圆柱坐标系面积元
柱面坐标面积微元

柱面坐标面积微元柱面坐标是一种常用的三维坐标系,它可以用来描述柱面形状的物体或者区域。
在柱面坐标系下,利用面积微元的概念,我们可以计算柱面坐标系中的面积。
1. 坐标转换在柱面坐标系中,一个点的坐标通常用 $(\\rho, \\phi, z)$ 表示。
其中,$\\rho$ 表示点到柱面轴的距离,$\\phi$ 表示点的极角,z表示点在轴向的位置。
如果我们想计算柱面坐标系下的面积,需要将坐标转换为直角坐标系的形式。
常见的转换公式如下:$$ x = \\rho \\cos(\\phi) $$$$ y = \\rho \\sin(\\phi) $$z=z2. 面积微元的计算考虑一个位于 $(\\rho, \\phi, z)$ 坐标的点,以点为中心的面积微元可以表示为dS。
对于微小的变化,我们可以将面积微元拆分为无穷小的矩形微元dS x和dS y。
由坐标转换公式可知,dS x和dS y的长度分别为 $d\\rho$ 和 $\\rho d\\phi$。
因此,面积微元可以表示为:$$ dS = dS_x \\cdot dS_y = d\\rho \\cdot \\rho d\\phi $$3. 计算例子为了更好地理解柱面坐标系的面积微元,我们来计算一个具体的例子。
假设我们有一个半径为 2 的柱体,高度为 3,且位于坐标原点处。
我们想计算该柱体的顶面的面积。
首先,我们注意到顶面可以表示为z=3的平面。
在柱面坐标系下,我们将该平面的方程转换为 $\\rho = 0$。
因此,顶面的极角范围为 $0 \\leq \\phi \\leq2\\pi$。
接下来,我们可以计算顶面的面积。
由于面积微元可以表示为 $dS = d\\rho\\cdot \\rho d\\phi$,我们可以将面积微元积分以计算整个面积:$$ S = \\int_0^{2\\pi} \\int_0^{\\infty} \\rho \\cdot d\\rho \\cdot d\\phi $$计算该积分后,可以得到顶面的面积为 $4\\pi$。
三种常用的正交坐标系程

张量分析
z
1、直角坐标系 坐标变量
z z0 (平面)
ez
x, y, z
o
坐标单位矢量 ex , e y , ez
位置矢量 线元矢量
ex
P
ey
点 P(x0,y0,z0)
y y y0(平面)
r ex x e y y ez z
dl ex dx ey dy ez dz
o
x
dx d y dSx exdydz
y
体积元
南京工业大学
dV dxdydz
直角坐标系的长度元、面积元、体积元
张量分析 2、圆柱面坐标系
坐标变量
, , z
坐标单位矢量 e , e , ez r e ez z 位置矢量 线元矢量 dl e d e d ez dz
x1 x 2 x 3 g1 1 i 1 j 1 k x x x x1 x 2 x 3 g2 2 i 2 j 2 k x x x x1 x 2 x 3 g3 3 i 3 j 3 k x x x
3
1
x3' g3 g2 O
1 v1 v v 2 r 2 v 2 0 r sin 2 v 3 r sin 2 v 3
面元矢量
dS e dl dl z e ddz dS e dl dl z e ddz dS z ez dl dl ez dd
体积元
南京工业大学
dV dddz
张量分析 3、球面坐标系 坐标变量
坐标单位矢量 er , e , e
第2章 矢量分析

工程电磁场基础第2 章矢量分析主讲人:陈德智dzhchen@华中科技大学电气与电子工程学院2011年2月第2章矢量分析1 关于矢量的一些约定2 矢量代数3 坐标系4 标量场的梯度5 矢量面积分,通量与散度6 矢量线积分,环量与旋度7 亥姆霍兹定理⑤矢量的坐标分量表示:⑥法向单位矢量与切向单位矢量:e n ,e t法向分量:A n 切向分量:A t关于矢量的基本约定④坐标单位矢量:直角坐标系(x , y , z ) :e x ,e y ,e z ;x x y y z zA A A =++A e e e2.矢量代数(1)点乘(标积):θcos :AB u =⋅=B A •A ∥B 时取最大值。
0=⋅B A •A ⊥B ⇔,矢量A 与B 正交。
B B A =⋅A e n n A =⋅A e •矢量的投影(分量):。
法向分量。
zz y y x x B A B A B A ++=⋅B A •直角坐标系中的计算公式:,×如果单位矢量为一平面的法向,则矢量与该法向•圆柱坐标系d d d d d d d z S z z ρφρφρρρφ=++e e e z ,,φρ坐标变量,,zρφe e e 坐标单位矢量z zρρ=+r e e 位置矢量d d d d z zρφρρφ=++l e e e 线元矢量zV d d d d φρρ=体积元面元矢量圆柱坐标系圆柱坐标系中的线元、面元和体积元球坐标系球坐标系中的线元、面元和体积元坐标系•在各种坐标系中,直角坐标系是唯一一种方向不变的坐标系。
•原则上,所有问题都可以使用直角坐标系描述。
但是根据问题的不同类型,选取不同的坐标系可能更方便,例如用圆柱坐标系描述轴对称问题,用球坐标系描述球对称问题等。
•直角坐标系中的运算公式要求熟练掌握;其它坐标系要求会用,不同坐标系中的转换关系可以查表解决。
4.标量场的梯度(1)标量场的图形表示——等值面(线)地形图与等高线()const f=r标量场的图示——绘制场图(草图)是工程电磁场中最重要和最常用的分析方法之一,也是最基本的技能。
圆柱坐标系dS

圆柱坐标系dS介绍在数学和物理学中,圆柱坐标系是一种常用的坐标系,用于描述三维空间中的点。
圆柱坐标系使用半径、极角和高度来表示一个点,相对于直角坐标系(x、y、z)更加方便描述某些问题。
圆柱坐标系中的dS表示面积元素,用于计算曲面的面积。
圆柱坐标系圆柱坐标系由三个坐标值表示一个点:半径(ρ)、极角(φ)和高度(z)。
这三个坐标值和直角坐标系中的x、y、z坐标值有一定的关系。
•半径(ρ)表示点到z轴的距离,可以是任意非负数。
当ρ等于0时,点位于z轴上。
•极角(φ)表示点到x轴的角度,范围是[0, 2π]。
当φ等于0时,点在x轴上。
•高度(z)表示点距离xy平面的距离。
可以是任意实数。
用数学的语言表示,点P在圆柱坐标系中可以表示为(Pρ, Pφ, Pz)。
圆柱坐标系与直角坐标系的转换圆柱坐标系和直角坐标系之间可以通过以下的转换公式相互转换:x = ρ * cos(φ) y = ρ * sin(φ) z = zρ = sqrt(x^2 + y^2) φ = arctan(y/x) z = z这些公式允许我们在两种坐标系之间自由切换。
圆柱坐标系中的面积元素dS在圆柱坐标系中,面积元素dS被定义为曲面在极坐标系下的面积。
它可以用于计算曲面的面积。
圆柱坐标系中的面积元素dS可以通过以下公式计算:dS = ρ * dφ * dρ其中,dφ是极角的微分,dρ是半径的微分。
dS表示一个面积元素,可以被视为一个极小的平行四边形的面积。
通过将许多小的面积元素累积起来,可以计算出一个曲面的总面积。
应用圆柱坐标系dS在数学和物理学中有广泛的应用。
它被用于求解各种问题,如电场和磁场的计算,流体力学问题以及曲面的面积计算等等。
在电场和磁场的计算中,圆柱坐标系dS可以帮助我们更方便地描述电荷分布和磁场分布,并计算出电场强度和磁场强度。
在流体力学中,圆柱坐标系dS可以用于描述流体的流动,计算流体的速度矢量、压力和流量等。
在计算曲面的面积时,圆柱坐标系dS可以在一定程度上简化计算过程。
圆柱,圆球坐标系
1 ∂ 1 ∂Fφ ∂Fz ∇ ⋅ F (ρ ,φ ,z) = (ρ Fρ ) + + ρ ∂ρ ρ ∂φ ∂z
1
ρ
eρ
eφ ∂ ∂φ ρ Fφ
1
ρ
ez
∇ × F (ρ ,φ ,z )
=
∂ ∂ρ Fρ
∂ ∂z Fz
1.8 圆柱坐标系与球坐标系
CQU
1.8.2 球面坐标系 坐标变量
r ,θ , φ
坐标单位矢量 er , eθ , eφ 位置矢量 线元矢量 面元矢量
= 0, ∂ρ ∂e z = 0, ∂ρ
= −eρ , ∂φ ∂e z = 0, ∂φ
1.8 圆柱坐标系与球坐标系
CQU
圆柱坐标系中的三度表达式
∇ = eρ
∇f =
∂ 1 ∂ ∂ + eφ + ez ∂ρ ρ ∂φ ∂z
∂f 1 ∂f ∂f eρ + eφ + ez ∂ρ ρ ∂φ ∂z
(ρ ≠ 0)
e ρ = cos φ e x + sin φ e y eφ = −sin φ e x + cosφ e y
∂e ρ ∂ρ ∂eφ = 0, ∂e ρ ∂φ ∂eϕ = eφ , =0 ∂z ∂eφ = 0 ∂z ∂e z =0 ∂z ∂e ρ
eρ、eφ、ez对坐标ρ、φ、z求偏导 求偏导
1.8 圆柱坐标系与球坐标系
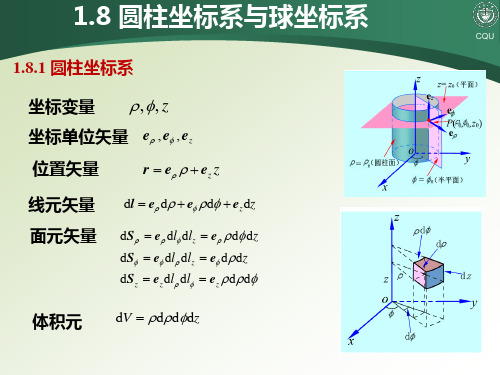
1.8.1 圆柱坐标系 坐标变量
1
CQU
ρ ,φ , z
r = eρ ρ + ez z
dl = eρ dρ + eφ ρ dφ + e z dz
坐标单位矢量 eρ , eφ , e z 位置矢量 线元矢量 面元矢量
圆柱坐标系和球坐标系

圆柱坐标系和球坐标系球坐标系的定义:球坐标是三维坐标系的一种,用以确定三维空间中点、线、面以及体的位置,它以坐标原点为参考点,由方位角、仰角和距离构成。
假设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数r,θ,φ来确定,其中r为原点O与点P间的距离,r∈[0,+∞)θ为有向线段OP与z轴正向的夹角,θ∈[0,π]φ为从正z轴来看自x轴按逆时针方向转到OM所转过的角,φ∈[0,2π]这里M为点P在xOy面上的投影。
这样的三个数r,φ,θ叫做点P的球面坐标。
当r,θ或φ分别为常数时,可以表示如下特殊曲面:r = 常数,即以原点为心的球面;θ= 常数,即以原点为顶点、z轴为轴的圆锥面;φ= 常数,即过z轴的半平面。
球坐标系与直角坐标系间的转换1).球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x= r sinθ cosφy= r sinθsinφz = r cosθ球坐标系下的微分关系在球坐标系中,沿基矢方向的三个线段元为:dl(r)=dr,dl(θ)=rdθ,dl(φ)=rsinθdφ球坐标的面元面积是:dS=dl(θ)* dl(φ)=r^2*sinθdθdφ体积元的体积为:dV=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ圆柱坐标系的定义:它是二维极坐标系往z-轴的延伸。
添加的第三个坐标专门用来表示P点离xy-平面的高低。
按照国际标准化组织建立的约定(ISO 31-11) ,径向距离、方位角、高度,分别标记为。
如图右,P 点的圆柱坐标是。
是P 点与z-轴的垂直距离。
是线OP 在xy-面的投影线与正x-轴之间的夹角。
与直角坐标的等值。
圆柱坐标系与直角坐标系间的转换1).圆柱坐标系(r,φ,z)与直角坐标系(x,y,z)的转换关系:x=r co sφy=r sinφz=z圆柱坐标系下的微分关系在球坐标系中,沿基矢方向的三个线段元为:dl(r)=dr,dl(φ)=rdφ,dl(z)= dz球坐标的面元面积是:dS=dl(θ)* dl(z)=r dφ dz体积元的体积为:dV=dl(r)*dl(φ)*dl(z)=r dr dφ dz。
三大坐标系

2
e
A
ez A Az 1 1 Az A e e z z z Az
两个矢量点积:A B= Ar Br A B A B ; 两个矢量叉积:
er A B Ar B r
e A B
e A A B A B er A Br Ar B e Ar B A Br e B
位置矢量:r = e ez z ;
其微分为:dr = d e d ez z e d de ez dz e d e d ez dz ;
2
它在 、 和 z 增加方向上的微分分别是: d 、 d 和 dz 。
(圆锥面)
0
z
er e
的投影。 与直角坐标系之间的变换关系:
r x 2 y 2 z 2, arccos z x 2 y 2 z 2 , arctan y x ; x r sin cos ,y r sin sin ,z r cos
位置矢量:r = er r ;其微分为:dr = d (er r ) er dr rder er dr e rd e r sin d ; 它在 er 、 e 和 e 增加方向上的微分分别是: dr 、 rd 和 r sin d 。
球坐标系中的坐标单位矢量 er 、 e 和 e 都不是常矢量,是 和 的函数,且
讲 柱坐标和球坐标系三重积分的计算

z dv
z r d
dv
dz
r
d
dr
r d
y
x r d dr r dr d
d
y
r sin
x
平面极坐标下的面积元素 ds
r sin d
28
在柱面坐标系下: dv r dr d dz,
f (x, y, z)d x d y dz
f (r cos , r sin , z) r dr d dz
在球面坐标系下: dv r 2 sin drd d ,
x2 y2 z2, 与平面z a (a 0)所围的立体.
解 1 采用球面坐标
za r a , cos
x2 y2 z2 ,
4
: 0 r a , 0 , 0 2,
cos
4
16
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
2r4
0
d
r
64 5
1
2 2
31
3. 计算
由 z 1 (x2 y2 ), z 1, z 4围成. 2
解:
利用对称性
1 2
(
x2
y2
)d
xd
yd
z
1
4
dz
( x2 y2 )d xd y
21
Dz
1
4
dz
2
d
2z r3 d r 21
21 0
0
其中
z 4
1
Dz
oy x
32
o
y
d
x
f ( cos , sin , z) dddz.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱坐标系面积元
1. 引言
圆柱坐标系是一种常见的三维坐标系,它由一个半径和一个高度组成。
在某些情况下,我们需要计算在圆柱坐标系中的一个面积元的大小。
本文将介绍如何计算圆柱坐标系中面积元的方法。
2. 圆柱坐标系
圆柱坐标系由一个径向(r)、一个方位角(θ)和一个高度(z)组成。
径向表示点到柱面中心的距离,方位角表示点在柱面上的位置,高度表示点在垂直于柱面方向的位置。
在圆柱坐标系中,可以使用三个参数(r, θ, z)来定位一个点。
3. 面积元的定义
在圆柱坐标系中,面积元是一个具有微小面积的区域。
它可以看作是一个微小的垂直于径向和方位角方向的矩形区域。
面积元的大小取决于两个因素:径向的长度(dr)和方位角的长度(dθ)。
4. 计算面积元的大小
要计算圆柱坐标系中面积元的大小,可以使用以下公式:
dA = r * dr * r * dθ
其中,dA表示面积元的面积,r表示径向的长度,dr表示径向的增量,θ表示方位角,dθ表示方位角的增量。
5. 示例计算
假设我们要计算位于圆柱坐标系中半径为3、方位角从0到π/2、高度从0到5的一个面积元的大小。
我们可以将r的范围从0到3、θ的范围从0到π/2代入上述公式并进行计算。
首先,我们将r的范围分成n等分,例如取n=100。
然后,我们计算r的每个增量dr的大小,即dr = (3-0)/n = 3/n。
对于θ,我们可以将其范围从0到π/2分成m等分,例如取m=50。
然后,计算θ的每个增量dθ的大小,即dθ = (π/2-0)/m = π/(2m)。
接下来,我们可以使用上述公式计算面积元的大小。
由于我们取的是等分,所以可以用一个双重循环来计算每个点的面积并将其累加。
最终得到面积元的大小。
6. 结论
本文介绍了如何计算圆柱坐标系中面积元的大小。
通过计算径向和方位角的增量,并使用公式dA = r * dr * r * dθ,可以得到面积元的大小。
通过将范围等分,并用双重循环计算每个点的面积,最终可以得到面积元的大小。
在实际应用中,计算圆柱坐标系中面积元的大小对于某些物理和数学问题是非常有用的。
通过了解这一概念和计算方法,我们可以更好地理解和分析这些问题。
