八年级上册数学第1课时“边边边”精选练习1
数学人教版八年级上册边边边课后作业

1.在△ABC 和△DEF 中,若AB =DE ,BC =EF ,AC =DF ,则△ABC ≌△DEF .2.若两个三角形全等,则它们的三边对应相等;反之,若两个三角形的三边对应相等,则这两个三角形全等.3.下列命题正确的是(A )A .有一边对应相等的两个等边三角形全等B .有两边对应相等的两个等腰三角形全等C .有一边对应相等的两个等腰三角形全等D .有一边对应相等的两个直角三角形全等4.已知AB =3,BC =4,AC =6,EF =3,FG =4,要使△ABC ≌△EFG ,则EG =6.小组讨论交流解题思路,小组活动后,小组代表展示活动成果.(10分钟)探究1 如图,AB =AD ,CB =CD ,求证:(1)△ABC ≌△ADC ;(2)∠B =∠D.证明:(1)连接AC ,在△ABC 与△ADC 中,⎩⎪⎨⎪⎧AB =AD ,AC =AC ,BC =DC ,∴△ABC ≌△ADC(SSS ).(2)∵△ABC ≌△ADC ,∴∠B =∠D.点拨精讲:在证明过程中善于挖掘如“公共边”这个隐含条件,可以考虑添加辅助线.探究2 如图,△ABC 是一个风筝架,AB =AC ,AD 是连接A 与BC 中点D 的支架,求证:AD ⊥BC.证明:∵点D 的BC 中点,∴BD =CD ,∴在△ABD 与△ACD 中,⎩⎪⎨⎪⎧AB =AC ,BD =CD ,BD =AC ,∴△ABD≌△ACD(SSS ),∴∠ADB =∠ADC ,∵∠ADB +∠ADC =180°,∴∠ADB =∠ADC =90°,∴AD ⊥BC.学生独立确定解题思路,小组内交流,上台展示并讲解思路.(5分钟)1.如图,AD =BC ,AC =BD ,求证:(1)∠DAB =∠CBA ;(2)∠ACD =∠BDC.证明:(1)在△ABD 与△BAC 中,⎩⎪⎨⎪⎧AB =BA ,AD =BC ,AC =BD ,∴△ABD ≌△BAC(SSS ),∴∠DAB =∠CBA.(2)在△ADC 与△BCD 中,⎩⎪⎨⎪⎧DC =CD ,AD =BC ,AC =BD ,∴△ADC ≌△BCD(SSS ),∴∠ACD =∠BDC.。
八年级上册数学第1课时“边边边”精选练习1

八年级上册数学第1课时“边边边”精选练习1“边边边”精选练习1第1课时 “边边边”一﹨选择题1.如图1,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A .120°B .125°C .127°D .104°DCBAODCBAFEDC BA[1] [2] [3]2.如图2,线段AD 与BC 交于点O ,且AC=BD ,AD=BC ,•则下面的结论中不正确的是( ) A .△ABC ≌△BAD B .∠CAB=∠DB A C .OB=OC D .∠C=∠D 二﹨填空题3.在△ABC 和△A 1B 1C 1中,已知AB=A 1B 1,BC=B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1.4.如图3,AB=CD ,BF=DE ,E ﹨F 是AC 上两点,且A E=CF .欲证∠B =∠D ,可先运用等式的性质证明AF =________,再用“SSS ”证明________≌_________•得到结论. 三﹨解题题5.如图,在四边形ABCD 中AB=CD ,AD=BC ,求证:①AB ∥CD ;②AD ∥BC .DCBA6.如图,已知AB=CD ,AC=BD ,求证:∠A =∠D .E DCBA7.如图,AC 与BD 交于点O ,AD=CB ,E ﹨F 是BD 上两点,且AE=CF ,DE=BF .•请推导下列结论:(1)∠D=∠B;(2)AE∥CF.O F ED CBA答案:1.C 2.C 3.AC=AC 4.CE;△ABF≌△CDE5.连接AC(或BD) 6.连接BC后证明△ABC≌△DCB7.①证明△ADE≌△CBF;②证明∠AEF=∠CFE。
1.5.1 “边边边” 浙教版八年级数学上册同步练习(含解析)

第1章 三角形的初步知识1.5 三角形全等的判定第1课时 “边边边”基础过关全练知识点1 “边边边”(或“SSS”)1.如图,在△ABC中,AB=AC,BE=EC,AE的延长线交BC于点D,直接使用“SSS”可判定( )A.△ABD≌△ACDB.△ABE≌△EDCC.△ABE≌△ACED.△BED≌△CED2.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )A.120°B.125°C.127°D.104°3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”判定△ABC≌△FED,还需添加的条件是 .4.(教材P28变式题)如图,在四边形ABCD中,AB=AD,CB=CD,∠B=105°,则∠D= °.知识点2 三角形的稳定性5.(2022浙江诸暨绍初教育集团期中)如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )A.两点之间,线段最短B.垂线段最短C.两直线平行,内错角相等D.三角形具有稳定性6.(2022浙江台州和合教育期中)如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .知识点3 角平分线的作法7.(2022浙江义乌绣湖中学期中)如图,AB∥CD,以点 B 为圆心,小于 DB 的长为半径作圆EF的长为半径作圆弧,两弧,分别交 BA、BD 于点 E、F,再分别以点 E、F 为圆心,大于12弧交于点 G,作射线 BG 交 CD 于点 H.若∠D=116°,则∠DHB=( )A.8° B.16°C.32° D.64°能力提升全练8.(2022独家原创)如图,点B,D,F,E在同一条直线上,且AB=AC,AD=AE,BD=CE,∠DAF=65°,∠BAE=105°,则∠BEC的度数为( )A.70°B.75°C.80°D.85°9.如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有 对.10.(2022浙江宁波镇海期末)如图,已知△ABC,请按下列要求作出图形.(1)用直角三角尺画BC边上的高线;(2)用直尺和圆规画∠B的平分线.11.(2022浙江杭州三墩中学期中)如图,AB=DC,AC=DB.(1)求证:△ABC≌△DCB;(2)求证:∠ABD=∠DCA.12.(2022浙江宁波春晓中学期中)如图,已知AB=AC,BD=CD.(1)求证:∠B=∠C;(2)若∠B=25°,∠A=2∠C,求∠BDC的度数.素养探究全练13.[数学建模]如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长为a米,FG的长为b米.若a=b,则说明∠B和∠C是相等的,他的这种做法合理吗?为什么?答案全解全析基础过关全练1.C 在△ABE与△ACE中,AB=AC,BE=CE,AE=AE,∴△ABE≌△ACE(SSS).故选C.2.C 在△ABC和△ADC中,AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC=12∠BAD=23°,∠ACD=∠ACB,∵∠BAC+∠B+∠ACB=180°,∴∠ACD=∠ACB=180°-30°-23°=127°.故选C.3.AB=FE(答案不唯一)解析 当AB=FE时,在△ABC和△FED中,AC=FD,BC=ED,AB=FE,∴△ABC≌△FED(SSS).答案不唯一.4.105解析 连结AC,在△ABC和△ADC中,AB=AD, CB=CD, AC=AC,∴△ABC≌△ADC(SSS),∴∠D=∠B=105°.5.D 人字梯中间一般设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性.故选D.6.三角形的稳定性解析 给凳子加了两根木条之后形成了三角形,而三角形具有稳定性,所以凳子比较牢固的数学原理是三角形的稳定性.7.C ∵AB∥CD,∴∠DHB=∠ABH,∠D+∠ABD=180°,∴∠ABD=180°-116°=64°,根据作图可得∠DBH=∠ABH=12∠ABD=32°,∴∠DHB=∠ABH=32°.故选C.能力提升全练8.D 在△ABD 和△ACE 中,AB =AC ,AD =AE ,BD =CE ,∴△ABD ≌△ACE(SSS),∴∠BAD=∠CAE=12(∠BAE-∠DAF)=20°,∠ADB=∠AEC,∵∠ADB=∠DAE+∠AED,∠AEC=∠AED+∠BEC,∴∠BEC=∠DAE=∠DAF+∠CAE=65°+20°=85°.故选D.9.3解析 在△ADC 和△CBA 中,AD =CB ,AC =CA ,CD =AB ,∴△ADC ≌△CBA(SSS).在△ADE 和△CBF 中,AD =CB ,DE =BF ,AE =CF ,∴△ADE ≌△CBF(SSS).∵AE=CF,∴AE+EF=CF+EF,∴AF=CE.在△DEC 和△BFA 中,DE =BF ,CE =AF ,DC =BA ,∴△DEC ≌△BFA(SSS).综上可知共有3对全等三角形.10.解析 (1)如图,AD 即为BC 边上的高.(2)如图,BE 即为∠ABC 的平分线.11.证明 (1)在△ABC 和△DCB 中,AB =DC ,AC =BD ,BC =CB ,∴△ABC ≌△DCB(SSS).(2)∵△ABC ≌△DCB,∴∠ABC=∠DCB,∠ACB=∠DBC,∴∠ABD=∠DCA.12.解析 (1)证明:如图,连结AD,并延长到E.在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS),∴∠B=∠C.(2)由(1)得△ABD≌△ACD,∴∠B=∠C,∠BAD=∠CAD,∵∠BAC=2∠C,∴∠BAD=∠CAD=∠C=∠B=25°,∵∠BDE=∠B+∠BAD=50°,∠CDE=∠CAD+∠C=50°,∴∠BDC=∠BDE+∠CDE=100°.素养探究全练13.解析 这种做法合理.理由:若在△BDE和△CFG中,BE=CG,BD=CF,DE=FG,则△BDE≌△CFG(SSS),∴∠B=∠C.。
2019秋人教版八年级数学上册作业课件:12.2 第1课时 “边边边”

15.如图,AD=CB,E,F是AC上的两动点,且有DE=BF. (1)若E,F运动至如图①所示的位置,有AF=CE, 求证:△ADE≌△CBF; (2)若E,F运动至如图②所示的位置,仍有AF=CE, 那么△ADE≌△CBF还成立吗?为什么? (3)若E,F不重合,且AF=CE,那么AD和CB平行吗?请说明理由.
AB=DE
5.(教材P45习题13变式)如图,AB=AC,DB=DC,EB=EC. (1)图中有几对全等三角形?请一一写出来; (2)选择(1)中的一对全等三角形加以证明.
解:(1)3 对,△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE (2)以△ABD≌△ACD 为例,
AB=AC, 证明:在△ABD 与△ACD 中,DB=DC,∴△ABD≌△ACD(SSS)
AD=AD,
6.如图是用直尺和圆规作一个角等于已知角的示意图, 要证明∠A′O′B′=∠AOB,就要先证明△C′O′D′≌△COD, 那么判定△C′O′D′≌△COD的依据是_______S_S_S.
7.已知∠AOB,点C是OB边上的一点. 用尺规作图画出经过点C与OA平行的直线.
解: ①以点O为圆心,任意长为半径,弧交OA于点E,交OB于点D; ②以点C为圆心,OD的长为半径画弧交OB于点G; ③以点G为圆心,DE的长为半径,交前弧于点H,连接CH,则CH∥OA.
则△_____≌△_____,∠2=___°.
ABD ACE
20
10.如图,在△ABC中,AB=AC,AD是BC边上的中线, 求证:△ABD≌△ACD.
解:∵AD 是 BC 边上的中线,∴BD=CD.
AB=AC, 在△ABD 和△ACD 中,AD=AD,∴△ABD≌△ACD(SSS)
人教版八年级数学上册边角边1同步练习题

第2课时 边角边一、选择题1. 如图,AB=AC ,AD=AE ,欲证△ABD ≌△ACE ,可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD2. 能判定△ABC ≌△A ′B ′C ′的条件是( ) A .AB=A ′B ′,AC=A ′C ′,∠C=∠C ′ B. AB=A ′B ′, ∠A=∠A ′,BC=B ′C ′ C. AC=A ′C ′, ∠A=∠A ′,BC=B ′C D. AC=A ′C ′, ∠C=∠C ′,BC=B ′C3. 如图,AD=BC ,要得到△ABD 和△CDB 全等,可以添加的条件是( ) A. AB ∥CD B. AD ∥BC C. ∠A=∠C D. ∠ABC=∠CDA4.如图,在△ABC 和△DEC 中,已知AB=DE ,还需添加两个条件才能使△ABC ≌△DEC ,不能添加的一组条件是( )A .BC=EC ,∠B=∠EB .BC=EC ,AC=DC C .BC=DC ,∠A=∠D D .AC=DC ,∠A=∠D5.如图,在四边形ABCD 中,AB=AD ,CB=CD ,若连接AC 、BD 相交于点O ,则图中全等三角形共有( )A .1对B .2对C .3对D .4对6.在△ABC 和C B A '''∆中,∠C =C '∠,b-a=a b '-',b+a=a b '+',则这两个三角形( )A. 不一定全等B.不全等C. 全等,根据“ASA ”D. 全等,根据“SAS ”第1题第3题图第4题图第5题图7.如图,已知AD 是△ABC 的BC 边上的高,下列能使△ABD ≌△ACD 的条件是( )A .AB=ACB .∠BAC=90°C .BD=ACD .∠B=45°8.如图,梯形ABCD 中,AD ∥BC ,点M 是AD 的中点,且MB=MC ,若AD=4,AB=6,BC=8,则梯形ABCD 的周长为( )A .22B .24C .26D .28 二、填空题9. 如图,已知BD=CD ,要根据“SAS ”判定△ABD ≌△ACD ,则还需添加的条件是 .10. 如图,AC 与BD 相交于点O ,若AO=BO ,AC =BD ,∠DBA=30°,∠DAB=50°, 则∠CBO= 度.11.西如图,点B 、F 、C 、E 在同一条直线上,点A 、D 在直线BE 的两侧,AB ∥DE ,BF =CE ,请添加一个适当的条件: , 使得AC =DF .12.如图,已知AD AB =,DAC BAE ∠=∠,要使 ABC △≌ADE △,可补充的条件是 (写出一个即可).第9题图第7题图第8题图第10题图第11题图13.(2005•天津)如图,OA=OB ,OC=OD ,∠O=60°,∠C=25°,则 ∠BED= 度.14. 如图,若AO=DO ,只需补充 就可以根据SAS 判定△AOB ≌△DOC.15. 如图,已知△ABC ,BA=BC ,BD 平分∠ABC ,若∠C=40°,则∠ABE 为度.16.在Rt △ABC 中,∠ACB=90°,BC=2cm ,CD ⊥AB ,在AC 上取一点E ,使EC=BC ,过点E 作EF ⊥AC 交CD 的延长线于点F ,若EF=5cm ,则 AE= cm .40D CBAE17. 已知:如图,DC=EA ,EC=BA ,DC ⊥AC , BA ⊥AC ,垂足分别是C 、A ,则BE 与DE 的位置关系是 .18. △ABC 中,AB=6,AC=2,AD 是BC 边上的中线,则AD 的取值范围是 .ACE B 0CEDB A第13题图第14题图第12题图第15题图第16题图第17题图D三、解答题19. 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.20.已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.求证:∠ACE=∠DBF.21.如图CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.22. 如图,AB=AC,点E、F分别是AB、AC的中点,求证:△AFB≌△AEC.23.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。
数学人教版八年级上册“边边边”判定三角形全等练习题

“边边边”判定三角形全等练习题一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△ D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( ) A.AC=BD B.AC=BC C.BE=CE D.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半 D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°5. 如图,线段AD 与BC 交于点O ,且AC=BD ,AD=BC , 则下面的结论中不正确的是( )A.△ABC ≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E 、F 是AC 上的两点,且AE=CF,DE=BF,,那么图中全等三角形共有( )对A .4对B .3对C .2对D .1对7. 如图 ,AB=CD ,BC=AD ,则下列结论不一定正确的是( ).AEDC第1题图第2题图第3题图第4题图第5题图A.AB ∥DCB. ∠B =∠DC. ∠A =∠CD. AB=BC8. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 等于( )A .73B .3C .4D .5 二、填空题9.工人师傅常用角尺平分一个任意角。
做法如下:如图,∠AOB 是一个任意角,在边OA ,OB 上分别取OM=ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合,过角尺顶点C 作射线OC 。
浙教版八年级数学上册__边边边(SSS)__同步练习(解析版)
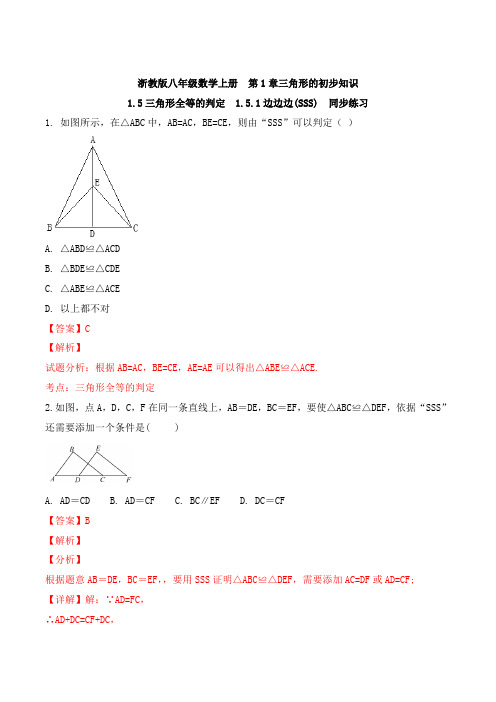
浙教版八年级数学上册第1章三角形的初步知识1.5三角形全等的判定 1.5.1边边边(SSS) 同步练习1. 如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定()A. △ABD≌△ACDB. △BDE≌△CDEC. △ABE≌△ACED. 以上都不对【答案】C【解析】试题分析:根据AB=AC,BE=CE,AE=AE可以得出△ABE≌△ACE.考点:三角形全等的判定2.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )A. AD=CDB. AD=CFC. BC∥EFD. DC=CF【答案】B【解析】【分析】根据题意AB=DE,BC=EF,,要用SSS证明△ABC≌△DEF,需要添加AC=DF或AD=CF;【详解】解:∵AD=FC,∴AD+DC=CF+DC,∴AC=DF,在△ABC和△FED中∴△ABC≌△DEF,故选:B.【点睛】本题考查了全等三角形的判定,证得AC=DF是解题的关键.3.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A. 垂线段最B. 两点之间线段最短C. 两点确定一条直线D. 三角形的稳定性【答案】D【解析】【分析】根据三角形的稳定性即可解答.【详解】一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是三角形的稳定性,故选:D.【点睛】本题考查了三角形的稳定性,利用三角形的稳定性是解题的关键.4.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )A. ①或②B. ②或③C. ①或③D. ①或④【答案】A【解析】由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,故①可以;若添加AB=FE,则可直接证明两三角形的全等,故②可以。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册数学第1课时“边边边”精选练习1
“边边边”精选练习1
第1课时 “边边边”
一﹨选择题
1.如图1,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )
A .120°
B .125°
C .127°
D .104°
D
C
B
A
O
D
C
B
A
F
E
D
C B
A
(1) (2) (3)
2.如图2,线段AD 与BC 交于点O ,且AC=BD ,AD=BC ,•则下面的结论中不正确的是( ) A .△ABC ≌△BAD B .∠CAB=∠DB A C .OB=OC D .∠C=∠D 二﹨填空题
3.在△ABC 和△A 1B 1C 1中,已知AB=A 1B 1,BC=B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1.
4.如图3,AB=CD ,BF=DE ,E ﹨F 是AC 上两点,且A E=CF .欲证∠B =∠D ,可先运用等式的性质证明AF =________,再用“SSS ”证明________≌_________•得到结论. 三﹨解题题
5.如图,在四边形ABCD 中AB=CD ,AD=BC ,求证:①AB ∥CD ;②AD ∥BC .
D
C
B
A
6.如图,已知AB=CD ,AC=BD ,求证:∠A =∠D .
E D
C
B
A
7.如图,AC 与BD 交于点O ,AD=CB ,E ﹨F 是BD 上两点,且AE=CF ,DE=BF .•请推导下列
结论:
(1)∠D=∠B;(2)AE∥CF.
O F E
D C
B
A
答案:
1.C 2.C 3.AC=AC 4.CE;△ABF≌△CDE
5.连接AC(或BD) 6.连接BC后证明△ABC≌△DCB
7.①证明△ADE≌△CBF;②证明∠AEF=∠CFE。
