均匀外电场中置入
《电磁场与电磁波》第4版(谢处方 编)课后习题答案 四章习题解答
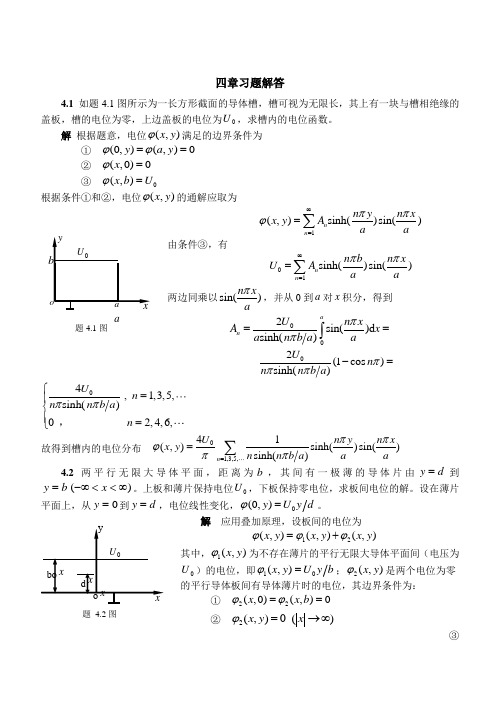
四章习题解答4.1 如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ=③ 0(,)x b U ϕ=根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a aππϕ∞==∑ 由条件③,有01sinh()sin()n n n b n x U A a aππ∞==∑ 两边同乘以sin()n xaπ,并从0到a 对x 积分,得到 002sin()d sinh()an U n xA x a n b a a ππ==⎰2(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩,故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:① 22(,0)(,)0x x b ϕϕ==②2(,)0()x y x ϕ=→∞③a题4.1图题 4.2图002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②,可设2(,)x y ϕ的通解为 21(,)sin()e n x b n n n y x y A b ππϕ∞-==∑ 由条件③有 00100(0)sin()()n n U U y y d n y bA U U b y y d y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑ 两边同乘以sin()n yb π,并从0到b 对y 积分,得到 0002211(1)sin()d ()sin()d d bn dU U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ 故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d nb b ππππ∞-=+∑ 4.3 求在上题的解中,除开0U y b 一项外,其他所有项对电场总储能的贡献。
电动力学-静电场答案

编号: 班级: 学号:姓名: 成绩:第1章 静电场1. 证明均匀介质内部的极化电荷体密度p ρ,总等于自由电荷体密度f ρ的 -(1-εε0)倍。
f ρ=⋅∇DE])[(E)(P 00εεεχρ-⋅-∇=⋅-∇=⋅-∇=e Pf P ρεεεεερ)(D])[(001--=-⋅-∇=2. 有一内外半径分别为21和r r 的空心介质球,介质的介电常数为ε,使介质内均匀带静止自由电荷f ρ,求 (1)空间各点的电场;(2)极化体电荷和极化面电荷分布。
解 1)由电荷分布的对称性可知:电场分布也是对称的。
电场方向沿径向 故:1r r<时0402==⎰dV r r fV ερπ)E( 或 0=)E(r21r r r <<时 球壳体内:dr r r D r ds rr f ⎰⎰⎰==⋅12244πρπ)(n D ])([)(3113r r rr D f -=ρ ])([)()(310013rr r r D r E f -==ερε 在2r r>的球形外:)()(212202023441421r r dr r r E r r rf -==⎰ρεππρεπ )()(2122203r r rr E -=ερ式中 r εεε0= 写在一起⎪⎪⎪⎩⎪⎪⎪⎨⎧>-<<-<=)(r )()(r])([)(E 22122302131013130r r r r r r r r r r r r f ερερ2) r ])([)(E D P 310013rrf --=-=ερεεε f p ρεεερ0--=⋅-∇=P (与第一题相符) 内表面:013031101011=-=--⋅-=-⋅-===])([]E )[(n )p (p n 12r rr f r r r r p ερεεσ 外表面:2222100013022r r r rr r r p )()(E])([n )p (p n 12--=--⋅-=-⋅-===ερεεεεσ3. 证明:当两种绝缘介质的分界面上不带面自由电荷时,电场线的偏折 满足:1212tan tan εεθθ= 式中1ε和2ε分别为两介质的介电常数,1θ和2θ分别为界面两侧电场线与法线的夹角。
电动力学复习总结电动力学复习总结答案

第二章 静 电 场一、 填空题1、若一半径为R 的导体球外电势为b a b ra,,+=φ为非零常数,球外为真空,则球面上的电荷密度为 。
答案: 02aRε2、若一半径为R 的导体球外电势为3002cos cos =-+E R E r rφθθ,0E 为非零常数,球外为真空,则球面上的电荷密度为 . 球外电场强度为 .答案:003cos E εθ ,303[cos (1)sin ]=-+-v v vr R E E e e rθθθ3、均匀各向同性介质中静电势满足的微分方程是 ;介质分界面上电势的边值关系是 和 ;有导体时的边值关系是 和 。
答案: σφεφσφεφεφφερφ-=∂∂=-=∂∂-∂∂=-=∇nc n n ,,,,1122212 4、设某一静电场的电势可以表示为bz y ax -=2φ,该电场的电场强度是_______。
答案:z y x e b e ax e axy ϖϖϖ+--225、真空中静场中的导体表面电荷密度_______。
答案:0nϕσε∂=-∂6、均匀介质部的体极化电荷密度p ρ总是等于体自由电荷密度f ρ_____的倍。
答案: -(1-εε0) 7、电荷分布ρ激发的电场总能量1()()8x x W dv dv rρρπε''=⎰⎰v v的适用于 情形.答案:全空间充满均匀介质8、无限大均匀介质中点电荷的电场强度等于_______。
答案: 34qRR πεv9、接地导体球外距球心a 处有一点电荷q, 导体球上的感应电荷在球心处产生的电势为等于 . 答案:04q aπε10、无电荷分布的空间电势 极值.(填写“有”或“无”) 答案:无11、镜象法的理论依据是_______,象电荷只能放在_______区域。
答案:唯一性定理, 求解区以外空间12、当电荷分布关于原点对称时,体系的电偶极矩等于_______。
答案:零13、一个外半径分别为R 1、R 2的接地导体球壳,球壳距球心a 处有一个点电荷,点电荷q 受到导体球壳的静电力的大小等于_______。
(完整版)电动力学-郭硕鸿-第三版-课后题目整理(复习备考专用)

电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性,推导下列公式:BA B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数,证明:u uf u f ∇=∇d d )(,uu u d d )(A A ⋅∇=⋅∇,uu u d d )(A A ⨯∇=⨯∇ 证明:3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x的距离,r 的方向规定为从源点指向场点。
(1)证明下列结果,并体会对源变量求微商与对场变量求微商的关系:r r r /'r =-∇=∇ ; 3/)/1(')/1(r r r r -=-∇=∇ ;0)/(3=⨯∇r r ;0)/(')/(33=⋅-∇=⋅∇r r r r , )0(≠r 。
(2)求r ⋅∇ ,r ⨯∇ ,r a )(∇⋅ ,)(r a ⋅∇ ,)]sin([0r k E ⋅⋅∇及)]sin([0r k E ⋅⨯∇ ,其中a 、k 及0E 均为常向量。
4. 应用高斯定理证明fS f ⨯=⨯∇⎰⎰SVV d d ,应用斯托克斯(Stokes )定理证明⎰⎰=∇⨯LSϕϕl S d d5. 已知一个电荷系统的偶极矩定义为 'd '),'()(V t t Vx x p ⎰=ρ,利用电荷守恒定律0=∂∂+⋅∇tρJ 证明p 的变化率为:⎰=V V t td ),'(d d x J p6. 若m 是常向量,证明除0=R 点以外,向量3/R)(R m A ⨯=的旋度等于标量3/R R m ⋅=ϕ的梯度的负值,即ϕ-∇=⨯∇A ,其中R 为坐标原点到场点的距离,方向由原点指向场点。
7. 有一内外半径分别为1r 和2r 的空心介质球,介质的电容率为ε,使介质球内均匀带静止自由电荷f ρ,求:(1)空间各点的电场;(2)极化体电荷和极化面电荷分布。
分析静电场中零势点的选择

分析静电场中零势点的选择作者:周明来源:《科学导报·学术》2019年第05期摘要:在静电场中,电势是一参考量,所以只有在零电势点确定后,才可谈空间中的电势,零电势选择得当可使问题简化,选择不当,则会使电势的表达形式比较繁琐甚至出现无确定的值。
本文将从几种典型电场的零电势位置的确定,说明选择零电势点的一般原则和方法。
关键词:静电场;零势点;选择一、电势零点选择的任意性和受限性1.电势零点选择的任意性电场中某点的电势是相对零电势点而言的,静电场力把单位正电荷从场点p处移到参考点处所作的功是。
例如带电量为正的点电荷电场,若选无穷远处为电势零点,则电场中任意点的电势为 = 其中是场点到点电荷的距离,若零电势点选在距点电荷rA处,则 = ()显然,电势零点选择位置不同,该点的电势值不同,但它们都有确定的物理意义,且零势点的选取不会影响电势的变化规律。
因此,对于点电荷,它的零电势点无论选在何处,电场,其性质没有变,所以我们可以这样说,对于点电荷电场,电势零点的选择具有任意性。
2.电势零点选择的受限性电势零点的选择虽然带有一定的任意性,但也受一定条件限制,这个条件是:电势零点一旦选定,电场中各个点电势必须具有确定的值,否则就毫无意义,即积分必须是收敛的,所以说电势零点的选择要依具体问题具体分析。
由一定带电体系所决定的电场,其场强是场点的矢量函数,它的形式一般为其中A是与场源电荷分布情况,场源电荷电量大小及选取单位有关的比例系数,r指场点至带电体或至带电体系中心的距离,m为整数,电场中某一点的电势可写为:= =从上式可以看出,电势参考点的选取由m决定,下面分三种情况讨论电势。
(1)当m>1时,零电势参考点的选取此时,电场中p点的电势可写为 = = =A ,对(1)式,当取无穷远处为电势零点时,当取电场中某一点为电势零点时,当取带电体本身的电势为零时,例如点电荷的电场,电偶极子的电场,电四极子的电场 =三式都是电荷分布在有限的区域内电场强度的表达式,且其中的m均大于1,只是在选无穷远的电势为零时,它的数学表达式最为简单,便于我们处理问题。
电磁场与电磁波思考题

思考与练习一1.证明矢量3ˆ2ˆˆz y x e e e−+=A 和z y x e e e ˆˆˆ++=B 相互垂直。
2. 已知矢量 1.55.8z y e ˆe ˆ+=A 和4936z y e ˆ.e ˆ+−=B ,求两矢量的夹角。
3. 如果0=++z z y y x x B A B A B A ,证明矢量A 和B 处处垂直。
4. 导出正交曲线坐标系中相邻两点弧长的一般表达式。
5.根据算符∇的与矢量性,推导下列公式:()()()()B A B A A B A B B A ∇⋅+×∇×+∇⋅+×∇×=⋅∇)(()()A A A A A 2∇⋅−∇=×∇×21 []H E E H H E ×∇⋅−×∇⋅=×⋅∇6.设u 是空间坐标z ,y ,x 的函数,证明:u du df u f ∇=∇)(, ()du d u u A A ⋅∇=⋅∇, ()du d u u A A ×∇=×∇,()[]0=×∇⋅∇z ,y ,x A 。
7.设222)()()(z z y y x x R ′−+′−+′−=′−=r r 为源点x ′到场点x 的距离,R 的方向规定为从源点指向场点。
证明下列结果,R R R R =∇′−=∇, 311R R R R−=∇′−=∇,03=×∇R R ,033=⋅∇′−=⋅∇RR R R )0(≠R (最后一式在0=R 点不成立)。
8. 求[])sin(0r k E ⋅⋅∇及[])sin(0r k E ⋅×∇,其中0E a ,为常矢量。
9. 应用高斯定理证明 ∫∫×=×∇v sd dV f s f ,应用斯克斯(Stokes )定理证明∫∫=∇×s Ldl dS ϕϕ。
10.证明Gauss 积分公式[]∫∫∫∫∫∇+∇⋅∇=⋅∇s Vdv d ψφψφψφ2s 。
论均匀电场中置入均匀带电绝缘介质球后的电场
这 一 叠 加 场 是 球 对 称 的 , 于 球 内 的 场 , 脚 对 用
标 1 表示 , 由高斯 定理 得 :
42 :  ̄ 导 xD r
D : p
球 心为 坐标原 点 , 均匀 外 电场 豆 方 向为 极轴 方 向 ( 对称轴 ) 建 立球 坐标 系 , 表示 场 点 与 坐标 原 点 , r
电 场 与 总 的极 化 场 的 叠 加 。
: 一
一
×3 :
…
一
二一
。
球 面上 的极化 电荷 面 密度
: 一
( : 一P. : P 1)
:( £一 e )p 。 I R
球 面 上 的 极 化 电荷 4 丌
,
下面, 我们 首 先 求 均匀 带 电球 所 产 生 的 电 场
= 。 ・ =
roO 这样 旌 一 1 也 等 于 : E电场s 。 表达质球 上 的 极 化 电荷 2( 所 产 生 的极化 c 的电势 ,介 式可 写 为 : )
=
球 外 的电势
,
:
f . r。 + .
xR ̄ o t l 4
一
q i
E ro 0 cs
P:e ∈E: 鲁 (-0 )
球 体 内的极化 电荷 密 度
P =一 V ・ P = 一 7 ・( P 。J ’( e一 £ e— e ) 0 。
二—
^
介质 球上 的 电荷 分 布不 会 有 什 么 影 响 。 绝 缘 介 设
质球 所带 均匀 自由 电荷 p 以及 介 质 球 上 所 产 生 , 的极化 电荷对 产 生均 匀外 电场 的 电荷分 布 的影 响 可以忽 略。 这样 , 匀带 电的绝缘 介质球 置 入均 匀 均 外 电场 以后 总 的外 电场 就是 庄 。与均 匀 带 电球 所产 生 的电场 的叠 加 , 两 个 外 电场 都 会 在 介 质 这 球 中产 生极化 现象 , 么 , 那 空间 的总 场就是 总 的外
1.6 电场强度与电势的微分关系
V E n
V E en n
V
V+dV
E与 V 的关系
V E 大小: n 方向:沿V 减小方向
V 大小:
V n
dln
e n
Q
q
dl
P
方向:沿V增大方向
E
V E e n gradV V n
E V
V V lim n n 0 n
U E
两方向微商的关系:
V V cos l n
P n l
Q R
U U
V V V V V lim lim lim cos cos l l 0 l n0 n / cos n0 n n
V Q 4 0 R 2 x 2
小
计算电势的方法
1、点电荷场的电势及叠加原理
结
计算场强的方法
1、点电荷场的场强及叠加原理
V
i
4 0 ri (分立)
qi
E
i
V
dq 4 0 r
Q
(连续)
E
2、可有
r dq (连续) Q 4 r 3 0
qi r 4 0 ri3 (分立)
§1.6 电场强度和电势梯度的关系 1.6.1 等势面
空间电势相等的点连接起来所形成的面称为等势面. 为了 描述空间电势的分布,规定任意两相邻等势面间的电势差相等. (等势面的疏密反映了场的强弱)
点 电 荷 的 等 势 面
V12 V23
V El
dl2 dl1
E2 E1
两平行带电平板的电场线和等势面
三.同一问题中能否选取不同的电势零点 例:均匀外电场 E0 中置入一点电荷 q 求空间任意一点的电势 .p 解:把坐标原点选取在点电荷所
静电场边值问题中唯一性定理的应用
静电场边值问题中唯一性定理的应用郑伟;高天附【摘要】在电磁场理论中,关于静电场边值问题的求解是重要而基本的.关于静电场边值问题的求解,在一般情况下可归结为在给定边界条件下求解场方程的问题,唯一性定理是求解静电场边值问题的理论基础.在电磁场相关课程中,静电场边值问题的求解都是教学中的重点和难点,但是作为判断场解正确性和唯一性的唯一性定理却经常被忽视.针对静电场边值问题的几种典型解法,以典型习题为例,深入分析了在各种解法中唯一性定理的应用及其重要意义,说明了在静电场边值问题中应用唯一性定理解题的思路和技巧.结合教学实践,指出了加强唯一性定理教学对于静态场教学的重要性,给出了关于唯一性定理教学的具体建议.%The solution of the boundary value problem for electrostatic field is important and essential in the electromagnetic field theory.Normally, the solution comes down to the problem of solving the field equations based on the given borderline condition.Moreover, the uniqueness theorem is the theoretical basis for solving the boundary value problem of the electrostatic field.In the interrelated courses of electromagnetic field, the solution of the boundary value problem in electrostatic field is the key and difficult point for teaching.But the uniqueness theory, which is used to judge the correctness and uniqueness of the solution, is often ignored.This paper is aimed at several typical solutions of the boundary value problem in electrostatic field, for example, the application and significant meaning of the uniqueness theorem are analyzed in various solutions of typical exercises.Moreover, this article intends to explain the solution ideal andtechniques for applying the uniqueness theorem in the boundary value problem of the electrostatic field.Based on the teaching practice, it points out the importance of uniqueness theorem in static field teaching, and gives some specific suggestions for the teaching of uniqueness theorem.【期刊名称】《沈阳师范大学学报(自然科学版)》【年(卷),期】2017(035)003【总页数】4页(P370-373)【关键词】唯一性定理;静电场;边值问题【作者】郑伟;高天附【作者单位】沈阳师范大学物理科学与技术学院, 沈阳 110034;沈阳师范大学物理科学与技术学院, 沈阳 110034【正文语种】中文【中图分类】O442静电场的求解方法和特殊函数是动态电磁场的边值问题求解的基础,关于静电场的求解在电磁场理论中是重要而基础的。
郭硕鸿《电动力学》课后答案
郭硕鸿《电动力学》课后答案第 2 页电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性,推导下列公式:B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇ A A A A )()(221∇⋅-∇=⨯∇⨯A 解:(1))()()(cc A B B A B A ⋅∇+⋅∇=⋅∇B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=cc c c B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=(2)在(1)中令B A =得:AA A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇,所以 A A A A A A )()()(21∇⋅-⋅∇=⨯∇⨯ 即 A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数,证明:u u f u f ∇=∇d d )( , u u u d d )(A A ⋅∇=⋅∇, uu u d d )(AA ⨯∇=⨯∇ 证明: (1)z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(zy x zuu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d du uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e(2)z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d du z u y u x u u A u A u A z y x z z y y x x dd)()d d d d d d (e e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++=第 3 页(3)u A u A u A zu y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=⨯∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=zx y y z x x y z yu A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=)(u A ⨯∇=3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离,r 的方向规定为从源点指向场点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安阳师范学院 物理与电气工程学院
景义林
郭硕鸿先生编著的《电动力学》 第二章习题2:
我们先来求解一下这道题:
以球心为坐标原点,均匀外电场 方向为 极轴建立球坐标系。
电场的边界条件。总场由三个场叠加而 成:
(1)均匀外电场 ; (2)导体球放入外电场 后的静电感应场
,这一场有这样的特征,导体球两侧球 面上的正负感应电荷相对于过球心且与
垂直的平面对称,在球内产生的电场场 强为 ,它与外电场 之矢量和为零; (3)导体球所带电荷 产生的电场(本 题即使是第一问,导体球上也可以是有 电荷的),导体球上的电荷 是均匀的 分布在球面上的,它在导体球内产生电 场的场强为零
故总场的电势:
(4)式带入(1)式,得 R R0 时任一点的电势
球外总电场的全部定解条件为
由于电场具有轴(8)对称性,故方 程(5bn R n1
)
Pn
(cos
)
(8)
边界条件(6)、(7)式带入 (8)式,即可得
E0R cos
0
Q
4 0 R0
Q
4 0 R
E0 R03 R2
cos
E0
R
0
Q
4 0 R0
Q
4 0 R
pR
4 0 R 3
(9)
谢谢各位
