(新课标)高考数学总复习第四章第八节正弦定理和余弦定理的实际应用练习文新人教A版

合集下载

2021年高考数学一轮复习 3.8 正弦定理、余弦定理的应用举例课时作业理(含解析)新人教A版

2021年高考数学一轮复习 3.8 正弦定理、余弦定理的应用举例课时作业理（含解析）新人教A 版一、选择题1．在同一平面内中，在A 处测得的B 点的仰角是50°，且到A 的距离为2，C 点的俯角为70°，且到A 的距离为3，则B 、C 间的距离为( )A.16B.17C.18D.19 解析：∵∠BAC ＝120°，AB ＝2，AC ＝3.∴BC 2＝AB 2＋AC 2－2AB ·AC cos ∠BAC ＝4＋9－2×2×3×cos 120°＝19.∴BC ＝19.答案：D2．(xx·厦门模拟)在不等边三角形ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，其中a 为最大边，如果sin 2(B ＋C )<sin 2B ＋sin 2C ，则角A 的取值范围为( )A.⎝ ⎛⎭⎪⎫0，π2B.⎝ ⎛⎭⎪⎫π4，π2C.⎝ ⎛⎭⎪⎫π6，π3 D.⎝ ⎛⎭⎪⎫π3，π2解析：由题意得sin 2A <sin 2B ＋sin 2C ，再由正弦定理得a 2<b 2＋c 2，即b 2＋c 2－a 2>0.则cos A ＝b 2＋c 2－a 22bc>0，∵0<A <π，∴0<A <π2.又a 为最大边，∴A >π3. 因此得角A 的取值范围是⎝ ⎛⎭⎪⎫π3，π2.答案：D3．某人在C 点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，则塔高为( )A．15米 B．5米 C．10米 D．12米解析：如图，设塔高为h，在Rt△AOC中，∠ACO＝45°，则OC＝OA＝h.在Rt△AOD中，∠ADO＝30°，则OD＝3h，在△OCD中，∠OCD＝120°，CD＝10，由余弦定理得：OD2＝OC2＋CD2－2OC·CD cos∠OCD，即(3h)2＝h2＋102－2h×10×cos 120°，∴h2－5h－50＝0，解得h＝10，或h＝－5(舍)．答案：C4．在湖面上高为10 m处测得天空中一朵云的仰角为30°，测得湖中之影的俯角为45°，则云距湖面的高度为(精确到0.1 m)( )A．2.7 m B．17.3 m C．37.3 m D．373 m解析：依题意画出示意图．则CM －10tan 30°＝CM ＋10tan 45°∴CM ＝tan 45°＋tan 30°tan 45°－tan 30°×10≈37.3 m. 答案：C5．如图，四边形ABCD 中，∠B ＝∠C ＝120°，AB ＝4，BC ＝CD ＝2，则该四边形的面积等于( )A. 3 B ．5 3 C ．6 3D ．7 3解析：连接BD ，在△BCD 中，BC ＝CD ＝2，∠BCD ＝120°， ∴∠CBD ＝30°，BD ＝23，S △BCD ＝12×2×2×sin 120°＝ 3.在△ABD 中，∠ABD ＝120°－30°＝90°，AB ＝4，BD ＝23，∴S △ABD ＝12AB ·BD ＝12×4×23＝43，∴四边形ABCD 的面积是5 3. 答案：B6．一艘海轮从A 处出发，以每小时40海里的速度沿东偏南50°方向直线航行，30分钟后到达B 处，在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是东偏南20°，在B 处观察灯塔，其方向是北偏东65°，那么B 、C 两点间的距离是( )A ．10 2 海里B ．10 3 海里C ．20 2 海里D ．20 3 海里解析：如图所示，由已知条件可得，∠CAB＝30°，∠ABC＝105°，∴∠BCA＝45°.又AB＝40×12＝20(海里)，∴由正弦定理可得20sin 45°＝BCsin 30°.∴BC＝20×1222＝102(海里)．答案：A二、填空题7．“温馨花园”为了美化小区，给居民提供更好的生活环境，在小区内的一块三角形空地上(如图，单位：m)种植草皮，已知这种草皮的价格是120元/m2，则购买这种草皮需要________元．解析：三角形空地的面积S＝12×123×25×sin 120°＝225，故共需225×120＝27 000元．答案：27 0008．江岸边有一炮台高30 m，江中有两条船，船与炮台底部在同一水平面上，由炮台顶部测得俯角分别为45°和60°，而且两条船与炮台底部连线成30°角，则两条船相距________m.解析：如图，OM ＝AO tan 45°＝30 (m)，ON ＝AO tan 30°＝33×30＝103(m)，在△MON 中，由余弦定理得，MN ＝ 900＋300－2×30×103×32＝300＝103(m)．答案：10 3 三、解答题9．(xx·广州综合测试(二))某单位有A 、B 、C 三个工作点，需要建立一个公共无线网络发射点O ，使得发射点到三个工作点的距离相等．已知这三个工作点之间的距离分别为AB ＝80 m ，BC ＝70 m ，CA ＝50 m ．假定A 、B 、C 、O 四点在同一平面内．(1)求∠BAC 的大小； (2)求点O 到直线BC 的距离．解：(1)在△ABC 中，因为AB ＝80 m ，BC ＝70 m ，CA ＝50 m ，由余弦定理得cos ∠BAC ＝AB 2＋AC 2－BC 22×AB ×AC ＝802＋502－7022×80×50＝12.因为∠BAC 为△ABC 的内角，所以∠BAC ＝π3.(2)因为发射点O 到A 、B 、C 三个工作点的距离相等，所以点O 为△ABC 外接圆的圆心．设外接圆的半径为R ，在△ABC 中，由正弦定理得BCsin A＝2R ，因为BC ＝70 m ，由(1)知A ＝π3，所以sin A ＝32.所以2R＝7032＝14033，即R＝7033.过点O作边BC的垂线，垂足为D，在△OBD中，OB＝R＝7033，BD＝BC2＝702＝35，所以OD＝OB2－BD2＝⎝⎛⎭⎪⎫70332－352＝3533.所以点O到直线BC的距离为3533m.10．甲船在A处观察乙船，乙船在它的北偏东60°的方向，两船相距a海里，乙船正向北行驶，若甲船是乙船速度的3倍，则甲船应沿什么方向行驶才能追上乙船？追上时甲船行驶了多少海里？解：如图所示，设到C点甲船追上乙船，乙到C地用的时间为t，乙船速度为v，则BC＝tv，AC＝3tv，B＝120°，由正弦定理知BC sin ∠CAB ＝ACsin B ，∴1sin ∠CAB ＝3sin 120°，∴sin ∠CAB ＝12，∴∠CAB ＝30°，∴∠ACB ＝30°，∴BC ＝AB ＝a ，∴AC 2＝AB 2＋BC 2－2AB ·BC cos 120°＝a 2＋a 2－2a 2·⎝ ⎛⎭⎪⎫－12＝3a 2，∴AC ＝3a .故甲船应沿北偏东30°方向行驶，追上乙船时甲行驶了3a 海里．11．(xx·安徽池州一中高三月考)在△ABC 中，AB ＝c ，AC ＝b ，D 为线段BC 上一点，且∠BAD ＝α，∠CAD ＝β，线段AD ＝l .(1)求证：sin αb＋sin βc＝sin α＋βl；(2)若AB ＝42，AC ＝4，∠BAD ＝30°，∠CAD ＝45°，试求线段AD 的长．解：(1)在△ABC 中，S △ABC ＝S △ABD ＋S △ACD ，得12bc sin(α＋β)＝12bl sin β＋12cl sin α，同除12bcl 即得证．(2)由(1)代入数据得sin45°＋30°l＝14，l ＝6＋ 2. [热点预测]12．(xx·无锡质检)如图，△ABC 为一个等腰三角形，腰AC 的长为3(百米)，底AB 的长为4(百米)，现拟在该空地内筑一条笔直的小路EF (宽度不计)，将该空地分成一个四边形和一个三角形．设分割的四边形和三角形的周长相等，面积分别为S 1，S 2.(1)若小路一端为AC 的中点，求此时小路的长度．(如图一) (2)若E ，F 点分别在两腰上，求S 1S 2的最小值．(如图二)解：(1)由题意知，点F 在底AB 上，且AF ＝72，AE ＝32，cos A ＝23，在△AEF 中，由余弦定理EF 2＝AE 2＋AF 2－2AE ·AF ·cos A ＝⎝ ⎛⎭⎪⎫322＋⎝ ⎛⎭⎪⎫722－2×32×72×23＝152，所以EF ＝302；(2)设CE ＝x ，则CF ＝5－x ，S 1S 2＝S △ABC －S 2S 2＝S △ABCS 2－1＝12AC ·BC ·sin C 12CE ·CF ·sin C －19x5－x－1≥9⎝ ⎛⎭⎪⎫x ＋5－x 22－1＝1125，当且仅当x ＝5－x ，即x ＝52时，S 1S 2的最小值是1125.36114 8D12 贒23697 5C91 岑21996 55EC 嗬)u29586 7392 玒34498 86C2 蛂21549 542D 吭40218 9D1A 鴚20125 4E9D 亝26099 65F3 旳O526014 659E 斞23250 5AD2 嫒。

高考数学总复习 38 正弦定理和余弦定理的应用备选练习文(含解析)新人教A版

1 【优化探究】2015届高考数学总复习 3-8 正弦定理和余弦定理的应用备选练习文（含解析）新人教A 版[B 组因材施教·备选练习](2014年青岛调研)某单位设计一个展览沙盘，现欲在沙盘平面内，设计一个对角线在l 上的四边形电气线路，如图所示．为充分利用现有材料，边BC ，CD 用一根长为5米的材料弯折而成，边BA ，AD 用一根长为9米的材料弯折而成，要求∠A 和∠C 互补，且AB ＝BC.(1)设AB ＝x 米，cos A ＝f (x )，求f (x )的解析式，并指出x 的取值范围；(2)求四边形ABCD 面积的最大值．解析：(1)在△ABD 中，由余弦定理得BD 2＝AB 2＋AD 2－2AB ·AD ·cos A .同理，在△CBD 中，BD 2＝CB 2＋CD 2－2CB ·CD ·cos C .∵∠A 和∠C 互补，∴cos C ＝－cos A ，∴AB 2＋AD 2－2AB ·AD ·cos A ＝CB 2＋CD 2＋2CB ·CD ·cos A .即x 2＋(9－x )2－2x (9－x )cos A ＝x 2＋(5－x )2＋2x (5－x )·cos A ，解得cos A ＝2x ，又∵5－x >0,9－x >0，且cos A <1， ∴x ∈(2,5)，即f (x )＝2x，其中x ∈(2,5)． (2)四边形ABCD 的面积为S ＝S △ABD ＋S △CBD＝12(AB ·AD ＋CB ·CD )sin A ＝12[x (9－x )＋x (5－x )]·1－cos 2A ＝x (7－x ) 1－⎝ ⎛⎭⎪⎫2x 2＝ x 2－47－x 2＝x 2－4x 2－14x ＋49. 记g (x )＝(x 2－4)(x 2－14x ＋49)，x ∈(2,5)．∴g ′ (x )＝2x (x 2－14x ＋49)＋ (x 2－4)(2x －14)＝2(x －7)·(2x 2－7x －4)＝2(x －7)(2x ＋1)(x －4)，令g ′(x )＝0，得x ＝4或x ＝7(舍)或x ＝－0.5(舍)．∴函数g (x )在区间(2,4)内单调递增，在区间(4,5)内单调递减．∴g (x )的最大值为g (4)＝12×9＝108，∴四边形ABCD 的面积S 的最大值为108＝63， ∴所求四边形ABCD 面积的最大值为63平方米．。

2024年高考数学一轮复习(新高考版) 第4章正弦定理、余弦定理

§4.8正弦定理、余弦定理考试要求1.掌握正弦定理、余弦定理及其变形.2.理解三角形的面积公式并能应用.3.能利用正弦定理、余弦定理解决一些简单的三角形度量问题．知识梳理1．正弦定理、余弦定理在△ABC 中，若角A ，B ，C 所对的边分别是a ，b ，c ，R 为△ABC 外接圆半径，则定理正弦定理余弦定理内容a sin A ＝bsinB ＝c sin C＝2R a 2＝b 2＋c 2－2bc cos A ；b 2＝c 2＋a 2－2ca cos B ；c 2＝a 2＋b 2－2ab cos C变形(1)a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ；(2)sin A ＝a 2R，sin B ＝b 2R ，sin C ＝c 2R；(3)a ∶b ∶c ＝sin A ∶sin B ∶sin Ccos A ＝b 2＋c 2－a 22bc ；cos B ＝c 2＋a 2－b 22ac ；cos C ＝a 2＋b 2－c 22ab 2．三角形解的判断A 为锐角A 为钝角或直角图形关系式a ＝b sin A b sin A <a <b a ≥b a >b 解的个数一解两解一解一解3．三角形中常用的面积公式(1)S ＝12ah a (h a 表示边a 上的高)；(2)S ＝12ab sin C ＝12ac sin B ＝12bc sin A ；(3)S ＝12r (a ＋b ＋c )(r 为三角形的内切圆半径)．常用结论在△ABC 中，常有以下结论：(1)∠A ＋∠B ＋∠C ＝π.(2)任意两边之和大于第三边，任意两边之差小于第三边．(3)a >b ⇔A >B ⇔sin A >sin B ，cos A <cos B .(4)sin(A ＋B )＝sin C ；cos(A ＋B )＝－cos C ；tan(A ＋B )＝－tan C ；sin A ＋B 2＝cos C2；cos A ＋B 2＝sin C 2.(5)三角形中的射影定理在△ABC 中，a ＝b cos C ＋c cos B ；b ＝a cos C ＋c cos A ；c ＝b cos A ＋a cos B .(6)三角形中的面积S ＝12(a ＋b ＋c 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)三角形中三边之比等于相应的三个内角之比．(×)(2)在△ABC 中，若sin A >sin B ，则A >B .(√)(3)在△ABC 的六个元素中，已知任意三个元素可求其他元素．(×)(4)当b 2＋c 2－a 2>0时，△ABC 为锐角三角形．(×)教材改编题1．在△ABC 中，AB ＝5，AC ＝3，BC ＝7，则∠BAC 等于()A.π6B.π3C.2π3D.5π6答案C解析在△ABC 中，设AB ＝c ＝5，AC ＝b ＝3，BC ＝a ＝7，由余弦定理得cos ∠BAC ＝b 2＋c 2－a 22bc ＝9＋25－4930＝－12，因为∠BAC 为△ABC 的内角，所以∠BAC ＝2π3.2．记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若△ABC 的面积为4，a ＝2，B ＝30°，则c 等于()A ．8B ．4C ．833D ．433答案A解析由S △ABC ＝12ac sin B ＝12×2c ×12＝4，得c ＝8.3．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知B ＝30°，b ＝2，c ＝2，则C ＝.答案45°或135°解析由正弦定理得sin C ＝c sin B b ＝2sin 30°2＝22，因为c >b ，B ＝30°，所以C ＝45°或C ＝135°.题型一利用正弦定理、余弦定理解三角形例1(12分)(2022·新高考全国Ⅰ)记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos A1＋sin A＝sin 2B1＋cos 2B.(1)若C ＝2π3，求B ；[切入点：二倍角公式化简](2)求a 2＋b 2c2的最小值．[关键点：找到角B 与角C ，A 的关系]思维升华解三角形时，如果式子中含有角的余弦或边的二次式，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式，则考虑用正弦定理，以上特征都不明显时，则要考虑两个定理都有可能用到．跟踪训练1(2022·全国乙卷)记△ABC的内角A，B，C的对边分别为a，b，c，已知sin C sin(A －B)＝sin B sin(C－A)．(1)证明：2a2＝b2＋c2；(2)若a＝5，cos A＝2531，求△ABC的周长．(1)证明方法一由sin C sin(A－B)＝sin B sin(C－A)，可得sin C sin A cos B－sin C cos A sin B＝sin B sin C cos A－sin B cos C sin A，结合正弦定理asin A＝bsin B＝csin C可得ac cos B－bc cos A＝bc cos A－ab cos C，即ac cos B＋ab cos C＝2bc cos A(*)．由余弦定理可得ac cos B＝a2＋c2－b22，ab cos C＝a2＋b2－c22，2bc cos A＝b2＋c2－a2，将上述三式代入(*)式整理，得2a2＝b2＋c2.方法二因为A＋B＋C＝π，所以sin C sin(A－B)＝sin(A＋B)sin(A－B)＝sin2A cos2B－cos2A sin2B＝sin2A(1－sin2B)－(1－sin2A)sin2B＝sin2A－sin2B，同理有sin B sin(C－A)＝sin(C＋A)sin(C－A)＝sin2C－sin2A.又sin C sin(A－B)＝sin B sin(C－A)，所以sin2A－sin2B＝sin2C－sin2A，即2sin2A＝sin2B＋sin2C，故由正弦定理可得2a2＝b2＋c2.(2)解由(1)及a2＝b2＋c2－2bc cos A得，a2＝2bc cos A，所以2bc＝31.因为b2＋c2＝2a2＝50，所以(b＋c)2＝b2＋c2＋2bc＝81，得b＋c＝9，所以△ABC的周长l＝a＋b＋c＝14.题型二正弦定理、余弦定理的简单应用命题点1三角形的形状判断例2(1)在△ABC中，角A，B，C所对的边分别是a，b，c，若c－a cos B＝(2a－b)cos A，则△ABC的形状为()A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形答案D解析因为c－a cos B＝(2a－b)cos A，C＝π－(A＋B)，所以由正弦定理得sin C －sin A cos B ＝2sin A cos A －sin B cos A ，所以sin A cos B ＋cos A sin B －sin A cos B ＝2sin A cos A －sin B cos A ，所以cos A (sin B －sin A )＝0，所以cos A ＝0或sin B ＝sin A ，所以A ＝π2或B ＝A 或B ＝π－A (舍去)，所以△ABC 为等腰三角形或直角三角形．(2)在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，c －a 2c ＝sin 2B2，则△ABC 的形状为()A ．直角三角形B ．等边三角形C ．等腰三角形或直角三角形D ．等腰直角三角形答案A解析由cos B ＝1－2sin 2B2，得sin 2B 2＝1－cos B2，所以c －a 2c ＝1－cos B 2，即cos B ＝a c .方法一由余弦定理得a 2＋c 2－b 22ac＝ac ，即a 2＋c 2－b 2＝2a 2，所以a 2＋b 2＝c 2.所以△ABC 为直角三角形，但无法判断两直角边是否相等．方法二由正弦定理得cos B ＝sin A sin C，又sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C ，所以cos B sin C ＝sin B cos C ＋cos B sin C ，即sin B cos C ＝0，又sin B ≠0，所以cos C ＝0，又角C 为△ABC 的内角，所以C ＝π2，所以△ABC 为直角三角形，但无法判断两直角边是否相等．延伸探究将本例(2)中的条件“c －a 2c＝sin 2B 2”改为“sin A sin B ＝ac ，(b ＋c ＋a )(b ＋c －a )＝3bc ”，试判断△ABC 的形状．解因为sin A sin B ＝a c ，所以由正弦定理得a b ＝ac，所以b ＝c .又(b ＋c ＋a )(b ＋c －a )＝3bc ，所以b 2＋c 2－a 2＝bc ，所以由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝bc 2bc ＝12.因为A ∈(0，π)，所以A ＝π3，所以△ABC 是等边三角形．思维升华判断三角形形状的两种思路(1)化边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状．(2)化角：通过三角恒等变换，得出内角的关系，从而判断三角形的形状．此时要注意应用A ＋B ＋C ＝π这个结论．命题点2三角形的面积例3(2022·浙江)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .已知4a ＝5c ，cos C ＝35.(1)求sin A 的值；(2)若b ＝11，求△ABC 的面积．解(1)由正弦定理a sin A ＝c sin C，得sin A ＝a ·sin Cc.因为cos C ＝35，所以sin C ＝45，又a c ＝54，所以sin A ＝5sin C 4＝55(2)由(1)知sin A ＝55，因为a ＝5c 4<c ，所以0<A <π2，所以cos A ＝255，所以sin B ＝sin(A ＋C )＝sin A cos C ＋sin C cos A ＝55×35＋45×255＝11525.因为b sin B ＝csin C，即1111525＝c 45，所以c ＝45，所以S △ABC ＝12bc sin A ＝12×11×45×55＝22.思维升华三角形面积公式的应用原则(1)对于面积公式S ＝12ab sin C ＝12ac sin B ＝12bc sin A ，一般是已知哪一个角就使用哪一个公式．(2)与面积有关的问题，一般要用到正弦定理或余弦定理进行边和角的转化．命题点3与平面几何有关的问题例4(2023·厦门模拟)如图，已知△ABC 的内角A ，B ，C 所对的边分别是a ，b ，c ，b (1＋cosC )＝3c sin ∠ABC 且△ABC 的外接圆面积为49π3.(1)求边c 的长；(2)若a ＝5，延长CB 至M ，使得cos ∠AMC ＝217，求BM .解(1)设△ABC 的外接圆半径为R ，由题意πR 2＝49π3，解得R ＝733.由题意及正弦定理可得sin ∠ABC (1＋cos C )＝3sin C sin ∠ABC ，因为sin ∠ABC ≠0，所以1＋cos C ＝3sin C ，即1，因为0<C <π，所以C －π6∈－π6，C －π6＝π6，即C ＝π3.故c ＝2R sin C ＝2×733×32＝7.(2)因为a ＝5，c ＝7，C ＝π3，故cos C ＝12＝25＋b 2－492×5×b ，得b 2－5b －24＝0，解得b ＝8(b ＝－3舍去)．在△ABC 中，由余弦定理可得cos ∠ABC ＝52＋72－822×5×7＝17，所以sin ∠ABC ＝437.由cos ∠AMC ＝217得sin ∠AMC ＝277.故sin∠BAM＝sin(∠ABC－∠AMC)＝sin∠ABC cos∠AMC－cos∠ABC sin∠AMC＝107 49，在△ABM中，由正弦定理可得BMsin∠BAM＝ABsin∠AMB，则BM＝7277×10749＝5.思维升华在平面几何图形中研究或求与角有关的长度、角度、面积的最值、优化设计等问题时，通常是转化到三角形中，利用正、余弦定理通过运算的方法加以解决．在解决某些具体问题时，常先引入变量，如边长、角度等，然后把要解三角形的边或角用所设变量表示出来，再利用正、余弦定理列出方程，再解方程即可．若研究最值，常使用函数思想．跟踪训练2(1)(多选)(2023·合肥模拟)已知△ABC的内角A，B，C所对的边分别为a，b，c，下列四个命题中正确的是()A．若a cos A＝b cos B，则△ABC一定是等腰三角形B．若b cos C＋c cos B＝b，则△ABC是等腰三角形C．若acos A＝bcos B＝ccos C，则△ABC一定是等边三角形D．若B＝60°，b2＝ac，则△ABC是直角三角形答案BC解析对于A，若a cos A＝b cos B，则由正弦定理得sin A cos A＝sin B cos B，∴sin2A＝sin2B，则2A＝2B或2A＋2B＝180°，即A＝B或A＋B＝90°，则△ABC为等腰三角形或直角三角形，故A错误；对于B，若b cos C＋c cos B＝b，则由正弦定理得sin B cos C＋sin C cos B＝sin(B＋C)＝sin A＝sin B，即A＝B，则△ABC是等腰三角形，故B正确；对于C，若acos A＝bcos B＝ccos C，则由正弦定理得sin Acos A＝sin Bcos B＝sin Ccos C，则tan A＝tan B＝tan C，即A＝B＝C，即△ABC是等边三角形，故C正确；对于D，由于B＝60°，b2＝ac，由余弦定理可得b2＝ac＝a2＋c2－ac，可得(a－c)2＝0，解得a＝c，可得A＝C＝B，故△ABC是等边三角形，故D错误．(2)在①b2＋2ac＝a2＋c2；②cos B＝b cos A；③sin B＋cos B＝2这三个条件中任选一个填在下面的横线中，并解决该问题．已知△ABC的内角A，B，C的对边分别为a，b，c，，A＝π3，b＝2，求△ABC的面积．解若选①，则由b2＋2ac＝a2＋c2，得2ac＝a2＋c2－b2.由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝2ac 2ac ＝22.因为B ∈(0，π)，所以B ＝π4.由正弦定理得a sin A ＝b sin B，即asin π3＝2sin π4，解得a ＝ 3.因为C ＝π－A －B ＝π－π3－π4＝5π12，所以sin C ＝sin 5π12＝＝sin π6cos π4＋cos π6sin π4＝6＋24，所以S △ABC ＝12ab sin C ＝12×3×2×6＋24＝3＋34.若选②，因为cos B ＝b cos A ，A ＝π3，b ＝2，所以cos B ＝b cos A ＝2cos π3＝22.因为B ∈(0，π)，所以B ＝π4.由正弦定理得a sin A ＝b sin B，即asin π3＝2sin π4，解得a ＝ 3.因为C ＝π－A －B ＝π－π3－π4＝5π12，所以sin C ＝sin 5π12＝＝sin π6cos π4＋cos π6sin π4＝6＋24，所以S △ABC ＝12ab sin C ＝12×3×2×6＋24＝3＋34.若选③，则由sin B ＋cos B ＝2，得2sin ＝2，所以 1.因为B ∈(0，π)，所以B ＋π4∈所以B ＋π4＝π2，所以B ＝π4.由正弦定理得a sin A ＝bsin B，即asin π3＝2sin π4，解得a ＝ 3.因为C ＝π－A －B ＝π－π3－π4＝5π12，所以sin C ＝sin 5π12＝＝sin π6cos π4＋cos π6sin π4＝6＋24，所以S △ABC ＝12ab sin C ＝12×3×2×6＋24＝3＋34.(3)(2022·重庆八中模拟)已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，在①c (sin A －sin C )＝(a －b )(sin A ＋sin B )；②2b cos A ＋a ＝2c ；③233ac sin B ＝a 2＋c 2－b 2三个条件中任选一个，补充在下面问题中，并解答．①若，求角B 的大小；②求sin A ＋sin C 的取值范围；③如图所示，当sin A ＋sin C 取得最大值时，若在△ABC 所在平面内取一点D (D 与B 在AC 两侧)，使得线段DC ＝2，DA ＝1，求△BCD 面积的最大值．解①若选①，因为c (sin A －sin C )＝(a －b )(sin A ＋sin B )，由正弦定理得c (a －c )＝(a －b )(a ＋b )，整理得a 2＋c 2－b 2＝ac ，所以cos B ＝a 2＋c 2－b 22ac ＝ac 2ac ＝12，又0<B <π，所以B ＝π3.若选②，因为2b cos A ＋a ＝2c ，由余弦定理得2b ·b 2＋c 2－a 22bc ＋a ＝2c ，化简得，a 2＋c 2－b 2＝ac ，所以cos B ＝a 2＋c 2－b 22ac ＝ac 2ac ＝12，又0<B <π，所以B ＝π3.若选③，因为233ac sin B ＝a 2＋c 2－b 2，由余弦定理得233ac sin B ＝2ac cos B ，化简得tan B ＝3，又0<B <π，所以B ＝π3.②由①得，A ＋C ＝2π3，则0<A <2π3，sin A ＋sin C ＝sin A ＋＝32sin A ＋32cos A ＝3sin 又π6<A ＋π6<5π6，所以12<sin 1，则sin A ＋sin C ，3.③当sin A ＋sin C 取得最大值时，A ＋π6＝π2，解得A ＝π3，又B ＝π3，所以△ABC 为等边三角形，令∠ACD ＝θ，∠ADC ＝α，AB ＝AC ＝BC ＝a ，则由正弦定理可得a sin α＝1sin θ，所以sin α＝a sin θ.又由余弦定理得，a 2＝22＋12－2×2×1×cos α，所以a 2cos 2θ＝a 2－a 2sin 2θ＝cos 2α－4cos α＋4，所以a cos θ＝2－cos α.S △BCD ＝12×a ×＝32a cos θ＋12a sin θ＝32(2－cos α)＋12sin α＝3＋≤3＋1，当且仅当α＝∠ADC ＝5π6时等号成立，所以△BCD 面积的最大值为3＋1.课时精练1．在△ABC 中，C ＝60°，a ＋2b ＝8，sin A ＝6sin B ，则c 等于()A.35B.31C ．6D ．5答案B解析因为sin A ＝6sin B ，则由正弦定理得a ＝6b ，又a ＋2b ＝8，所以a ＝6，b ＝1，因为C ＝60°，所以由余弦定理c 2＝a 2＋b 2－2ab cos C ，即c 2＝62＋12－2×6×1×12，解得c ＝31.2．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若(a ＋b )(sin A －sin B )＝(b ＋c )sin C ，a ＝7，则△ABC 外接圆的直径为()A ．14B ．7C.733D.1433答案D 解析已知(a ＋b )(sin A －sin B )＝(b ＋c )sin C ，由正弦定理可得(a ＋b )(a －b )＝(b ＋c )c ，化简得b 2＋c 2－a 2＝－bc ，所以cos A ＝b 2＋c 2－a 22bc ＝－bc 2bc＝－12，又因为A ∈(0，π)，所以A ＝2π3，所以sin A ＝sin2π3＝32，设△ABC 外接圆的半径为R ，由正弦定理可得2R ＝asin A ＝732＝1433，所以△ABC 外接圆的直径为1433.3．(2022·北京模拟)在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若3a sin B ＝b cos A ，且b ＝23，c ＝2，则a 的值为()A ．27B ．2C ．23－2D ．1答案B解析由已知及正弦定理得，3sin A sin B ＝sin B cos A 且sin B ≠0，可得tan A ＝33，又0<A <π，所以A ＝π6，又b ＝23，c ＝2，所以由余弦定理a 2＝b 2＋c 2－2bc cos A ＝16－12＝4，解得a ＝2.4．(2023·枣庄模拟)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，A ＝60°，b ＝1，S △ABC ＝3，则a ＋b ＋csin A ＋sin B ＋sin C等于()A.2393B.2633C.833D ．23答案A解析由三角形的面积公式可得S △ABC ＝12bc sin A ＝34c ＝3，解得c ＝4，由余弦定理可得a ＝b 2＋c 2－2bc cos A ＝13，设△ABC 的外接圆半径为r ，由正弦定理得a sin A ＝b sin B ＝csin C＝2r ，所以a ＋b ＋c sin A ＋sin B ＋sin C ＝2r (sin A ＋sin B ＋sin C )sin A ＋sin B ＋sin C＝2r ＝asin A ＝1332＝2393.5．(2023·马鞍山模拟)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，设(sin B ＋sin C )2＝sin 2A ＋(2－2)sin B sin C ，2sin A －2sin B ＝0，则sin C 等于()A.12B.32C.6－24 D.6＋24答案C解析在△ABC 中，由(sin B ＋sin C )2＝sin 2A ＋(2－2)sin B sin C 及正弦定理得(b ＋c )2＝a 2＋(2－2)bc ，即b 2＋c 2－a 2＝－2bc ，由余弦定理得cos A ＝b 2＋c 2－a 22bc＝－22，而0°<A <180°，解得A ＝135°，由2sin A －2sin B ＝0得sin B ＝22sin A ＝12，显然0°<B <90°，则B ＝30°，C ＝15°，所以sin C ＝sin(60°－45°)＝sin 60°cos 45°－cos 60°sin 45°＝6－24.6．(2023·衡阳模拟)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知2cos B (a cos C ＋c cos A )＝b ，lg sin C ＝12lg 3－lg 2，则△ABC 的形状为()A ．等腰三角形B ．直角三角形C ．等边三角形D ．等腰直角三角形答案C解析∵2cos B (a cos C ＋c cos A )＝b ，∴根据正弦定理得，2cos B (sin A cos C ＋cos A sin C )＝sin B ，∴2cos B sin(A ＋C )＝sin B ，∴2cos B sin(π－B )＝sin B ，即2cos B sin B ＝sin B ，∵B ∈(0，π)，∴sin B ≠0，∴cos B ＝12，∴B ＝π3.∵lg sin C ＝12lg 3－lg 2，∴lg sin C ＝lg32，∴sin C ＝32，∵C ∈(0，π)，∴C ＝π3或2π3，∵B ＝π3，∴C ≠2π3，∴C ＝π3，∴A ＝B ＝C ＝π3，即△ABC 为等边三角形．7．(2022·全国甲卷)已知△ABC 中，点D 在边BC 上，∠ADB ＝120°，AD ＝2，CD ＝2BD .当ACAB取得最小值时，BD ＝.答案3－1解析设BD ＝k (k >0)，则CD ＝2k .根据题意作出大致图形，如图．在△ABD 中，由余弦定理得AB 2＝AD 2＋BD 2－2AD ·BD cos ∠ADB ＝22＋k 2－2×2k k 2＋2k ＋4.在△ACD 中，由余弦定理得AC 2＝AD 2＋CD 2－2AD ·CD cos ∠ADC ＝22＋(2k )2－2×2×2k ·12＝4k 2－4k ＋4，则AC 2AB 2＝4k 2－4k ＋4k 2＋2k ＋4＝4(k 2＋2k ＋4)－12k －12k 2＋2k ＋4＝4－12(k ＋1)k 2＋2k ＋4＝4－12(k ＋1)(k ＋1)2＋3＝4－12k ＋1＋3k ＋1.∵k ＋1＋3k ＋1≥23(当且仅当k ＋1＝3k ＋1，即k ＝3－1时等号成立)，∴AC 2AB 2≥4－1223＝4－23＝(3－1)2，∴当ACAB取得最小值3－1时，BD ＝k ＝3－1.8．(2023·宜春模拟)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b sin C ＋c sin B ＝4a sinB sinC ，b 2＋c 2－a 2＝8，则△ABC 的面积为．答案233解析∵b sin C ＋c sin B ＝4a sin B sin C ，sin B sin C >0，结合正弦定理可得sin B sin C ＋sin C sin B ＝4sin A sin B sin C ，∴sin A ＝12，∵b 2＋c 2－a 2＝8，结合余弦定理a 2＝b 2＋c 2－2bc cos A ，可得2bc cos A ＝8，∴A 为锐角，且cos A ＝32，从而求得bc ＝833，∴△ABC 的面积为S ＝12bc sin A ＝12×833×12＝233.9．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且b cos C ＝(2a －c )cos B .(1)求B ；(2)若b ＝3，sin C ＝2sin A ，求△ABC 的面积．解(1)由正弦定理，得sin B cos C ＝2sin A cos B －cos B sin C ，即sin B cos C ＋cos B sin C ＝2sin A cos B ，∴sin(B ＋C )＝2sin A cos B ，∴sin A ＝2sin A cos B ，又∵sin A ≠0，∴cos B ＝12，∵B 为三角形内角，∴B ＝π3.(2)∵sin C ＝2sin A ，∴由正弦定理得c ＝2a ，∴由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝a 2＋4a 2－2a 2＝9，即3a 2＝9，∴a ＝3，c ＝23，∴△ABC 的面积为S ＝12ac sin B ＝12×3×23×32＝332.10．(2023·湖州模拟)在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，已知3b a sin B .(1)求角A 的大小；(2)若b ，a ，c 成等比数列，判断△ABC 的形状．解(1)∵3b a sin B ，由诱导公式得3b cos A ＝a sin B ，由正弦定理得3sin B cos A ＝sin A sin B ，∵sin B ≠0，∴3cos A ＝sin A ，即tan A ＝3，∵A ∈(0，π)，∴A ＝π3.(2)∵b ，a ，c 成等比数列，∴a 2＝bc ，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝b 2＋c 2－bc 2bc＝12，即b 2＋c 2－bc ＝bc ，∴(b －c )2＝0，∴b ＝c ，又由(1)知A ＝π3，∴△ABC 为等边三角形．11．(多选)对于△ABC ，有如下判断，其中正确的是()A ．若cos A ＝cosB ，则△ABC 为等腰三角形B ．若A >B ，则sin A >sin BC ．若a ＝8，c ＝10，B ＝60°，则符合条件的△ABC 有两个D ．若sin 2A ＋sin 2B <sin 2C ，则△ABC 是钝角三角形答案ABD解析对于A ，若cos A ＝cos B ，则A ＝B ，所以△ABC 为等腰三角形，故A 正确；对于B ，若A >B ，则a >b ，由正弦定理a sin A ＝b sin B＝2R ，得2R sin A >2R sin B ，即sin A >sin B 成立，故B 正确；对于C ，由余弦定理可得b ＝82＋102－2×8×10×12＝84，只有一解，故C 错误；对于D ，若sin 2A ＋sin 2B <sin 2C ，则根据正弦定理得a 2＋b 2<c 2，cos C ＝a 2＋b 2－c 22ab <0，所以C为钝角，所以△ABC 是钝角三角形，故D 正确．12．在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，sin A sin B sin C ＝18，△ABC 的面积为2，则下列选项错误的是()A ．abc ＝162B ．若a ＝2，则A ＝π3C ．△ABC 外接圆的半径R ＝22D ≥32sin C 答案B解析由题可得12ab sin C ＝2，则sin C ＝4ab，代入sin A sin B sin C ＝18，得4sin A sin B ab ＝18，即R 2＝8，即R ＝22，C 正确；abc ＝8R 3sin A sin B sin C ＝1282×18＝162，A 正确；若a ＝2，则sin A ＝a 2R ＝242＝14，此时A ≠π3，B 错误；因为sin A >0，sin B >0，所以(sin A ＋sin B )2≥4sin A sin B ，所以(sin A ＋sin B )2(sin A sin B )2≥4sin A sin B ，由sin A sin B sin C ＝18，得4sin A sin B＝32sin C ，所以(sin A ＋sin B )2(sin A sin B )2≥32sin C ，即≥32sin C ，D 正确．13．(2023·嘉兴模拟)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知c sin A ＝3a cos C ，c ＝23，ab ＝8，则a ＋b 的值是．答案6解析∵c sin A ＝3a cos C ，根据正弦定理得sin C sin A ＝3sin A cos C ，∵sin A ≠0，故tan C ＝3，∵C ∈(0，π)，∴C ＝π3，再由余弦定理得cos C ＝a 2＋b 2－c 22ab ＝(a ＋b )2－2ab －c 22ab ＝12，代入c ＝23，ab ＝8，得a ＋b ＝6.14．在△ABC 中，已知AB ＝4，AC ＝7，BC 边的中线AD ＝72，那么BC ＝.答案9解析在△ABD 中，结合余弦定理得cos ∠ADB ＝BD 2＋AD 2－AB 22BD ·AD，在△ACD 中，结合余弦定理得cos ∠ADC ＝CD 2＋AD 2－AC 22CD ·AD，由题意知BD ＝CD ，∠ADB ＋∠ADC ＝π，所以cos ∠ADB ＋cos ∠ADC ＝0，所以BD 2＋AD 2－AB 22BD ·AD ＋CD 2＋AD 2－AC 22CD ·AD ＝0，2×72CD 2×72CD 0，解得CD ＝92，所以BC ＝9.15．(多选)(2023·珠海模拟)已知△ABC 满足sin A ∶sin B ∶sin C ＝2∶3∶7，且△ABC 的面积S △ABC ＝332，则下列命题正确的是()A ．△ABC 的周长为5＋7B ．△ABC 的三个内角A ，B ，C 满足关系A ＋B ＝2C C ．△ABC 的外接圆半径为2213D ．△ABC 的中线CD 的长为192答案ABD解析因为△ABC 满足sin A ∶sin B ∶sin C ＝2∶3∶7，所以a ∶b ∶c ＝2∶3∶7，设a ＝2t ，b ＝3t ，c ＝7t ，t >0，利用余弦定理cos C ＝a 2＋b 2－c 22ab ＝4t 2＋9t 2－7t 212t 2＝12，由于C ∈(0，π)，所以C ＝π3.对于A ，因为S △ABC ＝332，所以12ab sin C ＝12·2t ·3t ·32＝332，解得t ＝1.所以a ＝2，b ＝3，c ＝7，所以△ABC 的周长为5＋7，故A 正确；对于B ，因为C ＝π3，所以A ＋B ＝2π3，故A ＋B ＝2C ，故B 正确；对于C ，利用正弦定理c sin C ＝732＝2213＝2R ，解得R ＝213，所以△ABC 的外接圆半径为213，故C 错误；对于D ，如图所示，在△ABC 中，利用正弦定理732＝2sin A ，解得sin A ＝217，又a <c ，所以cos A ＝277，在△ACD 中，利用余弦定理CD 2＝AC 2＋AD 2－2AC ·AD ·cos A ＝9＋74－2×3×72×277＝194，解得CD ＝192，故D 正确．16.如图，△ABC 的内角A ，B ，C 的对边分别是a ，b ，c .已知a 2＋c 2＝b 2＋ac ，则B ＝.若线段AC 的垂直平分线交AC 于点D ，交AB 于点E ，且BC ＝4，DE ＝ 6.则△BCE 的面积为．答案π323解析在△ABC 中，由余弦定理知cos B ＝a 2＋c 2－b 22ac，而a 2＋c 2＝b 2＋ac ，∴cos B ＝12，又0<B <π，则B ＝π3，在△BCE 中，设∠CEB ＝θ，则CE sin π3＝BC sin θ，可得CE ＝23sin θ，又AC 的垂直平分线交AC 于点D ，交AB 于点E ，则∠ECA ＝∠EAC ＝θ2，∴sin θ2＝DE CE ＝2sin θ2，可得cos θ2＝22，而0<θ<π，故θ2＝π4，即θ＝π2.∴CE ＝23，BE ＝2，故△BCE 的面积为12·CE ·BE ＝23.。

人教版高中数学必修第二册6.4.3.3 余弦定理、正弦定理在几何和生活应用举例同步精练(含解析)

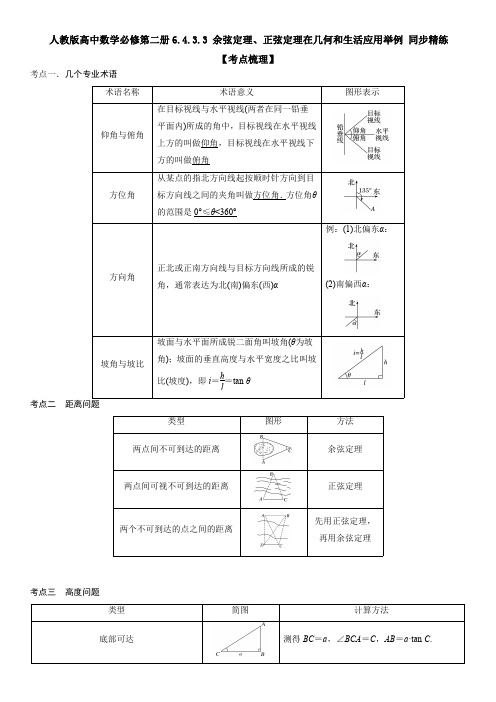
人教版高中数学必修第二册6.4.3.3余弦定理、正弦定理在几何和生活应用举例同步精练【考点梳理】考点一．几个专业术语术语名称术语意义图形表示仰角与俯角在目标视线与水平视线(两者在同一铅垂平面内)所成的角中，目标视线在水平视线上方的叫做仰角，目标视线在水平视线下方的叫做俯角方位角从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角．方位角θ的范围是0°≤θ<360°方向角正北或正南方向线与目标方向线所成的锐角，通常表达为北(南)偏东(西)α例：(1)北偏东α：(2)南偏西α：坡角与坡比坡面与水平面所成锐二面角叫坡角(θ为坡角)；坡面的垂直高度与水平宽度之比叫坡比(坡度)，即i ＝hl＝tan θ考点二距离问题类型图形方法两点间不可到达的距离余弦定理两点间可视不可到达的距离正弦定理两个不可到达的点之间的距离先用正弦定理，再用余弦定理考点三高度问题类型简图计算方法底部可达测得BC ＝a ，∠BCA ＝C ，AB ＝a ·tan C .底部不可达点B 与C ，D 共线测得CD ＝a 及C 与∠ADB 的度数.先由正弦定理求出AC 或AD ，再解三角形得AB 的值.点B 与C ，D 不共线测得CD ＝a 及∠BCD ，∠BDC ，∠ACB 的度数.在△BCD 中由正弦定理求得BC ，再解三角形得AB 的值.【题型归纳】题型一：正、余弦定理判定三角形的形状问题1．（2021·江苏宿迁·高一期末）在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若cos sin cos sin b c A Ba c B A-=-，则ABC的形状是（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形2．（2021·甘肃·庆阳第六中学高一期末）已知ABC 的内角A ，B ，C 所对的边分别为,,a b c ，满足cos a b C =，则ABC 的形状一定是（）A ．等腰直角三角形B ．等边三角形C ．等腰三角形D ．直角三角形3．（2021·全国·高一课时练习）在ABC 中，lg(sin sin )2lgsin lg(sin sin )A C B C A +=--，则ABC 的形状为（）A ．等腰三角形B ．直角三角形C ．等边三角形D ．等腰直角三角形题型二：求三角形的周长或者边长最值或范围问题4．（2021·天津市实验中学滨海学校高一期中）在锐角ABC 中，A ，B ，C 的对边分别是a ，b ，c ，若()12cos c b A =+，则ab的取值范围是（）A ．()1,3B ．()2,3C ．()2,2D ．13,22⎛⎫ ⎪ ⎪⎝⎭5．（2021·吉林·四平市第一高级中学高一期末）在ABC 中，角,,A B C 所对的边分别为,,a b c ，已知23a =，且ABC 的面积2222()2S b c a =+-，则ABC 周长的最大值是（）A ．6B ．623+C ．43D ．636．（2021·重庆南开中学高一阶段练习）ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若满足2c =，cos sin a C c A =的三角形ABC 有两个，则边BC 的长度的取值范围是（）A ．()1,2B ．()1,3C ．()3,2D ．()2,2题型三：几何图形中的计算7．（2021·重庆市育才中学高一期中）如图所示，在平面四边形ABCD 中，BCD △是等边三角形，2AD =，27BD =，23πBAD ∠=，则ABC 的面积为（）A ．73B ．33C ．143D ．638．（2021·安徽合肥·高一期末）如图，设ABC 的内角,,A B C 所对的边分别为,,a b c ，()cos co 3s 2sin a C c A b B +=，且.3CAB π∠=若点D 是ABC 外一点，1,2DC DA ==，则下列说法中错误的是（）A ．ABC 的内角3B π=B ．ABC 的内角3C π=C ．四边形ABCD 面积无最大值D ．四边形ABCD 面积的最大值为5324+9．（2021·辽宁·高一期末）在ABC 中，已知45B =︒，D 是BC 边上一点，如图，75,1,7BAD DC AC ∠=︒==，则AB =（）A ．5B ．6C ．2D ．3题型四：求三角形面积最值或者范围问题10．（2021·四川新都·高一期末）设锐角ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ，且()1cos 3sin c A a C +=，2b =，则ABC 的面积的取值范围是（）A ．()1,+∞B ．3,2⎛⎫+∞ ⎪ ⎪⎝⎭C ．3,232⎛⎫⎪ ⎪⎝⎭D ．()1,2311．（2021·江苏·南京市建邺高级中学高一期末）我国南宋时期数学家秦九韶发现了求三角形面积的“三斜求积”公式：设△ABC 内角A ，B ，C 所对的边分别为a ，b ，c ，面积2222221[()]42c a b S c a +-=-．若2b =，sin 2sin a B b C =，则△ABC 面积的最大值为（）A ．13B ．23C ．43D ．6312．（2021·江苏省丹阳高级中学高一阶段练习）已知a ，b ，c 分别为ABC 的三个内角A ，B ，C 的对边，2a =，且()()()2sin sin sin b A B c b C +-=-，则ABC 面积的最大值为（）A ．83B ．43C ．23D ．3题型五：正、余弦定理和三角函数综合问题13．（2021·河北·石家庄市第一中学东校区高一阶段练习）在锐角三角形ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2223a c ac b +=+，则cos sin A C +的取值范围为（）A ．33,22⎛⎫ ⎪ ⎪⎝⎭B ．3,32⎛⎤⎥ ⎝⎦C ．13,22⎛⎫ ⎪⎝⎭D ．3,22⎛⎤ ⎥⎝⎦14．（2021·江苏省苏州实验中学高一阶段练习）在ΔABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若c cos A +a cos C =2，AC 边上的高为3，则∠ABC 的最大值为（）A ．6πB ．3πC ．2πD ．23π15．（2021·广东·深圳中学高一期中）设锐角ABC 的内角,,A B C 所对的边分别为,,a b c ，若cos 2cos B a bC c-=，1c =，则22a b ab ++的取值范围为（）A ．1,33⎛⎤ ⎥⎝⎦B ．(1,3]C ．5,33⎛⎤ ⎥⎝⎦D ．7,33⎛⎤ ⎥⎝⎦题型六：测量距离问题16．（2021·全国·高一课时练习）如图所示，为测量某不可到达的竖直建筑物AB 的高度，在此建筑物的同一侧且与此建筑物底部在同一水平面上选择相距10米的C ，D 两个观测点，并在C ，D 两点处分别测得塔顶的仰角分别为45︒和60︒，且60BDC ∠=︒，则此建筑物的高度为（）A ．103米B ．53米C ．10米D ．5米17．（2021·河北邢台·高一阶段练习）一艘船航行到点B 处时，测得灯塔A 在其西北方向，如图，随后该船以20海里/小时的速度，按北偏东15的方向航行两小时后到达点C ，测得灯塔A 在其正西方向，此时船与灯塔A 间的距离为（）A ．203海里B ．403海里C ．206海里D ．406海里题型七：测量高度问题18．（2021·湖北·大冶市第一中学高一阶段练习）在高40m 的楼顶测得对面一塔顶的仰角为60°，塔基的俯角为45°，则这座塔的高度为（）A ．340(1)3+m B ．40(13)+mC ．20(62)+mD ．40(62)+m19．（2021·全国·高一课时练习）如图，地平面上有一根旗杆OP ，为了测得它的高度h ，在地面上取一基线AB ，AB=20m ，在A 处测得点P 的仰角∠OAP=30°，在B 处测得点P 的仰角∠OBP=45°，又测得∠AOB=60°，则旗杆的高度为（）A ．20（32-）mB ．204-2mC ．204-3m D ．10（32+）m题型八：测量角度问题20．（2021·江苏·南京市宁海中学高一阶段练习）如图所示，在坡度一定的山坡A 处测得山顶上一建筑物CD 的顶端C 对于山坡的斜度为15︒，向山顶前进100m 到达B 处，又测得C 对于山坡的斜度为45︒，若50m CD =，山坡对于地平面的坡度为θ，则cos θ等于（）A ．33B ．62-C ．31-D ．21-21．（2021·浙江·丽水外国语实验学校高一阶段练习）如图，某人在一条水平公路旁的山顶P 处测得小车在A 处的俯角为30°，该小车在公路上由东向西匀速行驶7.5分钟后，到达B 处，此时测得俯角为45°.已知此山的高1km PO =，小车的速度是20km/h ，则cos AOB ∠=（）A ．338-B ．58-C ．34-D ．104-题型九：正、余弦定理在几何中的综合性问题22．（2021·广东·中山市第二中学高一阶段练习）在ABC ∆中，设角,,A B C 的对边分别为,,a b c ，已知222cos sin cos sin sin A B C A B =++.（1）求角C 的大小；（2）若3c =，求ABC ∆周长的取值范围.23．（2021·重庆市江津中学校高一阶段练习）如图，在四边形ABCD 中，33CD =，7BC =，7cos 14CBD ∠=-.（1）求BDC ∠；（2）若3A π∠=，求 ABD △周长的最大值.24．（2021·广东·东莞市新世纪英才学校高一阶段练习）在ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，222sin sin sin sin sin A C B A C +=+.（1）求角B 的大小；（2）若ABC 为锐角三角形，3b =，求2a c -的取值范围.【双基达标】一、单选题25．（2021·全国·高一课时练习）如图所示，有四座城市A ，B ，C ，D ，其中B 在A 的正东方向，且与A 相距120km ，D 在A 的北偏东30°方向，且与A 相距60km ，C 在B 的北偏东30°方向，且与B 相距6013km ，一架飞机从城市D 出发，以360km/h 的速度向城市C 飞行，飞行了15min ，接到命令改变航向，飞向城市B ，此时飞机距离城市B 有（）A ．120kmB ．606kmC ．605kmD ．603km26．（2021·湖南·嘉禾县第一中学高一阶段练习）如图所示，为了测量湖中A 、B 两处亭子间的距离，湖岸边现有相距100米的甲、乙两位测量人员，甲测量员在D 处测量发现A 亭子位于西偏北75︒，B 亭子位于东北方向，乙测量员在C 处测量发现B 亭子位于正北方向，A 亭子位于西偏北30°方向，则A ，B 两亭子间的距离为（）A ．503米B ．1003米C ．506米D ．1006米27．（2021·全国·高一课前预习）如图，某人在一条水平公路旁的山顶P 处测得小车在A 处的俯角为30，该小车在公路上由东向西匀速行驶7.5分钟后，到达B 处，此时测得俯角为45．已知此山的高1km PO =，小车的速度是20km/h ，则cos AOB ∠=（）A ．338-B ．58C ．34-D ．104-28．（2021·全国·高一课前预习）今年第6号台风“烟花”于2021年7月25日12时30分前后登陆舟山普陀区.如图，A 点，正北方向的C 市受到台风侵袭，一艘船从A 点出发前去实施救援，以24 n mile/h 的速度向正北航行，在A 处看到S 岛在船的北偏东15︒方向，船航行3h 4后到达B 处，在B 处看到S 岛在船的北偏东45︒方向.此船从A 点到C 市航行过程中距离S 岛的最近距离为（）A ．92 n mile/hB ．()921n mile/h -C ．()931 n mile/h-D ．()932 n mile/h-29．（2021·全国·高一课时练习）为测量两塔塔尖之间的距离，某同学建立了如图所示的几何模型.若MA ⊥平面ABC ，NB ⊥平面ABC ，60m AC =，703m BC =，3tan 4MCA ∠=，14cos 15NCB ∠=，150MCN ∠=，则塔尖MN 之间的距离为（）A ．7510mB ．753mC ．757mD ．75m30．（2021·全国·高一课时练习）如图所示，为测一树的高度，在地面上选取A ，B 两点，从A ，B 两点分别测得树尖的仰角为30°，45︒，且A ，B 两点之间的距离为60m ，则树的高度为（）A ．(1533)m +B ．(30153)m +C ．(30303)m +D ．(15303)m+31．（2021·全国·高一课时练习）在某个位置测得某山峰仰角为θ，对着山峰在地面上前进600m 后测得仰角为2θ，继续在地面上前进2003m 以后测得山峰的仰角为4θ，则该山峰的高度为（）A ．200mB ．300mC ．400mD ．1003m32．（2021·安徽·安庆九一六学校高一阶段练习）空中有一气球，在它的正西方A 点测得它的仰角为45°，同时在它南偏东60°的B 点，测得它的仰角为30°，若A 、B 两点间的距离为266米，这两个观测点均离地1米，那么测量时气球到地面的距离CD 是（）A ．26677米B ．2667(1)7+米C ．266米D ．2667米33．（2021·重庆第二外国语学校高一阶段练习）在ABC 中，角,,A B C 所对的边分别为,,a b c ，满足2sin22C a ba-=，则ABC 的形状为（）A ．等边三角形B ．等腰三角形C ．等腰直角三角形D ．直角三角形34．（2021·江苏·泰州中学高一期中）泰州基督教堂，始建于清光绪二十八年，位于泰州市区迎春东路185号，市人民医院北院对面，总建筑面积2500多平方米.2017年被认定为省四星级宗教活动场所.小明同学为了估算泰州基督教堂的高度，在人民医院北院内找到一座建筑物AB ，高为()15315m -，在它们之间的地面上的点M （,,B M D 三点共线）处测得楼顶A ，教堂顶C 的仰角分别是15和60，在楼顶A 处测得塔顶C 的仰角为30，则小明估算泰州基督教堂的高度为（）A ．20mB ．30mC ．203mD ．303m【高分突破】一：单选题35．（2021·云南·昆明八中高一阶段练习）若()()3a b c b c a bc +++-=，且sin 2sin cos A B C =，那么ABC 是（）A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰直角三角形36．（2011·河南卫辉·高一期末）若△ABC 的三个内角满足sin A ∶sin B ∶sin C ＝3∶5∶7，则△ABC()A ．一定是锐角三角形B ．一定是直角三角形C ．一定是钝角三角形D ．可能是锐角三角形，也可能是钝角三角形37．（2021·黑龙江·哈尔滨三中高一阶段练习）若O 是ABC 垂心，6A π∠=且sin cos sin cos B C AB C BAC +2sin sin m B C AO =，则m =（）A ．12B ．32C ．33D ．3638．（2021·上海·高一专题练习）已知ABC ∆的三个内角,,A B C 所对的边分别为,,a b c ，满足222cos cos cos A B C -+1sin sin A C =+，且sin sin 1A C +=，则ABC ∆的形状为A ．等边三角形B ．等腰直角三角形C ．顶角为150的等腰三角形D ．顶角为120的等腰三角形39．（2020·辽宁·沈阳二中高一期末）如图，已知OPQ 是半径为1，圆心角为75的扇形，点,,A B C 分别是半径,OP OQ 及扇形弧上的三个动点（不同于,,O P Q 三点）,则ABC ∆周长的最小值是（）A ．612+B ．622+C ．2614+D ．2624+40．（2021·浙江·高一单元测试）如图，在ABC 中，∠BAC =23π，点D 在线段BC 上，AD ⊥AC ，14BD CD =，则sin C =（）A ．714B ．2114C ．77D ．21741．（2021·江苏·扬州中学高一期中）在ABC 中，2cos22B a cc+=（a ，b ，c 分别为角A ，B ，C 的对边），则ABC 的形状为A ．等边三角形B ．直角三角形C ．等腰三角形或直角三角形D ．等腰直角三角形42．（2021·江西·奉新县第一中学高一阶段练习）锐角ABC ∆中，角A 、B 、C 所对的边分别为a 、b 、c ，若220a b ac -+=，则sin sin AB的取值范围是（）A ．20,2⎛⎫ ⎪ ⎪⎝⎭B ．23,22⎛⎫ ⎪ ⎪⎝⎭C ．()2,3D ．32,32⎛⎫⎪ ⎪⎝⎭二、多选题43．（2021·江苏·高邮市第一中学高一阶段练习）在ABC 中，a ，b ，c 分别为A ∠，B Ð，C ∠的对边，下列叙述正确的是（）A ．若sin sin a bB A=，则ABC 为等腰三角形B ．若cos cos a bB A=，则ABC 为等腰三角形C ．若tan A tan tan 0B C ++<，则ABC 为钝角三角形D ．若sin cos a b C c B =+，则4C π∠=44．（2021·河北·沧州市一中高一阶段练习）如图，ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ．若a b =，且()3cos cos 2sin a C c A b B +=，D 是ABC 外一点，1DC =，3DA =，则下列说法正确的是（）A ．ABC 是等边三角形B ．若23AC =，则A ，B ，C ，D 四点共圆C ．四边形ABCD 面积最大值为5332+D ．四边形ABCD 面积最小值为5332-45．（2021·重庆·铜梁一中高一阶段练习）在ABC 中，内角,,A B C 所对的边分别为,,a b c ，3ABC π∠=，ABC ∠的平分线交AC 于点D ，且3BD =，则下列说法正确的是（）A ．ac 的最小值是4B ．ac 的最大值是4C ．3a c +的最小值是323+D ．3a c +的最小值是423+46．（2021·湖北·石首市第一中学高一阶段练习）在ABC 中，若3B π=，角B 的平分线BD 交AC 于D ，且2BD =，则下列说法正确的是（）A ．若BD BC =，则ABC 的面积是332+B ．若BD BC =，则ABC 的外接圆半径是22C ．若BD BC =，则312AD DC +=D ．AB BC +的最小值是833三、填空题47．（2020·安徽省岳西县店前中学高一开学考试）如图，为测量出高MN ，选择A 和另一座山的山顶C 为测量观测点，从A 点测得M 点的仰角060MAN ∠=，C 点的仰角045CAB ∠=以及075MAC ∠=；从C 点测得060MCA ∠=．已知山高100BC m =，则山高MN =__________m ．48．（2021·上海·高一期中）在锐角三角形ABC 中，已知2sin 2A+sin 2B =2sin 2C ，则111tan tan tan A B C++的最小值为___．49．（2020·全国·高一课时练习）如图，四边形ABCD 中，4AB =，5BC =，3CD =，90ABC ∠=︒，120BCD ∠=︒，则AD 的长为______50．（2021·上海·高一期中）在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且sin sin sin sin A C b cB C a--=+，3b =，则ABC 的周长的最大值是___________.51．（2020·吉林·辽源市第五中学校高一期末（理））对于ABC ，有如下命题：()1若sin2sin2A B =，则ABC 一定为等腰三角形．()2若sin sin A B =，则ABC 一定为等腰三角形．()3若222sin sin cos 1A B C ++<，则ABC 一定为钝角三角形．()4若tan tan tan 0A B C ++>，则ABC 一定为锐角三角形．则其中正确命题的序号是______.(把所有正确的命题序号都填上)四、解答题52．（2021·全国·高一单元测试）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知3,2,45a c B ===︒．（1）求sin C 的值；（2）在边BC 上取一点D ，使得4cos 5ADC ∠=-，求tan DAC ∠的值．53．（2021·吉林·汪清县汪清第四中学高一阶段练习）已知ABC ∆的内角分别为,,A B C ，其对应边分别是,,a b c ，且满足cos cos 2cos b C c B a B +=．（Ⅰ）求角B 的大小；（Ⅱ）若3b =，求2a c +的最大值.54．（2021·江苏·吴江汾湖高级中学高一阶段练习）在ABC 中，设角A ，B ，C 的对边长分别为a ，b ，c ，已知sin sin sin A B a cC a b--=+.（1）求角B 的值；（2）若ABC 为锐角三角形，且2c =，求ABC 的面积S 的取值范围.55．（2020·湖北省武昌实验中学高一阶段练习）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2223,3asinC ccosA a c b ac =+=+．()1求A 和B 的大小；()2若M ，N 是边AB 上的点，,43MCN b π∠==，求CMN 的面积的最小值．【答案详解】1．A 【分析】根据正弦定理把已知等式中的边转化为角的正弦，利用两角和公式化简得sin 2sin 2A B =，故22A B =或者22A B π+=，进而可判断出三角形的形状【详解】因为cos sin cos sin b c A B a c B A-=-，由正弦定理可得：sin sin cos sin sin sin cos sin B C A BA CB A -=-，整理可得：sin cos sin cos A A B B =，即sin 2sin 2A B =，所以22A B =或者22A B π+=，所以A B =或2A B π+=，而当2A B π+=时则2C π=，所以三角形ABC 为直角三角形，所以cos c B a ⋅=，则cos sin cos sin b c A Ba c B A-=-中，这时cos 0a c B -⋅=，分母为0无意义所以A B =，故选：A ．2．D 【分析】利用余弦定理将cos a b C =化为2222a b c a b ab+-=⋅，然后化简可得答案.【详解】cos a b C =，由余弦定理可得2222a b c a b ab+-=⋅，则22222a a b c =+-，则222a c b +=，所以ABC 为直角三角形.故选：D 3．B 【分析】利用给定条件结合对数运算可得222sin sin sin B C A =-，再利用正弦定理角化边即可判断得解.【详解】因lg(sin sin )2lgsin lg(sin sin )A C B C A +=--，则有222lg(sin sin )lgsin C A B -=，即有222sin sin sin C A B -=，于是得222sin sin sin C A B =+，在ABC 中，由正弦定理sin sin sin a b cA B C==得：222c a b =+，所以ABC 是直角三角形.故选：B 4．B 【分析】利用正弦定理化()12cos c b A =+转化为()sin sin 12cos C B A =+，根据三角恒等变换与三角形的内角和定理得出A 与B 的关系，化sin sin a A b B=，求出它的取值范围即可.【详解】解：锐角ABC 中，()12cos c b A =+，()sin sin 12cos C B A ∴=+，()sin sin 2cos sin A B B A B ∴+=+，sin cos cos sin sin 2cos sin A B A B B A B ∴+=+，()sin sin A B B ∴-=，A B B ∴-=，即2A B =，若A B B π-+=，则A π=，不符合题意舍去；sin 2sin cos 2cos sin sin a A B B B b B B ∴===，3A B C B C π++=+=，0,2C π⎛⎫∈ ⎪⎝⎭，32B π∴>，又22A B π=<64B ππ∴<<，22cos 3B ∴<<即ab的取值范围是()2,3.故选：B .5．B 【分析】由已知利用三角形的面积公式可求的22cos sin A A =，进而可得1cos 3A =，22sin 3A =，由余弦定理，基本不等式可求6b c +≤，根据三角形的周长即可求解其最大值．【详解】222221()(2cos )sin 222S b c a bc A bc A =-=⨯=+，即22cos sin A A =，又22cos sin 1A A +=，解得1cos 3A =，22sin 3A =，又23a =，由余弦定理可得：()()()()2222222821123333b c bc b c bc b c b c b c =+-=+-+-+=+ ，()236b c ∴+≤，即6b c +≤当且仅当b c =时取等号，则ABC 周长的最大值是623+，故选：B 6．D 【分析】由正弦定理及题意可得C 的值，再由余弦定理得关于边b 的二次方程，由方程有两个正根可求得结果【详解】解：因为cos sin a C c A =，所以由正弦定理得sin cos sin sin A C C A =,因为sin 0A ≠，所以tan 1C =，因为(0,)C π∈，所以4C π=，由余弦定理得，2222cos c a b ab C =+-，由于2c =，所以22220b ab a -+-=，因为满足条件的三角形有2个，所以方程有两个根，所以()2222(2)020a a a ⎧∆=-->⎪⎨⎪->⎩，即2242a a ⎧<⎨>⎩，解得22a <<，故选：D 7．D 【分析】设AB x =，在ABD △中，由余弦定理求得4x =，设ABD α∠=，结合正弦定理求得sin α，得到cos α，进而求得sin 3πα⎛⎫+ ⎪⎝⎭的值，利用三角形的面积公式，即可求解.【详解】在ABD △中，由余弦定理可知22222cos3BD AB AD AB AD π=+-⋅，整理可得22240x x +-=，解得4x =，设ABD α∠=，由正弦定理知2sin sin 3AD BDπα=，解得21sin 14α=，所以57cos 14α=，所以211573321sin sin cos cos sin 33314214214⎛⎫+=+=⨯+⨯= ⎪⎝⎭πππααα，所以11321sin 4276323214ABC S AB BC ⎛⎫=⋅+=⨯⨯⨯= ⎪⎝⎭△πα.故选：D.8．C 【分析】根据题设条件和正弦定理化简得23sin 2sin B B =，求得3B π=，得到3C π=，可判定A 、B正确；由四边形ABCD 面积等于53532sin 2434ABCACDS SADC π∠⎛⎫+=+-≤+ ⎪⎝⎭，可判定D 正确，C 错误．【详解】因为()3acos cos 2sin C c A b B +=，由正弦定理，可得()23sin cos sin cos 2sin A C C A B +=，所以()23sin 2sin A C B +=，即23sin 2sin B B =，因为(0,)B π∈，可得sin 0B >，所以3sin 2B =，解得3B π=，又因为3CAB π∠=，所以3C A B ππ=--=，所以A 、B 正确；由四边形ABCD 面积等于231sin 42ABC ACDS SAC AD DC ADC +=+⋅⋅∠(22312cos )sin 42AD DC AD DC ADC AD DC ADC =+-⋅⋅∠+⋅⋅∠()315353414cos 2sin 2sin 242434ADC ADC ADC π∠∠∠⎛⎫=+-⋅+⨯=+-≤+ ⎪⎝⎭，所以D 正确，C 错误．故选：C.9．B在ADC 中利用余弦定理求得2AD =，在ADB △中由正弦定理可求得AB ．【详解】04575120ADC ∠=︒+︒=，根据余弦定理22202cos120AC AD DC AD DC =+-⋅⋅，260AD AD +-=，2AD =，060ADB ∠=，根据正弦定理00sin 60sin 45AB AD=，则032sin 6026sin 4522AD AB ⨯===．故选：B 10．C 【分析】利用正弦定理、三角恒等变换求得3A π=，利用正弦定理求得31tan c B=+，求出角B 的取值范围，结合三角形的面积公式以及正切函数的基本性质可求得结果.【详解】因为()1cos 3sin c A a C +=，由正弦定理可得()sin 1cos 3sin sin C A A C +=，因为C 为锐角，则sin 0C >，所以，3sin cos 1A A -=，即2sin 16A π⎛⎫-= ⎪⎝⎭，所以，1sin 62A π⎛⎫-= ⎪⎝⎭，02A π<<Q ，663A πππ∴-<-<，则66A ππ-=，3A π∴=，2b =Q ，由正弦定理sin sin b cB C=，则有sin sin sin 3cos 331sin sin sin tan b B b C B B c B B B Bπ⎛⎫+ ⎪+⎝⎭====+，因为ABC 为锐角三角形，则0232B B πππ⎧<<⎪⎪⎨⎪+>⎪⎩，解得62B ππ<<，所以，3tan 3B >，所以，13333sin 1,23222tan 2ABC S bc A c B ⎛⎫⎛⎫===+∈ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭△.故选：C.11．C 【分析】由正弦定理边角关系得2ab bc =，则2a c =，由题设得22202569()994ABCc S--+=，结合二次函数的性质即可求△ABC 面积的最大值.【详解】∵sin 2sin a B b C =，∴由正弦定理得2ab bc =且0b ≠，即2a c =且2b =，∴2242242422025699()10415494016994[4()]42244ABCc c c c c c Sc --+-+---+-=-===，∴2209c =时，△ABC 面积取最大值43．故选：C ．12．D 【分析】先运用正弦定理边角互化得出边之间的关系，再结合余弦定理求出角A ，再用一次余弦定理结合不等式求解三角形面积最值.【详解】由2a =且()()()2sin sin sin b A B c b C +-=-.即()()()sin sin sin a b A B c b C +-=-.由正弦定理得：()()()a b a b c b c +-=-.所以222b c a bc +-=，故2221cos 22b c a A bc +-==，所以60A ∠=︒.则由余弦定理：2222242cos 2a b c bc A b c bc bc bc bc ==+-=+-≥-=.所以，4bc ≤，当且仅当2b c ==时等号成立.所以133sin 43244△==≤⨯=ABC S bc A bc ..故选D.【点睛】方法点睛：已知三角形中一角A 及其对边a 求三角面积最大值时，通常用如下的做法：第一步：由余弦定理，()2222cos 2221a b c bc A bc bccosA bc cosA =+-≥-=-从而()22·1cos a bc A ≤-，当且仅当b c =时等号成立.第二步：()211sin sin 222·1cos △=≤⨯-ABC a S bc A A A ..13．A【分析】先根据条件2223a c ac b +=+可得6B π=，然后把cos sin A C +化为3sin 3A π⎛⎫+ ⎪⎝⎭，结合角A的范围可得cos sin A C +的取值范围.【详解】由2223a c ac b +=+和余弦定理得2223cos 22a cb B ac +-==，又(0,)B π∈，∴6B π=．因为三角形ABC 为锐角三角形，则0202A C ππ⎧<<⎪⎪⎨⎪<<⎪⎩，即025062A A πππ⎧<<⎪⎪⎨⎪<-<⎪⎩，解得32A ππ<<．cos sin cos sin cos sin 66A C A A A A πππ⎛⎫⎛⎫+=+--=++ ⎪ ⎪⎝⎭⎝⎭1333cos cos sin sin cos 3sin22223A A A A A A π⎛⎫=++=+=+ ⎪⎝⎭，∵32A ππ<<，即25336A πππ<+<，所以，13sin 232A π⎛⎫<+<⎪⎝⎭则33cos sin 22A C <+<，因此，cos sin A C +的取值范围是33,22⎛⎫ ⎪ ⎪⎝⎭．故选：A 【点睛】三角形中的范围问题，一般有两个处理思路：（1）把目标式转化为关于边的代数式，结合基本不等式及三角形边长间的关系求解；（2）把目标式转化为单角函数式，结合角的范围求解.14．B 【分析】由余弦定理可求得2b =，再由等面积关系可得23sin ac B=，利用余弦定理结合基本不等式得出2cos 1B ac ≥-，即可求得3sin 32B π⎛⎫+≥ ⎪⎝⎭，再结合B 的范围即可得出结论.【详解】cos cos 2c A a C +=，由余弦定理可得222222222b c a a b c c a bc ab+-+-⋅+⋅=，整理可得2b =，又AC 边上的高为3，所以1123sin 22ac B ⨯⨯=，即23sin ac B=，222222cos 122a c b ac b B ac ac ac+--=≥=-，当且仅当a c =取等号，3cos 1sin 3B B ∴≥-，即3sin 3cos 3B B +≥，即3sin 32B π⎛⎫+≥⎪⎝⎭，()0,B π∈，4,333B πππ⎛⎫∴+∈ ⎪⎝⎭，则2,333B πππ⎛⎤+∈ ⎥⎝⎦，0,3B π⎛⎤∴∈ ⎥⎝⎦，故∠ABC 的最大值为3π.故选：B.【点睛】关键点睛：本题考查余弦定理的应用，解题的关键是等面积关系得23sin ac B=，由基本不等式得2cos 1B ac≥-.15．D 【分析】由给定条件结合正弦定理边化角，求出角C ，再利用正弦定理借助三角函数恒等变换即可作答.【详解】ABC 中，由正弦定理得：cos 22sin sin cos sin B a b A BC c C--==,整理变形得：2sin cos sin cos cos sin sin()sin A C B C B C B C A =+=+=，而sin 0A >，则1cos 2C =，0C π<<，于是得3C π=，则23A B π+=，令3A πθ=+，于是有3B πθ=-，因ABC 为锐角三角形，即66ππθ-<<，由正弦定理得sin 22sin(),sin()sin 3333c A a b C ππθθ==+=-，2222444sin ()sin ()sin()sin()3333333a b ab ππππθθθθ++=++-++-22431313131[(cos sin )(cos sin )(cos sin )(cos sin )]322222222θθθθθθθθ=++-++⋅-2224911(cos sin )(8cos 1)3443θθθ=+=+，而3cos 12θ<≤，则有278cos 19θ<+≤，即271(8cos 1)333θ<+≤，所以22a b ab ++的取值范围为7(,3]3.故选：D 16．B【分析】结合图形由余弦定理可得答案.【详解】设AB x =，则BC x =，33BD x =，在BCD △中，由余弦定理可得2222cos BC BD DC BD DC BDC =+-⋅∠，即22131100210332x x x =+-⨯⨯⨯，整理得2531500x x +-=，解得53x =或103x =-（舍），故选：B.17．C 【分析】由正弦定理可得答案.【详解】由题意可知60,45,40ABC A BC ∠∠===海里，由正弦定理可得sin sin BC ACA ABC=∠，即40sin45sin60AC =，解得206AC =，所以206AC =海里.故选：C.18．B 【分析】根据仰角与俯角概念列式求解.【详解】如图40,,43AB DE ADB BDC ππ==∠=∠=,由题意得这座塔的高为()33404034013AB BC AB BD AB AB +=+=+=+=+，故选：B.19．C 【分析】在直角三角形中表示出,AO BO ，然后由余弦定理求解．【详解】由已知，得3,AO h BO h ==，则在ABO 中，由余弦定理，得2222cos60AB AO BO AO BO =+-⋅⋅，即22240033h h h =+-，得()20m 43h =-.故选：C ．20．C 【分析】在ABC 中，由正弦定理得AC ＝1002m ，再在ADC 中，由正弦定理得解.【详解】由题知，15CAD ∠=︒，45CBD ∠=︒，所以30ACB ∠=︒，135ABC ∠=︒.在ABC 中，由正弦定理得sin 30sin135AB AC=，又100AB =m ，∴AC ＝1002m ．在ADC 中，90ADC θ∠=︒+，50CD =m ，由正弦定理得sin(90)sin15AC CD θ=+，∴()sin15cos sin 9031AC CDθθ⋅=+︒==-.故选：C.21．A 【分析】可由30OAP ∠=︒，1km OP =算得3km OA =,由45OBP ∠=︒，1km OP =算得1km OB =,由行使时间和速度算得AB ，再由余弦定理解出cos AOB ∠.【详解】由题意可得30OAP ∠=︒，45OBP ∠=︒，1km OP =，OP OA ⊥，OP OB ⊥，则3km OA =，1km OB =.因为157.520km 602AB =⨯⨯=，所以由余弦定理可知，222254334cos 2823OA OB AB AOB OA OB -+-∠===-⋅.故选：A.【点睛】解三角形应用题的一般步骤：(1)阅读理解题意，弄清问题的实际背景，明确已知与未知，理清量与量之间的关系．(2)根据题意画出示意图，将实际问题抽象成解三角形问题的模型．(3)根据题意选择正弦定理或余弦定理求解．(4)将三角形问题还原为实际问题，注意实际问题中的有关单位问题、近似计算的要求等.22．（1）23π；（2）(23,23⎤+⎦【分析】（1）由三角函数的平方关系及余弦定理即可得出（2）利用正弦定理、两角和差的正弦公式、三角函数的单调性转化为三角函数求值域即可得出.【详解】（1）由题意知2221sin sin 1sin sin sin A B C A B -=+-+，即222sin sin sin sin sin A B C A B +-=-，由正弦定理得222a b c ab+-=-由余弦定理得2221cos 222a b c ab C ab ab +--===-，又20,3C C ππ<<∴=.（2）32,2sin ,2sin 2sin sin sin sin 3a b c a A b BA B C π====∴==，则ABC ∆的周长()2sin sin 32sin sin 32sin 333L a b c A B A A A ππ⎡⎤⎛⎫⎛⎫=++=++=+-+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.230,,sin 1333323A A A πππππ⎛⎫<<∴<+<∴<+≤ ⎪⎝⎭，232sin 3233A π⎛⎫∴<++≤+ ⎪⎝⎭，ABC ∴∆周长的取值范围是(23,23⎤+⎦.【点睛】本题主要考查了三角函数的平方关系，正余弦定理，两角和差的正弦公式，三角函数的单调性，属于中档题.23．（1）6π；（2）12【分析】（1）在BCD △中，利用正弦定理可求得结果；（2）在BCD △中，由余弦定理可求得4BD =，在ABD △中，3A π∠=，设,AB x AD y ==，由余弦定理得22161cos 22x y A xy -+==，即2216x y xy -+=，利用基本不等式求得()max x y +，进而求出 ABD △周长的最大值.【详解】（1）在BCD △中，7cos 14CBD ∠=-Q ，273sin 1141421CBD ∠⎛⎫∴=--= ⎪ ⎪⎝⎭利用正弦定理得：sin sin CD BCCBD BDC=∠∠，37sin 1142sin 2331BC CBDBDC CD⨯⋅∠∴∠===又CBD ∠为钝角，BDC ∴∠为锐角，6BDC π∴∠=（2）在BCD △中，由余弦定理得22227277cos 2142733BC BD CD BD CBD BC BD ∠++===-⋅⨯--解得：4BD =或5BD =-（舍去）在ABD △中，3A π∠=，设,AB x AD y==由余弦定理得22222161cos 222AB AD D x y A AB B AD xy -+=⋅-+==，即2216x y xy -+=整理得：()2163x y xy +-=，又0,0x y >>利用基本不等式得：()()2231346x y x y xy +=≤-+，即()2416x y +≤，即()264x y +≤，当且仅当4x y ==时，等号成立，即()max 8x y +=，所以()max 8412AB AD BD ++=+=所以 ABD △周长的最大值为12【点睛】方法点睛：本题考查利用正余弦定理解三角形，及利用基本不等式求三角形周长的最值，利用条件最值的求解通常有两种方法：一是消元法，即根据条件建立两个量之间的函数关系，然后代入代数式转化为函数的最值求解；二是将条件灵活变形，利用常数“1”代换的方法构造和或积为常数的式子，然后利用基本不等式求解最值，考查学生的转化能力与运算解能力，属于中档题.24．（1）3B π=；（2）()0,3.【分析】（1）利用正弦定理边角互化，再利用余弦定理求出角B 的大小；（2）利用正弦定理结合三角恒等变换化简2a c -，再由锐角三角形得出C 的范围，进而得出答案．【详解】（1）由已知222sin sin sin sin sin A C B A C +=+，结合正弦定理，得222a c b ac +=+.再由余弦定理，得2221cos 222a cb ac B ac ac +-===，又()0,B π∈，则3B π=.（2）由3B π=，3b =，则由正弦定理，有224sin 2sin 4sin 2sin 3a c A C C Cπ⎛⎫-=-=-- ⎪⎝⎭224sin cos cos sin 2sin 23cos 33C C C Cππ⎛⎫=--= ⎪⎝⎭因为ABC 为锐角三角形，则62C ππ<<，则30cos 2C <<.所以2a c -的取值范围为()0,3.25．D 【分析】设15min 后飞机到了E 处，求出DE ，ABD △中由余弦定理求得BD ，由勾股定理逆定理知90ADB ∠=︒，这样易得,ABD DBC ∠∠，从而得出cos BDC ∠，然后在BDE 中由余弦定理得出BE ．【详解】设15min 后飞机到了E 处，则136090km 4DE =⨯=，由题意60DAB ∠=︒，//DA BC ，60AD =，120AB =，221601202601206032BD =+-⨯⨯⨯=，所以222AD BD AB +=，所以90DB ∠=︒，从而30ABD ∠=︒，于是90DBC ∠=︒2222(603)(6013)240DC BD BC =+=+=，6033cos 2404BD BDC CD ∠===，DBE 中，2222232cos (603)90260390360034BE BD DE BD DE BDE =+-⋅∠=+-⨯⨯⨯=⨯，603BE =．故选：D ．26．C 【分析】由条件解BCD △求BD ，在ACD △中利用正弦定理解求AD ，在ABD △中利用余弦定理求AB ，由此可得A ，B 两亭子间的距离.【详解】由题意，可得3010545ACD ADC BDC ∠︒=∠︒=∠=︒，，，∴45,60DAC ADB ∠∠=︒=︒．在等腰直角BCD △中，100CD =∴100BC =，1002BD =．在ACD △中，由正弦定理得100sin 45sin 30AD=︒︒，解得502AD =．连接AB ．在ABD △中，由余弦定理可得2222cos 6015000AB AD BD AD BD =+-⋅=︒，解得506AB =，即A 、B 两个亭子之间的距离为506米．故选：C.27．A 【分析】分析出POA 、POB 均为直角三角形，求出OA 、OB 的长，计算出AB 的长，再利用余弦定理可求得cos AOB ∠的值.【详解】由题意，得PO ⊥平面AOB ，AO 、BO ⊂平面AOB ，故PO AO ⊥，PO BO ⊥，所以，POA 、POB 均为直角三角形，且30PAO ∠=，45PBO ∠=，由1PO =，可得1OB =，3tan 30POOA ==．因为7.520 2.560AB =⨯=，所以22231 6.2533cos 28213OA OB AB AOB OA OB +-+-∠===-⋅⨯⨯．故选：A ．28．C 【分析】构造三角形运用正弦定理求解三角形即可得出结果.【详解】如图，SE AB ⊥ASB ，中，135ABS ∠=︒，324184AB =⨯=，15BAS ∠=︒，18030ASB ABS SAB ∠=︒-∠-∠=︒，由正弦定理得sin sin AS ABABS ASB=∠∠sin135182sin 30AB AS ︒∴==︒()n mile ，所以船与S 岛的最近距离：()()1cos30·sin 182sin15182931n mile 2SE SA SAB -︒=∠=︒=⨯=-故选：C.29．C 【分析】先在Rt MAC 中求得CM ，Rt BCN 中求得CN ，再在MNC 中利用余弦定理求MN 即可.【详解】依题意，在Rt MAC 中，60m AC =，3tan 4MCA ∠=，3tan 604AM AM MCA AC ∠===，可得45m AM =，则2222456075CM AM AC =+=+=，在Rt BCN 中，703m BC =，14cos 15NCB ∠=，则70375314cos 15BC CN NCB===∠，又MNC 中，150MCN ∠=，由余弦定理可得：则222cos MN CM CN CM CN MCN =+-⋅⋅∠()2275753275753cos150757=+-⨯⨯=.故塔尖MN 之间的距离为757m .故选：C.30．C 【分析】要求树的高度，需求PB 的长度，要求PB 的长度，在PAB △中利用正弦定理可得.【详解】解：在PAB △中，30,15,60,PAB APB AB ∠=∠==又()232162sin15sin 4530sin 45cos 30cos 45sin 302222-=-=-=⨯-⨯=４由正弦定理得：sin 30sin15PB AB=，()60130622624PB ∴=⨯=+-∴树的高度为()()2sin 453062303302PB m =+⨯=+31．B【分析】作出平面示意图：244PCO PBO PAO θ∠=∠=∠=且600,2003AB BC ==，应用余弦定理求cos 2θ，进而求sin 4θ，即可求该山峰的高度PO .【详解】由题设，若244PCO PBO PAO θ∠=∠=∠=且600,2003AB BC ==，∴600,2003PB AB PC BC ====，∴由余弦定理知：2223cos 222PB BC PC PB BC θ+-==⋅，又022πθ<<，∴1sin 22θ=，则3sin 42cos 2sin 22θθθ==，∴该山峰的高度sin 4300PO PC θ=⋅=米.故选：B32．B【分析】根据题意在ABD △中根据余弦定理即可求解.【详解】解：由题意知：D 为气球C 在过AB 且与地面平行的平面上的正投影，设CD x =米，45,30CAD CBD ∠=︒∠=︒，则AD x =米，3BD =米，在ABD △中，由余弦定理得：2222cos AB AD BD AD BD ADB =+-∠，即2222662(3)(3)··cos150x x x x =+-︒，解得：26677x =，故测量时气球到地面的距离是2667(1)7+米．33．D【分析】利用降次公式、余弦定理化简已知条件，由此确定正确选项.【详解】依题意2sin 22C a b a -=，即1cos 1222C b a-=-，所以cos bC a =，由余弦定理得2222a b c b ab a+-=，化简得222a b c =+，所以三角形ABC 是直角三角形.故选：D34．D【分析】在Rt ABM 求出AM ，在ACM △中利用正弦定理求出CM ，在Rt CDM △即可求得CD .【详解】在Rt ABM 中，sin15AB AM=，()232162sin15sin 453022224-=-=⨯-⨯=，所以153302sin1562415AB AM ==--=，在ACM △中，301545CAM ∠=+=，1801560105AMC ∠=--=，1804510530ACM ∠=--=，由正弦定理可得sin sin AM CM ACM CAM =∠∠即302sin 30sin 45CM =，所以2302302sin 452601sin 302CM ⨯===，在Rt CDM △中，3sin 60603032CD CM ==⨯=，所以估算泰州基督教堂的高度为303m ，故选：D.35．B。

(完整word版)高中数学高考总复习正弦定理与余弦定理应用举例习题及详解

高考总复习高中数学高考总复习正弦定理与余弦定理应用举例习题及详解、选择题1. （2010广东六校）两座灯塔A 和B 与海洋观察站=a 2 + a 2 — 2 a 2 — 2 = 3a 2••AB = .'3a.故选 D.［答案］A［解析］在△ABC 中，若sinA 〉*3」U/A>n 反之/ A>3时，不一定有sinA>¥，如5n ・n 丄,sinA sin sin^ o .6 6 2 （理）在厶ABC 中，角A 、B 所对的边长为 a 、b ,贝厂'a = b ”是“ acosA = bcosB ”的（A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件［答案］A［解析］当a = b 时，A = B ,•'acosA = bcosB ;当 acosA = bcosB 时,由正弦定理得C 的距离都等于akm ,灯塔A 在观察40°则灯塔 A 与灯塔B 的距离为 )km.( ) A . a B. ,'2aC . 2a D.'3a［答案］D［解析］依题意得/ ACB = 120 °.由余弦定理AC 2+ BC 2— AB 2cos120 = ------- 2AC BC••AB 2 = AC 2+ BC 2— 2AC BCcos1202.（文）（2010广东佛山顺德区质检）在厶ABC 中, “ sin A>宁” 是“/ A>n 的(A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件站C 的北偏东20°灯塔B 在观察站 C 的南偏东( OsinA cosA= sinB c osB,（理）（2010河北邯郸）在厶ABC 中，sin 2A + cos 2B = 1,贝U cosA + cosB + cosC 的最大值为（）A.5B. .'24•'si n2A = si n2B ,：2A = 2B 或 2A = n — 2B ,亠 n• A = B 或 A + B = 2则 a = b 或 a 2+ b 2= c 2.所以 “ a = b ” ? "acosA = bcosB ” ,“ acosA = bcosB ” ? / “ a = b ”，故选 A.3.已知A 、B 两地的距离为10km , B 、C 两地的距离为20km ，观测得/ ABC = 120 ° 则AC 两地的距离为（A . 10kmC . 10 .'5km［答案］D B. .'3km D . 10.； 7km［解析］如图，A ABC 中，AB = 10, BC = 20,Z B = 120 °由余弦定理得, =102+ 202 — 2 X 10X 20X 1 —2 =700,nA c — b 4.（文）在厶 ABC 中，sin 2^ =_2^（a 、b 、c 分别为角 A 、B 、C 的对应边），则△ ABC 的形状为（A •正三角形C .等腰直角三角形［答案］BB .直角三角形 D .等腰三角形 A 1 — cosA c — b b［解析］si 门号= 2 = ，：cosA = ^,b 2+c 2— a 22bc b2= c 2,故选 B.D*3 C. 1［答案］D ［解析］ Tsin 2A + COS 2B = 1,「.sin 2A = sin 2B , •.0<A , B< n -^si nA = sinB ,「.A = B. 故 cosA + cosB + COS C = 2COS A — COS 2A n 1 3 ••0<A<2，.・.O<COS A<1,.・.COS A = 2■时，取得最大值㊁. 5. （文）（2010广东汕头一中）已知△ ABC 的外接圆半径为 R ,角A 、B 、C 的对边分别为 a 、b 、c ,且 2R （sin 2A — sin 2C ）= （ .2a — b ）sinB ，那么角 C 的大小为（） n n A .§ B .2 n 2 n C ・4 ［答案］C ［解析］由正弦定理得，a 2— C 2= ,2ab — b 2, a 2 + b 2— C 2 迈 ©SC = 2ab =h ， '•0< C< n, —C =4. 1 （理）已知a 、b 、C 是厶ABC 三内角 A 、B 、C 的对边，且 A 为锐角，若sin 2A — COS 2A = ?, 则（） A . b + c<2a B . b + C < 2a C . b + C = 2a D . b + C >2a ［答案］B 2 2 1 1 ［解析］Tsin 2A — COS 2A = 2，—COS 2A =— ?, 又 A 为锐角，••• A = 60 ° —B + C = 120； B + C B — C b + C sinB + sinC 2sin 2 cos 2 …2a = 2sinA = 3 B — C =cos~2~ w 1 ,—b + c w 2a.=—2COS 2A + 2COS A + 1 = 1 2 3 2（COS A — ^）2 + 2,6. （2010北京顺义一中月考）在厶ABC中，已知COS A=寺，sinB = 5,则cosC的值为（）16A .65［答案］A5 12 3 ［解析］TcosA = 13，「.sinA =石电=sinB ,「.A>B ,16 cos(A + B) = sinAsi nB — cosAcosB =亦. ［点评］在△ABC 中，有 sinA>sinB? A>B. 7. 在地面上一点D 测得一电视塔尖的仰角为 45 °再向塔底方向前进100m ，又测得塔尖的仰角为60°，则此电视塔高约为 __________ m .（） A . 237 B . 227 C . 247 D . 257 ［答案］A ［解析］如图，/ D = 45° Z ACB = 60° DC = 100,/DAC = 15° 100 sin45 °in60 sin15 ° 100xg x 宁 ——-一-—〜237. •••选 A. ,6 —■ 2 n & （文）（2010青岛市质检）在厶ABC 中，/ B = 3，三边长a 、b 、c 成等差数列，且 ac = 6,则b 的值是（） A. '2 B. .'3 C. ；5 D. .'6 ［答案］ D ［解析］由条件2b = a + c , •4b 2 = a 2 + c 2 + 2ac = a 2 + c 2 + 12,56 B .65 16卡 56C.65或 65D . 16 65 ••SinB = 35, •••cosB = 4, 5 • cosC = cos ［ -n(A + B)］ ••AC = DC sin45 sin15 ° •'AB = AC s in60 又 cosB = a 2+ c 2- b 2 2ac ， 1 a 2+ c 2- b 2 2 = 12•'a2+ c2= 6+ b2,••4b 2= 18+ b 2,「.b = .6 （理）△ ABC 的内角A 、B 、C 的对边分别为 a 、b 、c.若a 、b 、c 成等比数列，且 c = 2a , 则 cosB =（） 1 3 A.4 B .4 C 亚 D 迟 C. 4 D. 3 ［答案］B ［解析］ "、b 、c 成等比数列，••• b 2= ac ,又T c = 2a , a 2+ c 2— b 2 a 2 + 4a 2— 2a 2 3 = 2（,.・.cosB = —莎一= 2a x 2a = 4. ［点评］在知识的交汇处命题是高考命题的基本原则•本题融数列与三角函数于一体，集中考查正弦定理、余弦定理、等比数列等基础知识•同时也体现了数列、三角函数等内容是高考中的热点问题，复习时要注意强化. 9.如图所示的曲线是以锐角△ ABC 的顶点B 、C 为焦点，且经过点 A 的双曲线，若△ csinA "v 3 ABC 的内角的对边分别为 a 、b 、c ,且a = 4, b = 6, ,则此双曲线的离心率为（） C . 3— ,7 ［答案］DD . 3+ .7B^于？孟=:=淤？sinC弋，因为C为锐角，所以C= n，2由余弦定理知c2= a2+ b2—2abcosC= 42+ 62—2 x 4X 6X 十=28,：c= 2,7e= =b —c 6—2X2 y2、10. （文）（2010山东济南）设F1、F2是双曲线申一器=1（a>0, b>0）的两个焦点，P在双曲线上，若P ?1 P F 2= 0, |P F 1||P F 2|= 2ac （c 为半焦距），则双曲线的离心率为（） 3 + 1 BP 5+ 1 D r ［答案］D ［解析］由条件知，|PF i |2+ |PF 2|2= |F i F 2|2，根据双曲线定义得： 4a 2= （|PF i |— |PF 2|）2 = |PF i |2+ |PF 2|2 — 2|PF i | |PF 2|= |F I F 2|2— 4ac = 4c 2 — 4ac , •*a 2+ ac — c 2= 0,「・1 + e — e 2= 0, V 5+1 e>1, .e = (理)(2010 安徽安庆联考)如图，在△ ABC 中,tanC = AH BC = 0, AB (CA + CB )= 0, 经过点B 以A 、H 为两焦点的双曲线的离心率为（） c C 1 叫 4 AH 1，A ta nC = 2C =3=AH ， 1 — tan ；A 4 2 C . 2 B. .5 — 1C. 5 + 1 5— 1 D h ［答［解••AH BC = 0 ,「.AH 丄 BC , ••tanC又T AB(CA+ CB)= 0, :.CA = CB ,.anB= tan 180—C = cotC = 2= AH,2 2 BH'3设BH = x,贝U AH = 2x,「.CH = AB = . 5x，由条件知双曲线中2C = AH = 2x,2a= AB—BH = ( ；5 — 1)x ,二、填空题 11. 如图，为了测定河的宽度，在一岸边选定两点 A , B 和对岸标记物C ,测得/ CAB =30° / CBA = 45° AB = 120米，则河的宽度为 ____________ 米.［答案］60( ,'3 — 1) ［解析］过 C 点作 CD 丄 AB 于 D ，设 BD = X ,贝U CD = x , AD = 120 — x ,又T /CAB = 30 ° 12. （2010福建三明一中）如图，海岸线上有相距 5海里的两座灯塔 A , B ，灯塔B 位于灯塔A 的正南方向•海上停泊着两艘轮船，甲船位于灯塔 A 的北偏西75°方向，与A 相距 3 ,'2海里的D 处；乙船位于灯塔B 的北偏西60。

高考数学总复习(人教版)：4-6正弦定理和余弦定理

4-6正弦定理和余弦定理基础巩固强化1.(文)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，如果c ＝3a ，B ＝30°，那么角C 等于( )A ．120°B ．105°C ．90°D ．75°[答案] A[解析] ∵c ＝3a ，∴sin C ＝3sin A ＝3sin(180°－30°－C )＝3sin(30°＋C )＝3⎝ ⎛⎭⎪⎫32sin C ＋12cos C ＝32sin C ＋32cos C ，即sin C ＝－3cos C ，∴tan C ＝－ 3.又C ∈(0°，180°)，∴C ＝120°.故选A.(理)(2011·郑州六校质量检测)△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若cb <cos A ，则△ABC 为( )A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等边三角形[答案] A[解析] 依题意得sin Csin B <cos A ，sin C <sin B cos A ，所以sin(A ＋B )<sin B cos A ，即sin B cos A ＋cos B sin A －sin B cos A <0，所以cos B sin A <0.又sin A >0，于是有cos B <0，B 为钝角，△ABC 是钝角三角形，选A.2．(文)(2011·湖北八校联考)若满足条件C ＝60°，AB ＝3，BC ＝a 的△ABC 有两个，那么a 的取值范围是( )A ．(1，2)B ．(2，3)C ．(3，2)D ．(1,2)[答案] C[解析] 由条件知，a sin60°<3<a ，∴3<a <2.(理)在△ABC 中，角A 、B 、C 的对边分别是a 、b 、c ，若a ＝2，b ＝22，且三角形有两解，则角A 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，π4 B.⎝ ⎛⎭⎪⎫π4，π2 C.⎝ ⎛⎭⎪⎫π4，3π4 D.⎝ ⎛⎭⎪⎫π4，π3 [答案] A[解析] 由条件知b sin A <a ，即22sin A <2，∴sin A <22， ∵a <b ，∴A <B ，∴A 为锐角，∴0<A <π4.3．(2011·福建质检)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若a ＝1，c ＝42，B ＝45°，则sin C 等于( )A.441B.45C.425D.44141[答案] B[解析] 依题意得b ＝a 2＋c 2－2ac cos B ＝5，又c sin C ＝b sin B ，所以sin C ＝c sin B b ＝42sin45°5＝45，选B. 4．(2012·天津理，6)在△ABC 中，内角A 、B 、C 所对的边分别是a 、b 、c ，已知8b ＝5c ，C ＝2B ，则cos C ＝( )A.725 B ．－725 C ．±725 D.2425[答案] A[解析] 由b sin B ＝csin C 及8b ＝5c ，C ＝2B 得，5sin2B ＝8sin B ，∴cos B ＝45，∴cos C ＝cos2B ＝2cos 2B －1＝725.5．(2011·辽宁理，4)△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，a sin A sin B ＋b cos 2A ＝2a ，则ba ＝( )A ．2 3B ．2 2 C. 3 D. 2 [答案] D[解析] ∵a sin A sin B ＋b cos 2A ＝2a ， ∴sin 2A sin B ＋sin B cos 2A ＝2sin A ， ∴sin B ＝2sin A ，∴b ＝2a ，∴ba ＝ 2.6．(文)在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ，若a 2－b 2＝3bc ，sin C ＝23sin B ，则A ＝( )A ．30°B ．60°C ．120°D ．150°[答案] A[解析] 由余弦定理得：cos A ＝b 2＋c 2－a 22bc ，由题知b 2－a 2＝－3bc ，c 2＝23bc ，则cos A ＝32，又A ∈(0°，180°)，∴A ＝30°，故选A.(理)△ABC 中，a 、b 、c 分别为∠A 、∠B 、∠C 的对边，如果a 、b 、c 成等差数列，∠B ＝30°，△ABC 的面积为0.5，那么b 为( )A ．1＋ 3B ．3＋ 3 C.3＋33 D ．2＋ 3[答案] C[解析] 12ac sin B ＝12，∴ac ＝2，又2b ＝a ＋c ，∴a 2＋c 2＝4b 2－4，由余弦定理b 2＝a 2＋c 2－2ac cos B 得，b ＝3＋33.7．在直角坐标系xOy 中，已知△ABC 的顶点A (－1,0)，C (1,0)，顶点B 在椭圆x 24＋y 23＝1上，则sin A ＋sin C sin B 的值为________．[答案] 2[解析] 由题意知△ABC 中，AC ＝2，BA ＋BC ＝4，由正弦定理得sin A ＋sin C sin B ＝BC ＋BAAC ＝2.8．(2011·广州一测)△ABC 的三个内角A 、B 、C 所对边的长分别为a 、b 、c ，已知c ＝3，C ＝π3，a ＝2b ，则b 的值为________．[答案]3[解析] 依题意及余弦定理得c 2＝a 2＋b 2－2ab cos C ，即9＝(2b )2＋b 2－2×2b ×b cos π3，解得b 2＝3，∴b ＝ 3.9．(文)(2012·石家庄质检)在△ABC 中，∠A ＝60°，BC ＝2，AC ＝263，则∠B ＝________.[答案] 45°[解析] 利用正弦定理可知：BC sin A ＝AC sin B ，即2sin60°＝263sin B ，∴sin B ＝22，∵2>263，∴BC >AC ，∴∠A >∠B ，∴∠B ＝45°.(理)(2012·北京西城区期末)在△ABC 中，三个内角A 、B 、C 的对边分别为a 、b 、c .若b ＝5，B ＝π4，tan C ＝2，则c ＝________.[答案] 2 2[解析]⎭⎪⎬⎪⎫sin 2C ＋cos 2C ＝1tan C ＝2⇒sin Ccos C ＝2⇒sin 2C ＝45⇒sin C ＝255.由正弦定理，得b sin B ＝c sin C ，∴c ＝sin Csin B ×b ＝2 2.10．(2012·河南商丘模拟)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且b cos C ＝(3a －c )cos B .(1)求cos B 的值；(2)若BA →·BC →＝2，且b ＝22，求a 和c 的值．[解析] (1)由正弦定理得，sin B cos C ＝3sin A cos B －sin C cos B ， ∴sin(B ＋C )＝3sin A cos B ，可得sin A ＝3sin A cos B . 又sin A ≠0，∴cos B ＝13.(2)由BA →·BC →＝2，可得ac cos B ＝2. 又cos B ＝13，∴ac ＝6.由b 2＝a 2＋c 2－2ac cos B ，及b ＝22，可得a 2＋c 2＝12，∴(a －c )2＝0，即a ＝c . ∴a ＝c ＝ 6.[点评] 本题主要考查正、余弦定理及三角运算等基础知识，同时考查运算求解能力.能力拓展提升11.(文)(2011·泉州质检)△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ，且a cos C ，b cos B ，c cos A 成等差数列，则角B 等于( )A ．30°B ．60°C ．90°D ．120°[答案] B[解析] 依题意得a cos C ＋c cos A ＝2b cos B ，根据正弦定理得，sin A cos C ＋sin C cos A ＝2sin B cos B ，则sin(A ＋C )＝2sin B cos B ，即sin B＝2sin B cos B ，又0°<B <180°，所以cos B ＝12，所以B ＝60°，选B.(理)在△ABC 中，内角A 、B 、C 对边的长度分别是a 、b 、c ，已知c ＝2，C ＝π3，△ABC 的面积等于3，则a 、b 的值分别为( )A ．a ＝1，b ＝4B ．a ＝4，b ＝1C ．a ＝4，b ＝4D ．a ＝2，b ＝2[答案] D[解析] 由余弦定理得，a 2＋b 2－ab ＝4，又因为△ABC 的面积等于3，所以12ab sin C ＝3，∴ab ＝4.联立⎩⎨⎧a 2＋b 2－ab ＝4，ab ＝4.解得a ＝2，b ＝2.12.(2011·天津理，6)如图，在△ABC 中，D 是边AC 上的点，且AB ＝AD,2AB ＝3BD ，BC ＝2BD ，则sin C 的值为( )A.33B.36C.63D.66[答案] D[解析] 如图，根据条件，设BD ＝2，则AB ＝3＝AD ，BC ＝4. 在△ABC 中，由正弦定理得3sin C ＝4sin A ，在△ABD 中，由余弦定理得， cos A ＝3＋3－42×3×3＝13，∴sin A ＝223，∴sin C ＝3sin A 4＝3×2234＝66，故选D. 13．(文)(2011·济南外国语学校质检)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若a ＝2，b ＝2，sin B ＋cos B ＝2，则∠A 的大小为________．[答案] π6[解析] ∵sin B ＋cos B ＝2sin(B ＋π4)＝2， ∴sin(B ＋π4)＝1， ∵0<B <π，∴B ＝π4，∵b sin B ＝a sin A ，∴sin A ＝a sin B b ＝2×222＝12， ∵a <b ，∴A <B ，∴A ＝π6.(理)(2011·河南质量调研)在△ABC 中，角A 、B 、C 所对应的边分别为a 、b 、c ，且满足cos A 2＝255，AB →·AC →＝3，则△ABC 的面积为________．[答案] 2[解析] 依题意得cos A ＝2cos 2A 2－1＝35，∴sin A ＝1－cos 2A ＝45，∵AB →·AC →＝AB ·AC ·cos A ＝3，∴AB ·AC ＝5，∴△ABC 的面积S ＝12AB ·AC ·sin A ＝2.14．(2011·安阳月考)在△ABC 中，C ＝60°，a 、b 、c 分别为A 、B 、C 的对边，则a b ＋c ＋b c ＋a＝________.[答案] 1[解析] ∵C ＝60°，∴a 2＋b 2－c 2＝ab ， ∴(a 2＋ac )＋(b 2＋bc )＝(b ＋c )(a ＋c )， ∴a b ＋c ＋b a ＋c＝1. 15．(2012·天津文，16)在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c .已知a ＝2，c ＝2，cos A ＝－24.(1)求sin C 和b 的值；(2)求cos(2A ＋π3)的值．[分析] (1)由cos A ＝－24及0<A <π，sin 2A ＋cos 2A ＝1可求sin A ，再由正弦定理求sin C ，由余弦定理a 2＝b 2＋c 2－2bc cos A ，可求b 的值．(2)由(1)知道sin A ，cos A ，用正弦、余弦二倍角公式求sin2A ，cos2A ，展开cos(2A ＋π3)代入即可．[解析] (1)在△ABC 中，由cos A ＝－24，可得sin A ＝144.又由a sin A ＝c sin C 及a ＝2，c ＝2，可得sin C ＝74. 由a 2＝b 2＋c 2－2bc cos A ，得b 2＋b －2＝0，因为b >0，故解得b ＝1. 所以sin C ＝74，b ＝1.(2)由cos A ＝－24，sin A ＝144得， cos2A ＝2cos 2A －1＝－34，sin2A ＝2sin A cos A ＝－74.所以，cos(2A ＋π3)＝cos2A cos π3－sin2A sin π3 ＝－3＋218.[点评] 本题主要考查同角三角函数的基本关系、二倍角的正弦与余弦关系、两角和的余弦公式以及正弦定理、余弦定理等基础知识．考查基本运算求解能力．16．(文)在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，向量m ＝(2sin B ，－3)，n ＝(cos2B,2cos 2B 2－1)且m ∥n . (1)求锐角B 的大小；(2)如果b ＝2，求△ABC 的面积S △ABC 的最大值．[分析] (1)问利用平行向量的坐标表示将向量知识转化为三角函数，利用三角恒等变换知识解决；(2)问利用余弦定理与基本不等式结合三角形面积公式解决．[解析] (1)∵m ∥n ，∴2sin B ⎝ ⎛⎭⎪⎫2cos 2B 2－1＝－3cos2B ， ∴sin2B ＝－3cos2B ，即tan2B ＝－3，又∵B 为锐角，∴2B ∈(0，π)，∴2B ＝2π3，∴B ＝π3.(2)∵B ＝π3，b ＝2，∴由余弦定理cos B ＝a 2＋c 2－b 22ac 得，a 2＋c 2－ac －4＝0，又∵a 2＋c 2≥2ac ，∴ac ≤4(当且仅当a ＝c ＝2时等号成立)，S △ABC ＝12ac sin B ＝34ac ≤3(当且仅当a ＝c ＝2时等号成立)．[点评] 本题将三角函数、向量与解三角形有机的结合在一起，题目新颖精巧，难度也不大，即符合在知识“交汇点”处命题，又能加强对双基的考查，特别是向量的坐标表示及运算，大大简化了向量的关系的运算，该类问题的解题思路通常是将向量的关系用坐标运算后转化为三角函数问题，然后用三角函数基本公式结合正、余弦定理求解．(理)已知A 、B 、C 分别为△ABC 的三边a 、b 、c 所对的角，向量m ＝(sin A ，sin B )，n ＝(cos B ，cos A )，且m ·n ＝sin2C .(1)求角C 的大小；(2)若sin A 、sin C 、sin B 成等差数列，且CA →·(AB →－AC →)＝18，求边c 的长．[解析] (1)m ·n ＝sin A ·cos B ＋sin B ·cos A ＝sin(A ＋B )．在△ABC 中，由于sin(A ＋B )＝sin C .∴m ·n ＝sin C .又∵m ·n ＝sin2C ，∴sin2C ＝sin C ，∴2sin C cos C ＝sin C .又sin C ≠0，所以cos C ＝12.而0<C <π，因此C ＝π3.(2)由sin A ，sin C ，sin B 成等差数列得，2sin C ＝sin A ＋sin B ，由正弦定理得，2c ＝a ＋b .∵CA →·(AB →－AC →)＝18，∴CA →·CB →＝18.即ab cos C ＝18，由(1)知，cos C ＝12，所以ab ＝36.由余弦定理得，c 2＝a 2＋b 2－2ab cos C ＝(a ＋b )2－3ab .∴c 2＝4c 2－3×36，∴c 2＝36.∴c ＝6.。

2024版高考数学总复习：正弦定理余弦定理及应用课件

4
2
.化简得BC2 ＋
1
3．若△ABC的两边长分别为2，3，其夹角的余弦值为，则△ABC
3
外接圆的半径为_________．
(1)A＋B＋C＝π.
(2)在三角形中大边对大角，大角对大边．
(3)任意两边之和大于第三边，任意两边之差小于第三边．
(4)sin (A＋B)＝sin C；cos (A＋B)＝－cos C；tan (A＋B)＝－tan C；
sin
+

+

＝cos ；cos
＝sin .
2
2
2
2
(5)tan A＋tan B＋tan C＝tan A·tan B·tan C.
余弦值．
二、基本技能·思想·活动经验
1．判断下列说法的正误，对的画“√”，错的画“×”．
(1)在三角形中，已知两角和一边或已知两边和一角都能解三角形．
( √ )

++
(2)在△ABC中，
＝
.
sin sin +sin +sin
( √ )
(3)在△ABC中，“a2 ＋b2>c2”是“△ABC为锐角三角形”的必要不
＝0，
则cos A＝0或sin B＝sin
π
A，所以A＝或B＝A.
2
1
2
3
4
5
3．在△ABC中，a＝3，b＝5，sin
1
A．
5
C．
B
1
A＝，则sin
3
B＝(
)
5
B．
9
5
3
D．1

3
5

高中数学高考总复习正弦定理与余弦定理应用举例习题及详解(2021年整理)

(完整版)高中数学高考总复习正弦定理与余弦定理应用举例习题及详解(word 版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)高中数学高考总复习正弦定理与余弦定理应用举例习题及详解(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)高中数学高考总复习正弦定理与余弦定理应用举例习题及详解(word版可编辑修改)的全部内容。

高中数学高考总复习正弦定理与余弦定理应用举例习题及详解一、选择题1．(2010·广东六校)两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为( )km。

( ）A．a B.错误!aC．2a D。

错误!a[答案] D[解析］依题意得∠ACB＝120°.由余弦定理cos120°＝错误!∴AB2＝AC2＋BC2－2AC·BC cos120°＝a2＋a2－2a2错误!＝3a2∴AB＝错误!a.故选D.2．(文）(2010·广东佛山顺德区质检)在△ABC中,“sin A〉错误!”是“∠A>错误!”的（)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件[答案] A［解析] 在△ABC中，若sin A〉错误!，则∠A>错误!，反之∠A>错误!时,不一定有sin A>错误!，如A＝错误!时，sin A＝sin错误!＝sin错误!＝错误!。

(理）在△ABC中，角A、B所对的边长为a、b，则“a＝b"是“a cos A＝b cos B”的( ) A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件［答案] A［解析] 当a＝b时，A＝B，∴a cos A＝b cos B;当a cos A＝b cos B时，由正弦定理得sin A·cos A＝sin B·cos B,∴sin2A＝sin2B，∴2A＝2B或2A＝π－2B，∴A＝B或A＋B＝错误!.则a＝b或a2＋b2＝c2.所以“a＝b”⇒“a cos A＝b cos B”,“a cos A＝b cos B"⇒/ “a＝b”，故选A。

完整word版高中数学高考总复习正弦定理与余弦定理应用举例习题及详解

高考总复习高中数学高考总复习正弦定理与余弦定理应用举例习题及详解一、选择题在观察，灯塔A与海洋观察站C(2010·广东六校的距离都等于)a两座灯塔km A和1B．的距离为A与灯塔B在观察站C的南偏东40°，则灯塔站C的北偏东20°，灯塔B)()km.( B.2a A．aD.3 a C．2aD答案][. ＝120°][解析依题意得∠ACB由余弦定理ABBC－＋222AC＝cos120°BC·2AC AC·BC cos120°－∴AB＝AC＋BC22221??－a2＝＝3aa＋a－2222??2D.故选＝∴AB3a.π3”是“∠A>”的(sin(2．文)(2010·广东佛山顺德区质检)在△ABC中，“A>) 23B．必要不充分条件．充分不必要条件AD．既不充分也不必要条件C．充要条件A[答案]ππ33，则∠A>，反之∠A>时，不一定有sin A>，如A＝>[解析A中，若在△ABC sin]2332π5π5π1＝sinsin A时，sin＝＝. 2666) ”的cos bB(＝cos”是“＝则“baBA中，在△理()ABC角、所对的边长为、，abaA．必要不充分条件．充分不必要条件A B D C．充要条件．既不充分也不必要条件A]答案[ ＝A时，＝当]解析[abB，cos＝A cos∴abB；＝cos a当A cos bB时，由正弦定理得A·A sincos·B sin＝B cos，含详解答案．高考总复习AB＝，∴sin2sin2 2B，或2A∴2＝Aπ＝－2Bπ＝A＋B∴A＝B或.2c＋b＝则a＝b或a222.B”，cos A＝b cos所以“a＝b”?“a A.”，故选/ “a＝ba“cos A＝b cos B”?，＝120°C两地的距离为20km，观测得∠ABC．已知A、B两地的距离为10km，B、3)则AC两地的距离为(3km B. A．10km7km5km ．10 DC．10D][答案，由余弦定120°ABC[解析]如图，△中，AB＝10，BC＝20，∠B＝理得，＝AB＋BC－2AB·BC·cos120°222AC1??－×10××2010，＝＋20－2＝70022??2D.∴选＝107km.∴ACbc－A2的ABCB、C的对应边)，则△在△4．(文)ABC中，sin、＝(ab、c分别为角A、c22)形状为(B ．直角三角形．正三角形AC．等腰直角三角形D．等腰三角形B [答案]b－cos Ac1－bA＝cos A，＝＝，∴2sin[解析]c22c2a＋c－222bb B.c，故选，∴a＋b＝∴＝222c2bc22的最大值为cos C＋，则cos A＋cos B中，河北邯郸(理)(2010·)在△ABC sin＋A cos＝B1)(5 2 A. B.43 1 D. ．C2含详解答案．高考总复习D答案][2222，∴sin BA＝sin[解析]∵sin A＋cos，B＝1. ＝B sin A＝sin B，∴A∵0<A，B<π，∴cos2A cos C ＝2cos A－故cos A＋cos B＋31 ，＋＝－2cos22)2(cos A－1A＋2cos A＋＝－22π31时，取得最大值＝0<cos A<1，∴cos A∵0<A<，∴.222的对边分别为C，角A、B、5．(文)(2010·广东汕头一中)已知△ABC的外接圆半径为R22) ，那么角C的大小为()＝(2a－b)sin a、b、c，且2R(sin－A sin BCππ B. A. 232ππ C. D. 34C[答案] ，2ab－－cb＝222a][解析由正弦定理得，c－＋b222a2 ，cos C＝＝∴22ab π＝，∴C0<C<π∵.4122，cos＝A为锐角，若sin AA－Ba、b、c是△ABC三内角A、、C的对边，且(理)已知2)则(B．b＋c≤2．b＋c<2a a AD ．b C．b＋c＝2a＋c≥2aB][答案11 ，＝－，∴cos2A22＝A][解析∵sin A－cos22 ，120°BA又A为锐角，∴＝60°，∴＋C＝C＋BCB－cos2sin C sin Bcb＋sin＋22＝∴＝Aa2sin23CB－cos＝.≤1，∴a2cb＋≤235) ．6(2010·cos则，B sin＝A已知中，ABC在△)北京顺义一中月考cos，＝C(的值为513含详解答案．高考总复习5616 A. B. 6565561616 C. D．－或656565A答案][3512 B，sin B，∴A>＝，∴sin A＝>∵cos A＝[解析]5131343)]＋B＝cos[π－(AB＝，∴cos B＝，∴cos C sin∵5516＝cos BB－cos A cos(A＋B)＝sin A sin＝－.65.BB?A>A点评]在△ABC中，有sin>sin[，又测得塔100m D测得一电视塔尖的仰角为45°，再向塔底方向前进7．在地面上一点)________m．(尖的仰角为60°，则此电视塔高约为227 ．237 B．A257D247 C．．A][答案＝100，∠DAC＝15°，，∠[解析]如图，∠D＝45°ACB＝60°，DC sin45°DC·＝，∵AC sin15°sin60°＝AC·AB∴sin60°sin45°100·＝sin15°32××10022＝A.237.∴选≈26－4π＝acb、c成等差数列，且B)在△ABC中，∠＝，三边长a、(8．文)(2010·青岛市质检3)b的值是(6，则 B.3 2 A.6C.5D.D][答案a＋＋＝ac2ac＝＋c12＋，22222b＝ba4，∴＋c2解析[]由条件b＋c－＋cb－222222aa1 ＝，，∴B又cos＝122ac2 ，＋＝c＋∴a6b222含详解答案．高考总复习6.4，∴bb＝∴＝18＋b22，ac＝的内角)△ABCA、B、C的对边分别为a、b、、c.若ab2、c成等比数列，且(理)＝(则cos B31 B. A. 4422 C. D.43B][答案，2a＝ac，又∵c＝2bca、b成等比数列，∴、解析[]∵a4a－－b＋2＋c222222aa3＝＝2a，∴cos B＝＝∴b22.42aca×22a在知识的交汇处命题是高考命题的基本原则．本题融数列与三角函数于一体，[点评]三角函数等内容余弦定理、等比数列等基础知识．同时也体现了数列、集中考查正弦定理、是高考中的热点问题，复习时要注意强化．的双曲线，若△为焦点，且经过点A9．如图所示的曲线是以锐角△ABC的顶点B、C3sin Ac)(＝6，＝，b、c，且a则此双曲线的离心率为＝4，b、ABC的内角的对边分别为a2a773－3＋B. A. 22 ．3－7 ．D3 ＋7CD ][答案π33accc sin A，为锐角，所以C＝＝＝＝，因为C＝?[解析]sin C?C23sin Aa2sin3217 228，∴c＝×＋46－2×46×＝cos－a由余弦定理知c＝＋b2abC＝2222226a7.＝3＋＝∴e＝7－26b－c22yx在双曲P的两个焦点，b>01(＝－是双曲线、F))(2010·(10．文山东济南设Fa，>0)2122ba含详解答案．高考总复习→→→→)(c为半焦距)线上，若，则双曲线的离心率为PF·PF＝0，|PF|·|PF|(＝2ac212113＋3－1 A.B. 221＋5 2 D. C ．2D答案][＝PF(|＝|PFF，根据双曲线定义得：4a＝＋|22222|)|由条件知，|PF|－|F||[解析PF]221112，4ac4－ac＝4c－＋|PF－2|PF2222|F||F＝||·|PF||PF212112，－e＝＝00，∴1＋e∴aac＋－c2221＋5＝ee>1，∴∵.21C→→→→→，)＝0AB·(CA＋CB·安徽安庆联考)如图，在△ABC中，tan＝，AHBC＝0，(理)(2010·22)(以A、H为两焦点的双曲线的离心率为经过点B15＋1 5－ A. B. 215－ 1 D.C.5 ＋2A][答案→→，，∴AH⊥BC＝0BC∵]AH·[解析C2tan2AH4C1 ＝＝，C∵tan＝，∴tan＝CH2C322tan1－2→→→CBAB＋又∵，CB0，∴CA·(CA＝)＝??180°－CAHC 2＝，＝cottan∴B＝tan＝??BH2??23＝CH2x，∴＝＝设BHx，则AHAB＝22AHC，由条件知双曲线中5ABx，＝x2＝＝x,a2含详解答案．高考总复习1)x，(－5BH－＝15＋2c A.＝＝，故选∴e＝2a15－二、填空题CABC，测得∠．如图，为了测定河的宽度，在一岸边选定两点A，B和对岸标记物11 ________米．AB＝120米，则河的宽度为30°＝，∠CBA＝45°，1)－]答案60(3[ ＝30°，－＝120x，又∵∠CAB则于⊥ABD，设BD＝x，CD＝x，AD点作][解析过CCD3x 1)．＝，解之得，x60(3－∴＝3x－120位于BA，B，灯塔如图，海岸线上有相距12．(2010·福建三明一中)5海里的两座灯塔相距A的北偏西75°方向，与灯塔A的正南方向．海上停泊着两艘轮船，甲船位于灯塔A则两艘轮船处．海里的B相距5C与B海里的32D处；乙船位于灯塔的北偏西60°方向，海里．之间的距离为________13答案][ ，＝，＝如图可知，∠][解析ABC60°ABBC含详解答案．高考总复习DAC45°BAC∴＝AC＝＝60°5，，∠，从而∠AD，∴由余弦定理得，＝3又213. ·cos45°2＝AD·AC＋AC－22AD＝CD，、cC所对的边分别是a、b山东日照模拟)在△ABC中，三个内角A、B、文13．()(2010·π________.b＝的面积等于3，则a＋已知c＝2，C＝，△ABC34][答案π1 4，3，∴ab＝＝sin由条件知，ab[解析]324－＋b22aπ，∵cos＝ab23 ，8＝16b＋2ab ＝8＋＋a∴＋b＝8，∴(a＋b)＝a222224.＝a＋b∴1222，a＝a10)，、c，面积S＝(bc＋若－、)(理在△ABC中，角A、BC的对边分别为a、b4 的最大值是______．则bc2＋50[答案]10011ac－＋222 )b，bc sin A＝([解析]由题意得，42π100又根据余弦定理得A＝，sin A ＝cos A，∴∠bc＝∴ab＋c－2sin A，结合余弦定理得，22241002.＋50，∴bc≤＝1002－＝b＋c2bc≥2bc－bc2222－海里的灯塔恰10)(2010·山东日照)一船向正北匀速行驶，看见正西方两座相距文14．(方向上，另一60°好与该船在同一直线上，继续航行半小时后，看见其中一座灯塔在南偏西小时．________海里/灯塔在南偏西75°方向上，则该船的速度是10答案][v3＝AC，，v＝[解析]设该船的速度为v海里AD/小时，如图由题意知，22tan30°tan45°＋＋3，2＝∵tan75°＝tan30°－1tan45°含详解答案．高考总复习v3＋102AB10. ＝＝，解得v tan75°＝，∴2＋3又vAD2的方位角为A处测得某岛M)(理)(2010·合肥质检如图，一船在海上自西向东航行，在范围n km角，后在B处测得该岛的方位角为北偏东β已知该岛周围北偏东α角，前进m km 时，该船没有触礁危险．α与满足条件β________内(包括边界)有暗礁，现该船继续东行．当)β>n cossin(α－β[答案]m cosαAMBAMB＝90°－α＋∠AMB－∠MAB＝90°α，∠MBC，∴∠＝90°－β＝∠MAB＋∠[解析] ＝α－β，αBMmm cos，BM＝ABM中，根据正弦定理得＝，解得由题可知，在△?－βsin?ααsin?90°－α?sin?－β?βαcos m cos＝)sin(90°－βBM要使船没有触礁危险需要α>n sin(α>n，所以α与β满足m coscosβ?β?αsin－)－β时船没有触礁危险．三、解答题AB＋cos bA、B、C所对的边，且ab15．(2010·河北唐山)在△ABC中，a、、cos c分别是角1.＝；求c(1)→→CB的最大值．B)＝－3，求CA·＋(2)若tan(A 1及正弦定理得，＋b cos A＝由[解析](1)a cos BB sin cc sin A 1，＋·cos A·＝cos BC sin C sin ，＝sin CB∴c sin(A＋) 0，)＝sin C≠C)sin(又A ＋B＝sin(π－1.＝∴c2π，＝A<π＋0<3)＋tan((2)∵AB＝－，AB，∴＋B3含详解答案．高考总复习π＝B∴)C＝π－(A＋.3 由余弦定理得，ab－ab≥2ab－ab＝＝＝a＋b－2ab cos Ca＋b2222211→→→→，＝2CA，∴CA≤·CB·CB2 ＝1时取“＝”号．当且仅当a＝b1→→的最大值是CA所以，.·CB2由于地形的C)广东玉湖中学如图，要计算西湖岸边两景点B与16．(的距离，文)(2010·＝14km，∠BAD＝10km，AB＝限制，需要在岸上选取A和⊥D两点，现测得ADCD，AD＝，30.1km)．参考数据：2＝1.414＝，∠BCD135°，求两景点B与C的距离(精确到60°2.236.5＝1.732，，xABD中，设BD＝[解析]在△，cos∠BDAADBD＋AD－2BD·则BA＝222·cos60°，－x＋102·10x14即＝222 0，＝－10x－96整理得：x2x解之得，)，x＝－6(舍去16＝，21由正弦定理得，BDBC，＝BCD∠∠CDB sinsin16＝∴BC11.3(km)82≈·sin30°＝sin135°11.3km.C的距离约为答：两景点B与经规划调长沙市某棚户区改造建筑用地平面示意图如图所示．理)(2010·湖南十校联考)(是原R的圆面．该圆的内接四边形ABCD研确定，棚改规划建筑用地区域可近似为半径是2CD6BC4ADAB棚户建筑用地，测量可知边界＝＝万米，＝万米，＝万米．含详解答案．高考总复习R的值；(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径可以调整．为了提高、BC(2)因地理条件的限制，边界AD、CD不能变更，而边界AB，使得棚户区改造的新建筑用地上设计一点P棚户区改造建筑用地的利用率，请在ABC APCD的面积最大，并求出其最大值．，由余弦ACABCD[解析](1)因为四边形内接于圆，所以∠ABC＋∠ADC＝180°，连接定理：＋＝46－2×4×6cos∠ABC222AC.＝4∠ADC×2×4cos＋2－222＝∠ABC∴cos.＝60°π)，∴∠ABC.∵∠ABC∈(0，211＝S则×sin60°＋sin120°6×4××2×4×ABCD四边形22 ＝83(万平方米)．中，由余弦定理：在△ABC∠ABC·2ABBC·cos AB＝＋BC－222AC17.＝2＝28AC，故＝16＋36－2×4×6×2 由正弦定理得，21212AC724＝R＝＝，∴(2R万米＝)．333ABC sin∠2 ＝S＋S，S(2)APC△APCD△ADC四边形1＝3.2CD·sin120°＝SAD·ADC△2 ＝，y，设AP＝xCP31则S＝xy·sin60°＝xy.APC△24又由余弦定理：AC＝x＋y－2xy cos60°222＝x＋y－xy＝28.22含详解答案．高考总复习.xy－≥2xyxy∴＝x＋y－xy22时取等号．28，当且仅当x＝y∴xy≤33＋＝23S∴时面积最大，其最大面积y，即当x＝＝xy≤23＋×2893APCD四边形44 万平方米．为93处各有一个CB、．17(2010·上海松江区模拟)如图所示，在一条海防警戒线上的点A、收到发自静止B50千米．某时刻，水声监测点，B、两点到点CA的距离分别为20千米和同时接收到该声波信号，已知声波在水中的传播速度CA、目标P的一个声波信号，8秒后秒．千米/是1.5的值．的距离，并求x的距离为(1)设A到Px千米，用x表示B、C到P千米)．(2)求P到海防警戒线AC的距离(结果精确到0.01 ，PC＝[解析](1)依题意，有PxA＝12. ＝x－1.5PB＝x－×820中，＝AB在△PAB?12?x＋AB－PB＋20－－222222xAP＝＝P cos AB∠20x2·2PAAB323x＋＝x550 ＝AC中，AC同理，在△Px＋PC50－＋AC－222222xPA25 ＝＝，＝AC cos∠Px·50A·AC2x2P，cos∠PACAB∵cos∠P＝32＋3x2531.x＝，解之得，＝∴x5x ADP中，⊥AC于D，在△PD(2)作25 得，PAD＝∠由cos31214 ，AD∠P ＝2cos1ADP∠sin＝－31含详解答案．高考总复习21431·＝421≈∠APD＝18.33千米，sin PPD∴＝A31答：静止目标P到海防警戒线AC的距离为18.33千米．含详解答案．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3.一艘海轮从 A 处出发,以每小时 40 海里的速度沿南偏东 40°的方向直线航行,30 分钟后到达 B 处,在 C 处有一座灯塔,海轮在 A 处观察灯塔,其方向是南偏东 70°,在 B 处观察灯塔,其方向是北偏东 65°,那么 B,C 两点间的距离是( )
A.10 海里 B.10 海里
C.20 海里 D.20 海里
=
,即
DB=100sin 15°=100×sin(45°-30°)=25 ×( -1),则在△BCD 中,由正弦定理得
=
,
即
=
,解得 cos θ= -1.
9.如图,为测量山高 MN,选择 A 和另一座山的山顶 C 为测量观测点.从 A 点测得 M 点的仰角∠MAN=60°,C 点的仰角∠CAB=45°以及∠MAC=75°,从 C 点测得∠MCA=60°.已知山高 BC=100 m,求山高 MN.
A.5 B.15
C.5 D.15
答案 D 在△BCD 中,∠CBD=180°-15°-30°=135°.
由正弦定理得
=
,所以 BC=15 .
在 Rt△ABC 中,AB=BCtan∠ACB=15 × =15 .故选 D.
6.一船自西向东匀速航行,上午 10 时到达灯塔 P 的南偏西 75°,距灯塔 68 海里的 M 处,下午 2 时到达这座灯塔
答案 A 如图所示,易知在△ABC 中,AB=20 海里,∠CAB=30°,∠ACB=45°,根据正弦定理得
=
,
解得 BC=10 海里.
4.地面上有两座相距 120 m 的塔,在矮塔塔底望高塔塔顶的仰角为 α,在高塔塔底望矮塔塔顶的仰角为 ,且在两塔底连线的中点 O 处望两塔塔顶的仰角互为余角,则两塔的高度分别为( ) A.50 m,100 m B.40 m,90 m C.40 m,50 m D.30 m,40 m 答案 B 设高塔高 H m,矮塔高 h m,在 O 点望高塔塔顶的仰角为 β.
A.240( -1)m B.180( -1)m C.120( -1)m D.30( +1)m
答案 C 如图,∠ACD=30°,∠ABD=75°,AD=60 m,在 Rt△ACD 中,CD=
=
=60 m,在 Rt△ABD
中,BD=
=
=
=60(2- )m,∴BC=CD-BD=60 -60(2- )=120( -1)m.
C.10 km D.10 km
答案 D 如图所示,由余弦定理可得:
AC2=100+400-2×10×20×cos 120°=700, 所以 AC=10 (km). 2.如图,从气球 A 上测得正前方的河流的两岸 B,C 的俯角分别为 75°,30°,此时气球的高是 60 m,则河流的宽度 BC 等于( )
(1)设 A 到 P 的距离为 x 千米,用 x 表示 B、C 到 P 的距离,并求 x 的值; (2)求 P 到海防警戒线 AC 的距离. 解析 (1)依题意,有 PA=PC=x,PB=x-1.5×8=x-12. 在△PAB 中,AB=20,
cos∠PAB=
=
=
.
同理,在△PAC 中,AC=50,
则 tan α= ,tan = ,
根据三角函数的倍角公式有 =
.①
因为在两塔底连线的中点 O 望两塔塔顶的仰角互为余角,
所以在 O 点望矮塔塔顶的仰角为 -β.
由 tan β= ,tan
=,
得 = .② 联立①②解得 H=90,h=40. 即两座塔的高度分别为 40 m,90 m. 5.如图所示,测量河对岸的塔高 AB 时可以选与塔底 B 在同一水平面内的两个测点 C 与 D,测得 ∠BCD=15°,∠BDC=30°,CD=30,并在点 C 测得塔顶 A 的仰角为 60°,则塔高 AB 等于( )
的坡角 θ,在山坡的 A 处测得∠DAC=15°,沿山坡前进 50 m 到达 B 处,又测得∠DBC=45°,根据以上数据可得
cos θ=
.
答案 -1
解析由∠DAC=15°,∠DBC=45°可得∠BDA=30°,∠DBA=135°,∠BDC=90°-(15°+θ)-30°=45°-θ,由三角
形内角和定理可得∠DCB=180°-(45°-θ)-45°=90°+θ,在△ABD 中,根据正弦定理可得
45°和 60°,而且两条船与炮台底部所连的线成 30°角,则两条船相距
m.
答案 10 解析由题意画示意图,如图,
OM=AOtan 45°=30(m),
ON=AOtan 30°= ×30=10 (m), 在△MON 中,由余弦定理得,
MN=
= =10 (m).
8.如图所示,在一个坡度一定的山坡 AC 的顶上有一高度为 25 m 的建筑物 CD,为了测量该山坡相对于水平地面
的东南方向的 N 处,则此船航行的速度为
海里/小时.Байду номын сангаас
答案解析如图,由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN 中,
=
,
∴MN=68× =34 海里. 又由 M 到 N 所用的时间为 14-10=4 小时,
∴此船的航行速度 v= = 海里/小时.
7.江岸边有一炮台高 30 m,江中有两条船,船与炮台底部在同一水平面上,在炮台顶部测得两条船的俯角分别为
解析由题意得,AC= BC=100 m. 在△MAC 中,∠CMA=180°-75°-60°=45°.
由正弦定理得
=
⇒ AM=100 m.
在△AMN 中, =sin 60°,
所以 MN=100 × =150 m.
10.如图,在一条海防警戒线上的点 A、B、C 处各有一个水声监测点,B、C 两点到 A 的距离分别为 20 千米和 50 千米,某时刻,B 收到发自静止目标 P 的一个声波信号,8 秒后 A、C 同时接到该声波信号,已知声波在水中的传播速度是 1.5 千米/秒.
（新课标）高考数学总复习第四章第八节正弦定理和余弦定理的实际应用练习文新人教 A 版
第八节正弦定理和余弦定理的实际应用
A 组基础题组
1.已知 A、B 两地间的距离为 10 km,B、C 两地间的距离为 20 km,现测得∠ABC=120°,则 A,C 两地间的距离为 ()
A.10 km
B.10 km
cos∠PAC=
=
=.
因为 cos∠PAB=cos∠PAC,

(新课标)高考数学总复习第四章第八节正弦定理和余弦定理的实际应用练习文新人教A版

2021年高考数学一轮复习 3.8 正弦定理、余弦定理的应用举例课时作业 理(含解析)新人教A版

高考数学总复习 38 正弦定理和余弦定理的应用备选练习 文(含解析)新人教A版

最新高考数学复习 正弦定理、余弦定理及其应用 理(含解析)新人教A版

2024年高考数学一轮复习(新高考版) 第4章 正弦定理、余弦定理

人教版高中数学必修第二册6.4.3.3 余弦定理、正弦定理在几何和生活应用举例 同步精练(含解析)