车位分配问题 数学建模
车位分配问题 数学建模
停车场车位分配问题研究一. 摘要某写字楼的停车位数目一定,主要提供写字楼办公人员办卡包年或包月使用,为了使停车场空置率减少,以及免于有卡却没有车位产生冲突的尴尬,我们必须对停车流量进行模拟分析,建立合理的最佳的车位分配管理方法,并得到最大的收益。
首先对附表中数据进行分析,因为我们得到的是四月份的停车流量,为了方便分析研究,我们应该把数据转化为停车量。
我们从中引入了概率进行模拟。
假设停在停车场中的车辆在各个时间段离开是按照泊松分布,即可分别求的到来的和离开的车辆数目,就可以方便得得到停车量这个关键的数据。
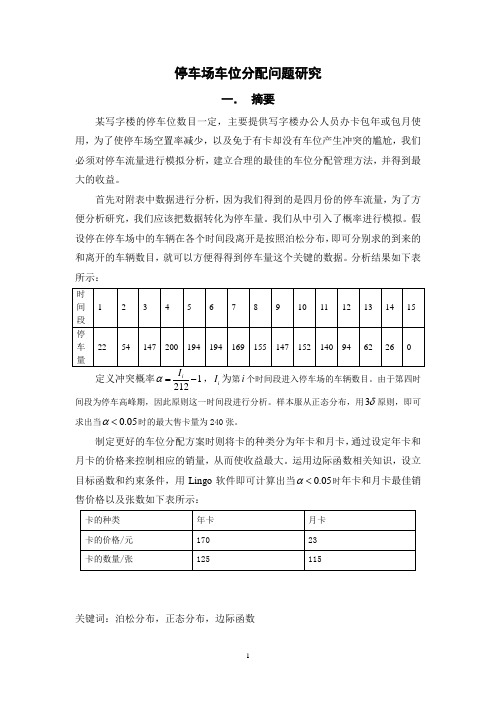
分析结果如下表所示:定义冲突概率1212iα=-,i I 为第i 个时间段进入停车场的车辆数目。
由于第四时间段为停车高峰期,因此原则这一时间段进行分析。
样本服从正态分布,用3δ原则,即可求出当0.05α<时的最大售卡量为240张。
制定更好的车位分配方案时则将卡的种类分为年卡和月卡,通过设定年卡和月卡的价格来控制相应的销量,从而使收益最大。
运用边际函数相关知识,设立目标函数和约束条件,用Lingo 软件即可计算出当0.05α<时年卡和月卡最佳销售价格以及张数如下表所示:关键词:泊松分布,正态分布,边际函数二.问题分析与重述问题一:题目要求模拟附表中停车流量,分析停车量的统计规律。
停车流量与停车量是两个不同的概念,要分析停车量的统计规律就必须弄清楚来到停车场的车辆数目以及离开停车场的车辆数目。
而题目所给的条件中我们只知道停车流量,也就是车离开与来到的总的次数,因此我们假设车的离开服从泊松分布,运用概率来求出单位时间内车辆离开的数目,这样也就可以知道单位时间内车辆到来的数目,它们两者的差值也就是我们所要求的停车量。
α=情形下,计算最大售卡量。
问题二:定义冲突概率,求若冲突概率低于0.05根据附表中停车流量数据,以及上题对停车量的分析,我们可以知道在第四个时间段,即早上9:00—10:00停车量是最多的,也就是在这段时间产生冲突的概率是最大的,为了计算最大售卡量,我们就取这段时间进行分析。
数学建模校车安排问题 标准答案 答案仅供参考

摘要根据对某市某一高校校车的老校区各区的距离和教师人数的调查资料,建立其数学模型,依据建立的停车站的位置及个数的不同而造成不同的满意程度,制定建立停车站的位置及数目,根据具体情况提出自己的的建议与意见。
模型一:最短距离模型。
通过对已知的两个不同区的距离,根据Dijkstra算法算出各个区之间的最短距离。
得到需要的分析数据。
模型二:多源最短距离。
通过模型一中得到的数据,用多源最短路径算法,求出建立不同个数的停车站时的最短路径。
再次考虑人的满意程度,求出最大满意度。
模型三:多目标最优规划。
通过以模型二的满意程度和最小数量的车为双目标,建立设有3个乘车站时的最优化解法。
[关键词]停车站;Dijkstra算法;满意度;多目标目标;最优解法校车安排问题1、问题重述许多学校都建有新校区,常常需要将老校区的教师和工作人员用校车送到新校区。
由于每天到新校区的教师和工作人员很多,往往需要安排许多车辆。
如何有效的安排车辆及让教师和工作人员尽量满意是个十分重要的问题。
现有如下问题请你设计解决。
假设老校区的教师和工作人员分布在50个区,各区的距离见表1(第3-4页)。
各区人员分布见表2(第6页)。
问题1:如要建立n个乘车点,为使各区人员到最近乘车点的距离最小,该将校车乘车点应建立在哪n个点。
建立一般模型,并给出2,3n=时的结果。
问题2:若考虑每个区的乘车人数,为使教师和工作人员满意度最大,该将校车乘车点应建立在哪n个点。
建立一般模型,并给出2,3n=时的结果。
问题3 若建立3个乘车点,为使教师和工作人员尽量满意,至少需要安排多少辆车?给出每个乘车点的位置和车辆数。
设每辆车最多载客47人。
问题4;关于校车安排问题,你还有什么好的建议和考虑。
可以提高乘车人员的满意度,又可节省运行成本。
2、模型假设(1)假设每个人的的满意程度只与距离有关。
(2)假设原数据没告诉的两个区之间没有道路,即只有经过其它的区往返。
(3)假设总的满意度是所有人的满意度之和。
2023高教杯数学建模c题

数学建模C题题目为"城市停车问题",是一个具有实际应用背景的问题,涉及到城市交通、土地利用、城市规划等多个方面。
本答案将采用层次分析法(AHP)来解决该问题。
首先,我们需要对问题进行详细的分析。
城市停车问题主要包括两个方面:一是寻找合适的停车位,二是考虑停车场的布局和数量。
针对这两个方面,我们可以从以下几个方面进行建模:1. 确定停车需求:根据城市的人口、车辆数量、交通状况等因素,确定不同区域的停车需求。
2. 确定停车场的布局:根据停车需求和停车场的特点(如占地面积、建设成本等),确定停车场的布局和数量。
3. 建立层次分析模型:将停车需求和停车场布局两个因素作为目标层,将其他相关因素作为准则层,建立层次分析模型。
4. 计算权重:根据层次分析模型,通过计算各因素的权重,为决策者提供参考。
接下来,我们将使用Python语言和相关的数学建模工具来实现上述建模过程。
首先,我们需要导入相关的库和模块,如numpy、scipy等。
假设我们已经收集了相关数据,包括城市的人口、车辆数量、交通状况、土地利用情况等。
我们可以使用这些数据来建立层次分析模型,具体步骤如下:1. 构建层次结构模型:将停车需求和停车场布局作为目标层,将土地利用情况、交通状况、停车场特点等作为准则层。
2. 构造判断矩阵:根据准则层因素对目标层的影响程度,构建判断矩阵。
可以使用专家打分等方法来确定各因素的权重。
3. 计算权重:使用scipy等库中的函数,根据判断矩阵计算各因素的权重。
4. 一致性检验:对判断矩阵进行一致性检验,确保各因素的权重合理。
5. 综合权重:将准则层因素的权重与目标层的权重相乘,得到综合权重。
最终,我们可以根据综合权重来评估不同方案的优劣,为决策者提供参考。
在实际应用中,我们还需要考虑其他因素,如政策支持、经济成本等,综合评估各种方案,选择最优方案来解决城市停车问题。
总之,通过层次分析法可以有效地解决城市停车问题,为决策者提供科学的参考依据。
校车乘车点的安排问题(数学建模)

装订线摘要研究在老校区设置校车停靠点的问题。
由于教职员工分布在许多不同的生活区域中,为了使其能够方便的乘坐校车,须要根据教职员工的分布设立多个校车停靠点。
现根据已有生活区域的分布,在使教职员工到校车停靠点的距离最小的前提下,尽可能安排最少的校车数量。
运用了Floyd算法、0-1整形规划、增加人数权重距离、概率分布与统计、状态转移图,对不同方案进行满意度比较,建立数学规划模型,得出优化方案,进行方案检验。
对于校车停靠点的设立,以题目给出的相关数据,假设没有给出数据的区域间没有直达路径,必须通过其余区域转达。
通过Floyd算法得到任意两区域之间的最短距离。
之后引入0-1状态变量,设定若某区域被选为校车停靠点则状态值为1,否则状态值为C n种方案,在确定校车停靠点的基0。
利用穷举法得到n个校车停靠点的设置分布的50础上,编程求出各个区域到离自己最近校车停靠点的距离之和。
根据题目要求,距离之最短的停靠点设置方案即为最优方案,此时得到2个停车点时设在区域18和区域31,3个停车点时设在区域15,区域21和区域31。
再考虑人数的时候,我们在第一问的基础上,对每个区域间的距离改为人数权值距离。
此时转化成与第一问相同的算法。
得到2个停车点时设在区域19和区域32,3个停车点时设在区域15,区域21和区域32。
研究校车数量的过程中,在增添校车和人员转移的取舍中,我们设定了增添校车的条件标准,从而计算出由人员转移距离和校车数量决定的满意度。
在此基础上,我们结合实际,分时段、分工种进行动态状态分析,不同工种的考虑增加了运送批数,缓解乘车高峰压力。
考虑课时的情况,则部分校车可以在时间允许范围内空车返回老校区接送下一批员工,此举增加了校车的流动性,从而减少了所需的校车数,在此考虑下,车辆数由最大需要量的54辆骤减到现如今27辆。
关键字:Floyd算法、0-1整形规划、人数权重距离、概率统计、状态转移图1.问题重述许多学校都建有新校区,常常需要将老校区的教师和工作人员用校车送到新校区。
(参考资料)停车场泊车位设计的数学建模

停车场泊车位设计姓名:鹿蕾 学号:1407021015班级:14数学与应用数学1班摘要:随着经济的发展,越来越多的人加入了有车一族,“停车难”也一直困扰着大家,但同时也引发了一系列城市管理问题,也带来了许多安全隐患。
解决停车位问题已经是迫在眉睫。
本文主要是针对停车场大小面积一定的情况下,合理利用停车场的有限空间尽可能多的停放车辆。
本模型先求的最佳停车角度,再进行停车场车位的合理分配。
根据模型,发现,当停车位与通道夹角69.94θ=︒ 时,可以使该停车场停放车辆达到最多。
关键词:泊车位设计;停车角度一、 问题重述由于城市泊车空间有限,因此合理地利用有现空间泊尽可能多的车辆,将有效缓解城市泊车困难。
如果将泊车位按照与停车线构成直角的方向设计,虽然能够在停车场内停放车辆达到最多,但按照这种方式停车实际上是有很大困难的,为了减少因停车造成意外损失的可能性,我们将研究出最佳停车角θ现有如图1所示的停车场,请你设计该停车场的泊车位设计方案。
图1某地面停车场规模示意图停车场车辆出入口二、合理假设与变量约定2.1合理假设1.进入停车场的车型只考虑小型车,小型车的详细指标参见名词解释2.假设每辆车都能按照规定停车3.每辆车的大小结构都是一样的4.每一位司机的驾驶能力都是一样的2.2、变量说明序号符号符号说明1A 每辆小汽车需要的面积2 停车位置的角度3 a 停车车位的宽度4 B 停车车位的长度5 X 车辆调整所需路面宽度三、模型建立与模型求解5.1 停车场泊车位规划模型5.1.1 单辆车停车位最佳角度LWR上图中,小轿车是自东向西行驶逆时针转角度驶入车位的。
小轿车具体驶入车位的情况,见下图,其中C 1为最小转弯半径,R 为通道的最小宽度。
我们假定小轿车的最外端在半径为C 1的原周上行驶,且此时轿车的最内端在半径为C 2的原周上随之移动,然后以角度进入停车位,所以通道的最小宽度12cos R C C θ=-每辆车均以角度停放,用W 表示小轿车停车位的宽度,L 表示停车位的长度(这里L 的最上方并没有渠道最下端,是考虑到车身以外的区域可以留给对面停车位使用),L 0表示停车位末端的距离,易知他们分别是停车角的函数,且有:absin θ(2b+acot θ)I/2 I/2θ这符合我们原来的假定。
车位分配数学建模
停车场车位分配问题【摘要】本文基于蒙特卡罗模拟法、正态总体、随机概率、线性规划等方法对停车场车位分配问题做了探讨。
根据已有的30天停车流量数据,分析其规律,最终达到合理分配车位,使得停车收益达到最大。
针对问题1:由于题目中统计资料以及相关数据较少,建立一个准确的数据模型比较困难,因此我们使用了蒙特卡罗模拟法,建立了蒙特卡罗模型。
同时我们以17:00—18:00为例说明,使用正态分布函数进行模拟,给出了100天的停车流量的模拟解;再计算其规律时,我们继续计算各时段的均值、标准差、偏度、峰度的统计量,观察这些数据我们有以下结论:1.停车量的高峰期出现在8:00到18:00的时间段里,值得注意的是9:00到12:00出现了停车量的最高峰;2.标准差也和停车量一样出现两边低中间高的情形,并且也是在9:00到12:00出现最大的标准差,进而说明在这三个小时内停车量很大同时汽车的流通量也很大,是一天当中最为繁忙的时间段。
3.偏度和峰度基本上比较接近,说明这些天之内出现停车流量忽高忽低的情况还是比较少的,停车流量还是比较平稳的。
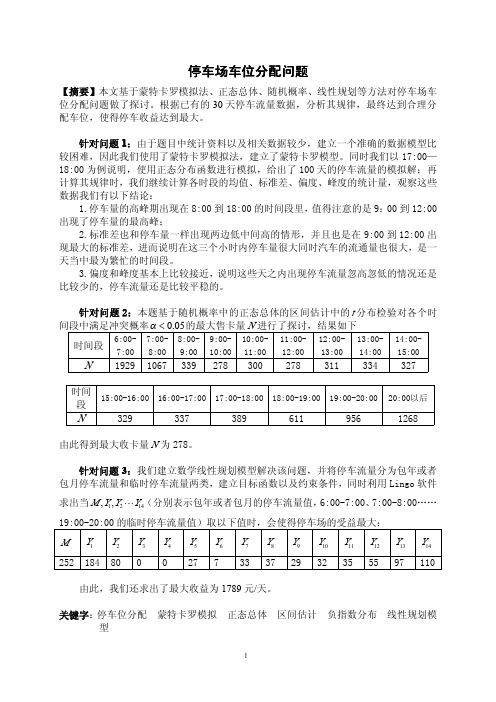
针对问题2:本题基于随机概率中的正态总体的区间估计中的t 分布检验对各个时间段中满足冲突概率05.0<α的最大售卡量N 进行了探讨,结果如下时间段6:00-7:007:00-8:008:00-9:009:00-10:0010:00-11:0011:00-12:0012:00-13:0013:00-14:0014:00-15:00N 19291067339278300278311334327时间段15:00-16:0016:00-17:0017:00-18:0018:00-19:0019:00-20:0020:00以后N3293373896119561268由此得到最大收卡量N 为278。
针对问题3:我们建立数学线性规划模型解决该问题,并将停车流量分为包年或者包月停车流量和临时停车流量两类,建立目标函数以及约束条件,同时利用Lingo 软件求出当1214,,M Y Y Y ⋯(分别表示包年或者包月的停车流量值,6:00-7:00、7:00-8:00……19:00-20:00的临时停车流量值)取以下值时,会使得停车场的受益最大:M 1Y 2Y 3Y 4Y 5Y 6Y 7Y 8Y 9Y 10Y 11Y 12Y 13Y 14Y 2521848027733372932355597110由此,我们还求出了最大收益为1789元/天。
MathorCup大学生数学建模挑战赛B题全国二等奖
2.问题分析
2.1 问题一的分析
根据查找的相关文献,我们提炼了几个与小区汽车停车位的分布合理有关的关键指 标。对于这几个指标,我们从“点”与“面”两个方面来考虑指标与判定车位分布的关 联。通过对指标的理解,我们在“面”的角度选择了多因素的决策模型。
2.2 问题二的分析
首先我们要对附件一所提供的内容进行理解,以及归纳总结。从附件一中得到有关 指标的所对应的判断标准及判断值。再从问题一中建立的模型出发,综合考虑停车位分 布的合理性,并对判断的结果进行相应的解释。
车位分布的优化设计与评价
摘要
现代社会经济的快速发展导致了小区内私家车数量的快速增长,因此小区内停车场 如何科学合理的分布成为了社会关注的问题。本文针对此问题,先建立了停车场综合评 价模型,再将所设计方案应用于已给附件,指出该小区停车场设计不合理,最终给出合 理分配方案,并与不合理的方案进行比较分析。 针对问题一:为了得到停车场车位的最优方案,我们采用多指标综合评价中的最优 回归构权法,先将评价停车场的指标分为分为三类,分别是方便性,实用性和舒适性。 其中方便性由效用时间和出口的位置决定;实用性由安全系数、紧急逃离和车位布置方 位决定;舒适性由排风口位置和场内环境决定。在选取的七个指标中,我们从“点”与 “面”两个方面来考虑指标与判定车位分布的关联。通过对指标的理解,我们在“面” 的角度选择了多因素的决策模型。 针对问题二:由于给出的附件为一张停车场的示意图,我们在查证现实生活中车位 的标准大小后确定所给图的大小,确定出比例尺为 1:500,并且将所给停车场分成 A 和 B 两个区域,分别对这两个区域再实行分区,最终得到 8 个区域,利用比例尺求得相 关数据。再根据问题一中所探讨出来的模型,分别进行点和面的分析,用 Matlab 处理 所求数据,再画出 A 和 B 两区域的评价得分图,车位得分情况呈下降趋势,故得出所 给停车分布并不合理。 针对问题三:由于在第二问中,我们算得车位分配并不是最优化,我们接下来对车 位最优化的方案进行探究。我们对 A 和 B 两个区域分别探讨,为了得到“均好”的效 果,我们重新分配车位的原则为 :对于得分高的车位,安排需要下楼时间长的户主。基于 这一原则,我们对问题二的车位得分情况以及不同楼层的下楼时间进行了简单的排序, 把得分高的车位对应与下楼时间长的户主,得到了重新修正过的等效时间。然后求出了 分配前后 A、B 区域的得分标准差,并且画出了重新分配前后的评价得分对比图,发现 优化后的分布方案显然更为科学合理。 关键词:多指标综合评价 最优化 评价得分
停车场规划数学建模
医院停车场规划问题摘要本题是个优化设计问题,通过合理设计停车场的停车方式和通道大小使得停车场在有限的区域下能停放的下更多的车辆,为医院患者解决停车难的问题。
针对于问题1,由于该医院挂号是从7:30开始,但8:00之后医生才开始门诊,每个患者平均门诊时间为1小时30分钟。
所以在7:30-8:00之间来的患者要到9:30才能离开医院,而在8:00之后来的患者只需门诊1小时30分钟就可离开医院。
于是,可通过用Excel表对表1数据进行处理和分析,以每五分钟为单位,统计此时停车场停放的车辆数。
因此,根据统计结果可知在周二9:30这个时刻医院的车辆数最多为229辆。
所以,医院至少需要有229个车位才能够使得每一位患者的车到停车场就有车位停车。
对于问题2,对于问题3,根据问题1结果可知医院至少要有229个车位才能使患者车到就有车位停车,而由问题2的结果可知,新建的停车场最多只有162个停车位,远远不能满足实际需要。
所以问题可转化为从政府部门、医院以及患者的角度提出一些可行性的建议来解决这个问题。
政府部门可以从建设新的停车场,开设便利的公交路线等方法来解决这一问题;医院可以通过合理利用医院内部的土地,为医护人员的上班提供便利等方法老解决这一问题;患者可以有意识的不占用停车位,按规定停车,尽可能的乘坐公交车或出租车来医院就诊。
关键词:一、问题重述问题背景:随着现代技术的发展,人民生活条件的不断改善,小轿车的普及率越来越高. 患者自己开车到医院看病的情况也越来越普遍. 然而, 福州市的医院普遍存在停车位不足, 患者停车难的问题.某医院原有若干个停车位, 零散分布于院内建筑楼房四周以及道路两侧. 现医院经重新规划整合,拆除部分旧楼,在门诊大楼旁整出一个长方形地块(见附录一),准备建公用停车场,用于患者停放小轿车.该医院8:00开始门诊, 挂号从7:30开始, 每个患者平均门诊时间1小时30分钟(包括候诊、问诊、缴费和取药). 表1(见附录二)是某一周每天从7:30-11:30每5分钟统计的到达车辆数据。
1987B停车场问题-赵轶星——大学生数学建模竞赛
1987:停车场问题在新英格兰镇有一个位于街角处、面积100×200平方英尺停车场,场主请你设计它的布局,即设场地上的线怎么画的方案。
容易理解,如果将汽车按照与停车线构成直角的方向,一辆紧挨一辆地排列成行,则可以在停车场内塞进最大数量的汽车。
但是对于缺乏经验的司机来说,按照这种方式停靠车辆是有困难的,它可能造成昂贵的保险费用支出。
为了减少因停车造成意外损失的可能性,场主可能不得不雇用一些技术熟练的司机专门停车。
另一方面,如果从通道进入停车位有一个足够大的转弯半径,那么,看来大多数的司机都可以毫无困难地一次停车到位。
当然,通道越宽,场内所能容纳的车辆数目也就越少,这将使得场主减少收入。
1解决一个新英格兰镇的停车场问题摘要给定一个100×200平方英尺的场地,我们分析的目标是确定一种停车场空间的配置方案使得从停车场获得的收入最大。
我们需要考虑专职停车和自助停车两种方案。
自助停车是更好的选择,但是需要一个服务员来收停车费。
为了求得停车场最大的停车数量,我们测试了停车空间的角度从45°到90°的情况。
在如果通道的转角的数量越少,能获得越多空间的假设下,停车场配置的预算的数量可以缩减为7,。
首先,我们分析不考虑入口,出口和服务员的情况。
我们找到了一种能容下76个停车位的配置。
当入口和收费所都考虑进来时,我们的配置相对其他的配置能有更多的停车位(75)。
在我们最后的方案中,移动的许可、下雪时暂时的布置和灯柱的空间都被考虑了。
问题重述1给定一个在新英格兰镇的100×200平方英尺的在转角处的停车场,设计一种配置方案使得停车位最大并且在车场里驾驶的难度最小。
基本假设1、车是自助停车的。
雇佣一个技术熟练的司机来停车的花费对于增加的停车位而增加的收入来说多太多了。
2、停车场里的路都是单向的,这是为了减少通道的宽度和路的总面积。
在这种方法下,停车场的空间可以最大化。
3、入口和出口的位置决定于停车场处于街道转角的位置。
停车场泊位设计数学模型模板
停车场的泊位设计数学建模学号:1407022046 班级:14数学与应用数学2班姓名:刘桃摘要:“停车场的泊位设计”数学模型是利用数学模型的计算来规划出一种使用更合理、利用率高的停车场车位停泊方案。
近几年来,随着人们生活水平的提高,私家车的数量越来越多,汽车的停泊就成为一个越来越重要的问题,如果汽车停泊问题不能合理的解决,将会影响到汽车的使用。
许多大型公司或者是商场门前,都设有自己的停车场,停车场的面积是有限的,而我们希望的就是在这有限的面积内尽可能停放更多的汽车。
当然,停放尽可能多的汽车只是建造停车场时一个需要解决的问题,一个比较成功的停车场还需要具备的就是良好的汽车疏导能力,这就需要在停车场设计时更合理的安排汽车的停放位置。
当停车场面积一定的时候,合理安排空间使得更多的车辆能够停泊进来。
此次建立的模型是通过探究车辆停放角度与停车场面积的方程,继而对面积函数进300*100m的停车场最佳泊位情况,进而行求解,得到车位最佳设计角度,解出2推广到一般的2*s tm,同时对车型进行分类,分别计算小轿车、小型车、大型车三种停车情况。
关键词:车辆停放角度;层次分析;最优方案。
正文1、问题重述1.1自20世纪90年代以来, 我国经济呈现出持续高速发展态势, 家用小汽车更以惊人的发展速度进入普通居民家庭。
但人们在享受汽车所带来的便利和快捷的同时, 又必须面对由此所引发的一系列问题, 其中停车问题就是越来越突出的问题之一。
停车场泊车位规划是指在有限的空间区域内,设计车位布局,尽可能多地发挥空间效率与时间效率。
停车泊位设计考虑的因素较多,如平均车位占面积,车辆出入泊位难易程度,停车场内部道路畅通程度等等。
请设计一个完整的指标体系对停车场效度进入评价。
现有如图1所示的停车场,请你设计该停车场的泊车位设计方案;如果图1中的停车场宽度和长度分别为未知量,s t米,请你重新设计你的方案。
100米300米3米停车场图1某地面停车场示意图1.2停车场的整体规划。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
停车场车位分配问题研究一. 摘要某写字楼的停车位数目一定,主要提供写字楼办公人员办卡包年或包月使用,为了使停车场空置率减少,以及免于有卡却没有车位产生冲突的尴尬,我们必须对停车流量进行模拟分析,建立合理的最佳的车位分配管理方法,并得到最大的收益。
首先对附表中数据进行分析,因为我们得到的是四月份的停车流量,为了方便分析研究,我们应该把数据转化为停车量。
我们从中引入了概率进行模拟。
假设停在停车场中的车辆在各个时间段离开是按照泊松分布,即可分别求的到来的和离开的车辆数目,就可以方便得得到停车量这个关键的数据。
分析结果如下表所示:定义冲突概率1212iα=-,i I 为第i 个时间段进入停车场的车辆数目。
由于第四时间段为停车高峰期,因此原则这一时间段进行分析。
样本服从正态分布,用3δ原则,即可求出当0.05α<时的最大售卡量为240张。
制定更好的车位分配方案时则将卡的种类分为年卡和月卡,通过设定年卡和月卡的价格来控制相应的销量,从而使收益最大。
运用边际函数相关知识,设立目标函数和约束条件,用Lingo 软件即可计算出当0.05α<时年卡和月卡最佳销售价格以及张数如下表所示:关键词:泊松分布,正态分布,边际函数二.问题分析与重述问题一:题目要求模拟附表中停车流量,分析停车量的统计规律。
停车流量与停车量是两个不同的概念,要分析停车量的统计规律就必须弄清楚来到停车场的车辆数目以及离开停车场的车辆数目。
而题目所给的条件中我们只知道停车流量,也就是车离开与来到的总的次数,因此我们假设车的离开服从泊松分布,运用概率来求出单位时间内车辆离开的数目,这样也就可以知道单位时间内车辆到来的数目,它们两者的差值也就是我们所要求的停车量。
α=情形下,计算最大售卡量。
问题二:定义冲突概率,求若冲突概率低于0.05根据附表中停车流量数据,以及上题对停车量的分析,我们可以知道在第四个时间段,即早上9:00—10:00停车量是最多的,也就是在这段时间产生冲突的概率是最大的,为了计算最大售卡量,我们就取这段时间进行分析。
将四月份这段时间的这些数据就行整理,做高峰期停车量与次数的柱状图,近似服从正态分布,求出均值后再用3δ原则,即可求出最多可以停车的数量,也就是最大售卡量。
问题三:此问要求设计出最佳车位分配管理方式,使得收益最大。
也就是在满足冲突概率低于一定值的条件下,找到它与收益的平衡点。
我们从售卡种类,价格,数量出发,设计方案将利润最大化。
首先将卡分为年卡和月卡,两者的价格和销量则按照经济学的编辑函数计算得出,列出目标函数和约束条件,用Lingo软件即可求出我们所需的数据。
三.建模过程1)问题一1.符号定义与说明表1.1符号定义与说明2. 模型假设①假设在第i 个时间段初了最后一个时间段来到停车场停车的车辆不会在这个时间段离开,都是在第(1)i +之后的时间段离开。
②假设在一天结束之后,所有车都离开停车场。
③假设车辆在各个时间段离开的数量服从泊松分布。
④假设售卡数量为212张。
3. 模型建立与求解已知各时间段的停车流量i T ,目的是要求出各个时间段的停车量i n 。
停车流量是单位时间内来到停车场的车辆数目与离开停车场的车辆数目的和,单位时间的停车量则是来到停车场的车辆数目与离开停车场的车辆数目的差值。
这两者的关系如下面两式所示:i i i T I O =+ (1) i i i N I O =- (2)由(1)式,(2)式可知:2i i i N I O =-(3)因此,问题的关键就是要求出i O 。
由假设第三条即:假设车辆在各个时间段离开的数量服从泊松分布:()(0,1,2,...)!kP X k e k k λλ-===再根据假设第一条即:假设在第i 个时间段初了最后一个时间段来到停车场停车的车辆不会在这个时间段离开,都是在第(1)i +之后的时间段离开,就可以列出以下式子: 第1个时间段:111I T N ==; 10O =;第2个时间段:21(1)O I P X =⨯=; 222I T O =-; 2222N T O =-;第3个时间段:312(2)(1)O I P X I P X =⨯=+⨯=;333I T O =-; 3332N T O =-;第i 个时间段:12(1)(2)...(1)i i O I P X i I P X i I P X =⨯=-+⨯=-++⨯=;i i i I T O =-; 2i i i N T O =-;用上述计算公式即可计算出单位时间内也就是每个时间段的进入停车场车辆的数目和离开停车场车辆的数目。
用折线图来表示如下图所示:图1.1各时间段停车场进出车辆数目根据上图容易得到各时间段停车量如图表所示:图1.2停车场各时间段停车量综上所述,各时间段的进入停车场的车辆的数目,离开停车场的车辆的数目以及停车量如下表所示:表1.2各时间段停车量与停车流量i1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 i T 22 42 131 161 148 160 143 134 138 135 132 114 72 46 35 i I2237112 107 71805960657060342055代表每个时间段进入停车场的车辆的数目? 代表每个时间段离开停车场的车辆的数目从图1.2和表1.2中可以看出,在9点以前停车量是不断上升的,在9点到10点之间有一个停车量最大值,然后就是稍稍下降和持平。
到了11点,出现一次明显的下降,在15点时有一个较小的峰值,等到16点之后,停车量迅速减小直至所有车都离开停车场。
2)问题二1.符号定义与说明表2.1符号定义与说明2.模型假设①假设汽车来到停车场的时间服从均匀分布。
②假设忽略工作日和休息日的区别。
③假设停车场现售出212张卡。
3.模型建立与求解a.定义冲突概率α:停车场发生冲突也就是来到停车场的车的数量比停车场车位的数量多。
定义可以有两种可能:①一天中有α的时间段出现车位不够的现象②当来到停车场的车辆数目大于车位数的1α+时为冲突 我们选用第二种方式定义冲突概率α,也就是:1212iI α=- b.求最大售卡量:由第一问可知,在第四时间段即9:00—10:00停车量是最多的,所以这个时间段发生冲突的概率最大,如果其他时间段发生了冲突,这个时间段必然也会发生冲突,因此,想要得到最大售卡量,只要考虑这个时间段即可。
以9:00—10:00这个时间段来到停车场的车辆数目为横坐标,以达到相同来车数目的次数为纵坐标作柱状图得到这个时间段即最高峰来车数分布直方图如下图所示:图2.1最高峰来车数分布直方图从上图可以看出,第四时间段来车分布近似服从正态分布。
整理第四个时间段数据得出:第4个时间段来到停车场车辆数目的均值为:199x =的方差为:4S =第4个时间段来到停车场车辆数目的中位数:181M =正态分布检验:Q 0.9 1.1Mx<< 3x δ>∴可认为样本大致呈正态分布根据正态分布的3δ原则,在3倍S 的区间内事情发生的概率为99%,也就是说有199+12=211辆车停在停车场的概率为99%。
由于该停车场有212各车位,允许发生冲突的概率为0.05,所以该时间段的停车上限为212*1.05=223,所以,加上冲突后可以多让233-211=22个人来停车。
假设持卡人来停车的概率为J ,那么计算最大售卡量的公式为:()2121182212L Jα⨯+-⎡⎤⎣⎦=+J 的得来:根据可能来到停车场中的车和在停车场中的车与时间段作散点图,并连成折线图如下图所示:实现代表可能到停车场的车,虚线代表已经在停车场中的车。
图2.2各时段停车场占用率折线图从图中可以看出,还没到停车场中的车辆数目也就是有卡却遭遇冲突的车辆数目,因此:10.20.8J =-=综上所述:当0.05α<时,最大售卡量240L =。
3)问题三 1.符号定义与说明表3.1符号定义与说明2.模型建立与求解将卡的种类分为年卡和月卡,它们价格和销量不同,我们通过设定年卡和月卡的价格来控制相应的销量,从而使收益最大。
运用经济学中边际函数的相关概念,我们可以得到以下关系式:9023y y m Q P P =-+(1) 704m m y Q P P =-+(2)偏边际:2y yQ P ∂=-∂;交叉边际:3y mQ P ∂=∂;偏边际表示当月卡的价格不变时,年卡的价格每增加1单位,年卡的销量就会降低2单位。
而交叉边际表示当年卡的价格不变时,月卡的价格每增加一个单位,年卡的销量就会增加3单位。
类似的我们有:偏边际:4mmQ P ∂=-∂ 交叉边际:1myQ P ∂=∂ 偏边际表示当年卡的价格不变时,年卡的价格每增加1单位,年卡的销量就会降低4单位。
而交叉边际表示当月卡的价格不变时,月卡的价格每增加一个单位,年卡的销量就会增加1单位。
一年的收益:12y y m m Y Q P Q P =⨯+⨯222125190840y m y m y m P P P P P P =--+++约束条件:0y P >;0m P ≥;且当0.05α<时有:240y m Q Q +≤用Lingo 软件计算得:170y P =;23m P =;将结果带入(1)、(2)两式得:125y Q =;115m Q =。
从该结果中可以得到,我们在售卡时在冲突概率小于0.05的条件下年卡卖125张,月卡卖112张,其中年卡单价为170,月卡单价为23。
这样得到收益最高的分配方式。
四.附录附录一:计算持卡人停车概率的程序:>>st=1:15;>>x0=[0.1,0.9];>> [t,x]=ode45('ill',st,x0);>> plot(t,x(:,1),'.',t,x(:,2),'-'),grid,pausefunction y=ill(t,x)if t>=1 & t<=4ab=1.2;bc=0.01;y=[ab*x(1)*x(2)-bc*x(1);-ab*x(1)*x(2)];else if t<=11ab=0.04;bc=0.035;y=[ab*x(1)*x(2)-bc*x(1);-ab*x(1)*x(2)];elseab=0.07;bc=0.35;y=[ab*x(1)*x(2)-bc*x(1);-ab*x(1)*x(2)];endend五.参考文献[]1姜启源,谢金星,叶俊编《数学模型(第三版)》,高等教育出版社。
