基于ansys的圣维南原理验证(附程序)
基于ANSYS Workbench的焊接机器人大臂预应力模态分析

基于ANSYS Workbench的焊接机器人大臂预应力模态分析王昆;刘进福;韩晶;莫贤【摘要】焊接机器人的大臂是整个机器人的受力最大的机构,作为机器人的重要部件,其刚度和强度直接影响到机器人的使用精度和寿命.在设计过程中必须保证它的强度和刚度及在运动过程中振动频率的影响.文中在有限元受力分析软件ANSYS 下对焊接机器人的大臂进行静力分析,为机器人整体设计和优化提供有效的理论支持.【期刊名称】《机械工程师》【年(卷),期】2014(000)002【总页数】2页(P159-160)【关键词】焊接机器人;大臂;有限元分析【作者】王昆;刘进福;韩晶;莫贤【作者单位】常州先进制造技术研究所,江苏常州213164;常州先进制造技术研究所,江苏常州213164;常州先进制造技术研究所,江苏常州213164;常州先进制造技术研究所,江苏常州213164【正文语种】中文【中图分类】TP2420 引言目前,在企业组织产品焊接中,大都采用手工焊接,其不足之处在于:手工焊接质量不稳定,工人劳动强度大;焊接时产生的烟雾对工人的呼吸系统产生损害,焊接时发出的亮光会对工人的眼角膜产生损害;手工焊接的生产效率低。
使用焊接机器人不仅能降低焊接对工人身体的危害,还能够有效地提高工作效率,降低劳动成本。
焊接机器人的大臂是整个机器人受力最大的机构,作为机器人的重要部件,其刚度和强度直接影响到机器人的使用精度和寿命。
在设计过程中必须保证它的强度和刚度及在运动过程中振动频率的影响。
本文在有限元受力分析软件ANSYS下对焊接机器人的大臂进行静力分析,为机器人整体设计和优化提供有效的理论支持。
1 模态分析理论基础有限元的模态分析就是建立模态模型进行数值分析的过程。
对于一般的多自由度结构系统而言,运动都可以由其自由振动的模态来合成。
由于系统结构阻尼主要发生在固定的或可动的连接部位,因此零件材料的内阻尼只是吸收和损耗能量的一部分[5]。
系统自由振动系统方程为:其中:[M]和[K]分别为油缸坯料搬运系统的质量矩阵和刚度矩阵,均为N×N阶方阵;{X}表示油缸坯料搬运系统的位移向量,同时还可以将式(1)写成位移向量的形式:经线性变换式{x}=[u]{y}对集合位置坐标{x}表示的耦合系统微分方程组进行解耦。
ansys复杂几何模型的系列网格划分

二、 映射网格划分
映射网格划分是对规整模型的一种规整网格划分方法,其原始概念是:对于面,只能是四边形面,网格划分数需在对边上保持一致,形成的单元全部为四边形;对于体,只能是六面体,对应线和面的网格划分数保持一致;形成的单元全部为六面体。在ANSYS中,这些条件有了很大的放宽,包括:
1 面可以是三角形、四边形、或其它任意多边形。对于四边以上的多边形,必须用LCCAT命令将某些边联成一条边,以使得对于网格划分而言,仍然是三角形或四边形;或者用AMAP命令定义3到4个顶点(程序自动将两个顶点之间的所有线段联成一条)来进行映射划分。
复杂几何模型的系列网格划分
众所周知,对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。在ANSYS中,大家知道,网格划分有三、划分网格。在这里,我们仅对网格划分这个步骤所涉及到的一些问题,尤其是与复杂模型相关的一些问题作简要阐述。
子结构(也称超单元)也是一种解决大型问题的有效手段,并且在ANSYS中,超单元可以用于诸如各种非线性以及装配件之间的接触分析等,有效地降低大型模型的求解规模。
巧妙地利用结构的对称性对实际工作也大有帮助,对于常规的结构和载荷都是轴对称或平面对称的问题,毫无疑问应该利用其对称性,对于一些特殊情况,也可以加以利用,比如:如果结构轴对称而载荷非轴对称,则可用ANSYS专门用于处理此类问题的25、83和61号单元;对于由多个部件构成装配件,如果其每个零件都满足平面对称性,但各对称平面又不是同一个的情况下,则可用多个对称面来处理模型(或至少可用此方法来减少建模工作量:各零件只需处理一半的模型然后拷贝或映射即可生成总体模型)。
2 面上对边的网格划分数可以不同,但有一些限制条件。
3 面上可以形成全三角形的映射网格。
弹性力学5-圣维南原理
P
P
P
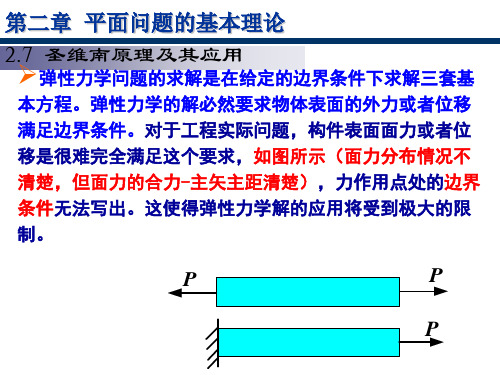
第二章 平面问题的基本理论 2.7 圣维南原理及其应用
低碳钢拉伸,轴力N是通过端部夹头的接触力得到的,
而接触力的分布情况是不清楚的,但面力的合成结果可以 确定,即轴力N,这个试件端部的精确的边界条件是无法写 出的,如何来求解这类问题?
为了扩大弹性力学解的适用范围,放宽这种限制,圣维南提 出了局部影响原理—圣维南原理。
图(a)
F
图(b) F
F
第二章 平面问题的基本理论 2.7 圣维南原理及其应用
圣维南原理的应用
注意:
边界力替换时必须满足静力等效条件。 只能在次要边界界
F
F/A
第二章 平面问题的基本理论 2.7 圣维南原理及其应用
圣维南原理的应用
(2)通过圣维南原理的使用,可以将一些难以处理 的边界条件转化为基本方程所能够满足的边界条件, 使得弹性力学问题得到解答。
h/2
h/2
∫ ∫ σ( ) −h/ 2
x x=±l
ydy ⋅1 = ±
−h/ 2
f x ( y) ydy ⋅1
h/2
h/2
∫ ∫ −h / 2 (τ xy ) x=±l dy ⋅1 = ± −h / 2 f y ( y)dy ⋅1
第二章 平面问题的基本理论 2.7 圣维南原理及其应用
h/2
h/2
第二章 平面问题的基本理论 边界条件写法小结
(2)直接写法(直接在图上标出)
例2.5 写出如图所示弹性体的应力边界条件。
左竖直边界:x=0 σ x x=0 = −γ y τ xy x=0 = 0 上水平边界:= y=0 σ y y 0= = −q τ xy y 0 = τ 0 右竖直边界:x=b
圣维南原理

几何方程
应变
协调条件
位移
位移求解: 位移
几何方程
应变
物理方程
应力
应力解法
未知数3个σx、σy、τxy,须联立平衡方程与 变形协调条件,以平面应力问题为例, 将虎克定律代入应变协调条件得到:
xy ( x y ) 2 ( y x ) 2(1 ) 2 y x xy
X Y x y x 2 y 2 ( x y ) (1 )
2 2
(1)
平面应力情形
控制方程
μ
μ/1-μ
平面应变情形
控制方程
1 X Y ( ) x y x 2 y 2 1 x y
i
这种等效只是从平衡的观点而言的,对刚体来而言完全正 确,但对变形体而言一般是不等效的。
2.圣维南原理
(Saint-Venant Principle)
原理: 若把物体的一小部分边界上的面力,变换为分布 不同但静力等效的面力,则近处的应力分布将有 显著改变,而远处所受的影响可忽略不计。 P P/2
P A
h( yx )y Nhomakorabea0dx P cos
可见,与前面结果相同。
§2-8 平面问题应力解法
上节回顾 应力解法 应力函数
上节回顾
平衡方程 基本方程 几何方程 物理方程 位移边界 边界条件 应力边界 混合边界 弹性力学问题的解
基本方程
1、平衡方程
xy x X 0 x y xy y Y 0 x y
P P/2
P A P A
P
3.圣维南原理的应用
圣维南原理的有限元模拟

圣维南原理的有限元模拟圣维南原理是电子学中的一项基本原理,用于描述电导体中电流分布情况的方法,常用于有限元模拟中来解决电磁场问题。
有限元模拟是一种基于数值方法的工程分析技术,通过将连续的物理问题离散化为有限数量的元素,再利用数值计算方法对这些元素进行求解,以模拟实际问题的行为和物理特性。
以下是关于圣维南原理在有限元模拟中的详细介绍。
圣维南原理(Saint-Venant’s Principle)主要用于描述电导体中的电流分布情况。
它是基于电流连续性方程和欧姆定律的基本原理,即电流在导体内部的分布是均匀且沿导体表面方向渐变。
根据这个原理,在有限元模拟中可以通过离散化导体为一系列有限元素来近似描述电流的分布情况。
在有限元模拟中,首先需要将导体区域划分为小块,称为有限元。
每个有限元都有一组自由度,用于描述电场强度或电势的分布情况。
在圣维南原理的约束下,任意两个相邻的有限元之间,在其界面上,电场强度或电势需要满足一定的连续性条件。
这些连续性条件可以通过将不同有限元之间的界面进行连接,构建整个导体区域的有限元模型。
有限元模型构建完成后,利用数值方法求解模型中的电场强度或电势分布。
通常采用有限元法的变分形式,通过求解最小化电场强度或电势的能量泛函来得到电场方程的离散形式。
然后,通过数值求解方法(如有限差分法等)对离散的电场方程进行求解,得到电场强度或电势分布的近似解。
由于圣维南原理的应用,有限元模拟能够较准确地描述导体中电流的分布情况。
采用有限元模拟方法,可以更好地理解和分析各种电磁场问题,如电磁传感器中的电流分布、电源线中的电压降等。
有限元模拟结果可以帮助工程师优化设计和制造过程,提高电子设备的性能和可靠性。
总之,圣维南原理作为电导体中电流分布的基本原理,在有限元模拟中扮演着关键的角色。
通过有限元模拟,可以准确地描述电流在导体中的分布情况,帮助工程师解决电磁场问题,从而优化设计和制造过程,提高电子设备的性能和可靠性。
基于ANSYS的换热器管板应力分析及其优化设计

基于ANSYS的换热器管板应力分析及其优化设计发布时间:2021-06-18T02:32:55.905Z 来源:《中国科技人才》2021年第9期作者:王宜亮[导读] 为研究换热器管板受力复杂的问题,基于ANSYS Workbench软件,以管板应力受管壳程温度载荷、压力载荷和管板厚度的影响为研究对象,研究了其应力分布情况,得出管板在换热器壳程先停工况时最危险;江苏自动化研究所江苏连云港 222061摘要:为研究换热器管板受力复杂的问题,基于ANSYS Workbench软件,以管板应力受管壳程温度载荷、压力载荷和管板厚度的影响为研究对象,研究了其应力分布情况,得出管板在换热器壳程先停工况时最危险;同时对此工况下各参数进行关联性分析和对管板进行优化分析。
结果表明:温度载荷对管板应力分布的影响程度最大,其次是管板厚度,压力载荷影响最小;管板可由原有的35mm厚度优化43%,在管板厚度降低至20mm后,仍满足安全要求,达到安全与经济兼顾。
关键词:管壳式换热器;管板;关联性分析;优化分析Stress analysis and optimization design of heat exchanger tube-sheet based on ANSYSWANG Yiliang( Jiangsu AutomationResearchInstitute, Lianyungang222061)Abstract: In order to study the complex stress on the tube-sheet of heat exchanger, the stress distribution of the tube-sheet was studied by using ANSYS Workbench and taking the influence of temperature load, pressure load and thickness of tube-sheet as the research object. It is concluded that tube-sheet is the most dangerous when the shell side of heat exchanger stops first. At the same time, the correlation analysis of the parameters and the optimization analysis of the tube-sheet are carried out. The results show that: the temperature load has the greatest influence on the stress distribution of the tube-sheet, followed by the thickness of the tube-sheet, and the pressure load has the least influence; the tube-sheet thickness can be optimized by 43% from the original 35mm thickness, and the safety requirements can still be met after the tube-sheet thickness is reduced to 20mm, which can achieve both safety and economy.Key words: Shell-and-tube heat exchanger; Tube-sheet; Relevance analysis; Optimization analysis0前言管壳式换热器管板的设计与优化是为了使换热器在实际运行中更加安全,能有效提高能源的利用率。
什么是圣维南原理及如何证明
弹塑性力学作业孙嘉粲建筑与土木工程2017级3班学号2170970036Q1:什么是圣维南原理?Q2:为什么需要圣维南原理?Q3:如何证明圣维南原理是正确的?Q1:什么是圣维南原理?答:圣维南原理(Saint Venant’s Principle)是弹性力学的基础性原理,是法国力学家圣维南于1855年提出的。
其内容是:分布于弹性体上一小块面积(或体积)内的荷载所引起的物体中的应力,在离荷载作用区稍远的地方,基本上只同荷载的合力和合力矩有关;荷载的具体分布只影响荷载作用区附近的应力分布。
还有一种等价的提法:如果作用在弹性体某一小块面积(或体积)上的荷载的合力和合力矩都等于零,则在远离荷载作用区的地方,应力就小得几乎等于零。
不少学者研究过圣维南原理的正确性,结果发现,它在大部分实际问题中成立。
因此,圣维南原理中“原理”二字,只是一种习惯提法。
有限元软件的模拟验证了这一点,如图1所示。
==图1 有限元计算得到的柱体在不同应力边界下得到的应力分布图Q2:为什么需要圣维南原理?问题的提出:弹性力学问题的求解是在给定的边界条件下求解基本方程。
使应力分量、应变分量、位移分量完全满足8个基本方程相对容易。
但对于工程实际问题,构件表面面力或者位移是很难满足边界条件要求。
这使得弹性力学解的应用将受到极大的限制。
为了扩大弹性力学解的适用范围,放宽这种限制,圣维南提出了局部影响原理。
圣维南原理的应用:对复杂的力边界,用静力等效的分布面力代替。
有些位移边界不易满足时,也可用静力等效的分布面力代替。
不论在弹性力学中还是在有限元中都广泛灵活的应用圣维南原理来处理和简化边界条件。
值得注意的是:圣维南原理只能适用于一小部分边界(小边界:尺寸相对很小的边界;次要边界:面力分布复杂的小边界)。
对于主要边界,圣维南原理不再适用。
例如对于较长的粱,其端部可以应用圣维南原理,而在粱的侧面,则不能应用。
Q3:如何证明圣维南原理是正确的?见附录1《圣维南原理证明》附录1《圣维南原理证明》1.Boussinesq 的陈述1855年Boussinesq 将圣维南的思想一般化,并冠“Saint-Venant’s Principle ”的名称,其内容为:施于弹性体上的任意平衡力系,如果其作用点限于某个给定的球内,那么该平衡力系在任意一个与球的距离远大于球半径的点上所产生的形变是可以忽略的。
发夹式换热器管板的应力分析与强度评定
第53卷第4期 辽 宁 化 工 Vol.53,No. 4 2024年4月 Liaoning Chemical Industry April,2024发夹式换热器管板的应力分析与强度评定孙梦莹,郭超越,李卓群,刘壮(沈阳化工大学 机械与动力工程学院,辽宁 沈阳 110142)摘 要:应用ANSYS有限元分析软件,考虑压力载荷和温度载荷对管板整体应力分布的影响,采用顺序耦合法对发夹式循环冷却器的热端管板在7种工况下进行有限元应力分析。
结果表明:在压力载荷与温度载荷共同作用下,管板最大等效应力为329.9 MPa,位于布管区内换热管与管板连接处。
壳程先停工况下管板的最大等效应力值最大值为332.5 MPa,是发夹式循环冷却器管板的最危险工况。
在对管板上最大等效应力处进行当量线性化处理,结合分析设计标准进行强度评定,评定结果均合格。
关 键 词:发夹式换热器;管板;有限元分析;应力线性化;强度评定中图分类号:TQ051.5 文献标识码: A 文章编号: 1004-0935(2024)04-0545-04发夹式换热器因其外形形似发夹而得名,其外形结构可视为单管程、单壳程、管束为U型的固定管板式换热器[1]。
与传统换热器相比,发夹式换热器具有换热效率高、管板温差应力小等优点[2]。
如何依据换热器形式以及选择合适的设计标准,进行管板设计是换热器设计工作中一项重要工作[3]。
随着计算机技术的发展,利用有限元软件辅助管板设计进行了很多工作[4-9]。
陈杰[5]等利用ANSYS 有限元软件对LNG绕管式换热器管板及其相连的管箱、换热器壳体进行了整体建模和多工况下的有限元应力分析。
通过增加短节厚度的方式解决了管箱短节处局部薄膜应力过大的问题。
张睿明[9]等利用ANSYS有限元软件中的Workbench模块针对U 型管换热器的管板进行了热固耦合分析,比较了三角形与正方形布管方式对管板热应力及机械应力的影响,为特定工况下选择合适的布管方式提供了理论依据。
ansys子模型介绍与应用实例
第五章子模型何为子模型子模型是得到模型部分区域中更加精确解的有限单元技术。
在有限元分析中往往出现这种情况,即对于用户关心的区域,如应力集中区域,网格太疏不能得到满意的结果,而对于这些区域之外的部分,网格密度已经足够了。
见图5-1。
图5-1 轮毂和轮辐的子模型 a)粗糙模型,b)叠加的子模型要得到这些区域的较精确的解,可以采取两种办法:(a)用较细的网格重新划分并分析整个模型,或(b)只在关心的区域细化网格并对其分析。
显而易见,方法a太耗费机时,方法b即为子模型技术。
子模型方法又称为切割边界位移法或特定边界位移法。
切割边界就是子模型从整个较粗糙的模型分割开的边界。
整体模型切割边界的计算位移值即为子模型的边界条件。
子模型基于圣维南原理,即如果实际分布载荷被等效载荷代替以后,应力和应变只在载荷施加的位置附近有改变。
这说明只有在载荷集中位置才有应力集中效应,如果子模型的位置远离应力集中位置,则子模型内就可以得到较精确的结果。
ANSYS程序并不限制子模型分析必须为结构(应力)分析。
子模型也可以有效地应用于其他分析中。
如在电磁分析中,可以用子模型计算感兴趣区域的电磁力。
除了能求得模型某部分的精确解以外,子模型技术还有几个优点:它减少甚至取消了有限元实体模型中所需的复杂的传递区域。
它使得用户可以在感兴趣的区域就不同的设计(如不同的圆角半径)进行分析。
它帮助用户证明网格划分是否足够细。
使用子模型的一些限制如下:只对体单元和壳单元有效。
子模型的原理要求切割边界应远离应力集中区域。
用户必须验证是否满足这个要求。
如何作子模型分析子模型分析的过程包括以下步骤:1. 生成并分析较粗糙的模型。
2. 生成子模型。
3. 提供切割边界插值。
4. 分析子模型。
5. 验证切割边界和应力集中区域的距离应足够远。
第一步:生成并分析较粗糙的模型第一个步骤是对整体建模并分析。
(注-为了方便区分这个原始模型,我们将其称为粗糙模型。
这并不表示模型的网格划分必须是粗糙的,而是说模型的网格划分相对子模型的网格是较粗糙的。
基于ANSYS的带孔钢板应力分析
基于ANSYS的带孔钢板应力分析戴雨;魏莉洁【摘要】对带孔钢板进行了有限元分析.通过ANSYS路径操作,分析了小孔周边应力、变形沿路径分布状态及变化规律,得出小孔周边应力集中的情况,为钢板的加工制作、质量控制及工程应用提供了可借鉴的方法.【期刊名称】《建材技术与应用》【年(卷),期】2011(000)006【总页数】3页(P4-6)【关键词】平面应力;有限元法;应力集中【作者】戴雨;魏莉洁【作者单位】南通航运职业技术学院,船舶与海洋工程系,江苏,南通,226010;南通航运职业技术学院,船舶与海洋工程系,江苏,南通,226010【正文语种】中文【中图分类】O343.1;TU311引言板是主要的工程构件,弹性板是土木工程、地下建筑工程和水利工程中较为常用的一种结构形式,尤其是钢板的应用更为普遍。
ANSYS是工程和教育方面非常流行的有限元软件[1],具有很高的应用价值,在机械工程、土木工程、航空航天工程和材料科学等领域都有所应用。
路径操作[2]是ANSYS通用后处理中一项较重要的内容,路径是模型上一系列由节点或坐标位置定义的轨迹,其作用是可以将结果数据映射到模型中一条由用户指定的路径上,对路径上的数据可以执行各种数学运算和微积分运算,许多计算结果对工程应用具有重要的实际意义。
利用ANSYS路径操作,分析小孔周边应力、变形沿路径分布状态及变化规律,得出小孔周边应力集中分布情况,为钢板在加工制作、质量控制、工程应用中提供可借鉴的方法,具有重要的实际意义。
1 钢板模型及特征参数[3]钢板长100 mm,宽20 mm,中心有一直径为2 mm的小圆孔,在左端固定,右端受水平方向5 kN的拉力作用,钢板弹性模量EX=2.06×105MPa,泊松比PRXY=0.3,密度(DENS)为7 850 kg/m3。
对该薄板使用PLANE42单元[4],单元尺寸划分边长控制为1 mm,实体模型见图1,有限元模型见图2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:张继刚学号:3116301035 班级:硕6008
圣维南原理验证
一、圣维南原理简介
圣维南原理(Saint Venant’s Principle)是弹性力学的基础性原理,是法国力学家圣维南于1855年提出的。
其内容是:分布于弹性体上一小块面积(或体积)内的荷载所引起的物体中的应力,在离荷载作用区稍远的地方,基本上只同荷载的合力和合力矩有关;荷载的具体分布只影响荷载作用区附近的应力分布。
二、建立实验模型
此次实验使用的是一根梁,材料为45#钢,长为800mm,截面尺寸为50x30mm,弹性模量为2e11Pa,泊松比为0.3,单元类型选择8nodessolid185 。
具体命令流为
finish
/clear,nostart
/prep7
et,1,185
mp,ex,1,2e11
prxy,1,0.3
dens,1,7800
block,0,30,0,50,0,800
esize,0,88
lesize,2,,,4
lesize,4,,,4
lesize,5,,,4
lesize,7,,,4
lesize,1,,,6
lesize,3,,,6
lesize,6,,,6
lesize,8,,,6
vmesh,1
三、分两种情况对比处理
1、对模型一端施加全约束,另一端的面中心点施加集中力1.5e6N,求解,显示z 方向的应力分布及大小。
具体命令流操作:
/solu
da,1,all
f,63,fz,1500000
solve
/post1
PLNSOL,s,z
2、对模型一端施加全约束,另一端面施加均布载荷1000N/m㎡,求解,显示z 方向的应力分布及大小。
具体操作命令流:
/solu
da,1,all
sfa,2,,pres,1000
solve
/post1
PLNSOL,s,z
四、分析并得出结论
比较两张应力分布图可以看出,两次不同的加载,远离作用区域的应力几乎不发生变化,集中力作用时在梁上的最小值为1055.42N,均匀载荷作用时在梁上最小值为1088.06N,二者几乎相等,且此值分布在远离作用域的大部分区域中,变化较大的只集中在作用区域附近。
说明作用于弹性体的载荷,改变其载荷分布情况,而不改变载荷总的合成值,且不引起主力矩变化,其载荷作用只影响作用区域附近,而对其它较远的部位几乎不会产生影响,即简单验证圣维南原理。
附图:位移变化图及总应力图。
