6流体动力学例题
[考研类试卷]流体力学(流体动力学)历年真题试卷汇编1.doc
![[考研类试卷]流体力学(流体动力学)历年真题试卷汇编1.doc](https://img.taocdn.com/s3/m/cf9792b8376baf1ffc4fadde.png)
(B)错误
29 (河海大学2005年考研试题)急变流不可能是均匀流。
(A)正确
(B)错误
30 (河海大学2005年考研试题)堰流是一种急变流。
(A)正确
(B)错误
五、填空题
请完成下列各题,在各题的空处填入恰当的答案。
31 (武汉大学2009年考研试题)当 =0时,水流为_________。
7 (北京航空航天大学2005年考研试题)一油箱如图3—4所示,油箱中装有其容积1/3的汽油,飞机以匀加速a水平运动,试求能使汽油自由面达箱底时的加速度值。
8 (天津大学2002年考研试题)对于ux=2xy,uy=a2+x2一y2的平面流动,a为常数。试分析判断:(1)是恒定流还是非恒定流? (2)是均匀流还是非均匀流? (3)是有旋流还是无旋流?
[考研类试卷]流体力学(流体动力学)历年真题试卷汇编1
1 (北京航空航天大学2007年考研试题)已知速度场 ,试确定(3,1,2)处的加速度。
2 (北京航空航天大学2007年考研试题)已知流体的流动速度为 ,试求t=0时过M(一1,一1)点的流线。
3 (北京航空航天大学2006年考研试题)已知速度场 ,试求在t=2时刻空间点(1,2,3)处的加速度。
13 (中国科学院一中国科技大学2007年考研试题)流动满足质量守恒的表达式是什么?不可压缩流体的方程被简化成什么形式?
14 (中国科学院一中国科技大学2007年考研试题)试述物质导数(又称随体导数)和当地导数的定义,并阐述两者的联系。
三、单项选择题
下列各题的备选答案中,只有一个是符合题意的。
15 (武汉大学2009年考研试题)均匀流的总水头线与测压管水头线的关系是( )。
9 (东南大学2005年考研试题)简要回答流体微团运动的基本形式有哪几种。
气动元件的流体动力学分析考核试卷

A.高效节能
B.安全可靠
C.简单易用
D.高成本
()
20.以下哪些情况下,需要重新调整气动系统的压力设定?()
A.系统工作压力不稳定
B.系统的工作负载发生变化
C.环境温度变化较大
D.系统元件老化
()
三、填空题(本题共10小题,每小题2分,共20分,请将正确答案填到题目空白处)
1.在流体力学中,流体受到的阻力与流体速度的平方成正比,这一规律称为______定律。
A.气阻影响系统的稳态特性,气容影响系统的动态响应
B.气容影响系统的稳态特性,气阻影响系统的动态响应
C.气阻和气容都只影响系统的稳态特性
D.气阻和气容都影响系统的动态响应
()
8.下列哪种流体流动状态是层流?()
A.高速流动
B.低速流动
C.高粘度流体流动
D.低粘度流体流动
()
9.气动执行元件中,哪种元件通常用来实现快速往复运动?()
3.结合流体动力学原理,解释为何在气动执行元件中会出现响应滞后现象,并讨论如何通过系统设计来减少这种滞后。
4.分析气动系统在不同工作条件(如温度、湿度变化)下可能出现的性能问题,并提出相应的解决措施。
标准答案
一、单项选择题
1. B
2. C
3. A
4. A
5. D
6. A
7. D
8. C
9. C
10. C
()
2.气动元件中的气缸根据其结构特点,可以分为______气缸和______气缸。
()
流体动力学 习题答案

流体动力学习题答案流体动力学习题答案流体动力学是研究流体运动规律以及与固体的相互作用的学科。
它广泛应用于航空航天、海洋工程、能源工程等领域。
在学习流体动力学的过程中,习题是不可或缺的一部分。
下面我将为大家提供一些流体动力学习题的答案,希望能帮助大家更好地理解和掌握这门学科。
1. 什么是流体的黏性?黏性对流体流动有什么影响?答:流体的黏性是指流体内部分子之间的相互作用力。
黏性对流体流动有重要影响。
当流体黏性较小时,流体流动较为快速,流线较为平滑;当流体黏性较大时,流体流动较为缓慢,流线较为弯曲。
黏性还会导致流体内部的能量损失,使得流体流动变得不稳定。
2. 什么是雷诺数?雷诺数的大小对流动有何影响?答:雷诺数是描述流体流动状态的一个无量纲参数,它由流体的惯性力和黏性力之比确定。
雷诺数越大,惯性力相对于黏性力的作用就越显著,流体流动越不稳定,容易产生湍流现象。
雷诺数越小,黏性力相对于惯性力的作用就越显著,流体流动越稳定,容易产生层流现象。
3. 什么是伯努利方程?它适用于哪些流动情况?答:伯努利方程是描述流体在无黏性、定常、不可压缩条件下流动的基本方程。
它表达了流体的动能、压力和重力势能之间的关系。
伯努利方程适用于流体在光滑管道中的流动、流体通过收缩管道的流动等情况。
4. 什么是流体的黏滞阻力?黏滞阻力与流体速度和黏性有何关系?答:流体的黏滞阻力是流体在流动过程中受到的阻碍力。
黏滞阻力与流体速度和黏性有密切关系。
当流体速度较小时,黏滞阻力较小;当流体速度较大时,黏滞阻力较大。
同时,黏滞阻力还与流体的黏性有关,黏性越大,黏滞阻力越大。
5. 什么是流体的旋转流?旋转流与无旋流有何区别?答:流体的旋转流是指流体在流动过程中存在旋转的情况。
旋转流与无旋流的区别在于流体速度场的旋度。
旋转流的旋度不为零,表示流体在流动过程中存在旋转;无旋流的旋度为零,表示流体在流动过程中没有旋转。
以上是对一些流体动力学习题的答案解析。
《流体力学》第六章气体射流

.
射流参数的计算
段 名
参数名称
符号
圆断面射流
平面射流
扩散角 主
α tg3.4a tg2.44a
体
段 射流直径 或半高度
D b
D d0
6.8
as d0
0.147
b b0
2.44
0.095 as 0.147
d0
v1 0.492
v0
as 0.41
b0
v2
v2 v0
as
0.23 0.147
d0
v2 v0
0.833 as 0.41 b0
.
段名 参数名称
符 号
圆断面射流
平面射流
起
流量
Q
2
QQ0 10.76ar0s1.32ar0s
Q Q0
1 0.43 as b0
始
v 断面平均 流速
B0Kx
tgKxK3.4a
x
紊流系数
起始段
主体段
C
B
A
R
M
α r0
核心
0
D X0
边 E
界 层
Sn
F
S
X
射流结构
.
紊流系数与 出口断面上 紊流强度有 关,也与出 口断面上速 度分布的均 匀性有关。 (表6-1)
紊流系数
喷嘴种类 带有收缩口的喷嘴
a
0.066 0.071
圆柱形管
带有导风板的轴流式通风机 带导流板的直角弯管
已知射流直径D, v2,d0,a, 求S和Q0
流体力学例题(动力学部分)
1000
q
49 7 m / s
d 2
4
v2
0 .12
4
7 55 10
3
m /s
3
2
6.一个100N的重物恰被一垂直水射 流所支承,其中d=6cm,出口速度 v=8m/s,不计沿程损失,求Y=? 解:水流接触重物后动量发生了变化
Fiy q ( 2 v y 2 1 v y 1 )
Fiy 100 N q v y2
d 2
4 0
v
0 . 06 2
z1 z 2 z
v2 q2
v1
q1
由伯努利方程: v1 v 2 v
v1 q1
令: 1 由动量方程:
v
A
F i 0 q1v q 2 v qv cos
q1 q 2 q cos v 2 q2 由连续性方程:q1 q 2 q
2 gH v
令: 2 1 1
带入动量方程: F q ( 2 v z 2 1v z1 )
F av ( v a A 2 gH v )
2
水流对水桶的作用为-F
W W 0 F W 0 av ( v a A 2 gH v )
4
8 0 . 0226 m / s
3
令: 2 1 1
则:
v y1
F
q
100 1000 0 . 0226
4 . 42 m / s
由出口和重物底面的伯努利方程:
z1 p
g
v1
流体运动练习题

流体运动练习题在学习流体力学相关知识时,进行练习题是非常重要的一部分。
通过练习题的解答,我们可以更加深入地理解流体运动的原理和应用。
下面是一些流体运动练习题,帮助大家加深对这一概念的理解。
练习题一:斜面上的流体流动假设有一个倾斜角度为θ的斜面,上面有一水平管道,管道之间有一段高度为h的竖直距离。
斜面上方的水箱中有一深度为H的水柱。
求当水流过管道时,出口的速度。
解答:设斜面的长度为L,管道的长度为d,管道入口处的面积为A1,出口处的面积为A2,管道入口处的速度为v1,出口处的速度为v2。
根据质量守恒定律,流入管道的质量等于流出管道的质量:ρ₁ * A₁ * v₁ = ρ₂ * A₂ * v₂其中ρ₁为水箱中的水密度,ρ₂为管道内的水密度。
由连续方程可知,流动过程中单位时间内流入管道的体积等于单位时间内流出管道的体积:A₁ * v₁ = A₂ * v₂通过以上两个方程,可以解得v₂的值。
练习题二:流体在水平管道中的流动假设有一水平管道,管道长度为L,截面积为A,有一段长度为d的管道内壁粗糙程度为ε。
当管道内液体流动速度为v时,求管道内壁受到的摩擦力F。
解答:根据达西定理,管道内壁受到的摩擦力可以通过以下公式计算:F = f * ρ * A * v² / 2其中f为管道内壁的摩擦系数,ρ为液体的密度。
在该问题中,管道内壁的粗糙程度为ε,可以利用密度函数方法计算摩擦系数f。
将管道内壁分成若干小区间,每个小区间的长度为Δx,宽度为Δy。
在每个小区间内,液体受到的正压力和摩擦力之和等于液体的密度乘以加速度。
通过计算每个小区间的摩擦力,再将其累加即可得到管道内壁受到的总摩擦力。
练习题三:流体的流速和流量关系假设有一管道,管道横截面积为A,液体的密度为ρ,管道内的液体流速为v。
求液体的流量Q。
解答:根据流量定义,流量Q等于单位时间内通过截面A的体积,可以通过以下公式计算:Q = A * v在流体力学中,流速是指流体通过单位时间内通过管道横截面的体积,而流量是指单位时间内通过管道横截面的体积。
流体力学例题及思考题-第三章
第三章流体运动学与动力学基础主要内容基本概念欧拉运动微分方程连续性方程——质量守恒*伯努利方程——能量守恒** 重点动量方程——动量守恒** 难点方程的应用第一节研究流体运动的两种方法流体质点:物理点。
是构成连续介质的流体的基本单位,宏观上无穷小(体积非常微小,其几何尺寸可忽略),微观上无穷大(包含许许多多的流体分子,体现了许多流体分子的统计学特性)。
空间点:几何点,表示空间位置。
流体质点是流体的组成部分,在运动时,一个质点在某一瞬时占据一定的空间点(x,y,z)上,具有一定的速度、压力、密度、温度等标志其状态的运动参数。
拉格朗日法以流体质点为研究对象,而欧拉法以空间点为研究对象。
一、拉格朗日法(跟踪法、质点法)Lagrangian method1、定义:以运动着的流体质点为研究对象,跟踪观察个别流体质点在不同时间其位置、流速和压力的变化规律,然后把足够的流体质点综合起来获得整个流场的运动规律。
2、拉格朗日变数:取t=t0时,以每个质点的空间坐标位置为(a,b,c)作为区别该质点的标识,称为拉格朗日变数。
3、方程:设任意时刻t,质点坐标为(x,y,z) ,则:x = x(a,b,c,t)y = y(a,b,c,t) z = z(a,b,c,t) 4、适用情况:流体的振动和波动问题。
5、优点: 可以描述各个质点在不同时间参量变化,研究流体运动轨迹上各流动参量的变化。
缺点:不便于研究整个流场的特性。
二、欧拉法(站岗法、流场法)Eulerian method1、定义:以流场内的空间点为研究对象,研究质点经过空间点时运动参数随时间的变化规律,把足够多的空间点综合起来得出整个流场的运动规律。
2、欧拉变数:空间坐标(x ,y ,z )称为欧拉变数。
3、方程:因为欧拉法是描写流场内不同位置的质点的流动参量随时间的变化,则流动参量应是空间坐标和时间的函数。
位置: x = x(x,y,z,t)y = y(x,y,z,t) z = z(x,y,z,t)速度: u x =u x (x,y,z,t )u y =u y (x,y,z,t ) u z =u z (x,y,z,t )同理: p =p (x,y,z,t ) ,ρ=ρ(x,y,z,t) 说明: x 、y 、z 也是时间t 的函数。
流体静力学流体动力学pre
复习牛顿粘性定律:dyud &μzg ——p /ρ——在同一静止流体中,处在不同位置流体的位能和静压能各不相同,但二者可以转换,其总和(势能)保持不变。
静力学方程:例题:斜管+倒U形管压差计——难点二、液位测量1. 液面管最原始的液位测量装置液面越高,h↓,R↓;当液面达到最高时,h=0,R=0ρ0ρ11’前提:管道中充满N 2, 其ρ较小u 气很慢0ABρ0ρp a p a3. 远距离液位测量装置液封作用:(1)确保设备安全:当设备内压力超过规定值时,气体从液封管排出,又称安全性液封;(2)设备为负压时,防止外界气体进入设备内。
三、液封高度的计算四、流向的判断流体由高势能向低势能流动例题h1’h2小结1.2静力学基本方程式:g z 211=+●放大读数:斜管式压差计、双液体压差计缩小读数:复式压差计静力学基本方程应用:●●应用条件北京化工大学●1.3 流体动力学1 流量volumetric flow ratemass flow rate2 流速average velocitymass velocity=uq V π4u 适宜u费用总费用设备费操作费3. 管径的估算steady state flowunsteady state flow121′2′equation of continuity⎜⎜==即不可压缩流体在管路中任意截面的流速与管内径的平方成反比。
例1-6=管路3a,3b (φ57×3.5mm):=(1)内能贮存于物质内部的能量流体具有的内能为mU ,J;(2)位能流体受重力作用在不同高度具有的能量m kg 流体具有的位能为mgZ ,J;(3)动能——流体因运动而具有的能量m kg 流体具有的动能为mu 2/2,J;(4)静压能使流体流动而对抗压力所作的功成为流体的静压能m kg 流体具有的静压能为pV ,J;(5)外加功——流体接受流体输送机械向流体作功或流体通过水力机械向外界作功。
流体运动学及动力学基础练习题
第三章 流体运动学及动力学基础练习题一、 单项选择题1. 定常流动中,流体质点的加速度等于( )A .等于零 B. 等于常量 C 随时间变化而变化 D 与时间无关2. 一维流动的连续性方程C VA =成立的必要条件是( )A 理想流体B 黏性流体C 可压缩流体D 不可压缩流体3. 均匀流是( )A 当地加速度为零B 迁移加速度为零C 向心加速度为零D 合加速度为零4. 均匀流过流断面上各点的( )等于常数A. PB. g p z ρ+C. g V g p 22+ρ D gV g p z 22++ρ 5. 用欧拉法研究流体运动时,流体质点的加速度a=( )A. 22dtr d B. t ∂∂U C )u u.∇( D )u u.U ∇+∂∂(t 6. 控制体是指相对于某个坐标系来说( )A 由确定的流体质点所组成的流体团B 有流体流过的固定不变的任何体积C 其形状、位置随时间变化的任何体积D 其形状不变而位置随时间变化的任何体积7. 恒定总流的连续方程、伯努利方程、动量方程中的流速为( )A 断面平均流速B 断面上的最大流速C 断面形心处的流速D 断面上压力中心处的流速8. 关于水流流向的正确说法是( )A 水一定是从高处往低处流B 水一定是从流速大处往流速小处流C 水一定是从机械能大处往机械能小处流D 水一定是从测压管水头高处往测压管水头低处流9. 非恒定流动中,流线与迹线( )A 一定重合B 一定不重合C 特殊情况下可能重合D 一定正交10. 在应用恒定总流的动量方程∑-=)(1122v v q F v ββρ解体时,∑F 中不应该包括( )A 重力B 压力C 阻力D 惯性力二 、思考题1. “均匀流和渐变流必为恒定流,急变流必为非恒定流”,这种说法对否?为什么?2. 在河道中,为什么自由航行的船只总是向水流较急的一侧河岸靠拢?三.计算题1. 如图所示一消防水枪,已知水管直径D=150mm,喷嘴直径d=75mm,水枪倾角α=30°,压力表读数P=3mH2O,若忽略水头损失,试求:(1)消防水枪的出口速度v0(2)消防水枪对消防队员的后坐力F;(3)消防水枪的最高射程H;(4)最高点处的射流水股直径d’。
流体力学流体动力学基础例题
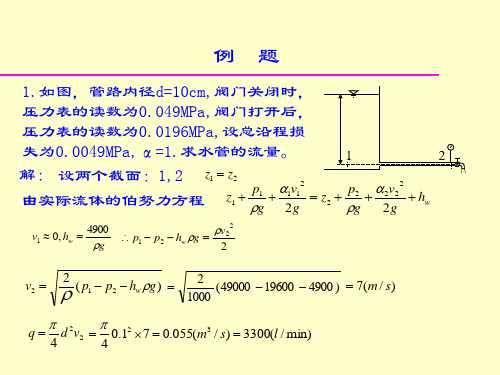
5
2024/10/12
6
【例】 有一贮水装置如图所示,贮水池足够大,当阀 门关闭时,压强计读数为2.8个大气压强。而当将阀门全 开,水从管中流出时,压强计读数是0.6个大气压强,试 求当水管直径d=12cm时,通过出口的体积流量(不计流动 损失)。
【解】 当阀门全开时列1-l、2-2截面的伯努利方程
当阀门关闭时,根据压强计的读数,应用流体静力学基本
试求管中流量qv。
【解】 首先计算1-1断面管路中心的压强。因为A-B为
等压面,列等压面方程得: Hg gh p1 gh1
p1 Hg gh gh1
则
p1
g
Hg
h h1
13.6 0.2 0.72 2
(mH2O)
列1-1和2-2断面的伯努利方程
z1
p1
g
V12 2g
z2
p2
g
V22 2g
H pa 0 0 pa 0.6 pa V22
g
g
2g
2024/10/12
1
方程求出H值
pa gH pa 2.8 pa则H 2.8 pa
g
2.8 98060 9806
28(mH 2O)
代入到上式
V2
2g
H
0.6 pa g
29.8062.8 0.698060 20.78(m/s)
9806
所以管内流量
qV
4
d
2V2
0.785 0.122 20.78 0.235(m3/s)
2024/10/12
2
2024/10/12
3
【例】 水流通过如图所示管路流入大气,已知:U形
测压管中水银柱高差Δh=0.2m,h1=0.72m H2O,管径
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F出 0, F进 0
例4
(3)做运动分析 沿0-1取流线如图,列伯努利方程 2 2 p0 v0 p1 v1 z0 z1 2g 2g 由于水流均暴露在大气中,p0=0,p1=0 在动量定理中,忽略质量力
v1 v0
同理,有:v2 = v0
例4
(4)应用动量定理
2 2
水
p1
v p2 v 2g 水 2g
2 1
d1 v2 v1 d2
2
汞 2 gh 1 水 v1 4 d1 1 d 2
例2
代入数据解得:
汞 2 gh 1 2 9.81 0.2 13.6 1 水 v1 3.49 m / s 4 4 0.15 d1 1 1 d 0.1 2
流体动力学习题课
一、伯努利方程问题解题思路 伯努利方程问题:求流量、流速 (1)取流线为研究对象 (2)做受力分析和运动分析 确定 p1、p2 ,确定 v1、v2 必要时可应用静水力学方程、连续方程 (3)列伯努利方程解
流体动力学习题课
二、动量定理问题解题思路
动量定理问题:求流体对固体壁面的作用力
如图,设有截面积为 A0=0.2 m2 的水柱, 以速度 V0= 5 m/s 向平板 AB 冲击,流速与平 板夹角α= 60°,水密度ρ=1000 kg/m3 。 求水柱对平板的作用力。
例4
解:(1)取虚线所围为控制体为研究对象,
坐标系如图
例4
(2)做受力分析 控制体受平板AB表面力R作用,其方向 指向流体并垂直于平板。 控制体除与平板接触 面外,其他表面均暴露 在大气中,表压为0, 故进、出端表面力:
p1 pa ,
p2 pa
∵ 桶水面面积比孔 口面积大很多
v1 0
例1
(3)列伯努利方程
H
水
p1
v p2 v ( H h) 2g 水 2g
2 1
2 2
代入解得:
v2 2gh
例1
(4)求射程R 水流自出口下落至地面, 落差为H-h,时间为t
1 2 2( H h) H h gt , t 2 g
Q
4
d v1
2 1
4
0.15 3.49 61.6 L / s
2
答:流量为61.6 升/秒。
例3(习题18-5)
利用虹吸管把水从 A 引到 B ,设每小时需 引水100m3,h = 3m,H = 6m,试确定虹吸 管的直径。
例3
解: (1)沿1-2取流线 (2)做受力分析 A、B池面压力均 为大气压,故:
F出 0, F进 0
例5
(3)做运动分析 沿0-1取流线如图,列伯努利方程 2 2 p1 v1 p21 v21 z1 z21 2g 2g 由于水流均暴露在大气中,p1=0,p21=0 在动量定理中,忽略质量力
v21 v1
同理,有:v22 = v1
例5
流入流量为:
p1 p2 h ( 汞 水 )
例2
(3)做运动分析 由连续方程得:
A1 v1 A2 v2 A1 A2
ቤተ መጻሕፍቲ ባይዱ
4 4
d
2 1 2 2
d
d1 v2 v1 d2
2
例2
(4)列伯努利方程
p1 p2 h ( 汞 水 )
答:水柱作用力为5.25KN
(1)取控制体为研究对象
(2)做受力分析和运动分析
确定 p1、p2 ,R,确定 v1、v2
必要时可应用连续方程、伯努利方程
(3)应用动量定理
例1(习题18-2)
开口大圆桶水深 H 恒为常量,在水下深 度 h 处壁上开一小孔(如图),试求由小孔 喷出的水流的射程R。
例1
解:由于H为恒量,故流动为定常。 (1)沿圆桶水面至孔口出口处取流线1-2 (2)做受力分析和运动分析
射流以 V1=19.8m/s 的速度从直径 d=10cm 的孔中射出, 射在固定的圆形曲线叶片上 ,角 度如图所示。求射流对叶片的冲击力。
例5
解:(1)取虚线所围为控制体为研究对象, 坐标系如图
例5
(2)做受力分析 控制体受叶片表面力R作用,其方向指 向流体并垂直于叶片。 控制体除与叶片接 触面外,其他表面均暴 露在大气中,表压为0, 故进、出端表面力:
v2 2 g ( H h) 2 9.81 (6 3) 7.67 m / s
例3
(5)求虹吸管的直径d:
Q
4
d V2
2
4Q 4 100 / 3600 d 0.068 m V2 3.14 7.67
答:虹吸管的直径d应为 6.8cm。
例4(例18-2)
F出y F进y R Q V出y Q V进y
R 0 Q (v0 sin ) A0 v sin
2 0
1000 0.2 5 sin 60
2
4330 N
答:水柱作用力为4330N,方向垂直并指向平板
例5(习题18-9)
Q1
4
d v1
2
4
0.12 19.8 0.155 m3 / s
由于叶片上下对称,在 忽略重力及粘性的情况下, 上下流出流量相等,即:
Q1 Q21 Q22 2
例5
(4)应用动量定理
F出x F进x R Q V出x Q V进x
R Q21 v21 cos 45 Q22 v22 cos 45 Q1 (v1 ) Q1 v1 (cos 45 1) 1 0.155 19.8 (cos 45 1) 5.25 KN
p1 p2 pa
例3
(3)做运动分析 由于A池很大,1点离进水口很远,故进 水口速度: V1≈0 V2为出水口速度
例3
(4)列伯努利方程
v p2 v z1 z2 2g 2g
取B点为 0 势位,则:
2 2
p1
2 1
2 2
v H h0 0 2g
例3
代入解得:
2 H h R v2 t 2 gh 2 ( H h) h g
例2(习题18-3)
文丘里管直径 d1=15cm , d2=10cm ,水 银比压计液面高差 h=20cm 。流管中流体为 水,求流量。
例2
解:(1)沿1-2取流线 (2)做受力分析
p A p1 ( H h) 水 pB p2 H 水 p A pB h 汞
