超弹材料本构模型实验研究
epdm薄膜橡胶包覆材料的粘-超弹本构模型研究

epdm薄膜橡胶包覆材料的粘-超弹本构模型研究摘要:本研究旨在分析epdm薄膜橡胶包覆材料的粘-超弹性本构模型。
为此,实验研究中采用了拉伸、压缩、剪切和滚动测试。
研究结果表明,在拉伸过程中,epdm薄膜橡胶的弹性模量在10kPa-1000kPa之间变化较大,而在压缩拉伸过程中,模量基本保持不变。
此外,剪切和滚动测试表明,由于EPDM薄膜橡胶具有优异的粘合弹性特性,因此可以应用于各种行业中。
例如,它可以用于制造高质量的密封件,可以帮助降低系统泄漏和损坏的风险。
同样,EPDM薄膜橡胶可以用于阻尼装置,可以减少由于强度变化而引起的冲击和振动。
除此之外,EPDM薄膜橡胶还可以用于家具和家用电器,以减少使用者受到的损伤。
而且,它还可以用来制作高性能的导热垫,可以有效地减少工厂的热损失。
此外,EPDM薄膜橡胶还用于制作软管和电缆线,可以增强其耐久性和抗拉强度,可以有效保护电气系统免受破坏。
因此,EPDM薄膜橡胶是一种多功能材料,可以满足各种应用要求。
此外,EPDM薄膜橡胶还可以用于建筑行业,主要是用于制作隔热材料,防止室内温度的变化对建筑物结构产生不利影响。
EPDM薄膜橡胶也可以用于过滤器或制作过滤器外壳,有效减少污染物的污染。
此外,它还可以用于船舶、汽车和其他交通工具,使之具有更强的抗老化性和耐腐蚀性。
最后,还可以将EPDM薄膜橡胶用于制造建筑材料,如PVC管道和橡胶地板,增强其耐磨性和抗氧化性。
因此,EPDM薄膜橡胶在各种行业中都有广泛的应用,为消费者提供了很多实用的解决方案。
此外,由于EPDM膜橡胶对温度有一定的要求,因此在使用过程中需要注意。
例如,当它暴露在115°C以上的高温环境中时,其性能会大大降低,而在低温下,其抗紫外线性能也会受到影响。
此外,它也不适合长期暴露于酸碱性材料中,因为它们会破坏EPDM薄膜橡胶的结构,减弱其性能。
因此,在使用EPDM薄膜橡胶时,应避免将其暴露于高温或酸碱性材料中,否则它的性能会受到不利影响。
workbench建立橡胶的超弹性和粘弹性本构模型
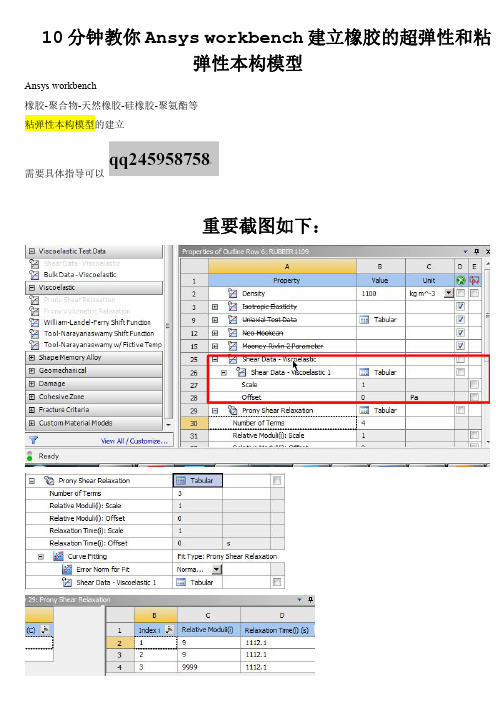
10分钟教你Ansys workbench建立橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建立需要具体指导可以重要截图如下:补充:ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分,在载荷作用下弹性部分是即时响应的,而粘性部分需要经过一段时间才能表现出来。
一般的,应力函数是由积分形式给出的,在小应变理论下,各向同性的粘弹性本构方程可以写成如下形式:()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰(1)其中σ=Cauchy 应力()G t =为剪切松弛核函数()K t =为体积松弛核函数e =为应变偏量部分(剪切变形)∆=为应变体积部分(体积变形)t =当前时间τ=过去时间I =为单位张量。
该式是根据松弛条件本构方程(1),通过将一点的应变分解为应变球张量(体积变形)和应变斜张量(剪切变形)两部分,推导而得的。
这里不再敖述,可参考相关文献等。
ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种,一种是广义Maxwell 单元(VISCO88和VISCO89)所采用的Maxwell 形式,一种是结构单元所采用的Prony 级数形式。
实际上,这两种表示方式是一致的,只是具体数学表达式有一点点不同。
1.2Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为:()1exp G n i G i i t G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑(2)()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑(3)其中,G ∞和i G 是剪切模量,K ∞和i K 是体积模量,G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。
再定义下面相对模量(Relative modulus)0G i i G G α=(4)0K i i K K α=(5)其中,0G ,0K 分别为粘弹性材质的瞬态模量,并定义式如下:()010G n i i G G t G G ∞====+∑(6)()010Kn i i K K t K K ∞====+∑(7)在ANSYS 中,Prony 级数的阶数G n 和K n 可以不必相同,当然其中的松弛时间G i τ和K i τ也不必相同。
胶黏剂超弹性理论与试验力学及ABAQUS仿真案例总结

胶黏剂超弹性理论及ABAQUS仿真案例总结摘要:一部胶黏剂固化后呈现的是橡胶这种超弹性状态,对齐固化后的性能研究与计算基本等于橡胶超弹性研究。
框架:一、超弹性材料本构模型理论二、橡胶材料力学行为的实验研究三、基于ABAQUS橡胶材料的工程实例仿真与实验验证方法四、基于COMSOL胶黏剂超弹性仿真案例一、超弹性材料本构模型理论对于固化后呈现软而韧的胶黏剂,基本可等同于橡胶超弹性材料。
二、橡胶材料力学行为的实验研究2.1引言试验设计与研究是材料设计的关键,主要研究各类配合剂与材料性能,诸如力学性能、功能性能、耐久性及加工性能等之间的相关性,进而从中解析材料组分的品种、类型和用量对橡胶材料性能的影响规律。
本章主要是通过对密封件橡胶试样EP7001和EP7118F进行单向拉伸的准静态力学实验,研究分析橡胶的各种力学行为,主要包括橡胶的Mullins效应及其能量损耗、橡胶材料的应力应变行为和起始模量、橡胶材料力学行为的调制应变相关性、橡胶材料变形行为的率相关性以及橡胶材料应力行为的应变历史相关性等。
另外,还特别针对9种不同体积含量的N330炭黑填充天然橡胶材料进行了单向拉伸的准静态力学实验,研究分析炭黑的填充对硫化橡胶相关力学行为的影响规律。
2.2橡胶材料试样的制备及实验准备在试验方法中,拉伸试验是评价力学、机械特性最基本的方法,所以在各国标准中都放在首要位置。
拉伸试验时,采用某橡胶制品公司生产的EP7001橡胶、EP7118F橡胶以及天然(NR)橡胶为原材料,所制备试样的形状与尺寸满足国家标准《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》(GB/T528-2009)中“1型”哑铃状试样的要求,试样狭窄部分的标准厚度为2mm。
试验在美特斯工业系统(中国)有限公司生产的CMT4104微机控制电子万能试验机上进行,如图2-1所示,其力值和位移精度均为0.5级,大变形传感器选用25mm标距,夹具选用偏心轮夹具PA103A,此夹具特别适用于橡胶材料的拉伸试验,随着拉伸力的增大,夹具钳口对试样的夹持也越来越紧,避免了试样夹持部分的打滑。
短纤维增强EPDM包覆薄膜超弹性本构模型

† (Tactical
Abstract Short fiber reinforced EPDM inhibitor film is used for a new winding coating process, which is mainly to solve the reliable problem in free loading solid rocket grains with complicated structure. Based on fiber reinforced continuum mechanics theory, a simple anisotropic hyperelastic constitutive model is proposed to describe their large deformation, highly non-linear and strongly anisotorpic mechanical behaviors in the work process of solid rocket motor. The unitvolume strain energy function is decomposed into two parts: representing the strain energy from isotropic rubber matrix and anisotropic fiber tensile deformation. By introducing fiber direction to modify fiber strain energy, the specific method of obtaining model parameters by uniaxial and off-axis tension data is presented.Results show that it is highly suitable to characterize their anisotropic mechanical behaviors in the fiber direction from 0◦ to 45◦ and the error is less than 5% compared with experimental data. It is concluded that the proposed model is highly accurate and easy to achieve numerical development, which can provide theoretical basis for the structural integrity analysis of solid rocket motor. Key words EPDM, inhibitor, anisotropic, hyperelastic, constitutive model
几种典型的橡胶材料超弹性本构模型及其适用性

⼏种典型的橡胶材料超弹性本构模型及其适⽤性橡胶材料具有良好的粘弹性,被⼴泛⽤作密封、减振部件。
橡胶作为⼀种超弹性材料,其物理化学性能与⾦属材料有很⼤差别。
橡胶材料的主要特点不可压缩性:橡胶材料的泊松⽐µ⼀般在0.45~0.4999范围内变化,接近于液体的泊松⽐(1) 不可压缩性:0.5,因此橡胶可以看作是⼀种体积近似不可压缩的材料。
⼤变形特性:橡胶⾼分⼦材料变形很⼤,⽽其弹性模量与⾦属材料相⽐却⼩很多。
橡胶材料(2) ⼤变形特性:的变形范围⼀般在200%~500%,甚⾄能够达到1000%,很多⾦属材料的变形则不⾜0.5%。
(3) ⾮线性:⾮线性:橡胶材料具有三重⾮线性,即⼏何⾮线性、材料⾮线性和边界⾮线性。
橡胶材料的应⼒-应变关系具有明显的⾮线性,其⼒学性能与环境条件、应变历程、加载速率等因素有很⼤关联,且随时间延长⽽不断变化。
本构模型及其适⽤性从20世纪40年代⾄今,国内外许多学者提出了许多橡胶材料的本构模型,⼤致可分为两⼤类:基于应变能函数的唯象模型和基于分⼦链⽹络的统计模型。
基于应变能函数的唯象模型⼜可分为两类。
⼀类是以应变不变量表⽰的应变能密度函数模型,这类模型在处理橡胶弹性时,可以把橡胶材料的变形看成是各向同性的均匀变形,从⽽将应变能密度函数表⽰成变形张量不变量的函数,⽐如:Mooney-Rivlin模型、Yeoh模型等。
另⼀类是以主伸长表⽰的应变能函数模型,⽐如:Valanis-Landel模型、Ogden模型等。
基于分⼦链⽹络的统计模型按照分⼦链的统计特性可分为两类:⾼斯链⽹络模型和⾮⾼斯链⽹络模型。
其中最具代表性的分⼦统计学模型包括Treloar模型以及Arruda-Boyce的8链模型。
下⾯对⼏种常见的本构模型进⾏简要介绍:Mooney-Rivlin模型Mooney-Rivlin模型是⼀个⽐较常⽤的模型,⼏乎可以模拟所有橡胶材料的⼒学⾏为。
其应变能密度函数模型为:对于不可压缩材料,典型的⼆项三阶展开式为:式中:N、Cij和dk为材料常数,由实验确定。
人体椎间盘纤维环各向异性超弹性材料本构模型的数值验证

量不变量。对于不可压缩的组织来说只需要知道 C10
这个参数就得其应变能函数 WM 。
纤维部分的应变能源于纤维的伸长。根据纤维
的伸长, 一个简单的非线性应变能函数 WF 定义如下
WF = C 2 ( I4 - 1) 2 + C 3 ( I4 - 1) 4 I4 > 1 ( 3)
0
I4 # 1
式中, I4 = a0 ∃ C ∃ a0 = F2, 其中 F 是纤维的拉伸
纤维环可以看作是由多层基质组织 组成的复合材
料, 每层基质组织中分别嵌入了一束平行排列的纤 维 ( 图 1), 并且不同层上的纤维排列方向是不同的。 P eng等 [ 7] 认为纤维环各向异性弹性变形的应变能
函数由 3个部分组成: 基质组织贡献的应变能; !
纤维贡献的应变能; ∀ 纤维和基质组织的相互剪切
I4 I3
( I5
-
I1 I4 +
I2 ) -
1
2
( 4)
式中 Ii ( i = 1, 2, 3, 4, 5)是主不变量, = tan2 !是定
义的新的不变量, !是基质和纤维的夹角。纤维 基
质剪切相互作用因子 f ( I 4 ) 可以根据 S 型函数定义 如下
f ( I4 )
=
1+
exp [ -
∀ #( F -
1 材料和方法
1 1 纤维环超弹性纤维加强材料本构模型
纤维环是 一种由同心薄层结构组成的坚硬物
质, 主要由非纤维基质和分布其中排列整齐的胶原
纤维束构成, 纤维束在与椎体横截面呈 30 和 150 方向分布 [ 12, 13] 。纤维束的 交叉重叠分布结构使纤
维环够承受较大的弯曲和扭转载荷。在进行模拟时
Abaqus超弹性材料分析
Abaqus超弹性材料分析模型了解:本案例所用模型如下:图1 模型认识其中,1为压块,结构刚材料,2为橡胶超弹性材料。
有限元分析流程分为3大步、3小步,如下图所示。
今天将以这种方式介绍使用workbench 实现齿轮啮合的分析流程。
图2 ABAQUS有限元分析流程介绍一、前处理1.1 几何模型的构建本案例中的几何模型较为简单,因此直接在abaqus中创建。
本例使用平面应力应变单元模拟实体的压缩过程,将Module切换到Part模块,单击create part创建压块部件,部件类型选择2D planar、Deformable、Shell,进入草图环境,绘制压块图形如图1,绘制完成后单击done完成压块的创建。
继续单击create part创建橡胶部件,部件类型也为2D planar、Deformable、Shell,进入草图环境,绘制橡胶图形如图1所示,绘制完成后单击done退出橡胶的创建。
1.2 材料参数的定义1.2.1 材料本构将Module切换到property模块。
单击create material创建材料,压块使用结构刚材料,密7850kg/m,杨氏模量为2.1e11Pa,泊松比为0.3。
度设置3橡胶使用超弹性材料,使用Mooney-Rivlin本构模型1.2.2 截面定义Abaqus赋予模型材料需要先定义截面属性,单击create section为压块以及橡胶各创建一个截面属性,类型为solid,Homogeneous,单击continue,在弹出的对话框中勾选,Plane stress/strain thickness,并为其指派厚度,如图3所示。
图3 截面属性创建1.2.3 截面指派当两个部件的截面创建完成后,便可以为其指派相应的截面属性。
1.3 网格系统的构建1.3.1 网格划分将Module切换到Mesh模块。
通过合理控制网格大小,得到如图所示的网格图4 网格系统模型1.3.2 单元类型设定对于本例,单元类型可以使用默认的单元类型1.3.3 装配将Module切换到Assembly模块,进入装配环境,按照图1所示位置关系进行装配。
形状记忆合金的力学性能与本构模型研究
形状记忆合金的力学性能与本构模型研究一、内容综述形状记忆合金(Shape Memory Alloys, SMA)是一类具有形状记忆效应(Shape Memory Effect, SMA)和超弹性(Superelasticity)特性的先进功能材料。
自20世纪70年代以来,形状记忆合金在生物医学、航空航天、电子器件等领域得到了广泛关注和应用。
本文从形状记忆合金的力学性能与本构模型两个方面进行综述,重点介绍近年来在这些领域的研究进展与挑战,并展望未来的发展趋势。
在力学性能方面,主要讨论了形状记忆合金的高温马氏体相变特性、超弹性行为、应力诱导相变等现象。
高温马氏体相变使得SMA在温度变化时发生可逆的形状记忆效应,而超弹性则赋予了材料在受到力的作用下发生显著形变的能力,同时在外力消失后又能够恢复到原始形状。
这些独特的力学性能使得SMA在各应用领域展现出了巨大的潜力。
在本构模型方面,重点介绍了各向同性、非各向同性以及各向异性等类型的本构模型。
各向同性本构模型可以描述形状记忆合金在单一取向下的力学行为,而非各向同性本构模型则需要考虑材料的各向异性效应,以更准确地描述其在不同方向上的力学响应。
一些学者还提出了包含塑性和蠕变效应在内的多尺度本构模型,以更全面地反映形状记忆合金在实际工程应用中的复杂力学行为。
值得注意的是,虽然目前对形状记忆合金的研究已取得了显著进展,但仍存在诸多挑战和问题需要进一步研究和解决。
如何提高材料的塑性以提高超弹性的使用范围,如何降低材料在长时间加载过程中的疲劳损伤等。
未来的研究应继续关注形状记忆合金在力学性能与本构模型方面的研究进展,并着眼于解决现有的问题和挑战,以实现其在各领域的广泛应用和更高性能表现。
1. 形状记忆合金的发展和应用形状记忆合金(SMA)是一种具有独特力学性能的材料,能够在受到外部刺激(如温度、电流、磁场等)时发生形状的改变和恢复。
这种材料在许多领域都有着广泛的应用前景,如航空航天、生物医学、机器人科学以及精密仪器等。
workbench建立橡胶的超弹性和粘弹性本构模型
workbench建⽴橡胶的超弹性和粘弹性本构模型10分钟教你Ansys workbench建⽴橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建⽴需要具体指导可以重要截图如下:补充:ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应⼒响应包括弹性部分和粘性部分,在载荷作⽤下弹性部分是即时响应的,⽽粘性部分需要经过⼀段时间才能表现出来。
⼀般的,应⼒函数是由积分形式给出的,在⼩应变理论下,各向同性的粘弹性本构⽅程可以写成如下形式:()()002t t de d G t d I K t d d d σττττττ?=-+-??(1)其中σ=Cauchy 应⼒()G t =为剪切松弛核函数()K t =为体积松弛核函数e =为应变偏量部分(剪切变形)=为应变体积部分(体积变形)t =当前时间τ=过去时间I =为单位张量。
该式是根据松弛条件本构⽅程(1),通过将⼀点的应变分解为应变球张量(体积变形)和应变斜张量(剪切变形)两部分,推导⽽得的。
这⾥不再敖述,可参考相关⽂献等。
ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表⽰⽅式主要有两种,⼀种是⼴义Maxwell 单元(VISCO88和VISCO89)所采⽤的Maxwell 形式,⼀种是结构单元所采⽤的Prony 级数形式。
实际上,这两种表⽰⽅式是⼀致的,只是具体数学表达式有⼀点点不同。
1.2Prony 级数形式⽤Prony 级数表⽰粘弹性属性的基本形式为:()1exp G n i G i i t G t G G τ∞=??=+-∑(2)()1exp K n i K i i t K t K K τ∞=??=+- ∑(3)其中,G ∞和i G 是剪切模量,K ∞和i K 是体积模量,G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。
非等温非牛顿黏弹性高分子熔体流动本构行为数值模拟和实验研究
非等温非牛顿黏弹性高分子熔体流动本构行为数值模拟和实验研究高分子成型加工过程中所涉及的应力场、压力场、温度场和化学反应效应不仅决定制品的外观、形状和质量,而且对分子链结构、超分子结构和织态结构的形成和演变具有极其重要的影响。
成型加工中由流动而诱发的高分子结晶及其取向可显著提高制品的力学和光学性能。
但另一方面,加工过程中时常出现的不稳定流动状态,将导致挤出物表面呈鲨鱼皮状或熔体破裂、共挤出物界面不稳定、注射制品表面有虎皮纹等影响最终制品性能和外观,因而是亟需解决的产品质量问题。
研究高分子材料成型加工中的流动过程,不仅对优化工艺条件、模具结构、挤出口模、机头结构,甚至对挤出机或注射成型机的螺杆等结构设计、对节约能耗、降低成本、提高产品竞争力都起着至关重要的作用。
因此,对高分子黏弹性流体流动的模拟和分析具有重要的工程实际意义。
一般,高分子加工过程是在三维非等温情况下进行的,并且材料在一些高应变和高应变率区域受到拉伸和剪切的双重作用,呈现复杂的流变行为和高度的非线性特征。
另外,流动分析中经常遇到具有尖角的模具或口模,这些几何奇异点容易导致高分子流体产生应力奇异行为,从而诱发不稳定流动;同时,一些加工过程,例如注塑充填过程中还要考虑材料自由面或多组分界面的追踪,这些都会给数值模拟黏弹性流动带来很大的挑战。
对成型加工过程中高分子流变行为的模拟研究,可为优化工艺条件、提高产品性能和更好理解高分子流体动力学提供科学依据,从而在高聚物结构—加工—产品三者之间起到桥梁作用,为高分子熔体加工的多尺度或跨尺度模拟,产品的高性能化奠定基础。
本研究用基于有限增量微积分(FIC)过程的压力稳定化迭代分步算法和DEVSS/SU方法,采用近年发展的能够较好描述支化高分子熔体的本构模型(XPP 模型、PTT-XPP模型、MDCPP模型以及作者提出的S-MDCPP模型)模拟了高分子加工过程中常遇到的收缩流和挤出胀大流问题,以及非等温非牛顿黏性流体注塑充填过程中熔体的流动行为等,分析了数值模拟这些工程问题所涉及的难点,提出了解决对策,为进一步发展高效、健壮的数值算法提供新的思路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超弹材料本构模型实验方法的研究黄友剑1, Kurt Miller2(1 株洲时代新材,2 Axel Products)摘要:有限元分析(FEA)所使用的材料本构模型并不能完全真实描述材料在任意工况下的应力-应变关系。
为定义与实际应用相适的材料行为,需要建立合适的实验方法,以便选择合理的材料模型。
因此,在设计实验时,与材料实际使用工况有关的信息,如应变率,,最大应变、应力松弛,循环加载和环境温度等因素都应在实验方案中加以考虑和体现,以便能准确地定义基于工程应用所需的材料本构模型。
关键词:有限元分析;本构模型;应力-应变关系有限元分析(FEA)材料本构模型并不能完全真实描述材料在各种应力工况下的力学属性,绝大部分FEA本构模型仅能模拟材料在特定工况下特定的应力-应变关系。
为此,本文将详细介绍为创建材料本构模型所需的各种力学实验,以及塑料、超弹材料在各种工况下的典型力学行为对FEA材料本构模型的影响。
同时,通过理解材料的这些典型行为,我们就能设计出合适的材料实验,从而为某一特定的模拟工况提供合适的应力-应变关系。
1材料本构模型所需的各种力学实验1.1常规力学实验为准确模拟材料的真实行为,需要利用合理的实验数据来拟合材料的本构模型。
当材料承受应力时,每一种本构模型仅能描述材料的某一特定行为[1],因此,为创建材料模型函数,实验时,应将材料试样加载到已知(给定)的应变状态,并将实验提供的应力-应变数据在材料模型中进行拟合。
Fig 1 Elastic – plastic curveFig 2 Super stress-strain curve对“硬”塑料来说,单向拉伸实验数据就已足够[2],工程应力-应变曲线通常如图1所示。
在实际应用中,根据使用需要可进行合理简化,线性强化模型和多线性强化模型是在有限元应用中使用较多的一种简化本构模型;而对超弹材料来说,需要形如单向拉伸、平面剪切、双向拉伸等多向应变状态实验[3],来充分定义其力学行为,典型的超弹材料的应力-应变曲线如图2所示。
1.2一次性失效实验对于塑料和超弹材料的物理实验,大部分都是一次性失效实验(即实验一直进行直到破坏),就超弹材料来说,实验是按照ASTM D412标准进行,而对塑料来说,实验则通常是按照ASTM D638标准进行。
某种工程橡胶的一次性单拉失效实验,其典型的应力-应变曲线如图3所示。
从图3可知,工程橡胶在应变不到250%就已拉断破坏。
而其弹性区域,是在其应变小于100%的范围内。
因此,这种工程橡胶承受的工程应变最好要小于100%。
当然,如果要确定最大失效应变,则需要用这条一次性单拉失效实验的应力-应变曲线。
Fig 3 Invalidation experiment curve1.3循环加载实验某一超弹材料的循环加、卸载过程如图4[4]所示:超弹材料先拉伸到应变状态为10%,然后卸载到零应力,再拉伸到应变状态为10%,然后又卸载到零应力,如此进行了3次应变为10%的循环加、卸载实验,然后在应变为20%条件下,往复加、卸载3次,接着在应变为30%的工况下加、卸载3次,实验依此进行,直到最大应变为100%。
Fig 4 Load and unload stable experiment curve 实验中,观察到2个很明显的现象,其一,循环拉伸试样到一特定的应变标准,其应力-应变曲线变柔软且曲线形状发生一次改变;其二,超弹材料每承受一个更大的应变状态,应力-应变曲线又一次变柔软,且曲线形状再次发生改变。
同时,当拉伸超弹材料试样第一次达到一个新的应变标准时,它的应力-应变曲线会落在一次性失效实验的应力-应变曲线上,因此一次性失效拉伸实验的应力应变曲线可认为是任意应变标准的一个最大应力边界。
从图4的循环加载实验数据中提取出稳定应变分别为10%、50%、100%时的拉伸实验数据,与一次性失效实验数据共同组成图5,由图5可知,由于发生了一定程度的塑性应变损失,因而每一条稳态应力-应变曲线都发生了一定程度的偏移[5],在材料模型中,如果要精确地模拟出材料的这种损伤行为,可以应用ABAQUS、MSC.MARC的损伤模块,利用图5所示的加、卸载实验数据来描述材料的这种行为。
显然,循环加载和卸载时的最大应变导致了应力-应变数据发生改变,因而需要用超弹材料模型来拟合这类材料行为。
Fig 5 Difference of circle and singleexperiment curve基于此,需要判断我们所关心的问题,是材料初次加载和最大应力工况,还是特定应变范围内的稳定荷载工况,如果是前者,那么一次性失效实验数据对我们来说是合适的;否则,稳定工况下的应力-应变数据对我们建立材料的本构模型更有意义。
1.4 应力松弛实验如果某一超弹材料被拉伸到某一特定的应变状态,然后维持这一应变状态不变,应力将随时间的延长而逐渐衰减,此效应称为应力松弛[6],它存在于平均应变保持不变的条件。
然而超弹材料本构模型并不能模拟这一特性,但ABAQUS、MARC可利用PRONEY公式对常应变工况下的时间-应力数据进行拟合,并在材料模型中将它作为一种粘弹单元来使用。
图6给出了一组时间-应力曲线图,图中每一条曲线都表示超弹材料被约束在某一特定的应变状态,并保持这一应变状态达2000秒之久,当然,在每一个特定应变下,第2000秒这一时刻都对应一应力值,如果把第2000秒时的应力值和与它对应的应变值在应力、应变坐标图上标识出来,就可创建出如图7所示的应力-应变松弛曲线,利用此曲线,我们能创建出超弹松弛本构模型。
这和利用单向拉伸、双向拉伸、平面拉伸实验获得的3条应力-应变曲线,创建出超弹材料本构模型类似。
因此,我们利用这组应力松弛数据,就能较精确地模拟出橡胶定位器、V型弹簧等这类大挠度产品的抗蠕变问题。
Fig 6 Time-stress relaxation curveFig 7 Stress-strain relaxation curve1.5 卸载特性实验从上图4可知,超弹材料拉伸时的应力-应变曲线明显比卸载时的应力-应变曲线要“坚硬”。
如果弹性元件对最小应力工况很敏感,设计时就应考虑这一特性,例如,汽车门密封圈在正常工作时,由于密封尺寸发生改变,汽车门密封圈需要维持一定的接触压力,因而维持最小密封压力是设计者设计时首先要关心的问题。
由于材料特性卸载时比在加载时“柔软”,因而在产品设计时,应给密封件一定的预压。
对工程塑料来说,材料在预定的应变范围按要求加、卸载,从而得到的力学实验数据是相当重要的,这是因为我们假定材料在加、卸载时是弹性的,材料在加、卸载时都具有相同的弹性模量,因此,我们需要判断出材料的弹性区域,为定义材料的弹性区域,简单而可行的方法是,卸载实验试片,分离出弹性和塑性应变,一个重复的弹性应变表示材料最大的弹性区域,虽然此时的模量已不是初始拉伸模量。
2实际使用工况对创建材料本构模型的影响2.1 温度影响温度对塑料和超弹材料力学性能的影响是强烈的。
在汽车应用中尤为如此,汽车在工作时,温度变化可能要达到2000℃。
面对一个如此大的温度变化,分析时并不是简单调整材料属性的问题。
图8[1]是一个汽车阀门弹性元件在经受循环荷载作用时的应力-应变曲线,从图8可看出,温度在23℃时,材料加、卸载仍可按超弹材料来处理,但温度为-40℃时,材料发生了几乎不可恢复的局部塑性应变,此时已不能将它视为超弹材料。
在不同温度范围内,材料属性发生了巨大变化,因此,在不同的温度范围,我们需要选用不同的材料模型。
Fig 8 Effect of temperature on circle loading property2.2应变速率的影响塑料和超弹材料的力学属性随加载速率的变化而变化[7],图9是一种普通工程塑料在拉伸时的应力-应变曲线,据实验可知,当应变速率的改变量超过10的3次方Fig 9 Effect of strain rate on stress-straincurve时,弹性模量对应变速率的变化反映的并不敏感,但应变速率对塑性屈服偏移和失效点位置变化的影响却很强烈。
因此,根据应力-应变曲线建立材料的本构模型时,应考虑应变速率的影响。
2.3应变幅值的影响弹性元件经常承受动态正弦载荷的作用,如:减震器、轴衬和密封体。
动态载荷的响应特性是:高频导致高刚度[8],然而,对大部分工程用弹性元件来说,平均应变幅效应和动态幅效应对弹性元件力学性能的影响会更大些[9]。
由图10可知,典型天然橡胶的贮能模量是频率和平均应变的函数,平均应变对动态模量的影响是巨大的,由图11可知,典型天然橡胶的贮能模量也是频率和动态应变的函数,动态应变对动态模量的影响也是巨大的[10]。
由于材料的这一力学行为,如果平均应变效应和动态正弦幅值效应对贮能模量的影响忽略不计的话,基于频率和应变率效应的分析预测将无法实现,这是由于DMA(动态力学分析)实验是在小幅值应变且平均应变接近为零的工况下进行的缘故[11]。
Fig 10 Effect of stress amplitude on dynamic modulusFig 11 Effect of dynamicstress amplitude on dynamic modulus3结论综上所述,一般情况下,建立塑料的本构模型时,只需要单向拉伸的应力-应变数据;建立超弹性材料的本构模型时,需要单向拉伸、双向拉伸、和平面剪切的应力应变数据。
但是,取什么状态下的这类应力-应变数据,还需根据材料的实际使用工况来决定。
例如,我们是为了分析材料在第一次变形时的力学行为,则应使用第一次的应力-应变数据;是为了分析材料在工作状况下的力学行为,则需用稳态下的实验数据;需要了解材料在最小应力工况下的力学行为时,则需使用卸载工况下的应力-应变曲线;如果是为了分析材料的力学松弛行为,则需使用应力-应变松弛曲线。
在考虑材料力学工况的同时,我们还应考虑到材料实际使用时的温度、应变速率、应变幅值等因素对材料模型的影响。
总之,虽然材料本构模型并不能全面描述材料在任意加载工况下的应力-应变关系,但是,我们却能够合理设计实验,创造适合的使用工况,从而获得相应的接近实际的材料分析本构模型。
参考文献:1Kurt M. Experimental Loading Conditions Used to Implement Hyperelastic and Plastic Material Models[C]. Testing and Analysis Report,Ann Arbor, MI, 20022Theory and User Information, MSC.Marc Volume A, Version K7.3, TheMSC.Software Corporation, Los Angeles,CA, 19983Kurt M. Measuring Material Properties to Build Material Models in FEA[C],Testing and Analysis Report, Ann Arbor,MI, 20014Kurt M. Using Slow Cyclic Loadings to Creat Stress Strain Curves for Input intoHyperelastic Curve Fitting Routines[C],Testing and Analysis Report, Ann Arbor,MI, 20005Kurt M. Testing Elastomers for Hyperelastic Material Models in FiniteElement Analysis[J], Rubber TechnologyInternational, 1999: 886范镜汉,高芝阵。
