第二章 地图的数学基础
合集下载
地图学第2章
（二）表示形式
1.数字式 2.文字式 3.图解式 4.其它
1. 数字式
• 用分数表示，分子是1，分母是100 用分数表示，分子是 ，分母是 的整数倍。 的整数倍。 例如 ：1/5000， 1/10000 ，
2.文字式 2.文字式
• 用文字来说明地图的比例尺 图上1cm的相当于实地100 1cm的相当于实地100米 如“图上1cm的相当于实地100米”
三种纬度关系： 三种纬度关系：
地心纬度
大地纬度
物体重心与地球重心的连线称为铅垂线
三种纬度关系： 三种纬度关系：
在大地测量学中， 在大地测量学中，常以天 文经纬度定义地理坐标。 文经纬度定义地理坐标。 在地图学中， 在地图学中，以大地经纬 度定义地理坐标。 度定义地理坐标。 在地理学研究及地图学的 小比例尺制图中， 小比例尺制图中，通常将椭球 体当成正球体看， 体当成正球体看，采用地心经 纬度。 纬度。
• 4、国家级基础测绘成果的转换与提供 2008年底前 完成1:5 年底前， 1:5万及以小比例尺地形图图幅坐标平 2008年底前，完成1:5万及以小比例尺地形图图幅坐标平 移量计算并提供使用。 移量计算并提供使用。 2009年底前 提供具有三套坐标系（1954年北京坐标系 年底前， 年北京坐标系、 2009年底前，提供具有三套坐标系（1954年北京坐标系、 1980西安坐标系 2000国家大地坐标系 下图廓、 西安坐标系、 国家大地坐标系） 1980西安坐标系、2000国家大地坐标系）下图廓、控制 格网等1:5万坐标参考模片电子版；计算并提供1:1 1:5万坐标参考模片电子版 1:1万地形 格网等1:5万坐标参考模片电子版；计算并提供1:1万地形 图图幅坐标平移量；开展2000国家大地坐标系下的1:5 2000国家大地坐标系下的1:5万 图图幅坐标平移量；开展2000国家大地坐标系下的1:5万 地形图编制印刷。 地形图编制印刷。 2010年底前 完成1:5 年底前， 1:5万 1:25万基础地理信息数据库坐 2010年底前，完成1:5万、1:25万基础地理信息数据库坐 标系的转换并向社会提供。 标系的转换并向社会提供。 2012年底前 完成2000国家大地坐标系下的1:5 年底前， 2000国家大地坐标系下的1:5万地形 2012年底前，完成2000国家大地坐标系下的1:5万地形 图编制印刷并提供使用。 图编制印刷并提供使用。
地图学课件第二章地图的数学基础
等距离投影是指投影前后，地图上的线段 长度保持不变的投影方式。
等方位投影
任意投影
等方位投影是指投影前后，地图上的方向 保持不变的投影方式。
任意投影是指根据实际需要，选择不同的 投影方式进行投影的过程，可以满足各种 不同的需求和应用场景。
02
常用地图投影
方位投影
总结词
方位投影是一种将地球表面投影到平 面上的方法，其特点是投影后各方向 保持相对方位不变。
多面投影
总结词
多面投影是一种将地球表面分割成多个部分，然后将每个部分分别投影到平面上 的方法。这种投影的特点是能够较好地保留地理特征的形状和面积。
详细描述
多面投影常用于制作大比例尺地图，尤其适用于制作特定地区的地图，如国家或 地区地图。由于多面投影可以针对特定区域进行优化，因此它能够更好地保留地 理特征的形状和面积，但制作过程相对复杂。
数字地图的坐标系
地理坐标系
以经纬度为基准，用于表示地球表面任意点的位置。
投影坐标系
将地球表面投影到平面上，形成二维坐标系，用于地图制作和地理信息系统。
数字地图的精度与比例尺
精度
地图上地理要素的详细程度和准确度， 与地图的制作技术和测量技术有关。
VS
比例尺
地图上的长度与实际地物长度之间的比例 关系，用于表示地图的缩放程度。
详细描述
方位投影通常用于制作小比例尺地图 ，因为它能够保持地理特征的相对方 向和距离。然而，方位投影在投影过 程中可能会产生较大的面积变形。
圆柱投影
总结词
圆柱投影是将地球表面投影到圆柱体表面，然后将圆柱体展 开成平面。这种投影的特点是投影后经度线保持等距离，而 纬度线则逐渐缩短。
详细描述
圆柱投影广泛应用于世界地图的制作，因为它在保持经度线 等距的同时，相对较好地保留了纬度方向的形状和面积。然 而，在靠近极点的区域，纬度线会变得非常密集，导致地图 扭曲。
第二章：地图的数
地球上的经纬线的长度的特点： 第一，纬线长度不等 第二，在同一条纬线上，经差相同的 纬线弧长相等 第三，所有经线长度相等
地球上的经纬线网格面积的特点：
第一，在同一纬度带内，经差相同的 球面网格面积相等
第二，在同一经度带内，纬度愈高，
网格面积愈小
地球上的经纬线角度的特点：
在地球上经线和纬线处处都呈直角相交
§2.5 地图的分幅与编号 主要内容：
1. 2. 3. 4. 地图编号 我国基本地形图的分幅和编号 地图分幅的概念和方法 地形图编号的计算方法
一、地图的分幅
1.为什么要分幅？ 区域表达，编图、印刷、保管和使用 的方便。 2.地图分幅的方法 矩形分幅
经纬线分幅
拼接 不拼接
矩形分幅
拼接分幅：
适用：挂图和大于1：2000的地形图
或1.5°经线范围内的经纬线投影到椭圆柱面上，
然后将椭圆柱面展开成平面即成。
中央子午线：与椭圆柱重合的子午线
两种常用的分带方式及中央子午线的计算 6°带：从0°子午线开始每6 °经差为一带，中间的子 午线为中央子午线 该投影带的中央子午线：L=6n-3 n为带号 3°带：从1°30′开始每3 °经差为一带，其中间的子午 线为中央子午线 该投影带的中央子午线：L=3n n为带号
2.4 地图比例尺
1. 地图比例尺的含义
地图比例尺：地图上一直线段长度与地面相应直线水平投影 长度之比。 可表达为（d为图上距离，D为实地距离）
d 1 D M
根据地图投影变形情况，地图比例尺分为：
主比例尺 ： 在投影面上没有变形的点或线上的比例尺。 局部比例尺： 在投影面上有变形处的比例尺。
2. 地图比例尺的形式
二、 椭球定位与定向
地图的数学基础new
大地坐标系：以参考椭球面为参考面，以法线为参考线，用大地经纬度表示地面点在参考椭球面上位置的空间坐标系
WGS-84世界大地坐标系 WGS-84是CTS, 坐标系的原点是地球的质心，Z 轴指向 BIH1984.0 CTP方向，X轴指向 BIH1984.0零子午面和 CTP 赤道的交点，Y 轴和 Z、X 轴构成右手坐标系
陕西省泾阳县永乐镇北洪流村为 “1980西安坐标系” 大地坐标的起算点——大地原点。
§2 地球坐标系与大地定位
① 天文经纬度 ② 大地经纬度 ③ 地心经纬度
2.1 地理坐标 —— 用地理经纬度表示地面点位的球面坐标。
地球表面上的定位问题，是与人类的生产活动、科学研究及军事国防等密切相关的重大问题。具体而言，就是球面坐标系统的建立。
地面支撑系统：1个主控站，3个注入站，5个监测站。它向GPS导航卫星提供一系列描述卫星运动及其轨道的参数；监控卫星沿着预定轨道运行；保持各颗卫星处于GPS时间系统及监控卫星上各种设备是否正常工作等。
用户设备部分：GPS接收机——接收卫星信号，经数据处理得到接收机所在点位的导航和定位信息。通常会显示出用户的位置、速度和时间。还可显示一些附加数据，如到航路点的距离和航向或提供图示。
大地控制网
平面控制网 : 按统一规范，由精确测定地理坐标的地面点组成，由三角测量或导线测量完成，依精度不同，分为四等。 由平面控制网和高程控制网组成，控制点遍布全国各地。
高程控制网 : 按统一规范，由精确测定高程的地面点组成，以水准测量或三角高程测量完成。依精度不同，分为四等。
中国高程起算面是 黄海平均海水面。 1956年在青岛观象山设立了水准原点，其他各控制点的绝对高程均是据此推算，称为1956年黄海高程系。 1987年国家测绘局公布： 启用《1985国家高程基准》 取代《黄海平均海水面》 其比《黄海平均海水面》 上升 29毫米。
WGS-84世界大地坐标系 WGS-84是CTS, 坐标系的原点是地球的质心，Z 轴指向 BIH1984.0 CTP方向，X轴指向 BIH1984.0零子午面和 CTP 赤道的交点，Y 轴和 Z、X 轴构成右手坐标系
陕西省泾阳县永乐镇北洪流村为 “1980西安坐标系” 大地坐标的起算点——大地原点。
§2 地球坐标系与大地定位
① 天文经纬度 ② 大地经纬度 ③ 地心经纬度
2.1 地理坐标 —— 用地理经纬度表示地面点位的球面坐标。
地球表面上的定位问题，是与人类的生产活动、科学研究及军事国防等密切相关的重大问题。具体而言，就是球面坐标系统的建立。
地面支撑系统：1个主控站，3个注入站，5个监测站。它向GPS导航卫星提供一系列描述卫星运动及其轨道的参数；监控卫星沿着预定轨道运行；保持各颗卫星处于GPS时间系统及监控卫星上各种设备是否正常工作等。
用户设备部分：GPS接收机——接收卫星信号，经数据处理得到接收机所在点位的导航和定位信息。通常会显示出用户的位置、速度和时间。还可显示一些附加数据，如到航路点的距离和航向或提供图示。
大地控制网
平面控制网 : 按统一规范，由精确测定地理坐标的地面点组成，由三角测量或导线测量完成，依精度不同，分为四等。 由平面控制网和高程控制网组成，控制点遍布全国各地。
高程控制网 : 按统一规范，由精确测定高程的地面点组成，以水准测量或三角高程测量完成。依精度不同，分为四等。
中国高程起算面是 黄海平均海水面。 1956年在青岛观象山设立了水准原点，其他各控制点的绝对高程均是据此推算，称为1956年黄海高程系。 1987年国家测绘局公布： 启用《1985国家高程基准》 取代《黄海平均海水面》 其比《黄海平均海水面》 上升 29毫米。
地图的数学基础
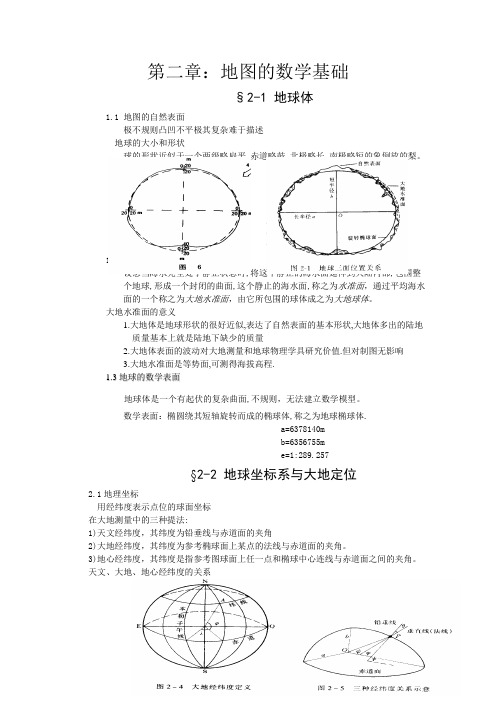
第二章：地图的数学基础§2-1 地球体1.1 地图的自然表面极不规则凸凹不平极其复杂难于描述地球的大小和形状球的形状近似于一个两级略扁平,赤道略鼓,北极略长,南极略短的象倒放的梨。
称“梨状体”（图 6）.1．2地球的物理表面设想当海水完全处于静止状态时,将这个静止的海水面延伸到大陆内部,包围整个地球,形成一个封闭的曲面,这个静止的海水面,称之为水准面，通过平均海水面的一个称之为大地水准面，由它所包围的球体成之为大地球体。
大地水准面的意义1.大地体是地球形状的很好近似,表达了自然表面的基本形状,大地体多出的陆地质量基本上就是陆地下缺少的质量2.大地体表面的波动对大地测量和地球物理学具研究价值.但对制图无影响3.大地水准面是等势面,可测得海拔高程.1.3地球的数学表面地球体是一个有起伏的复杂曲面,不规则，无法建立数学模型。
数学表面：椭圆绕其短轴旋转而成的椭球体,称之为地球椭球体.a=6378140mb=6356755me=1:289.257§2-2 地球坐标系与大地定位2.1地理坐标用经纬度表示点位的球面坐标在大地测量中的三种提法:1)天文经纬度，其纬度为铅垂线与赤道面的夹角2)大地经纬度，其纬度为参考椭球面上某点的法线与赤道面的夹角。
3)地心经纬度，其纬度是指参考图球面上任一点和椭球中心连线与赤道面之间的夹角。
天文、大地、地心经纬度的关系用经纬度表示点位的球面坐标：2.2球心坐标系：以椭球体球心O为坐标原点，用三维立体坐标X、Y、Z表示空间点位置。
2.3 我国的大地坐标系统历史上，一个国家或地区，可能采用过不同的坐标系；在使用其成果时，对坐标系的状况必须注意。
我国沿用了两个大地坐标系；即:(1) 1954年北京坐标系;我国于1954年以前苏联采用的克拉索夫斯基椭球元素(其坐标原点为苏联西部的普尔科夫42年定位)作为参考椭球体，以北京为原点，联测、平差后引伸到全国，这个过渡性的大地坐标系，称1954年北京坐标系。
02_地图数学基础
26
三、地图投影的变形
（五）面积比与面积变形
（2）面积变形
就是(dF’-dF)与dF之比，以VP表示面积变形， dF dF dF 则： VP 1 P 1 dF dF 面积变形表明了面积变形的程度，是衡量面积 变形的一个相对指标。它是一个>0,＝0,<0的 数，通常用百分比表示，如VP=-2%，即表示
(1)
等角投影 等积投影
地 图 投 影
(2)
(3) 任意投影
43
四、地图投影的分类
（3）任意投影（Aphylactic Projection）
概念：它是一种既不等角也不等积，长度、角 度和面积三种变形并存但变形都不大的投影类 型。
特点：角度变形：＜等积投影； 面积变形：＜等角投影； 是一种变形较为适中的投影。
研究各种投影的变形规律是通过把投影后的经纬线网与地 球仪上经纬线网格比较而实现的。地球仪是地球的真实缩 小。通过比较就会发现地球仪上的经纬网形状与投影后经 纬网的形状是不相同的。为了研究变形，首先让我们分析 一下地球仪上经纬网的特点： 1.所有经线都是通过两极的大圆且长度相等；所有纬 线都是圆，圆半径由赤道向两极递减，极地成为一点。 2.经线表示南北方向；纬线表示东西方向。 3.经线和纬线是相互垂直的。 4.纬差相等的经线弧长相等；同一条纬线上经差相等 的纬线弧长相等，在不同的纬线上，经差相等的纬线弧长 不等，由赤道向两极递减。 5.同一纬度带内，经差相同的经纬线网格面积相等， 同一经度带内，纬差相同的经纬线网格面积不等，纬度越 高，梯形面积越小（由低纬向高纬逐渐缩小）。
试验：
投影变形示意图
20
变形椭圆
21
三、地图投影的变形
（三）长度比和长度变形
三、地图投影的变形
（五）面积比与面积变形
（2）面积变形
就是(dF’-dF)与dF之比，以VP表示面积变形， dF dF dF 则： VP 1 P 1 dF dF 面积变形表明了面积变形的程度，是衡量面积 变形的一个相对指标。它是一个>0,＝0,<0的 数，通常用百分比表示，如VP=-2%，即表示
(1)
等角投影 等积投影
地 图 投 影
(2)
(3) 任意投影
43
四、地图投影的分类
（3）任意投影（Aphylactic Projection）
概念：它是一种既不等角也不等积，长度、角 度和面积三种变形并存但变形都不大的投影类 型。
特点：角度变形：＜等积投影； 面积变形：＜等角投影； 是一种变形较为适中的投影。
研究各种投影的变形规律是通过把投影后的经纬线网与地 球仪上经纬线网格比较而实现的。地球仪是地球的真实缩 小。通过比较就会发现地球仪上的经纬网形状与投影后经 纬网的形状是不相同的。为了研究变形，首先让我们分析 一下地球仪上经纬网的特点： 1.所有经线都是通过两极的大圆且长度相等；所有纬 线都是圆，圆半径由赤道向两极递减，极地成为一点。 2.经线表示南北方向；纬线表示东西方向。 3.经线和纬线是相互垂直的。 4.纬差相等的经线弧长相等；同一条纬线上经差相等 的纬线弧长相等，在不同的纬线上，经差相等的纬线弧长 不等，由赤道向两极递减。 5.同一纬度带内，经差相同的经纬线网格面积相等， 同一经度带内，纬差相同的经纬线网格面积不等，纬度越 高，梯形面积越小（由低纬向高纬逐渐缩小）。
试验：
投影变形示意图
20
变形椭圆
21
三、地图投影的变形
（三）长度比和长度变形
第二章地图的数学基础
第二章地图的数学基础地图的数学基础，是指使地图上各种地理要素与相应地面景物之间保持一定对应关系的经纬网、坐标网、大地控制点、比例尺等数学要素。
第一节地球的形状与大小地球的表面是一个不可展平的曲面，而地图是在平面上描述各种制图现象，这给地图工作者提出了一个问题，如何建立球面与平面间的对应关系。
要解决这个问题首先必须对地球的形状和大小进行研究。
一、地球的自然表面（自然球体）由地球自然表面所包围的形体我们称之为地球自然球体。
地球自然表面是一个崎岖不平的不规则表面，有高山、丘陵、平原、盆地和海洋。
世界第一高峰珠穆朗玛峰高出海平面8844.43m，而在太平洋西部的马利亚纳海沟的斐查兹海渊，低于海平面11034m。
人们对地球形状的认识曾经历了漫长的过程，古人在实现了环球航行后才发现地球是球形的，近代大地测量发现更接近于两极扁平的椭球。
长短半径大约差21km。
通过人造地球卫星对地球观察的资料分析，发现地球是一个不规则的“近似于梨形的椭球体”，它的极半径略短，赤道半径略长，北极略突出，南极略扁平(图2--1)。
这里所讲的梨形，是一种形象的夸张。
因为地球南北半球的极半径之差在近几十米范围之内，这与地球的自然表面起伏、极半径和赤道半径之差都在20 km左右相比是十分微小的。
所以，地球自然表面是一个极复杂而又不规则的球形曲面，不能用数学公式表达。
二、地球的物理表面（大地体）当海洋静止时，自由水面与该面上各点的重力方向（铅垂线）成正交，这个面叫水准面。
在众多的水准面中，有一个与静止的平均海水面相重合，并假想其穿过大陆、岛屿形成一个闭合曲面，这就是大地水准面。
它实际是一个起伏不平的重力等位面——地球物理表面(图2--2)。
由于地球的自然表面极其复杂与不规则，大地测量学家就引入了大地体的概念。
所谓大地体是由大地水准面所包围的地球形体。
大地水准面是地球形体的一级逼近。
由于地球引力的大小与地球内部的质量有关，而地球内部的质量分布又不均匀，致使地面上各点的铅垂线方向产生不规则的变化，因而大地水准面实际上是一个略有起伏的不规则曲面。
地图的数学基础(najin)
桑逊投影是一种经线为正炫曲线的正轴等 积伪圆柱投影 ,该投影的纬线为间隔相等的平 行直线，经线为对称于中央经线的正弦曲线, 是等面积投影，赤道和中央经线是两条没有变 形的线，离开这两条线越远，长度、角度变形 越大。因此，该投影中心部分变形较小，除用 于编制世界地图外，更适合编制赤道附近南北 延伸地区的地图，如非洲、南美洲地图等。
墨卡托投影属于正轴等角圆柱投影。该投 影设想与地轴方向一致的圆柱与地球相切或 相割，将球面上的经纬线网按等角的条件投 影到圆柱面上，然后把圆柱面沿一条母线剪 开并展成平面。经线和纬线是两组相互垂直 的平行直线，经线间隔相等，纬线间隔由赤 道向两极逐渐扩大（如图）。图上无角度变 形，但面积变形较大。
（2）空间斜轴墨卡托投影 （Space Oblique Mercator Projection）
假想一个扁率极小的椭 圆，绕大地球体短轴旋转所 形成的规则椭球体称之为地 球椭球体
地球椭球体三要素： 长半径 a 短半径 b 扁率f
图2-2 地球自然 表面、大 地水准面 和地球椭 球体的关 系
由于推算的年代、使用的方法以及测定地区
的不同，地球椭球体的数据并不一致，近一个世 纪来，世界上推出了几十种地球椭球体数据。
（3）长度比和长度变形
长度比 µ 是投影面上一微小线段ds’和椭
球面上相应微小线段ds之比。用公式表达为：
µ=ds’/d s
长度比用于表示投影过程中，某一方向上 长度变化的情况。µ>1，说明投影后长度拉长， µ<1，说明投影后长度缩短了；µ=1，则说明 特定方向上投影后长度没有变形。
注意长度比与比例尺区别：
1：295.0
埃及，加拿大，美国，墨西哥，法国
1：293.47
越南，罗马尼亚，法国，南非
墨卡托投影属于正轴等角圆柱投影。该投 影设想与地轴方向一致的圆柱与地球相切或 相割，将球面上的经纬线网按等角的条件投 影到圆柱面上，然后把圆柱面沿一条母线剪 开并展成平面。经线和纬线是两组相互垂直 的平行直线，经线间隔相等，纬线间隔由赤 道向两极逐渐扩大（如图）。图上无角度变 形，但面积变形较大。
（2）空间斜轴墨卡托投影 （Space Oblique Mercator Projection）
假想一个扁率极小的椭 圆，绕大地球体短轴旋转所 形成的规则椭球体称之为地 球椭球体
地球椭球体三要素： 长半径 a 短半径 b 扁率f
图2-2 地球自然 表面、大 地水准面 和地球椭 球体的关 系
由于推算的年代、使用的方法以及测定地区
的不同，地球椭球体的数据并不一致，近一个世 纪来，世界上推出了几十种地球椭球体数据。
（3）长度比和长度变形
长度比 µ 是投影面上一微小线段ds’和椭
球面上相应微小线段ds之比。用公式表达为：
µ=ds’/d s
长度比用于表示投影过程中，某一方向上 长度变化的情况。µ>1，说明投影后长度拉长， µ<1，说明投影后长度缩短了；µ=1，则说明 特定方向上投影后长度没有变形。
注意长度比与比例尺区别：
1：295.0
埃及，加拿大，美国，墨西哥，法国
1：293.47
越南，罗马尼亚，法国，南非
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精品课件
2-1 空间坐标系
人们对空间数据的一个基本应用就是获取事物在 地球空间中的位置信息，由此可了解地物与地理环境 的定位关系，而空间坐标系的选择则是给事物定位的 前提。
确定事物在空间中的位置，需要三个维量，分别 由坐标系统和高程系统来规定，其中坐标系用于确定 地物在地球椭球面和地图平面上的位置，高程系用于 确定陆地地形表面离高程起算面的高度或海底地形表 面离水深起算面的深度。
切基本定位计算，例如基本测量、航空、
航海以及全球定位系统（GPS）的定位。
地理坐标系统的建立与地球体形和地球le
通过天文大地测量、地球重力测量、卫星大地测量 等精密测量，发现：
地球并不是一个正球体，而是一个极半径略短、赤 道半径略长，北极略突出、南极略扁平，近于梨形的 椭球体。
精品课件
2-1 空间坐标系
目前，最常用的坐标系有两种： §地理坐标系 §平面直角坐标系
高程系根据陆高和水深的计量也分为两种： §陆高高程系 §水深高程系
精品课件
2-1 空间坐标系
一、地理坐标系
地理坐标系是一种较古老的按经纬度
计量的坐标系，是由公元前古希腊哲学
家和地理学家亚里士多德首先用于实践
的。这是一种基本坐标系统，被用于一
精品课件
地 球 的 自 然 表 面
精品课件
地球的自然表面是一个起伏不平，十分不规则的表 面。对于地球测量而言，地表是一个无法用数学公式 表达的曲面。
为了寻求一种规则的曲面来代替地球的自然表面， 人们设想当海洋静止时，平均海水面穿过大陆和岛屿， 形成一个闭合的曲面，该面上的各点与重力方向（铅 垂线）成正交，这就是大地水准面。大地水准面所包 围的球体，叫大地球体。 大地水准面是对地球形状的一级逼近
• 现在我国军用地图上所采用的就是“整体平差值的 1954年北京坐标系”，区别于从原苏联1942年坐 标系联测、平差推精算品到课件我国的“1954年北京坐标
精品课件
精品课件
精品课件
国家平面控制网布设示意图
精品课件
WGS-84世界大地坐标系
精品课件
2000 国家大地坐标系
地心坐标系 原点为包括海洋和大气的整个地球的质量中心。 Z轴指向BIH1984.0定义的协议极地方向（BIH国际时间局）
精品课件
2-1 空间坐标系
一、地理坐标系——椭球体的采用
各国根据适合本国的区域地球特点来采用椭球体。 §中国： • 1932年前采用白塞尔椭球，其后采用海福特椭球；
• 1952年采用克拉索夫斯基椭球；
• 1980年进行天文大地网平差时，采用国际大地测量 协会1975年推荐的GRS—75椭球，坐标原点设在 陕西西安——1980国家大地坐标系；
精品课件
短半径b (米) 6 356 075 6 356 079 6 356 534 6 356 515 6 356 912 6 356 863 6 356 750 6 356 755 6 356 752
扁 率 1∶300.80 1∶299.15 1∶294.98 1∶293.47 1∶297.00 1∶298.30 1∶298.26 1∶298.257 1∶298.257
精品课件
几个著名的地球椭球元素值
椭球名称 埃弗勒斯 白塞尔 克拉克 克拉克 海福特 克拉索夫斯基 WGS—72 GRS—75 GRS—80
年代 1830 1841 1866 1880 1909 1940 1972 1975 1979
长半径a (米) 6 377 276 6 377 397 6 378 206 6 378 249 6 378 388 6 378 245 6 378 135 6 378 140 6 378 137
扁 率 ab
a
第一偏心率
e2
(a2 b2) a2
第二偏心率
e'2
(a2 b2
b2
)
精品课件
2-1 空间坐标系
一、地理坐标系——地球椭球面
扁率和偏心率都反映了椭球的扁平程度。决定地 球椭球的形状和大小，只要知道上面五个基本元素 中的两个就够了，但其中至少必须有一个是长度元 素（a或b）。
这些基本元素，由于推求的年代不同，测定的地 区不同，其成果很不一致，因此地球椭球的元素值 有多种。
椭球面”。
精品课件
2-1 空间坐标系
一、地理坐标系——地球椭球面
这是一个纯粹的数学表面，用简 单的数学公式即可表达 ：
x2 y2 z2 a2 a2 b2 1
常用的符号有a、b、α、
e、e，这些符号的含义
叫做地球椭球的基本元
素。
精品课件
短 半 径
b
0
长半径a
地球椭球面
2-1 空间坐标系
一、地理坐标系——地球椭球面 其中 α 、e、e 的名称和公式为：
2-1 空间坐标系
一、地理坐标系——经纬线与地理坐标
纬线圈
B——纬度，从赤道起
P
算
A
L——经度，从格林尼
治首经线起算
起始经线
L
P＇
B
赤道
精品课件
地理坐标系中某点 的纬度和经度，是用大 地测量的方法测定的， 故又称这种地理坐标系 为大地地理坐标系，简 称大地坐标系。
2-1 空间坐标系
一、地理坐标系——经纬线与地理坐标
第二章 地图的数学基础（1）
精品课件
上一节 内容回顾
数字地图制图的流程
地图的分幅与编号
地图学的定义
地图学是研究地理信息的表达、处理和传输的理论和方法，以 地理信息可视化为核心，探讨地图的制作技术和使用方法。
地图学的学科体系，由哪些内容组成
地图学的发展趋势
精品课件
地图的数学基础
一、空间坐标系 二、地图比例尺 三、地图定向 四、地图投影
大地坐标的取得首先需要建立合适的大地坐标原 点，以此为测量基准来布设大地控制网，再由此逐点 推算各控制点的坐标，即大地经纬度。根据不同的坐 标原点推算出来的同名点的大地坐标是不同的，因此， 获取地面点的地理坐标信息时，不仅要获得其经纬度 坐标，还要知道该坐标所依据的地球椭球和大地坐标 原点。这些信息都可以从地形图的图外说明中得到。
精品课件
2-1 空间坐标系
一、地理坐标系——地球椭球面
§地球表面不规则，最大高差2万米；
§接近一个由大地水准面构成的大地体；
§这种形体的表面接近具有微小
短
半
扁率的旋转椭球面，即以椭圆
径 b
自然表面
大 地 水 准 面
的短轴（地轴）为旋转轴的椭 球面。这种椭球面是用来代表
长半径a
0 地球椭球面
地球形状的，因而又名“地球
2-1 空间坐标系
人们对空间数据的一个基本应用就是获取事物在 地球空间中的位置信息，由此可了解地物与地理环境 的定位关系，而空间坐标系的选择则是给事物定位的 前提。
确定事物在空间中的位置，需要三个维量，分别 由坐标系统和高程系统来规定，其中坐标系用于确定 地物在地球椭球面和地图平面上的位置，高程系用于 确定陆地地形表面离高程起算面的高度或海底地形表 面离水深起算面的深度。
切基本定位计算，例如基本测量、航空、
航海以及全球定位系统（GPS）的定位。
地理坐标系统的建立与地球体形和地球le
通过天文大地测量、地球重力测量、卫星大地测量 等精密测量，发现：
地球并不是一个正球体，而是一个极半径略短、赤 道半径略长，北极略突出、南极略扁平，近于梨形的 椭球体。
精品课件
2-1 空间坐标系
目前，最常用的坐标系有两种： §地理坐标系 §平面直角坐标系
高程系根据陆高和水深的计量也分为两种： §陆高高程系 §水深高程系
精品课件
2-1 空间坐标系
一、地理坐标系
地理坐标系是一种较古老的按经纬度
计量的坐标系，是由公元前古希腊哲学
家和地理学家亚里士多德首先用于实践
的。这是一种基本坐标系统，被用于一
精品课件
地 球 的 自 然 表 面
精品课件
地球的自然表面是一个起伏不平，十分不规则的表 面。对于地球测量而言，地表是一个无法用数学公式 表达的曲面。
为了寻求一种规则的曲面来代替地球的自然表面， 人们设想当海洋静止时，平均海水面穿过大陆和岛屿， 形成一个闭合的曲面，该面上的各点与重力方向（铅 垂线）成正交，这就是大地水准面。大地水准面所包 围的球体，叫大地球体。 大地水准面是对地球形状的一级逼近
• 现在我国军用地图上所采用的就是“整体平差值的 1954年北京坐标系”，区别于从原苏联1942年坐 标系联测、平差推精算品到课件我国的“1954年北京坐标
精品课件
精品课件
精品课件
国家平面控制网布设示意图
精品课件
WGS-84世界大地坐标系
精品课件
2000 国家大地坐标系
地心坐标系 原点为包括海洋和大气的整个地球的质量中心。 Z轴指向BIH1984.0定义的协议极地方向（BIH国际时间局）
精品课件
2-1 空间坐标系
一、地理坐标系——椭球体的采用
各国根据适合本国的区域地球特点来采用椭球体。 §中国： • 1932年前采用白塞尔椭球，其后采用海福特椭球；
• 1952年采用克拉索夫斯基椭球；
• 1980年进行天文大地网平差时，采用国际大地测量 协会1975年推荐的GRS—75椭球，坐标原点设在 陕西西安——1980国家大地坐标系；
精品课件
短半径b (米) 6 356 075 6 356 079 6 356 534 6 356 515 6 356 912 6 356 863 6 356 750 6 356 755 6 356 752
扁 率 1∶300.80 1∶299.15 1∶294.98 1∶293.47 1∶297.00 1∶298.30 1∶298.26 1∶298.257 1∶298.257
精品课件
几个著名的地球椭球元素值
椭球名称 埃弗勒斯 白塞尔 克拉克 克拉克 海福特 克拉索夫斯基 WGS—72 GRS—75 GRS—80
年代 1830 1841 1866 1880 1909 1940 1972 1975 1979
长半径a (米) 6 377 276 6 377 397 6 378 206 6 378 249 6 378 388 6 378 245 6 378 135 6 378 140 6 378 137
扁 率 ab
a
第一偏心率
e2
(a2 b2) a2
第二偏心率
e'2
(a2 b2
b2
)
精品课件
2-1 空间坐标系
一、地理坐标系——地球椭球面
扁率和偏心率都反映了椭球的扁平程度。决定地 球椭球的形状和大小，只要知道上面五个基本元素 中的两个就够了，但其中至少必须有一个是长度元 素（a或b）。
这些基本元素，由于推求的年代不同，测定的地 区不同，其成果很不一致，因此地球椭球的元素值 有多种。
椭球面”。
精品课件
2-1 空间坐标系
一、地理坐标系——地球椭球面
这是一个纯粹的数学表面，用简 单的数学公式即可表达 ：
x2 y2 z2 a2 a2 b2 1
常用的符号有a、b、α、
e、e，这些符号的含义
叫做地球椭球的基本元
素。
精品课件
短 半 径
b
0
长半径a
地球椭球面
2-1 空间坐标系
一、地理坐标系——地球椭球面 其中 α 、e、e 的名称和公式为：
2-1 空间坐标系
一、地理坐标系——经纬线与地理坐标
纬线圈
B——纬度，从赤道起
P
算
A
L——经度，从格林尼
治首经线起算
起始经线
L
P＇
B
赤道
精品课件
地理坐标系中某点 的纬度和经度，是用大 地测量的方法测定的， 故又称这种地理坐标系 为大地地理坐标系，简 称大地坐标系。
2-1 空间坐标系
一、地理坐标系——经纬线与地理坐标
第二章 地图的数学基础（1）
精品课件
上一节 内容回顾
数字地图制图的流程
地图的分幅与编号
地图学的定义
地图学是研究地理信息的表达、处理和传输的理论和方法，以 地理信息可视化为核心，探讨地图的制作技术和使用方法。
地图学的学科体系，由哪些内容组成
地图学的发展趋势
精品课件
地图的数学基础
一、空间坐标系 二、地图比例尺 三、地图定向 四、地图投影
大地坐标的取得首先需要建立合适的大地坐标原 点，以此为测量基准来布设大地控制网，再由此逐点 推算各控制点的坐标，即大地经纬度。根据不同的坐 标原点推算出来的同名点的大地坐标是不同的，因此， 获取地面点的地理坐标信息时，不仅要获得其经纬度 坐标，还要知道该坐标所依据的地球椭球和大地坐标 原点。这些信息都可以从地形图的图外说明中得到。
精品课件
2-1 空间坐标系
一、地理坐标系——地球椭球面
§地球表面不规则，最大高差2万米；
§接近一个由大地水准面构成的大地体；
§这种形体的表面接近具有微小
短
半
扁率的旋转椭球面，即以椭圆
径 b
自然表面
大 地 水 准 面
的短轴（地轴）为旋转轴的椭 球面。这种椭球面是用来代表
长半径a
0 地球椭球面
地球形状的，因而又名“地球