信号与系统系统函数与信号流图
第七讲数字信号处理系统函数流图
i0
M
•
H( z )
Y( X(
z) z)
1
br z r
r 0
N
ak zk
k 1
ARMA系统 IIR系统
M
• 若所有ak 0, H(z) br zr , 系统称为MA系统 －－－全零 r 0 点模型
h(n)为有限长序列－－－FIR系统（有限长单位脉冲响应）
• 若除b0 1外，所有br 0,
单位脉冲响 应的傅氏变
换
单位圆上的 系统函数
LTI系统的系统函数和ROC
因果系统
稳定系统 因果稳定系统
h(n)
h(n)=0,n<0 右边序列
H(z) Rx z 极点在某圆 内，收敛域 在此圆外
j Im(Z )
h(n)
n
h(n)=0,n<0
h(n)
n
H (e j ) 存在， 收敛域为
H(z)
1
N
1 ak zk
k 1
－－－全极点模型－－－AR 系统
h(n)为无限长序列－－－IIR系统（无限长单位脉冲响应）
一个稳定的LTI因果系统的差分方程为 y(n) 0.25y(n 1) 0.125y(n 2) x(n) x(n 1) 求系统函数H(z)，单位冲激响应h(n)
解：
i 1
系统频率响应 的几何确定
N
Ci
H (e j )
A
i 1 N
Di
i 1
N
N
() i i
i 1
i 1
当频率ω从零变化到2π时，这些向量的终点B沿单位圆逆时 针旋转一周，分别估算出系统的幅度特性和相位特性
N
M
有理系统分类 y(n) ai y(n i) bi x(n i)
§5-8 LTI系统的信号流图表示
2 1 s 1 s 2
于是级联实现
X (s)
∑
S -1
∑
S -1
3
∑
Y (s )
1
《Signals & Systems》
2
大连海事大学信息科学技术学院
《信号与系统》
§5-8 LTI系统的信号流图表示
或者
X (s)
∑
S -1
∑
S -1
3
∑
Y (s )
2
1
并联实现如下图
∑
S -1
2
自环：只有一条支路的闭环。
不接触环：环路之间，无公共节点的一类环。 前向通路：由源节点至阱节点的一条通路。
于是系统的级联模拟如下：
∑
z 1
0.2
0.5
∑
Y (z )
X (z )
∑
z 1
0.1
或者：
Y (z ) X (z )
∑
z 1
0.1
0.5
∑
∑
z 1
0.2
《Signals & Systems》
大连海事大学信息科学技术学院
《信号与系统》
§5-8 LTI系统的信号流图表示
系统的并联模拟如下：
4
∑
《信号与系统》
§5-8 LTI系统的信号流图表示
§5-8 LTI系统的信号流图表示
一、 LTI系统的模拟框图表示
第一章曾介绍过，将微分方程或差分方程用模拟框图表示。由 于方程中涉及的运算只有三种：加法、数乘和微分（或差分），因 此，模拟框图中的运算器件也只有三种：加法器、数乘器和积分器 （或单位延时器）。
H ( z)
b z
信号与系统课后习题参考答案
1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示，试作出下列各信号的波形图，并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示，试作出信号x(t)的波形图，并加以标注。
题图1-51- 6 试画出下列信号的波形图：1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图：⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角，并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下，试写出各自系统的输入输出方程。
信号与系统6-1
C
u1 (t )
s 解： U1 ( s ) 2 s 4
R
u2 (t )
1 s s LC U 2 ( s ) U1 ( s ) H ( s ) 2 s 4 s2 s 1 RC LC
2
将激励信号的极点抵消
2 2
则不会出现强迫响应分量
可见，欲使u2(t)中不出现强迫响应分量，则必须有
试证明系统的正弦稳态响应为：
yss (t ) | H ( j0 ) | Em cos[0t (0 )]
电信学院
第六章第1讲
22
系统函数与正弦稳态响应
证：激励函数可表示为
1 f (t ) Em (e j0t e j e j0t e j ) 2 1 e j e j F ( s ) Em 激励的拉氏变换 s j s j 2 0 0
( s j 2)( s j 2) s2 4 H ( s) H 0 H0 s( s j 4)( s j 4) s( s 2 16)
j2
0
- j2
又： h(0 ) lim h(t ) lim sH ( s) 1 可得：H0=1 t 0 s 故： H (s) s 2 4
t
j
( 2)
h(t )
a
2 0
j
t e a t (t )
h(t )
t
( s a)
2
0
a
e a t sin( 0t ) (t )
第六章第1讲
t
电信学院
11
系统函数的极点与冲激响应波形对应
信号与系统 (11)
它在使用中有一些不便： 1） 不能解决信号动态范围与精度之间的矛盾； 2） 不能解决频率范围与精度之间的矛盾；
波特图采用对数坐标，解决上面的问题。而且它有利 于系统综合。
二、 对数频率特性
假设： H ( jω ) = H ( jω ) e jϕ (ω ) 。对其取对数：
G(ω) = 20log[H ( jω) ]
单位：分贝(Deci-Bel,dB)。 奈培与分贝的转换关系：1 Np = 8.686 dB
在理论分析中，一般使用 Np；在实际应用中，一般使 用 dB
用分贝表示增益，解决了信号动态范围与精度之间的 矛盾。如果在频率坐标中同样使用对数坐标，则同样可以 解决频率的范围与精度之间的矛盾。
这样一来就形成了波特图。
H ( jω)
80dB 10000
60dB 1000
40dB 100
20dB 10
01
0.001 0.01 0.1
1
-20dB
10 100 1000 10000
ω
波特图的横坐标可以用 logω ，也可以用 log f ;
在波特图的横坐标上，一般直接标注频率值；
波特图的横坐标上只能表示 ω > 0 或者 f > 0 频率下
函函
电流传输函数：
数
数
电流 I1(s) 电流 I2(s)
Ti21(s)
=
I2(s) I1(s)
电压传输函数：
电压U1(s) 电压U2 (s)
Tu
21(s)
=
U2(s) U1(s)
三、 H (s) 、 H ( p) 、 H ( jω ) 、 h(t) 之间关系
控制系统的传递函数及信号流图和梅逊公式
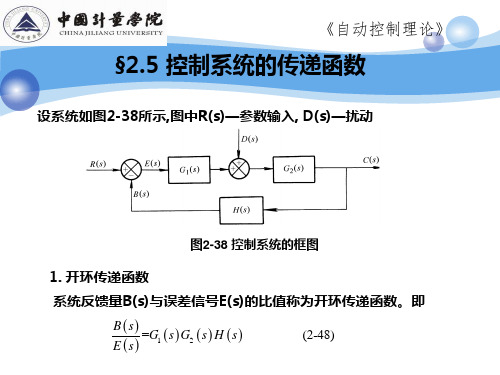
1 Ln LrLsLt
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
例2-7 试用梅逊公式求系统的闭环传递函数 C(S)
R(S)
图2-45 例2-7图
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
解： P1 G1G2G3.
路 开通路—通路与任一节点相交不多于一次
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
闭通路—通路的终点也是通路的起点，并且与任何其它节 点相交不多于一次
6）前向通路—从输入节点到输出节点的通路上，通过任何节 点不多于一次，此通路自然保护区为前向通路
7）回路—就是闭环通路 8）不接触回路—如果一些回路间没有任何公共节点 9）前向通路增益—在前向通路中多支路增益的乘积。 10）回路增益—回路中多支路增益的乘积。
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
信号流图的性质 (1)信号流图只适用于线性系统。 (2)支路表示一个信号对另一个信号的函数关系；信 号只能沿着支路上的箭头指向传递 (3)在节点上可以把所有输入支路的信号叠加，并把 相加后的信号传送到所有的输出支路。
(4)具有输入和输出支路的混合节点，通过增加一个具 有单位增益的支路，可以把它作为输出节点来处理。 (5)对于一个给定的系统，其信号流图不是唯一的， 这是由于描述的方程可以表示为不同的形式。
参考输入误差的传递函数为
CR(s) ER(s)G1(s)G2(s)
CR(s)
G1( s )G 2( s )
R(s) 1 G1(s)G2(s)H (s)
ER(s)G1(s)G2(s)
信号流图
（3）混联： ）混联：
X1 H1 H3 X3 X2 H2 X4
X2 H2H3 X1 H1H3 X4
X4=H3X3=H3(H1X1+ H2X2)= H1H3X1 + H2H3X2
H2 X1 H1 X2 H3 X4 X3
H1H2 X1 H1H3
X3
பைடு நூலகம்
X4
▲
■
第 7页
（4）自环的消除： ）自环的消除：
例 求下列信号流图的系统函数
H4
首先找出所有回路： 解 (1)首先找出所有回路： 首先找出所有回路 L1=H3G L2=2H1H2H3H5 L3=H1H4H5 (2)求特征行列式 求特征行列式
1
H1
H2
H3 G H5
2
1
△=1-（H3G+2H1H2H3H5+ H1H4H5）+ H3G H1H4H5 （ (3)然后找出所有的前向通路： 然后找出所有的前向通路： 然后找出所有的前向通路 1 p1=2H1H2H3 H = ( p1∆1 + p2 ∆2 ) ∆ p2=H1H4 (4)求各前向通路的余因子：△1 =1 ， △2 =1-GH3 求各前向通路的余因子： 求各前向通路的余因子 框图也可用梅森公式求系统函数。 框图也可用梅森公式求系统函数。 ▲ ■
▲ ■ 第 3页
3、信号流图的基本性质 、
（1）信号只能沿支路箭头方向传输。 ）信号只能沿支路箭头方向传输。 支路的输出=该支路的输入与支路增益的乘积 该支路的输入与支路增益的乘积。 支路的输出 该支路的输入与支路增益的乘积。 （2）当结点有多个输入时，该结点将所有输入支路 ）当结点有多个输入时， 的信号相加， 的信号相加，并将和信号传输给所有与该结点相连 的输出支路。 的输出支路。 x1 d x5 如：x4= ax1+bx2+cx3 x5= dx4 x6= ex4
信号与系统-8
信号与系统-8(总分：100.00，做题时间：90分钟)一、(总题数：23，分数：100.00)1.某单输入单输出的因果LTI 系统，当激励为e 1 (t)时，相应的零状态响应为r zs1 (t)=(8e -4t -9e -3t +e -t )ε(t)；当激励为e 2 (t)时，相应的零状态响应为r zs2 (t)=(e -4t -4e -3t +3e -2tε(t)。
其中e 1 (t)≠e2 (t)，且e 1 (t)和e 2 (t)均为指数单调衰减的有始函数。
若已知r(0 - )=7，r"(0 - )=-25，求该系统的零输入响应r zp (t)。
（分数：2.50）__________________________________________________________________________________________ 正确答案：()解析：4e -4t +3e -3t，t≥02.某线性非时变系统，其系统函数零极点图如下图所示。
试指出H(s)的可能收敛域，并对每一种收敛域确定系统的因果性，稳定性。
（分数：2.50） __________________________________________________________________________________________ 正确答案：()解析：ROC 1 ：Re[s]＜-2，系统是反因果的，不稳定的 ROC 2 ：-2＜Re[s]＜-1，系统是非因果的，不稳定的ROC 3 ：-1＜Re[s]＜2，系统是非因果的，稳定的ROC 4 ：Re[s]＞2，系统是因果的、不稳定的已知某线性非时变系统，在激励信号e(t)=δ(t)-4e 2t ε(-t)作用下产生的零状态响应为一双边信号r(t)，其拉氏变换为，（分数：10.00） (1).求系统函数H(s)及其收敛域；（分数：5.00）__________________________________________________________________________________________ 正确答案：()(2).若对于所有t ，e(t)=e 2t ，求响应r(t)。
信号与系统-系统函数与信号流图_图文_图文
对于负反馈，总有
二．信号流图
系统的信号流图是用一些点和有向线段来描述系统。变成信号流图形式 就是用线段端点代表信号，称为节点。有向线段表示信号传输的路径和方 向，一般称为支路，每一条支路上有增益，所以每一条支路相当于乘法器 。
信号流图中的节点可以有很多信号输入，它们是相加的关系， 而且可以有不同方向输出。
对于连续时间动态LTI系统的模拟，通常由加法器、标量乘 法器和积分器三种部件构成。
系统模拟可以理解为就是用这三种部件画出系统的信号流图 或是系统的方框图，使得流图或方框图实现了指定的系统函数。
四．系统模拟
例： 用加法器、标量乘法器和积分器三种部件模拟下面微分方程描
述的系统
解：首先考虑下面的系统
由线性时不变系统的性质知道存在下面关系
节点:
三．Mason公式
表示系统中的变量或信号的点称为节点。
支路:
连接两节点间的有向线段称为支路。 支路增益就是两节点间的增益。
输入节点（源点）: 仅有输出支路的节点， 一 般为系统的输入。
输出节点（阱点）: 仅有输入支路的节点，一般为系统的输出
混合节点:
既有输入支路又有输出支路的节点
三．Mason公式
四．系统模拟
方程两边积分三次得到
说明
是某信号积分三次得到，可以画出部分框图。
四．系统模拟
第一个积分器的输入信号实际是 可以画出部分系统框图
四．系统模拟
可以画出完整的系统框图
四．系统模拟
对应的信号流图为
其中
若 则
表示积分器（拉普拉斯变换的性质）
通路: 从任一节点出发沿着支路箭头方向连续地穿过 各相连支路到达另一节点的路径称为通路。
信号流图
[例]已知某三阶数字滤波器的系统函数为
5 1 2 2 3 z z 3 3 H ( z) 1 1 1 1 1 2 (1 z )(1 z z ) 3 2 2
试画出其直接型、级联型和并联型结构。
直接型
将系统函数H(z)表达为
5 1 2 2 3 z z 3 3 H (z) 1 1 1 2 1 3 1 z z z 6 3 6 x ( n) y ( n) 3 z 1 1/ 6 5/3 z 1 2/3 1/ 3 z 1 1/ 6
它的系统函数和差分方程一般有如下形式：
H ( z ) h( n) z
n 0 N 1 i 0
N 1
n
y (n) h(i) x(n i ) h(n i ) x(i )
i 0
N 1
基本的结构形式有下几种： （1）直接型（卷积型、横截型） 卷积型：差分方程是信号的卷积形式；
横截型：差分方程是一条输入x(n)延时链的横向 结构。
基本的结构形式有下几种： （1）直接型（卷积型、横截型） 直接由差分方程可画出对应的网络结构：
H ( z ) h(n) z n
n 0 N 1
y ( n) h(i ) x( n i )
i 0
N 1
直接型的转置：
（2）级联型（串联型） 当需要控制滤波器的传输零点时，可将系统函数分解 为二阶实系数因子的形式：
W z H1 z ai z X z i 0
N i
H 2 z
1 1 bi z i
i 1 N
wn ai xn i
i 0
N
yn wn bi yn i
i 1
N
信号与系统——系统函数
幅频: | H ( j) | bm B1B2...Bm
A1A2... An
相位:()=(1+…+m)-(1+…+n) 分析: 从0~∞
2019/11/20
22
例: u1(s) + -
R 1/sc
u2(s)
1 sc H(s)=u2(s)/ u1(s) = R 1 sc
11 = Rc s 1 Rc
写出网络转移函数表达式
Hs
V2 s V1 s
1 RC
s
1 1
RC
1 RC
2019/11/20
1 M1 ejθ1
V2 ej ω V1
M1
θ1
1 RC
jω
O
σ
30
频响特性 V2
jω
1 V1
M1
1
2
θ1
1 RC
O
σ
O1 RC
ω
H
Im[z] Z平面
2019/11/20
-1/3
1 2 Re[z]
13
极点位置与h(k)形状的关系
j Im z
1
O
1
Re z
2019/11/20
14
利用z～s平面的映射关系
s平面(单极点)
z平面(单极点)
极点位置 h(t)特点 极点位置 h(k)特点
虚轴上
等幅
单位圆上 等幅
原点时 左半平面
t 1
2019/11/20
28
结论:
凡极点位于左半开平面,零点位于右半开 平面,且所有的零点与极点对于j轴为一 镜像对称的系统函数即为全通函数.
吴大正 信号与线性系统分析 第7章 系统函数
系统函数H(· )与时域响应h(· )
(b) 若有一对共轭复极点p12= -α±jβ，则A(s)中有因 子[(s+α)2+β2] K e-αtcos(βt+θ)ε(t) (c) 若有r重极点， 则A(s)中有因子(s+α)r或[(s+α)2+β2]r，其响应为 Kiti e-αtε(t)或Kiti e-αtcos(βt+θ)ε(t) (i=0,1,2,…,r-1) 以上三种情况：当t→∞时，响应均趋于0→暂态分量。 系统的稳定性如何？
第 7页
Kitiε(t)或Kiticos(βt+θ)ε(t)(i=0,1,2,…,r-1)→递增函数
（3）在右半开平面 ：均为递增函数。
结 论
LTI连续因果系统的h(t)的函数形式由H(s)的极 极点确定。
① H(s)在左半平面的极点所对应的响应函数为衰减 的。即当t→∞时，响应均趋于0。 系统稳定？ ② H(s)在虚轴上的一阶极点所对应的响应函数为稳 态分量。系统稳定？
第七章
§7.1
系统函数
系统函数与系统特性
系统函数的零、极点分布图 系统函数H(· )与系统的因果性 系统函数与时域响应 系统函数与频率响应
第 1页
一、系统函数的零、极点分布图
LTI系统的系统函数是复变量s或z的有理分式，即
B () H () A()
A(.)=0的根p1，p2，…，pn称为系统函数H(.)的极点； B(.)=0的根1，2，…，m称为系统函数H(.)的零点。 将零极点画在复平面上 jω 得零、极点分布图。 j 例
第 23 页
第3行按下列规则计算：
an c n1 a0 a0 an
信号与系统4.7
b3 F(s) 1 b2 s-1 -a2 -a1 s-1 s-1 b1 b0 -a0 Y(s)
信号流图
1、直接型结构
H ( s)
H1 ( s ) 1
i 0
bn bn1 s
1
b1 s
( n 1)
b0 s
n
1 an1 s 1 a1 s ( n1) a0 s n
Y (s) 1 H (s) X (s) s a0
X (s )
sY (s)
1 s
Y (s)
a0
以上模拟图都未计初始条件，故是零状态响应！
直接型结构（一阶节）
b2 s b1 b2 b1s 1 H (s) s a1 1 a1s 1 b2 b1 s 1 1 1 Y (s) H (s) F (s) F ( s) (b2 b1s ) F (s) 1 1 1 a1 s 1 a1 s
系统的模拟是将系统分解为若干基本单元 (如果熟知各单元性能，将它们组合构成复 杂系统时，分析过程将得以简化)
二、线性系统的模拟方 法 1、模拟图用基本单元
①加法器:
x1( t ) X 1( s )
x 2(t ) X 2( s )
y (t ) Y (s)
y (t ) x1(t ) x 2(t ) Y ( s ) X 1( s) X 2( s)
H (s) H 2 ( s) H1 ( s)
并联系统的系统函数等于各子系统的系统函数的和
3)反馈
F (s )
E (s )
G(s)
Y (s )
H ( s)
Y ( s) E ( s) K ( s)
E (s) F (s) H (s)Y (s)
信号与系统系统函数与信号流图
数值计算误差分析与处理
截断误差
由于数值计算中采用有限项近似，导致计算结果与真实值之间的误差。可以通过增加计算项数、采用更高精度的算法 等方法减小截断误差。
舍入误差
由于计算机字长限制，进行数值运算时产生的误差。可以通过采用更高精度的数据类型、合理的运算顺序等方法减小 舍入误差。
稳定性分析
对于某些算法，随着计算步数的增加，误差可能会逐渐累积并导致计算结果失真。需要对算法进行稳定 性分析，选择合适的步长和算法参数以保证计算的稳定性。
信号与系统的关系
信号是系统的输入和输出
在信号处理中，通常将输入信号经过系统处理后得到的输出信号作 为研究对象。因此，信号与系统是密切相关的。
系统的性能影响信号的特性
不同的系统会对输入信号产生不同的影响，如放大、缩小、延迟、 失真等。因此，系统的性能会直接影响输出信号的特性。
信号与系统相互依存
没有输入信号就没有输出信号，而没有系统则无法对输入信号进行 处理。因此，信号与系统是相互依存的。
实验数据分析与结果讨论
数据预处理
对实验或仿真数据进行必要的预处理，如去噪、归一化等。
特征提取
提取数据的关键特征，如幅值、频率、相位等，以便进行后续分析。
结果可视化
利用图表、图像等方式将实验结果可视化，便于观察和分析。
结果讨论
根据实验或仿真结果，讨论系统性能、设计合理性以及可能存在的改进空间。
THANKS FOR WATCHING
感谢您的观看
输入节点和输出节点
分别表示系统的输入和输出信 号。
信号流图的绘制方法
根据系统方程或框图确定系统 的输入、输出和内部变量。
在支路上标注传输系数，以描 述信号通过该支路时的变化。
2.3 信号流图
前向通路增益 p1 = abc
前向通路增益
p2 = d
【回路】【单独回路】：起点和终点在同一节点，而且信号通过每个节
x2 x3 x2
回路1增益
l1 = ae l2 = bf l3 = g
回路2 x3 x4 x3 回路2增益 回路3 x5 x5 回路3增益 【不接触回路】：回路之间没有公共节点。 回路2和回路3 回路1和回路3
-
1 R1 1 R1
I1 ( s ) I (s)
1
1 C1s
1 C1s
u (s )
1
1 R2
1 R2
I 2 ( s)
1 C2 s
uo (s)
1
ui
ue
I1
1
I
a 1 b u
1 C2 s
I2
1
uo
讨论：信号流图中，a点和b点之间的传输为1，是否可以将该 两点合并。使得将两个不接触回路变为接触回路？如果可以的 话，总传输将不一样。
R
E
-
G1
H1
+
G2
+ -
G3
H2
C
[解]：在结构图上标出节点，如上。然后画出信号流图，如下：
R
G4 E G1 G2 H1
H1H 2
G3 C H2
R
C (s) 求 R(s) ：
G4 E G1 G2 H1
H1H 2
G3 C H2
前向通道有二，分别为: P G1G2G3 , P2 G3G4 1 回路有三，分别为： G1H1 ,G3 H 2 ,G1G2G3 H1H 2
1 m 0 l g 1 h e d k 1
信号与系统第三十讲
4 、x1→x4→x3 →x2 →x1, 增益 L4=−G1G2G3H4
L
j
j
G1 H1 G2 H 2 G3 H 3 G1G2G3 H 4
有一对两两不接触回路： x1→x2→x1 和x3→x4→x3
L
m,n
m
Ln L1 L3 G1G3 H1 H 3
1 L j Lm Ln Lp Lq Lr
j m, n p ,q ,r
L 所有不同回路增益之和
j j
L
m ,n p p ,q ,r
m
Ln 所有两个两两不接触回路的增益乘积之和
r
L L L 所有三个两两不接触回路的增益乘积之和
q
例7.3-2 求图7.3-6 所示信号流图的系统函数。
解：（1）求信号流图的特征行列式Δ 4 个回路： 1 、x1→x2→x1, 增益 L1=−G1H1 2 、x2→x3→x2, 增益 L2=−G2H2 3 、x3→x4→x3, 增益 L3=−G3H3
通路增益：通路中各支路增益的乘积称为 通路增益。
前向通路：从源点到汇点的开通路称为前 向通路。
注意：
1）除源点外，一个结点相当于一个加法器， 结点代表的变量为加法器的输出。 2）信号通过支路，将乘以支路的增益。 3）对同一系统，信号流图不唯一。
二、信号流图的化简（分析）
１、流图的性质
信号只能沿支路箭头方向传输，支路的输 出是该支路的输入与支路增益的乘积。
a b ac
c
bc
例7.3-1 求图7.3-5(a)所示信号流图的系统函数。
解： （1）将环分开化简为自环： 将 x1→x2→x1 环与 x1→x2→x3→x1 环从流图中分 开，按支路串联将x1→x2→x1 环化简成自环， 增益为 -a1s−1 ，将 x1→x2→x3→x1 环化简成自环， 增益为-a0s−2。
信号与系统_北京邮电大学中国大学mooc课后章节答案期末考试题库2023年
信号与系统_北京邮电大学中国大学mooc课后章节答案期末考试题库2023年1.关于信号【图片】描述正确的是（）。
参考答案:该信号的基波角频率是1 rad/s。
2.以频谱分割的方式进行频道划分，多路信号混合在一起传输，但每一信号占据着有限的不同频率区间，此区间不被其他信号占用。
这种复用方式称为频分复用。
参考答案:正确3.【图片】上图所示的周期矩形脉冲信号，其直流分量为【图片】。
参考答案:错误4.【图片】的能量是（）。
参考答案:55.对于具有矩形幅度特性和线性相位特性的理性低通滤波器，【图片】是其截止频率，其阶跃响应【图片】波形如下图所示。
下面说法中不正确的是（）【图片】参考答案:阶跃响应的上升时间为。
6.【图片】的收敛域是全s平面。
参考答案:正确7.因果信号【图片】的拉普拉斯变换为【图片】，则【图片】。
参考答案:正确8.【图片】的z变换为【图片】，收敛域为【图片】。
参考答案:正确9.线性时不变因果系统的单位阶跃响应【图片】与其单位冲激响应【图片】之间关系是【图片】。
参考答案:错误10.周期为T的冲激序列信号【图片】，有关该信号描述不正确的是（）。
参考答案:该信号的频谱满足离散性、谐波性和收敛性。
11.在区间【图片】余弦信号【图片】与正弦信号【图片】相互正交。
参考答案:正确12.已知某离散时间线性时不变系统的单位样值响应为【图片】，则当输入信号为【图片】时，系统的零状态响应为【图片】。
参考答案:正确13.某系统的信号流图如下图所示。
则该系统的系统函数可表示为【图片】。
【图片】参考答案:正确14.某连续系统的系统函数为【图片】，该系统可以既是因果的，又是稳定的。
参考答案:正确15.因果系统的系统函数为【图片】，R>0,C>0,则该系统属于( )网络。
参考答案:高通滤波网络16.下图所示反馈系统，已知子系统的系统函数【图片】，关于系统函数及稳定性说法正确的是（）。
【图片】参考答案:系统函数为，当时，系统稳定。
郑君里《信号与系统》(第3版)【教材精讲+考研真题解析】讲义 第11章 反馈系统 【圣才出品】
第11章反馈系统[视频讲解]11.1本章要点详解本章要点■反馈系统■信号流图重难点导学一、反馈系统反馈系统的研究是利用分解与互联概念而获得成功的典型范例。
1．连续时间信号反馈系统模型图11-1连续时间信号反馈系统模型2．离散时间信号反馈系统模型图11-2离散时间信号反馈系统模型3．反馈系统的基本特性及其应用（1）基本特性①前馈通路系统函数()A s （或()A z ）对整个系统函数()H s （或()H z ）的影响可忽略不计；②整个的系统函数()H s （或()H z ）近似等于反馈通路系统函数()F s （或()F z ）的倒数。
（2）应用①改善系统的灵敏度；②改善系统频响特性；③逆系统设计；④使不稳定系统成为稳定系统；⑤利用反馈系统产生自激振荡。
二、信号流图1．概述利用方框图可以描述系统（连续的或离散的），较微分方程或差分方程更为直观。
而将方框图进一步简化就可以得到流图。
其优点是系统模型的表示简明清楚、系统函数的计算过程明显简化。
2．系统的信号流图表示法信号流图是指用一些点和支路来描述系统，如图11-3所示。
图11-3用信号流图表示框图Y s称为结点。
线段表示信号传输的路径，称为支路。
信号的传输方向用箭X s、()()头表示，转移函数标在箭头附近，相当于乘法器。
3．流图术语（1）结点：表示系统中变量或信号的点。
（2）转移函数：两个结点之间的增益称为转移函数。
（3）支路：连接两个结点之间的定向线段，支路的增益即为转移函数。
（4）输入结点或源点：只有输出支路的结点，它对应的是自变量（即输入信号）。
（5）输出信号或阱点：只有输入支路的结点，它对应的是因变量（即输出信号）。
（6）混合结点：既有输入支路又有输出支路的结点。
（7）通路：沿支路箭头方向通过各相连支路的途径（不允许有相反方向支路存在）。
（8）开通路：通路与任一结点相交不多于一次。
（9）闭通路：如果通路的终点就是起点，并且与任何其他结点相交不多于一次。
信号与系统第四章习题
1 3
s +1 ) ，复频移性质、尺度变换、S 域微分 3
b
b ⎤ 1 s - s ⎡ (4) f (at − b) = f ⎢a(t − )⎥ ↔ F( )e a ，时移性质、尺度变换 a ⎦ a a ⎣
4．7 题图 4．2 所示为从 t=0 起始的周期信号。求 f(t)的单边拉氏变换。
解： (a) f (t ) = f a (t ) *
∑ δ (t − nT )
n =0
∞
- s 1 f a (t ) = ε (t ) − ε (t − T / 2) ↔ (1 - e 2 ) s - s 1 1 1- e 2 1 = = ∴ F(s) = (1 - e 2 ) T -s ⎞ s 1 - e -sT s 1 - e -sT ⎛ ⎜ s ⎜1 + e 2 ⎟ ⎟ ⎝ ⎠ T T - s
2
K1 =
2 jπ / 6 2 − jπ / 6 e , K2 = e 3 3
∴ h(t ) =
π 4 −t 2 −t e cos( 3t + )ε (t ) = e 6 3 3
2
(
3cos 3t - sin 3t ε (t )
)
当 u s (t ) = ε (t ) 时， U( s ) = H ( s) =
−2 t 解：(1) e f (2t ) ↔
1 s+2 F( ) ，复频移性质、尺度变换 2 2 ⎡1 ⎤
2 2 -2s (2) (t − 2) f ( t − 1) = (t − 2) f ⎢ (t − 2)⎥ ↔ 2F′′(2s)e ，时移性质、尺度变换、S 域微分 2 ⎣2 ⎦
1
−t (3) te f (3t ) ↔ − F′(
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§5.6.4 系统函数和信号流图
信号与系统
主要内容
•系统方框图 •信号流图 •Mason公式 •系统模拟（第5.8节）
信号与系统
一．系统方框图
一个系统的方框图可由许多子系统的框图作适当联接组成。
子系统的基本联接方式有级联、并联和反馈三种。
（1）级联 等效系统函数为
（2）并联 等效系统函数为
一．系统方框图
（3）反馈
等效系统函数为
H (s) H1(s) 1 H1(s)H2(s)
对于负反馈，总有
H (s) H1(s) 1 H1(s)H2(s)
X (s)
E(s)
Y (s)
H1(s)
B(s)
H 2 (s)
X (s)
H1(s)
Y (s)
1 H1(s)H2 (s)
信号与系统
二．信号流图
系统的信号流图是用一些点和有向线段来描述系统。变成信号流图形式 就是用线段端点代表信号，称为节点。有向线段表示信号传输的路径和方 向，一般称为支路，每一条支路上有增益，所以每一条支路相当于乘法器。
H (s) H1(s)H2 (s)
X (s)
Y1(s) H1(s)
H 2 (s)
Y (s)
X (s)
Y (s)
H1 (s)H 2 (s)
H (s) H1(s) H2(s)
X (s)
H1(s) Y1(s)
Y (s)
H2 (s) Y2 (s)
X (s)
Y (s)
H1(s) H2 (s)
信号与系统
X (s)
Y (s) H (s)
X (s)
H (s)
Y (s)
X 2 (s)
H 24
H14
H 45
X 5 (s)
X1(s)
X 3s
X 4 (s) H 34
H 46 X 6 (s)
多输入多输出节点
信号流图中的节点可以有很多信号输入，它们是相加的关系，
X 4 X1H14 X 2H24 X 3H34
述的系统
d3 y(t) dt 3
a2
d2 y(t) dt 2
a1
dy(t) dt
a0
y(t)
b2
d 2 x(t ) dt 2
b1
dx(t) dt
b0 x(t )
解：首先考虑下面的系统
d3 y1(t) dt 3
a2
d2 y1(t) dt 2
a1
dy1(t) dt
a0
y1(t)
x(t)
由线性时不变系统的性质知道存在下面关系
H1
H2
H3
G4
H5
Y
X
X1 G2 X 2
X 3 H4 X 4 G5
系统函数为
M
Pk (s)k (s)
H k1 (s)
H1H 2 H 3 H 4 H 5
1 H2G2 H4G4 H5G5 H2H3H4H5G1 H2H4G2G4 H2G2H5G5
信号与系统
三．Mason公式
G1
H1
H2
H3
G4
H5
X
X1 G2 X 2
X 3 H4 X 4 G5
Y
信号与系统
三．Mason公式
通路: 从任一节点出发沿着支路箭头方向连续地穿过 各相连支路到达另一节点的路径称为通路。
前向通路: 从输入节点到输出节点的通路。 前向通路中通过任何节点不多于一次。
开通路: 如果通路与任一节点相遇不多于一次，则称 为开通路。
三条前向通路之(1)
X X1 X2 X3 X4 Y
P1 H1H2H3H4H5
1 1 0 0 1
三条前向通路之(2)
X X1 X4 Y
P2 H1H5H6
2 1
信号与系统
三．Mason公式
三条前向通路之(3)
X X1 X2 Y
P3 H1H 2 H 7
3 1 H4G1
L4 H2H3H4H5G1
其中（L1、L2），（L1、L3）是两两不接触的回路，没有三三不接触的 回路。
信号与系统
三．Mason公式
G1
H1
H2
H3
G4
H5
Y
X
X1 G2 X 2
X 3 H4 X 4 G5
所以流图的特征式为
(s) 1 Li LiLj 1 (L1 L2 L3 L4) (L1L2 L1L3)
而且可以有不同方向输出。
信号与系统
节点:
三．Mason公式
表示系统中的变量或信号的点称为节点。
支路:
连接两节点间的有向线段称为支路。 支路增益就是两节点间的增益。
输入节点（源点）: 仅有输出支路的节点， 一 般为系统的输入。
输出节点（阱点）: 仅有输入支路的节点，一般为系统的输出
混合节点:
既有输入支路又有输出支路的节点
a1
d
y1(t) dt
a0
y1(t)
可以画出部分系统框图
d2 y1 t dy1 t
x t
dt 2
dt
y1t
a2 a1 a0
信号与系统
四．系统模拟
y(t)
b2
d
2 y1(t) dt 2
b1
d
y1(t) dt
b0
y1(t)
可以画出完整的系统框图
b2 b1
x(t)
y1t
b0
y(t)
a2 a1 a0
Pk (s)k (s)
k 1
X (s)
(s)
其中 H (s) 从输入节点到输出节点之间的系统函数
(s) 特征式 (s) 1 Li LiLj LiLjLk L
Li 所有不同回路增益之和 Li Lj 所有两两互不接触回路增益乘积之和 Li Lj Lk 所有三个互不接触回路增益乘积之和
Pk (s) 从输入节点到输出节点的第k条前向通路增益
k (s)
在 (s) 中，将与第k条前向通路相接触
的回路所在项去掉后余下的部分
信号与系统
三．Mason公式
例：用Mason公式求图所示系统的系统函数
G1
H1
H2
H3
G4
H5
Y
X
X1 G2 X 2
X 3 H4 X 4 G5
解：先求环路，一共有4个环路，即
L1 H2G2 L2 H4G4
L3 H5G5
方程两边积分三次得到
y1(t)
a2
d
2 y1(t) dt 2
a1
d
y1(t) dt
a0
y1 (t )
x(t)dt
说明 y1(t)是某信号积分三次得到，可以画出部分框图。
d2 y1 t dy1 t
dt 2
dt
y1 t
信号与系统
四．系统模拟
第一个积分器的输入信号实际是
x(t)
a2
d
2 y1(t) dt 2
四．系统模拟
系统模拟指用一些标准的部件通过一定的连接方式实现指定 的系统函数。
对于连续时间动态LTI系统的模拟，通常由加法器、标量乘 法器和积分器三种部件构成。
系统模拟可以理解为就是用这三种部件画出系统的信号流图 或是系统的方框图，使得流图或方框图实现了指定的系统函数。
信号与系统
四．系统模拟
例： 用加法器、标量乘法器和积分器三种部件模拟下面微分方程描
信号与系统
四．系统模拟
对应的信号流图为
1 X
1
1
s
s
a2
a1 a0
b2 b1
1
Y1
b0
s
1 Y
1
其中
表示积分器（拉普拉斯变换的性质）
s
若 Lx(t) X (s)
则
L
t
x(τ
)
d
τ
X (s) 1 ss
0 x( ) d τ
信号与系统
作业13-6-18
P183 5-16
二、 求下列微分方程描述系统的系统函数，并画出其零极点图。
1 (H2G2 H4G4 H5G5 H2H3H4H5G1) (H2H4G2G4 H2G2H5G5)
前向通路只有一条，即 X X1 X 2 X 3 X 4 Y
所有回路都和这条前向通路接触，所以
P1 H1H2H3H4H5
1 1 0 0 1
信号与系统
三．Mason公式
G1
2H
+
v1 ( t )
-
1F
题图
+
2
v2 (t)
-
其中L1、L4是两两不接触的回路，没有三个互不接触的回路
信号与系统
H6
H7
三．Mason公式
H1
H2
H3 X3 H4
H5
Y
可以求得流图的特征式 X
X1
X2
G1
X4
G2
1 Li LiLj 1 (L1 L2 L3 L4 ) (L1L4 )
1 H4G1 H2H3H4H5G2 H5H6G2 H2H7G2 H2H4H7G1G2
y(t)
b2
d2 y1(t) dt 2
b1
dy1(t) dt
b0
y1(t)
信号与系统
四．系统模拟
d
3 y1(t) dt3
a2
d
2 y1(t) dt 2
a1
d
y1(t) dt
ቤተ መጻሕፍቲ ባይዱ
a0
y1(t)
x(t)
d 3 y1(t) dt3
a2
d 2 y1(t) dt 2
a1