4.2 解一元一次方程(2)-去括号
合集下载
2022六年级数学上册 第四章 一元一次方程 2解一元一次方程（2）课件 鲁教版五四制
即
x-1=-2
x=-2+1 x=-1
练习
1.解下列方程： （1）2(3—x)=9; （2）−3(x +3) =24; （3）11x +1 =5(2x + 1); （4）5(x—1)=1;
x =-1.5 x =-11
x =4
x=1.2
（5）2 — (1—x)= —2;
5.某商店购进一批运动服，每件售价120元， 可获利20%，这种运动服每件的进价是多少 元？
解：设这种运动服每件的进价是X元。 根据题意，得（1+20%）X=120
120%X=120
X=100 答：这种运动服每件的进价是100元。
6.植树节某班要栽100棵树，有5名同学每人都栽了2棵， 其余的同学每人栽3棵，正好全部栽完，问这个班共有多 少名学生？
如果设一听果奶饮料x元，那么可列出方程 4（x+0.5）+x=10-3
想一想
（1）上面这个方程列的对吗？你还能列出不同的方程吗？
（2）怎样解所列的方程？
你知道一听果奶饮料多少 钱吗？解出你所列的方程。
例3 解方程:4(x+0.5)+x=7.
此方程与上课时所学方程有何差异?
方程中含 有括号
须先去括号
4.2 解一元一次方程（2）
小颖到超市准备买1听果奶饮料和4听可乐，营业员告诉她一 听可乐比一听果奶饮料多0.5元，小颖给了营业员10元钱，营 业员找回了3元，大家帮助小颖算算一听果奶饮料多少钱？
小颖到超市准备买1听果奶饮料和4听可乐，营业员告诉她一 听可乐比一听果奶饮料多0.5元，小颖给了营业员10元钱，营 业员找回了3元，大家帮助小颖算算一听果奶饮料多少钱？
合并同类项
七年级数学上第四章 4.2 解一元一次方程(2)
12．解一元一次方程：
(1)解方程： ；
(2)解方程： ．
13．单项式 ’与3x2y是同类项，则a–b的值为( )．
A. 2 B.0 C．–2 D．1
14．如果关于x的方程ax+b=2(2x+7)+1有无数多个解，那么a，b的值分别是( )．
A．a=4，b=15 B．a一=0，b=0 C．a=2，b=–15 D. a=–4, b=15
29．据《衢州日报》2009年5月2日报道：“家电下乡”农民得实惠．村民小郑购买一台双门冰箱，在扣除13％的政府财政补贴后，再减去商场赠送的“家电下乡”消费券100元，实际只花了1726.13元钱，那么他购买这台冰箱节省了___________元钱．
参考答案
1．A 2．C 3．B 4．D 5．A 6．A 7．6 9．8 10．
15．已知关于x的方程(3a+8b)x+7=0无解，则ab是( )．
A.正数B．非正数C．负数D.非负数
16．若方程(a+3)x –5=0是关于x的一元一次方程，则a=___________．
17．在等式3×口–2×口=15的两个方格内分别填入一个数，使这两个数互为相反数且等式成立．则第一个方格内的数是___________．
19．x=–3
20．由3[x–2(x– )]=4x，解得x= ．由 解得x= ．因为它们的解相同，所以 = ，解得a= ，所以x= =
21．因为|3a+1 |与(b–2)2互为相反数，所以|3a+1|+(b–2)2=0，又因为|3a+1|≥0且(b–2)2≥0，此时，只有0+0才能和为0，即|3a+1|=0，且(b–2)2=0，所以a= ，b=2．当a= ，b=2时，ab–ab=( )2–( ) 2= .
(1)解方程： ；
(2)解方程： ．
13．单项式 ’与3x2y是同类项，则a–b的值为( )．
A. 2 B.0 C．–2 D．1
14．如果关于x的方程ax+b=2(2x+7)+1有无数多个解，那么a，b的值分别是( )．
A．a=4，b=15 B．a一=0，b=0 C．a=2，b=–15 D. a=–4, b=15
29．据《衢州日报》2009年5月2日报道：“家电下乡”农民得实惠．村民小郑购买一台双门冰箱，在扣除13％的政府财政补贴后，再减去商场赠送的“家电下乡”消费券100元，实际只花了1726.13元钱，那么他购买这台冰箱节省了___________元钱．
参考答案
1．A 2．C 3．B 4．D 5．A 6．A 7．6 9．8 10．
15．已知关于x的方程(3a+8b)x+7=0无解，则ab是( )．
A.正数B．非正数C．负数D.非负数
16．若方程(a+3)x –5=0是关于x的一元一次方程，则a=___________．
17．在等式3×口–2×口=15的两个方格内分别填入一个数，使这两个数互为相反数且等式成立．则第一个方格内的数是___________．
19．x=–3
20．由3[x–2(x– )]=4x，解得x= ．由 解得x= ．因为它们的解相同，所以 = ，解得a= ，所以x= =
21．因为|3a+1 |与(b–2)2互为相反数，所以|3a+1|+(b–2)2=0，又因为|3a+1|≥0且(b–2)2≥0，此时，只有0+0才能和为0，即|3a+1|=0，且(b–2)2=0，所以a= ，b=2．当a= ，b=2时，ab–ab=( )2–( ) 2= .
课时编号4.2解一元一次方程.2(去括号)
用去括号、移项、合并同类项、系数化为1的方法解一些简单的一元一次方程
不要漏乘括号内的任何一项；
若括号前面是“－”号，记住去括号后括号内各项都变号
板书设计
情境创设
1、
2、
例1：……
……
……
例2：……
……
……
习题……
……
……
作业布置
P102
课后随笔
注意解法的灵活性，不要过分强求学生按固定格式来解，可适当引导学生找出较好的解题方法和书写过程.
共同概括
讲解矫正
适当拓展
解下列方程
3(y+4)12；2-(1-z)=-2；
2(3y-4)+7(4-y)=4y；4x-3(20-x)=6x-7(9-x)；
3(2y+1)=2(1+y)+3(y+3)
学用结合尝试解决
学生分析
学生讨论
利用乘除法互为逆运算；利用等式的基本性质；利用乘法分配律；利用去括号的方法等等
教学重点
去括号法则在解方程
教学难点
去括号法则在解方程中的熟练应用
教学过程
教学内容
教师活动
学生活动
小明说：“我姐姐今年的年龄是我去年的年龄的2倍少6，”已知姐姐今年20岁，问小明今年几岁？
若取小明今年为x岁，则依据下面的等量关系式列方程：姐姐今年的年龄=小明去年年龄的2倍－6.
得2（x－1）－6=20.
3.有什么收获？
初步掌握了解方程的一般步骤，培养自己的概括能力和耐心、细致的学习态度.
师提出问题，如何解方程？用上节课的知识能不能求解？有什么困难？如何去掉这个方程中的括号？谈谈你的想法.
教师把话题引到课本较为简单的例5上（见下面数学运用），引出去括号.
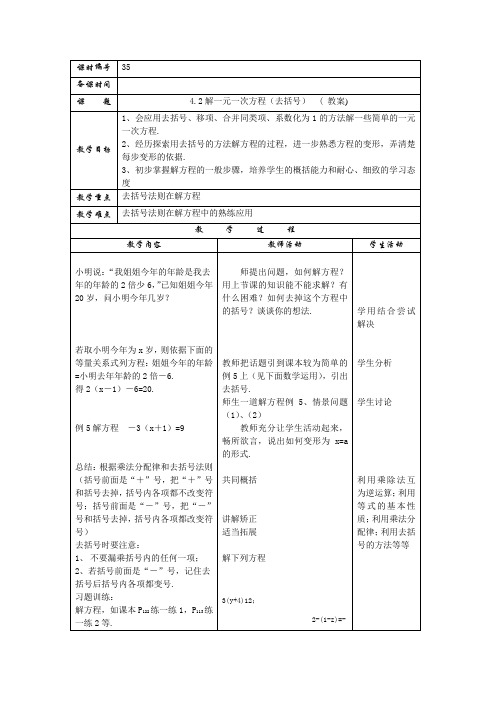
不要漏乘括号内的任何一项；
若括号前面是“－”号，记住去括号后括号内各项都变号
板书设计
情境创设
1、
2、
例1：……
……
……
例2：……
……
……
习题……
……
……
作业布置
P102
课后随笔
注意解法的灵活性，不要过分强求学生按固定格式来解，可适当引导学生找出较好的解题方法和书写过程.
共同概括
讲解矫正
适当拓展
解下列方程
3(y+4)12；2-(1-z)=-2；
2(3y-4)+7(4-y)=4y；4x-3(20-x)=6x-7(9-x)；
3(2y+1)=2(1+y)+3(y+3)
学用结合尝试解决
学生分析
学生讨论
利用乘除法互为逆运算；利用等式的基本性质；利用乘法分配律；利用去括号的方法等等
教学重点
去括号法则在解方程
教学难点
去括号法则在解方程中的熟练应用
教学过程
教学内容
教师活动
学生活动
小明说：“我姐姐今年的年龄是我去年的年龄的2倍少6，”已知姐姐今年20岁，问小明今年几岁？
若取小明今年为x岁，则依据下面的等量关系式列方程：姐姐今年的年龄=小明去年年龄的2倍－6.
得2（x－1）－6=20.
3.有什么收获？
初步掌握了解方程的一般步骤，培养自己的概括能力和耐心、细致的学习态度.
师提出问题，如何解方程？用上节课的知识能不能求解？有什么困难？如何去掉这个方程中的括号？谈谈你的想法.
教师把话题引到课本较为简单的例5上（见下面数学运用），引出去括号.
七年级数学上册教学课件《解一元一次方程(二)——去括号与去分母》(人教)
6x +6(x－2000) ＝150000
去括号
6x +6x－12000＝150000
移项
6x +6x＝150000+12000
合并同类项
12x＝162000
系数化为1
x＝13500
问题1 某工厂加强节能措施，前年下半年与上半年相比，月 平均用电量减少2000kW·h(千瓦·时)，全年用电15万kW·h。 这个工厂去年上半年每月平均用电多少？ (5)本题还有其他列方程的方法吗? 解：设下半年每月平均用电y kW· h。 根据题意，得 6y +6(y+2000) ＝150000 ② (6)试仿照解方程①方法解方程②。
实际问题的答案
检验
作业：教科书第91页习题3.3第1、6、7题。
随堂演练
1.方程4(a-x)-4(x+1)=60的解是x=-1，则a的值是( C ) A.-14 20 C. 14 D.-16 2.解方程5-5(x+8)=0的结果是 -7 。
3.解下列方程： (1) 5(x+8)-5=6(2x-7)； (2) 4(x-1)+3(2x+1)=10(1-2x)。 4.一架飞机在两城之间飞行，风速为24km/h，顺风飞行需要 2小时50分，逆风飞行需要3h。求无风时飞机的航速和两城之 间的航程。
回顾此题和问题1的解决过程，说一说列一元一次方
程解决实际问题的方法和步骤。
回顾此题和问题1的解决过程，说一说列一元 一次方程解决实际问题的方法和步骤。 实际问题 一元一次方程
解 方 程
设未知数，列方程
实际问题的答案
检验
一元一次方程的解 (x=a)
知识归纳
1.“去括号法”解一元一次方程的步骤：
六年级数学上册4.2解一元一次方程(第2课时) 精品优选PPT课件鲁教版五四制
2.解方程 1 x-1= 2 x去分母时,两边同乘6最合适.
3.方程
2
3
=3x,去分母得2x+1=3x.
(×)xΒιβλιοθήκη 14.方程 2去分母得3x+2x=1. ( × )
x + x = 1， 23
(√)
知识点一 解含括号的一元一次方程 【示范题1】解方程:(1)4x+2(x-2)=14-(x+4). (2)2(x-1)-(x+2)=3(4-x). 【思路点拨】去括号→移项→合并同类项→方程两边同除以未 知数的系数.
【自主解答】(1)去括号,得4x+2x-4=14-x-4, 移项,得4x+2x+x=14-4+4, 合并同类项,得7x=14, 方程两边同除以7,得x=2. (2)去括号,得2x-2-x-2=12-3x, 移项,得2x-x+3x=12+2+2, 合并同类项,得4x=16,方程两边同除以4,得x=4.
5.方程两边同除以未知数的系数得:__x_=__-_52__.
解一元一次方程的一般步骤
去分母、_去__括__号__、移项、_合__并__同__类__项__、未知数的系数化为1, 即最终将方程转化为“_x_=_a_”的形式.
【思维诊断】 (打“√”或“×”)
1.由2(x-2)-3(x+3)=1去括号得2x-4-3x+9=1. ( × )
【方法一点通】 解一元一次方程的步骤 1.去分母. 2.去括号. 3.移项. 4.合并同类项.
5.未知数的系数化为1. 但并不是解每一个方程都需要这五个步骤，这五个步骤的
先后顺序并非固定不变，要根据方程的特点，确定恰当的步骤， 灵活解方程.
2024年秋新苏科版七年级上册数学 4.2 一元一次方程及其解法 教学课件
标准，其中“元”指未知数，“次”指未知数的次数， “整式”指分母不含未知数.
例1
知1－练
2 解题秘方：利用一元一次方程的特点进行判断.
知1－练
解：①等号右边不是整式；③未知数x的最高次数为2；④ 化简后x的系数为0且等式不成立；⑥含有两个未知数；只 有②⑤是一元一次方程.
知1－练
方法 判断一个方程是否为一元一次方程的方法：
知识点 4 解一元一次方程——去分母
知4－讲
1. 解含有分母的一元一次方程时，方程两边乘各分母的最 小公倍数，从而约去分母，这个过程叫作去分母.
2. 去分母解一元一次方程的步骤 去分母→去括号→移项→合并同类项→系数化为1
特别解读 1. 去分母的依据是等式的性质2. 2. 去分母的目的是将分数系数化为整数系数.
注意：(1)去分母时，若分子是多项式，去分母后，分 子需要加上括号. (2)去分母时，不要漏乘不含分母的项.
知识点 5 解一元一次方程的一般步骤
知5－讲
1. 解一元一次方程的一般步骤 一般地，解一元一次方程的步骤是：去分母、去括号、
移项、合并同类项、把未知数的系数化为1 . 通过这些步骤 可以将一元一次方程转化为x＝c(c为常数)的形式.
第4章 一元一次方程
4.2 一元一次方程及其解法
1 课时讲解 一元一次方程
解一元一次方程——移项 解一元一次方程——去括号 解一元一次方程——去分母
2 课时流程 解一元一次方程的一般步骤
逐点 导讲练
课堂 小结
作业 提升
知识点 1 一元一次方程
知1－讲
2. 一元一次方程的特点
知1－讲
(1)只含有一个未知数；(2)未知数的次数都是1；(3)是
知4－讲
例1
知1－练
2 解题秘方：利用一元一次方程的特点进行判断.
知1－练
解：①等号右边不是整式；③未知数x的最高次数为2；④ 化简后x的系数为0且等式不成立；⑥含有两个未知数；只 有②⑤是一元一次方程.
知1－练
方法 判断一个方程是否为一元一次方程的方法：
知识点 4 解一元一次方程——去分母
知4－讲
1. 解含有分母的一元一次方程时，方程两边乘各分母的最 小公倍数，从而约去分母，这个过程叫作去分母.
2. 去分母解一元一次方程的步骤 去分母→去括号→移项→合并同类项→系数化为1
特别解读 1. 去分母的依据是等式的性质2. 2. 去分母的目的是将分数系数化为整数系数.
注意：(1)去分母时，若分子是多项式，去分母后，分 子需要加上括号. (2)去分母时，不要漏乘不含分母的项.
知识点 5 解一元一次方程的一般步骤
知5－讲
1. 解一元一次方程的一般步骤 一般地，解一元一次方程的步骤是：去分母、去括号、
移项、合并同类项、把未知数的系数化为1 . 通过这些步骤 可以将一元一次方程转化为x＝c(c为常数)的形式.
第4章 一元一次方程
4.2 一元一次方程及其解法
1 课时讲解 一元一次方程
解一元一次方程——移项 解一元一次方程——去括号 解一元一次方程——去分母
2 课时流程 解一元一次方程的一般步骤
逐点 导讲练
课堂 小结
作业 提升
知识点 1 一元一次方程
知1－讲
2. 一元一次方程的特点
知1－讲
(1)只含有一个未知数；(2)未知数的次数都是1；(3)是
知4－讲
苏科版(2024新版)七年级数学上册课件：4.2.3 解一元一次方程——去括号
解:去括号,得 6x+3－3x+1=7.
移项,得
6x－3x=7－3－1.
合并同类项,得 3x=3.
将x的系数化为1,得 x=1.
课堂小结： 解含括号的一 元一次方程
去括号
注意符号，防止漏乘
移项
移项要变号，防止漏项
合并同类项 计算要准确，防止合并出错 系数化为1 分子、分母不要颠倒了
苏科版 七年级(上册) 2024新版教材
4.2.3 一元一次方程及其解法 ——去括号
学习目标：
1.会应用去括号、移项、合并同类项、系数化为1的方法解一 些简单的一元一次方程； 2.经历探索用去括号的方法解方程的过程，进一步熟悉方程 的变形，弄清楚每步变形的依据； 3.体会解方程中的转化思想．
旧知回顾：
移项，得 －3x = 11 + 3 - 2.
合并同类项，得 － 3x = 12.
系数化为1 ，得 x = － 4.
还有没有别的 解法呢？
看做整体可解出
例4 解方程：2－3(x+1) = 11. 它，进而解出x
解法二：
移项，得
-3(x+1)=9
两边同除以-3,得 x+1 =－3.
移项，得
x=－3-1，
注意
去括号必须做到“两注意”： ① 如果括号外的因数是负数时，去括号后，原括号内各项
都要改变符号； ② 乘数与括号内多项式相乘时，乘数应乘以括号内每一项，
不要漏乘．
2.解下列方程：
（1）2(x-1)=6
解：去括号，得 2x-2=6
移项，得
2x=8
两边同时除以2，得x=4
（2）4-x=3(2-x)
新知探究：
问题：某工厂加强节能措施，去年下半年与上半年相比，月平均用 电量减少2 000 kW·h(千瓦·时）,全年用电15万kW·h(千瓦·时）, 这个工厂去年上半年每月平均用电多少度？
鲁教版(五四制)六年级上册4.2解一元一次方程(去括号与去分母)教案
3.3解一元一次方程(去括号与去分母)【目标导航】1.掌握有括号的一元一次方程的解法；2.通过列方程解决实际问题，感受到数学的应用价值；3.培养分析问题、解决问题的能力．【预习引领】1． 化简：⑴()()=+-+--33121y y ⑵()()=-+--a a 24523 2．问题 某工厂加强节能措施，去年下半年与上半年相比，月平均用电量减少2000度，全年用电15万度。
这个工厂去年上半年每月平均用电多少度？ 3．你会用方程解这道题吗？设上半年每月平均用电x 度，则下半年每月平均用电 度；上半年共用电 度，下半年共用电 度。
列方程为 。
4．这个方程与上一课所解方程有何不同点？怎样使这个方程向a x =的形式转化呢？【要点梳理】知识点: 有括号的一元一次方程的解法 引例：解方程()150********=-+x x 解：注：1.根据 ，先去掉等式两边的小括号，然后再移项、合并、系数化为12.本题用 的思想，将有括号的方程转化为已学的无括号的方程。
例1 解方程()()323173+-=--x x x注：运算过程中，特别防止符号的错误. 练习1：解下列方程()()()41232341+-=-+x x x()⎪⎭⎫ ⎝⎛--=+⎪⎭⎫ ⎝⎛-1317242162x x x例2 解方程，并说明每步的依据： ()[]{}()1082721324321--=+---x x注：⑴有多重括号，通用方法是由里向外依次去括号。
⑵在去括号的过程中，可以同时作合并变形。
练习2：解下列方程(1)()[]()21453123+-=---x x（2）()[]()51315.04210+-=----x x 例3【课堂操练】1． 将多项式()()24322+--+x x 去括号得 ，合并得 。
2．方程()()()x x x -=---1914322去括号得 ，这种变形的根据是 。
3．解方程： ⑴()62338=+-y y ⑵()33322+-=+-x x x⑶()()63734--=+x x⑷()()()36411223125+=+-+x x x⑸()()()121212345--=+--x x x⑹()[]()2321432-=+--x x x⑺()[]{}1720815432=----x⑻已知关于x 的方程()ax x =-+324无解，求a 的值。
4.2 解一元一次方程(2)
3、 11 x + 1 = 5 ( 2 x + 1 ) ;
4、 4 x – 3 ( 20 – x ) = 3 .
x=9
试一试
5、 5 ( x + 2 ) = 2( x + 7 ) ； 6、 3 ( 2y + 1) = 2 ( 1+ y) + 3 ( y + 3);
7、 3x – { 3 – [ 4x – (x – 1)+ 3x ] } = 8 ; 5、x = 4 – 3
边同时除以2再解，而非先去括号。
思考题
1、若方程 4x – 3 ( a – x ) = 5x – 7 ( a – x )
的解是 x = 3 ，求a的值.
2、解方程
2004 ( 5x + 8) – 2005 ( 2x + 8) = – 5x – 8
3、对于关于 x 的方程：2 k x = ( k + 1 ) x + 6 ，
10 7、x= 9
6、y = 8
例题2：解方程： – 2 ( x – 1 ) = 4 .
解法一： 去括号， 得– 2 x + 2 = 4。 移项，得 x = 4 – 2。 化简，得 – 2 x = 2。 方程两边同除以5， 得x = – 1。 解法二： 方程两边同除以– 2 ， 得x – 1 = – 2。 移项，得 x = – 2+ 1。
当整数k为何值时，方程的解为整数？
1、这一堂课我们学到了什么？
2、在解方程中去括号时应该 注意些什么？
这一堂课我们主要学习了含括号的
一元一次方程的解法，一般情况下是先
去括号，这样就转化为我们会解的不含 括号的类型。
1、去括号时， 一是要注意何时变号何时不变， 二是要注意不漏乘括号内的项；
苏科版2024新版七年级数学上册学案：4.2.3 解一元一次方程——去括号
课题：4.2 一元一次方程及其解法（3）——解一元一次方程——去括号班级：姓名：【学习目标】1.会应用去括号解简单的一元一次方程.2.知道解一元一次方程的基本步骤.【重点和难点】重点：正确使用去括号法则，掌握解一元一次方程的基本步骤.难点：正确使用去括号法则，掌握解一元一次方程的基本步骤.【创设情境】1.回忆去括号法则.2.某工厂加强节能措施，去年下半年与上半年相比，月平均用电量减少2000kW•h（千瓦•时），全年用电150000kW•h（千瓦•时），求这个工厂去年上半年每月的用电量.【合作探究】活动：解一元一次方程通过以上解方程的过程，你能总结出解含有括号的一元一次方程的一般步骤吗？归纳：【典型例题】例1：解方程：2-3（x+1）=11例2：解方程：2（x+1）=1-5（x-2）练习：课本P117【当堂反馈】1．解方程4（x -1）-x =2（x +21），步骤如下：①去括号，得4x -4-x =2x +1；②移项，得4x +x -2x =4+1；③合并同类项，得3x =5；④化系数为1，x =35．其中开始出现错误的一步是（ ） A ．① B ．② C ．③ D ．④2.当x 的取值不同时，整式ax -b （其中a ,b 是常数）的值也不同，部分对应值如表所示：则关于x 的方程ax =b +2的解为（ ）A ．x =-2B ．x =-1C ．x =0D ．x =13.若关于x 的方程3x +（1-10a ）=x -2（3a -2）的解是x =0，则a 的值为 .4.若方程3（2x -2）=2-3x 的解与关于x 的方程6-2k =2（x +3）的解相同，则k 的值为 .5.解方程：（1）5x+2=3(x+2) （2）3（y+2）-2(y -23)=5-4y（3）2-3（y +1）=1-2（1+0.5y ） （4）x -2［x -3（x -1）］=86. 设a ,b ,c ,d 为有理数，现规定一种新的运算,那么当时，求x 的值．【课堂小结】【课后作业】拓展提升：（1）若关于x 的方程2ax =（a +1）x +6的解为正整数，则整数a 的值为 .（2）已知关于x 的方程3a （x+2）=（2b-1）x+1有无数个解，则ab= 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解法二：方程两边同除以-2，得： x-1=-2 x=-2+1 移项，得 x=-1 合并同类项，得
议一议
观察上述两种解法， 说出它们的区别.
随堂练习
随堂练习
课本P129页 随堂练习
今天学习的 解含有括号 的一元一次 方程的一般 步 骤 是
去括号 移 项 合并同类项
系数化成1
1 、 解下列方程 （1） 3x- 7(x-1)=3-2(x+3) （2）2x-(x+10)=5x+2(x-1)
6x+ 6（x-2000）=150000 怎样解这个方程呢？
。
用框图表示解这个方程的具体过程
6x+ 6(x-2000)=150000
去括号
怎样使这个方 程向x=a转化？
6x+6x-12000=150000
移项
6x+6x=150000+12000
合并同类项
12x=162000
系数化成1
x=13500
x-3(y-2)= x-3y+6
.
.
法则：括号前是“－” 号，把括号和它前面 的“－”号去掉，括 号里各项都改变符号。
乘法分配律：a(b+c)=ab+ac
1 听 果 奶 多 少 钱 ？
如果设1听果奶x 元，可列出方程： 4(x+0.5)+x=20-3
想一想
4(x+0.5)+x=20-3
1.这个方程列得对吗？为什么？ 你还能列出不同的方程吗？ 2.怎样解所列的方程？ 方程中有括号怎么办? ——先去括号 例3 解方程：4(x+0.5)+x=17
-x=-45
系数化为1
x=45
要方程两边同时除以未知数前 面的系数（或乘以未知数系数 的倒数）
2、用去括号法则和乘法的分配律填空
a+(b+1)= a+b+1 .
2a+3(b-1)= 2a+3b-3 .
法则：括号前是“+” 号，把括号和它前面 的“+”号去掉，括 号里各项都不变符号。
m-(-a+b)= m+a-b
1、什么是一元一次方程？一元一次方程 的解法我们学了哪几步？
移项 → 合并同类项 → 系数化为1
移项要变号
方程 3x 20 4 x 25怎样解呢？
3x+20=4x-25
移项
3x-4x=-25-20
合并同类项
合并同类项时，只是把同类项的系数 相加作为所得项的系数，字母部分不 变，常数项直接相加。
2. 关于x的方程2-(1-x)=-2与方程mx3(5-x)=-3的解相同,则求m的值。
3、一艘船从甲码头到乙码头顺流航行,用 了2 小时;从乙码头到甲码头逆流航行,用了 2.5小时;已知水流的速度是3千米/小时,求船 在静水中的平均速度是多少千米/小时? 分析:等量关系是 甲码头到乙码头的路程=乙码头到甲码头的 路程
2(x+21)－39 +(x+21)+ x=416
金牌199枚；银牌119枚；铜牌98枚
还有其他列方程的方法，请同学们课后研究。
解：去括号，得： 4x+2+x=17 移项，得： 4x+x=17-2
合并同类项，得： 5x=15
方程两边同除以5，得： x=3
例 题 解 析
例4 解方程: -2(x—1)=4.
解法一：去括号，得
-2x+2=4
移项，得 -2x=4-2 合并同类项，得 -2x=2 x=-1 方程两边同除以-2，得
× 顺航时间=逆航速 也就是:顺航速度___ 度___ ×逆航时间
一艘船从甲码头到乙码头顺流航行,用了2 小 时;从乙码头到甲码头逆流航行,用了2.5小时; 已知水流的速度是3千米/小时,求船在静水中 的平均速度是多少千米/小时? × 逆航时间 顺航速度___ × 顺航时间=逆航速度___
解:设船在静水中的平均速度是X千米/小 (X+3) 千米/ 时,则船在顺水中的速度是______ (X-3) 千米/ 小时,船在逆水中的速度是_______ 小时.
2、解下列方程：
（1）4x + 3（2x – 3）=12 - （x +4） 1 1 (2)、6( x 4) 2 x 7 ( x 1) 2 3 (3) 2(x+3)=5x (4) 2-3(x+1)=1-2(1+0.5x)
能力提升 1. 已知关于x的方程3x + a = 0的解 比方程2x – 3 = x + 5的解大2，则 求a的值。
同学们都知道，2010年亚运会在广州召开，中国 体育健儿发扬奋勇拼搏的精神，再创佳绩，共获 得奖牌416枚，其中金牌数是银牌数的2倍少39枚， 银牌数比铜牌多21枚，你能求出中国队本次亚运 会获得的金、银、铜牌的枚数吗？ 提示：设获得铜牌x枚，则银牌有(x+21)枚，金牌有
[2(x+21)－39]枚，由题意得方程
2(X+3)=2.5(X-3)
4、 某车间有22名工人生产螺钉和螺母, 每人每天平均生产螺钉1200或螺母2000 个,一个螺钉要配两个螺母;为了使每天生 产的产品正好配套,应该分配多少名工人生 产螺钉,多少名工人生产螺母? 分析 :为了使每天的产品刚好配套应使生 产的螺母的数量是螺钉的______ 2倍 (22-X) 解:设有X名工人生产螺钉,则有_______ 名工人生产螺母;那么螺钉共生产 1200X 个,螺母共生产__________ 2000(22-X) 个. ________ 2000(22-X)=2×1200X
返回10章
5、某工厂加强节能措施，去年下半年与上半年相比， 月平均用电量减少2000度，全年用电15万度，这个工 厂去年上半年每月平均用电多少度？
等量关系是 上半年用电+下半年用电=15万度 。
分析：若设上半年每月平均用电x度，则下半年每 月平均用电 度；上半年共用电 6x 度， （x-2000） 下半年共用电 6(x-2000) 度 因为全年共用了15万度电，所以,可列方程
议一议
观察上述两种解法， 说出它们的区别.
随堂练习
随堂练习
课本P129页 随堂练习
今天学习的 解含有括号 的一元一次 方程的一般 步 骤 是
去括号 移 项 合并同类项
系数化成1
1 、 解下列方程 （1） 3x- 7(x-1)=3-2(x+3) （2）2x-(x+10)=5x+2(x-1)
6x+ 6（x-2000）=150000 怎样解这个方程呢？
。
用框图表示解这个方程的具体过程
6x+ 6(x-2000)=150000
去括号
怎样使这个方 程向x=a转化？
6x+6x-12000=150000
移项
6x+6x=150000+12000
合并同类项
12x=162000
系数化成1
x=13500
x-3(y-2)= x-3y+6
.
.
法则：括号前是“－” 号，把括号和它前面 的“－”号去掉，括 号里各项都改变符号。
乘法分配律：a(b+c)=ab+ac
1 听 果 奶 多 少 钱 ？
如果设1听果奶x 元，可列出方程： 4(x+0.5)+x=20-3
想一想
4(x+0.5)+x=20-3
1.这个方程列得对吗？为什么？ 你还能列出不同的方程吗？ 2.怎样解所列的方程？ 方程中有括号怎么办? ——先去括号 例3 解方程：4(x+0.5)+x=17
-x=-45
系数化为1
x=45
要方程两边同时除以未知数前 面的系数（或乘以未知数系数 的倒数）
2、用去括号法则和乘法的分配律填空
a+(b+1)= a+b+1 .
2a+3(b-1)= 2a+3b-3 .
法则：括号前是“+” 号，把括号和它前面 的“+”号去掉，括 号里各项都不变符号。
m-(-a+b)= m+a-b
1、什么是一元一次方程？一元一次方程 的解法我们学了哪几步？
移项 → 合并同类项 → 系数化为1
移项要变号
方程 3x 20 4 x 25怎样解呢？
3x+20=4x-25
移项
3x-4x=-25-20
合并同类项
合并同类项时，只是把同类项的系数 相加作为所得项的系数，字母部分不 变，常数项直接相加。
2. 关于x的方程2-(1-x)=-2与方程mx3(5-x)=-3的解相同,则求m的值。
3、一艘船从甲码头到乙码头顺流航行,用 了2 小时;从乙码头到甲码头逆流航行,用了 2.5小时;已知水流的速度是3千米/小时,求船 在静水中的平均速度是多少千米/小时? 分析:等量关系是 甲码头到乙码头的路程=乙码头到甲码头的 路程
2(x+21)－39 +(x+21)+ x=416
金牌199枚；银牌119枚；铜牌98枚
还有其他列方程的方法，请同学们课后研究。
解：去括号，得： 4x+2+x=17 移项，得： 4x+x=17-2
合并同类项，得： 5x=15
方程两边同除以5，得： x=3
例 题 解 析
例4 解方程: -2(x—1)=4.
解法一：去括号，得
-2x+2=4
移项，得 -2x=4-2 合并同类项，得 -2x=2 x=-1 方程两边同除以-2，得
× 顺航时间=逆航速 也就是:顺航速度___ 度___ ×逆航时间
一艘船从甲码头到乙码头顺流航行,用了2 小 时;从乙码头到甲码头逆流航行,用了2.5小时; 已知水流的速度是3千米/小时,求船在静水中 的平均速度是多少千米/小时? × 逆航时间 顺航速度___ × 顺航时间=逆航速度___
解:设船在静水中的平均速度是X千米/小 (X+3) 千米/ 时,则船在顺水中的速度是______ (X-3) 千米/ 小时,船在逆水中的速度是_______ 小时.
2、解下列方程：
（1）4x + 3（2x – 3）=12 - （x +4） 1 1 (2)、6( x 4) 2 x 7 ( x 1) 2 3 (3) 2(x+3)=5x (4) 2-3(x+1)=1-2(1+0.5x)
能力提升 1. 已知关于x的方程3x + a = 0的解 比方程2x – 3 = x + 5的解大2，则 求a的值。
同学们都知道，2010年亚运会在广州召开，中国 体育健儿发扬奋勇拼搏的精神，再创佳绩，共获 得奖牌416枚，其中金牌数是银牌数的2倍少39枚， 银牌数比铜牌多21枚，你能求出中国队本次亚运 会获得的金、银、铜牌的枚数吗？ 提示：设获得铜牌x枚，则银牌有(x+21)枚，金牌有
[2(x+21)－39]枚，由题意得方程
2(X+3)=2.5(X-3)
4、 某车间有22名工人生产螺钉和螺母, 每人每天平均生产螺钉1200或螺母2000 个,一个螺钉要配两个螺母;为了使每天生 产的产品正好配套,应该分配多少名工人生 产螺钉,多少名工人生产螺母? 分析 :为了使每天的产品刚好配套应使生 产的螺母的数量是螺钉的______ 2倍 (22-X) 解:设有X名工人生产螺钉,则有_______ 名工人生产螺母;那么螺钉共生产 1200X 个,螺母共生产__________ 2000(22-X) 个. ________ 2000(22-X)=2×1200X
返回10章
5、某工厂加强节能措施，去年下半年与上半年相比， 月平均用电量减少2000度，全年用电15万度，这个工 厂去年上半年每月平均用电多少度？
等量关系是 上半年用电+下半年用电=15万度 。
分析：若设上半年每月平均用电x度，则下半年每 月平均用电 度；上半年共用电 6x 度， （x-2000） 下半年共用电 6(x-2000) 度 因为全年共用了15万度电，所以,可列方程