3,1,2两角和与差的正弦,余弦,正切公式
高一数学(3.1.2两角和与差的正弦、余弦、正切公式)

1 + tan15 (3 ) o ; 1 - tan15
o
(4)tan17°+tan28°+tan17°tan28° tan17° tan28°+tan17°tan28°
3.公式都是有灵性的, 3.公式都是有灵性的,应用时不能生搬 公式都是有灵性的 硬套,要注意整体代换和适当变形. 硬套,要注意整体代换和适当变形.
�
a2 + b2 - 2 cos(a + b) = 2
思考2 思考2:若sinα+cosβ=a,cosα+sinβ= + = , + = b,则sin(α+β)等于什么? 等于什么? , + 等于什么
a2 + b2 - 2 sin(a + b) = 2
思考3 tanα+ 思考3:根据公式 Tα+β,tanα+tanβ 可变形为什么? 可变形为什么? tanα+tanβ=tan(α+β)(1- tanαtanβ) + 1 思考4 思考4:在△ABC中,tanA,tanB,tanC ABC中 tanA,tanB, 三者有什么关系? 三者有什么关系? tanA+tanB+tanC=tanAtanBtanC 思考5 sinx+cosx能用一个三角函数表 思考5:sinx+cosx能用一个三角函数表 示吗? 示吗? p sin x + cos x = 2 sin(x + ) 4
两角和与差的正弦, 3.1.2 两角和与差的正弦, 余弦,正切公式 余弦,
3.1.2 两角和与差的正弦、余弦、正切公式

第11课时 3.1.2 两角和与差的正弦、余弦、正切公式(1)【学习目标、理解考纲】能根据两角差的余弦公式推导出两角和与差的正弦、余弦公式,并能灵活运用.【知识梳理、双基再现】(阅读课本128-132页,回答下列问题)1.两角和与差的余弦公式=-)cos(βα ;=+)cos(βα .两者关系:)(βα-C )(βα+C .记忆口诀: .2.两角和与差的正弦公式=+)sin(βα ;=-)sin(βα .两者关系:)(βα+C )(βα-C )(βα-S )(βα+S 记忆口诀 : .【小试身手、轻松过关】(阅读课本128-132页,解答下列问题)【例1】求下列各式的值:(第2组)(1)sin15o ; (2)cos 75o ; (3)sin 75o .【例2】已知3cos ,,52πθθπ⎛⎫=-∈⎪⎝⎭,求sin 3πθ⎛⎫+ ⎪⎝⎭的值.(第3组)【例3】求下列各式的值:(第4组)(1)sin 72cos18cos72sin18+o o o o ; (2)cos72cos12sin 72sin12+o o o o ;(3)sin34sin 26cos34cos 26-o o o o ; (4)sin 20cos110cos160sin 70.+o o o o【例4】在三角形ABC 中,53sin ,cos 135A B ==,求cos C 的值.(第5组)【例5】已知,223,54)cos(,54)cos(πβαπβαβα<+<-=-=+,2πβαπ<-<求:α2cos 的值.(第6组)【例6】若1010sin ,55sin ==βα,且α、β为锐角,求βα+的值.(第1组)【基础训练、当堂检测】(时量:10分钟,每题20分,满分100分)1.=+)3045sin( ( )(A)212- (B)212+ (C)426- (D)426+2.已知),5sin ,5(cos ),35cos 2,35sin 2( -==则=⋅b a ( )(A)21 (B)1 (C)2 (D) 40sin 23.已知α、β都是锐角,135)cos(,54sin =+=βαα,则βsin 的值为( ) (A)6516 (B)6556 (C)658 (D)65474.在△ABC 中,若C A B sin sin cos 2=,则△ABC 的形状一定是( )(A)等腰直角三角形 (B )直角三角形(C)等腰三角形 (D )等边三角形5.已知,53)sin(,1312)cos(,432-=+=-<<<βαβαπαβπ求α2sin 的值.。
3.1.2两角和与差的正弦余弦正切公式

复习引入
1,两角差与和的余弦公式: 两角差与和的余弦公式:
cos(α ± β ) = cosα cos β sinα sin β
2,诱导公式五: 诱导公式五:
sin ( cos (
π
2 π
2
-α) = cosα -α) = sinα
sin (α + β )
π π π sin 求: α , cos + α , tan(α ) 4 4 4
例3, , π 4 3 (1)α , β ∈ (0, ), cos α = , cos(α + β ) = ) 2 5 5 (2)tan(α + β ) = 3, tan(α β ) = 2 ) 求: tan 2α , tan 2 β
探求新知
= sin α cos β + cos α sin β
sin (α β ) = sin α cos β cos α sin β
sin (α ± β ) = sinα cosβ )
tan α + tan β = 1 tan α tan β
y = 4sin x + 3cos x
y = a sin x + b cos x = a 2 + b 2 sin( x + φ )
其中,cosφ = a a 2 + b2 , sinφ = b a 2 + b2
6 证法1: 证法1: 右边=2(sin π cos α + cos π sin α ) 6 6 1 3 =2( cos α + sin α ) 2 2 =cos α + 3 sin α =左边 1 3 证法2: 证法2:左边=2( cos α + sin α ) 2 2 π π =2(sin cos α + cos sin α ) 6 6 π =2sin( + α ) =右边 6 化为某个角的一个 一个三角函数形式 注:该题将 cos α + 3 sin α 化为某个角的一个三角函数形式 π 即 cos α + 3 sin α = 2sin( + α ) 6
3.1.2两角和与差的正弦、余弦、正切公式

sin72。 cos 42。 cos 72。 sin 42。 1 sin(72 42 ) sin 30 ; 2
。 。 。
(2) cos 20。 cos 70。 sin 20。 sin 70。 cos(20。 70。 cos 90。 0 )
1 tan15。 tan 45。 tan15。 (3) 。 1- tan15 1- tan 45。 tan15。 tan(45。 15。 tan 60。 3 )
当cos cos 0时, 分子分母同时除以cos cos
tanα+ tanβ tan(α+β)= 1 - tanαtanβ
记:T( + )
tanα+ tanβ tan(α+β)= 1 - tanαtanβ
上式中以代得
tanα- tanβ tan tan( ) = tan[ ( )] 1 tan tan( ) 1+ tanαtanβ
在 △ ABC 中 , sinAcosB = 1 - cosAsinB , 则 △ABC的形状为________. [答案] 直角三角形 [解析] 由题意得sinAcosB+cosAsinB=1, 即sin(A+B)=1. π π 又∵0<A+B<π,∴A+B=2,即 C=2,
∴△ABC 为直角三角形.
3.1.2两角和与差的正弦、余弦、正切公式
复习:
OA=(cos,sin),OB=(cos,sin)£
,OB=(cos,sin)£
OA OB=coscos+sinsin于是有 cos(-)=cos cos+sinsin
cos ( – ) =cos cos + sinsin
3.1.2 两角和与差的正弦、余弦、正切公式

3.12 两角和与差的正弦、余弦、正切公式知识点一 两角和的余弦公式解决给角求值问题的策略(1)对于非特殊角的三角函数式求值问题,一定要本着先整体后局部的基本原则,如果整体符合三角公式的形式,则整体变形,否则进行各局部的变形.(2)一般途径有将非特殊角化为特殊角的和或差的形式,化为正负相消的项并消项求值,化分子.分母形式进行约分,解题时要逆用或变用公式.1.sin7°cos37°-sin83°sin37° 2.sin50°-sin20°cos30°cos20°3、sin14°cos16°+sin76°cos74°4、sin7°+cos15°sin8°cos7°-sin15°sin8°5、已知角α的终边经过点(-3,4),则sin ⎝ ⎛⎭⎪⎫α+π4的值为6.求函数f (x )=sin x -cos ⎝⎛⎭⎪⎫x +π6的值域.类型二 给值求值1、已知sin ⎝ ⎛⎭⎪⎫3π4+α=513,cos ⎝ ⎛⎭⎪⎫π4-β=35,且0<α<π4<β<3π4,求cos(α+β).2、已知cos ⎝⎛⎭⎪⎫x +π6=35,x ∈(0,π),求sin x 的值。
3.已知锐角α,β满足sin α=255,cos β=1010,求α+β。
类型三 辅助角公式对于形如y=asinx+bcosx 的三角式,可变形如下: y=asinx=bcosx =++++a b x a a bx b a b222222(sin cos )··。
上式中的a a b22+与b a b22+的平方和为1,故可记a a b22+=cos θ,b a b22+=sin θ,则。
)x sin(b a )sin x cos cos x (sin b a y 2222θ++=θ+θ+=1、求值(1)cos π12+3sin π12 (2)sin π12-3cos π12(3)2cos π12+6sin π12 (4)当函数y =sin x -3cos x (0≤x ≤2π)取得最大值时,求x.2、求周期求函数y x x x =+-+24432cos()cos()sin ππ的最小正周期。
3.1.2 两角和与差的正弦、余弦、正切公式
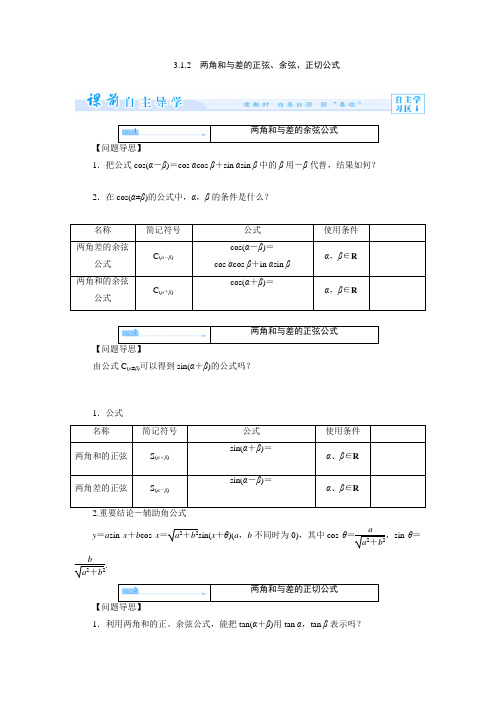
3.1.2两角和与差的正弦、余弦、正切公式两角和与差的余弦公式【问题导思】1.把公式cos(α-β)=cos αcos β+sin αsin β中的β用-β代替,结果如何?2.在cos(α±β)的公式中,α,β的条件是什么?名称简记符号公式使用条件两角差的余弦公式C(α-β)cos(α-β)=cos αcos β+in αsin βα,β∈R两角和的余弦公式C(α+β)cos(α+β)=α,β∈R两角和与差的正弦公式【问题导思】由公式C(α±β)可以得到sin(α+β)的公式吗?1.公式名称简记符号公式使用条件两角和的正弦S(α+β)sin(α+β)=α、β∈R两角差的正弦S(α-β)sin(α-β)=α、β∈R2.重要结论-辅助角公式y=a sin x+b cos x=a2+b2sin(x+θ)(a,b不同时为0),其中cos θ=aa2+b2,sin θ=ba2+b2.两角和与差的正切公式【问题导思】1.利用两角和的正、余弦公式,能把tan(α+β)用tan α,tan β表示吗?2.能用tan α,tan β表示tan(α-β)吗?3.公式中α,β为任意实数吗? 名称简记符号公式 使用条件两角和的正切T (α+β)tan(α+β)=tan α+tan β1-tan αtan βα,β,α+β≠k π+π2(k∈Z ) 且tan α·tan β≠1两角差的正切T (α-β)tan(α-β)=tan α-tan β1+tan αtan βα,β,α-β≠k π+π2(k∈Z ) 且tan α·tan β≠-1给角求值化简求值:(1)sin π12-3cos π12;(2)sin 15°-cos 15°cos 15°+sin 15°.1.公式T (α+β),T (α-β)是变形较多的两个公式,公式中有tan α·tan β,tan α+tan β(或tan α-tan β),tan(α+β)(或tan(α-β)).三者知二可表示或求出第三个.2.一方面要熟记公式的结构,另一方面要注意常值代换.求下列各式的值:(1)sin 14° cos 16°+sin 76°cos 74°; (2)tan 72°-tan 42°-33tan 72°tan 42°给值求值已知α、β是锐角,且sin α=437,cos(α+β)=-1114,求sin β的值.1.本题属于给值求值问题,求解时,关键是从已知角间的关系入手,分析出已知角和待求角的关系.如本题中巧用β=(α+β)-α这一关系.2.常见角的变换为(1)2α+β=(α+β)+α,2α-β=(α-β)+α; (2)α+β2=(α-β2)-(α2-β),α-β2=(α+β2)-(α2+β); (3)(π4+α)+(π4+β)=π2+(α+β); (4)(π4+α)+(π4-β)=π2+(α-β).将本例中条件“已知α、β是锐角”改为“α、β都是钝角”.仍求sin β的值.给值求角已知sin α=55,sin β=1010,且α,β为锐角,求α+β的值.1.求解该类问题常犯的错误是对角的范围讨论程度过大(小),导致求出的角不合题意或者漏解.2.求角的大小,要解决两点:(1)确定所求角的范围,(2)求角的某一三角函数值,特别是要根据角的范围确定取该角的哪一种三角函数值.若把本例题的条件改为“α∈(0,π2),β∈(-π2,0),且cos(α-β)=35,sin β=-210”,试求角α的大小.辅助角公式的应用将下列各式写成A sin(ωx +φ)的形式:(1)3sin x -cos x ; (2)24sin(π4-x )+64cos(π4-x ).1.对于形如sin α±cos α,3sin α±cos α的三角函数式均可利用特殊值与特殊角的关系,运用和差角正、余弦公式化简为含有一个三角函数的形式.2.在解法上充分体现了角的变换和整体思想,在三角函数求值化简的变换过程中,一定要本着先整体后局部的基本原则.化简:(1)2(cos x -sin x ); (2)315sin x +35cos x .忽略讨论角的范围致误已知在△ABC 中,sin A =35,cos B =513,求cos C .1.sin 21°cos 39°+cos 21°sin 39°等于( ) A.22 B.12 C.32D .12.若A 、B 是三角形ABC 的内角,并且(1+tan A )(1+tan B )=2,则A +B 等于 A.π4 B.3π4C.5π4D .k π+π4(k ∈Z )3.1+tan 15°1-tan 15°的值等于__________.4.已知α为锐角,sin α=35,β是第四象限角,cos(π+β)=-45.求sin(α+β)的值.一、选择题1.在△ABC 中,已知sin(A -B )cos B +cos(A -B )sin B ≥1,则△ABC 是( ) A .锐角三角形 B .钝角三角形 C .直角三角形 D .无法确定2.已知tan(α+π4)=3,则tan α的值为( )A.12 B .-12 C.14 D .-143.函数f (x )=sin x -cos(x +π6)的值域为( )A .[-2,2]B .[-3,3]C .[-1,1]D .[-32,32] 4.若α+β=3π4,则(1-tan α)(1-tan β)等于( )A .1B .-1C .2D .-25.已知sin α=12,α是第二象限的角,且tan(α+β)=-3,则tan β的值为( )A .- 3 B.3 C .-33 D.33二、填空题6.sin 7π18cos 2π9-sin π9sin 2π9=________7.sin (α+30°)-sin (α-30°)cos α的值为________.8.若cos(α+β)=15,cos(α-β)=35,则tan αtan β=________________________________________________________________________.三、解答题9.已知α、β∈(3π4,π),sin(α+β)=-35,sin(β-π4)=1213,求cos(α+π4)的值.10.图3-1-1如图,在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角α、β,它们的终边分别与单位圆交于A 、B 两点,已知A 、B 的横坐标分别为210、255. (1)求tan(α+β)的值;(2)求α+2β的值.11.已知函数f (x )=sin 2x +3cos 2x . (1)求出f (x )的最大值、最小值; (2)求出f (x )的单调增区间.。
两角和与差的正弦、余弦与正切公式
2
(sin
2
A.a>b>c
C.c>a>b
(2)已知
56°-cos 56°),c=
1-ta n 2 39°
,则 a,b,c 的大小关系是(
1+ta n 2 39°
B.b>a>c
D.a>c>b
π
cos(α-6 )+sin
4 3
α= 5 ,则
π
si(nα+6 )=
.
)
答案 (1)D
4
(2)
5
解析 (1)a=cos 50°cos 127°+cos 40°cos 37°
1
D.
2
.
答案 (1)B (2)D (3) 3
解析 (1)根据两角和的正弦公式展开得 sin
3
θ= sin
2
3
θ+ cos
2
θ=1,即
π
3sin(θ+ )=1,解得
6
π
θ+sin(θ+ )=sin
3
1
θ+ sin
2
π
3
sin(θ+ )= .故选
6
3
B.
(2)∵t=2sin 18°,
2cos2 27°-1
.
1+cos
5.积化和差公式
sin αcos
1
β=
2
sin( + ) + sin(-) ,
cos αsin
1
β=2
sin( + )-sin(-) ,
cos αcos
1
β=2
学案7:3.1.2 两角和与差的正弦、余弦和正切公式(二)
3.1.2 两角和与差的正弦、余弦和正切公式(二)【课前准备】1.课时目标(1)了解两角和的余弦公式,两角和与差的正弦公式、正切公式的推导过程,通过公式的推导了解角与角之间的内在联系;(2)正确理解与掌握两角和的余弦公式,两角和与差的正弦公式、正切公式,并会进行简单的化简、求值等应用.2.基础预探(1)两角和的余弦:cos (α+β)=__________;(2)两角和与差的正弦:sin (α+β)=__________;sin (α-β)=__________;(3)两角和与差的正切:tan (α+β)=__________;tan (α-β)=__________.【知识训练】1.满足cos αcos β=23+sin αsin β的一组α、β的值是( ) A .α=12π13,β=4π3 B .α=2π,β=3π C .α=2π,β=6π D .α=3π,β=6π 2.下列等式中成立的是( )A .2120sin 80sin 20cos 80cos =︒︒-︒︒B .2117sin 13cos 17cos 13sin =︒︒-︒︒ C .2220sin 25sin 25cos 70sin =︒︒+︒︒D .2320sin 50sin 20cos 140sin =︒︒+︒︒ 3.下列四个命题中的假命题是( )A .存在这样的α、β,使得cos (α+β)=cos αcos β+sin αsin βB .不存在无穷多个α、β,使得cos (α+β)=cos αcos β+sin αsin βC .对于任意的α、β,cos (α+β)=cos αcos β-sin αsin βD .不存在这样的α、β,使得cos (α+β)≠cos αcos β-sin αsin β4.已知sin αcos β=-31,cos αsin β=21,则sin (α+β),sin (α-β)的值分别为( ) A .61,65 B .-61,-65 C .61,-65 D .-61,65 5.若tan α=21,则tan (α+4π)=____________. 6.已知tan (4π+α)=2,求ααα2cos cos sin 21+的值.【学习引领】在两角和与差的三角函数公式中,对应的角α,β可以是单独的两个角,也可以是对应的两个整体部分所组成的角,比如α=(α+β)-β,β=(α+β)-α,2α=(α+β)+(α-β),2β=(α+β)-(α-β),(4π+α)+(4π-α)=2π等,同时在解答时要注意角的范围的讨论.在实际求解问题过程中,要注意对角的变形与整体思维的考虑.运用两角和与差的三角函数公式时的“四要”:一要审查公式成立的条件;二要弄清两角和与差的三角函数公式中角、函数的排列顺序及式中每一项的符号;三要熟练掌握公式的逆用、反用、变形用;四要注意和、差的相对性.【题型探究】题型一:公式的直接应用例1.已知α,β都是锐角,且sin α=55,cos β=10103,求α+β的值 思路导析:利用两角和的余弦公式分三步进行:①先求α+β的余弦值;②确定α+β所在的范围(或区间);③求角α+β的值.点评:其实,间接利用公式求解有关角的值的问题,可以结合不同的三角函数值加以解决:①求cos (α+β),在(0,π)内余弦值为22的角是唯一的,故可求之;②求sin (α+β),将角α+β的范围缩小到(0,2π)或更小,使之正弦值为22的角是唯一的;③求tan (α+β),在(0,π)内正切值为1的角也是唯一的.变式练习1:已知α,β是锐角,且sin α=51,cos β=101,求α-β的值.题型二:公式的整体应用例2.求sin (α+75º)+cos (α+45º)-3cos (α+15º)的值.思路导析:这道题的常规方法是利用两角和与差的公式直接展开,再加以必要的合并与化简,而这里的75º与15º均为非特殊角,又要通过必要的两角和与差的公式,最终达到求值的目的.而如果通过整体思维考查,令β=α+15º,通过换元转化加以运算,则更加简单、快捷.点评:这道题充分突出整体思维,通过整体换元,把非特殊角的三角函数的求值问题转化特殊角的三角函数的求值问题,从而使问题迎刃而解.变式练习2:设2)tan(=-βα,3)4tan(=-βπ,则)4tan(απ-等于( ) A .71 B .71- C .51 D .51- 题型三:公式的综合应用例3.已知sin α+sin β=22,求cos α+cos β的取值范围. 思路导析:先把cos α+cos β作为一个整体,利用条件中相关等式的变形与组合,结合同角三角函数基本关系式与两角和的余弦公式,利用三角函数的图象与性质加以综合.点评:综合利用同角三角函数基本关系式、两角和与差的三角公式、三角函数的图象与性质等来解决相关三角函数式的取值范围问题,关键在是等价变换与应用等.变式练习3:不查表,求下式的值:tan23︒+tan22︒+tan23︒tan22︒.【随堂练习】1.tan15°+cot15°等于( )A .2B .2+3C .4D .334 2.cos75°-cos15°的值等于( )A .26B .-26C .-22D .22 3.cos20ºcos110º+sin20ºsin110º的值为( )A .0B .-21 C .21 D .1 4.锐角βα,满足54cos =α,53)cos(=+βα,则βsin =________. 5.cos (45º+x )cos (15º-x )-cos (45º-x )sin (15º-x )=________.6.已知sin β=m sin (2α+β)(m ≠1),求证:tan (α+β)=mm -+11tan α.【参考答案】【课前准备】2.基础预探(1)cos αcos β-sin αsin β;(2)sin αcos β+cos αsin β,sin αcos β-cos αsin β;(3)βαβαtan tan 1tan tan -+,βαβαtan tan 1tan tan +-. 【知识训练】1.A ;【解析】由已知得cos (α+β)=23,代入检验得A ; 2.D ;【解析】根据两角和与差的公式加以判断;3.B ;【解析】由cos (α+β)=cos αcos β+sin αsin β=cos αcos β-sin αsin β,得sin αsin β=0,∴α=k π或β=k π(k ∈Z );4.C ;【解析】根据两角和与差的正弦公式加以求解;5.3;【解析】tan (α+4π)=4πtan tan 14πtantan ⋅-+αα=1211121⨯-+=3; 6.解 由tan (4π+α)=ααtan tan 1-1+=2,解得tan α=31, 于是ααα2cos cos sin 21+=ααααα222cos cos sin 2cos sin ++=1+1+ααtan 2tan 2=13121312+⨯+)(=32. 【典例导析】例1. 解 ∵α是锐角,sin α=55,∴cos α=α2sin 1-=552, ∵β是锐角,cos β=10103,∴sin β=β2cos 1-=1010, 那么cos (α+β)=cos αcos β-sin αsin β=552·10103-55·1010=22, ∵α,β是锐角,∴0<α+β<π,故α+β=4π.变式练习1:解 ∵α是锐角,sin α=51,∴cos α=α2sin 1-=552, ∵β是锐角,cos β=101,∴sin β=β2cos 1-=10103, 那么cos (α-β)=cos αcos β+sin αsin β=22, ∵α,β是锐角,∴-2π<α-β<2π, 又sin α=51<10103= sin β,则α<β,故α-β=-4π. 例2. 解 令β=α+15º,则sin (α+75º)+cos (α+45º)-3cos (α+15º)=sin (β+60º)+cos (β+30º)-3cos β=sin βcos60º+cos βsin60º+cos βcos30º-sin βsin30º-3cos β =21sin β+23cos β+23cos β-21sin β-3cos β=0. 变式练习2:A ; 【解析】)4tan(απ-=)]()4tan[(βαβπ---=)tan()4tan(1)tan()4tan(βαβπβαβπ--+---=23123⨯+-=71; 例3. 解析:令t =cos α+cos β, ①而sin α+sin β=22, ② 由①2+②2,得t 2+21=(cos α+cos β)2+(sin α+sin β)2=cos 2α+cos 2β+2cos αcos β+sin 2α+sin 2β+2sin α+sin β=2+2cos (α-β),∴2cos (α-β)=t 2-23∈[-2,2], ∴t ∈[-214,214],即cos α+cos β的取值范围为[-214,214].变式练习3:解 因为tan (23︒+22︒)=︒︒+︒+︒22tan 32tan 122tan 32tan ,所以tan23︒+tan22︒=tan (23︒+22︒)(1-tan23︒tan22︒), 原式=tan45︒ (1-tan23︒tan22︒)+tan23︒tan22︒=1-tan23︒ tan22︒+ tan23︒ tan22︒ =1;【随堂练习】1.C ;【解析】由tan15°=tan (45°-30°)=︒︒+︒-︒30tan 45tan 130tan 45tan =331331+-=3333+-,∴原式=3333+-+3333-+=4;2.C ;【解析】cos75°-cos15°=cos (45º+30º)-cos (45º-30º)=cos45ºcos30º-sin45ºsin30º-(cos45ºcos30º+sin45ºsin30º)=-2sin45ºsin30º=-22; 3.A ;【解析】cos20ºcos110º+sin20ºsin110º=cos (20º-110º)=cos (-90º)=cos90º=0;4.257;【解析】根据锐角βα,和条件,可得53sin =α,54)sin(=+βα,则βsin =])sin[(αβα-+=αβααβαsin )cos(cos )sin(+-+=257; 5.21;【解析】cos (45º+x )cos (15º-x )-cos (45º-x )sin (15º-x )=cos (45º+x )cos (15º-x )-cos[90º-(45º+x )]sin (15º-x )=cos (45º+x )cos (15º-x )-sin (45º+x )sin (15º-x )=cos[(45º+x )+(15º-x )]=cos60º=21; 6.证明:∵sin β=m sin (2α+β),∴sin [(α+β)-α]=m sin [(α+β)+α],∴sin (α+β)cos α-cos (α+β)sin α=m sin (α+β)cos α+m cos (α+β)sin α,∴(1-m )sin (α+β)cos α=(1+m )cos (α+β)sin α,∴tan (α+β)=m m -+11tan α.。
高中数学第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式(1)课件新人教A版必修4
2
2
(2) 3 sin x cos x.
解:(1)1 cos x 3 sin x (2) 3 sin x cos x
2
2
sin 30 cos x cos 30 sin x
2( 3 sin x 1 cos x)
2
2
sin(30 x);
2(sin x cos 30 cos x sin 30 )
解:原式 sin(72 18 ) sin 90 1.
第十三页,共31页。
例1 已知 sin 3 , 是第四象限角,求 sin( ),
5
4
cos( )的值.
4
解:由sin=-
3 5
,
是第四象限角,得
cos 1 sin2 1 ( 3)2 4 , 55
于是有sin( ) sin cos cos sin
第七页,共31页。
探究(tànjiū)二:两角和与差的正弦公式
1.利用哪些公式可以实现正弦(zhèngxián)、余弦的互 化?
提示(tíshìs)i:n cos( ) 2
sin(
)
cos
2
(
)
第八页,共31页。
2.由两角和与差的余弦公式如何推导两角和与 差的正弦(zhèngxián)公式?
(2) 2 cos x 6 sin x.
解:(1)原式 (2 2 sin x 2 cos x)
2
2
2sin(x ).
4
(2)原式 2 (2 1 cos x 3 sin x)
2
2
2 2 sin( x).
6
第二十一页,共31页。
1.(2015·四川高考)下列函数中,最小正周期为π且图象关
3.1.2第1课时 两角和与差的正弦、余弦公式 课件
栏目 导引
第三章 三角恒等变换
高效学习模型-内外脑模型
2
内脑- 思考内化
思维导图& 超级记忆法& 费曼学习法
1
外脑- 体系优化
知识体系& 笔记体系
内外脑高效学习模型
栏目 导引
第三章 三角恒等变换
超级记忆法
栏目 导引
第三章 三角恒等变换
超级记忆法-记忆规律
记忆前
第三章 三角恒等变换
3.1.2 两角和与差的正弦、余弦、正切 公式
第1课时 两角和与差的正弦、余弦公式
第三章 三角恒等变换
学习导航
学习目标
结合两角差 的余弦公式
―理―解→
两角和与差的正弦、 余弦推导过程及各 公式之间的联系
―掌―握→
两角和与差的正弦、 余弦公式的应用
重点难点 重点:公式的正用、逆用及变式应用. 难点:灵活运用公式解决相关的求值、化简.
=12sin x+ 23cos x+sin x- 3cos x+ 23cos x-32sin x
=(12+1-32)sin x+( 23-
3+
3 2 )cos
x=0.
栏目 导引
第三章 三角恒等变换
(2)原式=sin[α+β+α]s-in 2αcosα+βsin α
=sinα+βcos
α-cosα+βsin sin α
=csions 8100°°=1.
第三章 三角恒等变换
栏目 导引
第三章 三角恒等变换
【学习力-学习方法】
优秀同龄人的陪伴 让你的青春少走弯路
栏目 导引
第三章 三角恒等变换
小案例—哪个是你
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.2 两角和与差的正弦、余弦、正切公式[知识探究]1.两角和的余弦公式cos(α+β)= ,简记为C (α+β).思考1: C (α±β)公式有什么共同特征? (余弦在前,正弦在后,符号改变)2.两角和与差的正弦公式S (α+β):sin(α+β)= ;S (α-β):sin(α-β)= .思考2: S (α±β)有何特征?(异名乘,符号同)拓展提升:辅角公式(1)asin x+bcos x=ϕ)(其中tan ϕ=b a,ϕ为辅助角); ϕ)(其中tan ϕ=a b,ϕ为辅助角). 3.两角和与差的正切公式T (α+β):tan(α+β)= tan tan 1tan tan αβαβ+-;T (α-β):tan(α-β)= tan tan 1tan tan αβαβ-+. 思考3:使用T (α±β)的条件是什么?(公式T (α±β)只有在α≠π2+k 1π,β≠π2+k 2π,α±β≠π2+k 3π(k 1,k 2,k 3∈Z )时才成立,否则就不成立,这是由正切函数的定义域所决定的) 题型一 三角函数式的化简求值【例1】 (1)cos 105°;(2)sin 14°cos 16°+sin 76°cos 74°;(3)sin π12π12; (4)1tan 751tan 75+-. 名师导引:(1)将105°转化为两个特殊角的和或差,直接利用公式求解.(2)先利用诱导公式统一角度再逆用两角和的正弦公式 求解.(3)提取2后将12,逆用公式求解. (4)注意“1”的转化,逆用两角和的正切公式求解.解:(1)原式=cos(60°+45°)=cos 60°cos 45°-sin 60°sin 45°=12×22= (2)原式=sin 14°cos 16°+sin(90°-14°)cos(90°-16°)=sin 14°cos 16°+cos 14°sin 16°=sin(14°+16°)=sin 30°=12.(3)法一 原式=2(12sin π12cos π12) =2(sin π6sin π12-cos π6cos π12)=-2cos (π6+π12)=-2cos π4法二 原式=2(12sin π12π12) =2(cos π3sin π12-sin π3cos π12)=2sin (π12-π3)=-2sin π4 (4)原式=tan 45tan 751tan 45tan 75+-=tan(45°+75°)=tan 120°.题后反思 三角函数式的化简与求值主要是诱导公式、同角三角函数基本关系、两角和差的正余弦、正切公式的正用、逆用和变形用,观察式子结构特点选取合适公式是解题的关键.转化过程中注意“1”与“tan π4”、“”与“tan π3”、“ 12”与“cos π3”等特殊数与特殊角的函数值之间的转化. 跟踪训练11:(1)求sin(θ+75°)+cos(θ+45°)cos(θ+15°)的值;(2)(2014遵义四中期末)求tan 20°+tan 40°tan 20° tan 40°的值.解:(1)设α=θ+15°,则原式=sin(α+60°)+cos(α+30°α=(12sin αα)+cos α-12sin α)α =0.(2)原式=tan 60°(1-tan 20° tan 40°)+° tan 40°.题型二 三角函数的条件求值【例2】 已知π2<β<α<34π,cos(α-β)= 1213,sin(α+β)=- 35,求cos 2α的值. 名师导引:(1)寻找角的关系2α=(α+β)+(α-β);(2)借助同角三角函数关系及两角和的余弦公式求解.解:∵π2<β<α<34π,∴-34π<-β<-π2, ∴0<α-β<π4,π<α+β<32π,∴sin(α-β)=513,cos(α+β)=-45. ∴cos 2α=cos[(α-β)+(α+β)]=cos(α-β)cos(α+β)-sin(α-β)sin(α+β) =1213×(-45)-513×(-35)=-3365, 即cos 2α=-3365. 题后反思 (1)解决三角函数条件求值问题的关键是寻找已知角与所求角之间的关系,恰当地拆角凑角、合理地选用公式.(2)常见角的变换有α=(α+β)-β、α=β-(β-α)、2α=(α+β)+(α-β)等.跟踪训练21:(2014洛阳期末)已知tan (π4+α)=2,tan(α-β)= 12,α∈(0,π4),β∈(-π4,0). (1)求tan α的值;(2)求212sin cos cos ααα+的值; (3)求2α-β的值.解:(1)tan (π4+α)=1tan 1tan αα+-=2,得tan α=13; (2)212sin cos cos ααα+=222sin cos 2sin cos cos ααααα++ =2tan 12tan 1αα++=23; (3)因为tan(2α-β)=tan[α+(α-β)]=tan tan()1tan tan()ααβααβ+---=1, 又α∈(0,π4),β∈(-π4,0),得2α-β∈(0, 3π4),所以2α-β=π4. 题型三 辅角公式的应用【例3】 当函数≤x<2π)取得最大值时,x= .解析:函数为(x-π3), 当0≤x<2π时,-π3≤x-π3<5π3, 所以当y 取得最大值时,x-π3=π2,所以x=5π6. 答案:5π6题后反思 辅角公式ϕ)(或asin x+bcos x=ϕ))可以将形如 asin x+bcos x(a,b 不同时为零)的三角函数式写成一个角的三角函数式.这样有利于三角函数式的化简求值,更有助于研究三角函数的性质.跟踪训练31:函数f(x)=sin x-cos (x+π6)的值域为( B )(A)[-2,2](C)[-1,1] ] 解析:f(x)=sin x-cos (x+π6)12sin x=32sin (x-π6),所以函数f(x)的值域为,].故选B.【自主练习】1. 已知sin(α+β)=12,sin(α-β)=13,求tan tan αβ的值. 解:∵sin(α+β)=12,∴sin αcos β+cos αsin β=12.①∵sin(α-β)=1 3 ,∴sin αcos β-cos αsin β=13.②由①,②解得sin αcos β=512, cos αsin β=112,∴tantanαβ=sin coscos sinαβαβ=512112=5.2.已知α,β都是锐角,且cos αsin β=12,求α-β的值.解:法一由α,β都是锐角及cos αβ=12,得sin αβ.所以sin(α-β)=sin αcos β-cos αsin β.又由α,β都是锐角,即0<α<π2,0<β<π2,所以-π2<α-β<π2.所以α-β=π4 .法二由α,β都是锐角及cos αβ=12,得sin αβ.cos(α-β)=cos αcos β+sin αsin β1 2,3.(2014清远期末)化简:sin 21°cos 81°-cos 21° sin 81°等于( D )(A)12 (B)-12解析:原式=sin(21°-81°)=-sin 60°故选D. 4.已知α是锐角,sin α=35,则cos (π4+α)等于( B )(D) 解析:因为α是锐角,sin α=35, 所以cos α=45,所以cos (π4+α)×45×35.故选B. 5.sin 255°= .解析:sin 255°=-sin 75°=-sin(45°+30°)=-答案: 6.1tan12tan 72tan12tan 72--= .解析:1tan12tan 72tan12tan 72+-=-()1tan 7212-=-答案:5.已知α+β=45°,求(1+tan α)·(1+tan β)的值. 解: (1+tan α)·(1+tan β )=1+tan αtan β+tan α+tan β=1+tan αtan β+tan(α+β)(1-tan αtan β)=2。
