XX届高三数学3月二轮研讨会专题复习-函数应用题
基本初等函数、函数与方程 专项练习-2023届高三数学二轮专题复习(含解析)

冲刺2023年高考二轮 基本初等函数、函数与方程(原卷+答案)1.函数y =log 2(4+3x -x 2)的一个单调增区间是( ) A .⎝ ⎛⎭⎪⎫-∞,32 B .⎣⎢⎡⎭⎪⎫32,+∞ C .⎝ ⎛⎭⎪⎫-1,32 D .⎣⎢⎡⎭⎪⎫32,4 2.已知函数f (x )=⎩⎨⎧ax 2-x -14,x ≤1log a x -1,x >1,是R 上的单调函数,则实数a 的取值范围为( )A .⎣⎢⎡⎭⎪⎫14,12B .⎣⎢⎡⎦⎥⎤14,12 C .⎝ ⎛⎦⎥⎤0,12 D .⎝ ⎛⎭⎪⎫12,1 3.若不等式x 2-log a x <0在⎝⎛⎭⎪⎫0,12 内恒成立,则a 的取值范围是( )A .116 ≤a <1B .116 <a <1 C .0<a ≤116 D .0<a <1164.若函数f (x )=x +ax -1在(0,2)上有两个不同的零点,则a 的取值范围是( )A .⎣⎢⎡⎦⎥⎤-2,14B .⎝ ⎛⎭⎪⎫-2,14C .⎣⎢⎡⎦⎥⎤0,14D .⎝ ⎛⎭⎪⎫0,145.中国的5G 技术领先世界,5G 技术的数学原理之一便是著名的香农公式:C =W log 2⎝ ⎛⎭⎪⎫1+S N .它表示,在受噪音干扰的信道中,最大信息传递速度C 取决于信道带宽W ,信道内信号的平均功率S ,信道内部的高斯噪声功率N 的大小,其中SN 叫作信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,增加带宽,提高信号功率和降低噪声功率都可以提升信息传递速度,若在信噪比为1 000的基础上,将带宽W 增大到原来的2倍,信号功率S 增大到原来的10倍,噪声功率N 减小到原来的15 ,则信息传递速度C 大约增加了( )(参考数据:lg 2≈0.3) A .87% B .123% C .156% D .213%6.已知函数f (x )=⎩⎪⎨⎪⎧||log 2x ,x >0,-x 2-4x +4,x <0. 若函数g (x )=f (x )-m 有四个不同的零点x 1,x 2,x 3,x 4,则x 1x 2x 3x 4的取值范围是( )A .(0,4)B .(4,8)C .(0,8)D .(0,+∞)7.已知函数f (x )是定义在R 上的奇函数,满足f (x +2)=f (-x ),且当x ∈[0,1]时,f (x )=log 2(x +1),则函数y =f (x )-x 3的零点个数是( )A .2B .3C .4D .5 8.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量y (mg/m 3)与时间t (h )的函数关系为y =⎩⎪⎨⎪⎧kt ,0<t <12,1kt ,t ≥12, (如图所示)实验表明,当药物释放量y <0.75(mg/m 3)时对人体无害.(1)k =________;(2)为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过________分钟人方可进入房间.9.函数f (x )=⎩⎪⎨⎪⎧x 3+2,x ≤0x -3+e x,x >0 的零点个数为________. 10.已知函数f (x )=⎩⎪⎨⎪⎧4x -1,x ≤1log 2x ,x >1 ,若1<f (a )≤2,则实数a 的取值范围为________.11.已知函数f (x )=⎩⎪⎨⎪⎧10x -2-102-x ,x ≤2||x -3-1,x >2,则不等式f (x )+f (x -1)<0的解集为________.12.对实数a 和b ,定义运算“⊗”:a ⊗b =⎩⎪⎨⎪⎧a ,a -b ≤1,b ,a -b >1.设函数f (x )=(x 2-2)⊗(x -1),x ∈R .若函数y =f (x )-c 恰有两个零点,则实数c 的取值范围是________.13.已知f (x )是定义在R 上的偶函数,f ′(x )是f (x )的导函数,当x ≥0时,f ′(x )-2x >0,且f (1)=3,则f (x )>x 2+2的解集是( )A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(1,+∞)C .(-1,0)∪(0,1)D .(-∞,-1)∪(0,1)14.定义在R 上的偶函数f (x )满足f (2-x )=f (2+x ),且当x ∈[0,2]时,f (x )=⎩⎨⎧2x-1,0≤x ≤12sin π2x -1,1<x ≤2,若关于x 的方程m ln ||x =f (x )至少有8个实数解,则实数m 的取值范围是( )A .⎣⎢⎡⎭⎪⎫-1ln 6,0 ∪⎝ ⎛⎦⎥⎤0,1ln 5B .⎣⎢⎡⎦⎥⎤-1ln 6,1ln 5 C .⎝ ⎛⎭⎪⎫-1ln 6,0 ∪⎝ ⎛⎭⎪⎫0,1ln 5 D .⎝ ⎛⎭⎪⎫-1ln 6,1ln 5参考答案1.解析:函数y =log 2(4+3x -x 2)的定义域为(-1,4). 要求函数y =log 2(4+3x -x 2)的一个单调增区间, 只需求y =4+3x -x 2的增区间,只需x <32 . 所以-1<x <32 .所以函数y =log 2(4+3x -x 2)的一个单调增区间是⎝ ⎛⎭⎪⎫-1,32 .故选C.答案:C2.解析:当函数f (x )=⎩⎪⎨⎪⎧ax 2-x -14,x ≤1,log a x -1,x >1是R 上的单调递减函数,所以⎩⎪⎨⎪⎧0<a <112a ≥1a -54≥-1,解得14 ≤a ≤12 ,因为a >0且a ≠1,所以当x ≤1时,f (x )不可能是增函数, 所以函数f (x )在R 上不可能是增函数, 综上:实数a 的取值范围为⎣⎢⎡⎦⎥⎤14,12 ,故选B.答案:B3.解析:当a >1时,由x ∈⎝ ⎛⎭⎪⎫0,12 ,可得log a x <0,则-log a x >0,又由x 2>0,此时不等式x 2-log a x <0不成立,不合题意; 当0<a <1时,函数y =log a x 在⎝ ⎛⎭⎪⎫0,12 上单调递减,此时函数y =-log a x 在⎝ ⎛⎭⎪⎫0,12 上单调递增,又由y =x 2在⎝ ⎛⎭⎪⎫0,12 上单调递增,要使得不等式x 2-log a x <0在⎝ ⎛⎭⎪⎫0,12 内恒成立,可得⎝ ⎛⎭⎪⎫12 2-log a 12 ≤0,解得116 ≤a <1.故选A.答案:A4.解析:函数f (x )=x +ax -1在(0,2)上有两个不同的零点等价于方程x +ax -1=0在(0,2)上有两个不同的解,即a =-x 2+x 在(0,2)上有两个不同的解.此问题等价于y =a 与y =-x 2+x (0<x <2)有两个不同的交点.由下图可得0<a <14 .故选D. 答案:D5.解析:提升前的信息传递速度C =W log 2S N =W log 21 000=3W log 210=3Wlg 2≈10W ,提升后的信息传递速度C ′=2W log 210S 15N =2W log 250SN =2W log 250 000=2W ·4+lg 5lg 2 =2W ·5-lg 2lg 2 ≈94W 3 ,所以信息传递速度C 大约增加了C ′-CC =943W -10W 10W ≈2.13=213%.故选D.答案:D6.解析:函数g (x )有四个不同的零点等价于函数f (x )的图象与直线y =m 有四个不同的交点.画出f (x )的大致图象,如图所示.由图可知m ∈(4,8).不妨设x 1<x 2<x 3<x 4,则-4<x 1<-2<x 2<0,且x 1+x 2=-4.所以x 2=-x 1-4,所以x 1x 2=x 1(-x 1-4)=-(x 1+2)2+4∈(0,4),则0<x 3<1<x 4,因为||log 2x 3 =||log 2x 4 ,所以-log 2x 3=log 2x 4,所以log 2x -13 =log 2x 4,所以x 3·x 4=1,所以x 1·x 2·x 3·x 4=x 1·x 2∈(0,4).故选A. 答案:A7.解析:由f (x +2)=f (-x )可得f (x )关于x =1对称, 由函数f (x )是定义在R 上的奇函数,所以f (x +2)=f (-x )=-f (x )=-[-f (x -2)]=f (x -2), 所以f (x )的周期为4,求函数y =f (x )-x 3的零点问题即y =f (x )-x 3=0的解, 即函数y =f (x )和y =x 3的图象交点问题,根据f (x )的性质可得如图所示图形,结合y =x 3的图象,由图象可得共有3个交点,故共有3个零点,故选B. 答案:B8.解析:(1)由题图可知,当t =12 时,y =1,所以2k =1,所以k =2. (2)由(1)可知,y =⎩⎪⎨⎪⎧2t ,0<t <12,12t ,t ≥12,当t ≥12 时,y =12t ,令y <0.75,得t >23 ,所以在消毒后至少经过23 小时,即40分钟人方可进入房间.答案:(1)2 (2)409.解析:当x ≤0时,令x 3+2=0,解得x =3-2 ,3-2 <0,此时有1个零点;当x >0时, f (x )=x -3+e x ,显然f (x )单调递增,又f ⎝ ⎛⎭⎪⎫12 =-52 +e 12 <0,f (1)=-2+e>0,由零点存在定理知此时有1个零点;综上共有2个零点.答案:210.解析:若a ≤1,则f (a )=4a -1,故1<4a -1≤2,解得12 <a ≤log 43,故12 <a ≤log 43;若a >1,则f (a )=log 2a ,故1<log 2a ≤2,解得2<a ≤4; 综上:12 <a ≤log 43或2<a ≤4. 答案:⎝ ⎛⎦⎥⎤12,log 43 ∪(2,4]11.解析:①当x ≤2时,x -1≤1,∵f (x )=10x -2-102-x 在(-∞,2]上单调递增,∴f (x )≤f (2)=0,又f (x -1)≤f (1)<f (2)=0, ∴f (x )+f (x -1)<0恒成立;②当2<x ≤3时,1<x -1≤2,f (x )=||x -3 -1=2-x <0, 又f (x -1)≤f (2)=0,∴f (x )+f (x -1)<0恒成立;③当3<x ≤4时,2<x -1≤3,f (x )=||x -3 -1=x -4,f (x -1)=||x -4 -1=3-x ;∴f (x )+f (x -1)=-1<0恒成立;④当x >4时,x -1>3,f (x )=||x -3 -1=x -4,f (x -1)=||x -4 -1=x -5,∴f (x )+f (x -1)=2x -9<0,解得x <92 ,∴4<x <92 ; 综上所述:不等式f (x )+f (x -1)<0的解集为⎝ ⎛⎭⎪⎫-∞,92 .答案:⎝ ⎛⎭⎪⎫-∞,92 12.解析:因为a ⊗b =⎩⎨⎧a ,a -b ≤1,b ,a -b >1.,所以f (x )=(x 2-2)⊗(x -1)=⎩⎨⎧x 2-2,-1≤x ≤2x -1,x <-1或x >2 ,由图可知,当-2<c ≤-1或1<c ≤2时,函数f (x )与y =c 的图象有两个公共点,∴c 的取值范围是(-2,-1]∪(1,2]. 答案:(-2,-1]∪(1,2] 13.解析:令g (x )=f (x )-x 2, 因为f (x )是定义在R 上的偶函数, 所以f (-x )=f (x ),则g (-x )=f (-x )-(-x )2=g (x ), 所以函数g (x )也是偶函数, g ′(x )=f ′(x )-2x ,因为当x ≥0时,f ′(x )-2x >0,所以当x ≥0时,g ′(x )=f ′(x )-2x ≥0, 所以函数g (x )在(0,+∞)上递增, 不等式f (x )>x 2+2即为不等式g (x )>2, 由f (1)=3,得g (1)=2, 所以g (x )>g (1),所以||x >1,解得x >1或x <-1,所以f (x )>x 2+2的解集是(-∞,-1)∪(1,+∞). 故选B. 答案:B14.解析:因为f (2-x )=f (2+x ),且f (x )为偶函数, 所以f (x -2)=f (x +2),即f (x )=f (x +4), 所以函数f (x )是以4为周期的周期函数,作出y=f(x),y=m ln x在同一坐标系的图象,如图,因为方程m ln ||x=f(x)至少有8个实数解,所以y=f(x),y=m ln |x|图象至少有8个交点,根据y=f(x),y=m ln |x|的图象都为偶函数可知,图象在y轴右侧至少有4个交点,由图可知,当m>0时,只需m ln 5≤1,即0<m≤1ln 5,当m<0时,只需m ln 6≥-1,即-1ln 6≤m<0,当m=0时,由图可知显然成立,综上可知,-1ln 6≤m≤1ln 5.故选B.答案:B。
届数学统考第二轮专题复习第1讲函数的图像与性质的简单应用学案理含解析
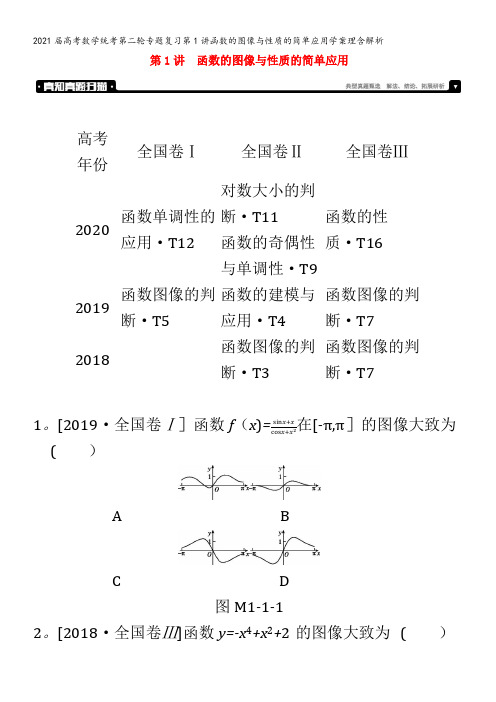
第1讲 函数的图像与性质的简单应用高考年份全国卷Ⅰ 全国卷Ⅱ 全国卷Ⅲ2020函数单调性的应用·T12对数大小的判断·T11 函数的奇偶性与单调性·T9函数的性质·T162019 函数图像的判断·T5函数的建模与应用·T4 函数图像的判断·T7 2018函数图像的判断·T3函数图像的判断·T71。
[2019·全国卷Ⅰ]函数f (x )=sinx+x cosx+x 2在[-π,π]的图像大致为( )A BC D图M1-1-12。
[2018·全国卷Ⅲ]函数y=-x 4+x 2+2的图像大致为 ( )图M1-1-23。
[2019·全国卷Ⅱ]若a〉b,则 ()A。
ln(a—b)>0 B。
3a〈3bC。
a3—b3〉0 D.|a|>|b|4。
[2020·全国卷Ⅱ]若2x-2y〈3—x-3-y,则()A.ln(y-x+1)〉0B.ln(y—x+1)〈0C.ln|x-y|〉0D。
ln|x-y|〈05.[2020·北京卷]已知函数f(x)=2x—x—1,则不等式f(x)〉0的解集是()A.(—1,1)B。
(-∞,—1)∪(1,+∞)C.(0,1)D。
(-∞,0)∪(1,+∞)6.[2020·全国新高考Ⅰ卷]若定义在R的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是()B。
[—3,—1]∪[0,1]C.[—1,0]∪[1,+∞)D.[-1,0]∪[1,3]7.[2020·全国卷Ⅲ]已知55〈84,134<85。
设a=log53,b=log85,c=log138,则()A。
a<b〈c B.b<a〈cC。
b<c〈a D.c<a〈b8。
[2020·全国卷Ⅲ]Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎,累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=K1+e-0.23(t-53)其中K为最大确诊病例数。
高三理科数学二轮复习专题能力提升训练:函数、导数、不等式的综合问题(含答案解析).pdf

训练 函数、导数、不等式的综合问题 一、选择题(每小题5分,共25分) 1.下面四个图象中,有一个是函数f(x)=x3+ax2+(a2-1)x+1(aR)的导函数y=f′(x)的图象,则f(-1)等于( ). A. B.- C. D.-或 2.设直线x=t与函数f(x)=x2,g(x)=ln x的图象分别交于点M,N,则当|MN|达到最小时t的值为( ). A.1 B. C. D. 3.已知函数f(x)=x4-2x3+3m,xR,若f(x)+9≥0恒成立,则实数m的取值范围是( ). A. B. C. D. 4.已知函数f(x)=x2-ax+3在(0,1)上为减函数,函数g(x)=x2-aln x在(1,2)上为增函数,则a的值等于( ). A.1 B.2 C.0 D. 5.设aR,若函数y=eax+3x,xR有大于零的极值点,则( ). A.a>-3 B. a<-3 C.a>- D.a<- 二、填空题(每小题5分,共15分) 6.若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于________. 7.函数f(x)=x3-x2+ax-5在区间[-1,2]上不单调,则实数a的范围是________. 8.关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________. 三、解答题(本题共3小题,共35分) 9.(11分)已知函数f(x)=x3-x2+bx+a.(a,bR)的导函数f′(x)的图象过原点. (1)当a=1时,求函数f(x)的图象在x=3处的切线方程; (2)若存在x<0,使得f′(x)=-9,求a的最大值. 10.(12分)已知a,b为常数,且a≠0,函数f(x)=-ax+b+axln x,f(e)=2(e=2.718 28…是自然对数的底数). (1)求实数b的值; (2)求函数f(x)的单调区间; (3)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t[m, M],直线y=t与曲线y=f(x)都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由. 11.(12分)已知f(x)=xln x,g(x)=-x2+ax-3. (1)求函数f(x)在[t,t+2](t>0)上的最小值; (2)对一切的x(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围; (3)证明:对一切x(0,+∞),都有ln x>-.参考答案 1.D [f′(x)=x2+2ax+a2-1,f′(x)的图象开口向上,若图象不过原点,则a=0时,f(-1)=,若图象过原点,则a2-1=0,又对称轴x=-a>0,a=-1,f(-1)=-.] 2.D [|MN|的最小值,即函数h(x)=x2-ln x的最小值,h′(x)=2x-=,显然x=是函数h(x)在其定义域内唯一的极小值点,也是最小值点,故t=.] 3.A [因为函数f(x)=x4-2x3+3m,所以f′(x)=2x3-6x2,令f′(x)=0,得x=0或x=3,经检验知x=3是函数的一个最小值点,所以函数的最小值为f(3)=3m-,不等式f(x)+9≥0恒成立,即f(x)≥-9恒成立,所以3m-≥-9,解得m≥.] 4.B [函数f(x)=x2-ax+3在(0,1)上为减函数,≥1,得a≥2.又g′(x)=2x-,依题意g′(x)≥0在x(1,2)上恒成立,得2x2≥a在x(1, 2)上恒成立,有a≤2,a=2.] 5.B [令f(x)=eax+3x,可求得f′(x)=3+aeax,若函数在xR上有大于零的极值点,即f′(x)=3+aeax=0有正根.当f′(x)=3+aeax=0成立时,显然有a<0,此时x=ln.由x>0,解得a<-3,a的取值范围为(-∞,-3).] 6.解析 由题得f′ (x)=12x2-2ax-2b=0,f′(1)=12-2a-2b=0,a+b=6.a+b≥2,6≥2,ab≤9,当且仅当a=b=3时取到最大值. 答案 9 7.解析 f(x)=x3-x2+ax-5,f′(x)=x2-2x+a=(x-1)2+a-1,如果函数f(x)=x3-x2+ax-5在区间[-1,2]上单调,那么a-1≥0或f′(-1)=3+a≤0且f′(2)=a≤0,a≥1或a≤-3.于是满足条件的a(-3,1). 答案 (-3,1) 8.解析 由题意知使函数f(x)=x3-3x2-a的极大值大于0且极小值小于0即可,又f′(x)=3x2-6x=3x(x-2),令f′(x)=0得,x1=0,x2=2,当x<0时,f′(x)>0;当0<x<2时,f′(x)<0;当x>2时,f′(x)>0,所以当x=0时,f(x)取得极大值,即f(x)极大值=f(0)=-a;当x=2时,f(x)取得极小值,即f(x)极小值=f(2)=-4-a,所以,解得-4<a<0. 答案 (-4,0) 9.解 由已知,得f′(x)=x2-(a+1)x+b. 由f′(0)=0,得b=0,f′(x)=x(x-a-1). (1)当a=1时,f(x)=x3-x2+1,f′(x)=x(x-2),f(3)=1, f′(3)=3. 所以函数f(x)的图象在x=3处的切线方程为y-1=3(x-3), 即3x-y-8=0. (2)存在x<0,使得f′(x)=x(x-a-1)=-9,-a-1=-x-=(-x)+≥2=6,a≤-7,当且仅当x=-3时,a=-7. 所以a的最大值为-7. 10.解 (1)由f(e)=2,得b=2. (2)由 (1)可得f(x)=-ax+2+axln x. 从而f′(x)=aln x. 因为a≠0,故 当a>0时,由f′(x)>0,得x>1,由f′(x)<0得, 0<x<1; 当a<0时,由f′(x)>0,得0<x<1,由f′(x)<0得,x>1. 综上,当a>0时,函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1);当a<0时,函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞). (3)当a=1时,f(x)=-x+2+xln x,f′(x)=ln x. 由(2)可得,当x在区间内变化时,f′(x),f(x)的变化情况如下表: x1(1,e)ef′(x) -0 +f(x)2-单调递减极小值1单调递增2又2-<2, 所以函数f(x)的值域为[1,2]. 据此可得,若则对每一个t[m,M],直线y=t与曲线y=f(x)都有公共点; 并且对每一个t(-∞,m)(M,+∞),直线y=t与曲线y=f(x)都没有公共点. 综上,当a=1时,存在最小的实数m=1,最大的实数M=2,使得对每一个t[m,M],直线y=t与曲线y=f(x)都有公共点. 11.(1)解 f′(x)=ln x+1. 当x时,f′(x)<0,f(x)单调递减; 当x时,f′(x)>0,f(x)单调递增. 则当0<t<t+2<时,t无解; 当0<t<<t+2,即0<t<时, [f(x)]min=f=-; 当≤t<t+2,即t≥时, f(x)在[t,t+2]上单调递增. 所以[f(x)]min=f(t)=tln t.所以[f(x)]min= (2)解 2f(x)≥g(x),即2xln x≥-x2+ax-3, 则a≤2ln x+x+.设h(x)=2ln x+x+(x>0), h′(x)=. 当x(0,1)时,h′(x)<0,h(x)单调递减; 当x(1,+∞)时,h′(x)>0,h(x)单调递增. 所以[h(x)]min=h(1)=4.因为对一切x(0,+∞),2f(x)≥g(x)恒成立, 所以a≤[h(x)] min=4.故实数a的取值范围是(-∞,4]. (3)证明 问题等价于证明xln x>-,x(0,+∞). 由(1)可知f(x)=xln x,x(0,+∞)的最小值为-, 当且仅当x=时取得.设m(x)=-,x(0,+∞),则m′(x)=,易得[m(x)]max=m(1)=-. 从而对一切x(0,+∞),都有ln x>-成立.。
2019-2020学年高三数学第二轮专题复习 专题三 函数题型分析与预测(二)教案.doc

2019-2020学年高三数学第二轮专题复习 专题三 函数题型分析与预测(二)教案【专题目标】:函数是高中阶段数学重要的基础知识,是高考考查的重中之重,因为它是贯穿整个中学数学的一根主线,许多内容都和它有联系,都能够用其思想与方法解决问题。
函数问题成为高考永恒的热点,从考试来看对函数内容的考查主要有以下形式和特点:1.考查集合的概念及运算,简易逻辑的理解,条件充要性的判断,命题真假的判定,以及映射、函数的概念,常以选择题、填空题形式出现,属中、低档题,能力要求不高。
2.考查一次函数、二次函数、反比例函数、指数函数和对数函数等常见初等函数的图象和性质及应用。
考查内容主要是关于函数的定义域、值域(最值)、单调性、奇偶性、周期性、对称性、反函数、图象以及图象的变换。
以上纯函数内容的考查也常以选择题、填空题出现,属中档题。
3.二次函数是中学生在初中、高中阶段所学过的最正规、最完备的函数之一;二次函数几乎涉及学生在高中阶段所学过的各种数学思想,所以它最能体现学生对函数思想的把握。
许多重要的数学方法,如配方法、换元法、参数分类讨论法、基本不等式法、赋值法,都与它有着密切的联系;一元二次方程的根的分布与讨论,一元二次不等式解集的讨论;二次曲线交点问题,也与二次函数息息相关。
【知识网络】:1.从2005年全国和各地高考试卷看,函数试题进一步创新,试题设计新颖、灵活、思维力度增大,运算量减少,这部分内容分值约占部分的20%--25%。
自2004年以来,高考命题权下放,高考模式增多,涉及二次函数问题的试题更是举不胜举,且有些问题难度较大,因此在学习中对二次函数的有关性质及应用的训练要深入、广泛并达到一定的深度。
2.考查函数与方程、不等式、三角、数列、曲线方程等知识的交叉渗透及应用,属中、高档题,特别要注意加强导数、向量、线性规划、概率等新增知识与函数的交汇问题的剖析与训练。
3.考查以函数为模型的实际应用问题,让考生从数学角度观察事物、阐释现象,分析解决问题,属中档题。
高三数学二轮复习专题3

高三数学二轮复习专题3:《函数与导数》[专题内容]1、函数与导数的基础知识、基本方法归纳梳理;2、三个基本问题(函数的三要素问题;函数的性质及图象应用问题;利用导数研究函数的性质问题)的解决方法与途径;[知识归纳]要点1、函数的三要素(定义域、值域、对应法则):①掌握求函数定义域的原则及规律:列表法、图象法、解析式、实际问题、复合函数的定义域。
x 2 x 2[范例1](06,湖北,4)设f(X) lg——,则f(—) f(—)的定义域为______________2 x 2 x②掌握求函数值域的基本方法,如直接法、二次函数法、反函数法、换元法、配方法、判别式法、图象法、数形结合法、不等式法、导数法等。
[范例2](08,宣武)定义在N*上的函数f(x)满足f(1) 1,且1-f (n), n为偶数f(n 1) 则f (22) _________2f (n), n为奇数[范例3]已知f(x) 2 log s x,x [1,9],试求函数y [f(x)]2 f (x2)的值域。
③掌握求函数解析式的基本方法(待定系数法、换元法及实际问题)2[范例4]已知f( 1) lg x,求f(X)。
x要点2、函数的性质:① 函数的单调性:(重点掌握单调性的概念、判断方法、复合函数的单调 性)。
♦定义:注意定义是相对与某个具体的区间而言。
♦判定方法有:定义法(作差比较和作商比较);导数法(适用于 多项式函数);复合函数法和图像法。
♦应用:比较大小,证明不等式,解不等式。
°a )X 1,X 1是R 上的增函a x , x 1数,贝U a 的取值范围是 ______ .② 函数的奇偶性:(重点掌握函数奇偶性概念、判断方法、图象的特点)。
♦定义:注意区间是否关于原点对称,比较f(x)与f(-x)的关系。
f(x) — f(-x)=0 f(x) =f(-x)f(x)为偶函数;f(x)+f(-x)=0 f(x) =— f(-x) f(x)为奇函数。
江苏省天一中学高三数学二轮复习函数应用题

学海无涯,精做知识 专题9.1:函数应用题【拓展探究】探究1:以分式函数为载体的函数应用题1. 工厂生产某种产品,次品率p 与日产量x (万件)间的关系为:10,623x c x p x c ⎧<≤⎪⎪-=⎨⎪>⎪⎩(c 为常数, 且0<c <6). 已知每生产1件合格产品盈利3元,每出现1件次品亏损1.5元.(1)将日盈利额y (万元)表示为日产量x (万件)的函数; (2)为使日盈利额最大,日产量应为多少万件?(注:次品率=次品数产品总数×100%) 【解】(1)若c x ≤<0,则)6(293623)6(3x x x x x x x x y --=-⋅---=, 若c x >,则03223)32(3=⋅--=x x x y , cx c x >≤<0(2)当c x ≤<0,则222')6()9)(3(3))6()1)(29()6)(49(23x x x x x x x x y ---=------⋅= 若30≤<c ,则0'>y ,函数在(]c ,0上为增函数,)6(2)29(3,2max c c c y c x --==∴ 若63<<c ,在)3,0(上为增函数,在),3(c 上为减函数,∴当3=x 时,29max )3(==f y .综上,若30≤<c ,则当日产量为c 万件时,日盈利额最大;若63<<c ,则当日产量为3万件时,日盈利额最大.2. 近年来,某企业每年消耗电费约24万元, 为了节能减排, 决定安装一个可使用15年的太阳能供电设备接入本企业电网, 安装这种供电设备的工本费(单位: 万元)与太阳能电池板的面积(单位: 平方米)成正比, 比例系数约为0.5. 为了保证正常用电, 安装后采用太阳能和电能互补供电的模式. 假设在此模式下, 安装后该企业每年消耗的电费C (单位:万元)与安装的这种太阳能电池板的面积x (单位:平方米)之间的函数关系是()(0,20100k C x x k x =≥+为常数). 记F 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.(1)试解释(0)C 的实际意义, 并建立F 关于x 的函数关系式;。
备战高考数学二轮专题复习 专题1第3讲函数、方程及函数的应用课件 文 新人教版
第3讲 │ 主干知识整合
二、二分法 1.二分法的条件:函数 y=f(x)在区间[a,b]上的图 象是连续不断的一条曲线,并且 f(a)f(b)<0. 2.二分法的思想:通过二等分,无限逼近. 3.二分法的步骤:其中给定精确度 ε 的含义是区间 (a,b)长度|a-b|<ε,不能认为是函数零点近似值的精度.
第3讲 │ 要点热点探究
【解答】 (1)设相遇时小艇的航行距离为 S 海里,则 S= 900t2+400-2·30t·20-cos90°-30° = 900t2-600t+400 = 900t-132+300. 故当 t=13时 Smin=10 3,v=101 3=30 3,
3 即小艇以 30 3海里/小时的速度航行,相遇时小艇的航行 距离最小.
第3讲 │ 要点热点探究
【点评】 关于解决函数的实际应用问题,首先要在阅 读上下功夫,一般情况下,应用题文字叙述比较长,要耐心、 细心地审清题意,弄清各量之间的关系,再建立函数关系式, 然后借助函数的知识求解,解答后再回到实际问题中去.本 题中弄清“销量”、“售价”、“生产成本”、“促销费”、 “利润”等词的含义后列出函数关系式是解决本题的关键.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的 大小应为多少?
(2)为保证小艇在 30 分钟内(含 30 分钟)能与轮船相遇,试 确定小艇航行速度的最小值;
(3)是否存在 v,使得小艇以 v 海里/小时的航行速度行驶, 总能有两种不同的航行方向与轮船相遇?若存在,试确定 v 的 取值范围;若不存在,请说明理由.
又 t=0 时,x=1. ∴3-1=0+k 1,解得 k=2. ∴x 与 t 的关系式是 x=3-t+2 1(t≥0).
第3讲 │ 要点热点探究
二轮专题复习三应用题
二轮专题之三-------函数应用专题秭归县职教中心袁德【考纲导读】了解函数的简单实际应用,基本题型为解应题,高考具有选拔功能的压轴题。
【考点示例】例1.我国是一个缺水的国家,很多城市的生活用水远远低于世界的平均水平,为了加强公民的节水意识,某城市制订了每户每月用水收费(含用水费和污水处理费)标准如下表所示。
试写出每户每月用水量x(m3)与应交水费y(元)之间的例2.某城市出租汽车的收费标准是:当行程不超过3km时,收费7元;行程超过3km,但不超过10km时,在收费7元的基础上,超过3km的部分每公里收费元;行程超过10km时,超过10km的部分每公里收费元,试求车费y(元)与x(km)之间的函数解析式,并作出函数图象。
例3.我国平信计费标准是:投寄外埠平信,每封信的质量不超过20g ,付邮资元;质量超过20g 后,每增加20g (不足20g 按照20g 计算)增加元。
试建立每封平信应付的邮资y(元)与信的质量x(g)之间的函数关系(设0<x ≤60),并作出函数图象。
例4.有一种礼花的升空高度h(m)与飞行时间t(s)的关系式是h=120252++-t t ,若这种礼花在点火升空到最高点时引爆,求从点火升空到引爆所需要的时间。
例5.某服装经销商经营某品牌的牛仔裤,采用打折的方法促销:5条以上享受批发价,可以打9折;10条以上可以打折;20条以上可以打折;50条以上可以打6折,试建立顾客享受折扣价与购买牛仔裤数量之间的函数关系式,并作出函数的图像。
例6.某城市固定电话市内通话的收费标准是:每次通话3分钟以内,收费元,超过3分钟后,每分钟(不足1分钟按1分钟计算)收费元,如果通话时间不超过6分钟,试建立通话应付费与通话时间之间的函数关系式,并作出函数图象。
例7.为了鼓励居民节约用水,某市改革居民用水的收费办法,每月收费的表尊如下:月用水量不超过20m 3时,按2元/ m 3计费;月用水量超过20m 3时,其中的20m 3按2元/ m 3计费,超过的部分按元/ m 3计费.设每户月用水量为x m 3,应缴水费为y 元。
2021-2022年高三数学第二轮专题复习专题三函数题型分析与预测(一)教案
2021年高三数学第二轮专题复习专题三函数题型分析与预测(一)教案【专题目标】:函数是高中阶段数学重要的基础知识,是高考考查的重中之重,因为它是贯穿整个中学数学的一根主线,许多内容都和它有联系,都能够用其思想与方法解决问题。
函数问题成为高考永恒的热点,从考试来看对函数内容的考查主要有以下形式和特点:1.考查集合的概念及运算,简易逻辑的理解,条件充要性的判断,命题真假的判定,以及映射、函数的概念,常以选择题、填空题形式出现,属中、低档题,能力要求不高。
2.考查一次函数、二次函数、反比例函数、指数函数和对数函数等常见初等函数的图象和性质及应用。
考查内容主要是关于函数的定义域、值域(最值)、单调性、奇偶性、周期性、对称性、反函数、图象以及图象的变换。
以上纯函数内容的考查也常以选择题、填空题出现,属中档题。
3.二次函数是中学生在初中、高中阶段所学过的最正规、最完备的函数之一;二次函数几乎涉及学生在高中阶段所学过的各种数学思想,所以它最能体现学生对函数思想的把握。
许多重要的数学方法,如配方法、换元法、参数分类讨论法、基本不等式法、赋值法,都与它有着密切的联系;一元二次方程的根的分布与讨论,一元二次不等式解集的讨论;二次曲线交点问题,也与二次函数息息相关。
【知识网络】:1.从xx年全国和各地高考试卷看,函数试题进一步创新,试题设计新颖、灵活、思维力度增大,运算量减少,这部分内容分值约占部分的20%--25%。
自xx年以来,高考命题权下放,高考模式增多,涉及二次函数问题的试题更是举不胜举,且有些问题难度较大,因此在学习中对二次函数的有关性质及应用的训练要深入、广泛并达到一定的深度。
2.考查函数与方程、不等式、三角、数列、曲线方程等知识的交叉渗透及应用,属中、高档题,特别要注意加强导数、向量、线性规划、概率等新增知识与函数的交汇问题的剖析与训练。
3.考查以函数为模型的实际应用问题,让考生从数学角度观察事物、阐释现象,分析解决问题,属中档题。
高三数学二轮复习建议专题五函数与导数
21.涉与用导 大小;考查特殊值法、 21.涉与用导数讨
思想 求极值、最值的基本方 21.涉与用导数 数求曲线的切线问 排除法.
论单调性和根据零点个
法.
求曲线的切线问题 题和函数零点个数 21.涉与根据零点数求参数范围问题;考
能力 21.涉与用导数求 和证明函数不等式 问题;考查零点存 个数求参数范围与极 查考查考查零点存在定
(一)近五年高考题的统计与分析——文科
年份
2013年
2014年
2015年
2016年
2017年
题目 与难
度
9—中 12—难 20—中难
5—易 12—难 15—中难 21—难
10—中 12—难 21—难
8—中 9—中 12—难 21—难
8—中 9—中难 14—易 21—难
总分 值
22分
27分
22分
27分
论函数零点个数 和证明函数不等
题;考查转化能力、数形 结合思想.
力.
21.涉与用导数讨
20.涉与用导数 存在成立求参数范围 式问题;考查零 21.涉与用导数讨论 论单调性和不等式恒成
求曲线的切线、单调 问题;考查利用导数 点存在定理与利 函数单调性和由零点个数 立求参数范围问题;考
性、极值问题;考查 求函数最值的基本方 用导数研究函数 求参数范围问题;考查零 查考查考查利用导数研
除法. 12.涉与由函数单调
法. 14.考查用导数求
思想
式恒成立求参数范围 问题;考查转化与化
考查运算能力和分类 讨论思想数范围、三角函数 与二次函数交汇恒成立问
曲线切线的问题;考查 转化能力和运算求解能
能力
归思想、数形结合思 想解决问题的能力.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
XX届高三数学3月二轮研讨会专题复习-函
数应用题
函数应用题专题复习
【填空题】
.已知某产品今年年产量是a件,计划以后每年的产量比上一年增加20%,则x年后该产品的年产量y与x之间的函数关系式为__________.
.如图,某飞行器在4千米高空水平飞行,从距着陆点A的水平距离10千米处下降,已知下降飞行轨迹为某三次函数图象的一部分,则下列函数模型适合题意的是__________.
.某商品进货单价为40元,按单价每个50元售出,能卖出50个.若零售价在50元的基础上每上涨1元,其销售量就减少一个,则零售价上涨到__________元时,这批货物能取得最高利润.
.如图所示,是一块曲线部分为抛物线段且为轴对称形的钢板,其底边AB长为2,顶点到底边之距为1,若将此钢板切割成等腰梯形的形状,则该梯形面积为S的最大值是__________2.
二、典例分析
例1某科研所帮助一民营企业研发了一种新产品,据分
析预测该产品可以帮助该企业获得10万元~1000万元的投资收益,因此该企业决定对科研室所进行奖励.奖励方案为:奖金y随投资收益x的增加而增加,但最多不超过9万元,同时也不得超过投资收益的20%.现有两套模拟计算方法,问这两套计算方法是否符合奖励方案要求?为什么?
例2销售A、B两种商品所得的利润是P和Q,它们与投入资金t的关系为.现将3万元资金投入经营这两种商品,问应该如何投资最为合理?说明理由.
例3如图,oA、oB为两条直通景点o的公路,∠AoB=1350.在公路oA上距o点30的G点处有一个以G为中心、半径为5的文物保护区.为繁荣旅游事业,现拟修建一条笔直的高速公路,要求景点o距高速公路的最短距离为10,且分别在o、G之间设一出口E,在oB上设一出口F.求两出口间的最短距离;
若要确保高速公路不经过文物保护区,出口E应如何选址?说明理由.
【巩固训练】
.如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接,已知环湖弯曲路段为某三次函数图像的一部分,则该函数的解析式为__________.
.将一个长宽分别是a,b的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,若这个长方体的外
接球的体积存在最小值,则ab的取值范围是__________..为了节能减排的需要,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用c与隔热层厚度x满足关系:,若不建隔热层,每年能源消耗费用为8万元.设f为隔热层建造费用与20年的能源消耗费用之和.
求的值及f的表达式.试求隔热层多厚时,总费用f达到最小,并求最小值.
.某种水平放置的长方体形枕木,其安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.
将此枕木翻转90°,枕木的安全负荷会发生变化吗?为什么?
现有一根横断面为半圆的木材,用它来截取成长方体形的枕木,其长度即为枕木规定的长度,问如何截取,可使安全负荷最大?
.某渔场有一边长为20的正三角形湖面ABc,计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验.
为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?6.如图,一块弓形余布料EF,点为弧的中点,其所在圆o的半径为4d,∠EoF=.将弓形余布料裁剪成尽可能大的矩形ABcD,AD∥EF,且点A、D在弧上,设∠AoD=.求矩形ABcD的面积S关于的函数关系式;
当矩形ABcD的面积最大时,求cos的值.。
