Grover量子搜索算法中的最速降线问题研究
量子搜索算法Groversearch

量⼦搜索算法Groversearch问题定义:Problem :f :{0,1,2,3,……,N −1}→{0,1}找到 f (x )=1 的x解法经典解法:经典解法很简单,就是把每⼀个都看⼀遍,如果只有⼀个x 对应的f(x)=1,那么平均是要看⼀半,才能找到那个x 。
时间复杂度O(N)量⼦解法:使⽤Grover search 算法,时间复杂度在 O (√N )Grover search 算法Grover search 算法⼀共分为两步:1. Phase Inversion2. Inversion about the Mean然后不断的迭代这两步我们就能够得到结果了。
⾸先我们先看看这两个步骤分别在做什么:我们把 f (x )=1 的 |x ⟩ 称为 x ∗ ,我们要找的也就是这个 x ∗ 。
Phase Inversion:这⼀步主要是把 x ∗ 的概率幅翻转,变成负数,⽽其他的保持不变。
即,把 ∑x αx |x ⟩ 变成 ∑x ≠x ∗αx |x ⟩−αx ∗|x ∗⟩Inversion about the Mean这⼀步呢,就是把 αx 变成 2µ−αxµ 是所有概率幅的平均值,µ=∑x αxN ⽤图可能更好表达这两个步骤究竟在做什么:图1到图2,就是Phase Inversion ,把x ∗的概率幅翻转到了下⾯,图2中的虚线就是我的概率幅的平均值,图2到图3 就是我们的Inversion about the Mean ,对着平均值翻转⼀次,其余x 的概率幅是⾼于平均值的,所以 2µ−αx 让他们变⼩了,⽽我们的 x ∗ 他的概率幅是个负数,所以 2µ−αx 后他增加了。
不断的重复这个步骤, x ∗ 他的概率幅会越来越⼤,最后我们测量的时候就会很容的找到他。
进⾏了 √N 后,他的概率幅就会达到 1√2 ,算概率就是1/2。
那么接下来的问题就是,这些操作是怎么实现的?Phase Inversion:这个步骤要做的事情就是,把 ∑x αx |x ⟩ 变成 ∑x ≠x ∗αx |x ⟩−αx ∗|x ∗⟩符号是和f(x)是否为1相关的,进⼀步化简就是 ∑x (−1)f (x )αx |x ⟩有没有⼀丝熟悉感?把f(x)的结果给放到相位上去,这是我们在中就遇到的问题。
最优化方法第二章_线搜索算法_最速下降法
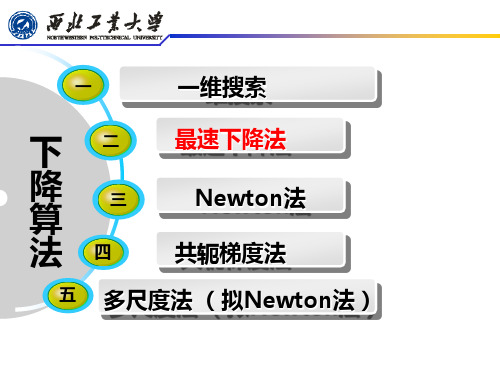
f x1 , x2 c, c>0,
2
改写为:
x12 2c 1
2 x2
2c 2
2
1
二、最速下降法
x2
这是以
2c
1
和
2c
2
为半轴的椭圆
2c
2c
2
2
从下面的分析可见 两个特征值的相对
x1
大小决定最速下降法的收敛性。
(1)当 1 2 时,等值线变为圆
2 2
4 f x , 2
2 x1 2 x2 4 f ( x) , 2 x1 +4x2
4 d = f x , 2
0 0
=40 2 20 3 令 0= ' ( ) 80 20, 得 0 =1/4,
一
一维搜索
二 三 四
下 降 算 法
五
最速下降法 Newton法 共轭梯度法
多尺度法 (拟Newton法)
二、最速下降法 假设 f 连续可微,取 线搜索方向
k
d f ( x )
k
步长k 由精确一维搜索得到。 从而得到第 k+1次迭代点,即
f ( x k k d k ) min f ( x k d k )
(推论)在收敛定理的假设下,若f (x)为凸函数,则最速下降 法或在有限迭代步后达到最小点;或得到点列 x k ,它的任 何聚点都是 f (x)的全局最小点。
二、最速下降法
最速下降法特征:相邻两次迭代的方向互相垂直。
令
( ) f ( x d ), 利用精确一维搜索,可得
Grover算法在单道量子计算模型下的实现的开题报告

Grover算法在单道量子计算模型下的实现的开题报告题目:Grover算法在单道量子计算模型下的实现摘要:Grover算法是在量子计算中被广泛使用的一种算法,其在搜索未排序数据库的时候能够提供极大的加速效果。
随着量子计算技术的逐步成熟,研究者开始尝试在不同的量子计算模型下实现Grover算法。
其中,单道量子计算模型是一种被广泛使用的模型。
本文将探讨Grover算法在单道量子计算模型下的实现,包括Grover算法的原理、单道量子计算模型的基本概念、算法的具体实现方法等。
关键词:Grover算法;单道量子计算模型;实现方法1. 引言量子计算技术是近年来发展迅猛的领域之一,其能够在一些特定的问题上提供极大的加速效果。
Grover算法是在量子计算中比较常见的一种算法,其在搜索未排序数据库时能够提供极大的加速效果 [1]。
随着量子计算技术的逐步成熟,研究者开始尝试在不同的量子计算模型下实现该算法。
其中,单道量子计算模型是一种被广泛使用的模型之一。
本文将探讨Grover算法在单道量子计算模型下的实现。
2. Grover算法的原理Grover算法是一种在经典计算机上很难高效实现的搜索算法,但是在量子计算机上却可以实现线性加速。
其主要思路是通过遍历未排序的数据库来寻找某个特定的项 [2]。
具体来说,假设有一个未排序的数据库,其中包含n个元素,我们要在其中寻找某一个特定的元素x。
首先,我们用方波函数来表示所有元素的平均值,然后将其作为初始状态。
接下来,我们使用一个Oracle操作,用于标记目标元素x。
具体实现方法是,在整个数据库上应用一种判断函数f(x),该函数在x为目标元素时返回1,否则返回0。
接下来,我们将目标元素x的振幅增加到一个足够大的值,然后对整个数据库进行相位反转操作。
这样一来,目标元素x的振幅就会变得足够大,从而使我们在测量时,以非常高的概率测量到目标元素x。
这样,我们就成功实现了对未排序数据库的搜索。
量子计算中的量子搜索算法与优化问题求解

量子计算中的量子搜索算法与优化问题求解量子计算是一门新兴的领域,将经典计算与量子力学相结合,利用量子特性来进行计算。
在传统计算机无法高效解决的问题上,量子计算显示出巨大的潜力。
其中,量子搜索算法和优化问题求解是量子计算中两个重要的研究领域。
量子搜索算法是指使用量子计算机来寻找未排序数据库中的特定项。
与经典计算机的线性搜索不同,量子搜索算法能够在O(sqrt(N))的时间复杂度内找到目标项,其中N是数据库的大小。
著名的量子搜索算法是Grover算法,它的关键思想是利用量子叠加态和量子相干性来加快搜索速度。
Grover算法在某些应用领域,如密码学、数据挖掘和图像处理中具有重要意义。
量子优化问题求解则是利用量子计算来解决组合优化问题,如旅行商问题、最大割问题和费马大定理等。
在经典计算中,这些问题往往需要穷举所有可能的解来找到最优解,这在大规模问题上是非常耗时的。
而量子优化问题求解通过量子并行处理和量子叠加态的优势,能够在相对较短的时间内找到全局最优解或近似最优解。
量子搜索算法和优化问题求解在实际应用中有着广泛的潜力。
例如,在网络搜索中,量子搜索算法可以快速找到目标网页,提高搜索引擎的效率。
在材料科学中,量子优化问题求解可以用于寻找新型材料的最佳组合,从而设计出更高效的能源储存材料或催化剂。
此外,量子搜索算法和优化问题求解还可以用于金融领域的投资组合优化、交通路线规划以及基因序列分析等。
尽管量子计算在搜索和优化问题求解方面具有巨大的潜力,但实现其在实际应用中的效果仍面临挑战。
首先,量子计算的硬件仍处于早期阶段,存在噪声和误差。
这些问题限制了量子计算的规模和稳定性,使得解决大规模问题仍然具有挑战性。
其次,量子算法的设计和优化需要深入的数学和物理知识,以及计算机科学和优化理论的交叉研究。
这使得量子计算研究变得复杂和困难。
为了克服这些挑战,迫切需要加大对量子计算的研究和投资。
目前,许多科研机构和公司都在积极探索量子算法和量子计算机的发展。
最速降线问题

解 且y(0)=0,y(p)=q 这样 其E-L方程为 由于 所以有 则可得 上式对θ求导,所以 根据曲线过原点(0,0)及(p,q)可求出x0=0及r,这样,所求曲线为
应用
最速降线无论在数学上还是物理上都进行过严格的证明,对工程来说,其物理原理为在同一高度滚下的两个球, 两球下滚的原因都是受重力分力的作用,沿直线下滚的球,下滑的加速度保持不变,速度稳定地增加。沿着旋轮线 下滑时,开始的一段的坡度非常大,使得下滑的球在非常短的时间内取得的下滑速度非常大。虽然,在下滑的后半 阶段,坡度逐渐变小、速度增加变缓,但此时的下滑速度已经变得很大。所以,沿着旋轮线下滑在整个下滑阶段的 平均速度很大。即使旋轮线的长度比直线的长度大,沿着旋轮线下滑的时间也比直线短。
求解
列出表达式
最终解答
图1设 O, A是高度不同,且不在同一铅垂线上的两定点,如果不计摩擦和空气阻力,一质点 m在重力作用下 从 O点沿一曲线降落至。A(p,q) A点,问曲线呈何种形状时,质点降落的时间最短。
设曲线为 y=y(x),坐标如图1所示,质点由 O点开始运动,它的速度 v与它的纵坐标有关系 式中, g是重力加速度。 在曲线上点 (x, y)处,质点的运动速度为 式中, s表示曲线的弧长, t表示时间,于是 由于点 O, A的横坐标分别是 0, p,则质点 m从 O点运动到 A点所需时间为 这样,质点由 O点运动到 A点所需时间 t是 y(x)的函数,最速降线问题就是满足边界条件的 所有连续函数 y(x)中,求出一个函数 y使泛函式取最小值。 对泛函求极值的问题称为变分问题,使泛函取极值的函数称为变分问题的解,也称为极值函数。
旋轮线与1673年荷兰科学家惠更斯讨论的摆线相同。因为钟表摆锤作一次完全摆动所用的时间相等,所以摆 线(旋轮线)又称等时曲线。
量子计算中的Grover算法及其应用

量子计算中的Grover算法及其应用量子计算是一种相对于传统计算机的新兴计算模式,它利用量子特性来实现高效的计算和数据处理。
其中,Grover算法是一种重要的量子算法,被广泛应用于搜索问题的求解。
本文将介绍Grover算法的原理,并探讨其在实际应用中的潜力。
一、Grover算法的原理Grover算法是1996年由美国计算机科学家L. Grover提出的一种搜索算法,其核心思想是通过量子特性来实现快速搜索。
与传统的搜索算法相比,Grover算法具有更快的速度和更高的效率。
Grover算法的基本步骤如下:1. 初始化:将量子比特(qubit)初始化为均匀分布的状态。
假设有N个可能的搜索目标,通过N个量子比特可以表示2^N个状态。
2. 反转操作:通过应用受控反转门(controlled-NOT)来反转搜索空间中目标状态的幅度。
3. 反射操作:对搜索空间中的所有状态进行关于平均值的对称操作。
4. 重复以上两个步骤:进行若干次重复操作,直到找到目标状态。
二、Grover算法的应用1. 数据库搜索Grover算法在数据库搜索中有着广泛的应用。
传统的搜索算法的时间复杂度为O(N),而Grover算法只需O(√N)的时间复杂度。
这使得Grover算法能够更高效地搜索数据库,加快数据检索的速度。
2. 密码破解Grover算法还可以应用于密码学领域。
传统的密码破解方法使用穷举法,时间复杂度极高。
而使用Grover算法,可以在较短的时间内找到密码的正确答案,为密码破解提供了一种新的解决方案。
3. 组合优化问题组合优化问题在实际应用中广泛存在,例如旅行商问题(TSP)和背包问题。
传统的解法需要枚举所有可能的解,时间复杂度较高。
而Grover算法通过量子并行的方式,大幅度提高了求解组合优化问题的效率。
三、Grover算法的挑战与展望虽然Grover算法在搜索问题的求解中具有较高的效率,但其应用仍面临一些挑战。
其中最主要的挑战之一是量子比特的错误率。
一种Grover量子搜索算法的改进策略
Ke wo ds y r :Gr e l ort m ;p s a c n ov ra g ih ha e m t hi g;q a u s a c ng;qu nt m omputng u nt m e r hi a u c i
f rt i p o l m s a a y e n t i p p r n n i r v d m e s r a e n t en w h s t h n o — o h s r b e i n l z d i h s a e ,a d a mp o e a u e b s d o h e p a e ma c i g c n d to s p o o e . I h e p a e ma c i g c n ii n,t e a p iu e f t h s o a i n r h i n i r p s d n t e n w h s t h n o d t i o h m l d s o WO p a e r t to s a e t e t
Da i g P t oe m n t u e q n e r lu I s i t ,Da i g 1 3 1 t qn 6 3 8,Ch n ) ia
Ab ta t sr c :W h nt ec r e tGr v rag rt m sa p id t e r h s meo jc si n u s re u n u d — e h u r n o e lo ih i p l os a c o b t n a n o t dq a t m a e e
tb s , h rb bl yo ret bet s al l t eices f h e rh do jcs a a e t e o a it f o rc o jcsu u l f l wi t ra e esac e bet.Th e sn p i c yas hh n ot erao
grover算法简单解释
grover算法简单解释Grover算法是一种量子算法,用于在无序数据库中搜索特定的目标项。
它由Lov Grover于1996年提出,是对传统算法中的经典搜索算法进行量子加速的一种方法。
传统的搜索算法,例如线性搜索,需要逐个检查数据库中的每个项,平均需要搜索N/2个项才能找到目标(其中N是数据库中的项数)。
相比之下,Grover算法只需要大约√N次的查询即可找到目标项,实现了量子加速。
Grover算法的基本思想是利用量子叠加和干涉的原理,通过反转目标项的幅度来实现搜索。
算法的步骤如下:1.初始化:将量子计算机的n个量子比特都置于一个特殊的状态,称为均匀叠加态(Uniform Superposition)。
这可以通过应用Hadamard门来实现。
2.应用Oracle操作:通过一个称为Oracle的量子门操作,将目标项标记为负相位。
Oracle操作会在目标项上施加一个相位反转。
3.应用Diffusion操作:通过一个称为Diffusion的量子门操作,将非目标项的幅度反转。
Diffusion操作会改变均匀叠加态的相对幅度,使目标项的幅度增加,非目标项的幅度减小。
4.重复步骤2和3:重复应用Oracle和Diffusion操作,直到目标项的幅度接近最大值。
5.测量:最后,对量子比特进行测量,得到目标项的索引。
Grover算法的时间复杂度为O(√N),相比于传统算法的O(N/2),实现了量子加速。
然而,需要注意的是,Grover算法并不提供指数级的加速,仅仅是对某些特定问题的搜索提供了加速效果。
总结起来,Grover算法是一种使用量子计算机进行搜索的算法,通过利用量子叠加和干涉的原理,在无序数据库中高效地搜索目标项。
这种算法在量子计算领域具有重要的应用和研究价值。
量子计算中的Grover搜索算法及其应用潜力
量子计算中的Grover搜索算法及其应用潜力量子计算作为一种新兴的计算模式,拥有极高的计算速度和强大的并行处理能力,引起了广泛的关注。
Grover搜索算法作为量子计算中的一种重要算法,被广泛应用于数据搜索和优化问题的解决上。
本文将介绍Grover搜索算法的原理,探讨其在不同领域的应用潜力。
量子计算的出现带来了巨大的潜力,能够以数量级的速度执行任务。
然而,传统的计算机算法往往需要指数级的计算时间来解决一些问题,这限制了传统计算机在某些领域的应用。
Grover搜索算法的诞生填补了这一空白。
Grover搜索算法的核心思想是利用量子并行性和量子态叠加的特性,在一组数据中快速找到目标项。
传统的搜索算法需要遍历整个数据集,其时间复杂度为O(N),而Grover算法的时间复杂度只有O(√N),在某些情况下可以达到指数级的优势。
该算法的实现需要三个基本元素:量子态叠加、量子态干涉和量子态反转。
首先,通过叠加量子比特,将计算机的初始状态转化为量子态叠加的状态。
然后,通过量子干涉,将目标项与其他项进行干涉,使目标项的幅值加大,从而达到区分的目的。
最后,通过对量子态进行反转操作,使得目标项在度量的过程中概率更大地被测量出来,从而完成搜索。
Grover搜索算法的应用潜力非常广泛。
例如,在数据库搜索方面,传统的算法需要遍历整个数据库才能找到目标项,而Grover算法只需要O(√N)的时间复杂度,大大提高了搜索的效率。
在密码破解方面,Grover算法可以在较短的时间内找到一个密钥的可能值,从而加快破解的速度。
此外,Grover算法还可以用于图像识别、优化问题求解等领域。
然而,Grover搜索算法也存在一些限制。
首先,需要找到的目标项必须事先定义好,并且目标项的数量必须是唯一的。
其次,该算法的应用在大规模问题上面临着困难,因为Grover算法的时间复杂度依然是随问题规模的增加而线性增长的。
此外,由于量子计算的误差和噪声问题,实际应用中可能会出现误差积累、干涉消失等情况。
量子算法中的Grover搜索算法解析
量子算法中的Grover搜索算法解析量子计算作为一种新兴的计算模型,具有在某些特定问题上具有优势的潜力。
其中,Grover搜索算法是一种非常重要的量子算法,被广泛应用于搜索问题的求解。
本文将对Grover搜索算法进行详细解析,包括其原理、实现方法以及应用领域。
一、Grover搜索算法的原理Grover搜索算法是由美国计算机科学家Lov Grover于1996年提出的,用于在未排序的数据库中搜索目标元素。
与传统的经典搜索算法相比,Grover搜索算法具有更高的搜索效率。
Grover搜索算法的核心思想是利用量子叠加态和干涉效应,通过一系列的量子操作,将目标元素的概率幅度放大,从而实现更快速的搜索。
其基本步骤如下:1. 初始化:将n个量子比特初始化为均匀叠加态,即处于所有可能状态的叠加态。
2. 目标元素标记:通过一个特殊的量子门(称为标记相位翻转门),将目标元素的相位进行翻转,使其与其他元素区分开来。
3. 幅度放大:通过一系列的量子操作,将目标元素的概率幅度放大,同时抑制其他元素的概率幅度。
4. 重复操作:重复进行第2步和第3步,直到找到目标元素。
二、Grover搜索算法的实现方法Grover搜索算法的实现主要包括量子门的设计和量子操作的执行。
其中,量子门的设计是保证算法正确性的关键。
1. 标记相位翻转门:标记相位翻转门是Grover搜索算法中的关键操作,用于将目标元素的相位进行翻转。
其设计方法是通过目标元素的特征,构造一个特殊的量子门,使得目标元素的相位与其他元素不同。
2. 幅度放大操作:幅度放大操作是Grover搜索算法中的另一个关键操作,用于放大目标元素的概率幅度。
其设计方法是通过一系列的量子操作,使得目标元素的概率幅度逐步增大,同时抑制其他元素的概率幅度。
3. 量子操作的执行:量子操作的执行需要借助量子计算机或者量子模拟器。
在实际操作中,需要满足量子比特的高保真度和低误差率,以确保算法的正确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E= sin −
θ (z) θ (z)
2 2
q ⊥ + cos q⊥
cos E= +
q 2 θ (z) − 是绝热量子 N
θ (z)
这里我们稍作讨论,当 z = 0 时绝热量子系统 H ( 0 ) = H i ,此时 = φ 系 统 的 初 始 基 态 , 相 应 的 系 统 参 数 为 ∆ = 1, cos θ = −1 +
令
∆ (z) = cos θ (= z)
(1 − 2 z )
2
+
4 z (1 − z ) N
1 1 1 − 2 (1 − z ) 1 − N ∆ (z)
2 1 1 sin θ ( z ) = 1− (1 − z ) N ∆ (z) N
则 H ( z ) 有如下紧凑形式
收稿日期:2018年10月25日;录用日期:2018年11月6日;发布日期:2018年11月13日
摘
要
Grover量子搜索算法是近二十年最著名的量子算法,其已经被证明无法被任何经典算法所超越,展示出 极强的量子加速特性。Grover量子搜索算法可以被两种等价的途径所实现,即线路模型Grover算法和绝 热 Grover 算法。本文从绝热 Grover 算法的角度出发,运用变分法中广为人知的最速降线问题来探讨
Keywords
Grover’s Quantum Search Algorithm, Adiabatic Quantum Computation, Brachistochrone Problem
Grover量子搜索算法中的最速降线问题研究
崔晓东,刘存海,宿德志,柳 叶
海军航空大学,航空基础学院,理化教研室,山东 烟台
θ 1,= sin θ 0 , 意 味着 = 绝 热 量 子 系 统 H (1) = H q 并 查 询 到 目 标 态 q , 相 应 的 系 统 参 数 = 为 ∆ 1, cos
θ = 0 mod 2π 。由于绝热演化的基态 E− 是绝热量子计算唯一关心的态,那么我们将它稍作调整,令 θ= ( z ) α ( z ) + π ,则 H ( z ) 变为
文章引用: 崔晓东, 刘存海, 宿德志, 柳叶. Grover 量子搜索算法中的最速降线问题研究[J]. 应用物理, 2018, 8(11): 455-460. DOI: 10.12677/app.2018.811058
崔晓东 等
Grover量子搜索算法,得到了其量子加速特性的一个必要原因,这使得按照该算法的实质来设计其他量 子算法成为可能。
关键词
Grover量子搜索算法,绝热量子计算,最速降线问题
Copyright © 2018 by authors and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
首先,我们给出 Hilbert 空间的最速降线问题。
DOI: 10.12677/app.2018.811058 457
应用物理
崔晓东 等
问 题 : 给 定 N 维 Hilbert 空 间 N
ψ ( ⋅) ∈ : =
{
C⊂ | C (τ 1 ) = ψ 1 , C (τ 2
N
( )
θ (z)
2
q ⊥ − sin
θ (z)
2
q
(1)
而当 z = 1 时则恰处于所要查询的目标态 q 这样的好处是当 z = 0 时绝热量子系统处于平均态 φ 上, 上。 下面我们说明由(1)式所描述的绝热基态与变分法中广为熟知的最速降线问题的联系并给出本文结果。
3. 绝热 Grover 算法与最速降线问题
( N ) 。对 n 量子比特 Grover 量子搜索算法,其可搜索的条目总数为 N = 2
Hi = 1 − φ φ
n
。按照绝热
这里 1 表示单位矩阵, 平均态 φ = 被搜索到的概率都为
1 N
∑
x =0
N −1
x 表示初始时各条目 x ( x 0,1, 2, , N − 1) 处于等同地位, =
| x 0,1, 2, , N − 1} 代表要搜索的结果,称为目标态,则将编码该目标态到查询哈密顿 假定 q ∈ { x =
Hq 为
1 = ,同时 { x | x 0,1, 2, , N − 1} 构成一组标准正交基。 N
Hq = 1 − q q
则绝热演化哈密顿 H ( z ) 就可以描述为
H (z) = (1 − z ) H i + zH q
Open Access
1. 引言
1982 年,Feynman 提出了量子计算机的想法,其目的是克服经典计算机在模拟量子力学过程中经典 算法本质上存在的困难[1]。1994 年,Shor 提出了量子计算机的第一个量子算法[2],用于求极大整数的 因子分解,其效率明显优于目前的最先进的经典因子分解算法,但无法证明不存在经典算法比 Shor 量子 因子分解算法更高效。1997 年,Grover 量子搜索算法横空出世[3],打破了人们关于经典算法可以替代量 子算法的疑惑[4]。Grover 量子搜索算法可由量子线路模型和绝热量子计算两种等价的方法实现。简单地 讲,量子线路模型通过各种通用量子酉门的时序组合来编码并求解得到最终结果;而绝热量子计算则通 过制备初始哈密顿及其基态, 并将结果编码进查询哈密顿的基态, 在量子绝热定理的保证下来得到结果。 本文从绝热量子计算角度来探讨 Grover 量子搜索算法,得到了其量子加速特性的一个必要原因,这一结 果使得按照该算法的实质来设计其他量子算法成为可能。
2. 绝热 Grover 算法
在数据库中存在 N 个未排序的条目,这里 N 极大,目标是在这 N 个条目中找到指定的一个条目,并 且查询的次数最少。处理该问题时,经典算法的平均查询次数为 O ( N ) ,而 Grover 量子搜索算法的平均 查询次数仅为 O 量子计算的方法[5],初始哈密顿 H i 为
( ) 中的两个量子态 ψ ,ψ ,寻找一条测地线 0 ,其中 J ( ψ ( ⋅) ) 是关于 ψ ( ⋅) 的 ) = ψ } 使得 δ J ( ψ (⋅) ) =
1 2
2
一个指标泛函。 上述问题是变分法中的最速降线问题在 Hilbert 空间中的一般描述,它的提出与绝热量子计算是有联 系的,因为实际上问题中的 ψ 1 和 ψ 2 分别对应绝热量子计算的平均态 φ 和目标态 q ,找到了最速降 线也就找到了使得平均态 φ 到达目标态 q 的最快路径。问题的核心在与如何确定指标泛函 J ψ ( ⋅) , 而这需要考察量子态的物理。 由于归一化量子态的物理等价性, 即 ψ 和c ψ 空间 因此对于 N 维 Hilbert ( c = 1) 描述的是同一个物理态,
= H ( z)
相应地, E− 变为
= E− cos
2 2 N −1 , sin θ = ,当 N 足够大时, N N cos θ ≈ −1, sin θ ≈ 0 意味着 θ ≈ π ;依据量子绝热定理, E− 应始终是绝热演化过程的基态,且当 z = 1 时
1 ∆ ( z ) cos α ( z ) sin α ( z ) − 2 2 sin α ( z ) − cos α ( z )
Applied Physics 应用物理, 2018, 8(11), 455-460 Published Online November 2018 in Hans. /journal/app https:///10.12677/app.2018.811058
th th th
Abstract
Grover’s quantum search algorithm is the most famous quantum algorithm in the last twenty years, which exhibits a strong quantum speedup and has been proved not to be able to be outperformed by any classical algorithm. Grover’s quantum search algorithm can be implemented by two equivalent ways, which are circuit model Grover’s algorithm and adiabatic Grover’s algorithm, and the latter is the start point of the paper. We here apply the well-known brachistochrone problem in calculus of variations to investigate and obtain a necessary condition of Grover’s quantum search algorithm, which makes possible to design new efficient quantum algorithms.
由于 q 与其他 x , x ≠ q 都正交,故可将绝热演化哈密顿 H ( z ) 在 q 与其正交态 q ⊥ =
1 ∑x N − 1 x≠q
应用物理
DOI: 10.12677/app.2018.811058
456
崔晓东 等
构成的子空间上表示出来,有
1 1 1 1− −1 + 2 (1 − z ) 1 − 2 (1 − z ) N N 1 1 N = − H (z) 2 2 1 1 1 1− 1 − 2 (1 − z ) 1 − 2 (1 − z ) N N N
