[精选PPT]物理 振动阻尼与受迫振动及振动合成
合集下载
高中物理 1.4 阻尼振动 受迫振动课件
❖ 答案 不变．周期与振幅无关．
预习导学
❖ 二、受迫振动
❖ 1．驱动周力期：性
的外力．
❖ 2．受迫振动：驱系动统力在 动．
作用下的振
驱动力
❖ 3 ． 振 动 稳 定 后 受 迫 振 没动有的 周 期 总 等 于 的周期，受迫振动稳定后的频率与物体的固 有频率 等于关系．
❖ 三、共振
共振
❖ 驱动力的频率
预习导学 课堂讲义 对点练习
[探背景]
第4讲 阻尼振动 受迫振动
本文选自《汉字王国》。该书以图文并茂的形式讲述中国文字的起源和特点，
选取 200 多个与人的生活有关的字进行细致的讲解，如与人的身体、住房、器
皿、丝和麻、家畜、农具、车船、道路等有关的字，同时分析和描述中国人的
生活方式和风俗习惯，从而使人加深对文字的理解，把学术性与趣味性熔于一
这会让孩子们学习语文、学习国语的积极性、自觉性和趣味性，得到空前推进
和提升，正如歌曲《中国话》所唱到的，“最爱说的话永远是中国话，字正腔圆
落地有声说话最算话；最爱写的字是先生教的方块字，横平竖直堂堂正正做人
要像它”。高考语文分数增加，可以让祖国语言文字自豪感、民族文化自豪感、
民族文化自信力，得到现代化的继承和发扬光大。
【答案】 (1)清楚 (2)清晰
预习导学 课堂讲义 对点练习
第4讲 阻尼振动 受迫振动
第 4 步辨熟语——于细微处细斟酌 请判断下列加点的成语使用是否正确。 (1)这里的森林遭到严重破坏，由于经济贫困，群众生态保护意识淡薄，过 度开发，导致土壤严重流失，沙漠化的土地荒．无．人．烟．。( ) 理由：
预习导学 课堂讲义 对点练习
第 3 步用词语——送你一双慧眼
第4讲 阻尼振动 受迫振动
预习导学
❖ 二、受迫振动
❖ 1．驱动周力期：性
的外力．
❖ 2．受迫振动：驱系动统力在 动．
作用下的振
驱动力
❖ 3 ． 振 动 稳 定 后 受 迫 振 没动有的 周 期 总 等 于 的周期，受迫振动稳定后的频率与物体的固 有频率 等于关系．
❖ 三、共振
共振
❖ 驱动力的频率
预习导学 课堂讲义 对点练习
[探背景]
第4讲 阻尼振动 受迫振动
本文选自《汉字王国》。该书以图文并茂的形式讲述中国文字的起源和特点，
选取 200 多个与人的生活有关的字进行细致的讲解，如与人的身体、住房、器
皿、丝和麻、家畜、农具、车船、道路等有关的字，同时分析和描述中国人的
生活方式和风俗习惯，从而使人加深对文字的理解，把学术性与趣味性熔于一
这会让孩子们学习语文、学习国语的积极性、自觉性和趣味性，得到空前推进
和提升，正如歌曲《中国话》所唱到的，“最爱说的话永远是中国话，字正腔圆
落地有声说话最算话；最爱写的字是先生教的方块字，横平竖直堂堂正正做人
要像它”。高考语文分数增加，可以让祖国语言文字自豪感、民族文化自豪感、
民族文化自信力，得到现代化的继承和发扬光大。
【答案】 (1)清楚 (2)清晰
预习导学 课堂讲义 对点练习
第4讲 阻尼振动 受迫振动
第 4 步辨熟语——于细微处细斟酌 请判断下列加点的成语使用是否正确。 (1)这里的森林遭到严重破坏，由于经济贫困，群众生态保护意识淡薄，过 度开发，导致土壤严重流失，沙漠化的土地荒．无．人．烟．。( ) 理由：
预习导学 课堂讲义 对点练习
第 3 步用词语——送你一双慧眼
第4讲 阻尼振动 受迫振动
物理 第6章 振动2(阻尼与受迫振动及振动合成)
10
（3）共振的危害与利用
危害：军队过桥的情况、火车速度的限制，……
利用：超声清洗、音箱设计、振荡电路、核磁共 振……
塔科马海峡桥的倒塌
11
§6.6 同一直线上同频率简谐运动的合成 1. 分振动: x1 A1 cos( t 1 ) x2 A2 cos( t 2 ) 2. 合振动: x x1 x2 A1 cos( t 1 ) A2 cos( t 2 )
故所求的合振动表达式为
4 x 5 cos( 2t ) 5
cm
21
（2）当 3 1 2k
(k 0,1,2,) 时
即x1与x3相位相同时，合振动的振幅最大， 由于 1 故
3 2k
(k 0,1,2,)
当 3 1 (2k 1)
(k 0,1,2,) 时
即x1与x3相位相反时，合振动的振幅最小， 由于 1 故 3 (2k 1) 即
(k 0,1,2,)
3 2k
(k 0,1,2,)
22
§6.7 同一直线上不同频率简谐运动的合成 x1 A1 cosω1 t 1. 分振动: x2 A2 cosω2t A2 A 2. 合振动: x x1 x2 当 (ω2 ω1 ) t 2kπ 3
时间常量与品质因数： 在欠阻尼情况下， 振幅
振动能量E： E
A A0e
t
E0 e
2 t
( E A2 )
时间常量
1 2
（振动系统的能量减 小到起始能量的1/e时 所经过的时间）
（时间常量内振动 次数的2倍）
稳定受迫振动的运动方程65受迫振动共振驱动力的角频率受迫振动的振幅由系统的固有频率w阻尼系数以及驱动力幅h决定对一定的振动系统改变驱动力的频率w当驱动力频率为某一值时振幅会达到极大值特点
（3）共振的危害与利用
危害：军队过桥的情况、火车速度的限制，……
利用：超声清洗、音箱设计、振荡电路、核磁共 振……
塔科马海峡桥的倒塌
11
§6.6 同一直线上同频率简谐运动的合成 1. 分振动: x1 A1 cos( t 1 ) x2 A2 cos( t 2 ) 2. 合振动: x x1 x2 A1 cos( t 1 ) A2 cos( t 2 )
故所求的合振动表达式为
4 x 5 cos( 2t ) 5
cm
21
（2）当 3 1 2k
(k 0,1,2,) 时
即x1与x3相位相同时，合振动的振幅最大， 由于 1 故
3 2k
(k 0,1,2,)
当 3 1 (2k 1)
(k 0,1,2,) 时
即x1与x3相位相反时，合振动的振幅最小， 由于 1 故 3 (2k 1) 即
(k 0,1,2,)
3 2k
(k 0,1,2,)
22
§6.7 同一直线上不同频率简谐运动的合成 x1 A1 cosω1 t 1. 分振动: x2 A2 cosω2t A2 A 2. 合振动: x x1 x2 当 (ω2 ω1 ) t 2kπ 3
时间常量与品质因数： 在欠阻尼情况下， 振幅
振动能量E： E
A A0e
t
E0 e
2 t
( E A2 )
时间常量
1 2
（振动系统的能量减 小到起始能量的1/e时 所经过的时间）
（时间常量内振动 次数的2倍）
稳定受迫振动的运动方程65受迫振动共振驱动力的角频率受迫振动的振幅由系统的固有频率w阻尼系数以及驱动力幅h决定对一定的振动系统改变驱动力的频率w当驱动力频率为某一值时振幅会达到极大值特点
阻尼受迫振动振动合成课件——大连理工大学
二、单摆
一根长为L的无伸缩得细线,上端固定,下端悬挂一个很小的重 物(其线度<<L,可视为质点),质量为m,将重物略加移动后,重物 就在竖直平面内来回摆动,这种装置称为单摆。 `O——平衡位置 O 平衡位置 `单摆右偏时θ为正，左偏θ为 单摆右偏时θ 单摆右偏时 为正，左偏θ θ 负。 l `重力产生的回复力矩： 重力产生的回复力矩： 重力产生的回复力矩 ` M=－mgsinθ·l M=－mgsinθ l mgsinθ 0 p mgcosθ `“－”：力矩方向与角位移θ方向 力矩方向与角位移θ － 相 M = Jβ = ml2 ⋅ β 反。 有转动定律： 有转动定律：
o
t
(b) β 〉ω0 , β = ω0
时的阻尼振动
（3）当β
= ω0 时：临界阻尼状态
（也不发生振动） 也不发生振动）
ξ (t) = ( At + B)e−βt
方程（ ）解为： 方程（1）解为：
一单摆的摆球在一粘滞性很大的油中运动（例蓖麻油）， 例如 一单摆的摆球在一粘滞性很大的油中运动（例蓖麻油）， 小球只会逐渐回到平衡位置，而不会摆到另一边去， 小球只会逐渐回到平衡位置，而不会摆到另一边去，当它回到 平衡位置时，所具有的能量都已消耗在阻尼上了。 平衡位置时，所具有的能量都已消耗在阻尼上了。 如果阻尼刚好大到使摆球不能振动的程度，称临界阻尼。 如果阻尼刚好大到使摆球不能振动的程度，称临界阻尼。 超过这个程度：过阻尼。 超过这个程度：过阻尼。
b
f
x o′
ξ
∑F=mg-kx =kb-kx =-k(x-b) =-kξ
物体受到的力就是回复力和阻尼力的合力：
P
ξ
dξ d 2ξ − kξ − r =m 2 dt dt
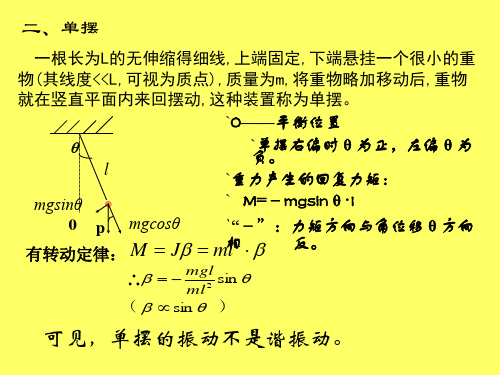
一根长为L的无伸缩得细线,上端固定,下端悬挂一个很小的重 物(其线度<<L,可视为质点),质量为m,将重物略加移动后,重物 就在竖直平面内来回摆动,这种装置称为单摆。 `O——平衡位置 O 平衡位置 `单摆右偏时θ为正，左偏θ为 单摆右偏时θ 单摆右偏时 为正，左偏θ θ 负。 l `重力产生的回复力矩： 重力产生的回复力矩： 重力产生的回复力矩 ` M=－mgsinθ·l M=－mgsinθ l mgsinθ 0 p mgcosθ `“－”：力矩方向与角位移θ方向 力矩方向与角位移θ － 相 M = Jβ = ml2 ⋅ β 反。 有转动定律： 有转动定律：
o
t
(b) β 〉ω0 , β = ω0
时的阻尼振动
（3）当β
= ω0 时：临界阻尼状态
（也不发生振动） 也不发生振动）
ξ (t) = ( At + B)e−βt
方程（ ）解为： 方程（1）解为：
一单摆的摆球在一粘滞性很大的油中运动（例蓖麻油）， 例如 一单摆的摆球在一粘滞性很大的油中运动（例蓖麻油）， 小球只会逐渐回到平衡位置，而不会摆到另一边去， 小球只会逐渐回到平衡位置，而不会摆到另一边去，当它回到 平衡位置时，所具有的能量都已消耗在阻尼上了。 平衡位置时，所具有的能量都已消耗在阻尼上了。 如果阻尼刚好大到使摆球不能振动的程度，称临界阻尼。 如果阻尼刚好大到使摆球不能振动的程度，称临界阻尼。 超过这个程度：过阻尼。 超过这个程度：过阻尼。
b
f
x o′
ξ
∑F=mg-kx =kb-kx =-k(x-b) =-kξ
物体受到的力就是回复力和阻尼力的合力：
P
ξ
dξ d 2ξ − kξ − r =m 2 dt dt
阻尼振动和受迫振动ppt课件
但是，随着振幅的增大，阻力的功率也不 断增大，最后与强迫力的功率相抵，从而 使振幅保持恒定。从能量观点看在共振时， 这能量转变为共振质点的能量，也叫共振 吸收。
陆果一书讨论阻尼弹簧振子的相图。p168
21
通常称 A p 与 p 的关系曲线为频率响应曲线。
当 Ap maxAp()/ 2时，即相对振幅为 0.707 (即相对强度为1/2) 处曲线宽度，定义为共振 峰的宽度 或共振带宽。可证明在弱阻尼的情
18
讨论：p 0, ApH p /2mp h2 较小
p 0,
H/m H
Ap 2 0
k
p0, Ap 2 H/ m 0 若很小，A p 很大。
3-2 共振
求振幅 Ap 得出
h
对频率的极值，
(02p2)242p2
振幅有极大值：
Ar 2
h
02 2
共振的振幅。
pr 02 22 共振的角频率。
19
pr 02 22 共振的角频率。
k2 A20co 2xsd x1k2 A
2T0 0
4
4
求出势能的时间平均值:
E pT 10 T1 2k2 A co 2(s0t0)d t
k2 A20co 2xsd x1k2 A
2T0 0
4
结论：
* 即弹簧振子的动能和势能的平均值相等，且 等于总机械能的一半
* 任一简谐振动总能量与振幅的平方成正比
co s co s2 co s co s
2
2
合成振动表达式：
x ( t) A co 1 t s ) A (co 2 t s )(
30
附录：三角函数关系式的证明
4 cos cos
22
陆果一书讨论阻尼弹簧振子的相图。p168
21
通常称 A p 与 p 的关系曲线为频率响应曲线。
当 Ap maxAp()/ 2时，即相对振幅为 0.707 (即相对强度为1/2) 处曲线宽度，定义为共振 峰的宽度 或共振带宽。可证明在弱阻尼的情
18
讨论：p 0, ApH p /2mp h2 较小
p 0,
H/m H
Ap 2 0
k
p0, Ap 2 H/ m 0 若很小，A p 很大。
3-2 共振
求振幅 Ap 得出
h
对频率的极值，
(02p2)242p2
振幅有极大值：
Ar 2
h
02 2
共振的振幅。
pr 02 22 共振的角频率。
19
pr 02 22 共振的角频率。
k2 A20co 2xsd x1k2 A
2T0 0
4
4
求出势能的时间平均值:
E pT 10 T1 2k2 A co 2(s0t0)d t
k2 A20co 2xsd x1k2 A
2T0 0
4
结论：
* 即弹簧振子的动能和势能的平均值相等，且 等于总机械能的一半
* 任一简谐振动总能量与振幅的平方成正比
co s co s2 co s co s
2
2
合成振动表达式：
x ( t) A co 1 t s ) A (co 2 t s )(
30
附录：三角函数关系式的证明
4 cos cos
22
大学物理机械振动课件
03 阻尼振动
阻尼振动的定义与特点
定义
阻尼振动是指振动系统受到阻力 作用，使得振动能量逐渐减少的
振动过程。
特点
随着时间的推移，振幅逐渐减小， 频率逐渐降低，直至振动停止。
阻尼力
阻尼振动过程中，系统受到的阻力 称为阻尼力，它与振动速度成正比， 方向与振动速度方向相反。
阻尼振动的描述方法
微分方程
阻尼振动的运动方程通常表示为二阶常微分方程，形式为 `m * d²x/dt² + c * dx/dt + k * x = 0`，其中 m、c、k 分别为质量、
振动压路机
利用共振原理来提高压实效果。
振动输送机
利用共振来输送物料，提高输送效率。
受迫振动与共振的能量转换
能量转换过程
外界周期性力对系统做正 功，系统动能增加；阻尼 使系统能量耗散，系统势 能减小。
转换关系
在振动过程中，外界对系 统的总能量输入等于系统 动能和势能的变化之和。
影响因素
阻尼系数、驱动力频率、 物体固有频率等。
能量耗散途径
阻尼振动的能量耗散途径 主要包括与周围介质之间 的摩擦、空气阻力、内部 摩擦等。
能量耗散的意义
阻尼振动的能量耗散有助 于减小系统振幅，避免因 过大振幅导致的结构破坏 或噪声污染等问题。
04 受迫振动与共振
受迫振动的定义与特点
定义：在外来周期性力的持 续作用下，物体发生的振动
称为受迫振动。
确定各简谐振动的振幅、相位差和频 率，在复平面内绘制振动相量，通过 旋转和位移操作找到合成振动的相量 表示。
振动合成的能量法
描述
能量法是通过分析各简谐振动的能量分布和转化，来研究振 动合成过程中的能量传递和平衡。
【正式版】阻尼振动受迫振动共振PPT
T 2 2 m
K
由于振动系统要不断克服阻力作功，所以要逐渐
损耗振动的能量使振幅逐渐变小直至振动停止。
1.阻尼振动方程（低速）
以弹簧一维振动为例
振动系统受介质的粘滞阻力与速度大小成正比，
与其方向相反。
v
fr
v
dx dt
F弹, f x
FF弹frk xv ma o x
d2x mdt2
k
x
dx dt
弹性力或准弹性力和上述阻力作用下的动力学方程：
阻尼振动受迫振动 共振
一、阻尼振动
实际振动过程存在着阻力，这种由弹性恢复力和阻 力共同作用的振动叫阻尼振动。
•当物体低速运动时，阻力 f cv
弹簧、单摆振动过程，受到的阻力与速度正比反向。
•当物体高速运动时，阻力 f cv2
子弹运动、卫星发射过程，受到的阻力与速度平方正
比反向。 • 无阻尼的自由振动 • 谐振子的阻尼振动
2 在受迫振动中，振子因外力对它作功而获得能量，同时又因有阻尼而损耗能量。
第二项为策动力产生的周期振动。
dx dx 受迫振动方程---二阶常系数非齐次微分方程
2
2 xhco ts 2 0 在阻尼振动中，要维持振动，外界需加一个周期的强迫力------策动力。
弹簧、单摆振动过程，受到的阻力与速度正比反向。
d d22 xtm d dx t m kxH mcop st
k H 2
临界阻尼情况是振动系统刚刚不能作准周期振动，而很快回到平衡位置的情况，应用在天平调衡中。
令 2 , , h 两项都衰减，不是周期振动。
0
m m m 受迫振动方程---二阶常系数非齐次微分方程
受迫振动可以看成是两个振动合成的。
大学物理-12第十二讲简谐振动的合成、阻尼、受迫振动（001）
解得 ω = ωr = ω02 − 2β 2
则
A=
2mβ
F0
ω02 − β 2
= Amax
A
β2 β3
β1
ω
β1 > βω2 0> β3
23
2.速度共振—使速度振幅达最大值的状态
v = dx = − Aω sin(ωt − δ )
dt
速度振幅 vm = Aω
而 Aω =
F0ω
m (ω02 − ω2 ) + 4β 2ω2
●合振幅A的大小由两个分振动的初相差决定。
当 Δϕ = ϕ2 − ϕ1 = ±2kπ
(k = 0，1，2") 同相
Y ωK
A2
ωK
A ωK
A = A1 + A2 = Amax
θ2
Δθ θ1
A1
合振动加强
x2 θ x1 x x
4
当 Δϕ = ϕ2 −ϕ1 = ±(2k +1)π 反相
(k = 0，1，2")
ϕ =0
t
19
2. β =ω0（临界阻尼） x = e −βt (C1 + C 2t)
●在临界阻尼时，质点到达平衡位置时速度即减为 零，振动不可能发生。
◆原理常用于阻尼天平等，以减少摆动时间.
3. β >ω0（过阻尼）
x = e − βt (C 1e ω1t + C 2 e −ω1t )
●过阻尼时，质点的速度 x
F强 = F0 cosωt
v = dx = Aω cos ωt v与强迫力同位相。
dt
●在整个周期内外力的方向和物体运动方向一致， 不断对物体作正功，使振动最强。 ◆外力的周期性变化与物体的固有振动“合拍”。
阻尼振动和受迫振动简介分析ppt课件.ppt
4
大学物理 第三次修订本
第6章 机械振动基础
受迫振动微分方程的稳态解为
x Acos(t ) 为驱动力角频率。
为受迫振动与驱动力之间的相位差。
A
f
(02 2 ) 4n22
tan
2n 02 2
受迫振动是谐振动，其角频率与驱动力
的角频率相同。
受迫振动的振幅 A， 以及它与驱动力间
的相位差，都与起始条件无关。
第6章 机械振动基础
令 / m 2n,2 k / m
d2 dt
x
2
2n
dx dt
2
x
0
n — 阻尼常量
阻尼振动运动方程
x Aent cos( 2 n2 t )
振幅衰减随时间按指数衰减。
角频率 2 n2
1
大学物理 第三次修订本
第6章 机械振动基础
x Aent cos(' t )
' 2 n2
r越接近于系统的 固有频率 0 ，同
时共振振幅 Ar也 越大。
共振频率
A 小阻尼
0阻尼
大阻尼
o
r0
P
7
大学物理 第三次修订本
第6章 机械振动基础
1940年11月,华盛顿州的Tacoma Narrows 桥, 由于桥面刚度太差,在45 mph风速的情形下,产 生“Galloping Gertie”(驰振）.
三种阻尼情况
（1）小阻尼 2 n2
x 阻尼振动位移时间曲线
A
Aent
Aent cos t
O
t
( 0)
A
（2）大阻尼 2 n2 x
三种阻尼
b
（3）临界阻尼 2 n2
阻尼振动及受迫振动 3
§9.3阻尼振动和受迫振动一. 阻尼振动1. 阻尼力x μf-=2. 振动的微分方程(以弹簧振子为例)x μkx x m--=022=++x ωx n x 阻尼系数: 2 n = μ/ m3. 阻尼振动的振动方程、表达式和振动曲线（2）过阻尼和临界阻尼（1）小阻尼( n 2 < ω02 ))cos(220ϕ+-=-t n ωAex nt202ω=n 202ω>n 临界阻尼:过阻尼:在过阻尼和临界阻尼时,无振动.1.振幅特点振幅随t 衰减2.周期特点阻尼振动的特点:严格讲，阻尼振动不是周期性振动，更不是简谐振动，但阻尼振动有某种重复性。
质点经一次完全振动所经历的时间称为衰减振动的周期>220π2nT -='ω0π2ω=T二.受迫振动（在外来策动力作用下的振动）1. 系统受力弹性力阻尼力xμ-周期性策动力tF x μkx x m cos 0ω+--= kx -2. 受迫振动的微分方程tf x x n x ωωcos 220=++ tF F ωcos 0=其中mF f mn mk 002===μωFkxF 1-=x μF2-=3.受迫振动微分方程的稳态解为:)cos(ϕ-=t ωA x 下面用旋转矢量叠加的方法求稳态的解振幅和初相(将稳态解代入到振动微分方程中有) :tωf t ωA ωt ωA n t ωA ω cos ) cos( ) sin( 2) cos( 202=-+----ϕϕωϕ令( 同时画出t 时刻对应的矢量图)：tωf t y cos )(=[y ( t )]f)π cos()(21+-=ϕt ωA ωt yϕ[y 1 ( t )]2A ω)2/π cos( 2)(2+-=ϕt ωnA ωt y [y 2 ( t )]2A n ω)cos()(203ϕ-=t ωA ωt y [y 3 ( t )]20A ω因而：)()()()(321t y t y t y t y ++=根据t 时刻的旋转矢量图，可得稳态时的振幅和初相：2/1222202]4)[(ωn ωωfA +-=2202tan ωωn ω-=ϕ（1）位移共振(振幅取极值)讨论（振幅共振曲线）共振频率:2202nr -=ωω共振振幅:2202nn fA r -=ω结论:受迫振动的振幅A 及受迫振动与驱动力的相位差ϕ都与起始条件无关。