人教新课标六年级数学下册第三单元1第三课时圆柱的体积课件
合集下载
六年级数学下册课件3.1.3圆柱的体积人教版共20张PPT
答:这个圆柱的体积是785立方厘米
分享收获
这节课我收获 了……
这节课我知道 了……
0.9米=90厘米
V=Sh
=75×90 =6750(立方厘米) 答:它的体积是6750立方厘米。
解决问题
2、一根圆柱形的木料,横截面的半径是5厘米, 长是150厘米。这根木料的体积是多少立方厘米?
3.14×5²×150
=3.14×25×150
150cm
=78.5×150
=11775(cm³)
5cm
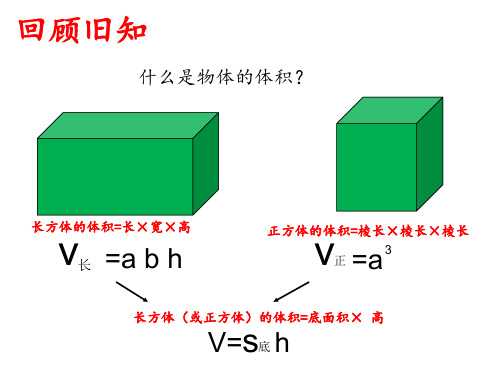
回顾旧知
什么是物体的体积?
长方体的体积=长×宽×高
v长 =a b h
正方体的体积=棱长×棱长×棱长
v正 =a3
长方体(或正方体)的体积=底面积× 高
V=s底 h
怎样求水泥 柱的体积呢?
下面长方体、正方体和圆柱的底面积都相等,高 也相等
想一想:谁和谁的体积相等?为什高么? 猜一猜:圆柱的体积和长方体、正方体的体积相等吗?
S=π r 2
r
πr
S=πr ×r =π r 2
自主探究
以小组为单位,结合手中的学具,探究圆柱的体 积
温馨提示: 1、圆柱体可以转化成已经学过的那种立体图形? 2、观察转化后的立体图形与原来的圆柱体有什么 关系?
如果把底面平均分的份数越多,结果会怎样呢?
把圆柱的底面平均分的份数越多,切拼 成的立体图形越接近长方体。
答:这根木料的体积是11775 cm³
解决问题
3、李家庄挖了一口圆柱形水井,地面 以下的井深10m,底面直径为1m。挖出 的土有多少立方米?
3.14 ×(1 ÷2)² ×10 =3.14 ×0.5² ×10 =3.14 ×0.25 ×10 =0.785 ×10 =7.85(m³)
分享收获
这节课我收获 了……
这节课我知道 了……
0.9米=90厘米
V=Sh
=75×90 =6750(立方厘米) 答:它的体积是6750立方厘米。
解决问题
2、一根圆柱形的木料,横截面的半径是5厘米, 长是150厘米。这根木料的体积是多少立方厘米?
3.14×5²×150
=3.14×25×150
150cm
=78.5×150
=11775(cm³)
5cm
回顾旧知
什么是物体的体积?
长方体的体积=长×宽×高
v长 =a b h
正方体的体积=棱长×棱长×棱长
v正 =a3
长方体(或正方体)的体积=底面积× 高
V=s底 h
怎样求水泥 柱的体积呢?
下面长方体、正方体和圆柱的底面积都相等,高 也相等
想一想:谁和谁的体积相等?为什高么? 猜一猜:圆柱的体积和长方体、正方体的体积相等吗?
S=π r 2
r
πr
S=πr ×r =π r 2
自主探究
以小组为单位,结合手中的学具,探究圆柱的体 积
温馨提示: 1、圆柱体可以转化成已经学过的那种立体图形? 2、观察转化后的立体图形与原来的圆柱体有什么 关系?
如果把底面平均分的份数越多,结果会怎样呢?
把圆柱的底面平均分的份数越多,切拼 成的立体图形越接近长方体。
答:这根木料的体积是11775 cm³
解决问题
3、李家庄挖了一口圆柱形水井,地面 以下的井深10m,底面直径为1m。挖出 的土有多少立方米?
3.14 ×(1 ÷2)² ×10 =3.14 ×0.5² ×10 =3.14 ×0.25 ×10 =0.785 ×10 =7.85(m³)
人教版小学数学六年级下册 第三课 圆柱的体积(课件)

3.14×(40÷2)2×50 = 3.14×400×50 = 62800(cm3) = 62.8 (L) 答:它的容积是62.8升。
0.85×62.8=53.38(千克)
答:这个油桶可 装53.38千克柴油。
拓展提高
有一块长方形的铁皮,按图剪下阴影 部分,正好制成一个圆柱形状的油漆 桶,这个油漆桶的容积是多少?
杯子的底面积: 3.14 ×(8÷2)2 =3.14 ×16 =50.24(cm3)
杯子的容积: 50.24 ×15=753.6( cm3 )
= 0.7536(L) 1L > 0.7536 L 答:带这杯水不够。
探究新知
一个直径是8cm的瓶子里,水的高度是7cm, 把瓶盖拧紧倒置放平,无水部分是圆柱形, 高度是18cm。这个瓶子的容积是多少?
作业布置 教材29页7、10、12题。
板书设计
圆柱的体积
圆柱的体积=底面积×高 V=Sh
容积是指容器所能容纳物体的体积。
同桌比赛: 看谁做得又对又快。
探究新知
这个瓶子不是一个 完整的圆柱,无法 直接计算容积。
能不能转化 成圆柱呢?
瓶子里水的体积倒置后没变, 水的体积加上18cm高圆柱的 体积就是瓶子的容积。
探究新知
也就是把瓶子的容积转 化成了两个圆柱的容积。
3.14 × (8 ÷2 )2 ×7+3.14 × (8 ÷2 )2 ×18 =3.14 ×16 ×(7+18) = 3.14 ×16 ×25 =1256( cm3 ) =1256(mL) 答:这个瓶子的容积是1256mL。
男女生比ቤተ መጻሕፍቲ ባይዱ:看谁做的又对又快。
探究新知
容积是指容器所能容纳物体的体积
杯子的底面积: 3.14 ×(8÷2)2 =3.14 ×16 =50.24(cm3)
人教版六年级数学下册第三单元圆柱与圆锥-圆柱的体积PPT课件

说一说:根据圆柱的体积公式,"你知道哪些条件就可以求出圆
柱的体积?
V =Sh
底面半径和高: V=πr2h
2
2h
V=π
(
)
底面直径和高:
底面周长和高: V=π(
2
)2h
课堂练习
李家庄挖了一口圆柱形井,地面以下的井深10m底面直径为1m。挖出
的土有多少立方米?
已知底面直径和高求圆柱体积。
2
V=π( )2h
两个花坛的体积
7.065×0.5×2=3.5325×2=7.065(m³)
答:两个花坛中共需要填土7.065立方米。
课堂小结
圆柱的体积
V =sh
V=πr2h
2
ቤተ መጻሕፍቲ ባይዱ
V=π( )2h
V=π(
2
)2h
第3单元 圆柱与圆锥
课 程 结 束
人教版部编版六年级数学下册
授课老师:xx
= 3.14×(1÷2)2×10
= 7.85(立方米)
答:挖出的土有7.85立方米。
课堂练习
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
8cm
杯子的底面积:
3.14 ×(8÷2)2
=3.14 ×16
=50.24(cm3)
杯子的容积:
50.24 ×10
10cm
思考:1.已知什么?2.要求什么?3.要注意什么?
=0.628(m3)
0.628÷0.02=31.4(张)
答:这根木料最多能做31张课桌。
课堂练习
一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重
柱的体积?
V =Sh
底面半径和高: V=πr2h
2
2h
V=π
(
)
底面直径和高:
底面周长和高: V=π(
2
)2h
课堂练习
李家庄挖了一口圆柱形井,地面以下的井深10m底面直径为1m。挖出
的土有多少立方米?
已知底面直径和高求圆柱体积。
2
V=π( )2h
两个花坛的体积
7.065×0.5×2=3.5325×2=7.065(m³)
答:两个花坛中共需要填土7.065立方米。
课堂小结
圆柱的体积
V =sh
V=πr2h
2
ቤተ መጻሕፍቲ ባይዱ
V=π( )2h
V=π(
2
)2h
第3单元 圆柱与圆锥
课 程 结 束
人教版部编版六年级数学下册
授课老师:xx
= 3.14×(1÷2)2×10
= 7.85(立方米)
答:挖出的土有7.85立方米。
课堂练习
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
8cm
杯子的底面积:
3.14 ×(8÷2)2
=3.14 ×16
=50.24(cm3)
杯子的容积:
50.24 ×10
10cm
思考:1.已知什么?2.要求什么?3.要注意什么?
=0.628(m3)
0.628÷0.02=31.4(张)
答:这根木料最多能做31张课桌。
课堂练习
一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重
数学六年级下人教新课标版3-1-3圆柱的体积课件(12张)

=395.64毫升 答:这杯茶有395.64毫升。
请完成教材第26页做一做第2题,第28页练习五 第5题、第8题、第10题。
归纳总结:
圆柱形容器的容积的计算方法与体积的 计算方法相同,只是所需数据必须从容器的 里面测量。
小试牛刀
小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面
量底面直径是8cm,高是15cm。如果两人游玩期间要喝
1L水,带这杯水够喝吗?
保温杯的底面积: 3.14×(8÷2)2
= 3.14×42
= 3.14×16
A 表面积
B 体积
C 容积
D占地面积
(2)下面( B )杯中的饮料最多。
(1)容积的计算方法和体积的计算方法完全 相同。 ( × )
(2)容积的单位只有升和毫升。 ( × ) (3)一个纸盒的体积是6立方分米,它的容积
也是6立方分米。( × )
妈妈的茶杯形状如下图,一天豆豆给妈妈倒满一 杯茶,这杯茶有多少毫升?(杯子厚度忽略不计) 6÷2=3(厘米) 3.14×3ቤተ መጻሕፍቲ ባይዱ=28.26(平方厘米) 28.26×14=395.64(立方厘米)
3 圆柱与圆锥
3.1.3 圆柱的体积(2)
我们已经学习了圆柱体积的计算公式,能说 一说推导过程吗?
底面积
高
高
圆柱体积=底面积×高 V=Sh=πr2h
1 课堂探究点
利用圆柱的体积公式求容积
2 课时流程
探索 新知
课堂 小结
当堂 检测
课后 作业
10cm
探究点 利用圆柱的体积公式求容积
下图中的杯子能不能装下这袋牛奶?(数据是从杯子 里面测量得到的。)
8cm
请先自杯己子独的立容解积答。,然请后你同想桌一之想间,交要流回。 答这个问题,先要 计算出什么?
请完成教材第26页做一做第2题,第28页练习五 第5题、第8题、第10题。
归纳总结:
圆柱形容器的容积的计算方法与体积的 计算方法相同,只是所需数据必须从容器的 里面测量。
小试牛刀
小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面
量底面直径是8cm,高是15cm。如果两人游玩期间要喝
1L水,带这杯水够喝吗?
保温杯的底面积: 3.14×(8÷2)2
= 3.14×42
= 3.14×16
A 表面积
B 体积
C 容积
D占地面积
(2)下面( B )杯中的饮料最多。
(1)容积的计算方法和体积的计算方法完全 相同。 ( × )
(2)容积的单位只有升和毫升。 ( × ) (3)一个纸盒的体积是6立方分米,它的容积
也是6立方分米。( × )
妈妈的茶杯形状如下图,一天豆豆给妈妈倒满一 杯茶,这杯茶有多少毫升?(杯子厚度忽略不计) 6÷2=3(厘米) 3.14×3ቤተ መጻሕፍቲ ባይዱ=28.26(平方厘米) 28.26×14=395.64(立方厘米)
3 圆柱与圆锥
3.1.3 圆柱的体积(2)
我们已经学习了圆柱体积的计算公式,能说 一说推导过程吗?
底面积
高
高
圆柱体积=底面积×高 V=Sh=πr2h
1 课堂探究点
利用圆柱的体积公式求容积
2 课时流程
探索 新知
课堂 小结
当堂 检测
课后 作业
10cm
探究点 利用圆柱的体积公式求容积
下图中的杯子能不能装下这袋牛奶?(数据是从杯子 里面测量得到的。)
8cm
请先自杯己子独的立容解积答。,然请后你同想桌一之想间,交要流回。 答这个问题,先要 计算出什么?
六年级数学下册课件-3.1.3 圆柱的体积24-人教版(共53张PPT) (1)

桶能装140千克水吗?
谈一谈,通过本节课的学习, 你又有什么新的收获?在哪些方面 的表现很好,在哪些方面表现不够 ,以后要注意的是:—————— —。
谢谢
(3)底面周长是25.12分米,高是2分米。
2、 一根圆柱形钢材,底面积是50平方厘米,
高是2.1米。它的体积是多少? A、50×2.1=105(立方厘米)
B、2.1米=210厘米 50×210=10500(平方厘米)
C、2.1米=210厘米 50×210=10500(立方厘米 )
D、50平方厘米=0.005平方米 0.005×2.1=0.0105(立方米)
讨论
1.已知圆柱体的底面半径和高,怎样求体积?
S=∏r2 v=sh
2.已知圆柱体的底面直径和高,怎样求体积?
r= d
2
S=∏r2 v=sh
3.已知圆柱体的底面周长和高,怎样求体积?
r=c÷2∏ S=∏r2 v=sh
巩固新知 1:、计算下列各圆柱的体积。
(1)底面直径8厘米,高是5厘米。
(2)底面半径是3分米,高是1.3米。
长方体的底面积等于圆柱的 底面积 ,高等于圆柱的 高 。
长方体体积=底面积×高 圆柱体积 V=Sh
=
学贵有疑地 方或者又产生了哪些新的疑问, 请大胆提出来大家共同探讨。
试一试
一根圆柱形钢材的 底面直径是10分米, 高是2.5米,这根 钢材的体积是多少
立方分米?
圆柱的体积
学习目标:
理解并掌握圆柱的体积计算 公式,并能运用公式解决实
际问题。
自探提示:
认真看课本25页内容,思考: 圆柱的体积计算公式是什么?
它是怎样推导出来的?
(
等分的份数越多, 拼成的越接近长方 体。
谈一谈,通过本节课的学习, 你又有什么新的收获?在哪些方面 的表现很好,在哪些方面表现不够 ,以后要注意的是:—————— —。
谢谢
(3)底面周长是25.12分米,高是2分米。
2、 一根圆柱形钢材,底面积是50平方厘米,
高是2.1米。它的体积是多少? A、50×2.1=105(立方厘米)
B、2.1米=210厘米 50×210=10500(平方厘米)
C、2.1米=210厘米 50×210=10500(立方厘米 )
D、50平方厘米=0.005平方米 0.005×2.1=0.0105(立方米)
讨论
1.已知圆柱体的底面半径和高,怎样求体积?
S=∏r2 v=sh
2.已知圆柱体的底面直径和高,怎样求体积?
r= d
2
S=∏r2 v=sh
3.已知圆柱体的底面周长和高,怎样求体积?
r=c÷2∏ S=∏r2 v=sh
巩固新知 1:、计算下列各圆柱的体积。
(1)底面直径8厘米,高是5厘米。
(2)底面半径是3分米,高是1.3米。
长方体的底面积等于圆柱的 底面积 ,高等于圆柱的 高 。
长方体体积=底面积×高 圆柱体积 V=Sh
=
学贵有疑地 方或者又产生了哪些新的疑问, 请大胆提出来大家共同探讨。
试一试
一根圆柱形钢材的 底面直径是10分米, 高是2.5米,这根 钢材的体积是多少
立方分米?
圆柱的体积
学习目标:
理解并掌握圆柱的体积计算 公式,并能运用公式解决实
际问题。
自探提示:
认真看课本25页内容,思考: 圆柱的体积计算公式是什么?
它是怎样推导出来的?
(
等分的份数越多, 拼成的越接近长方 体。
人教版六年级数学下册3.1.3 圆柱的体积 (共41张PPT)

长方体体积=底面积×高
=
圆柱体积
V=Sh
32 返回
V=Sh
33 返回
智慧城堡
加油啊!
34 返回
闯关一
计算下面各圆柱的体积。
底面积
(平方米)
高
(米)
圆柱体积
(立方米)
15
3
45
6.4
4
25.6
35 返回
闯关二
火眼金睛判对错。
(1)圆柱体的底面积越大,它的体积越大。(× )
(2)长方体、正方体、圆柱体的体积都可以
圆的面积
近似长方形的面积
转化、推导是常用的数学研究方法。
9 返回
(1)你准备把圆柱体转化成什么立体图形? (2)你是怎样转化成这个立体图形的? (3)转化以后的立体图形和圆柱体之间有什么关 系?
10 返回
11 返回
12 返回
13 返回
14 返回
15 返回
16 返回
17 返回
18 返回
19 返回
20 返回
21 返回
22 返回
23 返回
24 返回
25 返回
26 返回
27 返回
单击此处编辑母版标题样式
28 返回
29 返回
30 返回
把圆柱的底面平均分的份数越多,切拼成的立体图 形越接近长方体。
31 返回
长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。
用底面积乘高的方法来计算。 ( √ )
(3)一个圆柱的底面积是10平方厘米,高是5米, 它的体积是10×5=50平方厘米( )
(1)5米=500厘米 (2)10×500=5000(立方厘米)
36 返回
=
圆柱体积
V=Sh
32 返回
V=Sh
33 返回
智慧城堡
加油啊!
34 返回
闯关一
计算下面各圆柱的体积。
底面积
(平方米)
高
(米)
圆柱体积
(立方米)
15
3
45
6.4
4
25.6
35 返回
闯关二
火眼金睛判对错。
(1)圆柱体的底面积越大,它的体积越大。(× )
(2)长方体、正方体、圆柱体的体积都可以
圆的面积
近似长方形的面积
转化、推导是常用的数学研究方法。
9 返回
(1)你准备把圆柱体转化成什么立体图形? (2)你是怎样转化成这个立体图形的? (3)转化以后的立体图形和圆柱体之间有什么关 系?
10 返回
11 返回
12 返回
13 返回
14 返回
15 返回
16 返回
17 返回
18 返回
19 返回
20 返回
21 返回
22 返回
23 返回
24 返回
25 返回
26 返回
27 返回
单击此处编辑母版标题样式
28 返回
29 返回
30 返回
把圆柱的底面平均分的份数越多,切拼成的立体图 形越接近长方体。
31 返回
长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。
用底面积乘高的方法来计算。 ( √ )
(3)一个圆柱的底面积是10平方厘米,高是5米, 它的体积是10×5=50平方厘米( )
(1)5米=500厘米 (2)10×500=5000(立方厘米)
36 返回
【新】人教版六年级数学下册《圆柱体积》优质课课件.ppt
结论
1、拼成的长方体的体积与原来的圆柱体体积相等。 2、它的底面积没有发生变化。 3、它的高也没有发生变化。
圆柱体积的大小与哪些条件有关?
底面积
高
例4 (1)一根圆柱形木料,底面 积为75平方厘米,长90厘米, 它的体积是多厘米。
判断并说明理由.
圆柱体的体积
—— (人教版)六年制小学数学第十二册
数学课件
考一考
你会计算下面哪些图形的体积呢?
真 棒!
高 宽
长
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
v长=a b h
v正 =a 3
V=s底 h
这是什么图形? 怎样求它的体积?
??
圆柱体的体积
数学课件
讨论题
1、拼成的长方体的体积与原来的圆柱体体积是否相等? 2、它的底面积变了吗? 3、它的高变了吗?
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
1、用绳子量出饮料罐底面的周长,然后通过周长求半径。
2、用直尺量出直径(最长一条为直径),再通过直径求出半 径。
再见
▪ 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/152020/12/15Tuesday, December 15, 2020
六年级数学下册课件-3.1.3 圆柱的体积13-人教版(共28张PPT) (1)
能不能把圆柱转化成我 们已经学过的形体来求出它 的体积?
长方体的体积=底面积 ×高 底面积
长方体的体积= 底面积 × 高
圆柱体的体积= 底面积 × 高
结论:
圆柱体通过切拼,圆柱体转化成近似的长方
体。这个长方体的底面积等于圆柱 的 底面,积高等
于高圆,柱所体以的圆柱体。的高因体为积长等方于体的体积等底用于面字底积母面乘积表高乘示
圆柱的体积
一、复习导入:圆的面积公式推导 过程
圆的面积公式推导过程:
S=π r 2
一、复习
导入:
高
宽
长
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
底面积
用“S”表示底面积,正方体、长方体的体积计算 公式都可以写成:
V=sh
二、探究新知
例5、圆柱体体积公式怎样 推导呢?
讨论:
(2)长方体、正方体和圆柱体
都可用底面积乘高来计算
它们的体积。
( √
(3)体积相等的两个圆柱体, 它们的底面积一定相等。( )×
(4)高相等的两个圆柱体,
底面半径长的那个圆柱
体体积大。
() √
四、作业
作业: 第28页练习五, 第2题、第6题。
兴趣作业:
整理并熟记 3.14的2至9倍、 11至29的平方、
为
。
V=sh
圆柱的体积
长方体的体积=底面积×高 圆柱的体积=底面积×高
V=Sh=πr2h
二、探究新知
下图的杯子能不能装下这袋牛奶?(数 据是从杯子里面测量得到的。)
8cm
10cm
二、探究新知
杯子的底面积: 3.14×(8÷2) =3.14×4² =3.14×16 =50.24 (cm2 )
长方体的体积=底面积 ×高 底面积
长方体的体积= 底面积 × 高
圆柱体的体积= 底面积 × 高
结论:
圆柱体通过切拼,圆柱体转化成近似的长方
体。这个长方体的底面积等于圆柱 的 底面,积高等
于高圆,柱所体以的圆柱体。的高因体为积长等方于体的体积等底用于面字底积母面乘积表高乘示
圆柱的体积
一、复习导入:圆的面积公式推导 过程
圆的面积公式推导过程:
S=π r 2
一、复习
导入:
高
宽
长
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
底面积
用“S”表示底面积,正方体、长方体的体积计算 公式都可以写成:
V=sh
二、探究新知
例5、圆柱体体积公式怎样 推导呢?
讨论:
(2)长方体、正方体和圆柱体
都可用底面积乘高来计算
它们的体积。
( √
(3)体积相等的两个圆柱体, 它们的底面积一定相等。( )×
(4)高相等的两个圆柱体,
底面半径长的那个圆柱
体体积大。
() √
四、作业
作业: 第28页练习五, 第2题、第6题。
兴趣作业:
整理并熟记 3.14的2至9倍、 11至29的平方、
为
。
V=sh
圆柱的体积
长方体的体积=底面积×高 圆柱的体积=底面积×高
V=Sh=πr2h
二、探究新知
下图的杯子能不能装下这袋牛奶?(数 据是从杯子里面测量得到的。)
8cm
10cm
二、探究新知
杯子的底面积: 3.14×(8÷2) =3.14×4² =3.14×16 =50.24 (cm2 )
圆柱的体积ppt课件-数学六年级下第三章圆柱与圆锥第3节人教版
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
计
算
长
方
体
和
正
方
体
的
体
积
0.06m2
解:长方体体积=底面积×高 =0.06 ×5 =0.3m3
长方体和正方体的体积
1
一块正方体石料,一个面的面积是36dm2,这块石料的体
积是多少立方分米?
计
算
长
方
因为:36=6×6
体
和
所以:棱长是6
正
方
体
V=
Sh
的
体
=36×6
积
=216(dm3) 答:这块石料的体积是216 dm3。
是多少?
81÷4.5×3 = 54(dm3) 答: 它的体积是 54 dm3。
9、一块蜂窝煤大约需要 用煤多少立方分米? (得数保留整数。)
课堂练习
( )12×223.14×9
= 1 017.36 (cm3)
( )2×2 3.14×9×12 2
= 339.12 (cm3)
1 017.36 - 339.12 = 678.24 (cm3) 答: 一块蜂窝煤大约需要用煤 1 dm3。
圆柱的体积ppt课件-数学六年级下第三章圆柱 与圆锥第3节人教版
第三章 圆柱与圆锥 第3节 圆柱的体积
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
3
圆 的 体 积 公 式 推 导 过 程
探究新知
计
算
长
方
体
和
正
方
体
的
体
积
0.06m2
解:长方体体积=底面积×高 =0.06 ×5 =0.3m3
长方体和正方体的体积
1
一块正方体石料,一个面的面积是36dm2,这块石料的体
积是多少立方分米?
计
算
长
方
因为:36=6×6
体
和
所以:棱长是6
正
方
体
V=
Sh
的
体
=36×6
积
=216(dm3) 答:这块石料的体积是216 dm3。
是多少?
81÷4.5×3 = 54(dm3) 答: 它的体积是 54 dm3。
9、一块蜂窝煤大约需要 用煤多少立方分米? (得数保留整数。)
课堂练习
( )12×223.14×9
= 1 017.36 (cm3)
( )2×2 3.14×9×12 2
= 339.12 (cm3)
1 017.36 - 339.12 = 678.24 (cm3) 答: 一块蜂窝煤大约需要用煤 1 dm3。
圆柱的体积ppt课件-数学六年级下第三章圆柱 与圆锥第3节人教版
第三章 圆柱与圆锥 第3节 圆柱的体积
人教版小学数学六年级下册《第三单元圆柱与圆锥:3.圆柱的体积》PPT1
169.56立方分米。
判断:
1、圆柱的体积比表面积大。( ) ×
2、等底等高的正方体、长方体和圆柱,它们的体积
都相等。( √ )
3、一个圆柱的底面半径扩大到原来的3倍,体积也
4、体积相等的两个圆柱不一定是等底等高。(√ )
扩到原来的3倍。( × )
判断:
5、高不变,圆柱体的底面积越大,它的体积就
人教版六年级数学下册第三单元
圆柱的体积练习课
知识回顾:
圆柱的体积公式是怎样推导出来的?
转化
长方体的体积= 底面积 × 高 圆柱的体积= V
底面积 S
圆柱体积计算公式是:
V
×
高 h
已知圆柱的底面积和高,怎样求圆柱的体积?
V=s×h
已知圆柱的体积和高,怎样求圆柱的底面积?
s=V÷h
已知圆柱的体积和底面积,怎样求圆柱的高?
越大。( √ )
6、圆柱体的高越长,它的体积越大。( × ) 7、圆柱体的底面直径和高可以相等。(√ )
巩固练习:
将一个棱长为6分米的正方 体钢材熔铸成底面半径为1 分米的圆柱体,这个圆柱有 多长?(得数保留整数)
思考:正方体与熔铸成的圆柱体体积有什么关系? 正方体的体积:6×6×6=216(dm3) 圆柱的长:216÷(3.14×1×1) =216÷3.14 ≈69(分米)
=18×3 =54(dm3)
答:它的体积是54dm3。
练一练:
把一个棱长6分米的正方体木块切削成一个体积最 大的圆柱体,这个圆柱的体积是多少立方分米?
d 2 思考:圆柱的直径和高 V ( ) h 2 是正方体的什么? =3.14×(6÷2)2×6 =3.14×32×6 3) =169.56 ( dm 答:这个圆柱的体积是
判断:
1、圆柱的体积比表面积大。( ) ×
2、等底等高的正方体、长方体和圆柱,它们的体积
都相等。( √ )
3、一个圆柱的底面半径扩大到原来的3倍,体积也
4、体积相等的两个圆柱不一定是等底等高。(√ )
扩到原来的3倍。( × )
判断:
5、高不变,圆柱体的底面积越大,它的体积就
人教版六年级数学下册第三单元
圆柱的体积练习课
知识回顾:
圆柱的体积公式是怎样推导出来的?
转化
长方体的体积= 底面积 × 高 圆柱的体积= V
底面积 S
圆柱体积计算公式是:
V
×
高 h
已知圆柱的底面积和高,怎样求圆柱的体积?
V=s×h
已知圆柱的体积和高,怎样求圆柱的底面积?
s=V÷h
已知圆柱的体积和底面积,怎样求圆柱的高?
越大。( √ )
6、圆柱体的高越长,它的体积越大。( × ) 7、圆柱体的底面直径和高可以相等。(√ )
巩固练习:
将一个棱长为6分米的正方 体钢材熔铸成底面半径为1 分米的圆柱体,这个圆柱有 多长?(得数保留整数)
思考:正方体与熔铸成的圆柱体体积有什么关系? 正方体的体积:6×6×6=216(dm3) 圆柱的长:216÷(3.14×1×1) =216÷3.14 ≈69(分米)
=18×3 =54(dm3)
答:它的体积是54dm3。
练一练:
把一个棱长6分米的正方体木块切削成一个体积最 大的圆柱体,这个圆柱的体积是多少立方分米?
d 2 思考:圆柱的直径和高 V ( ) h 2 是正方体的什么? =3.14×(6÷2)2×6 =3.14×32×6 3) =169.56 ( dm 答:这个圆柱的体积是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
想:要回答这个问题,先 要计算出杯子的容积。
杯子的底面积: 3.14×(8÷2)² =3.14×4² =3.14×16 =50.24(cm²)
杯子的容积: 50.24×10 =502.4(cm³) =502.4(mL) 答:因为502.4大于498,所以杯子能装下这袋牛奶。
随堂练习
1.一根圆柱形木料,底面积为75cm²,长90cm。它的体积是 多少? 75×90=6750(cm³) 答:它的体积是6750cm³。
把拼成的长方体与原来的圆柱比 较,你能发现什么?
长方体的底面积等于圆柱的 底面积 ,高等于圆柱的 高。
长方体的体积= 底面积×高
=
圆柱的体积= 底面积×高
如果知道圆柱的底面半径r和高h, 你能写出圆柱的体积公式吗?
圆柱的体积计算公式是:
V= π r²h ,
6.下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面 测量得到的。)
2.李家庄挖了一口圆柱形水井,地面以下的井深10m,底面直 径为1m。挖出的土有多少立方米? 3.14×(1÷2)²×10=7.85(m³) 答:挖出的土有7.85立方米。
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量 底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水, 带这杯水够喝吗? 3.14×(8÷2)²×15=753.6(cm³)=0.7536(L) 0.7536L<1L 答:带这杯水不够喝。 2.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌 用去木料0.02m³。这根木料最多能做多少张课桌? 3.14×(0.4÷2)²×5=0.628(m³) 0.628÷0.02≈31(张) 答:这根木料最多能做31张课桌。
第3单元 圆柱与圆锥
第3课时 圆柱的体积
新课导入
放入石头后发生了什么?
水位变高了
你能用一句话说说什么
是圆柱的体积吗? 圆柱所占空间的大小就是圆柱的体积
探索新知
我们会计算长方体和正方体的体积,圆柱的体积 怎样计算呢?能不能将圆柱转化成我们学过的立体图 形,计算出它的体积呢?
把圆柱的底面平均分的份数越多,切拼成的立体图形越 接近长方体。
杯子的底面积: 3.14×(8÷2)² =3.14×4² =3.14×16 =50.24(cm²)
杯子的容积: 50.24×10 =502.4(cm³) =502.4(mL) 答:因为502.4大于498,所以杯子能装下这袋牛奶。
随堂练习
1.一根圆柱形木料,底面积为75cm²,长90cm。它的体积是 多少? 75×90=6750(cm³) 答:它的体积是6750cm³。
把拼成的长方体与原来的圆柱比 较,你能发现什么?
长方体的底面积等于圆柱的 底面积 ,高等于圆柱的 高。
长方体的体积= 底面积×高
=
圆柱的体积= 底面积×高
如果知道圆柱的底面半径r和高h, 你能写出圆柱的体积公式吗?
圆柱的体积计算公式是:
V= π r²h ,
6.下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面 测量得到的。)
2.李家庄挖了一口圆柱形水井,地面以下的井深10m,底面直 径为1m。挖出的土有多少立方米? 3.14×(1÷2)²×10=7.85(m³) 答:挖出的土有7.85立方米。
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量 底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水, 带这杯水够喝吗? 3.14×(8÷2)²×15=753.6(cm³)=0.7536(L) 0.7536L<1L 答:带这杯水不够喝。 2.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌 用去木料0.02m³。这根木料最多能做多少张课桌? 3.14×(0.4÷2)²×5=0.628(m³) 0.628÷0.02≈31(张) 答:这根木料最多能做31张课桌。
第3单元 圆柱与圆锥
第3课时 圆柱的体积
新课导入
放入石头后发生了什么?
水位变高了
你能用一句话说说什么
是圆柱的体积吗? 圆柱所占空间的大小就是圆柱的体积
探索新知
我们会计算长方体和正方体的体积,圆柱的体积 怎样计算呢?能不能将圆柱转化成我们学过的立体图 形,计算出它的体积呢?
把圆柱的底面平均分的份数越多,切拼成的立体图形越 接近长方体。
