模糊控制系统讲解
离散控制系统中的模糊控制设计

离散控制系统中的模糊控制设计离散控制系统是指控制对象和控制器都是离散时间的系统。
在离散控制系统中,模糊控制设计是一种有效的控制方法。
本文将介绍离散控制系统中模糊控制设计的原理和应用。
一、模糊控制的基本原理模糊控制是一种基于模糊逻辑的控制方法,其设计思想源于人脑的模糊推理过程。
模糊控制系统由模糊化、模糊推理和解模糊化三部分组成。
1. 模糊化:模糊化是将输入变量用模糊集合进行描述,将连续的输入映射为隶属度的形式。
常用的模糊化方法包括三角隶属度函数和高斯隶属度函数等。
2. 模糊推理:模糊推理是基于一组模糊规则对输入进行推理,得到输出变量的隶属度。
常用的模糊推理方法包括Mamdani模糊推理和T-S模糊推理等。
3. 解模糊化:解模糊化将模糊推理得到的隶属度翻译为实际的输出值。
常用的解模糊化方法包括最大隶属度法和平均隶属度法等。
二、离散控制系统中的模糊控制设计步骤离散控制系统中的模糊控制设计步骤包括以下几个方面:1. 系统建模:首先需要对离散控制系统进行建模,确定系统的输入、输出和状态变量。
根据系统的数学模型,进行离散化处理,得到离散时间的系统模型。
2. 设计控制规则:根据系统的特性和控制目标,设计模糊控制器的控制规则。
控制规则是模糊控制系统的核心,它决定了输入变量和输出变量之间的映射关系。
3. 设置隶属函数:为输入变量和输出变量设置适当的隶属函数,以描述变量之间的模糊关系。
不同的隶属函数可以描述不同的模糊集合,用于表征输入输出变量的不确定性。
4. 进行模糊推理:根据输入变量的隶属度和控制规则,进行模糊推理,得到输出变量的隶属度。
模糊推理可以使用模糊关系矩阵或者模糊推理引擎进行计算。
5. 解模糊化:将模糊推理得到的输出变量隶属度翻译为实际的输出值,从而得到模糊控制器的输出。
解模糊化可以使用最大隶属度法或者平均隶属度法等方法。
6. 仿真与优化:通过对模糊控制器的仿真,评估其性能并进行优化。
可以通过调整隶属函数的形状、增加控制规则的数目等方式改进控制器的性能。
控制系统的模糊控制理论与应用

控制系统的模糊控制理论与应用控制系统是指通过对特定对象的操作,以达到预期目标的过程。
在控制系统中,模糊控制理论是一种常用的控制方法。
本文将介绍控制系统的模糊控制理论以及其应用。
一、模糊控制理论的基本概念模糊控制理论是一种基于模糊逻辑的控制方法,它模拟了人类的思维和决策过程。
与传统的精确控制方法相比,模糊控制理论能够应对现实世界中存在的模糊不确定性和非线性关系。
1. 模糊集合模糊集合是模糊控制理论的基础,它是对现实世界中一类事物或对象的模糊描述。
不同于传统的集合理论,模糊集合允许元素以一定的隶属度或可信度属于这个集合。
2. 模糊逻辑模糊逻辑是模糊控制理论的核心,它用于描述和处理具有模糊性质的命题和推理。
模糊逻辑采用模糊集合的运算规则,能够处理模糊不确定性和非精确性的信息。
3. 模糊控制器模糊控制器是模糊控制系统的核心组件,它基于模糊逻辑进行决策和控制。
模糊控制器通常由模糊规则库、模糊推理机和模糊输出函数组成。
二、模糊控制理论的应用领域模糊控制理论具有广泛的应用领域,并在许多实际问题中取得了良好的效果。
1. 工业控制在工业控制领域,模糊控制理论可以应对复杂的非线性系统和参数不确定性。
例如,在温度控制系统中,模糊控制器可以根据当前的温度和环境条件,控制加热器的输出功率,以使温度保持在设定范围内。
2. 智能交通在智能交通系统中,模糊控制理论可以用于交通信号灯控制、车辆路径规划和交通流量优化。
通过根据交通状况和道路条件动态调整信号灯的时序,可以提高交通效率和道路安全性。
3. 机器人技术在机器人技术中,模糊控制理论可以用于机器人路径规划、动作控制和感知决策。
通过将环境信息模糊化,机器人可以根据当前的感知结果和目标任务制定合理的动作策略。
4. 金融风险控制在金融风险控制中,模糊控制理论可以用于风险评估和交易决策。
通过建立模糊规则库和模糊推理机制,可以根据不确定和模糊的市场信息制定合理的交易策略。
三、模糊控制理论的优势和发展方向模糊控制理论具有以下几个优势,使其在实际应用中得到了广泛的应用和研究:1. 简化建模过程:相比传统的控制方法,模糊控制理论能够简化系统的建模过程,减少系统的复杂性。
第四章 模糊控制系统

常规反馈控制系统结构
今天, 今天,常规的反馈控制方法在实际过程中已经得到广泛 应用,例如在阿波罗登月舱的姿态控制、宇宙飞船、 应用,例如在阿波罗登月舱的姿态控制、宇宙飞船、导弹制 导以及在工业生产过程控制等。但是, 导以及在工业生产过程控制等。但是,对于常规反馈控制系 统,控制器的设计无论是采用经典控制理论还是现代控制理 都需要事先知道被控制对象精确的数学模型。 论,都需要事先知道被控制对象精确的数学模型。也就是说 系统的分析与综合都是建立在数学模型的基础上。 系统的分析与综合都是建立在数学模型的基础上。 然而,在实际控制中被控对象的精确数学模型很难建立, 然而,在实际控制中被控对象的精确数学模型很难建立, 甚至无法建立。例如,交通系统、经济系统及生物发酵过程 甚至无法建立。例如,交通系统、 这样,基于数学模型的控制方法则陷入了困境。 等。这样,基于数学模型的控制方法则陷入了困境。值得注 意的是对于上述的复杂过程, 意的是对于上述的复杂过程,有经验的专家或操作人员用手 动控制的方式,却可以收到令人满意的效果。 动控制的方式,却可以收到令人满意的效果。面对这样的事 人们考虑能否让计算机模拟人的思维方式, 实,人们考虑能否让计算机模拟人的思维方式,对这些复杂 过程进行控制决策。 过程进行控制决策。
x = (ω ,θ ) ɺ x = f ( x, u )
u1 u= u 2
其中u为一个有约束的控制向量, 为前轮的角度, 其中 为一个有约束的控制向量,u1为前轮的角度, u2为车 为一个有约束的控制向量 速。
如果把邻近两辆车定义为 x(执行中的约束),用集合 (执行中的约束) 表示,而两辆停着的车之间的空隙定义为Г( 表示,而两辆停着的车之间的空隙定义为 (允许的终端状 态的集合) 那么, 停车问题就转化为寻找一个控制律u(t), 态的集合 ) 。 那么 , 停车问题就转化为寻找一个控制律 , 使其在满足各种约束的条件下把初始状态转移到终端状态Г 使其在满足各种约束的条件下把初始状态转移到终端状态 中去。对于这个问题若采用基于数学模型的精确方法来求解, 中去。对于这个问题若采用基于数学模型的精确方法来求解, 由于约束条件过多,求解过程将异常复杂。 由于约束条件过多,求解过程将异常复杂。 但在实际停车时,汽车司机并不考虑控制律u(t)的求解。 的求解。 但在实际停车时,汽车司机并不考虑控制律 的求解 而是凭借以往的经验,先让车向前运动, 而是凭借以往的经验,先让车向前运动,前轮先向右而后向 然后使车向后运动,前轮仍先向右而后向左, 左,然后使车向后运动,前轮仍先向右而后向左,经过多次 反复,车将横向移动一个所需要的距离, 反复,车将横向移动一个所需要的距离,最后向前开停在空 隙处。这样,汽车司机通过一些不精确的观察,执行一些不 隙处。 这样, 汽车司机通过一些不精确的观察, 精确的控制,却达到了准确停车的目的。 精确的控制,却达到了准确停车的目的。
控制系统模糊逻辑

控制系统模糊逻辑控制系统模糊逻辑是一种基于模糊集合理论的控制方法,它采用了多值逻辑和模糊推理的思想,能够更好地应对现实世界中存在的不确定性和模糊性问题。
本文将介绍控制系统模糊逻辑的基本原理、应用领域以及其在现代工业中的重要性。
一、控制系统模糊逻辑的基本原理控制系统模糊逻辑的基本原理是将模糊集合理论应用于控制系统中,通过定义模糊规则、模糊变量和模糊推理等方法,实现对非精确信息的处理和控制。
具体来说,控制系统模糊逻辑包含以下几个要素:1. 模糊集合:模糊集合是一种介于二值集合和连续集合之间的数学概念,它用来描述现实世界中的模糊性和不确定性。
在控制系统中,模糊集合可以表示输入、输出和中间变量等。
2. 模糊规则:模糊规则是一种基于经验和专家知识的规则集合,用来描述输入和输出之间的关系。
每个模糊规则由若干个前提和一个结论组成,通过匹配输入与规则的前提条件,进行模糊推理得到模糊输出。
3. 模糊推理:模糊推理是根据模糊规则和输入,通过模糊逻辑运算得到模糊输出的过程。
常用的模糊逻辑运算包括模糊交、模糊并以及模糊推理的合成等。
4. 模糊控制:模糊控制是指将模糊逻辑应用于控制系统中,通过模糊规则和模糊推理来实现对系统的控制。
模糊控制具有适应性强、鲁棒性好等优势,在许多现实环境中具有广泛的应用价值。
二、控制系统模糊逻辑的应用领域控制系统模糊逻辑可以应用于许多领域,其中包括但不限于以下几个方面:1. 工业控制:在现代工业中,控制系统模糊逻辑被广泛应用于各种自动化控制系统中,如温度、湿度、流量等变量的控制。
相比传统的控制方法,模糊逻辑能够更好地处理非精确的输入和模糊的输出,提高控制系统的性能和鲁棒性。
2. 交通系统:交通系统是一个典型的复杂系统,其中包含了大量的不确定性和模糊性因素。
控制系统模糊逻辑可以应用于交通信号灯控制、路况预测和交通流优化等方面,实现交通系统的智能化管理和优化。
3. 金融系统:金融市场中存在着大量的不确定性和模糊性,模糊逻辑可以应用于金融系统中的风险评估、投资决策和交易策略等方面,提供更准确和可靠的决策支持。
模糊控制系统课件
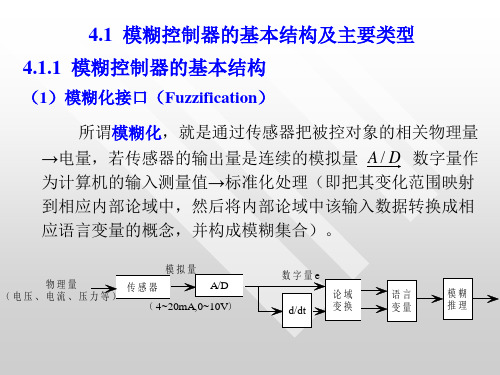
(1)模糊化接口(Fuzzification)
所谓模糊化,就是通过传感器把被控对象的相关物理量 →电量,若传感器的输出量是连续的模拟量 A / D 数字量作 为计算机的输入测量值→标准化处理(即把其变化范围映射 到相应内部论域中,然后将内部论域中该输入数据转换成相 应语言变量的概念,并构成模糊集合)。
量化因子:K e
2n1 eH eL
, Kec
2n2 eH eL
,
比例因子:
Ku
uH uL 2m
注:误差和误差变化这两个变量的连续值与其论域中的离散值
并不是一一对应的。
(2)模糊推理机(Inference engine) 模糊推理机由知识库(数据库和规则库)与模糊
推理决策逻辑构成。这是基本部分。 ①知识库(Knowledge base)=数据库(Date base) +语言控制规则库(Rule base)
缺点:不同被控对象,控制规则不变,控制效果不好。
图4.3 简单模糊控制器的结构
⑵模糊自调整控制器----二维模糊控制器中加入修正因子
(规则自调整模糊控制器)
u e 1 e
低阶控制系统: >0.5 高阶控制系统: <0.5
当误差较大时,控制系统的主要任务是消除误差,加快响 应速度,这时对误差的加权应该大些;
的概念? 3、常用的模糊控制器有哪些? 4、二维FC的工作原理?优缺点? 5、FC设计的两种实现方式及其特点? 6、设计模糊控制器的步骤?
4.2模糊控制器的结构设计
4.2.1模糊控制器的结构设计 实质:模糊控制器输入语言变量及输出语言变量的选取和模糊控制器的不同
计算机控制系统第5章模糊控制课件

与其隶属
度 A(xi ) 之间的对应关系;“+”也不表示“求和”,而是表示
模糊集合在论域上的整体。
2024/8/6
5
2.几种典型的隶属函数 (1)高斯型隶属函数
( xc)2
f (x; ,c) e 2 2
2024/8/6
6
(2)S形隶属函数
f
(x;
a,
c)
1
1 ea(xc)
2024/8/6
7
(3)梯形隶属函数
第一节 模糊控制系统
一、模糊控制系统的组成
模糊控制系统的结构与一般计算机控制系统基本相似, 通常由模糊控制器、输入输出接口、广义被控对象和测量装 置四个部分组成。
基本模糊控制器
给定值 +
e
-
输 入 量
化
模
糊 化
e~
处
理
模
糊 u~
推
理
反 模 糊 化 处
理
输 出 量
化
u
D/A
A/D
传感器
被控对象
执行机构
所谓论域就是被考虑客体所有元素的集合。在模糊控制系
统中,把模糊控制器的输入变量偏差 e 及其变化率 ec 的实际范
围称为这些变量的基本论域。基本论域内的量为精确量,需要 对它们进行量化处理。
在实际控制系统中,需要通过所谓量化因子进行量化处理, 实现论域变换。量化因子的定义为:
ke
2n be ae
kec
a,
b)
1 2( 2(b
x b
x
a a
)2 )2
ba
0
xa
a a
x b
a x
2
b
模糊控制系统简介

模糊理论在模糊控制中的应用——模糊控制系统摘要:模糊控制技术对工业自动化的进程有着极大地推动作用。
本文简要的讲述了模糊控制理论的起源及基本原理,详细分析了模糊控制器的设计方法,最后就典型的模糊控制系统原理和新型模糊控制系统应用进行了分析正文:一:模糊理论1.1模糊理论概念:模糊理论(Fuzzy Theory)是指用到了模糊集合的基本概念或连续隶属度函数的理论。
它可分类为模糊数学,模糊系统,不确定性和信息,模糊决策这五个分支,它并不是完全独立的,它们之间有紧密的联系。
1.2模糊理论产生:1965年,模糊理论创始人,美国加州福尼亚大学伯克利分校的自动控制理论专家L.A.Zadeh教授发表了题为“Fuzzy Set”的论文,这标志着模糊理论的诞生。
这一理论为描述和处理事务的模糊性和系统中的不确定性,以及模拟人所特有的模糊逻辑思维功能,从定性到定量,提供了真正强有力的工具。
1966年,马里诺斯发表了模糊逻辑的研究报告,而Zadeh进一步提出了著名的模糊语言值逻辑,并于1974年进行了模糊逻辑推理的研究。
由于这一研究和观点反映了客观世界中普遍存在的事务,它一出现便显示出强大的生命力和广阔的发展前途,在自然科学,其他科学领域及工业中得到了迅速的广泛的应用。
二:模糊控制理论2.1模糊控制理论的产生:在控制技术的应用过程中,对于多变量、非线性、多因素影响的生产过程,即使不知道该过程的数学模型,有经验的操作人员也能够根据长期的实践观察和操作经验进行有效地控制,而采用传统的自动控制方法效果并不理想。
从这一点引申开来,是否可将人的操作经验总结为若干条控制规则以避开复杂的模型建造过程?模糊控制理论与技术由此应运而生。
20世纪70年代模糊理论应用于控制领域的研究开始盛行,并取得成效。
其代表是英国伦敦大学玛丽皇后分校的E.H.Mamdani教授将IF-THEN型模糊规则用于模糊推理,并把这种规则型模糊推理用于蒸汽机的自动运转中。
模糊控制系统讲解29页PPT

模糊控制系统讲解
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿பைடு நூலகம் 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
● 对iv、viii、xii 区,应防止超调,减小谷点的峰值,u 0。
根据以上规则,我们可以选择和设计模糊控制器 的规则表
规则号 e
△e
△u 参 考 点
1
PB ZE PB
a
2
PM ZE PM
e
3
PS ZE PS
i
4
ZE NB NB
b
5
ZE NM NM
f
6
ZE NS NS
u
u
过程
yk
- yk
• 模糊控制在MATLAB中的实现
假定被控对象的传递函数为:
G2
s
0.5
4.228 s2 1.64s
8.456
• 设计一模糊控制器,查看其阶跃响应。
• 步骤
1. 确定e,de和u的论域 2. e,de和u语言变量的选取 3. 规则的制定 4. 推理方法的确定
利用MATLAB的Toolbox工具
●对交叉点, △u符号和△e符号一样。
对b, f , j,u 0
对d, h, l,u 0
●对峰、谷点,△u符号和e符号一样。
对c, g, k,u 0
对e,i, m,u 0
6
● 对i 、v、ix区,当e大时,要缩短上升时间,u 0; 当接近设定值时,u 0或 0。
● 对ii、vi、x区,应防止超调,u 0 ● 对iii 、vii、xi 区,当e大时,要缩短上升时间,u 0;
3.模糊规则确定
e
U
NB
NM
NS
NZ
PZ
PS
PM
PB
PB
PL
PM
NM
NM
NM
NL
NL
NB
PM
PL
PM
NM
NM
NM
NS
NS
NB
PS
PL
PM
NS
NS
NS
NS
NM
NB
de Z
PL
PM
PS
Z
Z
NS
NM
NB
NS
PL
PM
PS
PS
PS
PS
NM
NB
NM
PL
PL
PS
PS
PM
PM
NM
NB
NB
PL
PL
PL
PM
PM
PM
NM
c
g k
b
d
f
h
j
l
m i
e
i ii iii iv v vi vii viii ix x x i xii a
根据e和△e的方向和大小,选择控制量的增量△u的大 小和方向。
有四种情况:
1. e 0 e 0 2. e 0 e 0 3. e 0 e 0 4. e 0 e 0
(相当于i 、v、ix区); (相当于ii 、vi、x 区); (相当于iii 、vii、xi区); (相当于iv、viii、xii 区);
• 1. 根据系统实际情况,选择e,de和u的论域 e range : [-1 1] de range: [-0.1 0.1] u range: [0 2]
• 2. e,de和u语言变量的选取 e 8个:NB,NM,NS,NZ,PZ,PS,PM,PB de 7个:NB,NM,NS,Z,PS,PM,PB U 7个:NB,NM,NS,Z,PS,PM,PB
有交叉点和峰、谷点。
交叉点:1. e 0 e 0, e 0 (b, f , j)
2. e 0 e 0, e 0 (d, h,l)
峰点:e 0,e 0 (c, g, k)
谷点:e 0,e 0 (e,i, m)
控制规则:
1。如果e和△e二者都为零,△u=0, 保持现状。 2。如果e以满意的速率趋向零, △u=0, 保持现状。 3。如果e不是自校正, △u不为零,取决于e和△e的符号和大小。
● 模糊控制系统的设计
1. 模糊化的策略 ▲ 采用单点模糊化
▲ 选择合适的模糊函数 ☆ 考虑噪声的概率密度函数。使 W f 5 n
(u)
1
(u )
1
Wf
Wf
0
U
0
U
2 n 2 n
P(u)
(a)
P(u) (b)
☆ 模糊变量术语集合的数目选取。在细分和粗分之间进 行折中。一般为2~10。
2. 模糊规则的合理调整 按照系统的动态行为可以合理地选择和确定模糊规则:
NB
4. 隐含和推理方法的制定
• 隐含采用 ‘mamdani’方法: ‘max-min‘ • 推理方法, 即 ‘min‘ 方法 • 去模糊方法:重心法。 • 选择隶属函数的形式:三角型
MATLAB
-1
1
-0.1
0.1
0
2
也可以用viewsurf菜单命令看模糊控制器的输出量
仿真程序:
j
7
NB ZE NB
c
8
NM ZE NM g
9
NS ZE NS
k
10
ZE PB PB
d
11
ZE PM PM
h
12
ZE PS PS
i
13
ZE
ZE
ZE 设置点
3 . 模糊规则的完整性、一致性 ●对过程的每一状态,都能推导出一个合适的控制规则,
——控制规则的完整性。
● 子集的并,应该以一定程度覆盖有关论域——控制
规则的 完整性。 0.5.
.5
● 规则之间不存在矛盾.
模糊控制器应用的模式
● 模糊PID 控制器
yr +
-
yk
模糊PID控制器
控制信号
过程
yk
●模糊PID控制器
常规模糊PID控制器
e
yr + 比较 e 模糊 u
处理
e 推理
过程
yk
- yk
增量模糊PID控制器
e
yr +
比较 处理
e
2e
模糊 推理
▲模糊化部件 ▲知识库 ▲推理逻辑—模糊控制系统的核心 ▲去模糊化部件
模糊控制中,推理逻辑按专家知识,以语言规则描述: 一般规则表示如下:
R1 : if x1 是 A11, x2 是A21 , ,xn 是 An1 , then y 是 C1 R2 : if x1 是 A12 , x2 是A22 , ,xn 是 An2 , then y 是 C 2 Rn : if x1 是 A1n , x2 是A2n , ,xn 是 Ann , then y 是 C n
系统输出
误差及其变化率 模糊控制器输出
模糊控制的基本原理和方法
● 模糊逻辑控制器的基本结构 ● 模糊控制系统的设计 ● PID模糊控制器模糊 ●利用MATLAB设计模糊控制器
● 模糊逻辑控制器的基本结构
设定值
yr +
y-k
模糊控制器
知识
库
精
模
确 值
模
糊 值
计算e和e 糊
化
模 糊
去
决策逻辑
值
模 糊
化
精 确 值
模糊推理单元
输出
过程
在采样时刻k, 误差和误差的变化定义为: ek yr yk ek ek ek1
