历年全国人教版数学高考真题与模拟题分类汇编 c单元 三角函数(文科2013年) 含答案
2013年全国各地高考文科数学试题分类汇编:三角函数
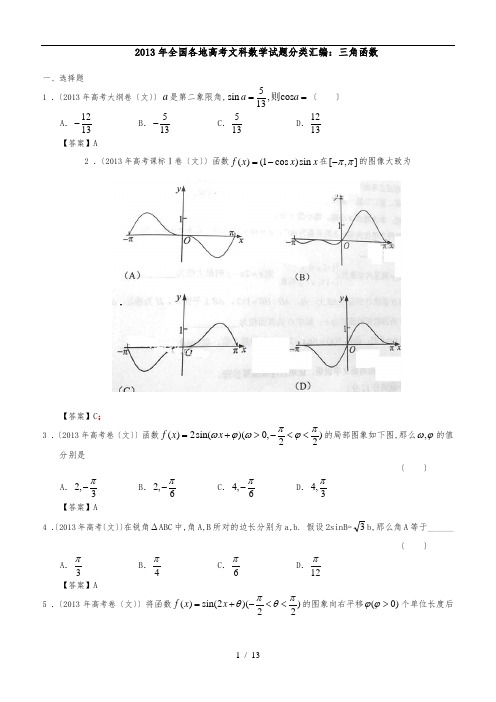
2013年全国各地高考文科数学试题分类汇编:三角函数一、选择题1 .〔2013年高考大纲卷〔文〕〕a 是第二象限角,5sin ,cos 13a a ==则〔 〕 A .1213-B .513-C .513D .1213【答案】A2 .〔2013年高考课标Ⅰ卷〔文〕〕函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为【答案】C ;3 .〔2013年高考卷〔文〕〕函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的局部图象如下图,那么,ωϕ的值分别是〔 〕A .2,3π-B .2,6π-C .4,6π-D .4,3π 【答案】A4 .〔2013年高考〔文〕〕在锐角∆ABC 中,角A,B 所对的边长分别为a,b. 假设2sinB=3b,那么角A 等于______〔 〕A .3πB .4πC .6πD .12π【答案】A5 .〔2013年高考卷〔文〕〕将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,假设)(),(x g x f 的图象都经过点)23,0(P ,那么ϕ的值可以是〔 〕 A .35π B .65π C .2πD .6π【答案】B6 .〔2013年高考卷〔文〕〕设△ABC 的角A , B , C 所对的边分别为a , b , c , 假设cos cos sin b C c B a A +=, 那么△ABC 的形状为〔 〕A .直角三角形B .锐角三角形C .钝角三角形D .不确定【答案】A7 .〔2013年高考卷〔文〕〕在ABC ∆,角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=,a b B >∠=且则〔 〕A .6πB .3π C .23π D .56π【答案】A8 .〔2013年高考课标Ⅱ卷〔文〕〕△ABC 的角A,B,C 的对边分别为a,b,c,b=2,B=,C=,那么△ABC 的面积为〔 〕 A .2+2B .+1C .2-2D .-1【答案】B9 .〔2013年高考卷〔文〕〕3sincos 23αα==若,则〔 〕 A .23-B .13-C .13D .23【答案】C10.〔2013年高考卷〔文〕〕ABC ∆的角A B C 、、的对边分别是a b c 、、,假设2B A =,1a =,3b =,那么c =〔 〕 A .23B .2C .2D .1【答案】B11.〔2013年高考课标Ⅱ卷〔文〕〕sin2α=,那么cos 2(α+)=〔 〕A .B .C .D .【答案】A12.〔2013年高考卷〔文〕〕51sin()25πα+=,那么cos α=〔 〕A .25-B .15-C .15D .25【答案】C13.〔2013年高考卷〔文〕〕将函数3cos sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,那么m 的最小值是〔 〕 A .π12B .π6C .π3D .5π6【答案】B14.〔2013年高考大纲卷〔文〕〕假设函数()()sin0=y x ωϕωω=+>的部分图像如图,则〔 〕A .5B .4C .3D .2【答案】B15.〔2013年高考卷〔文〕〕函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是〔 〕A .1-B .22-C .22D .0【答案】B16.〔2013年高考〔文〕〕设ABC ∆的角,,A B C 所对边的长分别为,,a b c ,假设2,3sin 5sin b c a A B +==,那么角C =〔 〕 A .3πB .23πC .34πD .56π 【答案】B 17.〔2013年高考课标Ⅰ卷〔文〕〕锐角ABC ∆的角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,那么b =〔 〕A .10B .9C .8D .5【答案】D18.〔2013年高考卷〔文〕〕函数f(x)=sin xcos x+32cos 2x 的最小正周期和振幅分别是 〔 〕A .π,1B .π,2C .2π,1D .2π,2【答案】A19.〔2013年高考卷〔文〕〕在△ABC 中,3,5a b ==,1sin 3A =,那么sin B =〔 〕 A .15B .59C 5.1 【答案】B20.〔2013年高考卷〔文〕〕函数x x x y sin cos +=的图象大致为【答案】D 二、填空题21.〔2013年高考卷〔文〕〕设sin 2sin αα=-,(,)2παπ∈,那么tan 2α的值是________.【答案】322.〔2013年高考课标Ⅱ卷〔文〕〕函数cos(2)()y x ϕπϕπ=+-≤<的图像向右平移2π个单位后,与函数sin(2)3y x π=+的图像重合,那么||ϕ=___________.【答案】56π23.〔2013年高考数学试题〔文科〕〕ABC ∆的角A 、B 、C 所对的边分别是a ,b ,c .假设2220a ab b c ++-=,那么角C 的大小是________(结果用反三角函数值表示).【答案】23π24.〔2013年高考数学试题〔文科〕〕假设1cos cos sin sin 3x y x y +=,那么()cos 22x y -=________. 【答案】79-25.〔2013年高考课标Ⅰ卷〔文〕〕设当x θ=时,函数()sin 2cos f x x x =-取得最大值,那么cos θ=______.【答案】255-; 26.〔2013年高考卷〔文〕〕设f(x)=sin3x+cos3x,假设对任意实数x 都有|f(x)|≤a,那么实数a 的取值围是_____._____【答案】2a ≥三、解答题27.〔2013年高考大纲卷〔文〕〕设ABC ∆的角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=.(I)求B(II)假设31sin sin 4A C =,求C .【答案】(Ⅰ)因为()()a b c a b c ac ++-+=,所以222a cb ac +-=-.由余弦定理得,2221cos 22a cb B ac +-==-, 因此,0120B =.(Ⅱ)由(Ⅰ)知060A C +=,所以cos()cos cos sin sin A C A C A C -=+ cos cos sin sin 2sin sin A C A C A C =-+cos()2sin sin A C A C =++131224-=+⨯32=, 故030A C -=或030A C -=-, 因此,015C =或045C =.28.〔2013年高考〔文〕〕函数f(x)=(1) 求2()3f π的值; (2) 求使1()4f x <成立的x 的取值集合【答案】解: (1) 41)212cos 232(sin 21)3sin sin 3cos(cos cos )(+⋅+⋅=⋅+⋅⋅=x x x x x x f ππ41)32(.414123sin 21)32(41)62sin(21-==-=+=⇒++=ππππf f x 所以. (2)由(1)知,)2,2()62(0)62sin(4141)62sin(21)(f ππππππk k x x x x -∈+⇒<+⇒<++=.),12,127(.),12,127(Z k k k Z k k k x ∈--∈--∈⇒ππππππππ所以不等式的解集是:29.〔2013年高考卷〔文〕〕在△ABC 中, 角A , B , C 所对的边分别是a , b , c . sin 3sin b A c B =, a = 3, 2cos 3B =. (Ⅰ) 求b 的值;(Ⅱ) 求sin 23B π⎛⎫- ⎪⎝⎭的值.【答案】30.〔2013年高考卷〔文〕〕函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 假设33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【答案】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-,1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.31.〔2013年高考卷〔文〕〕设函数2()sin cos (0)f x x x x ωωωω=->,且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π,(Ⅰ)求ω的值 (Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值 【答案】32.〔2013年高考卷〔文〕〕在锐角△ABC 中,角A,B,C 的对边分别为a,b,c,且2asinB=3b .(Ⅰ)求角A 的大小;(Ⅱ) 假设a=6,b+c=8,求△ABC 的面积.【答案】解:(Ⅰ)由得到:2sin sin 3sin A B B =,且3(0,)sin 0sin 22B B A π∈∴≠∴=,且(0,)23A A ππ∈∴=;(Ⅱ)由(1)知1cos 2A =,由得到:222128362()3366433623b c bc b c bc bc bc =+-⨯⇒+-=⇒-=⇒=,所以1283732323ABCS =⨯⨯=; 33.〔2013年高考卷〔文〕〕如图,在等腰直角三角形OPQ ∆中,90OPQ ∠=,22OP=,点M 在线段PQ 上.(1)假设3OM =,求PM 的长;(2)假设点N 在线段MQ 上,且30MON ∠=,问:当POM ∠取何值时,OMN ∆的面积最小?并求出面积的最小值.【答案】解:(Ⅰ)在OMP ∆中,45OPM∠=︒,OM =OP =,由余弦定理得,2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒, 得2430MP MP -+=,解得1MP =或3MP =.(Ⅱ)设POM α∠=,060α︒≤≤︒, 在OMP ∆中,由正弦定理,得sin sin OM OPOPM OMP=∠∠, 所以()sin 45sin 45OP OM α︒=︒+,同理()sin 45sin 75OP ON α︒=︒+故1sin 2OMN S OM ON MON ∆=⨯⨯⨯∠ ()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+ ()()1sin 45sin 4530αα=︒+︒++︒====()131sin 23042α=++︒因为060α︒≤≤︒,30230150α︒≤+︒≤︒,所以当30α=︒时,()sin 230α+︒的最大值为1,此时OMN ∆的面积取到最小值.即230POM ∠=︒时,OMN ∆的面积的最小值为843-.34.〔2013年高考卷〔文〕〕向量1(cos ,),(3sin ,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b . (Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最小正周期ππ==22T .所以),62sin()(π-=x x f 最小正周期为π. (Ⅱ)上的图像知,在,由标准函数时,当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈.]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f . 所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-.35.〔2013年高考卷〔文〕〕(本小题总分值13分,(Ⅰ)小问4分,(Ⅱ)小问9分)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且2223a b c ab =++. (Ⅰ)求A ;(Ⅱ)设3a =,S 为△ABC 的面积,求3cos cos S B C +的最大值,并指出此时B 的值.【答案】36.〔2013年高考卷〔文〕〕在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A c ---+=-.(Ⅰ)求sin A 的值;(Ⅱ)假设42a =,5b =,求向量BA 在BC 方向上的投影.【答案】解:(Ⅰ)由3cos()cos sin()sin()5A B B A B A c ---+=- 得53sin )sin(cos )cos(-=---B B A B B A ,那么 53)cos(-=+-B B A ,即 53cos -=A又π<<A 0,那么 54sin =A(Ⅱ)由正弦定理,有 BbA a sin sin =,所以22sin sin ==a A b B , 由题知b a >,那么 B A >,故4π=B .根据余弦定理,有 )53(525)24(222-⨯⨯-+=c c , 解得 1=c 或 7-=c (负值舍去),向量BA 在BC 方向上的投影为=B BA cos 22 37.〔2013年高考卷〔文〕〕在△ABC 中,角A,B,C 的对边分别为a,b,c,sinAsinB+sinBsinC+cos2B=1.(1)求证:a,b,c 成等差数列;(2) 假设C=23π,求ab的值. 【答案】解:(1)由得sinAsinB+sinBsinC+1-2sin 2B=1.故sinAsinB+sinBsinC=2sin 2B因为sinB 不为0,所以sinA+sinC=2sinB 再由正弦定理得a+c=2b,所以a,b,c 成等差数列(2)由余弦定理知2222cos c a b ac C =+-得2222(2)2cos3b a a b ac π-=+-化简得35a b = 38.〔2013年高考卷〔文〕〕在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c . cos23cos()1A B C -+=.(Ⅰ)求角A 的大小; (Ⅱ)假设△ABC 的面积53S =,5b =,求sin sin B C 的值.【答案】(Ⅰ)由cos 23cos()1A B C -+=,得22cos 3cos 20A A +-=,即(2cos 1)(cos 2)0A A -+=,解得1cos 2A = 或cos 2A =-(舍去). 因为0πA <<,所以π3A =. (Ⅱ)由1133sin 53,2224S bc A bc bc ==⋅==得20bc =. 又5b =,知4c =. 由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故21a =.又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.39.〔2013年高考〔文〕〕设函数()sin sin()3f x x x π=++.(Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合;(Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化得到.【答案】解:(1)3sincos 3cossin sin )(ππx x x x f ++=x x x x x cos 23sin 23cos 23sin 21sin +=++=)6sin(3)6sin()23()23(22ππ+=++=x x当1)6sin(-=+πx 时,3)(min -=x f ,此时)(,234,2236Z k k x k x ∈+=∴+=+πππππ所以,)(x f 的最小值为3-,此时x 的集合},234|{Z k k x x ∈+=ππ.(2)x y sin =横坐标不变,纵坐标变为原来的3倍,得x y sin 3=; 然后x y sin 3=向左平移6π个单位,得)6sin(3)(π+=x x f 40.〔2013年高考卷〔文〕〕函数21(2cos 1)sin 2cos 42f x x x x =-+(). (I)求f x ()的最小正周期与最大值;(II)假设(,)2παπ∈,且22f α=(),求α的值. 【答案】解:(I)因为21(2cos 1)sin 2cos 42f x x x x =-+()=1cos 2sin 2cos 42x x x + =1(sin 4cos 4)2x x +=2)24x π+,所以()f x 的最小正周期为2π,最大值为22.(II)因为2f α=(),所以sin(4)14πα+=. 因为(,)2παπ∈,所以9174(,)444πππα+∈,所以5442ππα+=,故916πα=. 41.〔2013年高考数学试题〔文科〕〕此题共有2个小题.第1小题总分值6分,第2小题总分值8分.函数()2sin()f x x ω=,其中常数0ω>. (1)令1ω=,判断函数()()()2F x f x f x π=++的奇偶性并说明理由;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再往上平移1个单位,得到函数()y g x =的图像.对任意的a R ∈,求()y g x =在区间[,10]a a π+上零点个数的所有可能值.【答案】法一:解:(1)()2sin 2sin()2sin 2cos )24F x x x x x x ππ=++=+=+ ()F x 是非奇函数非偶函数.∵()0,()44F F ππ-==∴()(),()()4444F F F F ππππ-≠-≠-∴函数()()()2F x f x f x π=++是既不是奇函数也不是偶函数.(2)2ω=时,()2sin 2f x x =,()2sin 2()12sin(2)163g x x x ππ=++=++,其最小正周期T π=由2sin(2)103x π++=,得1sin(2)32x π+=-,[来源:学,科,网] ∴2(1),36k x k k Z πππ+=--⋅∈,即(1),2126k k x k Z πππ=--⋅-∈ 区间[],10a a π+的长度为10个周期,假设零点不在区间的端点,那么每个周期有2个零点;假设零点在区间的端点,那么仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点; 故当(1),2126k k a k Z πππ=--⋅-∈时,21个,否那么20个. 法二:42.〔2013年高考卷〔文〕〕设向量()()3sin ,sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)假设.a b x =求的值;(II)设函数()(),.f x a b f x =求的最大值【答案】。
2013年全国各省(市)高考数学真题(文)分类汇编与解析(一)三角函数与数列

2013年全国各省(市)高考真题数学(文)分类汇编与解析(一)三角函数与数列(黑龙江zhnagyajun131@)2013年6月24日1.(2013年安徽卷16题)(本小题满分12分)设函数()sin sin()3f x x x π=++.(Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合; (Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化得到.【解析】(1)3sin cos 3cos sin sin )(ππx x x x f ++=x x x x x cos 23sin 23cos 23sin 21sin +=++= )6sin(3)6sin()23()23(22ππ+=++=x x当1)6sin(-=+πx 3,此时34,2236x k x =∴+=+ππππ所以,)(x f 的最小值为},234|Z k k x ∈+=ππ. (2)x y sin =倍,得x y sin 3=; 然后x y sin 3=6)6sin(3π+x【考点定位】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力,中等难度.2. (2013年北京卷18题) (本小题共13分)已知函数2()sin cos f x x x x x =++。
(Ⅰ)若曲线()y f x =在点(,())a f a 处与直线y b =相切,求a 与b 的值。
(Ⅱ)若曲线()y f x =与直线y b =有两个不同的交点,求b 的取值范围。
3.(2013年福建卷17题)(本小题满分12分)已知等差数列{}n a 的公差1d =,前n 项和为n S . (1)若131,,a a 成等比数列,求1a ; (2)若519S a a >,求1a 的取值范围.本小题主要考查等比等差数列、等比数列和不等式等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想.满分12分. 解:(1)因为数列{}n a 的公差1d =,且131,,a a 成等比数列, 所以2111(2)a a =⨯+,即21120a a --=,解得11a =-或12a =. (2)因为数列{}n a 的公差1d =,且519S a a >,所以21115108a a a +>+; 即2113100a a +-<,解得152a -<<4. (2013年广东卷16题).(本小题满分12分)已知函数(),f x x x R π⎛⎫=-∈ ⎪⎝.(1) 求3f π⎛⎫ ⎪⎝⎭的值;(2) 若33cos ,,252πθθ⎛=∈⎝【解析】(1)13f π⎛⎫= ⎪⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-, 1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.【解析】这个题实在是太简单,两角差的余弦公式不要记错了.5.( 2013年广西卷17题).(本小题满分10分)等差数列{}n a 中,71994,2,a a a ==(I )求{}n a 的通项公式; (II )设{}1,.n n n nb b n S na =求数列的前项和6.(全国新课标二卷17题).(本小题满分12分)△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB。
2013年全国各地高考数学试题及解答分类汇编大全(08 三角函数 三角恒等变换)

2013年全国各地高考数学试题及解答分类汇编大全 (08三角函数 三角恒等变换)一、选择题:1.(2013福建文) 将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是( ) A .35π B .65π C .2π D .6π 【答案】B【解析】本题考查的三角函数的图像的平移.把)23,0(P 代入)22)(2sin()(πθπθ<<-+=x x f ,解得3πθ=,所以)232sin()(ϕπ-+=x x g ,把)23,0(P 代入得,πϕk =或6ππϕ-=k ,观察选项,故选B2.(2013广东文) 已知51sin()25πα+=,那么cos α= A .25- B .15- C .15 D .25【解析】:考查三角函数诱导公式,51sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭,选C.3、(2013湖北文、理) 将函数()sin y x x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是( )A. 12πB. 6πC. 3πD. 56π【解析与答案】解析 y =3cos x +sin x =2sin(x +π3)向左平移m 个单位长度后得到y =2sin(x +π3+m )它关于y 轴对称可得sin(π3+m )=±1, ∴π3+m =k π+π2,k ∈Z ,∴m =k π+π6,k ∈Z ,∵m >0,∴m 的最小值为π6. 答案 B【相关知识点】三角函数图象及其变换4. (2013江西文) sincos 23αα==若 ( )A. 23-B. 13-C. 13D.23[答案]:C[解析]:211cos 12sin12233αα=-=-⨯=5. (2013江西文) 如图。
2013年数学高考题分类三角函数-推荐下载

首先判断函数的奇偶性进行排除,然后再根据函数的图象特征取最佳值进行验证排除.,即x x x f sin )cos 1()(--=-)(f x f -=-关于原点对称,所以函数为奇函数,排除B.又当)(x f ,排除A. 当时012sin >=π43π=x 123+π等问题,合理利用管线敷设技术。
线缆敷设原则:在分线盒处,当不同电压回路交叉时,应采用金属隔板进行隔开处理;同一线槽内,强电回路须同时切断习题电源,线缆敷设完毕,要进行检查和检测处理。
调试工作并且进行过关运行高中资料试卷技术指导。
对于调试过程中高中资料试卷技术问题,作为调试人员,需要在事前掌握图纸资料、设备制造厂家出具高中资料试卷试验报告与相关技术资料,并且了解现场设备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
护装置调试技术,要求电力保护装置做到准确灵活。
对于差动保护装置高中资料试卷调试技术是指发电机一变压器组在发生内部故障时,需要进行外部电源高中资料试卷切除从而采用高中资料试卷主要保护装置。
A. B.54【解题指南】观察图象可知,【解析】选B.由图像可知,2.(2013·山东高考理科π移个单位后,得到一个偶函数的图象,则C.D.4,6π-4,对函数,ωϕ()2sin(f x ω=.,根据图象可知359()412312T πππ=--==B.2,-D.4,3π式,为解决高中语文电气课件中管壁薄、接口不严等问题,合理利用管线敷设技术。
线缆敷设原则:在分线盒处,当不同电压回路交叉时,应采用金属隔板进行隔开处理;同一线槽内,强电回路须同时切断习题电源,线缆敷设完毕,要进行检查和检测处理。
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料试卷相互作用与相互关案;对整套启动过程中高中资料试卷电气设备进行调试工作并且进行过关运行高中资料试卷技术指导。
2013年高中数学全国各地高考真题分类汇编文科数学C单元 三角函数

C 单元 三角函数C1 角的概念及任意的三角函数14.C1,C2,C6[2013·四川卷] 设sin 2α=-sin α,α∈π2,π,则tan 2α的值是________.14.3 [解析] 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,又α∈⎝ ⎛⎭⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2 α=2×(-3)1-3= 3.方法二:同上得cos α=-12,又α∈⎝ ⎛⎭⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3= 3.C2 同角三角函数的基本关系式与诱导公式2.C2[2013·全国卷] 已知α是第二象限角,sin α=513,则cos α=( )A .-1213B .-513 C.513 D.12132.A [解析] cos α=-1-sin 2 α=-1213.16.C2,C5[2013·广东卷] 已知函数f(x)=2cos ⎝ ⎛⎭⎪⎫x -π12,x ∈R .(1)求f ⎝ ⎛⎭⎪⎫π3的值;(2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝ ⎛⎭⎪⎫θ-π6.16.解:14.C1,C2,C6[2013·四川卷] 设sin 2α=-sin α,α∈π2,π,则tan 2α的值是________.14.3 [解析] 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,又α∈⎝ ⎛⎭⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2α=2×(-3)1-3= 3. 方法二:同上得cos α=-12,又α∈⎝ ⎛⎭⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3= 3.C3 三角函数的图像与性质1.C3[2013·江苏卷] 函数y =3sin ⎝⎛⎭⎪⎫2x +π4的最小正周期为________.1.π [解析] 周期为T =2π2=π.17.C3[2013·辽宁卷] 设向量a =(3sin x ,sin x),b =(cos x ,sin x),x ∈0,π2.(1)若|a|=|b|,求x 的值; (2)设函数f(x)=a·b ,求f(x)的最大值.17.解:(1)由|a |2=(3sin x)2+(sin x)2=4sin 2 x , |b |2=(cos x)2+(sin x)2=1. 及|a|=|b |,得4sin 2 x =1.又x ∈0,π2,从而sin x =12,所以x =π6.(2)f(x)=a·b =3sin x ·cos x +sin 2x =32sin 2x -12cos 2x +12=sin2x -π6+12,当x =π3∈0,π2时,sin2x -π6取最大值1. 所以f(x)的最大值为32.9.C3[2013·山东卷] 函数y =xcos x +sin x 的图像大致为( )图1-39.D [解析] ∵f(-x)=-xcos(-x)+sin(-x)=-(xcos x +sin x)=-f(x),∴y =xcos x +sin x 为奇函数,图像关于原点对称,排除选项B ,当x =π2,y =1>0,x =π,y =-π<0,故选D.16.C3、C5、C9[2013·新课标全国卷Ⅰ] 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.16.-2 55 [解析] f(x)=sin x -2cos x =5⎝⎛⎭⎫15sin x -25cos x ,令cos α=15,sin α=25,则f(x)=5sin(x -α).当θ-α=2k π+π2,即θ=2k π+π2+α(上述k 为整数)时,f(x)取得最大值,此时 cos θ=-sin α=-2 55.C4 函数 的图象与性质16.C4[2013·安徽卷] 设函数f(x)=sin x +sin ⎝ ⎛⎭⎪⎫x +π3.(1)求f(x)的最小值,并求使f(x)取最小值的x 的集合;(2)不画图,说明函数y =f(x)的图像可由y =sin x 的图像经过怎样的变化得到. 16.解:(1)因为f(x)=sin x +12sin x +32cos x =32sin x +32cos x =3sinx +π6,所以当x +π6=2k π-π2(k ∈Z ),即x =2k π-2π3(k ∈Z )时,f(x)取得最小值- 3.此时x 的取值集合为x 错误!x =2k π-错误!,k ∈Z .(2)先将y =sin x 的图像上所有点的纵坐标伸长到原来的3倍(横坐标不变),得y =3sin x 的图像;再将y =3sin x 的图像上所有的点向左平移π6个单位,得y =f(x)的图像.15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x ·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4. 所以4α+π4=5π2.故α=9π16.9.C4[2013·全国卷] 若函数y =sin(ωx +φ)(ω>0)的部分图像如图1-1所示,则ω=( )图1-1A .5B .4C .3D .29.B [解析] 根据对称性可得π4为已知函数的半个周期,所以2πω=2×π4,解得ω=4.9.C4[2013·福建卷] 将函数f(x)=sin(2x +θ)⎝ ⎛⎭⎪⎫-π2<θ<π2的图像向右平移φ(φ>0)个单位长度后得到函数g(x)的图像.若f(x),g(x)的图像都经过点P ⎝⎛⎭⎫0,32,则φ的值可以是( ) A.5π3 B.5π6C.π2D.π69.B [解析] g(x)=f(x -φ)=sin[2(x -φ)+θ],由sin θ=32,-π2<θ<π2,得θ=π3,又sin(θ-2φ)=32,结合选项,知φ的一个值为5π6,故选B.6.C4[2013·湖北卷] 将函数y =3cos x +sin x(x ∈R )的图像向左平移m(m >0)个单位长度后,所得到的图像关于y 轴对称,则m 的最小值是( )A.π12B.π6C.π3D.5π66.B [解析] 结合选项,将函数y =3cos x +sin x =2sin ⎝ ⎛⎭⎪⎫x +π3的图像向左平移π6个单位得到y =2sin ⎝ ⎛⎭⎪⎫x +π2=2cos x ,它的图像关于y 轴对称,选B.13.C4[2013·江西卷] 设f(x)=3sin 3x +cos 3x ,若对任意实数x 都有|f(x)|≤a ,则实数a 的取值范围是________.13.a ≥2 [解析] |f(x)|max =2,则a ≥2.16.C4[2013·新课标全国卷Ⅱ] 函数y =cos(2x +φ)(-π≤φ<π)的图像向右平移π2个单位后,与函数y =sin ⎝⎛⎭⎪⎫2x +π3的图像重合,则φ=________.16.5π6 [解析] 由已知,y =cos(2x +φ)的图像向右平移π2得到y =cos(2x -π+φ)=-cos(2x +φ).y =sin ⎝ ⎛⎭⎪⎫2x +π3=-cos ⎝ ⎛⎭⎪⎫π2+2x +π3=-cos ⎝⎛⎭⎫2x +56π,两个函数图像重合,故φ=56π. 18.C4,C7[2013·山东卷] 设函数f(x)=32-3sin 2 ωx -sin ωx cos ωx(ω>0),且y =f(x)图像的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f(x)在区间π,3π2上的最大值和最小值.18.解:(1)f(x)=32-3sin 2ωx -sin ωxcos ωx =32-3·1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -12sin 2ωx =-sin ⎝⎛⎭⎪⎫2ωx -π3.因为图像的一个对称中心到最近的对称轴的距离为π4,又ω>0, 所以2π2ω=4×π4.因此ω=1.(2)由(1)知f(x)=-sin ⎝⎛⎭⎪⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3.所以-32≤sin ⎝⎛⎭⎪⎫2x -π3≤1. 因此-1≤f(x)≤32. 故f(x)在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.6.C4[2013·天津卷] 函数f(x)=sin2x -π4在区间0,π2上的最小值为( )A .-1B .-22C.22D .06.B [解析] ∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴2x -π4∈⎣⎢⎡⎦⎥⎤-π4,3π4,当2x -π4=-π4时,f(x)有最小值-22.图1-36.C4[2013·四川卷] 函数f(x)=2sin(ωx +φ)ω>0,-π2<φ<π2的部分图像如图1-3所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π36.A [解析] 由半周期T 2=11π12-5π12=π2,可知周期T =π,从而ω=2,于是f(x)=2sin(2x+φ).当x =5π12时,f ⎝ ⎛⎭⎪⎫5π12=2,即sin ⎝ ⎛⎭⎪⎫5π6+φ=1,于是5π6+φ=2k π+π2(k ∈Z ),因为-π2<φ<π2,取k =0,得φ=-π3.16.F3,C4[2013·陕西卷] 已知向量a =⎝⎛⎭⎫cos x ,-12,b =(3sin x ,cos 2x),x ∈R ,设函数f(x)=a·b .(1)求f(x)的最小正周期;(2)求f(x)在⎣⎢⎡⎦⎥⎤0,π2上的最大值和最小值.16.解: f(x)=⎝⎛⎭⎫cos x ,-12·(3sin x ,cos 2x)=3cos xsin x -12cos 2x =32sin 2x -12cos 2x =cos π6sin 2x -sin π6cos 2x =sin ⎝⎛⎭⎪⎫2x -π6.(1)f(x)的最小正周期为T =2πω=2π2=π,即函数f(x)的最小正周期为π.(2)∵0≤x ≤π2,∴-π6≤2x -π6≤5π6.由正弦函数的性质,当2x -π6=π2,即x =π3时,f(x)取得最大值1.当2x -π6=-π6,即x =0时,f(0)=-12,当2x -π6=56π,即x =π2时,f ⎝ ⎛⎭⎪⎫π2=12,∴f(x)的最小值为-12.因此,f(x)在0,π2上最大值是1,最小值是-12.6.C4[2013·浙江卷] 函数f(x)=sin xcos x +32cos 2x 的最小正周期和振幅分别是( ) A .π,1 B .π,2C .2π,1D .2π,26.A [解析] f(x)=12sin 2x +32cos 2x =sin2x +π3,则最小正周期为π;振幅为1,所以选择A.C5 两角和与差的正弦、余弦、正切15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4. 所以4α+π4=5π2.故α=9π16.16.C2,C5[2013·广东卷] 已知函数f(x)=2cos ⎝ ⎛⎭⎪⎫x -π12,x ∈R .(1)求f ⎝ ⎛⎭⎪⎫π3的值;(2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝ ⎛⎪⎫θ-π6.16.解:3.C5[2013·江西卷] 若sin α2=33,则cos α=( )A .-23B .-13C.13D.233.C [解析] cos α=1-2sin 2 α2=13,故选C.17.C5,C8,F1[2013·四川卷] 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B)cos B -sin(A -B)sin(A +C)=-35.(1)求sin A 的值;(2)若a =4 2,b =5,求向量BA →在BC →方向上的投影. 17.解:(1)由cos(A -B)cos B -sin(A -B)sin(A +C)=-35,得cos(A -B)cos B -sin(A -B)sin B =-35.则cos(A -B +B)=-35,即cos A =-35.又0<A<π,则sin A =45.(2)由正弦定理,有a sin A =b sin B, 所以,sin B =bsin A a =22.由题知a>b ,则A>B ,故B =π4.根据余弦定理,有(4 2)2=52+c 2-2×5c ×⎝⎛⎭⎫-35, 解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.16.C3、C5、C9[2013·新课标全国卷Ⅰ] 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.16.-2 55 [解析] f(x)=sin x -2cos x =5⎝⎛⎭⎫15sin x -25cos x ,令cos α=15,sin α=25,则f(x)=5sin(x -α).当θ-α=2k π+π2,即θ=2k π+π2+α(上述k 为整数)时,f(x)取得最大值,此时 cos θ=-sin α=-2 55.18.C5和C8[2013·重庆卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2=b 2+c 2+3bc. (1)求A ;(2)设a =3,S 为△ABC 的面积,求S +3cos Bcos C 的最大值,并指出此时B 的值.18.解:(1)由余弦定理得cos A =b 2+c 2-a 22bc =-3bc 2bc =-32.又因为0<A<π,所以A =5π6.(2)由(1)得sin A =12,又由正弦定理及a =3得S =12bcsin A =12·asin B sin A·asin C =3sin Bsin C ,因此,S +3cos Bcos C =3(sin Bsin C +cos Bcos C)=3cos(B -C). 所以,当B =C ,即B =π-A 2=π12时,S +3cos Bcos C 取最大值3.C6 二倍角公式15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x ·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4.所以4α+π4=5π2.故α=9π16.6.C6[2013·新课标全国卷Ⅱ] 已知sin 2α=23,则cos 2⎝ ⎛⎭⎪⎫α+π4=( )A.16B.13 C.12 D.236.A [解析] cos 2⎝ ⎛⎭⎪⎫α+π4=1+cos ⎝⎛⎭⎪⎫2α+π22=1-sin 2α2=16,故选A.14.C1,C2,C6[2013·四川卷] 设sin 2α=-sin α,α∈π2,π,则tan 2α的值是________.14.3 [解析] 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,又α∈⎝ ⎛⎭⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2α=2×(-3)1-3= 3. 方法二:同上得cos α=-12,又α∈⎝ ⎛⎭⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3= 3.15.C6、E1和E3[2013·重庆卷] 设0≤α≤π,不等式8x 2-(8sin α)x +cos 2α≥0对x ∈R恒成立,则α的取值范围为________.15.⎣⎢⎡⎦⎥⎤0,π6∪⎣⎢⎡⎦⎥⎤5π6,π [解析] 根据二次函数的图像可得Δ=(8sin α)2-4×8cos 2α≤0,即2sin 2 α-cos 2α≤0,转化为2sin 2 α-(1-2sin 2 α)≤0,即4sin 2α≤1,即-12≤sinα≤12.因为0≤α≤π,故α∈⎣⎢⎡⎦⎥⎤0,π6∪⎣⎢⎡⎦⎥⎤5π6,π.C7 三角函数的求值、化简与证明15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x ·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4. 所以4α+π4=5π2.故α=9π16.18.C7、C8[2013·全国卷] 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c)(a -b +c)=ac.(1)求B ;(2)若sin Asin C =3-14,求C.18.解:(1)因为(a +b +c)(a -b +c)=ac , 所以a 2+c 2-b 2=-ac.由余弦定理得cos B =a 2+c 2-b 22ac =-12,因此B =120°.(2)由(1)知A +C =60°, 所以cos (A -C)=cos Acos C +sin Asin C=cos Acos C -sin Asin C +2sin Asin C =cos(A +C)+2sinAsin C=12+2×3-14 =32, 故A -C =30°或A -C =-30°, 因此C =15°或C =45°.18.C4,C7[2013·山东卷] 设函数f(x)=32-3sin 2 ωx -sin ωx cos ωx(ω>0),且y =f(x)图像的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f(x)在区间π,3π2上的最大值和最小值.18.解:(1)f(x)=32-3sin 2ωx -sin ωxcos ωx =32-3·1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -12sin 2ωx =-sin ⎝⎛⎭⎪⎫2ωx -π3.因为图像的一个对称中心到最近的对称轴的距离为π4,又ω>0, 所以2π2ω=4×π4.因此ω=1.(2)由(1)知f(x)=-sin ⎝⎛⎭⎪⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3.所以-32≤sin ⎝⎛⎭⎪⎫2x -π3≤1.因此-1≤f(x)≤32. 故f(x)在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.16.C7,C8[2013·天津卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.已知bsin A =3csin B ,a =3,cos B =23.(1)求b 的值; (2)求sin2B -π3的值.16.解:(1)在△ABC 中,由a sin A =bsin B ,可得bsin A =asin B ,又由bsin A =3csin B ,可得a =3c ,又a =3,故c =1.由b 2=a 2+c 2-2accos B ,cos B =23,可得b = 6.(2)由cos B =23,得sin B =53,进而得cos 2B =2cos 2 B -1=-19,sin 2B =2sin Bcos B =4 59. 所以sin2B -π3=sin 2Bcos π3-cos 2Bsin π3=4 5+318.C8 解三角形9.C8[2013·安徽卷] 设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,若b +c =2a ,3sin A =5sin B ,则角C =( )A.π3B.2π3C.3π4D.5π69.B [解析] 根据正弦定理,3sin A =5sin B 可化为3a =5b ,又b +c =2a ,解得b =3a 5,c =7a5.令a =5t(t>0),则b =3t ,c =7t ,在△ABC 中,由余弦定理得cos C =a 2+b 2-c 22ab =25t 2+9t 2-49t 22×5t ×3t=-12,所以C =2π3.5.C8[2013·北京卷] 在△ABC 中,a =3,b =5,sin A =13,则sin B =( )A.15B.59C.53D .1 5.B [解析] 由正弦定理得a sin A =b sin B ,即313=5sin B ,解得sin B =59. 18.C7、C8[2013·全国卷] 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c)(a -b +c)=ac.(1)求B ;(2)若sin Asin C =3-14,求C. 18.解:(1)因为(a +b +c)(a -b +c)=ac , 所以a 2+c 2-b 2=-ac.由余弦定理得cos B =a 2+c 2-b 22ac =-12,因此B =120°.(2)由(1)知A +C =60°, 所以cos (A -C)=cos Acos C +sin Asin C=cos Acos C -sin Asin C +2sin Asin C =cos(A +C)+2sinAsin C =12+2×3-14 =32, 故A -C =30°或A -C =-30°, 因此C =15°或C =45°.21.C8,C9[2013·福建卷] 如图1-6,在等腰直角△OPQ 中,∠POQ =90°,OP =2 2,点M 在线段PQ 上.(1)若OM =5,求PM 的长;(2)若点N 在线段MQ 上,且∠MON =30°,问:当∠POM 取何值时,△OMN 的面积最小?并求出面积的最小值.图1-621.解:(1)在△OMP 中,∠OPM =45°,OM =5,OP =2 2, 由余弦定理得,OM 2=OP 2+MP 2-2OP·MP·cos 45°,得MP 2-4MP +3=0, 解得MP =1或MP =3.(2)设∠POM =α,0°≤α≤60°,在△OMP 中,由正弦定理,得OM sin ∠OPM =OPsin ∠OMP ,所以OM =OPsin 45°sin (45°+α),同理ON =OPsin 45°sin (75°+α).故S △OMN =12OM ·ON ·sin ∠MON=14×OP 2sin 2 45°sin (45°+α)sin (75°+α) =1sin (45°+α)sin (45°+α+30°)=1sin (45°+α)⎣⎡⎦⎤32sin (45°+α)+12cos (45°+α)=1 32sin 2(45°+α)+12sin (45°+α)cos (45°+α) =134[1-cos (90°+2α)]+14sin (90°+2α) =134+34sin 2α+14cos 2α =1 34+12sin (2α+30°). 因为0°≤α≤60°,30°≤2α+30°≤150°,所以当α=30°时,sin(2α+30°)的最大值为1,此时△OMN 的面积取到最小值.即∠POM =30°时,△OMN 的面积的最小值为8-4 3.18.C8[2013·湖北卷] 在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c.已知cos 2A -3cos(B +C)=1.(1)求角A 的大小;(2)若△ABC 的面积S =5 3,b =5,求sinB sin C 的值.18.解:(1)由cos 2A -3cos(B +C)=1,得2cos 2A +3cos A -2=0, 即(2cos A -1)(cos A +2)=0,解得cos A =12或cos A =-2(舍去).因为0<A <π,所以A =π3.(2)由S =12bc sin A =12bc ·32=34bc =5 3,得bc =20,又b =5,知c =4.由余弦定理得a 2=b 2+c 2-2bc·cos A =25+16-20=21,故a =21. 又由正弦定理得sin Bsin C =b a sin A ·c a sin A =bc a 2sin 2A =2021×34=57.5.C8[2013·湖南卷] 在锐角△ABC 中,角A ,B 所对的边长分别为a ,b.若2asin B =3b ,则角A 等于( )A.π3B.π4C.π6D.π125.A [解析] 由正弦定理可得2sin Asin B =3sin B .又sin B ≠0,所以sin A =32.因为A 为锐角,故A =π3,选A.17.C8[2013·江西卷] 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知sin Asin B +sin Bsin C +cos 2B =1.(1)求证:a ,b ,c 成等差数列;(2)若C =2π3,求ab的值.17.解:(1)证明:由题意得sin Asin B +sin Bsin C =2sin 2 B ,因为sin B ≠0,所以sin A +sin C =2sin B ,由正弦定理,有a +c =2b ,即a ,b ,c 成等差数列. (2)由C =2π3,c =2b -a 及余弦定理得(2b -a)2=a 2+b 2+ab ,即有5ab -3b 2=0,所以a b =35.6.C8[2013·辽宁卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c.若asin Bcos C +csin Bcos A =12b ,且a>b ,则∠B =( )A.π6B.π3C.2π3D.5π66.A [解析] 由正弦定理可以得到sin Asin Bcos C +sin Csin Bcos A =12sin B ,所以可以得到sin Acos C +sin Ccos A =12,即sin(A +C)=sin B =12,则∠B =π6,故选A.4.C8[2013·新课标全国卷Ⅱ] △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b =2,B =π6,C =π4,则△ABC 的面积为( )A .2 3+2 B.3+1 C .2 3-2 D.3-14.B [解析] b sin B =c sin Cc =2 2.又A +B +C =π,∴A =712π,∴△ABC 的面积为12×2×2 2×sin 7π12=22×6+24=3+1.7.C8[2013·山东卷] △ABC 的内角A ,B ,C 所对的边分别为a ,b ,c.若B =2A ,a =1,b =3,则c =( )A .2 3B .2 C. 2 D .17.B [解析] 由正弦定理a sinA =b sinB ,即1sinA =3sinB =32sinAcosA ,解之得cosA =32,∴A =π6,B =π3,C =π2,∴c =a 2+b 2=()32+12=2.9.C8[2013·陕西卷] 设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若bcos C +ccos B =asin A ,则△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定9.A [解析] 结合已知bcos C +ccos B =asin A ,所以由正弦定理可知sin Bcos C +sin Ccos B =sin Asin A ,即sin (B +C)=sin 2A sin A =sin 2A sin A =1,故A =90°,故三角形为直角三角形.16.C7,C8[2013·天津卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.已知bsin A =3csin B ,a =3,cos B =23.(1)求b 的值; (2)求sin2B -π3的值.16.解:(1)在△ABC 中,由a sin A =bsin B ,可得bsin A =asin B ,又由bsin A =3csin B ,可得a =3c ,又a =3,故c =1.由b 2=a 2+c 2-2accos B ,cos B =23,可得b = 6.(2)由cos B =23,得sin B =53,进而得cos 2B =2cos 2 B -1=-19,sin 2B =2sin Bcos B =4 59. 所以sin2B -π3=sin 2Bcos π3-cos 2Bsin π3=4 5+318.17.C5,C8,F1[2013·四川卷] 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B)cos B -sin(A -B)sin(A +C)=-35.(1)求sin A 的值;(2)若a =4 2,b =5,求向量BA →在BC →方向上的投影. 17.解:(1)由cos(A -B)cos B -sin(A -B)sin(A +C)=-35,得cos(A -B)cos B -sin(A -B)sin B =-35.则cos(A -B +B)=-35,即cos A =-35.又0<A<π,则sin A =45.(2)由正弦定理,有a sin A =b sin B, 所以,sin B =bsin A a =22.由题知a>b ,则A>B ,故B =π4.根据余弦定理,有(4 2)2=52+c 2-2×5c ×⎝⎛⎭⎫-35, 解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.15.H1,C8,E8[2013·四川卷] 在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),D(7,-1)的距离之和最小的点的坐标是________.15.(2,4) [解析] 在以A ,B ,C ,D 为顶点构成的四边形中,由平面几何知识:三角形两边之和大于第三边,可知当动点落在四边形两条对角线AC ,BD 交点上时,到四个顶点的距离之和最小.AC 所在直线方程为y =2x ,BD 所在直线方程为y =-x +6,交点坐标为(2,4),即为所求.10.C8[2013·新课标全国卷Ⅰ] 已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2 A +cos 2A =0,a =7,c =6,则b =( )A .10B .9C .8D .510.D [解析] 由23cos 2A +cos 2A =0,得25cos 2A =1.因为△ABC 为锐角三角形,所以cos A =15.在△ABC 中,根据余弦定理,得49=b 2+36-12b ×15,即b 2-125b -13=0,解得b =5或-135(舍去). 18.C8[2013·浙江卷] 在锐角△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2asin B = 3b.(1)求角A 的大小;(2)若a =6,b +c =8,求△ABC 的面积.18.解:(1)由2asin B = 3b 及正弦定理a sin A =b sin B,得 sin A = 32.因为A 是锐角,所以A =π3. (2)由余弦定理a 2=b 2+c 2-2bc cos A 得b 2+c 2-bc =36.又b +c =8,所以bc =283. 由三角形面积公式S =12bcsin A ,得△ABC 的面积为7 33. 18.C5和C8[2013·重庆卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2=b 2+c 2+3bc.(1)求A ;(2)设a =3,S 为△ABC 的面积,求S +3cos Bcos C 的最大值,并指出此时B 的值.18.解:(1)由余弦定理得cos A =b 2+c 2-a 22bc =-3bc 2bc =-32. 又因为0<A<π,所以A =5π6. (2)由(1)得sin A =12,又由正弦定理及a =3得 S =12bcsin A =12·asin B sin A·asin C =3sin Bsin C , 因此,S +3cos Bcos C =3(sin Bsin C +cos Bcos C)=3cos(B -C).所以,当B =C ,即B =π-A 2=π12时,S +3cos Bcos C 取最大值3.C9 单元综合21.C8,C9[2013·福建卷] 如图1-6,在等腰直角△OPQ 中,∠POQ =90°,OP =2 2,点M 在线段PQ 上.(1)若OM =5,求PM 的长;(2)若点N 在线段MQ 上,且∠MON =30°,问:当∠POM 取何值时,△OMN 的面积最小?并求出面积的最小值.图1-621.解:(1)在△OMP 中,∠OPM =45°,OM =5,OP =2 2,由余弦定理得,OM 2=OP 2+MP 2-2OP·MP·cos 45°,得MP 2-4MP +3=0,解得MP =1或MP =3.(2)设∠POM =α,0°≤α≤60°,在△OMP 中,由正弦定理,得OM sin ∠OPM =OP sin ∠OMP, 所以OM =OPsin 45°sin (45°+α),同理ON =OPsin 45°sin (75°+α). 故S △OMN =12OM ·ON ·sin ∠MON =14×OP 2sin 2 45°sin (45°+α)sin (75°+α)=1sin (45°+α)sin (45°+α+30°)=1sin (45°+α)⎣⎡⎦⎤32sin (45°+α)+12cos (45°+α) =1 32sin 2(45°+α)+12sin (45°+α)cos (45°+α) =1 34[1-cos (90°+2α)]+14sin (90°+2α) =1 34+34sin 2α+14cos 2α =1 34+12sin (2α+30°). 因为0°≤α≤60°,30°≤2α+30°≤150°,所以当α=30°时,sin(2α+30°)的最大值为1,此时△OMN 的面积取到最小值.即∠POM =30°时,△OMN 的面积的最小值为8-4 3.18.C9[2013·江苏卷] 如图1-4,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C.现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C.假设缆车匀速直线运动的速度为130 m/min ,山路AC 长为1 260 m ,经测量,cos A =1213,cos C =35. (1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?图1-418.解:(1)在△ABC 中,因为cos A =1213,cos C =35, 所以sin A =513,sin C =45, 从而sin B =sin[π-(A +C)]=sin(A +C)=sin Acos C +cos Asin C=513×35+1213×45=6365. 由正弦定理AB sin C =AC sin B,得 AB =AC sin B ×sin C =1 2606365×45=1 040(m). 所以索道AB 的长为1 040 m.(2)假设乙出发t 分钟后,甲、乙两游客距离为d ,此时,甲行走了(100+50t)m ,乙距离A 处130t m ,所以由余弦定理得d 2=(100+50t)2+(130t)2-2×130t ×(100+50t)×1213=200(37t 2-70t +50). 因为0≤t ≤1 040130,即0≤t ≤8, 故当t =3537(min)时,甲、乙两游客距离最短. (3)由正弦定理BC sin A =AC sin B,得 BC =AC sin B ×sin A =1 2606365×513=500(m). 乙从B 出发时,甲已走了50×(2+8+1)=550(m),还需走710 m 才能到达C.设乙步行的速度为v m/min ,由题意得-3≤500v -71050≤3,解得1 25043≤v ≤62514,所以为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎣⎡⎦⎤1 25043,62514(单位:m/min)范围内. 15.C9[2013·江苏卷] 已知a =(cos α,sin α),b =(cos β,sin β),0<β<α<π.(1)若|a -b |=2,求证:a ⊥b ;(2)设c =(0,1),若a +b =c ,求α,β的值.15.解:(1)由题意得|a -b|2=2,即(a -b )2=a 2-2a·b +b 2=2.又因为a 2=b 2=|a|2=|b|2=1,所以2-2a·b =2,即a·b =0,故a ⊥b.(2)因为a +b =(cos α+cos β,sin α+sin β)=(0,1),所以⎩⎪⎨⎪⎧cos α+cos β=0,sin α+sin β=1, 由此得,cos α=cos(π-β),由0<β<π,得0<π-β<π,又0<α<π,故α=π-β.代入sin α+sin β=1得,sin α=sin β=12,而α>β,所以α=5π6,β=π6. 16.C3、C5、C9[2013·新课标全国卷Ⅰ] 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.16.-2 55[解析] f(x)=sin x -2cos x = 5⎝⎛⎭⎫15sin x -25cos x ,令cos α=15,sin α=25, 则f(x)=5sin(x -α).当θ-α=2k π+π2, 即θ=2k π+π2+α(上述k 为整数)时, f(x)取得最大值,此时 cos θ=-sin α=-2 55. 9.C9[2013·新课标全国卷Ⅰ] 函数f(x)=(1-cos x)·sin x 在[-π,π]的图像大致为( )图1-29.C [解析] 函数f(x)是奇函数,排除选项B.当x ∈[0,π]时f(x)≥0,排除选项A.对函数f(x)求导,得f′(x)=sin xsin x +(1-cos x)cos x =-2cos 2 x +cos x +1=-(cos x -1)(2cos x +1),当0<x<π时,若0<x<2π3,则f′(x)>0,若2π3<x<π,则f′(x)<0,即函数在(0,π)上的极大值点是x=错误!,故只能是选项C中的图像.。
2013年全国各地高考文科数学试题分类汇编3:三角函数

A.
答案
B.
C.
D.
A
文
令以. 2013 年高考广东卷
已知 sin(
A. −
2 5
C
B. −
1 5
5π 1 + α ) = ,那么 cos α = 2 5 1 2 C. D. 5 5
答案
令3. 2013 年高考湖北卷
文
将函数 y = 3 cos x + sin x ( x ∈ R ) 的 象向左 移 m ( m > 0) 个单位长度后,所
答案
C; 函数 f ( x ) = 2 sin(ω x + ϕ )(ω > 0, −
3 . 2013 年高考四川卷 文
π
2
<ϕ <
π
2
) 的部分 象如 所示,则 ω , ϕ
的值分别是
A. 2, −
答案
π
3
A
B. 2, −
π
6
C. 4, −
π
6
D. 4,
π
3
4 .2013 年高考湖南 文
在锐角 ∆ ABC 中,角 A,B 所对的边长分别为 a,b. 若 以sinB称 3 b,则角 A 等于______
D.
5π 6
A
卷 文
8 . 2013 年高考课标
△ABC 的内角 A,B,C 的对边分别为 a,b,c,已知 b称以,B称 ,C称 ,则△ABC 的
面
为 +以 B
文
A.以
答案
B.
+令
C.以
-以
D.
-令
9 . 2013 年高考江西卷
若 sin 1 3
全国各地高考文科数学试题分类汇编三角函数

2013年全国各地高考文科数学试卷分类汇编:三角函数一、选择题1 .(2013年高考大纲卷(文))已知a 是第二象限角,5sin ,cos 13a a ==则( ) A .1213-B .513-C .513D .1213【答案】A2 .(2013年高考课标Ⅰ卷(文))函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为【答案】C 。
3 .(2013年高考四川卷(文))函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )A .2,3π-B .2,6π-C .4,6π-D .4,3π【答案】A4 .(2013年高考湖南(文))在锐角∆ABC 中,角A,B 所对的边长分别为a,b. 若2sinB=3b,则角A 等于______( )A .3πB .4πC .6πD .12π【答案】A5 .(2013年高考福建卷(文))将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是( ) A .35πB .65πC .2πD .6π 【答案】B6 .(2013年高考陕西卷(文))设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=,则△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定 【答案】A7 .(2013年高考辽宁卷(文))在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=,a b B >∠=且则( )A .6πB .3πC .23πD .56π【答案】A8 .(2013年高考课标Ⅱ卷(文))△ABC 的内角A,B,C 的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为( ) A .2+2B .+1C .2-2D .-1【答案】B9 .(2013年高考江西卷(文))sincos 2αα==若( ) A .23-B .13-C .13D .23【答案】C10.(2013年高考山东卷(文))ABC ∆的内角A B C 、、的对边分别是a b c 、、,若2B A =,1a =,b =,则c =( )A .B .2CD .1【答案】B11.(2013年高考课标Ⅱ卷(文))已知sin2α=,则cos 2(α+)=( )A .B .C .D .【答案】A12.(2013年高考广东卷(文))已知51sin()25πα+=,那么cos α=( ) A .25-B .15-C .15D .25【答案】C13.(2013年高考湖北卷(文))将函数sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )A .π12B .π6C .π3D .5π6【答案】B 14.(2013年高考大纲卷(文))若函数()()sin0=y x ωϕωω=+>的部分图像如图,则()A .5B .4C .3D .2【答案】B15.(2013年高考天津卷(文))函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是( )A .1-B .CD .0 【答案】B16.(2013年高考安徽(文))设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2,3sin 5sin b c a A B +==,则角C =( ) A .3πB .23πC .34πD .56π 【答案】B17.(2013年高考课标Ⅰ卷(文))已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,则b =( )A .10B .9C .8D .5 【答案】D18.(2013年高考浙江卷(文))函数f(x)=sin xcos x+32cos 2x 的最小正周期和振幅分别是( ) A .π,1B .π,2C .2π,1D .2π,2 【答案】A19.(2013年高考北京卷(文))在△ABC 中,3,5a b ==,1sin 3A =,则sin B =( )A .15B .59C .1【答案】B20.(2013年高考山东卷(文))函数x x x y sin cos +=的图象大致为【答案】D 二、填空题21.(2013年高考四川卷(文))设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是________.【答案】322.(2013年高考课标Ⅱ卷(文))函数cos(2)()y x ϕπϕπ=+-≤<的图像向右平移2π个单位后,与函数sin(2)3y x π=+的图像重合,则||ϕ=___________.【答案】56π23.(2013年上海高考数学试卷(文科))已知ABC ∆的内角A 、B 、C 所对的边分别是a ,b ,c .若2220a ab b c ++-=,则角C 的大小是________(结果用反三角函数值表示).【答案】23π24.(2013年上海高考数学试卷(文科))若1cos cos sin sin3x y x y +=,则()cos 22x y -=________.【答案】79-25.(2013年高考课标Ⅰ卷(文))设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______.【答案】5-。
2013届全国各地高考押题数学(文科)精选试题分类汇编3三角函数

2013届全国各地高考押题数学(文科)精选试题分类汇编3:三角函数一、选择题1 .(2013届重庆省高考压轴卷数学文试题)函数11y x=-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于 ( )A .2B .4C .6D .8【答案】解析:图像法求解.11y x =-的对称中心是(1,0)也是2sin (24)y x x π=-≤≤的中心,24x -≤≤他们的图像在x=1的左侧有4个交点,则x=1右侧必有4个交点.不妨把他们的横坐标由小到大设为1,2345678,,,,,,x x x x x x x x ,则182736452x x x x x x x x +=+=+=+=,所以选D2 .(2013届上海市高考压轴卷数学(文)试题)已知锐角,A B 满足)tan(tan 2B A A +=,则B tan 的最大值为 ( )A .22B .2C .22D .42 【答案】D【解析】AA A A AB A A B A A B A B tan 2tan 1tan 21tan tan )tan(1tan )tan(])tan[(tan 2+=+=++-+=-+=,又0tan >A ,则22tan 2tan ≥+AA 则42221tan =≤B . 【注】直接按和角公式展开也可.3 .(2013届陕西省高考压轴卷数学(文)试题)函数 ln 1yx =-的图像与函数()2cos 24y x x π=--≤≤的图像所有交点的横坐标之和等于( )A .8B .6C .4D .2【答案】B 【解析】画出两函数图象可知均关于直线1=x 对称,所以在[]4,2-内所有交点横坐标之和为.632=⨯4 .(2013届福建省高考压轴卷数学文试题)将函数sin 2y x =的图像向左平移4π个单位长度,所得函数是( )A .奇函数B .偶函数C .既是奇函数又是偶函数D .既不是奇函数也不是偶函数【答案】B5 .(2013届山东省高考压轴卷文科数学)设sin(4πθ+)=13,sin2θ= ( )A .79-B .19-D .19 D .79【答案】A【解析】因为sin(4πθ+)=13,即1,sin cos 3θθθθ+=+所以,两边平方,得:2+sin cos =9θθ12,所以7sin 2=-9θ2. 6 .(2013届湖北省高考压轴卷 数学(文)试题)如图,正五边形ABCDE 的边长为2,甲同学在ABC ∆中用余弦定理解得AC =,乙同学在Rt ACH ∆中解得1cos 72AC =,据此可得cos72的值所在区间为().0.1,0.2A().0.2,0.3B().0.3,0.4C().0.4,0.5D【答案】C【解析】:因为1cos 72=,令cos 72t =,则1t=,所以328810t t +-=.令()32881f t t t =+-,则当0t >时,()224160f t t t '=+>,所以()32881f t t t =+-在()0,+∞上单调递增.又因为()()0.30.40f f ⋅<,所以()32881f t t t =+-在()0.3,0.4上有唯一零点,所以cos 72的值所在区间为()0.3,0.4.故选C .7 .(2013届全国大纲版高考压轴卷数学文试题(二))若1sin sin 3x y +=,则2sin cos y x -的取值范围为 ( )A .112[,]123-- B .24[,]33-C .24[,]39-D .114[,]129-【答案】D8 .(2013届四川省高考压轴卷数学文试题)函数22sin ()14y x π=--是( )A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为2π的奇函数D .最小正周期为2π的偶函数【答案】A9 .(2013届海南省高考压轴卷文科数学)若点(a,9)在函数y=3x的图象上,则tan的值为 ( )A .0B .C.1 D .【答案】答案:D考点:指数函数的图像与性质.分析:先将点代入到解析式中,解出a 的值,再根据特殊三角函数值进行解答.解答:解:将(a,9)代入到y=3x 中,得3a=9, 解得a=2. ∴=.10.(2013届全国大纲版高考压轴卷数学文试题(二))为得到函数cos()3y x π=+的图象,只需将函数sin y x =的图象( )A .向左平移6π个长度单位 B .向右平移6π个长度单位C .向左平移56π个长度单位D .向右平移56π个长度单位【答案】C11.(2013届天津市高考压轴卷文科数学)已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示,则ω等于()A.13B.1C.32D.2【答案】C【解析】由图象可知153122888Tπππ=-=,所以3Tπ=,又23Tππω==,所以23ω=,选C.12.(2013届海南省高考压轴卷文科数学)函数的图象大致是()A .B .C .D .【答案】答案:C考点:函数的图象.分析:根据函数的解析式,我们根据定义在R上的奇函数图象必要原点可以排除A,再求出其导函数,根据函数的单调区间呈周期性变化,分析四个答案,即可找到满足条件的结论.解答:解:当x=0时,y=0﹣2sin0=0故函数图象过原点,可排除A又∵y'=故函数的单调区间呈周期性变化分析四个答案,只有C满足要求13.(2013届安徽省高考压轴卷数学文试题)若1sin()34xπ+=,则sin(2)6xπ+的值()A.78B.78-CD.【答案】B【解析】本题考查诱导公式和二倍角公式,227sin(2)cos(2)cos(2)2sin ()1626338x x x x πππππ+=-++=-+=+-=-14.(2013新课标高考压轴卷(一)文科数学)设向量()()cos ,1,2,sin a b αα=-=,若ab ⊥,则tan 4πα⎛⎫- ⎪⎝⎭等于 ( )A .13-B .13C .3-D .3【答案】B【解析】因为a b ⊥,所以2cos sin 0a b αα=-=,即tan 2α=.所以tan 1211tan()41tan 123πααα---===++,选 B .15.(2013届上海市高考压轴卷数学(文)试题)已知函数sin ,sin cos ,()cos ,sin cos ,x x x f x x x x ≥⎧=⎨<⎩则下面结论中正确的是( )A .()f x 是奇函数B .()f x 的值域是[1,1]-C .()f x 是偶函数D .()f x 的值域是[ 【答案】D【解析】在坐标系中,做出函数()f x 的图象如图,由图象可知选 D .16.(2013届新课标高考压轴卷(二)文科数学)现有四个函数:①x x y sin =②x x y cos =③cox x y =④xx y 2=的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )A .④①②③B .①④③②C .①④②③D .③④②①【答案】C17.(2013届新课标高考压轴卷(二)文科数学)把函数)6sin(π+=x y 图象上各点的横坐标缩短到原来的21倍(纵坐标不变),再将图象向右平移3π个单位,那么所得图象的一条对称轴方程为 ( )A .8π=xB .4π-=xC .2π-=xD .4π=x【答案】C18.(2013届陕西省高考压轴卷数学(文)试题)下列函数一定是偶函数的是( )A .cos(sin )y x =B .sin cos y x x =C .()cos ln y x =D .cos sin y x x =-【答案】A 【解析】由偶函数定义可知,函数cos(sin )y x =中,x 的定义域关于原点 对称且cos(sin())cos(sin )x x -=.19.(2013届新课标高考压轴卷(二)文科数学)已知函数①x x y cos sin +=,②x x y cos sin 22=,则下列结论正确的是( )A .两个函数的图象均关于点(,0)4π-成中心对称 B .①的纵坐标不变,横坐标扩大为原来的2倍,再向右平移4π个单位即得②C .两个函数在区间(,)44ππ-上都是单调递增函数 D .两个函数的最小正周期相同 【答案】C20.(2013届全国大纲版高考压轴卷数学文试题(一))将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是 ( )A .cos 2y x =B .22cos y x = C .)42sin(1π++=x yD .22sin y x =【答案】B21.(2013届上海市高考压轴卷数学(文)试题)本题共2小题,第(Ⅰ)小题6分,第(Ⅱ)小题6分.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数a .①22sin 13cos 17sin13cos17︒︒︒︒+-; ②22sin 15cos 15sin15cos15︒︒︒︒+-; ③22sin 18cos 12sin18cos12︒︒︒︒+-; ④22sin (18)cos 48sin(18)cos 48︒︒︒︒-+--; ⑤22sin (25)cos 55sin(25)cos55︒︒︒︒-+--. (Ⅰ)试从上述五个式子中选择一个,求出常数a ;(Ⅱ)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.【答案】解:(Ⅰ)选择②式计算:4330sin 21115cos 15sin 15cos 15sin 22=︒-=︒︒-︒+︒=a .(Ⅱ)猜想的三角恒等式为:43)30cos(sin )30(cos sin 22=-︒--︒+αααα. 证明:)30cos(sin )30(cos sin 22αααα-︒--︒+22sin (cos30cos sin 30sin )sin (cos30cos sin 30sin )αααααα=+︒+︒-︒+︒2222311sin cos cos sin cos sin 442αααααααα=+++--22333sin cos 444αα=+=. 二、填空题22.(2013届江西省高考压轴卷数学文试题)函数()sin sin()3f x x x π=-的最小正周期为______. 【答案】4323.(2013届海南省高考压轴卷文科数学)已知函数y=sin(ωx+ϕ)(ω>0, -π≤ϕ<π)的图像如图所示,则 ϕ=________________【答案】解析:由图可知,()544,,2,1255T x πωπϕ⎛⎫=∴=+ ⎪⎝⎭把代入y=sin 有:89,510ππϕϕ⎛⎫+∴=⎪⎝⎭1=sin 答案:910π 24.(2013届上海市高考压轴卷数学(文)试题)在ABC ∆中,若2,60,a B b ︒=∠==,则c =_______________.【答案】3【解析】由余弦定理得2222cos 60b a c ac =+-,即2174222c c =+-⨯⨯整理得2230c c --=,解得3c =.25.(2013届北京市高考压轴卷文科数学)已知3cos ,05ααπ=<<,则tan 4πα⎛⎫+= ⎪⎝⎭____ 【答案】7-【解析】因为3cos 0,05ααπ=><<,所以0,sin 02παα<<>,所以4sin ,5α=故4tan ,3α=所以41tan tan34tan()7441tan tan 143παπαπα+++===--⋅-. 26.(2013新课标高考压轴卷(一)文科数学)已知函数,给出下列四个说法: ①若,则; ②的最小正周期是; ③在区间上是增函数;④的图象关于直线对称. 其中说法正确的序号为____________【答案】③④【解析】函数1()sin cos sin 22f x x x x ==,若12()=()f x f x -,即1211sin 2=sin 222x x -,所以12sin 2=sin 2x x -,即12sin 2=sin(2)x x -,所以122=22x x k π-+或122=22,x x k k Z ππ-+∈,所以①错误;2,ω=所以周期2T ππω==,所以②错误;当44x ππ-≤≤时,222x ππ-≤≤,函数递增,所以③正确;当34x π=时,313131()sin 2)=sin =424222f πππ=⨯-(为最小值,所以④正确,所以说法正确的序号为③④.27.(2013届全国大纲版高考压轴卷数学文试题(一))若35sin ,,0,cos 524a πααπ⎛⎫⎛⎫=-∈-+ ⎪ ⎪⎝⎭⎝⎭则= _______________;【答案】1027-解析:由3sin ,(,0)52παα=-∈-得4cos 5α=, 所以555cos()cos cos sin sin 444πππααα+=-=43)55+= 28.(2013届重庆省高考压轴卷数学文试题)在ABC V 中,60,B AC ==,则2AB BC +的最大值为____【答案】解析:00120120A C C A +=⇒=-,0(0,120)A ∈, 22sin sin sin BC ACBC A A B ==⇒=022sin 2sin(120)sin sin sin AB ACAB C A A A C B ==⇒==-=+;2AB BC ∴+=5sin ))A A A A ϕϕ+=+=+,故最大值是29.(2013届广东省高考压轴卷数学文试题)已知ABC ∆中,A ∠,B ∠,C ∠的对边分别为a ,b ,c ,若1a =,b =,2B A =,则A =_________.【答案】由正弦定理sin sin a bA B=,又∵2B A =,∴sin 2sin cos a b A A A =,∴cos 2b A a ==,∴π6A =. 30.(2013新课标高考压轴卷(一)文科数学)在△ABC 中,角A,B,C 所对的边分别为a,b,c,若222sin A sin C sin B A sinC +-=,则角B 为_______【答案】6π【解析】由正弦定理可得222a cb +-=,所以222cos 2a c b B ac +-===所以6B π=. 三、解答题31.(2013届新课标高考压轴卷(二)文科数学)设ABC ∆中的内角A ,B ,C 所对的边长分别为a ,b ,c ,且54cos =B ,2=b . (Ⅰ)当35=a 时,求角A 的度数;(Ⅱ)求ABC ∆面积的最大值.【答案】解:(Ⅰ)因为54cos =B ,所以53sin =B .因为35=a ,2=b ,由正弦定理B b A a sin sin =可得21sin =A . 因为b a <,所以A 是锐角,所以o 30=A . (Ⅱ)因为ABC ∆的面积ac B ac S 103sin 21==, 所以当ac 最大时,ABC ∆的面积最大.因为B ac c a b cos 2222-+=,所以ac c a 58422-+=. 因为222a c ac +≥,所以8245ac ac -≤, 所以10≤ac ,(当a c ==)所以ABC ∆面积的最大值为. 3sin 21==B ac S 32.(2013届福建省高考压轴卷数学文试题)函数()sin()4f x M x πω=-(0,0M ω>>)的部分图像如右图所示.(Ⅰ)求函数()f x 的解析式;(Ⅱ)ABC ∆中,角,,A B C 的对边分别为,,a b c ,若()28A f π+=其中(0,)2A π∈,且222a c b ac +-=,求角,,A B C 的大小.【答案】解:(Ⅰ)由图像可知2M =且34824T πππ=-= ∴T π= ∴ 22Tπω==故函数()f x 的解析式为()2sin(2)4f x x π=-(Ⅱ)由(Ⅰ)知()2sin 28A f A π+==∴sin A = (0,)2A π∈ 3A π∴=由余弦定理得:2221cos 222a cb ac B ac ac +-===(0,)B π∈ 3B π∴=从而()3C A B ππ=-+=∴3A B C π===33.(2013届辽宁省高考压轴卷数学文试题)在ABC ∆中,C B A ,,的对边分别是c b a ,,,已C B B C A cos sin cos sin 2sin 23+=, (Ⅰ)求A sin 的值;(Ⅱ)若332cos cos ,1=+=C B a ,求边c 的值. 【答案】解答:(Ⅰ)由C B B C A cos sin cos sin 2sin 23+=得A C B A A sin )sin(cos sin 3=+=, , 由于ABC ∆中0sin >A ,1cos 3=∴A ,31cos =A ,322cos 1sin 2=-=∴A A , (Ⅱ)由332cos cos =+C B 得332cos )cos(=++-C C A , 即332cos cos cos sin sin =+-C C A C A ,332cos 32sin 322=+∴C C 得3cos sin 2=+C C ,C C sin 23cos -=,平方得36sin =C , 由正弦定理得23sin sin ==A C a c 34.(2013届山东省高考压轴卷文科数学)(2013济南市一模)在ABC ∆中,边a 、b 、c 分别是角A 、B 、C 的对边,且满足cos (3)cos b C a c B =-. (Ⅰ)求B cos ;(Ⅱ)若4BC BA ⋅=,b =,求边a ,c 的值.【答案】【解析】(1)由正弦定理和cos (3)cos b C a c B =-,得sin cos (3sin sin )cos B C A C B =-, 化简,得sin cos sin cos 3sin cos B C C B A B +=即sin3sin cos B C A B +=(), 故sin 3sin cos A A B =.所以1cos =3B (2)因为4BC BA ⋅=, 所以4cos ||||=⋅⋅=⋅B 所以12BC BA ⋅=,即12ac =. (1)又因为2221cos =23a cb B ac +-=, 整理得,2240a c +=. (2)联立(1)(2) 224012a c ac ⎧+=⎨=⎩,解得26a c =⎧⎨=⎩或62a c =⎧⎨=⎩35.(2013届浙江省高考压轴卷数学文试题)已知函数()sin (0)f x m x x m =+>的最大值为2.(1)求函数()f x 在[0,]π上的单调递减区间;(2)△ABC 中,()()sin 44f A f B A B ππ-+-=,角A 、B 、C 所对的边分别是a 、b 、c,且C=60︒,c=3,求△ABC 的面积.【答案】【解析】(1)由题意,()f x .而0m >,于是m =π()2sin()4f x x =+.()f x 为递减函数,则x 满足ππ3π2π+2π+242k x k +≤≤ ()k ∈Z ,即π5π2π+2π+44k x k ≤≤()k ∈Z .所以()f x 在[]0π,上的单调递减区间为ππ4⎡⎤⎢⎥⎣⎦,.(2)设△ABC 的外接圆半径为R ,由题意,得32=23sin sin 60c R C ==化简ππ()()sin 44f A f B A B -+-=,得sin sin sin A B A B +=.由正弦定理,得()2R a b +=,a b +=. ① 由余弦定理,得229a b ab +-=,即()2390a b ab +--=. ② 将①式代入②,得()22390ab ab --=. 解得3ab =,或 32ab =-(舍去).1sin 2ABC S ab C ∆==. 36.(2013届广东省高考压轴卷数学文试题)已知函数()sin 2x f x A ϕ⎛⎫=+⎪⎝⎭()0,0A ϕπ><<的最大值是1,且()01f =.(1)求函数()f x 的最小正周期; (2)求()f x 的解析式;(3)已知锐角ABC ∆的三个内角分别为A ,B ,C ,若()()3522513f A f B π=+=-,,求()2f C 的值.【答案】解:(1)函数()f x 的最小正周期是2412T ππ==(2)∵函数()f x 的最大值是1,0A > ∴1A = ∵()0sin 1f ϕ==又∵0ϕπ<<∴2πϕ=∴()f x 的解析式是()sin cos222x x f x π⎛⎫=+= ⎪⎝⎭ (3)()32cos 5f A A ==,()()152cos2cos sin 2213f B B B B πππ⎛⎫+=+=+=-=- ⎪⎝⎭,∴5sin 13B =∵,0,2A B π⎛⎫∈ ⎪⎝⎭∴4sin 5A ===,12cos 13B ===∴()()2cos cos f C C A B π==-+⎡⎤⎣⎦()cos A B =-+cos cos sin sin A B A B=-+312451651351365=-⨯+⨯=-37.(2013届陕西省高考压轴卷数学(文)试题)已知函数2()sincossin(0,0)2222x x x f x ωϕωϕωϕπωϕ+++=+><<.其图象的两个相邻对称中心的距离为2π,且过点(,1)3π.(I) 函数()f x 的解析式;(Ⅱ) 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a c A C c a b --=---. 且()f A =,求角C 的大小.【答案】【解析】(Ⅰ)[]1())1cos()2f x x x w j w j =++-+ π1sin()62x w j =+-+. Q 两个相邻对称中心的距离为π2,则πT =,2ππ,>0,=2||w w w \=\Q ,又()f x 过点π(,1)3,2ππ1π1sin 1,sin 36222j j 骣骣鼢珑\-++=+=鼢珑鼢珑桫桫即,1cos 2j \=, πππ10,,()sin(2)2362f x x j j <<\=\=++Q . (Ⅱ)在△ABC 中,222222sin 2cos cosB sin cos 2sin sin 2cos cos sin cos C b a c ac B c C B A C ab C b C B Cc a b ---====----, 因为sin 0C ≠,所以sin cos 2sin cos sin cos B C A B C B =-,所以2sin cos sin cos sin cos sin()sin A B B C C B B C A =+=+=, 因为sin 0A ≠,所以1cos 2B =,因为0πB <<,所以π3B =.而由()f A =得4A π=,所以5.4312C ππππ=--=38.(2013届湖南省高考压轴卷数学(文)试题)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A -2cos Ccos B=2c -ab.(1)求sin C sin A的值;(2)若cos B =14,b =2,求△ABC 的面积S .【答案】解: (1)由正弦定理,设asin A =bsin B =csin C=k ,则2c -a b =2k sin C -k sin A k sin B =2sin C -sin Asin B. 所以cos A -2cos C cos B =2sin C -sin A sin B即(cos A -2cos C )sin B =(2sin C -sin A )cos B ,化简可得sin(A +B )=2sin(B +C )又A +B +C =π,所以sin C =2sin A .因此sin Csin A =2(2)由sin C sin A=2得c =2a .由余弦定理b 2=a 2+c 2-2ac cos B 及cos B =14,b =2,得4=a 2+4a 2-4a 2×14解得a =1,从而c =2又因为cos B =14,且0<B <π,所以sin B =154.因此S =12ac sin B =12×1×2×154=15439.(2013届全国大纲版高考压轴卷数学文试题(二))已知函数2()sin ()(0,0,0)2f x A x A πωϕωϕ=+>><<,且()y f x =的最大值为2.其图象相邻两对称轴之间的距离为2,并过点(1,2)(1)求函数()f x 的解析式;(2)求(1)(2)(2009)f f f +++.【答案】解:(1) ()cos(22)22A Af x x ωϕ=-+ ()y f x =的最大值为2,222A A∴+=,即2A =又∵相邻对称轴之间的距离为122,2,224ππωω∴⋅=∴=由于(1,2)在图像上,1cos(2)22πϕ∴-+=,即sin 21ϕ=,(0,),24ππϕϕ∈∴=,即2()2sin ()44f x x ππ=+(2) 2()2sin ()1sin 442f x x x πππ=+=+ 242T ππ∴==,(1)(2)(2009)4502(1)2010f f f f ∴+++=⨯+=40.(2013届北京市高考压轴卷文科数学)已知a b c ,,为ABC △的内角A B C ,,的对边,满足A CB AC B cos cos cos 2sin sin sin --=+,函数()sin f x x ω=(0)ω>在区间[0,]3π上单调递增,在区间2[,]33ππ上单调递减. (Ⅰ)证明:a c b 2=+;(Ⅱ)若A f cos )9(=π,证明ABC △为等边三角形.【答案】解:(Ⅰ)ACB AC B cos cos -cos -2sin sin sin =+ ∴sin cos sin cos 2sin -cos sin -cos sin B A C A A B A C A += ∴sin cos cos sin sin cos cos sin 2sin B A B A C A C A A +++=sin ()sin ()2sin A B A C A +++=sin sin 2sin C B A += 所以2b c a +=(Ⅱ)由题意知:由题意知:243ππω=,解得:32ω=, 因为1()sin cos 962f A ππ===, (0,)A π∈,所以3A π=由余弦定理知:222-1cos 22b c a A bc +==所以222-b c a bc += 因为2b c a +=,所以222-()2b c b c bc ++=, 即:22-20b c bc +=所以b c = 又3π=A ,所以ABC △为等边三角形41.(2013届天津市高考压轴卷文科数学)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,已知向量),2(),cos ,(cos a b c n B A m +==,且n m ⊥.(Ⅰ) 求角A 的大小;(Ⅱ)若a =8b c +=,求△ABC 的面积.【答案】解:(Ⅰ)⊥∴ 0),2()cos ,(cos =+∙=∙a b c B A即0cos cos )2(=++B a A b c由正弦定理可得0cos sin cos )sin sin 2(=++B A B B C 整理得0cos sin 2sin =+A C C32,21cos 0sin ,0ππ=∴-=∴>∴<<A A C C(II)由余弦定理可得 ,cos 2222A bc c b a -+=22248()64b c bc b c bc bc =++=+-=- 即16bc =故11sin 16222S bc A ∆==⨯⨯= 42.(2013届江西省高考压轴卷数学文试题)如图,在ABC ∆中,AD BC ⊥,垂足为D ,且::2:3:6BD DC AD =.(Ⅰ)求BAC ∠的大小;(Ⅱ)设E 为AB 的中点,已知ABC ∆的面积为15,求CE 的长.EDCBA【答案】解:(I)由已知得11tan ,tan 32BAD CAD ∠=∠=, 则1132tan tan()111132BAC BAD CAD +∠=∠+∠==-⨯,EDCBA又(0,)BAC π∠∈,故4BAC π∠=(II)设2(0)BD t t =>,则3,6DC t AD t ==,由已知得21515t =,则1t =,故2BD =,3,6DC AD ==,则2ABAE AC ===,由余弦定理得5CE =43.(2013届四川省高考压轴卷数学文试题)已知函数,2()cos ()1(0,0,0)2f x A x A πωϕωϕ=++>><<的最大值为3,()f x 的图像的相邻两对称轴间的距离为2,在y 轴上的截距为2. (1)求函数()f x 的解析式; (2)求()f x 的单调递增区间.【答案】解:(Ⅰ)()()2122cos 2Ax A x f +++=ϕω 依题意2A ,3212=∴=++AA 又 4T , 22==得T 4422πωωπ==∴()222cos +⎪⎭⎫⎝⎛+=∴ϕπx x f令 x=0,得 22 20, 222cos πϕπϕϕ=∴<<=+又所以函数()x f 的解析式为x x f 2sin2)(π-= (还有其它的正确形式,如:2)22cos()(,1)44(cos 2)(2++=++=ππππx x f x x f 等)(Ⅱ)当322222k x k πππππ+<<+,k Z ∈时()f x 单调递增 即4143k x k +<<+,k Z ∈ ------10分∴()f x 的增区间是(41,43),k k k Z ++∈44.(2013届全国大纲版高考压轴卷数学文试题(一))已知函数()f x =(Ⅰ)求函数()f x 的定义域; (Ⅱ)若()2f x =,求sin 2x 的值.【答案】解:Ⅰ)由题意,sin 0x ≠,所以,()x k k ≠π∈Z.函数()f x 的定义域为{,}x x k k ≠π∈Z(Ⅱ)因为()2f x=,1)2sin43x xπ+-=,1)2sin3x x x-=,1cos sin3x x-=,将上式平方,得11sin29x-=,所以8sin29x=45.(2013届湖北省高考压轴卷数学(文)试题)已知()()cos sin,2cos,cos sin,sinm x x x n x x x=+=--.(1)求()f x m n=⋅的最小正周期和单调递减区间;(2)将函数()y f x=的图象向右平移8π个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数()y g x=的图象.在ABC∆中,角,,A B C的对边分别为,,a b c,若()0,22Af g B b⎛⎫===⎪⎝⎭,求a的值.【答案】(1)()()()cos sin cos sin2sin cosf x m n x x x x x x=⋅=+--22cos sin sin2x x x=--cos2sin2x x=-32244x xππ⎛⎫⎛⎫=-=+⎪ ⎪⎝⎭⎝⎭.所以()f x的最小正周期Tπ=.又由()33222242k x k k Zπππππ+≤+≤+∈,得()388k x k k Zππππ-≤≤+∈,故()f x的单调递减区间是()3,88k k k Zππππ⎡⎤-+∈⎢⎥⎣⎦.(2)由02Af⎛⎫=⎪⎝⎭,34Aπ⎛⎫+=⎪⎝⎭,所以()34A k k Zππ+=∈,因为0Aπ<<,所以4Aπ=,将函数()y f x=的图象向右平移8π个单位,得到3222842y x x x πππ⎡⎤⎛⎫⎛⎫=-+=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数()y g x x ==的图象,因为()g B =,所以B =,即1cos 2B =,又0B π<<,所以3B π=,由正弦定理sin sin a b A B=,得2sinsin 4sin sin 3b A a B ππ===. 46.(2013届重庆省高考压轴卷数学文试题)已知ABC ∆内角A ,B ,C 的对边分别为a ,b ,c ,其中2=a ,3=c .(Ⅰ)若33sin =C ,求A sin 的值; (Ⅱ)设C C C C f 2cos cos sin 3)(-=,求)(C f 的取值范围.【答案】解(Ⅰ)由正弦定理得sin 2,sin sin sin 3a c a CA A C c=∴=== 5(Ⅱ)在A B C D 中,由余弦定理,2222cos ,AB AC BC AC BC C =+-⋅2344cos ,AC AC C ∴=+-即24cos 10,AC C AC -⋅+=有题知关于AC 的一元二次方程应该有解,7令21=cos -40cos -2C ∆≥≤(4C ),得(舍去)或者1cos 023C C π≥<<,所以 91cos 21()2sin(2)262C f C C C π+=-=-- 1(2),1(662.)2C f C πππ-<-≤∴-<≤ 11 47.(2013届安徽省高考压轴卷数学文试题)( )在ABC ∆中,A B C ∠∠∠、、所对的边分别是a b c 、、,S表示三角形的面积,且2sin(2)2sin()2sin 222B B B ππ++-+=(1)求角B 的大小;(2)若4a S ==,,求b 的值.【答案】【解析】(1)由2sin(2)2sin()2sin 222B B B ππ++-+=得 2cos 22cos 2(1sin )B B B +=-,即222cos 12cos 2cos B B B -+=,1cos (0)2B B π=∈,,63B π=分(2)1sin 42S ac B c ===,由余弦定理得 2222222cos 44244cos 163b a c ac B b π=+-∴=+-⨯⨯⨯=,所以4b =12分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C 单元 三角函数
C1 角的概念及任意的三角函数
14.C1,C2,C6 设sin 2α=-sin α,α∈π2
,π,则tan 2α的值是________. 14. 3 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,
又α∈⎝ ⎛⎭
⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2 α=2×(-3)1-3
= 3. 方法二:同上得cos α=-12,又α∈⎝ ⎛⎭
⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3
= 3. C2 同角三角函数的基本关系式与诱导公式
2.C2 已知α是第二象限角,sin α=
513,则cos α=( ) A .-1213 B .-513 C.513 D.1213
2.A cos α=-1-sin 2 α=-
1213. 16.C2,C5 已知函数f(x)=2cos ⎝
⎛⎭⎪⎫x -π12,x ∈R. (1)求f ⎝ ⎛⎭
⎪⎫π3的值; (2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝
⎛⎭⎪⎫θ-π6. 16.解:
14.C1,C2,C6 设sin 2α=-sin α,α∈π2
,π,则tan 2α的值是________.
14. 3 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,
又α∈⎝ ⎛⎭
⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2 α=2×(-3)1-3
= 3. 方法二:同上得cos α=-12,又α∈⎝ ⎛⎭
⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3
= 3. C3 三角函数的图像与性质
1.C3 函数y =3sin ⎝
⎛⎭⎪⎫2x +π4的最小正周期为________. 1.π 周期为T =2π2
=π. 17.C3 设向量a =(3sin x ,sin x),b =(cos x ,sin x),x ∈0,
π2. (1)若|a|=|b|,求x 的值;
(2)设函数f(x)=a ·b ,求f(x)的最大值.
17.解:(1)由|a|2=(3sin x)2+(sin x)2=4sin 2 x ,
|b|2=(cos x)2+(sin x)2=1.
及|a|=|b|,得4sin 2 x =1.
又x ∈0,π2,从而sin x =12,所以x =π6
. (2)f(x)=a ·b =3sin x ·cos x +sin 2x =32sin 2x -12cos 2x +12
=sin2x -π6+12,当x =π3∈0,π2时,sin2x -π6
取最大值1. 所以f(x)的最大值为32
.
9.C3 函数y =xcos x +sin x 的图像大致为( )
图1-3
9.D ∵f(-x)=-xcos(-x)+sin(-x)=-(xcos x +sin x)=-f(x),∴y =xcos x +sin x 为奇函数,图像关于原点对称,排除选项B ,当x =π2
,y =1>0,x =π,y =-π<0,故选D.
16.C3、C5、C9 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.
16.-2 55 f(x)=sin x -2cos x = 5⎝ ⎛⎭⎪⎫15sin x -25cos x ,令cos α=15,sin α=25
, 则f(x)=5sin(x -α).当θ-α=2k π+
π2, 即θ=2k π+π2
+α(上述k 为整数)时, f(x)取得最大值,此时 cos θ=-sin α=-
2 55. C4 函数 的图象与性质
16.C4 设函数f(x)=sin x +sin ⎝
⎛⎭⎪⎫x +π3. (1)求f(x)的最小值,并求使f(x)取最小值的x 的集合;
(2)不画图,说明函数y =f(x)的图像可由y =sin x 的图像经过怎样的变化得到. 16.解:(1)因为f(x)=sin x +12sin x +32cos x =32sin x +32cos x =3。
