九年级全国中考材料问题复习及答案
人教版九年级化学中考总复习 专题3 身边的化学物质 含答案及解析

专题三身边的化学物质专题提升演练1.实验室有四个药品橱,已存放如下药品,实验室新购进的活性炭,应将它存放在()A.①B.②C.③D.④解析:活性炭属于非金属单质。
四个药品橱中,①橱是酸,②橱是碱,③橱是非金属单质,④橱是金属单质,故活性炭应该放于③橱中。
答案:C2.用如图所示装置进行实验,有关说法及分析不正确的是()A.烘干的木炭粉末与CuO粉末需混合均匀B.网罩的作用是集中火焰,提高温度C.可观察到澄清石灰水变浑浊D.产生的气体一定没有CO解析:为使反应充分,木炭粉末与CuO粉末需混合均匀,故A正确;酒精灯网罩的作用是提高温度,故B正确;木炭粉末与CuO粉末反应产生二氧化碳,二氧化碳能使澄清石灰水变浑浊,故C正确;木炭粉末与CuO粉末反应产生二氧化碳,当木炭粉末过量时可能会产生一氧化碳,故D不正确。
答案:D3.下列物质的用途与性质对应关系错误的是()金刚石做玻璃刀石墨做电池电极不锈钢做水壶钛合金制造船舶设备金刚石硬度大石墨很软不锈钢有导热性钛合金抗腐蚀性强解析:石墨做电池电极是由于石墨具有导电性,故B错误。
答案:B4.(2022四川凉山州中考)除去下列物质中的少量杂质,所用试剂及方法正确的是()答案:B5.下列是分析久置于空气中的NaOH固体成分的相关实验(不考虑水分),其中合理的是()A.①②B.①③C.②④D.③④解析:氢氧化钠与空气中的二氧化碳反应生成碳酸钠,因此向样品中加入足量稀盐酸,若观察到有气泡产生,证明氢氧化钠变质,故①正确;向样品固体中,加入石灰水,生成白色沉淀,确定有碳酸钠,过滤后再向滤液中滴加酚酞溶液,酚酞溶液显红色,由于氢氧化钙与碳酸钠反应生成氢氧化钠,故无法确定样品中是否含有氢氧化钠,故②错误;取a g样品与足量氯化钡溶液充分反应,由于碳酸钠与氯化钡反应生成碳酸钡沉淀,因此将沉淀过滤、洗涤、干燥,得到m g固体,由碳酸钡的质量可求出碳酸钠的质量,进而求出纯度,故③正确;取固体,加水溶解,滴加氯化钙溶液至恰好完全反应,过滤后溶液中有新杂质氯化钠,故④错误。
中考英语总复习九年级(全)Units 7-8 教材知识梳理

九年级(全)Units7-8安徽中考真题精选Ⅰ.单项填空1.(2017·安徽第33题)The New Silk Road will offer a good for more nations to communicate.(A)A.chanceB.habitC.questionD.price2.(2017·安徽第39题)—Mom,I’ve signed for the box.What’s in it?—I’m not sure.It be a present from your uncle.(C)A.needB.mustC.mayD.will3.(2015·安徽第44题)—Do you have any plans for this Sunday?—I’m not sure.I go to the countryside to see my grandmother.(C)A.canB.mustC.mayD.need4.(2013·安徽第46题)Thanks to the Internet,different kinds of information in a short time.(A)A.can be learnedB.has been learnedC.can learnD.has learnedⅡ.单词拼写1.(2019·安徽第93题)The six⁃year⁃old American girl has learned hundreds of Chinese poems (诗).2.(2015·安徽第92题)When swimming,you should put safety (安全) first.熟词生义1.field熟义:n.田野;场地生义:n.领域(1)—In the field of 5G technology,China’s company Huaiwei is the great leader in the world.—Amazing!I’m really proud of our country. 领域 (2)There is a baseball field and two football fields. 场地 (3)In summer,they watched Bird and Squirrel(松鼠) play in the field.(2020·安徽) 田野 2.support熟义:v.& n.支持生义:v.帮助;养活;支撑(1)My host family supported me greatly when I studied abroad. 帮助 (2)In a weightless environment,astronauts don’t need to use their muscles to support themselves,so their muscles start shrinking(萎缩).(2020·广东东莞) 支撑 (3)We will always be there to support whatever you wish to do. v.支持 (4)His mother found it difficult to support the large family.(2017·安徽) 养活 3.circle熟义:n.圆圈v.圈出生义:n.圆;圈子v.盘旋(1)—My uncle has a large circle of good friends in his daily life.—Sounds like he is an active and welcome man. 圈子 (2)This island is almost shaped like a circle.(2020·安徽) 圆 (3)The plane circled the airport before landing. 盘旋 (4)Alice likes circling the important dates on her calendar. 圈出 4.energy熟义:n.力量;精力生义:n.能量;能源(1)Solar panels(太阳能电池板) take energy from the sun and turn it into electricity.(2020·湖南长沙) 能量 (2)He sleeps for only five to six hours a day,but he is still full of energy.(2020·山东聊城) 精力 (3)Renewable energy is the energy that can be used again and again. 能源 5.position熟义:n.位置;地方生义:n.地位;职位;名次(1)As the sun moved across the sky,the position of the shadow changed.(2020·山东德州) 位置 (2)They make China own an important and even top position in the history of human civilization(文明).(2020·湖北黄冈) 地位 (3)We all think Carl is the proper man for the position. 职位 (4)My brother finished the race in second position. 名次 名师考点精讲考点1 get in the way of的用法【教材原句】But sometimes these can get in the way of their schoolwork...有时这些(爱好)会妨碍他们的学业……(P54)get in the way of意为“挡……的路;碍事”。
精编九年级中考历史知识点精题精练--三次工业革命复习题(含答案)

A. 飞梭 B. 珍妮机 C. 蒸汽机 D. 发电机
是最野蛮的。”该材料无法反映工业革命( )
3. 1492 年哥伦布从欧洲到美洲历时 37 天,1838 年人们乘船从欧洲到美洲仅需
A. 创造了巨大财富
B. 带来了环境污染
19 天。这一巨大变化得益于( )
C. 开拓了世界市场
D. 加深了殖民掠夺
好题精练
①用机械力取代了自然力,把人类带入“蒸汽时代” ②标志着工业革命的完成
1. 马克思说:“市场总是在扩大,需求总是在增加。甚至工场手工业也不能满 ③为汽船、火车的发明提供了动力,促进了交通运输业的革新 ④确立起西方先
足需要了。于是,蒸汽和机器引起了工业生产的革命。”以上材料说的是工业革命的 进,东方落后的格局 ⑤出现了机器化大生产,提高了生产效率
精编九年级中考历史知识点精题精练--三次工业革命复习题
第一次工业革命 1. 阅读下图,促使英国城市人口占总人口比例在某一时期增长最快的主要原因 是( )
4. 材料一 英国固定式动力源装机容量统计表(单位:千马力) 1760 年 1800 年 1830 年 1870 年
蒸汽机 5
35
160 2 060
科学技术和文化
1. 科技进步影响着人们的生产生活方式。下列现象按其出现的
先后顺序排列正确的是
( )
①机器轰鸣,铁路速度 ②车马劳顿,家书万金
③在线购物,网络订票 ④楼上楼下,电灯电话
A. ①②③④
B. ②①③④
九年级数学中考复习压轴题专题训练含答案解析二次函数小综合抛物线中的定线问题
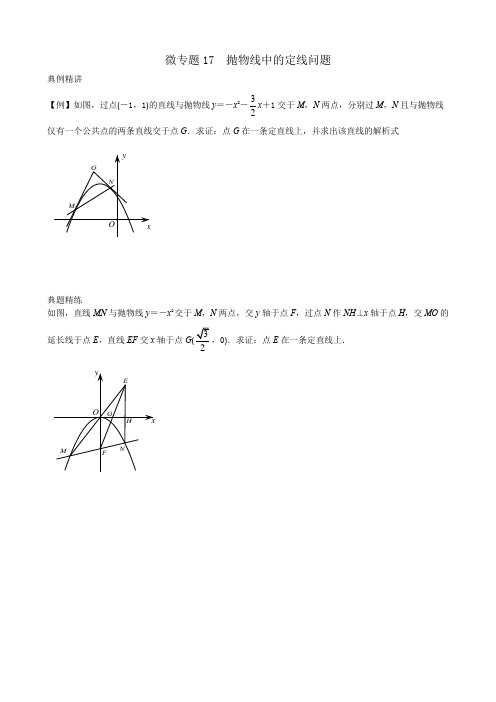
典例精讲【例】如图,过点(-1,1)的直线与抛物线y=-x2-32x+1交于M,N两点,分别过M,N且与抛物线仅有一个公共点的两条直线交于点G.求证:点G在一条定直线上,并求出该直线的解析式典题精练如图,直线MN与抛物线y=-x2交于M,N两点,交y轴于点F,过点N作NH⊥x轴于点H,交MO的延长线于点E,直线EF交x轴于点G(2,0).求证:点E在一条定直线上.典例精讲【例】如图,过点(-1,1)的直线与抛物线y =-x 2-32x +1交于M ,N 两点,分别过M ,N 且与抛物线 仅有一个公共点的两条直线交于点G .求证:点G 在一条定直线上,并求出该直线的解析式【解答】设直线MN :y =k (x +1)+1=kx +k +1,直线MG :y =k 1x +b 1,M (x 1,y 1),N (x 2,y 2),联立23121y x x y kx k ⎧=--+⎪⎨⎪=++⎩,∴x 2+(32+k )x +k =0,∴x 1+x 2=-32-k ,x 1⋅x 2=k , 联立211312y x x y k x b ⎧=--+⎪⎨⎪=+⎩,∴2x 1=-32-k 1,x 12=b 1-1,∴直线MG :y =(-2x 1-32)x +x 12+1,同理,直线NG :y =(-2x 2-32)x +x 22+1, 由2112223(2)1,23(2)12y x x x y x x x ⎧=--++⎪⎪⎨⎪=--++⎪⎩解得x =122x x +=-34-2k ,y =-x 1x 2-34(x 1+x 2)+1=-4k +178, 消去k 可得y =12x +52,∴点G 在定直线y =12x +52上.典题精练如图,直线MN 与抛物线y =-x 2交于M ,N 两点,交y 轴于点F ,过点N 作NH ⊥x 轴于点H ,交MO 的延长线于点E ,直线EF 交x 轴于点G,0).求证:点E 在一条定直线上.解:设M(x1,-x22),N(x,-x22),则MN:y=(-x1-x2)x+x1x2,OM:y=-x1x,∴F(0,x1x2),又∵G的坐标为0),可得FG:y(x∵NH⊥x轴,∴x E=x2,∴y E=-x1x2(x2),解得x2=x E∴点E在定直线x。
2024年九年级语文中考名著阅读复习《经典常谈》检测卷附答案

2024年九年级语文中考名著阅读复习《经典常谈》检测卷一、单选题(每题1分,共17分)1.《经典常谈》是朱自清先生的作品,全书共()篇。
A.15B.18C.13D.302.《诗经》被称作“诗三百”,现在实存()篇。
A.300B.301C.303D.3053.下列不属于四书的是()A.《大学》B.《中庸》C.《论语》D.《春秋》4.《史记》共一百三十篇,()占了全书的过半数。
A.本纪B.世家C.列传D.表5.下列不属于五经的是()A.《易》B.《书》C.《大学》D.《春秋》6.()这部书中虽用鲁国纪元,所记的却是各国的事,所以也是我们第一部通史。
A.《左传》B.《春秋》C.《公羊传》D.《战国策》7.杜预作《春秋序》,论到(),说“其文缓,其旨远”,“缓”是委婉,“远”是含蓄。
这不但是好史笔,也是好文笔。
所以这部书不但是史学的权威,也是文学的权威。
A.《左传》B.《春秋》C.《公羊传》D.《战国策》8.反对侵略战争,但是擅长制造战争器械的专家是()A.老子B.庄子C.韩非子D.墨子9.中国文字相传是()造的。
A.黄帝B.炎帝C.尧D.仓颉10.在人家门头上,在小孩的帽饰上,我们常见到八卦那种东西。
讲八卦的便是()这部书。
A.《春秋》B.《诗经》C.《中庸》D.《周易》11.()是中国最古的记言的历史。
包括虞、夏、商、周四代。
A.《春秋》B.《尚书》C.《左转》D.《战国策》12.我国现存的第一部编年史是()A.《春秋》B.《资治通鉴》C.《左转》D.《战国策》13.下列不是儒家代表人物的是()A.孔子B.墨子C.荀子D.孟子14.()不但是老、庄的信徒,也是佛的信徒,他是第一个在诗里用全力刻画山水的人。
A.陶渊明B.孟浩然C.谢灵运D.陶弘景15.善于写“民间的实在痛苦,社会的实在问题,国家的实在状况,人生的实在希望与恐惧”,给诗开辟了新世界的诗人是()A.李白B.杜甫C.孟浩然D.李商隐16.下面对《经典常谈》中相关内容解说不正确的一项是()A.全书包括《说文解字》《周易》《尚书》《诗经》等经史子集共十三部分内容,详细介绍了中国古代文学的发展与历史脉络,是介绍传统文化的典范之作。
人教版九年级化学中考总复习 第10单元 酸和碱 含答案及解析

第十单元酸和碱知能优化训练中考回顾1.(2021浙江宁波中考)不同品牌洗手液的pH一般不同,25 ℃时四种洗手液的pH如图所示。
下列说法错误的是()A.洗手液a用蒸馏水稀释后pH减小B.洗手液b的酸性比洗手液a的酸性弱C.洗手液c能使石蕊溶液变蓝色D.洗手液d和洗手液a的混合液的pH可能等于7答案:A2.(2021广东深圳中考)小明在探究稀硫酸性质,下列有关说法正确的是()A.稀硫酸与紫色石蕊溶液反应后,溶液变蓝B.若能与X反应制取H2,则X是CuC.与金属氧化物反应,有盐和水生成D.若与Y发生中和反应,则Y一定是NaOH答案:C3.(2020辽宁本溪中考)某物质能使紫色石蕊溶液变为蓝色,关于该物质的下列说法中正确的是()A.该物质可能是氢氧化铜B.该物质一定是纯碱的水溶液C.可以将pH试纸放入该物质的稀溶液中测其pHD.向该物质的水溶液中滴加稀盐酸,溶液的pH一定变小答案:D4.(2021湖北荆州中考)物质X与Ba(OH)2在溶液中反应的化学方程式为X+Ba(OH)2 BaSO4↓+2Y,下列说法正确的是()A.X可能为氯化铁B.X只能为硫酸C.Y可以为氢氧化铜D.Y不一定是水答案:D5.(2021福建中考)甲、乙、丙三种物质有如下转化关系:甲乙丙。
在不断搅拌下,往装有甲溶液的容器中逐滴加入稀盐酸依次发生了①②反应,同时测定容器中液体的透光强度(液体越浑浊,透光强度越小),结果如图。
下列分析错误的是()A.乙难溶于水B.甲可能是NaOHC.QM段对应的反应是②D.E、F对应的液体组成不同答案:B6.(2020吉林中考)若利用碱的性质进行下列实验,不能达到相应目的的是()A.分别加入少量Mg(OH)2固体,根据是否溶解,可鉴别稀盐酸和Na2CO3溶液B.分别加入适量水溶解,根据温度是否明显升高,可鉴别NaOH固体和NaCl固体C.分别加入Ba(OH)2溶液,根据是否产生沉淀,可鉴别MgCl2溶液和Na2SO4溶液D.分别加入熟石灰粉末研磨,根据是否产生氨味,可鉴别(NH4)2SO4固体和K2SO4固体答案:C7.(2019四川自贡中考)氧化铜与稀盐酸发生反应时,容器中溶液总质量随时间的变化曲线如图所示。
九年级中考语文模拟复习测试题(附答案)
九年级中考语文模拟复习测试题(附答案)一、积累与运用(共26分)1.(6分)阅读下面的文字,完成问题。
狂妄自大的民族不喜欢聆.听,___,贪欲和傲漫..(遮挡/遮盖)了他们的视线;闭关自守....的民族不喜欢聆听,___,浅陋.和愚昧妨.碍了他们的(进攻/进取);急攻近利....的民族不喜欢聆听,___,浮躁..和短视制约了他们的识见。
因此,只有喜欢聆听的民族,才是富有智慧的民族。
(1)文中加点字的注音和字形,全都正确的一项是A.聆.听(líng)傲漫B.妨.碍(fǎng)闭关自守C.浅陋.(lòu)浮躁D.狂妄.(wàng)急攻近利(2)依次选用文中括号里的词语,最恰当的一项是A.遮挡进取B.遮挡进攻C.遮盖进取D.遮盖进攻(3)在文中两处横线上依次填入句子,衔接最恰当的一项是①他们只会穷兵黩武②他们只会坐井观天③他们只会浅尝辄止A.①②③B.②③①C.③①②D.①③②2.(2分)下列各句中,没有语病的一项是()A.5月15日,天问一号探测器成功着陆火星,实现了从地月系到行星际的跨越。
B.我国将采取多种节能减排,力争提前实现2060年二氧化碳“零排放”的承诺。
C.为提高学生审美能力,颖滨中学开设了陶艺、书法等超过30余门美育选修课。
D.社区物业应增强社区管理和服务水平,增加群众的获得感、幸福感、安全感。
3.(2分)下列有关传统文化常识的表述,不正确的一项是()A.《蒹葭》《关雎》均选自《诗经》,《诗经》是我国最早的一部诗歌总集,收录了从西周到春秋时期的诗歌305篇,又称“诗三百”。
B.古时住宅旁常栽桑树、梓树,后人就用“桑梓”指家乡;“长河落日圆”中的“河”指黄河;“晋太元中”的“太元”是年号;《范文正公集》中的“文正”是谥号。
C.古人把山的南面、水的北面称为“阳”,山的北面、水的南面称为“阴”。
如“河阳”指的就是黄河的北岸,“汉阴”指的就是汉水的南岸。
D.“特别想念那东坡的月光,梦想跟随在放翁的身旁。
2023年春九年级数学中考复习《几何图形变换综合压轴题》专题提升训练(附答案)
2023年春九年级数学中考复习《几何图形变换综合压轴题》专题提升训练(附答案)1.如图,在△ABC中,∠BAC=90°,AB=AC,点D为线段AB上一点,线段CD绕点C 逆时针旋转90°能与线段CE重合,点F为AC与BE的交点.(1)若BC=5,CE=4,求线段BD的长;(2)猜想BD与AF的数量关系,并证明你猜想的结论;(3)设CA=3DA=6,点M在线段CD上运动,点N在线段CA上运动,运动过程中,DN+MN的值是否有最小值,如果有,请直接写出这个最小值;如果没有,请说明理由.2.阅读下列材料,并完成相应的学习任务:图形旋转的应用图形的旋转是全等变换(平移、轴对称、旋转)中重要的变换之一,利用图形旋转中的对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变等性质,可以将一般图形转化成特殊图形,从而达到解决问题的目的.如图1,在Rt△ABC中,∠ACB=90°,CE平分∠ACB,且AC=4,BC=3.过点E作互相垂直的两条直线,即EF⊥ED,EF交AC于点F,ED交BC于点D,求四边形EFCD 的面积.分析:将∠FED以点E为旋转中心顺时针旋转,使得旋转后EF的对应线段所在直线垂直于AC,并且交AC于点M,旋转后ED的对应线段所在直线交BC于点N.则容易证明四边形MENC为正方形.因为∠EMF=∠END=90°,ME=NE,∠MEF=∠NED,所以△MEF≌△NED,所以S四边形EFCD=S正方形MENC.学习任务:(1)四边形EFCD的面积等于;(2)如图2,在Rt△ABC中,∠ACB=90°,①作出△ABC的外接圆O;②作∠ACB的平分线,与⊙O交于点D.要求:尺规作图,不写作法,但保留作图痕迹.(3)在(2)的基础上,若BC+AC=14,则四边形ACBD的面积等于.3.△ABC为等边三角形,AB=4,AD⊥BC于点D,点E为AD的中点.(1)如图1,将AE绕点A顺时针旋转60°至AF,连接EF交AB于点G,求证:G为EF中点.(2)如图2,在(1)的条件下,将△AEF绕点A顺时针旋转,旋转角为α,连接BE,H为BE的中点,连接DH,GH.当30°<α<120°时,猜想∠DHG的大小是否为定值,并证明你的结论.(3)在△AEF绕点A顺时针旋转过程中,H为BE的中点,连接CH,问线段CH何时取得最大值,请说明理由,并直接写出此时△ADH的面积.4.如图,已知△ABC中,∠ABC=45°,CD是边AB上的高线,E是AC上一点,连接BE,交CD于点F.(1)如图1,若∠ABE=15°,BC=+1,求DF的长;(2)如图2,若BF=AC,过点D作DG⊥BE于点G,求证:BE=CE+2DG;(3)如图3,若R为射线BA上的一个动点,以BR为斜边向外作等腰直角△BRH,M 为RH的中点.在(2)的条件下,将△CEF绕点C旋转,得到△CE'F',E,F的对应点分别为E',F',直线MF'与直线AB交于点P,tan∠ACD=,直接写出当MF'取最小值时的值.5.如图1,已知△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点B逆时针旋转一定的角度α得到△A1BC1.(1)若α=90°,则AA1的长为.(2)如图2,若0°<α<90°,直线A1C1分别交AB,AC于点G,H,当△AGH为等腰三角形时,求CH的长.(3)如图3,若0°<α<360°,M为边A1C1的中点,N为AM的中点,请直接写出CN的最大值.6.问题发现:(1)如图1,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D为AB上一点,且AD=2DB,过点D作DE∥BC,填空:=,=;类比探究:(2)如图2,在(1)的条件下将△ADE绕点A逆时针旋转得到△AMN,连接DM,BM,EN,CN,请求出,的值;拓展延伸:(3)如图3,△ABC和△DEF同为等边三角形,且AB=3EF=6,连接AD,BE,将△DEF绕AC(DF)的中点O逆时针自由旋转,请直接写出在旋转过程中BE﹣AD的最大值.7.【问题提出】如图1,在等边三角形ABC内部有一点P,P A=3,PB=4,PC=5.求∠APB的度数.【数学思考】当图形中有一组邻边相等时,通过旋转可以将分散的条件集中起来解决问题.【尝试解决】(1)将△APC绕点A逆时针旋转60°,得到△AP'B,连接PP',则△APP'为等边三角形.∵P'P=P A=3,PB=4,P'B=PC=5,∴P'P2+PB2=P'B2,△BPP'为三角形,∴∠APB的度数为.(2)如图2,在等边三角形ABC外部有一点P,若∠BP A=30°,求证:P A2+PB2【类比探究】=PC2.【联想拓展】(3)如图3,在△ABC中,∠BAC=90°,AB=AC.点P在直线BC上方且∠APB=45°,PC=BC=2,求P A的长.8.如图(1),已知△ABC中,∠BAC=90°,AB=AC;AE是过A的一条直线,且B,C 在AE的异侧,BD⊥AE于D,CE⊥AE于E.(1)求证:BD=DE+CE;(2)若直线AE绕A点旋转到图(2)位置时(BD<CE),其余条件不变,问BD与DE,CE的数量关系如何?请给予证明.(3)若直线AE绕A点旋转到图(3)位置时(BD>CE),其余条件不变,问BD与DE,CE的数量关系如何?请直接写出结果,不需证明;(4)根据以上的讨论,请用简洁的语言表达直线AE在不同位置时BD与DE,CE的数量关系.9.(1)如图1,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,作DE垂直DF交BC于点F,求证:DE=DF.(2)如图2,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,求证:点F在线段BC上;(3)如图3,直角△ABC,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,若AB=6,BC=8,①直接写出线段EF=时,BE的长;②直接写出△ACF是等腰三角形时,BE的长;③直接写出△BEF面积的最大值.10.在平面直角坐标系中,O为原点,点A(﹣4,0),点B(0,3),△ABO绕点B顺时针旋转,得△A'BO',点A、O旋转后的对应点为A'、O',记旋转角为α.(1)如图①,α=90°,边OA上的一点M旋转后的对应点为N,当OM=1时,点N 的坐标为;(2)在(1)的条件下,当O'M+BN取得最小值时,在图②中画出点M的位置,并求出点N的坐标.(3)如图③,P为AB上一点,且P A:PB=2:1,连接PO'、P A',在△ABO绕点B顺时针旋转一周的过程中,△PO'A'的面积是否存在最大值和最小值,若存在,请求出;若不存在,请说明理由.11.如图①,△ABC为直角三角形,∠ACB=90°,∠BAC=30°,点D在AB边上,过点D作DE⊥AC于点E,取BC边的中点F,连接DF并延长到点G,使FG=DF,连接CG.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)问题发现:(1)填空:CE与CG的数量关系是,直线CE与CG所夹的锐角的度数为.探究证明:(2)将△ADE绕点A逆时针旋转,(1)中的结论是否仍然成立,若成立,请仅就图②所示情况给出证明,若不成立,请说明理由;问题解决:(3)若AB=4,AD=3,将△ADE由图①位置绕点A逆时针旋转α(0°<α<180°),当△ACE是直角三角形时,请直接写出CG的值.12.如图,两直角三角形ABC和DEF有一条边BC与EF在同一直线上,且∠DFE=∠ACB =60°,BC=1,EF=2.设EC=m(0≤m≤4),点M在线段AD上,且∠MEB=60°.(1)如图1,当点C和点F重合时,=;(2)如图2,将图1中的△ABC绕点C逆时针旋转,当点A落在DF边上时,求的值;(3)当点C在线段EF上时,△ABC绕点C逆时针旋转α度(0<α<90°),原题中其他条件不变,则=.13.在△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,连接DE,将△AED 沿直线AE翻折得到△AEF(点D与点F为对应点),连接DF,过点D作DG⊥DE交BE于点G.(1)如图1,求证:四边形DFEG为平行四边形;(2)如图2,连接CF,若tan∠ABE=,在不添加任何辅助线与字母的情况下,请直接写出图2中所有正切值等于2的角.14.在△ABC中,∠BAC=90°,点E为AC上一点,AB=AE,AG⊥BE,交BE于点H,交BC于点G,点M是BC边上的点.(1)如图1,若点M与点G重合,AH=2,BC=,求CE的长;(2)如图2,若AB=BM,连接MH,∠HMG=∠MAH,求证:AM=2HM;(3)如图3,若点M为BC的中点,作点B关于AM的对称点N,连接AN、MN、EN,请直接写出∠AMH、∠NAE、∠MNE之间的角度关系.15.(1)如图1.在Rt△ACB中,∠ACB=90°,CA=8,BC=6,点D、E分别在边CA,CB上,且CD=3,CE=4,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CG所在直线与线段BD所在直线的位置关系是.(提示:延长CF到点M,使FM=CF,连接AM)(2)将△DCE绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将△DCE绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为.16.在△ABC和△AEF中,∠AFE=∠ABC=90°,∠AEF=∠ACB=30°,AE=AC,连接EC,点G是EC中点,将△AEF绕点A顺时针旋转.(1)如图1,若E恰好在线段AC上,AB=2,连接FG,求FG的长度;(2)如图2,若点F恰好落在射线CE上,连接BG,证明:GB=AB+GC;(3)如图3,若AB=3,在△AEF旋转过程中,当GB﹣GC最大时,直接写出直线AB,AC,BG所围成三角形的面积.17.如图,在等腰Rt△ABC中,∠ACB=90°,点D,E分别在AB,BC上运动,将线段DE绕点E按顺时针方向旋转90°得到线段EF.(1)如图1,若D为AB中点,点E与点C重合,AF与DC相交于点O,求证:OE=OD;(2)如图2,若点E不与C,B重合,点D为AB中点,点G为AF的中点,连接DG,连接BF,判断线段BF,CE,AD的数量关系并说明理由;(3)如图3,若AB=4,AD=3BD,点G为AF的中点,连接CG,∠GDE=90°,请直接写出CE的长.18.如图,在平面直角坐标系中,点O为坐标原点,点A(x,y)中的横坐标x与纵坐标y 满足+|y﹣8|=0,过点A作x轴的垂线,垂足为点D,点E在x轴的负半轴上,且满足AD﹣OD=OE,线段AE与y轴相交于点F,将线段AD向右平移8个单位长度,得到线段BC.(1)直接写出点A和点E的坐标;(2)在线段BC上有一点G,连接DF,FG,DG,若点G的纵坐标为m,三角形DFG 的面积为S,请用含m的式子表示S(不要求写m的取值范围);(3)在(2)的条件下,当S=26时,动点P从D出发,以每秒1个单位的速度沿着线段DA向终点A运动,动点Q从A出发,以每秒2个单位的速度沿着折线AB→BC向终点C运动,P,Q两点同时出发,当三角形FGP的面积是三角形AGQ面积的2倍时,求出P点坐标19.如图:直线l1:y=﹣x+6与x轴交于点A,与y轴交于点B,将△AOB沿直线l1翻折后,设点O的对应点为点C,已知双曲线y=(x>0)经过点C.(1)求点A,B的坐标.(2)求k的值.(3)将直线l1绕着点A逆时针旋转得到直线l2.直线l2与y轴交于点B′,将△AOB′沿直线l2翻折得到△AB′C',当四边形OAC′B′为正方形时停止转动,求转动过程中点C运动到点C′的路径长.20.图形的旋转变换是研究数学相关问题的重要手段之一.小华和小芳对等腰直角三角形的旋转变换进行研究.如图(1),已知△ABC和△ADE均为等腰直角三角形,点D,E分别在线段AB,AC上,且∠C=∠AED=90°.(1)观察猜想小华将△ADE绕点A逆时针旋转,连接BD,CE,如图(2),当BD的延长线恰好经过点E时,①的值为;②∠BEC的度数为度;(2)类比探究如图(3),小芳在小华的基础上,继续旋转△ADE,连接BD,CE,设BD的延长线交CE于点F,请求出的值及∠BFC的度数,并说明理由.(3)拓展延伸若AE=DE=,AC=BC=,当CE所在的直线垂直于AD时,请你直接写出BD 的长.参考答案1.解:(1)在Rt△ABC中,AB=AC,BC=5,∴AB=AC=BC=5,由旋转知,CD=CE=4,在Rt△ADC中,AD===,∴BD=AB﹣AD=5﹣;(2)猜想:BD=2AF,理由:如图1,延长BA至G,使AG=AB,连接EG,则CG=CB,∴∠ABC=∠AGC,在Rt△ABC中,AB=AC,∴∠ABC=45°,∴∠AGC=45°,∴∠BCG=90°,由旋转知,CD=CE,∠DCE=90°=∠BCG,∴∠BCD=∠GCE,∴△BCD≌△GCE(SAS),∴BD=GE,∠CBD=∠CGE=45°,∴∠BGE=∠CGB+∠CGE=90°=∠BAC,∴AC∥GE,∴,∴=,∴EG=2AF,∴BD=2AF;(3)存在,如图2,延长DA至P,使AP=AD,∵∠BAC=90°,∴点P,点D关于AC对称,∴MN+DN=MH+PN,过点P作PH⊥CD于H,要使MN+DN最小,则点P,N,M在同一条线上,且PM⊥CD,即MN+DN的最小值为PH,∵CA=3DA=6,∴AD=2,∴DP=2AD=4,CD===2,连接CP,∴S△CDP=DP•AC=CD•PH,∴PH===,即DN+MN的最小值为.2.解:(1)如图1中,∵EC平分∠ACB,EM⊥AC,EN⊥BC,∴EM=EN,∵∠EMC=∠DNC=∠MCN=90°,∴四边形EMCN是矩形,∵EM=EN,∴四边形EMCN是正方形,设正方形的边长为m,则×AC×BC=×AC×m+×BC×m,解得m=,∵EF⊥ED∴∠MEN=∠FED=90°,∴∠MEF=∠NDF,∵∠EMF=∠END=90°,∴△EMF≌△END(AAS),∴S四边形EFCD=S正方形EMCN=,故答案为:;(2)①如图2中,⊙O即为所求作.②如图2中,射线CD即为所求作.(3)如图2中,过点D作DM⊥CB交CB的延长线于M,DN⊥AC于N.∵∠DMC=∠DNC=∠MCN=90°,∴四边形DMCN是矩形,∵DC平分∠ACB,DM⊥CB,DN⊥AC,∴DM=DN,∴四边形DMCN是正方形,∴CM=CN,∵∠ACD=∠BCD,∴=,∴DB=DA,∵DM=DN,∠DMB=∠DNA=90°,∴Rt△DMB≌Rt△DNA(HL),∴BM=AN,S四边形ACBD=S正方形DMCN,∴AC+BC=CM﹣BM+CN﹣AN=2CM=14,∴CM=7,∴S四边形ACBD=49.故答案为:49.3.(1)证明:∵△ABC是等边三角形,AD⊥BC,∴∠BAD=∠CAD=∠BAC=30°,∵∠EAF=60°,∴∠GAE=∠GAF=30°,∵AE=AF,∴FG=EG.(2)解:结论:∠EHD=120°,是定值.理由:如图2中,连接BF,CE.∵AB=AC,AD⊥BC,∴BD=CD,∵BH=EH,∴DH∥EC,∴∠HDB=∠ECB,∵FG=GE,EH=HB,∴GH∥BF,∴∠EHG=∠EBF,∵∠EAF=∠BAC=60°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE(SAS),∴∠ACE=∠ABF,∵∠EHD=∠HDB+∠HBD,∴∠DHG=∠EHG+∠EHD=∠EBF+∠HDB+∠HBD=∠ABF﹣∠ABE+∠ECB+∠ABD+∠ABE=∠ACE+∠ECB+∠ABD=∠ACB+∠ABC=120°.(3)解:如图3中,取AB的中点N,连接AH,HN,CH,CH交AD于M,过点H作HT⊥AD于T.∵EH=BH,AN=BN,∴NH为△ABE的中位线,∴HN=AE=,∴点H在以N为圆心,为半径的圆上,当C,N,H共线时,CH的值最大,∵△ABC是等边三角形,∴CN⊥AB,∴∠ACM=∠MCB=30°,∵AD=2,∴CN=AD=2,在Rt△CMD中,CD=2,∠MCD=30°,∴CM==,∴MN=CN﹣CM=,∴HM=HN+MN=+=,∴HT=HM•sin60°=,∴S△ADH=•AD•HT=.4.(1)解:如图1中,过点F作FH⊥BC于H.∵CD⊥AB,∴∠BDC=90°,∵∠DBC=45°,∴∠DCB=90°﹣45°=45°,∵FH⊥CH,∴∠FHC=90°,∴∠HFC=∠HCF=45°,∴CH=FH,设FH=CH=m,∵∠ABE=15°,∴∠FBC=45°﹣15°=30°,∴BH=HF=m,∴m+m=+1,∴m=1,∴CF=CH=,∵CD=BC=,∴DF=CD﹣CF=﹣=.(2)证明:如图2中,连接DE,过点D作DH⊥DE交BE于H.∵∠ADC=∠FDB=90°,DB=DC,BF=AC,∴Rt△BDF≌Rt△CDA(HL),∴∠DBF=∠ACD,∵∠BFD=∠CFE,∴△BFD∽△CFE,∴=,∴=,∵∠DFE=∠BFC,∴△DFE∽△BFC,∴∠DEF=∠BCF=45°,∵DH⊥DE,∴∠HDE=90°,∴∠DHE=∠DEH=45°,∴DH=DE,∵∠BDC=∠EDH=90°,∴∠BDH=∠CDE,∵DB=DC,DH=DE,∴△BDH≌△CDE(SAS),∴BH=EC,∵DH=DE,DG⊥EH,∴GH=EG,∴DG=EH,∴BE=BH+HE=EC+2DG.(3)解:如图3中,过点M作MJ⊥BC于J,过点P作PK⊥BC于K.∵△BHR,△DBC都是等腰直角三角形,∴∠DBC=∠HBR=45°,∴∠HBC=90°,∵∠H=∠HBJ=∠MJB=90°,∴四边形BHMJ是矩形,∴BH=MJ,HM=BJ,∵BH=HR,HM=MR,∴MJ=2BJ,∴tan∠MBJ==2,∴点M的在射线BM上运动,∴当C,F′,M共线,且CM⊥BM时,F′M的值最小.设AD=m,∵tan∠ACD==,∴CD=BD=3m,DF=AD=m,CF=CF′=2m,BC=3m,∵∠CMB=90°,tan∠CBM==2,∴BM=m,CM=m,∴BJ=HM=m,JM﹣BH=HR=m,∴MR=m,设BK=PK=n,CK=2n,∴n=m,∴BK=PK=m,CK=2m,PC=m,∴PF′=PC﹣CF′=m﹣2m,∴==.5.解:(1)∵∠C=90°,AC=4,CB=3,∴AB===5,∵α=90°,∴△ABA1是等腰直角三角形,AA1=AB=5.故答案为:5.(2)如图2﹣1中,当AG=AH时,∵AG=AH,∴∠AHG=∠AGH,∵∠A=∠A1,∠AGH=∠A1GB,∴∠AHG=∠A1BG,∴∠A1GB=∠A1BG,∴AB=AG=5,∴GC1=A1G﹣C1G=1,∵∠BC1G=90°,∴BG===,∴AH=AG=AB﹣BG=5﹣,∴CH=AC﹣AH=4﹣(5﹣)=﹣1.如图2﹣2中,当GA=GH时,过点G作GM⊥AH于M.同法可证,GB=GA1,设GB=GA1=x,则有x2=32+(4﹣x)2,解得x=,∴BG=,AG=5﹣=,∵GM∥BC,∴=,∴=,∴AM=,∵GA=GH,GM⊥AH,∴AM=HM,∴AH=3,∴CH=AC﹣AM=1.综上所述,满足条件的CH的值为﹣1或1.(3)如图3中,取AB的中点J,连接BM,CJ,JN.∵AJ=BJ,∠ACB=90°,∴CJ=AB=,∵BC1=BC=3,MC1=MA1=2,∠BC1M=90°,∴BM===,∵AJ=BJ,AN=NM,∴JN=BM=,∵CN≤CJ+JN,∴CN≤,∴CN的最大值为.6.解:(1)如图1中,在Rt△ABC中,,∵AD=2DB,∴AB=AD+DB=3DB,∵DE∥BC,∴,∵,∴,即,∴,故答案为:,.(2)由旋转性质可知:AD=AM,AE=AN,∠BAM=∠CAN,∵,∠BAM=∠CAN,∴△ABM∽△ACN,∴,∠ABM=∠ACN,∵,∠ABM=∠ACN,∴△DBM∽△ECN,∴.(3)如图3中,连接OB,OE,由三线合一性质可知∠BOC=∠DOE=90°,∴∠BOD=∠COE,∴∠AOB+∠BOD=∠BOC+∠COE,即∠AOD=∠BOE,∵,∠AOD=∠BOE,∴△AOD∽△BOE,∴,∵AB=3EF=6,∴,,在△BOE中,由三边关系可得,BE<BO+OE,当B、O、E三点共线时,BE存在最大值为,∵,∴当BE存在最大值时,BE﹣AD的最大值=.7.(1)解:如图1,将△APC绕点A逆时针旋转60°,得到△AP′B,连接PP′,则△APP′为等边三角形.∵PP′=P A=3,PB=4,P′B=PC=5,∴P′P2+PB2=P′B2.∴△BPP′为直角三角形.∴∠APB的度数为90°+60°=150°.故答案为:直角;150°.(2)证明:如图2中,将△P AB绕点B逆时针旋转60°得到△TCB,连接PT.∵BP=BT,∠PBT=60°,∴△PBT是等边三角形,∴PT=PB,∠PTB=60°,由旋转的性质可知:△P AB≌△TCB,∴∠APB=∠CTB=30°,P A=CT,∴∠PTC=∠PTB+∠CTB=60°+30°=90°,∴PC2=PT2+CT2,∵PB=PT,P A=CT,∴P A2+PB2=PC2.(3)解:过点C作CT⊥PB于T,连接AT,设CT交AB于O.∵PC=BC=2,CT⊥PB,∴PT=BT,∵∠CAO=∠BTO=90°,∠AOC=∠BOT,∴∠ACT=∠ABP,∠ATC=∠ABC=45°,∵∠CTB=90°,∴∠ATP=∠CTA=∠APT=45°∵AC=AB,∴△CAT≌△BAP(AAS),∴CT=PB=2PT,∵PC2=PT2+CT2,∴(2)2=m2+(2m)2,解得m=2或﹣2(舍弃),∴PT=2,∴P A=PT=.8.解:(1)∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°,∴∠ABD+∠BAD=90°,又∵∠BAC=90°,∴∠EAC+∠BAD=90°,∴∠ABD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(AAS),∴BD=AE,AD=EC,∴BD=DE+CE.(2)∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°,∴∠ABD+∠BAD=90°,又∵∠BAC=90°,∴∠EAC+∠BAD=90°,∴∠ABD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(AAS),∴BD=DE﹣CE.(3)同(2)的方法得出,BD=DE﹣CE.(4)归纳:由(1)(2)(3)可知:当B,C在AE的同侧时,BD=DE﹣CE.当B,C在AE的异侧时,BD=DE+CE.9.(1)证明:如图1中,连接BD.∵△ABC是等腰直角三角形,AD=DC,∴BD⊥AC,BD=DA=DC,∴BD⊥AC,∵ED⊥DF,∴∠EDF=∠BDC=90°,∴∠EDB=∠FDC,∵∠DBE=∠C=45°,∴△EDB≌△FDC(ASA),∴DE=DF.(2)证明:如图2中,连接DB,CF.∵∠BDC=∠EDF=90°,∴∠BDE=∠CDF,∵DB=DC,DE=DF,∴△EDB≌△FDC(SAS),∴∠DBE=∠DCF=45°,∴点F在线段BC上.(3)①如图3﹣1中,过点D作DT⊥AB于T.∵∠ATD=∠ABC=90°,∴DT∥CB,∵AD=DC,∴AT=TB=3,∴DT=BC=4,∵△DEF是等腰直角三角形,EF=,∴DE=DF=,∴ET===1,∴BE=TB+ET=3+1=4,当点E在点T的下方时,BE=3﹣1=2,综上所述,满足条件的BE的值为4或2.②如图3﹣2中,∵△ACF是等腰三角形,又∵AD=DC=DF,∴∠AFC=90°,∴△AFC是等腰直角三角形,∴点E与A重合,∴BE=6.③如图3﹣3中,过点D作DT⊥AB于T,过点F作FR⊥DT于R.∵∠DTE=∠FRD=90°,∠EDT=∠DFR,DE=DF,∴△DTE≌△FRD(AAS),∴ET=DR,DT=FR=4,设ET=DR=m,则RT=4﹣m,∴S△EFB=(3+m)(4﹣m)=(﹣m2+m+12)=﹣(m﹣)2+,∵﹣<0,∴△BEF的面积有最大值,最大值为.10.解:(1)∵点A(﹣4,0),点B(0,3),∴OA=4,OB=3,由旋转的性质可知,BO=BO′=3,OM=O′N=1,∠OBO′=90°,∴N(﹣3,4).故答案为:(﹣3,4).(2)如图②中,∵BM=BN,∴O′M+BN=O′M+BM,作点B关于OA的对称点B′,连接O′B′交OA于M,连接BM,O′M+BM的值最小.∵O′(﹣3,3),B′(0,﹣3),∴直线O′B′的解析式为y=﹣2x﹣3,∴M(﹣,0),∴O′N=OM=,∴N(﹣3,).(3)存在.理由:如图③﹣1中,当点O′落在AB的延长线上时,△PO′A′的面积最大.由题意,OA=4,OB=3,∴AB===5,∴P A:PB=2:1,∴PB=,∴PO′=PB+PO′=,∴△PO′A′的面积的最大值=×4×=.如图③﹣2中,当点O′落在AB上时,△PO′A′的面积最小,最小值为×4×(3﹣)=.11.解:(1)如图①中,过点D作DT⊥BC于T.∵DE⊥AC,∴∠DEC=∠ECT=∠DTC=90°,∴四边形ECTD是矩形,∴DT=EC,DT∥AC,∴∠TDB=∠A=30°,∴DT=BD,∵FC=FB,∠CFG=∠BFD,FG=FD,∴△CFG≌△BFD(SAS),∴CG=BD,∠FCG=∠B=60°,∴EC=CG,∴∠ACG=90°+60°=150°,∴直线CE与CG所夹的锐角的度数为30°,故答案为:EC=CG,30°.(2)成立.理由如下:连接CD,BG,延长BD交CE的延长线于H,设BH交AC于点O.在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=30°,∴cos∠BAC==,cos∠EAD==,∠EAC=∠DAB,∴==,∴△ACE∽△ABD,∴==,∠ACE=∠ABD,∵∠HOC=∠AOB,∴∠H=∠OAB=30°,∵CF=FB,DF=FG,∴四边形DCGB是平行四边形,∴CG=BD,CG∥BH,∴∠1=∠H=30°,∴EC=CG,直线CE与CG所夹的锐角的度数为30°.(3)如图③﹣1中,当∠AEC=90°时,由题意AC=AB=2,AE=AD=,∴EC===,∴CG=EC=,如图③﹣2中,当∠EAC=90°时,可得EC==,∴CG=EC=5.综上所述,CG的值为或5.12.解:(1)由题意得,在Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=1,∴AC=2,BC=,在Rt△DEC中,∠DEC=90°,∠DCE=60°,EF=2,∴DC=4,DE=2,∴∠DCA=180°﹣∠DCE﹣∠ACB=60°,∴AC=EF,∠DCE=∠DCA,DC=DC,∴△DEF≌△DAC(SAS),∴AD=DE=2,∠EDC=∠CDA=30°,∵∠MEC=60°,∴∠DEM=30°,∴∠DME=180°﹣∠DEM﹣∠EDM=180°﹣∠DEM﹣2∠EDC=90°,∴DM=DE=,∴AM=AD﹣DM=,∴=1,故答案为:1;(2)如图2,连接AE,∵AC=EF=2,∠ACE=60°,∴△AEC是等边三角形,∴AE=2,∠EAC=∠AEC=60°,∴∠AEB+∠BEC=∠AEC=60°,∵∠MEB=60°,∴∠AEB+∠MEA=60°,∴∠BEC=∠MEA,∵∠DAE=∠ECB=120°,AE=EC,∴△AME≌△CBE(ASA),∴AM=BC=1,∵AD=DC﹣AC=2,∴DM=AD﹣AM=1,∴=1;(3)如图3,过点B作BG⊥BE交EM延长线于点G,连接AG,BG,∵∠CBA=∠EBG=90°,∴∠EBC=∠GBA,∵∠MEB=∠ACB=60°,∴,∴△ECB∽△GAB,∴,∠AGB=∠CEB,∴AG=m,∵∠CEB+∠DEG=30°,∠AGB+∠EGA=30°,∴∠AGM=∠DEM,∴AG∥DE,∴△AGM∽△DEM,∴,∵DE=EF=2,∴==.故答案为:.13.(1)证明:如图1中,∵∠ABC=45°,AD⊥BC于点D,∴∠BAD=90°﹣∠ABC=45°,∴△ABD是等腰直角三角形,∴AD=BD,∵BE⊥AC,∴∠GBD+∠C=90°,∵∠EAD+∠C=90°,∴∠GBD=∠EAD,∵∠ADB=∠EDG=90°,∴∠ADB﹣∠ADG=∠EDG﹣∠ADG,即∠BDG=∠ADE,∴△BDG≌△ADE(ASA),∴BG=AE,DG=DE,∵∠EDG=90°,∴△EDG为等腰直角三角形,∴∠AED=∠AEB+∠DEG=90°+45°=135°,∵△AED沿直线AE翻折得△AEF,∴△AED≌△AEF,∴∠AED=∠AEF=135°,ED=EF,∴∠DEF=360°﹣∠AED﹣∠AEF=90°,∴△DEF为等腰直角三角形,∴∠GDE=∠DEF=90°,DG=DE=EF,∴DG∥EF,∴四边形DFEG是平行四边形.(2)解:如图2中,设AD交BE于P,过点P作PT⊥AB于T.∵tan∠ABE==,∴可以假设PT=a,BT=3a,∵△ABD是等腰直角三角形,∴∠P AT=45°,∵PT⊥AB,∴∠ATP=90°,∴∠P AT=∠APT=45°,∴AT=PT=a,∴P A=a,AB=4a,AD=BD=2a,∴P A=PD=a,∴tan∠BPD==2,∵BE⊥AC,∴∠ADC=∠PEC=90°,∴∠EPD+∠ACD=180°,∵∠EPD+∠BPD=180°,∴∠BPD=∠ACD,根据对称性可知,∠ACD=∠ACF,∠ADF=∠AFD,AC⊥DF,∴∠ACD=∠ACF=∠BPD,∵∠ADF+∠CDF=90°,∠CDF+∠ACD=90°,∴∠ADF=∠ACD,∴∠ACD=∠ACF=∠ADF=∠AFD=∠BPD,∴正切值等于2的角有:∠ACD,∠ACF,∠ADF,∠AFD.14.解:(1)∵∠BAC=90°,AB=AE,∴△BAE为等腰直角三角形,∵AG⊥BE,∴AH是△BAE的中线,∴BE=2AH=4,∵∠BEA=45°,∴∠BEC=135°,在△BCE中,过点C作CD⊥BE交BE的延长线于点D,如图1,∵∠DEC=45°,∴△DEC是等腰直角三角形,设ED=x,则DC=x,CE=x,在Rt△BCD中,BC2=BD2+DC2,即,∴x1=1或x2=﹣5(舍去),∴CE=;(2)如图2,过H作HD⊥HM交AM于点D,连接BD,∵AB=AE,∠BAC=90°,∴△ABE是等腰直角三角形,∵AG⊥BE,∴△ABH为等腰直角三角形,∴BH=AH,∠BAN=45°,∠BHA=90°,∵AB=BM,∴∠BAM=∠BMA,∵∠HMG=∠MAH,∴∠BAM﹣∠MAH=∠BMA﹣∠HMG,即∠BAH=∠AMH=45°,∵HD⊥HM,∴△DHM为等腰直角三角形,∴DH=HM,∠DHM=90°,∵∠BHD=∠BHA+∠AHD,∠AHM=∠DHM+∠AHD,∴∠BHD=∠AHM,在△BHD与△AHM中,,∴△BHD≌△AHM(SAS),∴∠DBH=∠MAH,BD=AM,∴∠BHA=∠BDA=90°,∵BA=BM,∴D是AM的中点,∴AM=2DM=2HM,即AM=2HM;(3)∵H是BE的中点,M是BC的中点,∴MH是△BCE的中位线,∴MH∥CE,∴∠AMH=∠MAC,∵∠BAC=90°,∴AM=BM,∴∠MAB=∠ABM,∵点B与点N关于线段AM对称,∴∠ABM=∠ANM,AB=AN,∴AE=AN,∴∠AEN=∠ANE,在△AEN中,∠NAE+2∠ANE=180°①,∵∠ANE=∠ANM+∠MNE,∠ABM=∠ANM=∠MAB=90°﹣∠MAC,∴∠ANE=90°﹣∠MAC+∠MNE,∴∠ANE=90°﹣∠AMH+∠MNE②,将②代入①,得:∠NAE+2×(90°﹣∠AMH+∠MNE)=180°,∴∠NAE+180°﹣2∠AMH+2∠MNE=180°,∴∠NAE+2∠MNE=2∠AMH.15.解:(1)结论:CG⊥BD.理由:延长CF到点M,使得FM=CF,连接AM.∵F A=FE,∠AFM=∠EFC,FM=FC,∴△AMF≌△ECF(SAS),∴AM=CE=4,∠AMF=∠ECF,∴AM∥CE,∴∠MAC=∠DCB=90°,∵==,∴△MAC∽△DCB,∴∠DBC=∠ACM,∵∠ACM+∠GCB=90°,∴∠DBC+∠GCB=90°,∴∠CGB=90°,∴CG⊥BD.故答案为:CG⊥BD.(2)结论仍然成立.理由:延长CF到点M,使得FM=CF,连接AM.∵F A=FE,∠AFM=∠EFC,FM=FC,∴△AMF≌△ECF(SAS),∴AM=CE=4,∠AMF=∠ECF,∴AM∥CE,∴∠MAC+∠ACE=180°,∴∠MAC=180°﹣∠ACE,∵∠DCB=∠DCE+∠ACB﹣∠ACE=90°+90°﹣∠ACE=180°﹣∠ACE,∴∠MAC=∠DCB,∵==,∴△MAC∽△DCB,∴∠DBC=∠ACM,∵∠ACM+∠GCB=90°,∴∠DBC+∠GCB=90°,∴∠CGB=90°,∴CG⊥BD.(3)如图3中,当点E在线段BD上时,∵△AMC∽△CDB,∴==,在Rt△DCE中,CD=3,CE=4,∴DE===5,∵CG⊥DE,∴CG==,在Rt△CGB中,CB=6,CG=中,∴BG===,在Rt△DCG中,DG===,∴BD=BG+DG=,∴CM=BD=,∴CF=CM=如图4中,当点E在线段BD的延长线上时,同法可得CF=CM=.综上所述,满足条件的CF的值为或.16.(1)解:如图1中,过点F作FH⊥AE于H.在Rt△ABC中,∠ACB=90°,AB=2,∠C=30°,∴AC=2AB=4,BC=AB=2,∵AE=EC=AC=2,EG=GC,∴EG=CG=1,∵∠AFE=90°,∠AEF=30°,∴EF=AE•cos30°=,∴FH=EF=,HE=FH=,∴GH=HE+EG=,∴FG===.(2)证明:如图2中,取AC的中点M,连接BM,GM,BF.∵AM=MC,∠ABC=90°,∴BM=AM=CM,∵AC=2AB,∴AB=AM=BM,∴∠BAM=∠AMB=∠ABM=60°,∴∠BMC=120°,∵AE=2AF,∠EAF=60°,∴∠BAF=120°+∠EAC,∵AM=MC,EG=GC,∴GM=AE=AF,GM∥AE,∴∠CMG=∠EAC,∴∠BMG=120°+∠CMG=120°+∠EAC=∠BAF,∴△BAF≌△BMG(SAS),∴∠ABF=∠MBG,BF=BG,∴∠FBG=∠ABM=60°,∴△BFG是等边三角形,∴BG=FG,∴BG=EF+EG=AE+CG=AB+CG.(3)解:如图3中,取AC的中点M,连接BM,GM,BF.在MC上取一点D,使得MD=MG,连接DG,BD.同法可证:△BAF≌△BMG(SAS),∴∠ABF=∠MBG,BF=BG,∴∠FBG=∠ABM=60°,∴△BFG是等边三角形,∴BG=FG,∵AM=CM,EG=CG,∴MG=AE,∵AB=3,∠ABC=90°,∠ACB=30°,∴AC=2AB=6,AM=CM=3,∵AE=AC=3,MG=,∴MD=MG=,∵==,∠DMG=∠GMC,∴△MDG∽△MGC,∴==,∴DG=CG,∴GB﹣CG=GB﹣DG≤BD,∴当B,D,G共线时,BG﹣CG的值最大,最大值为BD的长,∴直线AB,AC,BG围成的三角形为△ABD,∵AD=AM+DM=3+=,∴S△ABD=××=,∴当GB﹣GC最大时,直线AB,AC,BG所围成三角形的面积为.17.(1)证明:如图1中,∵CA=CB,∠ACB=90°,AD=DB,∴CD⊥AB,CD=AD=DB,∵∠DEF=∠ADC=90°,DE=EF,∴AD=EF,∵∠AOD=∠EOF,∴△AOD≌△FOE(AAS),∴OE=OD.(2)解:结论:AD﹣BF=CE.理由:如图2中,过点E作ET⊥BC交AB于T,过点T作TR⊥AC于R.则四边形ECRT 是矩形,△ART,△EBT都是等腰直角三角形,可得EC=RT,AT=RT=EC.∵∠TEB=∠DEF=90°,∴∠TED=∠BEF,∵ET=EB,ED=EF,∴△TED≌△BEF(SAS),∴DT=BF,∵AD﹣DT=AT,∴AD﹣BF=CE.(3)解:如图3中,取AB的中点R,连接GR,BF,过点E作EM⊥AB于M.设GR =x,EM=BM=y.由(2)可知,△TED≌△BEF(SAS),∴∠ETD=∠EBF=45°,∴∠ABC=45°,∴∠FBA=90°,∵AG=GF,AR=RB=2,∴GR∥BF,BF=2GR=2x,∴∠GRA=∠FBA=90°,∵GR⊥AB,∵AB=4,AD=3BD,∴AD=3,BD=,∴DR=AD﹣AR=3﹣2=,∵∠GRD=∠EMD=∠EDG=90°,∴∠GDR+∠DGR=90°,∠GDR+∠EDM=90°,∴∠DGR=∠EDM,∴△DRG∽△EMD,∴=,∴=①又∵AD﹣BF=CE,∴3﹣2x=(4﹣y)②,由①②可得y=(不合题意的解已经舍弃).∴EC=4﹣()=.18.解:(1)∵+|y﹣8|=0,又∵≥0,|y﹣8|≥0,∴x=2,y=8,∴A(2,8),∵AD⊥x轴,∴OD=2,AD=8,∵AD﹣OD=OE,∴OE=6,∴E(﹣6,0).(2)如图1中,连接OG.由题意G(10,m).∵AD=DE=8,∠ADE=90°,∴∠AED=45°,∴∠OEF=∠OFE=45°,∴OE=OF=6,∴F(0,6),∴S=S△ODG+S△OFG﹣S△OFD=×2×m+×6×10﹣×2×6=m+24(0≤m≤8).(3)如图2中,设FG交AD于J,P(2,t),当点P在DJ上,点Q在AB上时,当S=26时,m=2,∴G(10,2),∵F(0,6),∴直线FG的解析式为y=﹣x+6,∴J(2,),由题意,•(﹣t)×10=2××2t×6,解得t=,∴P(2,),当点P在AJ上,点Q在BG上时,同法可得,•(t﹣)×10=2××(14﹣2t)×8,解得t=,∴P(2,).综上所述,满足条件的点P的坐标为(2,)或(2,).19.解:(1)当x=0时,y=6,∴B(0,6),当y=0时,﹣x+6=0,∴x=6,∴A(6,0);(2)如图1,过点C作CM⊥x轴于M,Rt△ABO中,OA=6,OB=6,∴AB==12,∴∠ABO=30°,由翻折得:∠ABC=∠ABO=30°,∠AOB=∠ACB=90°,AC=OA=6,∴∠CAM=60°,∴∠ACM=90°﹣60°=30°,∴AM=AC=3,CM=3,∴C(9,3),∴k=9×3=27;(3)分两种情况:①如图2,当点B'在y轴的负半轴上时,。
广西壮族自治区2023年九年级中考备考语文专题复习:综合性学习题(含答案)
广西壮族自治区2023年九年级中考备考语文专题复习:综合性学习题(2022·广西梧州·统考一模)某班开展以“保护环境从垃圾分类开始”为主题的综合性学习活动,下面是某同学为活动搜集的四则材料。
请你按照要求,完成下面小题。
【材料一】目前,我国某些城市的垃圾分类标准不够具体,分类回收的垃圾桶也不统一,“混装”“混运”现象严重,导致终端处理成本大大增加,而且垃圾终端处理多为就近填埋,这不仅会占用大量的土地,还会严重污染土地及水源。
【材料二】生活垃圾分类处理流程图【材料三】许多国家在垃圾处理方面取得了一些成效。
有的国家制定了《资源复原法》《固定废弃物处置法》等法律法规,并严格执行有的国家在各个学段均开设专门的环境教育课程;还有一个国家的每个家庭中都分设三个颜色不同的垃圾桶等。
1.根据【材料一】的内容,概括目前我国某些城市垃圾处理方式带来的弊端。
2.结合以上相关材料,请你提出4条环保建议。
3.(2022·广西河池·统考一模)综合性学习。
材料一:2021年国庆档,电影票房排名:电影档期票房票房占比排片占比《长津湖》32.04亿元73% 47.7%《我和我的父辈》9.65亿21.9% 29.2%《皮皮鲁与鲁西西之罐头小人》4185.2万0.9% 3.5%材料二:2021年的国庆档,除了中美合作的《拯救甜甜圈:时空大营救》外,其余7部新片均为国产电影。
在众多影片中,《我和我的父辈》从小人物视角切入,反映时代的变迁和民族精神的传承延续。
《长津湖》全景还原历史级战役,无论是题材类型、主创阵容,还是制作规格,都足以“领跑”国庆档期。
材料三:评论员张雪峰向记者表示:“近年来,我国正处于走向中华民族伟大复兴的关键时期,中国的经济、文化、教育、科技等等,都逐渐走向世界领先的位置,年轻人对于国家越来越有自信心,对于民族越来越有认同感。
”(1)从以上三则材料中说说你的发现。
(2)随着爱国电影的热播,以“长津湖”为代表的一系列影视剧中塑造的“中国英雄”“中国硬汉”形象,点燃了国人爱国情怀,激发了许多人内心深处的英雄情结。
人教版九年级数学上册中考专题复习题含答案全套
人教版九年级数学上册中考专题复习题1.类比归纳专题:配方法的应用2.类比归纳专题:一元二次方程的解法3.易错易混专题:一元二次方程中的易错问题4.考点综合专题:一元二次方程与其他知识的综合5.解题技巧专题:抛物线中与系数a,b,c有关的问题6.易错易混专题:二次函数的最值或函数值的范围7.难点探究专题:抛物线与几何图形的综合(选做)8.抛物线中的压轴题9.易错专题:抛物线的变换10.解题技巧专题:巧用旋转进行计算11.旋转变化中的压轴题12.类比归纳专题:圆中利用转化思想求角度13.类比归纳专题:切线证明的常用方法14.解题技巧专题:圆中辅助线的作法15.解题技巧专题:圆中求阴影部分的面积16.考点综合专题:圆与其他知识的综合17.圆中的最值问题18.抛物线与圆的综合19.易错专题:概率与放回、不放回问题类比归纳专题:配方法的应用——体会利用配方法解决特定问题◆类型一 配方法解方程1.一元二次方程x 2-2x -1=0的解是( )A .x 1=x 2=1B .x 1=1+2,x 2=-1- 2C .x 1=1+2,x 2=1- 2D .x 1=-1+2,x 2=-1- 22.用配方法解下列方程时,配方有错误的是( )A .x 2-2x -99=0化为(x -1)2=100B .x 2+8x +9=0化为(x +4)2=25C .2t 2-7t -4=0化为⎝⎛⎭⎫t -742=8116 D .3x 2-4x -2=0化为⎝⎛⎭⎫x -232=1093.利用配方法解下列方程:(1)(2016·淄博中考)x 2+4x -1=0;(2)(x +4)(x +2)=2;(3)4x 2-8x -1=0;(4)3x 2+4x -1=0.◆类型二 配方法求最值或证明 4.代数式x 2-4x +5的最小值是( ) A .-1 B .1 C .2 D .55.下列关于多项式-2x 2+8x +5的说法正确的是( )A .有最大值13B .有最小值-3C .有最大值37D .有最小值1 6.(2016-2017·夏津县月考)求证:代数式3x 2-6x +9的值恒为正数.7.若M =10a 2+2b 2-7a +6,N =a 2+2b 2+5a +1,试说明无论a ,b 为何值,总有M >N .◆类型三 完全平方式中的配方 8.如果多项式x 2-2mx +1是完全平方式,则m 的值为( )A .-1B .1C .±1D .±29.若方程25x 2-(k -1)x +1=0的左边可以写成一个完全平方式,则k 的值为( )A .-9或11B .-7或8C .-8或9D .-6或7◆类型四 利用配方构成非负数求值 10.已知m 2+n 2+2m -6n +10=0,则m +n 的值为( )A .3B .-1C .2D .-211.已知x 2+y 2-4x +6y +13=0,求(x +y )2016的值.答案:类比归纳专题:一元二次方程的解法——学会选择最优的解法◆类型一 一元二次方程的一般解法方法点拨: 形如(x +m )2=n (n ≥0)的方程可用直接开平方法;当方程二次项系数为1,且一次项系数为偶数时,可用配方法;若方程移项后一边为0,另一边能分解成两个一次因式的积,可用因式分解法;如果方程不能用直接开平方法和因式分解法求解,则用公式法.1.用合适的方法解下列方程:(1)⎝⎛⎭⎫x -522-14=0;(2)x 2-6x +7=0;(3)x 2-22x +18=0;(4)3x (2x +1)=4x +2.◆*类型二 一元二次方程的特殊解法 一、十字相乘法方法点拨:例如:解方程:x 2+3x -4=0.第1种拆法:4x -x =3x (正确), 第2种拆法:2x -2x =0(错误), 所以x 2+3x -4=(x +4)(x -1)=0,即x +4=0或x -1=0,所以x 1=-4,x 2=1. 2.解一元二次方程x 2+2x -3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程____________.3.用十字相乘法解下列一元二次方程: (1)x 2-5x -6=0; (2)x 2+9x -36=0.二、换元法方法点拨:在已知或者未知条件中,某个代数式几次出现,可用一个字母来代替它从而简化问题,这就是换元法,当然有时候要通过变形才能换元.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.4.若实数a ,b 满足(4a +4b )(4a +4b -2)-8=0,则a +b =_______.5.解方程:(x 2+5x +1)(x 2+5x +7)=7.1.解:(1)移项,得⎝⎛⎭⎫x -522=14, 两边开平方,得x -52=±14, 即x -52=12或x -52=-12,∴x 1=3,x 2=2;(2)移项,得x 2-6x =-7,配方,得x 2-6x +9=-7+9,即(x -3)2=2, 两边开平方,得x -3=±2, ∴x 1=3+2,x 2=3-2;(3)原方程可化为8x 2-42x +1=0. ∵a =8,b =-42,c =1,∴b 2-4ac =(-42)2-4×8×1=0, ∴x =-(-42)±02×8=24,∴x 1=x 2=24; |(4)原方程可变形为(2x +1)(3x -2) =0,∴2x +1=0或3x -2=0, ∴x 1=-12,x 2=23.2. x -1=0或x +3=0.3.解:(1)原方程可变形为(x -6)(x +1) =0,∴x -6=0或x +1=0, ∴x 1=6,x 2=-1;(2)原方程可变形为(x +12)(x -3) =0,∴x +12=0或x -3=0, ∴x 1=-12,x 2=3. 4.-12或15.解:设x 2+5x +1=t ,则原方程化为t (t +6)=7,∴t 2+6t -7=0,解得t =1或-7.当t =1时,x 2+5x +1=1,x 2+5x =0, x (x +5)=0,∴x =0或x +5=0,∴x 1=0,x 2=-5; 当t =-7时,x 2+5x +1=-7,x 2+5x +8=0,∴b 2-4ac =52-4×1×8<0,此时方程 无实数根.∴原方程的解为x 1=0,x 2=-5.易错易混专题:一元二次方程中的易错问题◆类型一 利用方程或其解的定义求待定系数时,忽略“a ≠0”1.(2016-2017·江都区期中)若关于x的方程(a +3)x |a |-1-3x +2=0是一元二次方程,则a 的值为______.【易错1】2.关于x 的一元二次方程(a -1)x 2+x +a 2-1=0的一个根是0,则a 的值是( )A .-1B .1C .1或-1D .-1或0 3.已知关于x 的一元二次方程(m -1)x 2+5x +m 2-3m +2=0的常数项为0.(1)求m 的值; (2)求方程的解.◆类型二 利用判别式求字母取值范围时,忽略“a ≠0”及“a 中的a ≥0”4.(2016-2017·抚州期中)若关于x 的一元二次方程(m -2)2x 2+(2m +1)x +1=0有解,那么m 的取值范围是( )A .m >34B .m ≥34C .m >34且m ≠2D .m ≥34且m ≠25.已知关于x 的一元二次方程x 2+k -1x -1=0有两个不相等的实数根,则k的取值范围是________.6.若m 是非负整数,且关于x 的方程(m -1)x 2-2x +1=0有两个实数根,求m 的值及其对应方程的根.◆类型三 利用根与系数关系求值时,忽略“Δ≥0”7.(2016·朝阳中考)关于x 的一元二次方程x 2+kx +k +1=0的两根分别为x 1,x 2,且x 21+x 22=1,则k 的值为_______.【易错2】 8.已知关于x 的方程x 2+2(m -2)x +m 2+4=0有两个实数根,且这两根的平方和比两根的积大21,求m 的值.【易错2】◆类型四 与三角形结合时忘记取舍 9.已知三角形两边长分别为2和9,第三边的长为一元二次方程x 2-14x +48=0的根,则这个三角形的周长为( )A .11B .17C .17或19D .1910.在等腰△ABC 中,三边分别为a ,b ,c ,其中a =5,若关于x 的方程x 2+(b +2)x +6-b =0有两个相等的实数根,求△ABC 的周长.考点综合专题:一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1.(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是()A.5 B.7 C.5或7 D.102.(广安中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的根,则该等腰三角形的周长是()A.12 B.9C.13 D.12或93.(罗田县期中)菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为()A.16 B.12 C.16或12 D.244.(烟台中考)等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为()A.9 B.10C.9或10 D.8或105.(齐齐哈尔中考)△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是________.6.(西宁中考)若矩形的长和宽是方程2x2-16x+m=0(0<m≤32)的两根,则矩形的周长为_________.【方法8】7.已知一直角三角形的两条直角边是关于x的一元二次方程x2+(2k-1)x+k2+3=0的两个不相等的实数根,如果此直角三角形的斜边是5,求它的两条直角边分别是多少.【易错4】◆类型二一元二次方程与一次函数的综合8.(泸州中考)若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是()9.(安顺中考)若一元二次方程x2-2x -m=0无实数根,则一次函数y=(m+1)x +m-1的图象不经过()A.第四象限B.第三象限C.第二象限D.第一象限10.(葫芦岛中考)已知k、b是一元二次方程(2x+1)(3x-1)=0的两个根,且k>b,则函数y=kx+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限11.(广元中考)从3,0,-1,-2,-3这五个数中抽取一个数,作为函数y=(5-m2)x和关于x的一元二次方程(m+1)x2+mx+1=0中m的值.若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m的值是______.◆类型三一元二次方程与二次根式的综合12.(达州中考)方程(m-2)x2-3-mx +14=0有两个实数根,则m的取值范围为()A.m>52B.m≤52且m≠2C.m≥3 D.m≤3且m≠213.(包头中考)已知关于x的一元二次方程x2+k-1x-1=0有两个不相等的实数根,则k的取值范围是______.答案:12.B 13.解题技巧专题:抛物线中与系数a,b,c有关的问题◆类型一由某一函数的图象确定其他函数图象的位置1.二次函数y=-x2+ax-b的图象如图所示,则一次函数y=ax+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限第1题图第2题图2.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是()3.已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是()第3题图第4题图4.如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是()◆类型二由抛物线的位置确定代数式的符号或未知数的值5.(2016·新疆中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是【方法10】()A.a>0B.c<0C.3是方程ax2+bx+c=0的一个根D.当x<1时,y随x的增大而减小第5题图第7题图6.(2016·黄石中考)以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是【方法10】()A.b≥54B.b≥1或b≤-1C.b≥2 D.1≤b≤27.(2016·孝感中考)如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是()A.1个B.2个C.3个D.4个8.(2016·天水中考)如图,二次函数y =ax2+bx+c(a≠0)的图象与x轴交于A,B 两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②b2-4ac4a>0;③ac-b+1=0;④OA·OB =-ca .其中正确结论的序号是____________.答案:易错易混专题:二次函数的最值或函数值的范围——类比各形式,突破给定范围求最值◆类型一 没有限定自变量的范围求最值 1.函数y =-(x +1)2+5的最大值为_______. 2.已知二次函数y =3x 2-12x +13,则函数值y 的最小值是【方法11】( )A .3B .2C .1D .-13.已知函数y =x(2-3x),当x 为何值时,函数有最大值还是最小值?并求出最值.◆类型二 限定自变量的取值范围求最值4.(2016-2017·双台子区校级月考)函数y =x 2+2x -3(-2≤x ≤2)的最大值和最小值分别是( )A .4和-3B .-3和-4C .5和-4D .-1和-45.二次函数y =-12x 2+32x +2的图象如图所示,当-1≤x ≤0时,该函数的最大值是【方法11】( )A .3.125B .4C .2D .06.已知0≤x ≤32,则函数y =x 2+x +1( ) A .有最小值34,但无最大值B .有最小值34,有最大值1C .有最小值1,有最大值194D .无最小值,也无最大值◆类型三 限定自变量的取值范围求函数值的范围7.从y =2x 2-3的图象上可以看出,当-1≤x ≤2时,y 的取值范围是( )A .-1≤y ≤5B .-5≤y ≤5C .-3≤y ≤5D .-2≤y ≤18.已知二次函数y =-x 2+2x +3,当x ≥2时,y 的取值范围是( )A .y ≥3B .y ≤3C .y >3D .y <39.二次函数y =x 2-x +m(m 为常数)的图象如图所示,当x =a 时,y <0;那么当x =a -1时,函数值CA .y <0B .0<y <mC .y >mD .y =m◆类型四 已知函数的最值,求自变量的取值范围或待定系数的值10.当二次函数y =x 2+4x +9取最小值时,x 的值为( )A .-2B .1C .2D .911.已知二次函数y =ax 2+4x +a -1的最小值为2,则a 的值为( )A.3 B.-1C.4 D.4或-112.已知y=-x(x+3-a)+1是关于x 的二次函数,当x的取值范围在1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是()A.a=9 B.a=5 C.a≤9 D.a≤513.在△ABC中,∠A,∠B所对的边分别为a,b,∠C=70°.若二次函数y=(a+b)x2+(a+b)x-(a-b)的最小值为-a2,则∠A=_______度.14.★已知函数y=-4x2+4ax-4a-a2,若函数在0≤x≤1上的最大值是-5,求a的值.答案:难点探究专题:抛物线与几何图形的综合(选做)——代几结合,突破面积及点的存在性问题◆类型一二次函数与三角形的综合一、全等三角形的存在性问题1.如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;(2)若抛物线与x轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点D,使得△ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由.二、线段(或周长)的最值问题及等腰三角形的存在性问题2.(2016·凉山州中考)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P 的坐标;(3)点M也是直线l上的动点,且△MAC 为等腰三角形,请直接写出所有符合条件的点M的坐标.◆类型二二次函数与平行四边形的综合3.如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,A点在B点左侧.若点E在x轴上,点P 在抛物线上,且以A,C,E,P为顶点的四边形是平行四边形,则符合条件的点P有()A.1个B.2个C.3个D.4个4.如图,抛物线y=12x2+x-32与x轴相交于A,B两点,顶点为P.(1)求点A,B的坐标;(2)在抛物线上是否存在点E,使△ABP 的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由;(3)坐标平面内是否存在点F,使得以A,B,P,F为顶点的四边形为平行四边形?直接写出所有符合条件的点F的坐标.◆类型三 二次函数与矩形、菱形、正方形的综合5.如图,在平面直角坐标系中,点A 在抛物线y =x 2-2x +2上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连接BD ,则对角线BD 的最小值为________.第5题图 第6题图6.如图,抛物线y =ax 2-x -32与x 轴正半轴交于点A(3,0).以OA 为边在x 轴上方作正方形OABC ,延长CB 交抛物线于点D ,再以BD 为边向上作正方形BDEF.则a =,点E 的坐标是_________________.7. (2016·新疆中考)如图,对称轴为直线x =72的抛物线经过点A(6,0)和B(0,-4). (1)求抛物线的解析式及顶点坐标; (2)设点E(x ,y)是抛物线上一动点,且位于第一象限,四边形OEAF 是以OA 为对角线的平行四边形,求平行四边形OEAF 的面积S 与x 之间的函数关系式;(3)当(2)中的平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形.8.(2016·百色中考)正方形OABC 的边长为4,对角线相交于点P ,抛物线l 经过O ,P ,A 三点,点E 是正方形内的抛物线l 上的动点.(1)建立适当的平面直角坐标系,①直接写出O ,P ,A 三点的坐标; ②求抛物线l 的解析式;(2)求△OAE 与△OCE 面积之和的最大值.答案:拔高专题抛物线中的压轴题一、基本模型构建常见模型思考在边长为1的正方形网格中有A, B, C三点,画出以A,B,C为其三个顶点的平行四边形ABCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9年级上册 第10课《资本主义时代的曙光》(12分)阅读下列材料,回答问题。
材料一 哥伦布说:“黄金是一切商品中最宝贵的,黄金是财富,谁占有了黄金,就能获得他在世上所有的一切。
”材料二 图一:位于西班牙的哥伦布纪念碑,上有“光荣属于哥伦布”“向哥伦布致敬”两行大字。
图二:2007年10月拉美各地印第安人游行示威,要求将“哥伦布日”改为“土著人民抵抗日”,他们把哥伦布塑像披上塑料外套,要求世界重新评价哥伦布。
(1)依据相关知识回答,在新航路开辟的过程中,哥伦布做出了什么贡献?材料一表明,哥伦布航海的动机是什么?(4分)(2)材料二表明,在如何评价哥伦布的问题上,欧洲人和美洲印第安人持不同的观点。
试依据新航路开辟的影响谈谈导致不同观点的原因。
(8分)(6分)哲人们认为,思想是地球上最美丽的花朵,一个拥有伟大思想的民族,才能拥有不断前进的动力。
阅读下列图文材料:材料一材料二 难道农民的儿子生来颈上带着圈,而贵族的儿子生来在腿上带着踢马刺吗?……一切享有各种天然能力的人,显然是平等的。
……除了法律以外,不依赖任何别的东西,这就是自由人。
——《伏尔泰语录》材料三……西洋人因为拥护德、赛两先生,闹了许多事,流民许多血,德、赛两先生才渐渐从黑暗中把他们救出来,引到光明世界。
我们现在认定,只有这两两位先生可以救治中国政治上、道德上、学术上、思想上一切的黑暗。
——陈独秀《本志罪案之答辨书》请回答:(1)材料一两幅作品体现了什么时代精神?(1分)(2)材料二体现了什么思想主张?有何进步意义?(2分)(3)材料三的主要观点是什么?(2分)(3)概括指出上述思想在人类历史进程中有什么共同影响?(1分)相隔数百年,欧洲、中国都经历了一场思想文化运动,都爆发了一次有重要影响的革命,通过一些法律的制定,巩固了革命成果。
结合所学知识,回答问题。
(14分)材料一在14—16世纪的西欧,人们认为:“人类可以成就伟大的事业。
”文学巨匠莎士比亚说:“人具有高贵的理性,人具有伟大的力量,人的行为像天使,人的智慧像天使。
”(1)材料一显示14一l6世纪的西欧广为流传的一种思潮是什么?(2分)材料二陈独秀在新文化运动时期启示青年,必须树立变革现实的思想,要有探索勇气和创新的胆识。
“应战胜恶社会,而不被恶社会所征服”。
(2)陈独秀为“战胜恶社会”,希望青年们高举的两面大旗是什么?(2分)这两场“思想文化运动”有什么共同作用?(2分)材料三为追求资产阶级民主政治,许多国家爆发了革命,为巩固革命成果制定了法律性文件。
下面是某法律条文的摘要和某次革命时的情景。
起义军占领楚望台军械库图一图二(3)图一中的条文出自哪一法律性文件?(2分)图二中的情景出现在哪次革命中?(2分)制定图一文件的革命与图二所示的这次革命,从影响上看有哪些相似点?(4分)(10分)从专制到民主、从人治到法治是人类历史发展的必然趋势。
阅读下列材料,结合所学知识,回答问题。
材料一我们的政治制度不是从我们邻人的制度中模仿而来的,我们的制度是别人的模范……我们的制度之所以称为民主政治,因为政权是在全体公民手中,而不是在少数人手中。
解决私人争执的时候,每个人在法律上都是平等的……——伯里克利材料二 凡未经议会同意,以国王权威停止法律或停止法律实施之僭越权力,为非法权力。
……凡未经议会准许,借口国王特权,为国王而征收,或供国王使用而征收金钱,超出议会准许之时限或方式者,皆为非法。
材料三美国政治权力结构示意图(1)材料一中“我们的政治制度”开启了西方民主政治的先河。
请据材料一指出这一制度民主性的表现。
(2分)(2)材料二的内容出自哪部文献?(1分)其核心思想是什么?(1分)该文献的颁布使该国的政体发生了怎样的变化?(2分)(3)材料三体现了启蒙运动中的哪一学说? (1分)结合所学知识,指出美国确立这一政体的法律文件。
(1分)(4)西方民主政治从产生起就存在局限性,请举两例说明。
(2分)阅读材料:材料一 经过漫长的航行后,他和同伴于1492年10月12日突然发现远处有陆地,于是高兴地前往,到了近处一看,原来是座海岛,这个岛就是现在美洲加勒比海上巴哈马群岛中的瓜纳哈尼岛。
材料二请回答:(1)材料一中的“他”是指哪一位航海家?(1分)(2)材料二中有A 、B 、C 三条航线,哪一条是环球航行路线?(1分)率领这支环球航行船队的航海家是谁?(1分)(3)最早开辟新航路的是哪两个国家?(2分)(4)谈谈新航路开辟的影响。
(2分)17—18世纪,英、法、美等国家发生了巨大的变革,纷纷走上了发展资本主义的道路。
阅读材料,回答问题。
(5分)材料一:1649年1月30日下午,伦敦天气格外阴冷。
白金汉宫外广场上,人头攒动。
一位衣着华丽的犯人被推上了断头台,掀开了英国历史重要的一页。
材料二:1789年7月14日,巴黎城中枪声四起,愤怒的市民拿起武器同军警展开激战……这一天揭开了法国大革命的序幕,成为法国的国庆日。
———摘自人教版《世界历史》九年级上材料三:我们以这些殖民地的善良人民的名义和权力,谨庄严宣告:这些联合殖民地从此成为,而且名正言顺地应当成为自由独立的合众国,它们解除与英王的一切隶属关系,而它们与大不列颠王国之间的一切政治关系也应从此完全废止。
———《独立宣言》(1)材料一中的“一位衣着华丽的犯人”指的是谁?英国资产阶级革命后,通过什么文献确立了君主立宪制的政体?(2分)(2)7月14日是法国的国庆日,请你说出法国大革命开始的标志?拿破仑是法国历史上的一位风云人物,他为巩固资产阶级统治颁布了什么文献?(2分)(3)材料三这一文献的发表标志着什么?(1分)四、分析说命题(本题共12分)19、材料:17-18世纪,英、美、法的资产阶级在血与火的洗礼中建立了自己的政治统治。
从此,自由与平等、民主与法制的理念逐渐深入人心,深刻影响了世界历史发展的进程。
依据材料,结合所学知识回答问题。
(1)说出为17-18世纪欧美资产阶级革命准备理论武器的历史事件。
(2分)(2)归纳英、美、法资产阶级革命的主要成果,并逐一说明其作用。
(6分)(3)列举受资产阶级思想理论的影响,发生在欧美和中国的资产阶级革命或改革各一例。
(2分)(4)从资产阶级革命过程中,你得到哪些启示?(2分)简答题(8分)38.(1)世界近代史上最早的资产阶级思想解放运动是什么?它产生了怎样的影响?(3分)(2)18世纪欧洲出现的第二次思想解放运动是什么?在这一运动影响下,18世纪后半期发生了哪两场资产阶级革命?并相应地写出这两场资产阶级革命中颁布的体现启蒙思想的文件各一个。
(5分)37.【纵览世界巨变】(6分)阅读大事年表,回答问题。
1789年,法国大革命爆发。
1792年,法兰西第一共和国成立。
1799年,拿破仑发动政变,夺取了政权。
1812年,拿破仑率领军队远征俄罗斯。
(1)在法国大革命爆发前,世界上已经建立了哪几种类型的资产阶级政权?(2分)(2)法国大革命爆发的标志是什么?谁掌握政权后,采取一系列措施,把法国大革命推向高潮?(2分)(3)请你分别写出法国大革命和拿破仑帝国对世界历史发展的积极影响。
(2分)34.(9分)阅读下列材料:材料一第一条凡未经议会同意,以国王权威停止法律或停止法律实施之僭越权力,为非法权力。
第二条近来以国王权威擅自废除法律或法律实施之僭越权力,为非法权力。
材料二我们认为下面这些真理是不言而喻的:人人生而平等,造物者赋予他们若干不可剥夺的权利,其中包括生命权、自由权和追求幸福的权利。
我们以这些殖民地的善良人民的名义和权力,谨庄严宣告:这些联合殖民地从此成为,而且名正言顺地应当成为自由独立的合众国,……材料三第一条在权利方面,人们生来是而且始终是自由平等的。
第三条国家主权属于人民。
第六条法津是公共意志的表现,在法律面前,所有的公民都是平等的。
第十七条私人财产神圣不可侵犯。
请回答:(1)材料一、二、三分别出自欧美资产阶级革命中的哪三部文件?(3分)(2)材料一法律文件颁布的目的是什么?这一法律文件的颁布,标志着这个国家建立了什么政治制度?(2分)(3)材料二的文件是在何时颁布的(写出年月日)?这一文件的颁布有何重要意义?(2分)(4)材料三的文件是由资产阶级革命中哪一机构通过的?(1分)(5)综合上述材料,请你写出它们在政治思想方面的共同之处。
(1分)36.阅读下列材料:材料一“不经议会的批准,国王不能征税,也不能在和平时期维持常备军;同时,还规定国王既不能随意废除法律,也不能停止法律的执行。
”材料二“我们以这些殖民地的善良人民的名义和权力,谨庄严宣告:这些联合殖民地从此成为、而且名正言顺地应当成为自由独立的合众国,他们解除了对英王的一切隶属关系,而它们与大不列颠王国之间的一切政治联系也应从此完全废止。
”材料三“在权利面前,人们生来是而且始终是自由平等的。
……法律是公共意志的表现,所有公民有权参与法律的制定。
……在法律面前,所有公民都是平等的。
”——上述三则材料均摘自人教版《世界历史》九年级上册请回答:(1)材料一、材料二、材料三的内容分别出自什么重要文献?(3分)(2)这三部重要文献分别于欧美哪些资产阶级革命事件直接相关?(3分)15.阅读下列材料(10分)材料一所有成年男子都有选举权;进行无记名投票;平等选区;评论员选举废除财产资格要求;议员应有报酬;议员每年六月进行大选。
----------《人民宪章》材料二让统治阶级在共产主义革命面前发抖吧。
无产者在这个革命中失去的只是锁链。
他们获得的将是整个世界。
-----------《共产党宣言》材料三起来,饥寒交迫的奴隶;起来,全世界受苦的人!满腔的热血已经沸腾,要为真理而斗争。
-------------《国际歌》请回答:(1)材料一是哪一次工人运动的革命纲领?工人阶级提出了怎样的要求?(3分)(2)据材料二概述《共产党宣言》的主要内容。
它的发表有什么意义?(4分)(3)材料三是为了纪念哪一次革命运动而创作的?它反映出怎样的革命精神?(3分)[参考答案] [11年新疆中考]第15题15.(1)①英国宪章运动。
(1分)②要求取得普选权(或:选举权),参与国家的管理。
(2分) (2)①《共产党宣言》揭示了资本主义必然要被社会主义代替客观规律,号召全世界无产者,为获得自己的解放而斗争。
(2分)②它的发表标志着马克思主义的诞生。
从此,在科学理论的指导下,国际工人运动进入一个新的历史时期。
(2分)(3)①巴黎公社(1分)②无产阶级追求真理、无私无畏的革命英雄主义精神和伟大的创造精神。
(意思相近即可,2分)辨析题巴黎公社是无产阶级第一次取得胜利的革命,对20世纪的历史进程产生了深刻影响。
[参考答案] [11年福建莆田中考]第25题不正确。
