单调性及幂函数
《幂函数》PPT课件

(4) y x
1 2
(5) y x
1
(-2,4)
4
y=x3
(2,4) y=x2 y=x (4,2)
1
3
y=x 2
2
1
(-1,1)
-6 -4 -2
(1,1)
2
y=x-1
4 6
-1
(-1,-1)
-2
幂函数的图象都通过点(1,1) α为奇数时,幂函数为奇函数, α为偶数时,幂函数为偶函数.
在第一象限内,
-3
-4
a >0,在(0,+∞)上为增函数; a <0,在(0,+∞)上为减函数.
练习:利用单调性判断下列各值的大小。 (1)5.20.8 与 5.30.8 (2)0.20.3-2 与 0.30.3 -2
(3)
2.5
5
与 2.7
5
解:(1)y= x0.8在(0,∞)内是增函数, ∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,∞)内是增函数
二、五个常用幂函数的图像和性质
3 2 y x y x (1) (2) y x (3)
(4) y x
1 2
(5) y x
1
函数
y x的图像
定义域: 值 域:
R R
奇偶性: 在R上是奇函数
单调性:在R上是增函数
函数 y x 的图像
2
定义域:
R
值 域: [0,) 奇偶性: 在R上是偶函数
高中数学必修 ①人教版A
§2.3幂函数
y x 中 x 前面的系数是1,后面没有其它项。
一、幂函数的定义: 一般地,我们把形如 y x 的函数叫做 x为自变量, 幂函数,其中 为常数。
幂函数知识点
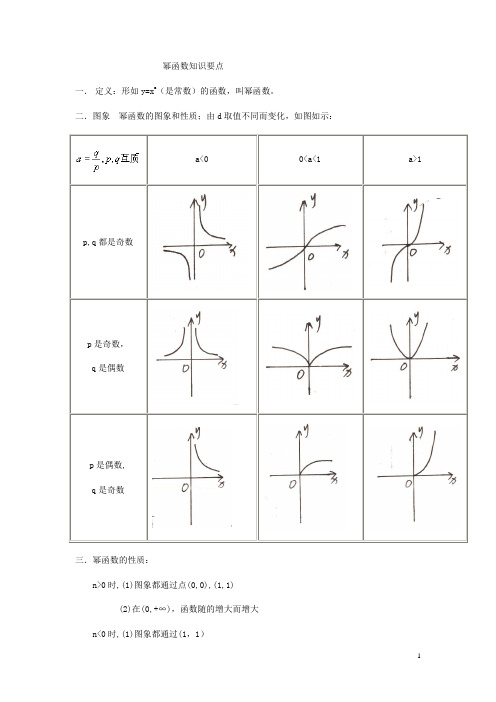
幂函数知识要点一.定义:形如y=x a(是常数)的函数,叫幂函数。
二.图象幂函数的图象和性质;由d取值不同而变化,如图如示:三.幂函数的性质:n>0时,(1)图象都通过点(0,0),(1,1)(2)在(0,+∞),函数随的增大而增大n<0时,(1)图象都通过(1,1)(2)在(0,+∞),函数随x的增加而减小(3)在第一象限内,图象向上与y轴无限地接近,向右与x轴无限地接近。
注意事项:1.判断幂函数的定义域的方法可概括为(对指数)“先看正负,是负去零,再看奇偶,是偶非负”2.根据幂函数的定义域,值域及指数特点画其图象。
函数位于第一象限的图象在“n>1”时,往上翘;0<n<1,往右拐;n<0向下滑。
四.例析:分析:底数分别不同而指数相同,可以看作是和。
两个幂函数,利用幂函数的单调性质去理解。
解:(1)(0,+∞)是递增的又∵1.1<1.4 ∴利用幂函数的性质比较数的大小。
例3.比较的大小。
分析:三个量比较大小,先考虑取值的符号。
启示:当直接比较大小难以进行时,可以考虑借助一些中间量特殊值,如0,1或其他数来解决。
分析:在指数运算中,注重运算顺序和灵活运用乘法合成。
启示:此处化简过程可与初中代数式的运算联系。
五.自测题:1.计算的值()2.下列命题中正确的是()A.当n=0时,函数y=x n的图象是一条直线B.幂函数的图象都经过(0,0),(1,1)两点C.若幂函数y=x n的图象关于原点对称,则y=x n在定义域内y随x的增大而增大D.幂函数的图象不可能在第四象限3.实数a,b满足0<c<b<1,则下列不等式正确的是()A.a b<ba B.a-b<b-b C.a-a<b-b D.b b<a a4.在幂函数y=x a,y=x b,y=x c,y=x d在第1象限的图象中(右图),的大小关系为()A.a>b>c>d B.d>b>c>a C.d>c>b>aD.b>c>d>a5.下列函数中是幂函数的是)6.设幂函数y=x n的图象经过(8,4),则函数y=x n的值域为_______。
高三幂函数知识点

高三幂函数知识点幂函数是数学中常见的一类函数,其中最为典型的就是高三幂函数。
高三幂函数是指幂指数为3的函数,可以表示为f(x) = ax^3 + bx^2 + cx + d的形式。
在高三数学学习中,掌握高三幂函数的相关知识点对于解题和理解函数的性质非常重要。
本文将从定义、图像、性质以及函数应用等方面来介绍高三幂函数的知识要点。
一、定义高三幂函数是由幂指数为3的变量函数所构成的,函数表达式为f(x) = ax^3 + bx^2 + cx + d,其中a、b、c、d为常数,a≠0。
其中,a决定了函数的开口方向,正值开口向上,负值开口向下;b、c、d分别对应二次项、一次项和常数项的系数。
二、图像特点高三幂函数的图像特点与其系数a的正负值有关。
当a>0时,函数图像开口朝上;当a<0时,函数图像开口朝下。
而且,当幂函数为3次时,其图像可能与x轴交于三个不同的点,也可能与x轴相切于某一点。
这些交点或者切点被称为函数的零点。
三、性质1. 零点和与坐标轴的交点:在图像上,高三幂函数的零点是与x轴交点的横坐标值,也是函数的解;与y轴的交点为函数的截距点,对应的坐标为(0, d)。
2. 单调性:当a>0时,高三幂函数在定义域上单调递增,当a<0时,高三幂函数在定义域上单调递减。
3. 奇偶性:高三幂函数在定义域上为奇函数,即满足f(-x) = -f(x)的性质。
4. 极值点:由于高三幂函数的图像可能存在局部最小值或者最大值,因此其极值点可以通过求导数或者观察图像得到。
5. 函数的拐点:高三幂函数的拐点是函数图像从凹向上凸或者从凸向上凹的点,对应的坐标为(x, f(x))。
四、函数应用高三幂函数在实际问题中具有广泛的应用,下面列举一些常见的应用场景:1. 物体的运动问题:高三幂函数可用于描述物体的运动状态,如自由落体运动、弹性碰撞等。
2. 经济学中的成本、收益分析:高三幂函数可以用来分析成本和收益之间的关系,从而对经济决策进行评估和优化。
函数的单调性知识点

函数的单调性知识点函数的单调性是数学分析中的一个重要概念,用来描述函数在定义域上的增减特性。
具体而言,一个函数可以是严格递增的、递增的、严格递减的或递减的。
函数的单调性具有广泛的应用,在求解极值、解方程、绘制函数图像等问题中起到重要的作用。
本文将介绍函数的单调性的概念、判定方法以及一些常见的单调函数。
一、函数的单调性概念函数的单调性是指函数在定义域上的增减变化规律。
具体而言,一个函数在某个区间上单调递增,意味着随着自变量的增大,函数的取值也随之增大;而在单调递减的区间上,函数的取值随着自变量的增大而减小。
二、函数单调性的判定方法1. 导数法导数是函数单调性判定的重要工具之一。
对于可导函数,函数在某个区间上单调递增的充要条件是导数恒大于等于零;函数在某个区间上单调递减的充要条件是导数恒小于等于零。
2. 一阶差分法对于分段连续的函数,可以通过一阶差分的正负来判断函数的单调性。
若一阶差分恒大于零,则函数在该区间上单调递增;若一阶差分恒小于零,则函数在该区间上单调递减。
3. 二阶导数法对于二次可导函数,函数在某个区间上的单调性可以通过二阶导数的正负来判断。
若二阶导数恒大于零,则函数在该区间上单调递增;若二阶导数恒小于零,则函数在该区间上单调递减。
三、常见的单调函数1. 线性函数线性函数是最简单的单调函数,其定义域为实数集,函数的图像为一条直线。
线性函数在整个定义域上均为单调递增或单调递减。
2. 指数函数指数函数为形如 f(x) = a^x (a>0, a≠1)的函数,指数函数在定义域上分为两类:当a>1时,函数为单调递增函数;当0<a<1时,函数为单调递减函数。
3. 对数函数对数函数为形如 f(x) = loga(x) (a>0, a≠1)的函数。
当0<a<1时,对数函数为单调递增函数;当a>1时,对数函数为单调递减函数。
4. 幂函数幂函数为形如 f(x) = x^a (a为常数)的函数。
幂函数知识点

幂函数1.幂函数:一般地,形如y=x a(a∈R)叫做幂函数,其中x是自变量,a是常数.要准确理解幂函数的定义,注意以下四点:(1)幂函数具有严格的形式,形如 y=mx a, y=(mx)a, y=x a+m,y=(x+m)a(以上m均为不等于零的常数,且前两个函数中的m也不等于1)的函数都不是幂函数,二次函数中只有y=x2是幂函数,其他的二次函数都不是幂函数,幂函数y=x a要满足三个特征:○1幂x a前的系数是1;○2底数只能是自变量x,指数是常数;○3项数只有一项,只有满足这三个特征,才是幂函数;(2)求函数解析式时,若已知待求函数是幂函数,则可根据待定系数法设函数为f(x)=x a,根据条件求出a即可.(3)不要把幂函数与指数函数混淆,幂函数的底数为自变量,指数为常数,而指数函数恰好相反,底数为常数,指数为自变量.当遇到一个有关幂的形式的问题时,要先看自变量所在的位置,然后决定是用幂函数知识解决,还是用指数函数知识解决.2.幂函数在第一象限的图象:幂函数在其他象限的图象,可由幂函数的奇偶性根据对称性做出.α=n/m (其中m∈N*,n∈Z且m,n互质).(1)当n为偶数时,f(x)为偶函数,其图象关于y轴对称.(2)当m,n都为奇数时,f(x)为奇函数,其图象关于原点对称.(3)当m为偶数,n为奇数时,f(x)为非奇非偶函数,其图象只能在第一象限.3.幂函数当α=1,2,3,0.5,-1时的图象与性质.(1)图象(如图所示)(2)性质(如表)4.幂函数的性质:(1)所有的幂函数在(0,+∞)上都有定义,并且图像都通过点(1,1);(2)如果a>0,则幂函数的图像过原点,并且在区间(0,+∞)上为增函数;(3)如果a<0,则幂函数的图像在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于零时,图像在y轴右方无限逼近y轴,当x趋向于无穷大时,图像在x轴上方无限逼近x轴;(4)当a为奇数时,幂函数为奇函数;当a为偶数时,幂函数为偶函数.(5)①α>0,图像都过定点(0,0)和(1,1);在区间(0,+∞)上单调递增;②α<0,图像都过定点(1,1);在区间(0,+∞)上单调递减;③当O<a<l时,曲线上凸,当a>l时,曲线下凸.④当a=l时,图象为过点(0,0)和(1,1)的直线.⑤当a=0时,y=x a表示过点(1,1)且平行于x轴的直线(除去点(0,1))5.幂函数图象的其他性质:(1)图象的对称性:把幂函数y=x a的幂指数a(只讨论a是有理数的情况)表示成既约分数的形式(整数看作是分母1的分数),则不论a>0还是a<0,幂函数y=x a的图象的对称性用口诀记为:“子奇母偶孤单单;母奇子偶分两边;分子分母均为奇,原点对称莫忘记”,(2)图象的形状:①若a>0,则幂函数y=x a的图象为抛物线形,当a>l时,图象在[0,+∞)上是向下凸的(称为凸函数);当O<a<l时,图象在[o,+∞)上是向上凸的(称为凹函数).②若a<0,则幂函数y=x“的图象是双曲线形,图象与x轴、y轴无限接近,在(0,+∞)上图象都是向下凸的。
第五讲 一次函数和幂函数

第五讲 一次函数和幂函数【基础回顾】 一、基础知识: 知识点一:一次函数1.一次函数的表达式为 ,图像是 . 2.单调性:当k>0时,函数y=kx+b 在),(+∞-∞上 ;当k<0时,函数y=kx+b 在),(+∞-∞上 .3.奇偶性:当b=0时,为 ;b ≠0时,为 . 知识点二:幂函数1.幂函数的定义:一般地,我们把形如 的函数称为幂函数,其中 是自变量, 是常数.注意:幂函数与指数函数的区别. 2.幂函数的图像和性质:(1)当0>α时,幂函数y x α=有下列性质:①图象都通过点 ;②在第一象限内都是 ; ③在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的; ④在第一象限内,过点)1,1(后,图象向右上方无限伸展. (2)当0<α时,幂函数y x α=有下列性质: ①图象都通过点 ;②在第一象限内都是 ,图象是向下凸的;③在第一象限内,图象向上与 无限地接近;向右无限地与 无限地接近;④在第一象限内,过点)1,1(后,α越大,图象下落的速度越 .无论α取任何实数,幂函数y x α=的图象必然经过第 象限,并且一定不经过第 象限.二、基础自测:1.已知幂函数)(x f 的图象过)22,2(,则=)4(f .2.设21,y a x a =+-当11x -≤≤时,y 的值有正有负,则实数a 的取值范围是 .3.设11,1,,32a ⎧⎫∈-⎨⎬⎩⎭,则使函数y x α=的定义域为R 且为奇函数的所有α值为 .4. 比较下列各组数的大小:(1)237.0 236.0; (2)32)2.1(-- 32)25.1(--;(3)3.02.0 2.03.0; (4)b a ,a b ,b b .5.函数21554(32)y x x x =++≥-的值域是 .6.已知函数b ax x f -=)(的零点是2,则函数2)(bx ax x g +=的零点是 . 【典型例题】例题1:若p=(x-1)a log 23-6x a log3+x+1,在区间[0,1]上恒为正值,求实数a 的范围.解:设f(x)=p=(a log23-6a log3+1)x+(-a log 23+1),∴由题意,得⎩⎨⎧>>0)1(f 0)0(f ,∴⎩⎨⎧>+->+-02a log 601a log 323,∴-1<log 3a<31,∴31331<<a .例2:比较大小:(1)11221.5,1.7;(2)33( 1.2),( 1.25)--;(3)1125.25,5.26,5.26---;(4)30.530.5,3,log 0.5.解:(1)∵12y x =在[0,)+∞上是增函数,1.5 1.7<,∴11221.5 1.7< ;(2)∵3y x =在R 上是增函数, 1.2 1.25->-,∴33( 1.2)( 1.25)->-;(3)∵1y x -=在(0,)+∞上是减函数,5.25 5.26<,∴115.25 5.26-->;∵ 5.26x y =是增函数,12->-,∴125.265.26-->;综上,1125.255.265.26--->> ;(4)∵300.51<<,0.531>,3log 0.50<,∴30.53log 0.50.53<<.注: 若两个数是同一个函数的两个函数值,则可用函数的单调性比较大小;若两个数不是同一个函数的函数值,则可利用0,1等数架设桥梁来比较大小.例题3:已知幂函数()y f x =经过点1(2,)8.(1)试求函数解析式;(2)判断函数的奇偶性并写出函数的单调区间;(3)试解关于x 的不等式(32)(24)0f x f x ++->. 解:(1)由题意,得 1(2)238a f a ==⇒=- 故函数解析式为3()f x x-=.(2)定义域为()(),00,-∞+∞ ,关于数0对称 33()()()f x x x f x ---=-=-=- 故该幂函数为奇函数. 其单调减区间为:()(),0,0,-∞+∞. (3)由(2)得(32)(24)(42)f x f x f x +>--=-即232034202232425x x x x x x x ⎧+>⇒>-⎪⎪->⇒<⎨⎪⎪+<-⇒<⎩或232034202232425x x x x x x x ⎧+<⇒<-⎪⎪-<⇒>⎨⎪⎪+<-⇒<⎩或232034202x x x x ⎧+>⇒>-⎪⎨⎪-<⇒>⎩ 解得2235x -<<或2x >故原不等式的解集为222 35x x x ⎧⎫-<<>⎨⎬⎩⎭或. 例4:已知幂函数)()(22Z m xx f m m ∈=--是偶函数,且在区间),0(+∞上是减函数,求)(x f 的解析式,并讨论)()()(x xf b x f a x -=ϕ的奇偶性(R b a ∈,).解: ∵)()(22Z m x x f m m∈=--在),0(+∞上是减函数,∴022<--m m , ∴Z m m ∈<<-且21,∴m=0或m=1,∴当m=0或m=1时,2)(-=x x f 是偶函数,且在区间),0(+∞上是减函数.则)()()(x xf b x f a x -=ϕbx xa -=,)(x -ϕbx xa +=,∴当a=b=0时,)(x ϕ0)(=-=x ϕ,)(x ϕ既是奇函数又是偶函数;当a=0,0≠b 时,)(x ϕ是奇函数不是偶函数;当0≠a ,b=0时,)(x ϕ为偶函数不是奇函数;当0≠a ,0≠b 时,)(x ϕ是非奇非偶函数. 【巩固练习】1.已知f(x)是一次函数,且f[f(x -1)]=4x+5,则f(x)= .2.方程x x =32的实数解的个数是_________________.3.若函数f(x)=ax+2a+1的值在-1≤x ≤1时有正也有负,则实数a 的范围是 .4.函数122(1)y x =-的值域是 .5.设,a b 满足01a b <<<,下列不等式中正确的是 . (1)a b a a < (2)a b b b < (3)a a a b < (4)b b b a <6.图中曲线是幂函数y x α=在第一相限的图象,已知α取12±,2± 四个值,则相应与曲线1C 、2C 、3C 、4C 的α值依次为 .7.给出下列四个函数:13(1)y x =;13(2)y x-=;1(3)y x -=;23(4)y x =,其中定义域和值域相同的是 .(写出所有满足条件的函数的序号) 8. 函数221m my x --=在第二象限内单调递增,则m 的最大负整数是 .9. 函数215524(32)y x x x =++≥-的值域是 .10.函数*)(,112N m x y m m ∈=++的定义域是_________,奇偶性_________,单调性______.11. 比较下列几组数大小(1)131.5,131.7,1; (2)23(2--,2310()7-,431.1-.12.已知1133(3)(12)x x ---<+,求x 的取值范围.13.已知幂函数)()(322Z m x x f m m ∈=--的图象与x 轴、y 轴都无交点,且关于原点对称,求m 的值.分析:幂函数图象与x 轴、y 轴都无交点,则指数小于或等于零;图象关于原点对称,则函数为奇函数.结合m Z ∈,便可逐步确定m 的值.14.已知函数)()(22N k x x f k k∈=++-满足)3()2(f f <.(1)求k 的值并求出相应的)(x f 的解析式;(2)对于(1)中得到的函数)(x f ,试判断是否存在q ,使函数x q x qf x g )12()(1)(-+-=在区间]2,1[-上的值域为]817,4[-?若存在,求出q ;若不存在,说明理由.【拓展提高】★1.已知点在幂函数()f x 的图象上,点124⎛⎫- ⎪⎝⎭,在指数函数()g x 的图象上.问方程()()0f x g x -=有 个根,当x ≥0时不等式()()f x g x ≥和()()f x g x <的解集分别是 、 .★2.已知函数a x xx f -+=221)( (常数+∈R a ),(Ⅰ)判断)(x f 的奇偶性并说明理由;(Ⅱ)试研究函数)(x f 在定义域内的单调性,并利用单调性的定义给出证明.【总结反思】。
大一高数幂函数知识点归纳

大一高数幂函数知识点归纳幂函数是大一高数中重要的概念之一,它在数学和科学领域具有广泛的应用。
在本文中,将对大一高数幂函数的知识点进行归纳总结,以帮助读者更好地理解和掌握这一内容。
一、幂函数的定义幂函数是指形如f(x) = x^n的函数,其中x为自变量,n为常数指数。
幂函数的特点是自变量x的幂次,它决定了函数的增长趋势和性质。
幂函数可以分为正幂函数和负幂函数两种情况。
正幂函数:当指数n为正数时,幂函数随着x的增大而增大,随着x的减小而减小。
例如,f(x) = x^2是一个正幂函数,其图像为开口向上的抛物线。
负幂函数:当指数n为负数时,幂函数随着x的增大而减小,随着x的减小而增大。
例如,f(x) = x^(-2)是一个负幂函数,其图像为开口向下的抛物线。
二、幂函数的性质1. 定义域和值域:对于幂函数f(x) = x^n,当n为正数时,定义域是整个实数集;当n为负数时,定义域是正实数集。
值域在正幂函数和负幂函数的情况下有所不同。
2. 奇偶性:当指数n为偶数时,幂函数是关于y轴对称的偶函数;当指数n为奇数时,幂函数是关于原点对称的奇函数。
3. 单调性:正幂函数在定义域上是递增的,负幂函数在定义域上是递减的。
4. 零点:当幂函数中的指数n为正数时,零点为x=0;当指数n为负数时,零点不存在。
5. 渐近线:对于正幂函数和负幂函数,它们都有y轴作为渐近线。
当幂函数的指数n为正数时,还可能有x轴作为渐近线。
三、幂函数的图像1. 正幂函数的图像:正幂函数在定义域上为开口向上的抛物线,图像越接近x轴,增长速度越慢。
当指数n越大时,抛物线的开口越窄。
2. 负幂函数的图像:负幂函数在定义域上为开口向下的抛物线,图像越接近x轴,减小速度越慢。
当指数n越小时,抛物线的开口越窄。
四、幂函数的应用1. 物理学中的应用:幂函数在物理学中具有广泛的应用,例如在力学中描述物体的抛体运动、空气阻力、电子流强度与电位差的关系等。
通过研究幂函数的性质和图像,可以帮助我们更好地理解这些物理现象。
高中数学《幂函数》课件

课前预习
课堂互动
课堂反馈
规律方法 判断函数为幂函数的方法 (1)只有形如y=xα(其中α为任意实数,x为自变量)的函数才 是幂函数,否则就不是幂函数. (2)判断一个函数是否为幂函数的依据是该函数是否为y= xα(α为常数)的形式,函数的解析式为一个幂的形式,且: ①指数为常数,②底数为自变量,③底数系数为1.形如y= (3x)α,y=2xα,y=xα+5…形式的函数都不是幂函数.反过 来,若一个函数为幂函数,则该函数也必具有这一形式.
2 2
D. 2
课前预习
课堂互动
课堂反馈
解析 设幂函数为 y=xα,∵幂函数的图象经过点4,12,∴12=
4α,∴α=-12,∴y=x-12
1
,∴f(2)=2-2
=
22,故选 C.
答案 C
课前预习
课堂互动
课堂反馈
2.下列函数中,其定义域和值域不同的函数是( )
1
A.y=x3
1
B.y=x-2
5
C.y=x3
课前预习
课堂互动
课堂反馈
规律方法 解决幂函数图象问题应把握的两个原则 (1)依据图象高低判断幂指数大小,相关结论为: ①在(0,1)上,指数越大,幂函数图象越靠近 x 轴(简记为指大图 低);②在(1,+∞)上,指数越大,幂函数图象越远离 x 轴(简 记为指大图高). (2)依据图象确定幂指数 α 与 0,1 的大小关系,即根据幂函数在
D.-1,1,3
课前预习
课堂互动
课堂反馈
解析 当 a=-1 时,y=x-1 的定义域是{x|x≠0},且为奇函数;
当 a=1 时,函数 y=x 的定义域是 R 且为奇函数;当 a=12时,
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 - 函数的单调性 知能点全解: 知能点一: 函数单调性的定义 1、图形描述: 从函数2xy的图象(图1)看到:图象在 y轴的右侧部分是从左向右连续上升的,也就 是说,当x在区间[0,+)上取值时,随着x的 增大,相应的y值也随着增大,即如果任取21,xx0,,得到1y=)(1xf,2y=)(2xf,那么当1x<2x时,有1y<2y。这时我们就说函数)(xf=2x在[0,+ )上是增函数。 图象在y轴的左侧部分是从左向右连续下降的,也就是说, 当x在区间,0上取值时,随着x的增大,相应的y值反而随着减小,即如果任取21,xx,0,得到1y=)(1xf,2y=)(2xf,那么当1x<2x时,有1y>2y。这时我们就说函数)(xf=2x在(-,0)上是减函数. 2、定量描述 对于函数)(xf的定义域I内某个区间D上的任意两个自变量的值21,xx, (1)若当1x<2x时,都有)(1xf<)(2xf,则说)(xf在区间D上是增函数; (2)若当1x<2x时,都有)(1xf>)(2xf,则说)(xf在区间D上是减函数。 3、单调性与单调区间 若函数y=)(xf在某个区间是增函数或减函数,则就说函数)(xf在这一区间具有(严格的)单调性,这一区间叫做函数)(xf的单调区间。此时也说函数是这一区间上的单调函数。在单调区间上,增函数的图象是上升的,减函数的图象是下降的。 特别提醒: 1、函数是增函数还是减函数,是对定义域内某个区间而言的。有的函数在一些区间上是增函数,而在另一些区间上不是增函数.例如函数2xy(图1),当x∈[0,+)时是增函数,当x∈(-,0)时是减函数。而有的函数在整个定义域上都是单调的,如图2。 2、函数的单调区间是其定义域的子集; 3、21,xx应是该区间内任意的两个实数,忽略需要任意取值这个条件,就不能保证函数是增函数(或减函数)。 例 1 如图是定义在闭区间[-5,5]上的函数)(xfy的图象,根据图象说出)(xfy的单
调区间,以及在每一单调区间上,函数)(xfy是增函数还是减函数。
知能点二:用定义证明函数的单调性 例 2 :证明函数3)(xxfxR是增函数。
例 3:证明函数1fxxx在0,1上是减函数
特别提醒:定义法证明函数在某个区间上是增(减)函数是最基本方法其步骤是: (1)取值,即设21,xx是区间上的任意两个实数,且1x<2x;
(2)作差变形,即12fxfx,并通过因式分解、配方、有理化等方法,向有利于判断差的符号的方向变形; (3)判断12fxfx的正负,当正负不确定时,可以分区间进行讨论,判断正负; (4)根据定义得出结论。 及时演练: 1、判断并证明下列函数的单调性 (1)23)(xxf xR (2)()32fxx xR
(3)()fxx (4)()fxx 2、讨论下列函数的单调性,指出其单调区间并予以证明
(1)1fxx (2)3fxx (3)223fxxx (4)232fxxx 3、判断下列各函数在给定的单调区间上是增函数还是减函数
531-2-5
xO
y - 2 - (1)2,(0,)yxx (2)1,(1,0]1yxx (3)21yx x),( (4).1xxy),1( 4、讨论函数322axxf(x)在(-2,2)内的单调性
知能点三:判断较复杂函数的单调性的几条有用的结论 1、函数yfx与函数yfx的单调性相反
2、当fx恒为正或恒为负时,函数1yfx与函数yfx的单调性相反 3、在公共区间内,增函数+增函数=增函数,增函数-减函数=增函数,减函数-增函数=减函数。
例 4:求函数20xafxax的单调区间。
及时演练: 1、下列函数中,在区间0,2上为增函数的是( )
A、3yx B、21yx C、1yx D、yx 2、在,0上单调递减的函数是( ) A、1xyx B、21yx C、23yx D、22xx
3、函数211xxyx的单调递减区间是 。 4、已知,fxgx定义在同一区间上,fx是增函数,gx是减函数,且0gx,则
( ) A、fxgx为减函数 B、fxgx为增函数
C、fxgx为减函数 D、fxgx为增函数 5、223fxxx的单调减区间是 。 6、二次函数2yaxbxc的递增区间为,2,则二次函数2ybxaxc的递减区间为 。 7、已知函数222913fxxx,则使函数fx是减函数的区间是 。 8、设fx是定义在区间U上的增函数,且0fx,则下列函数:①1yfx;②
1yfx③2yfx;④yfx中,是减函数的有 (把序号填在横线上)。
知能点四:复合函数单调性的判断 对于函数)(ufy和)(xgu,如果)(xgu在区间),(ba上是具有单调性,当),(bax时,),(nmu,且)(ufy在区间),(nm上也具有单调性,则复合函数))((xgfy在区间),(ba具有单调性的规律见下表:
)(ufy ),(nmu 增 ↗ 减 ↘ )(xgu ),(bax 增 ↗ 减 ↘ 增 ↗ 减 ↘ ))((xgfy ),(bax 增 ↗ 减 ↘ 减 ↘ 增 ↗ 以上规律还可总结为:“同向得增,异向得减”或“同增异减”。 例 5:求函数xxy20042的单调递增区间.
拓展知识点:函数(0,0)byaxabx的单调性 (1)单调增区间:bb,,,aa (2)单调减区间:bb0,,,0aa (3)图像的两条渐进线分别为0x和yax (4)图像如右: - 3 -
典型题型全解 题型一:利用函数单调性比较函数值的大小 例 6:如果函数2fxxbxc,对任意实数t都有22ftft,比较
1,2,4fff的大小。
及时演练 1、 已知4,fxfxxR,当2x时, fx为增函数,设
1,4,2afbfcf,则,,abc的大小关系为 。
2、若12,,0xx,且12xx,函数1fxx,则1fx与2fx的大小关系为_ 3、函数2fxxpxq对任意x均有11fxfx,那么0,1,1fff的大小关系为 。 题型二:利用函数单调性求参数的范围 例 7:已知2212fxxax在,4上是减函数,求实数a的取值范围。 及时演练: 1、若函数ymxb在,上是增函数,则有( ) A、0b B、0b C、0m D、0m 2、若22fxxax与1agxx在区间1,2上都是减函数,则a的取值范围是( ) A、1,00,1 B、1,00,1 C、0,1 D、0,1 3、已知函数25yxax在1,上递增,则a的取值范围是 。 4、已知函数268,1,fxxxxa,并且fx的最小值为fa,则实数a的取值范围是 。 5、函数2201fxxaxx的最大值是2a,那么实数a的取值范围为 。 6、函数245fxxmx在区间2,上是增函数,则1f的取值范围是 。 题型三:利用函数单调性求函数的最值 例 8:(1)求函数1yxx的值域; (2)已知1,1Abb,对于函数21112fxx,若xA时,fxA,求b的值。 及时演练: 1、函数1yx在2,2上的最大值与最小值分别为 。 2、已知函数24,1,5fxxxx,则这个函数的值域为 。 题型四:函数单调性定义逆命题及其应用 逆命题:已知函数yfx在定义域的某个区间上为增函数(减函数),若12xx,则12fxfx(12fxfx) 例 9:已知函数yfx在0,上是减函数,试比较34f与21faa的大小。
及时演练: 1、函数223fxxmx在2,上为增函数,在,2上为减函数,则m= 。 2、2221fxxaxa在,2上为增函数,在2,上为减函数,则2f= 。 3、若函数yfx在R上单调递减,且21fmfm,则实数m的取值范围是 。 4、已知函数在区间,ab上具有单调性,且0fafb,则方程0fx在区间,ab上( ) A、至少有一实根 B、至多有一实根 C、没有实根 D、必有唯一实根 5、函数fx在,0和0,上递减,且220ff,则10fx的解集是 。 6、fx是定义在0,上的增函数,则不等式82fxfx的解集为
题型五:抽象函数单调性的判断 例 10:已知函数fx的定义域为R,满足10fxfx,且gxfxc(c为
常数)在区间,ab上是减函数,判断并证明gx在区间,ba上的单调性。
