Chapter1-3(电磁场边值关系-电磁场的能量和能流)PPT课件
合集下载
电磁场PPT模板 (5)

L I
说明:若回路由N匝线圈绕成,则线圈的总磁通量为各单匝线 圈磁通量之和,称为磁链。若N匝线圈密绕,回路总磁通量为:
N 为单匝线圈磁通量
第3章 静态电磁场及其边值问题的解
2、自感
若某回路C载流为I,其产生的磁场穿过回路C所形成的自感 磁链为 ,则定义回路C的自感系数为:
L (H) I
Wm
1 2
L1I12
Wm
1 2
L1I12
1 2
L2
I
2 2
MI1I2
第3章 静态电磁场及其边值问题的解
1 N N
Wm
2
j 1
M kj I j Ik
k 1
1
2
NN
I j j
j1 k 1
N
j M kjik k 1
j
B dS
S
说明:1)回路自感仅与回路自身的几何形状、尺寸和媒质磁
导率有关,与回路中载流无关。
2)若回路为N匝线圈密绕,则 L N 2L0
L0为单匝线圈电感
讨论:若回路导线直径较粗,则 L Li Lo
式中: Li 为回路内自感,即导体内部磁场与部分电流交链所形 成电感。Lo 为回路外自感,即导体外磁场与回路交链所形成电感。
E2
J
2
[ 2
1U0 ln(b / a) 1 ln(c / b)]r
er
(b r c)
c
2 r E2 dr (b r c)
2c
2b
2a
b
c
1 r E1 dr b E2 dr
(a r b)
说明:若回路由N匝线圈绕成,则线圈的总磁通量为各单匝线 圈磁通量之和,称为磁链。若N匝线圈密绕,回路总磁通量为:
N 为单匝线圈磁通量
第3章 静态电磁场及其边值问题的解
2、自感
若某回路C载流为I,其产生的磁场穿过回路C所形成的自感 磁链为 ,则定义回路C的自感系数为:
L (H) I
Wm
1 2
L1I12
Wm
1 2
L1I12
1 2
L2
I
2 2
MI1I2
第3章 静态电磁场及其边值问题的解
1 N N
Wm
2
j 1
M kj I j Ik
k 1
1
2
NN
I j j
j1 k 1
N
j M kjik k 1
j
B dS
S
说明:1)回路自感仅与回路自身的几何形状、尺寸和媒质磁
导率有关,与回路中载流无关。
2)若回路为N匝线圈密绕,则 L N 2L0
L0为单匝线圈电感
讨论:若回路导线直径较粗,则 L Li Lo
式中: Li 为回路内自感,即导体内部磁场与部分电流交链所形 成电感。Lo 为回路外自感,即导体外磁场与回路交链所形成电感。
E2
J
2
[ 2
1U0 ln(b / a) 1 ln(c / b)]r
er
(b r c)
c
2 r E2 dr (b r c)
2c
2b
2a
b
c
1 r E1 dr b E2 dr
(a r b)
(电磁场PPT)第三章 恒定磁场

7 0
图3.1.1 两载流回路间的相互作用力
元电流段:
元电流段:
源点元电流段 场点元电流段 I dl I dl 1 1 2 2
电流元 即在载流导线上沿电流流向取一段长度为dl的 线元,若线元中通过的恒定电流强度为I,则我们就把 Idl表示为矢量Idl,Idl的方向沿着线元中的电流流向。 这一载流线元矢量Idl为电流元 计算磁场的基本方法: 与在静电场中计算带电体的电 场时的方法相仿,为了求恒定电流的磁场,我们也可 将载流导线分成无限多个小的载流线元,每个小的载 流线元的电流情况可用Idl来表征,称为电流元。电流 元可作为计算电流磁场的基本单元。
图3.1.4 圆形载流回路轴线上的 磁场分布
I R 0 2 π R e x 2 2 2 2 4 π ( R x) R x
0IR2
2(R x )
2 2 3/ 2
ex
B
2 IR 0
2 (R x )
2
2 3/2
ex
如果载流圆线圈是由半径都是R的N匝线圈重叠而成, 则在圆心处激发的磁感强度为:
注意类比法的应用。
恒定磁场的知识结构。 基本实验定律 (安培力定律)
磁感应强度(B)(毕奥—沙伐定律)
H 的旋度
基本方程
分界面衔接条件 边值问题
B 的散度
磁位( m )
磁矢位(A) 解析法 镜像法
数值法
有限差分法
有限元法
分离变量法
电感的计算
磁场能量及力
本章要求
深刻理解磁感应强度、磁通、磁化、磁场强度 的概念。 掌握恒定磁场的基本方程和分界面衔接条件。 了解磁位及其边值问题。
l 0
2 I 2 I 2 π I 2 π 1 1
图3.1.1 两载流回路间的相互作用力
元电流段:
元电流段:
源点元电流段 场点元电流段 I dl I dl 1 1 2 2
电流元 即在载流导线上沿电流流向取一段长度为dl的 线元,若线元中通过的恒定电流强度为I,则我们就把 Idl表示为矢量Idl,Idl的方向沿着线元中的电流流向。 这一载流线元矢量Idl为电流元 计算磁场的基本方法: 与在静电场中计算带电体的电 场时的方法相仿,为了求恒定电流的磁场,我们也可 将载流导线分成无限多个小的载流线元,每个小的载 流线元的电流情况可用Idl来表征,称为电流元。电流 元可作为计算电流磁场的基本单元。
图3.1.4 圆形载流回路轴线上的 磁场分布
I R 0 2 π R e x 2 2 2 2 4 π ( R x) R x
0IR2
2(R x )
2 2 3/ 2
ex
B
2 IR 0
2 (R x )
2
2 3/2
ex
如果载流圆线圈是由半径都是R的N匝线圈重叠而成, 则在圆心处激发的磁感强度为:
注意类比法的应用。
恒定磁场的知识结构。 基本实验定律 (安培力定律)
磁感应强度(B)(毕奥—沙伐定律)
H 的旋度
基本方程
分界面衔接条件 边值问题
B 的散度
磁位( m )
磁矢位(A) 解析法 镜像法
数值法
有限差分法
有限元法
分离变量法
电感的计算
磁场能量及力
本章要求
深刻理解磁感应强度、磁通、磁化、磁场强度 的概念。 掌握恒定磁场的基本方程和分界面衔接条件。 了解磁位及其边值问题。
l 0
2 I 2 I 2 π I 2 π 1 1
电磁场课件--第一章电磁场的媒质边界条

,
汇报人:
01
02
03
04
05
06
电磁场与媒质的相互作用是电 磁场理论的重要内容
媒质边界条件是描述电磁场与 媒质相互作用的重要工具
媒质边界条件包括电边界条件 和磁边界条件
媒质边界条件在电磁场计算和 工程应用中具有重要意义
理想边界条件:假设边界上不存在任何电磁场
非理想边界条件:假设边界上存在电磁场,但场强和场矢量满 足一定的条件
电场强度:在媒质分界面上,电场 强度必须连续
电荷密度:在媒质分界面上,电荷 密度必须连续
添加标题添加标题来自添加标题添加标题磁场强度:在媒质分界面上,磁场 强度必须连续
电流密度:在媒质分界面上,电流 密度必须连续
电场强度:在媒质分界面上,电场强度必须连续 磁场强度:在媒质分界面上,磁场强度必须连续 电荷密度:在媒质分界面上,电荷密度必须连续 电流密度:在媒质分界面上,电流密度必须连续
边界条件:描述媒质分界面上的电磁场性质 连续性条件:描述媒质分界面上电磁场的连续性 数学表达形式:通过数学公式表示边界条件 应用实例:在电磁场课件中,通过实例讲解边界条件的数学表达形式
理想导体:电场 强度为零,电流 密度无穷大
绝缘体:电场强 度不为零,电流 密度为零
边界条件:理想 导体与绝缘体之 间的边界上,电 场强度和电流密 度必须满足连续 性条件
数据采集:记录实验过程中的 数据,包括电磁场强度、温度、 湿度等
实验设计:选择合适的实验 设备,设计实验方案
数据分析:对采集到的数据进 行处理和分析,验证边界条件
的准确性
应用实例:介绍边界条件在实 际应用中的案例,如电磁屏蔽、
电磁兼容等
边界条件是电 磁场理论中的 重要概念,用 于描述电磁场 在媒质边界上
汇报人:
01
02
03
04
05
06
电磁场与媒质的相互作用是电 磁场理论的重要内容
媒质边界条件是描述电磁场与 媒质相互作用的重要工具
媒质边界条件包括电边界条件 和磁边界条件
媒质边界条件在电磁场计算和 工程应用中具有重要意义
理想边界条件:假设边界上不存在任何电磁场
非理想边界条件:假设边界上存在电磁场,但场强和场矢量满 足一定的条件
电场强度:在媒质分界面上,电场 强度必须连续
电荷密度:在媒质分界面上,电荷 密度必须连续
添加标题添加标题来自添加标题添加标题磁场强度:在媒质分界面上,磁场 强度必须连续
电流密度:在媒质分界面上,电流 密度必须连续
电场强度:在媒质分界面上,电场强度必须连续 磁场强度:在媒质分界面上,磁场强度必须连续 电荷密度:在媒质分界面上,电荷密度必须连续 电流密度:在媒质分界面上,电流密度必须连续
边界条件:描述媒质分界面上的电磁场性质 连续性条件:描述媒质分界面上电磁场的连续性 数学表达形式:通过数学公式表示边界条件 应用实例:在电磁场课件中,通过实例讲解边界条件的数学表达形式
理想导体:电场 强度为零,电流 密度无穷大
绝缘体:电场强 度不为零,电流 密度为零
边界条件:理想 导体与绝缘体之 间的边界上,电 场强度和电流密 度必须满足连续 性条件
数据采集:记录实验过程中的 数据,包括电磁场强度、温度、 湿度等
实验设计:选择合适的实验 设备,设计实验方案
数据分析:对采集到的数据进 行处理和分析,验证边界条件
的准确性
应用实例:介绍边界条件在实 际应用中的案例,如电磁屏蔽、
电磁兼容等
边界条件是电 磁场理论中的 重要概念,用 于描述电磁场 在媒质边界上
《工程电磁场第一章》PPT课件

4 π0V ' R
4 π0S' R
令 p P 极化电荷体密度
p Pen 极化电荷面密度
(r)1 4 π0V '
p (r')d V '1
R
4 π0S '
p R (r')d S '30
返回 上页 下页
思考 根据电荷守恒定律,极化电荷的总和为零
V ' P d V 'S 'P e n d S ' 0
i定ty义):电场强度 E 等于单位正电荷所受的电场力F
lim E(x,y,z) F(x,y,z) V/m ( N/C )
qt 0
qt
(a) 单个点电荷产生的电场强度
Fq
Ep(R)qt 4π0R2eR V/m
一般表达式为
图1.1.2 点电荷的电 场
Ep(r)4π0qrr'2
rr' rr'
4π0
q rr'
S 面上的 E 是由
系统中全部电荷产
生的。
24
图1.2.2 闭合面外的电荷对场的影响
返回 上页 下页
1.2.2. 电介质中的高斯定律 (Gauss’s Theorem in Dielectri 1. 静电场中导体的性质
导体内电场强度 E 为零,静电平衡;
导体是等位体,导体表面为等位面; 电场强度垂直于导体表面,电荷分布在导体表面,
当 L L 1 L 2 时 ,
E (,
0
,z)E e E zez
2π 0
e
无限长直导线产生的电场
Ε
2π0
e
平行平面场。
9
返回 上页 下页
电磁场边界条件ppt课件
lim
h0
D t
e hl
0
如果分界面的薄层内有自由电流, 则在回路所围的面积上,
lim J ds s
J e hl
h0
Js e l
e en (H1 H2 ) Js e
2
en (H1 H2 ) Js
D1n D2n 0
电位移矢量的法向分量 在边界面上才是连续的。
9
电磁场的边界条件
en
(H1
H
2
)
Js
en (B1 B2 ) 0
en
(
E1
en (D1
E2
)
D2 )
0
s
相应的标量形式为
H1t H2t B1n B2n
en
(E1
E2
)
0
en (D1 D2 ) 0
相应的标量形式为
H1t H2t B1n B2n
E1t E2t D1n D2n
12
3、漏电媒质:
Biblioteka en (H1H
2
)
Js
en (B1 B2 ) 0
en
(
E1
将积分形式的磁通连续性原理即如果分界面的薄层内有自由电荷则圆柱面内包围的总电荷为得电位移矢量的法向分量边界条件的矢量形式为limlim电位移矢量的法向分量在边界面上是不连续的
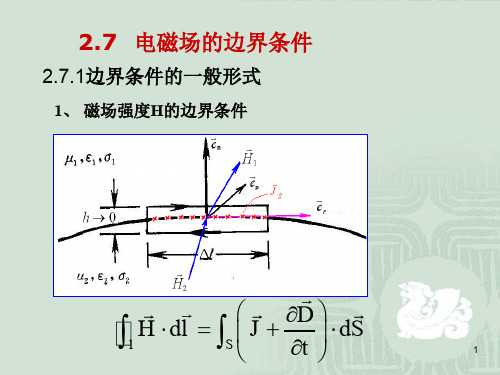
2.7 电磁场的边界条件
2.7.1边界条件的一般形式
1、 磁场强度H的边界条件
电动力学-第一章-1.5 电磁场边值关系

j
0
t
2、库仑定律
F
1
4 0
V1 V2
12
r3
rd1d 2
1 Q1Q2 r.
40 r3
3、毕奥——萨伐尔定律
r B
xr
0 4
V
Jr
xr ' rr
r3
dV
'
4、法拉第定律
L
E
dl
S
B ds t
5、洛仑兹力
F Fe Fm q(E v B)
整体
f
(
E
v
B)
4
3
r23 r13
f
D
r23 r13 3
f
1 r2
,
r
r2
ÑS E dS V f dV
P e0E
D 1 e 0E E
4 r2D 4 3
r3 r13
f
D
r3 r13 3
f
1 r2
, r2
r
r1
E D
P
1
0
D
注意球内球外的ε不同
D 0,r r1
r
f
0
P
理想导体表面边界条件σ=∞
• 设介质1为理想导体,理想导体内电场为 0(否则J为∞),对应的磁场也为0
• 介质2边界上的场强满足
en H ar en E 0
en D f
en B 0
理想介质σ=0
• 如果媒质1和2为理想介质,在求时变场时 认为表面不存在自由面电荷和面电流
D 0E P P e0E
H B M
0
M
D
mH
0
1
e
【实用】电磁场的能流密度与动量PPT文档
D t H j0
B E t
t(DEBH)2[E(H)H(E)j0E] t(DEBH)2[(EH)]2j0E
d d W t V (EH )dVV j0E dV
j0
j0E d V (j0 2j0K )d V
S
V
V
j0 (E K )
E j0 K
(j02 j0K)dVj02Slj0KSl
被照射面全吸收(绝对黑体)
1 光压为:
F ( S S ) 第六章 麦克斯韦电磁理论 入
反
c 天体物理中,星体层外收到核心部分的万有引力相当大一部分靠核心部分的辐射产生的光压平衡。
第六章 麦克斯韦电磁理论
1 发射电磁波,粒子一定要有加速度.
P | S S | 光压非常小,很难观察到。入
反
第六章 麦克斯韦电磁理论
§3. 电磁场的能流密度与动量
电磁场的能量原理
➢在空间任一体积 V ,其表面为 Σ . ➢体积V内电磁能为:
1
W W eW m2V (D EBH )dV ddW t 1 2V t(DEBH)dV
t(DEBH)0t(EE)0t(HH) 20EE t 20HH t 2ED t 2HB t
相当大一部分靠核心部分的辐射产生的光压平衡。 ➢ 原子物理中,光在电子上散射时与电子交换动量
(康普顿散射)。
Thanks
第六章 麦克斯韦电磁理论来自v结果分析S a2
S
1 r2
S sin 2
偶极振子的辐射
➢偶极振子:偶极矩p作简谐振荡的偶极子
pp0cost
偶极振子辐射的能流密度空间分布
能流密度S
1. Sa2 2. Sr12 3. Ssin2 S4
电磁场的动量
1.6.ppt
电磁场具有能量,是物质的一种形态。
Sz
S 几乎垂直进入负载内部。
(2)在电源附近电磁场能量的传输:
S 从电源侧面流出。
S
E
_
H
J
+
结论:在闭合直流电路中,能量从电源表面流向空间的电磁场, 在空间电磁场中沿着导线方向传递给负载。
例2.计算正在缓慢充电的电容器的能流.
解:设电容器由半径为R的两块圆形平板构成,间距为h.由于
E E t ez,J f 0,
a r b的介质中应用安培环路定理:
H I 2 r
b I I
a
2 rH I
E 0
忽略导线电阻时,σ→∞, J E, J 有限
Ez 0
设内导线表面单位长度的电荷为τ,应用高斯 定理 Er 2 r
I S E H Er H eZ ez 2 2 4 r
1 1 1 2 2 w E D B H 真空中: w 0E B 得: 2 2 0
思 考
E H 0 是否一定有能流?
例:在同一空间中存在静止电荷的静电场和永久磁铁
的磁场.此时可能存在 E H 矢量,但没有能流。可以
证明,对于任一闭合表面有: E H dS 0
b.恒定情况下,负载前后电流I处处相等.
c.在交流电路中,电流的方向发生变化但能量传输方向不变. 结论:电磁场能量无论是在电磁波情形和电路情形都 是在电磁场中传播的。
例1.同轴传输线半径为a ,外导线半径为 b ,两导线间
为均匀绝缘介质,导线载有电流I,两导线间的电压为U. (1)忽略导线的电阻,计算介质中的能流 S 和传输功率. (2)计及内导线的有限电导率,计算通过内导线表面进入 导线内的能流,证明它等于导线的损耗功率. 解:(1)在
磁场的矢势方程和边值关系省名师优质课赛课获奖课件市赛课一等奖课件
一、矢势 A
B 0
H
j
D t
B=0
H = j
f 0
n
•
(B2
-
B1
)
0
n (H2 - H1)
静磁场
令 B A
(1)
2
A称为磁场旳矢势(Vector potential of magnetic field)
根据(1)式,由矢势能够完全拟定磁场,但是,由磁场却不
能唯一地拟定矢势。
第四章 静磁场
Chapter 4 Static Magnetic Field
1.在静磁场理论中引入矢势 A,建立有关旳微 分方程,并经过求解矢势 A 而得到磁场 B 。
2.使用与解静电场相同旳措施—磁标势法来求解 静电场问题。
3.简介矢势 A 旳多极展开式。
1
基本内容
§4.1 磁场旳矢势方程和边值关系
设 A A
A A A B
B A
所以,相应拟定磁场 B 它旳矢势能够有 A ,A …无穷多种。
在静磁场问题中,一般要求
A 0
(2)
3 这个限制条件称为规范条件。
§4.1 磁场旳矢势方程和边值关系
二、矢势 A 旳微分方程
B=0 H = j
B H
B A
B j
A2n A1n
• A 0
(10)
§4.1 磁场旳矢势方程和边值关系
由(9)、(10)得:
A1 A2
(11)
即在分界面上,矢势 A是连续旳,边值关系(11)
式能够用来替代(7)式。
12
8
§4.1 磁场旳矢势方程和边值关系
四、矢势 A 旳边值关系
n • (B2 B1) 0
电磁场与电磁波第3章ppt_图文
q
4 0
1 rP
1 rQ
O
选参考点位于无穷远处,即令rQ ,得 P
rP q
4 0rP
P
由此得到点电荷电位的一般表达式 q 4 0r
对于位于r的点电荷,电位表达式为
q
q
40 r r 40R
无限长线电荷:设线电荷l在原点,参考点Q,场点 (电位
微分形式:
D
E 0
本构关系:D E
边界条件
en E1 E2 0
en
D1
D2
S
或
E1t E2t
D1n
D2 n
S
对于理想介质,有
en E1 E2
0 或
en D1 D2 0
x a 处,φ2 (a) = 0
x b处,φ1(b) =φ2 (b),
2 ( x)
x
1(x)
x
xb
S0 0
所以 D1 = 0
C2a + D2 = 0
C1b + D1 = C2 b + D2
C2
-
C1
=
-ρS0 ε0
由此解得
C1
=
-ρS0 (b ε0a
证明 对于单个点电荷产生的场
把试探电荷q0从P移到Q 设电荷q0 受到的电场力为F, 在该力作用下的位移为dl,
则电场力做功为 dW F dl qE dl
WPQ
Q
F dl
P
Q
Q
F cos θdl Fdr
