哈工大概率论与数理统计课后习题答案五
概率论和数理统计大学课后题答案

7习题七1.设总体X 服从二项分布b 〔n ,p 〕,n ,X 1,X 2,…,X n 为来自X 的样本,求参数p 的矩法估计.【解】1(),(),E X np E X A X ===因此np =X所以p 的矩估计量 ˆXpn= 2.设总体X 的密度函数f 〔x ,θ〕=22(),0,0,.x x θθθ⎧-<<⎪⎨⎪⎩其他X 1,X 2,…,X n 为其样本,试求参数θ的矩法估计.【解】23022022()()d ,233x x E X x x x θθθθθθθ⎛⎫=-=-= ⎪⎝⎭⎰令E (X )=A 1=X ,因此3θ=X 所以θ的矩估计量为 ^3.X θ=3.设总体X 的密度函数为f 〔x ,θ〕,X 1,X 2,…,X n 为其样本,求θ的极大似然估计.〔1〕 f 〔x ,θ〕=,0,0,0.e x x x θθ-⎧≥⎨<⎩〔2〕 f 〔x ,θ〕=1,01,0,.x x θθ-⎧<<⎨⎩其他【解】〔1〕 似然函数111(,)ee eniii n nx x nn ii i L f x θθθθθθ=---==∑===∏∏1ln ln ni i g L n x θθ===-∑由1d d ln 0d d ni i g L n x θθθ===-=∑知 1ˆnii nxθ==∑所以θ的极大似然估计量为1ˆXθ=. (2) 似然函数11,01nni i i L x x θθ-==<<∏,i =1,2,…,n.1ln ln (1)ln ni i L n x θθ==+-∏由1d ln ln 0d ni i L nx θθ==+=∏知 11ˆln ln nniii i n nxx θ===-=-∑∏所以θ的极大似然估计量为 1ˆln nii nxθ==-∑【解】0.094x =-0.101893s =9n =0.094.EX x ==-由222221()()[()],()ni i x E X D X E X E X A n==+==∑知222ˆˆ[()]E X A σ+=,即有 ˆσ=于是 ˆ0.101890.0966σ=== 所以这批股民的平均收益率的矩估计值及标准差的矩估计值分别为-0.94和0.966. 5.随机变量X 服从[0,θ]上的均匀分布,今得X 的样本观测值:0.9,0.8,0.2,0.8,0.4,0.4,0.7,0.6,求θ的矩法估计和极大似然估计,它们是否为θ的无偏估计. 【解】(1)()2E X θ=,令()E X X =,那么ˆ2X θ=且ˆ()2()2()E E X E X θθ===, 所以θ的矩估计值为ˆ220.6 1.2x θ==⨯=且ˆ2X θ=是一个无偏估计.(2) 似然函数8811(,)i i L f x θθ=⎛⎫== ⎪⎝⎭∏,i =1,2, (8)显然L =L (θ)↓(θ>0),那么18max{}i i x θ≤≤=时,L =L (θ)最大,所以θ的极大似然估计值ˆθ=0.9. 因为E(ˆθ)=E (18max{}i i x ≤≤)≠θ,所以ˆθ=18max{}ii x ≤≤不是θ的无偏计. 6.设X 1,X 2,…,X n 是取自总体X 的样本,E 〔X 〕=μ,D 〔X 〕=σ2,2ˆσ=k 1211()n i i i XX -+=-∑,问k 为何值时2ˆσ为σ2的无偏估计. 【解】令 1,i i i Y X X +=-i =1,2,…,n -1,那么 21()()()0,()2,i i i i E Y E X E X D Y μμσ+=-=-==于是 1222211ˆ[()](1)2(1),n ii E E k Yk n EY n k σσ-===-=-∑那么当22ˆ()E σσ=,即222(1)n k σσ-=时, 有 1.2(1)k n =-7.设X 1,X 2是从正态总体N 〔μ,σ2〕中抽取的样本112212312211311ˆˆˆ;;;334422X X X X X X μμμ=+=+=+ 试证123ˆˆˆ,,μμμ都是μ的无偏估计量,并求出每一估计量的方差. 【证明】〔1〕11212212121ˆ()()(),333333E E X X E X E X μμμμ⎛⎫=+=+=+= ⎪⎝⎭21213ˆ()()()44E E X E X μμ=+=, 31211ˆ()()(),22E E X E X μμ=+= 所以123ˆˆˆ,,μμμ均是μ的无偏估计量. (2) 22221122145ˆ()()(),3399D D X D X X σμσ⎛⎫⎛⎫=+== ⎪ ⎪⎝⎭⎝⎭222212135ˆ()()(),448D D X D X σμ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭()223121ˆ()()(),22D D X D X σμ⎛⎫=+= ⎪⎝⎭8.某车间生产的螺钉,其直径X ~N 〔μ,σ2〕,由过去的经历知道σ2=0.06,今随机抽取6枚,测得其长度〔单位mm 〕如下: 14.715.014.814.915.115.2试求μ的置信概率为0.95的置信区间.【解】n =6,σ2=0.06,α=1-0.95=0.05,0.25214.95, 1.96,a x u u ===,μ的置信度为0.95的置信区间为/2(14.950.1 1.96)(14.754,15.146)x u α⎛±=±⨯= ⎝.9.总体X ~N (μ,σ2),σ2,问需抽取容量n 多大的样本,才能使μ的置信概率为1-α,且置信区间的长度不大于L ?【解】由σ2可知μ的置信度为1-α的置信区间为/2x u α⎛± ⎝,/2u α,/2u α≤L ,得n ≥22/224()u L ασ 10.设某种砖头的抗压强度X ~N 〔μ,σ2〕,今随机抽取20块砖头,测得数据如下〔kg ·cm -2〕:64694992559741848899 846610098727487844881〔1〕 求μ的置信概率为0.95的置信区间.〔2〕 求σ2的置信概率为0.95的置信区间.【解】76.6,18.14,10.950.05,20,x s n α===-==/20.025222/20.0250.975(1)(19) 2.093,(1)(19)32.852,(19)8.907t n t n ααχχχ-==-===(1) μ的置信度为0.95的置信区间/2(1)76.6 2.093(68.11,85.089)a x n ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭(2)2σ的置信度为0.95的置信区间222222/21/2(1)(1)1919,18.14,18.14(190.33,702.01)(1)(1)32.8528.907n s n s n n ααχχ-⎛⎫--⎛⎫=⨯⨯= ⎪⎪--⎝⎭⎝⎭ 11.设总体X ~f (x )=(1),01;10,.x x θθθ⎧+<<>-⎨⎩其中其他X 1,X 2,…,X n 是X 的一个样本,求θ的矩估计量及极大似然估计量.【解】(1)1101()()d (1)d ,2E X xf x x x x θθθθ+∞+-∞+==+=+⎰⎰ 又1(),2X E X θθ+==+ 故21ˆ1X Xθ-=-所以θ的矩估计量 21ˆ.1X Xθ-=- (2) 似然函数11(1) 01(1,2,,)()()0n n ni i i i i x x i n L L f x θθθ==⎧+<<=⎪===⎨⎪⎩∏∏其他. 取对数11ln ln(1)ln (01;1),d ln ln 0,d 1nii i ni i L n x x i n L n x θθθθ===++<<≤≤=+=+∑∑所以θ的极大似然估计量为1ˆ1.ln nii nXθ==--∑12.设总体X ~f (x )= 36(),0;0,.xx x θθθ⎧-<<⎪⎨⎪⎩其他X 1,X 2,…,X n 为总体X 的一个样本〔1〕 求θ的矩估计量;〔2〕 求ˆ()D θ.【解】(1) 236()()d ()d ,2x E X xf x x x x θθθθ+∞-∞=-=⎰⎰令 ,2EX X θ==所以θ的矩估计量 ˆ2.X θ= (2)4ˆ()(2)4(),D D X D X DX nθ===, 又322236()63()d ,2010x x E X x θθθθθ-===⎰于是222223()()(),10420D XE X EX θθθ=-=-=,所以2ˆ().5D nθθ=13.设某种电子元件的使用寿命X 的概率密度函数为f (x ,θ)= 2()2,;0,.x x x θθθ--⎧>⎨≤⎩e其中θ(θ>0)为未知参数,又设x 1,x 2,…,x n 是总体X 的一组样本观察值,求θ的极大似然估计值.【解】似然函数12()12e 0;1,2,,;()0ln ln 22(),;1,2,,,ni i x n i n i i i x i n L L L n x x i n θθθθ=--=⎧∑⎪⋅≥===⎨⎪⎩=--≥=∑其他.由d ln 20ln (),d Ln L θθ=>↑知 那么当01ˆˆmin{}ln ()max ln ()ii nx L L θθθθ>≤≤==时 所以θ的极大似然估计量1ˆmin{}ii nx θ≤≤=其中θ(0<θ<2)是未知参数,利用总体的如下样本值3,1,3,0,3,1,2,3,求θ的矩估计值和极大似然估计值. 【解】813ˆ(1)()34,()4 28ii x E X E X x x x θθ=-=-====∑令得又 所以θ的矩估计值31ˆ.44x θ-== 〔2〕 似然函数86241(,)4(1)(12).ii L P x θθθθ===--∏2ln ln 46ln 2ln(1)4ln(1),d ln 628628240,d 112(1)(12)L L θθθθθθθθθθθθ=++-+--+=--==---- 解2628240θθ-+=得1,272θ±=. 由于71,122> 所以θ的极大似然估计值为 ˆθ=15.设总体X 的分布函数为F 〔x ,β〕=1,,0,.x xx ββααα⎧->⎪⎨⎪≤⎩其中未知参数β>1,α>0,设X 1,X 2,…,X n 为来自总体X 的样本 〔1〕 当α=1时,求β的矩估计量; 〔2〕 当α=1时,求β的极大似然估计量; 〔3〕 当β=2时,求α的极大似然估计量.【解】当α=1时,11,1;(,)(,1,)0, 1.x x f x F x x x ββββ+⎧≥⎪==⎨⎪<⎩当β=2时,2132,;(,)(,,2)0,.x x f x F x x x ααααα⎧≥⎪==⎨⎪<⎩(1) 111()d 11E X x x x βββββββ+∞-+∞===--⎰令()E X X =,于是ˆ,1XX β=- 所以β的矩估计量ˆ.1XX β=- (2) 似然函数(1)1111,1,(1,2,,);()(,)0,.ln ln (1)ln ,d ln ln 0,d n n ni i i i i n i i ni i x x i n L L f x L n x L n x ββββββββ-+====⎧⎛⎫>=⎪ ⎪===⎨⎝⎭⎪⎩=-+=-=∏∏∑∑其他所以β的极大似然估计量1ˆ.ln nii nxβ==∑(3) 似然函数23112,,(1,2,,);(,)0,.n ni nn i i i i x i n L f x x ααα==⎧≥=⎪⎪⎛⎫==⎨ ⎪⎝⎭⎪⎪⎩∏∏其他显然(),L L α=↑那么当1ˆmin{}i i nx α≤≤=时,0ˆ()max ()a L L L αα>== , 所以α的极大似然估计量1ˆmin{}i i nx α≤≤=.16.从正态总体X~N〔3.4,62〕中抽取容量为n的样本,如果其样本均值位于区间〔1.4,5.4〕的概率不小于0.95,问n至少应取多大?2/2()dz tz tϕ-=⎰【解】26~ 3.4,X Nn⎛⎫⎪⎝⎭,那么~(0,1),XZ N={1.4 5.4}33210.95333ZP X PPZΦΦΦ<<<<=⎧=-<<⎨⎩⎭⎛⎫⎛⎛⎫=-=-≥-⎪ ⎪⎝⎭⎝⎭⎝⎭于是0.975Φ≥ 1.96≥,∴n≥35.17. 设总体X的概率密度为f(x,θ)=,01,1,12,0,.xxθθ<<⎧⎪-≤<⎨⎪⎩其他其中θ是未知参数〔0<θ<1〕,X1,X2,…,X n为来自总体X的简单随机样本,记N为样本值x1,x2,…,x n中小于1的个数.求:〔1〕θ的矩估计;〔2〕θ的最大似然估计.解(1)由于1201(;)d d(1)dEX xf x x x x x xθθθ+∞-∞==+⎰⎰⎰-133(1)222θθθ=+-=-.令32Xθ-=,解得32Xθ=-,所以参数θ的矩估计为32Xθ=-.(2)似然函数为1()(;)(1)nN n NiiL f xθθθθ-===-∏,取对数,得ln ()ln ()ln(1),L N n N θθθ=+--两边对θ求导,得d ln ().d 1L N n Nθθθθ-=-- 令 d ln ()0,d L θθ=得 Nnθ=,所以θ的最大似然估计为Nnθ=.。
概率论重点及课后题答案5
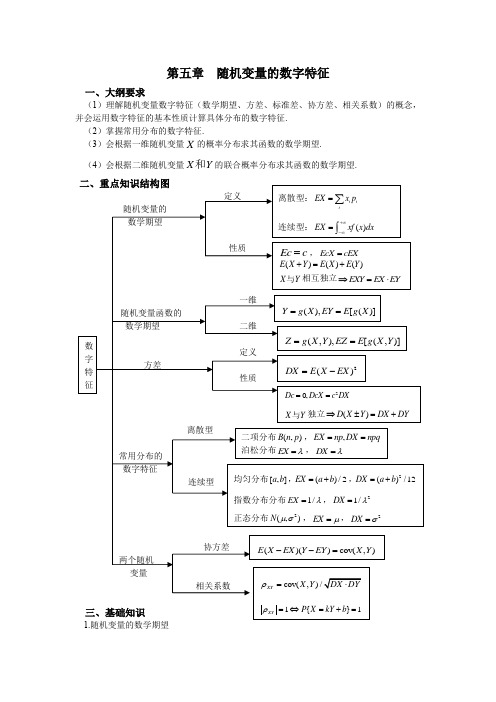
第五章随机变量的数字特征一、大纲要求(1)理解随机变量数字特征(数学期望、方差、标准差、协方差、相关系数)的概念,并会运用数字特征的基本性质计算具体分布的数字特征.(2)掌握常用分布的数字特征.(3)会根据一维随机变量X的概率分布求其函数的数学期望.和的联合概率分布求其函数的数学期望.(4)会根据二维随机变量X Y1.随机变量的数学期望(1)离散型随机变量的数学期望 定义若离散型随机变量X 的分布律是{}i i p P X x ==,(1,2,)i = ,且级数i i ix p ∑绝对收敛,则称此级数的和为X 的数学期望(或均值),记为EX .即i i iEX x p =∑简单地说,离散型随机变量的数学期望等于各个取值与对应概率的乘积之和. (2)连续型随机变量的数学期望 定义若随机变量X 有概率密度函数()f x ,并且积分()xf x dx +∞-∞⎰绝对收敛,则称此积分为X 的数学期望,记为EX ,即()EX xf x dx +∞-∞=⎰2.随机变量函数的数学期望(1)离散型随机变量函数的数学期望 设二维离散型随机变量(,)X Y 的分布律为{,}i j ij P X x Y y p ===(,1,2,)i j =如果,(,)ijiji jg x y p∑绝对收敛,则(,)g X Y 的数学期望存在,且有,(,)(,)i j ij i jEg X Y g x y p =∑(2)连续型随机变量函数的数学期望设二维连续型随机变量(,)X Y 的分布密度函数为(,)f x y ,如果(,)(,)g x y f x y dxdy +∞+∞-∞-∞⎰⎰绝对收敛,则(,)g X Y 的数学期望存在,且有(,)(,)(,)Eg X Y g x y f x y dxdy +∞+∞-∞-∞=⎰⎰特别有(,)(,)()X EXxf x y dxdy x f x y dy dx xf x dx +∞+∞+∞+∞+∞-∞-∞-∞-∞-∞⎡⎤===⎢⎥⎦⎣⎰⎰⎰⎰⎰ 式中,()X f x 为X 的分布密度函数.3.数学期望的性质性质1一个常数c 的数学期望等于这个常数,即Ec c =. 性质 2 设c 是常数,若随机变量X 的数学期望EX 存在,则EcX 也存在,并且有EcX cEX =.性质 3 若随机变量(,)X Y 的数学期望存在,则X Y +的数学期望也存在,并且有()E X Y EX EY +=+.性质4 若性质3的条件成立,且X Y 与相互独立,则EXY 存在,且有()E XY EX =EY .4.方差和标准差定义设X 是一个随机变量,若2()E X EX -存在,则称2()E X EX -为X 的方差,记作DX ,即2()DXE X EX =-.X 的标准差或均方差.对于离散型随机变量X ,若有分布律i p ,则2()i i iDX x EX p =-∑.对于连续型随机变量X ,若有密度函数()f x ,则2()()DX x EX f x dx +∞-∞=-⎰5. 方差的性质性质10Dc =(c 是常数). 性质22DcXc DX =(c 是任意常数).性质3当X Y 与相互独立时,()()()D X Y D X D Y ±=+.性质40DX =的充要条件是X 以概率1取常数c ,即{}1P X c ==(显然,应有EX c =).6.协方差与相关系数 对于随机变量X Y 与,若()()E X E X Y E Y --存在,则称其为随机变量X Y 与的协方差,记作c o v (,)[()(X Y E X E X Y E Y=--.若X Y 与的方差都不等于零.称cov(,)/XY X Y ρ=为随机变量X Y 与的相关系数.定理1对给定的二维随机变量(,)X Y , (1)若X Y 与独立,则cov(,)0X Y =; (2)[]2cov(,)()()X Y D X D Y ≤.定理2 对给定的二维随机变量(,)X Y ,XY ρ为X Y 与的相互系数, (1)若X Y 与独立,则0XY ρ=;(2)11XYρ-≤≤,当且仅当X Y 与有严格的线性关系时,等号成立.若(,)X Y 服从二维正态分布,则X Y 与独立的充要条件是X Y 与不相关,即0XY ρ=.定理3 若(,)X Y 是二维随机变量,则(1)()cov(,)E XY EX EY X Y =⋅+;(2)()()()2cov(,)D XY D X D Y X Y +=++.对不相关的随机变量X Y 与,必有()E XY EX EY =⋅,()()()D X Y D X D Y +=+若12,,,n X X X 是两两独立的随机变量,则必有11()n nk k k k D X DX ===∑∑7.矩定义设X 为随机变量,c 为常数,k 为正整数,则[()]kE x c -称为X 关于c 点的k 阶矩.(1)当0c =时,()k k a E X =称为X的k 阶原点矩;(2)当()c E X =时,[()]k k E X EX μ=-称为X 的k 阶中心矩.四、典型例题例1 设随机变量X 在区间[1,2]-上服从均匀分布,随机变量100010X Y X X >⎧⎪==⎨⎪-<⎩当当当则方差()D Y =_________. 解X 的密度函数为112()30x f x ⎧-≤≤⎪=⎨⎪⎩当其他2012{0}33P X dx >==⎰,0111{0}33P X dx -<==⎰,{0}0P X ==因此211100(1)333EY =⨯+⨯+-⨯=222221100(1)133EY =⨯+⨯+-⨯=2218()199DY EY EY =-=-= 例2设随机变量X Y 与的方差存在且不等于0,则()D X Y DX DY +=+是X Y 与(). (A )不相关的充分条件,但不是必要条件(B )独立的必要条件,但不是充分条件 (C )不相关的充分必要条件 (D )独立的充分必要条件 解若X Y 与独立,则一定有()D XY DX DY +=+.但若()D X Y DX DY +=+ ,则X Y 与不一定独立.因此()D XY DX DY +=+是X Y 与独立的充分条件,但不是必要条件.因此B 项不正确.从而D 项也不正确. 例3设随机变量X 的概率密度为2330(,)0x x f x θθθ⎧<<⎪=⎨⎪⎩当其他已知7{1}8P X>=,求θ和EX 的值解由7{1}8P X>=,得71{1}1{1}188P X P X ≤=->=-= 又因为211331{1}(,)8x P Xf x dx dx θθ-∞≤===⎰⎰所以2θ=,3233()82x EXxf x dx dx +∞-∞===⎰⎰例4 设A B 、是两个事件,则随机变量11A X A ⎧=⎨-⎩当出现当不出现,11B Y B ⎧=⎨-⎩当出现当不出现试证明随机变量X Y 与不相关的充分必要条件是A B 与相互独立. 证设1212(),(),()P A p P B p P AB p ===,由数学期望定义可得11()(1)()()()21EX P A P A P A P A p =⨯+-⨯=-=-同理221EYp =-由于XY 只取两个可能值1和-1,可见{1}()()()()P XY P AB P AB P AB P A B ==+=+()1()P AB P A B =+-()1()()()P AB P A P B P AB =+--+121221p p p =--+1212{1}1{1}2P XY P XY p p p =-=-==+-所以12121{1}(1){1}4221EXYP XY P XY p p p =⨯=+-⨯=-=--+从而1212cov(,)44X Y EXYEX EY p p p =-⋅=-又因为X Y 与不相关的充要条件为cov(,)0X Y =,即12121212440p p p p p p -=⇒=即A B 与相互独立.例5若连续型随机变量X 的密度函数为201()0ax bx c x f x ⎧++<<=⎨⎩当其他 已知12EX=,320DX =,求系数a b c 、、. 解由于()1f x dx +∞-∞=⎰,所以120()1ax bx c dx ++=⎰,即11132a b c ++=(1) 已知12EX =,所以有1201()2x ax bx c dx ++=⎰,即11114322a b c ++=(2) 由22()DX EX EX =-知225EX =,所以12202()5x ax bx c dx ++=⎰,即11125435a b c ++=(3) 联立式(1)(2)(3),解得12,12,3a b c ==-=.例6假设在国际市场上每年对我国某种出口商品的需求量是随机变量X (单位:t ),已知X 服从[2000,4000]上的均匀分布,设每售出这种商品1t ,可为国家挣得外汇3万元,但若销售不出而囤积于仓库,则每吨需浪费保养费1万元,问应组织多少货源,才能使国家的收益最大?解用y 表示预备某年出口的此种商品量(20004000y ≤≤),Y 表示获得的收益(单位:万元),则3()3()yx y Y H x x y x x y≥⎧==⎨--<⎩当当从而每年平均收益为4000200011()()(4)320002000y X y EY H x f x dx y dx ydx +∞-∞==-+⎰⎰⎰ 26211(7000410)[825000(3500)]10001000y y y =-+-⨯=-- 故当3500yt =时,可使平均收益达到最大.例7 设袋中有k 号的球k 个(1,2,,)k n = ,从中摸出一球,试求所得号码的数学期望.解以X 表示摸出一球的号码数,注意袋中球的总数为12n +++ ,即有2{}12(1)k kP X k n n n ===++++ (1,2,,)k n =从而,X 的数学期望为112{}(1)nni i kEX kP X k kn n =====+∑∑ 2(1)(21)21(1)63n n n n n n +++==+ 例8设X 为n 次独立试验中事件A 出现的次数,在第i 次试验中事件A 出现的概率为i p (1,2,,)i n = ,求DX ,并证明:在11ni i p p n ==∑(常数)的条件下,当且仅当12n p p p p ==== 时,DX 达到最大.[分析]在证明是,将DX 进行正确的合并时解答本题的关键. 解设10ii A X i A ⎧=⎨⎩第次试验中事件出现第次试验中事件不出现则i X 互相独立且具有相同的分布:i X 0 1P 1i p -i p于是i i EX p =,(1)i i i DX p p =-(1,2,,)i n =由于1ni i Xx ==∑,则11(1)n ni i i i i DX DX p p ====-∑∑当11ni i p p n ==∑时,有 22111()nnni i i i i i DX p p np p p p ====-=--+∑∑∑221[()2()]ni i i np p p p p p p ==--+-+∑21(1)2()ni i np p p p p ==---∑所以,当且仅当i p p =时,DX 最大.例9设随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3P X <<=,求{0}P X<.[分析]求正态分布的概率时,先将其转化为标准正态分布,在查表,即可求得结果.所用定理为:若2~(,)XN μσ,则~(0,1)X N μσ-.这个定理一定要熟练掌握.解由于22242{24}X P X P σσσ---⎧⎫<<=<<⎨⎬⎩⎭()200.3φφσ⎛⎫=-= ⎪⎝⎭所以有()200.30.50.30.8φφσ⎛⎫=+=+=⎪⎝⎭因此2022{0}X P XP φσσσ---⎧⎫⎛⎫<=<=⎨⎬ ⎪⎩⎭⎝⎭2110.80.2φσ⎛⎫=-=-= ⎪⎝⎭例10设X 在11,22⎡⎤-⎢⎥⎣⎦上服从均匀分布,ln 0()00x x y g x x >⎧==⎨≤⎩当当,求随机变量()Y g X =的数学期望及方差.解X 的概率密度为111()220x f x ⎧-≤≤⎪=⎨⎪⎩当其他于是120[()]()()ln EY E g X g x f x dx xdx +∞-∞===⎰⎰11/22011[ln ](1ln 2)2x x x dx x =-=-+⎰112221/2220ln [ln ]2ln EY xdx x x xdx ==-⎰⎰21ln 2ln 212=++ 所以222211()ln 2ln 21(1ln 2)24DY EY EY =-=++-+2113ln 2ln 2424=++ 例11游客乘电梯从电视塔底层到顶层观光,电梯于每个整点的5分钟、15分钟和55分钟从底层起行,假设一游客在早上8点的第X 的分钟到达底层电梯处,且X 在[0,60]上服从均匀分布,求该游客等候时间的数学期望.解已知X 在[0,60]上服从均匀分布,则其密度函数为1060()60x f x ⎧≤≤⎪=⎨⎪⎩当其他 设Y 为游客等候电梯的时间(单位:分),则50525525()5525556055560x x x x Y g x x x x x -<≤⎧⎪-<≤⎪==⎨-<≤⎪⎪-+<≤⎩当当当当因此601[()]()()()60EY E g x g x f x dx g x dx +∞-∞===⎰⎰52555600525551(5)(25)(55)(605)60x dx x dx x dx x dx ⎡⎤=-+-+-+-+⎢⎥⎣⎦⎰⎰⎰⎰ 1(12.520045037.5)11.67()60=+++=分 例12 设ξ在(,)ππ-上服从均匀分布,sin Xξ=,cos Y ξ=,求X Y 与的相关系数XY ρ.解根据随机变量函数的数学期望的计算公式,有1sin 02EX d ππθθπ-==⎰,1cos 02EY d ππθθπ-==⎰ 所以2211sin 22DX EX d ππθθπ-===⎰ 2211cos 22DY EY d ππθθπ-===⎰又因为1sin cos 02EXYd ππθθθπ-==⎰从而得cov(,)0X Y EXY EX EY =-⋅=于是XYρ==五、课本习题全解5-1 (1)1111210(1)12666EX=⨯+⨯+⨯+-⨯=,222211117210(1)26663EX=⨯+⨯+⨯+-⨯=,11(21)(221)(211)(201)26E X-+=-⨯+⨯+-⨯+⨯+-⨯+⨯11(2(1)1)166+-⨯-+⨯=-;(2)224()3DX EX EX=-=,()Xσ==.5-2 (1)00;k kk kqEX kpq pq qp∞∞=='⎛⎫===⎪⎝⎭∑∑(2)22222210000k k k kk k k k EX k pq pq k q pq q pq kq∞∞∞∞--====''⎛⎫===+⎪⎝⎭∑∑∑∑200k kk kpq q pq q∞∞=='''⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭∑∑222q qp p=+2222222q q q q qDXp p p p p=+-=+5-3 (1)1()02xEX xf x dx x e dx+∞+∞--∞-∞===⎰⎰;(2)2221()2(3)22xDX EX EX x e dx+∞-=-==Γ=⎰.5-4 (1)0(1)1EX p p p =⨯-+⨯=,0(1)1EY p p p =⨯-+⨯=;(2)由于20(1)1EXp p p =⨯-+⨯=,20(1)1EY p p p =⨯-+⨯=;22()(1)DX EX EX p p =-=-,22()(1)DY EY EY p p =-=-;(3)由于00(1)11EXYp p p =⨯⨯-+⨯⨯=,故2cov(,)(1)X Y EXY EX EY p p p p =-⋅=-=-.5-5222()()2g t E X t EX tEX t =-=-+, ()220dg t t EX dt=-=, 因此,t EX =,即t EX =时,()g t 达到最小值为DX .5-6 当2YX =时,022x EY xe dx +∞-==⎰;当3XYe-=时,3014x x EYe e dx +∞--==⎰. 5-7222()/2(ln 2)/2xx u a EY a dx a e μσσ+∞---∞==⎰22()DY EY EY =-222222()/2(ln 2)/222ln 2ln 2()()(1)xx u a u a a a dx a e a e e μσσσσ+∞---∞=-=-⎰5-8 由于12102()23EXx x dx x dx ϕ+∞-∞===⎰⎰,(5)20()y EY y y dy ye dy ϕ+∞+∞---∞==⎰⎰6=,且X Y 与相互独立,所以有2643EXY EX EY =⋅=⨯=,220(+)+633E X Y EX EY ==+=5-9 证明)0EYE EX EX==-= 22221()()1DY EY EY E E X EXDX =-==-=5-10证明0XYρ===()()0E X EX Y EY ⇒--=()0E XY Y EX X EY EX EY ⇒-⋅-⋅+⋅=0EXY EX EY ⇒-⋅=()2cov(,)D X Y DX DY X Y DX DY ⇒+=++=+5-15 (1)由于220(,)sin()x y dxdy A x y dxdy ππϕ+∞+∞-∞-∞=+⎰⎰⎰⎰20cos cos 2A x x dx ππ⎡⎤⎛⎫=-+- ⎪⎢⎥⎝⎭⎣⎦⎰21A ==,故12A =. (2)22200011sin()cos cos 2224EX x x y dxdy x x x x dx πππππ⎡⎤⎛⎫=+=++= ⎪⎢⎥⎝⎭⎣⎦⎰⎰⎰, 由于X Y 与相互对称,故有4EYEX π==;2222222200011sin()[sin cos ]22282EX x x y dxdy x x x x dx πππππ=+=+=+-⎰⎰⎰22222()22824162DX EX EX πππππ⎛⎫=-=+--=+- ⎪⎝⎭由于X Y 与相互对称,故有22162DYππ=+-.(3)222000112sin()sin cos 222EXY xy x y dxdy x x x dx ππππ-⎛⎫=+=+ ⎪⎝⎭⎰⎰⎰22π-=2cov(,)1162X Y EXY EX EY ππ=-⋅=-+-2211622162XYππρππ-+-==+-5-12 二维随机变量(,)X Y的联合分布函数为1(,)(,)x y Af x y∈⎧=⎨⎩当其他12(1)12(1)000012,33x xEX xdydx EY ydydx--====⎰⎰⎰⎰12(1)0016xEXY xydydx-==⎰⎰.5-13 设抽到次品所需要次数为X,则X服从下列分布:X 1 2 3 kP2n221nn n-⋅-23212n nn n n--⋅⋅--2(2)(3)()(1)(2)(1)n n n kn n n n k-------即2{}1n kP X kn n-==⋅-,因此11112{}1n nk kn kEX k P X k kn n--==-=⋅==⋅⋅-∑∑1121121(2)3n nk knkn kn n--==+⎛⎫=-=⎪-⎝⎭∑∑122121nkn kEX kn n-=-=⋅⋅-∑11231121(1)(2)6n nk kk n k n nn n--==⎛⎫=-=+⎪-⎝⎭∑∑221()(1)(2)18DX EX EX n n=-=+-5-15 (1)11005(2)12EX x x y dydx=--=⎰⎰,512EY EX==.1122001(2)4EX x x y dydx=--=⎰⎰,2214EY EX==2211()144DX DY EX EX ==-= 11001(2)6EXY xy x y dydx =--=⎰⎰2151cov(,)612144X Y EXY EX EY ⎛⎫=-⋅=-=- ⎪⎝⎭5()2cov(,)36D X Y DX DY X Y +=++=(2)103()(2)2X f x x y dy x =--=-⎰,103()(2)2Y f y x y dx y =--=-⎰可见,()()(,)X Y f x f y f x y ≠,所以两者不独立.111441111144XYρ-===-故两者相关. 5-16(5)5()22y X f x xedy x +∞--==⎰,1(5)(5)0()2y y Y f y xe dx e ----==⎰可见,()()(,)X Y f x f y f x y =,故两者独立.1(5)054y EXY xye dydx +∞--==⎰⎰5-17 两台仪器无故障时间的密度分布为1511150()0x e x f x -⎧>=⎨⎩当其他,2522250()0x e x f x -⎧>=⎨⎩当其他联合密度函数为125()121212250,0(,)()()0x x e x x f x x f x f x -+⎧>>==⎨⎩当其他 设无故障工作时间为12y x x =+,则联合分布函数为1125()5512210(,)()2551y y x x x y y F x x F y e dx dx ye e --+--===--+⎰⎰5()()25y df y F y e y dy-==所以密度函数为5250()0y e y y f y -⎧>=⎨⎩当其他 2502255y EY y e dy +∞-==⎰,235062525y EY y e dy +∞-==⎰ 262225525DY ⎛⎫=-= ⎪⎝⎭5-18 根据题意有()EXP A =,()EY P B =,()EXY P AB ={1}()P XY P AB ==,{0}1()P XY P AB ==-已知0XYρ=,所以cov(,)0X Y =,即cov(,)()()()0X Y EXY EX EY P AB P A P B =-⋅=-=故()()()P AB P A P B =.事件A B 与相互独立,由事件的独立性定理可得:A ,A ,B ,B 两两相互独立,即{11}{1}{1}P X Y P X P Y =====, {10}{1}{0}P X Y P X P Y =====, {01}{0}{1}P X Y P X P Y =====, {00}{0}{0}P X Y P X P Y =====,因此,X Y 和相互独立. 5-19 已知11~0,,~0,22XN Y N ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,由正态分布的性质可知:()1D X Y DX DY -=+=,()0E X Y -=故()()~0,1XY N -,令Z X Y=-,则()~0,1ZN.22()z E Z z e dz +∞--∞==22222()()()()1D Z EZ E Z DZ EZ E Z π=-=+-=-⎡⎤⎡⎤⎣⎦⎣⎦六、自测题及答案1.设随机变量X 的密度函数为()()0ba x x a f x a x a ⎧-<⎪=⎨⎪≥⎩当当且已知1DX=,则常数a =____________,b =____________.2.设随机变量X 的方差为1DX =,(,)Y X αβαβ=+为非零常数,则DY =__________.3.设X 表示10次独立重复射中目标的次数,每次射中目标的概率为0.4,则2EX =__________.4.设随机变量123X X X 、、相互独立,其中2123~(0,6),~(0,2),~(3)X U X N X P,记12323YX X X =-+,则DY =_________.5.设随机变量X 服从于参数为λ的泊松分布,且已知[(1)(2)]1E X X --=,则λ=___________.6.设X 是一个随机变量,其概率密度为110()1010x x f x x x +-≤≤⎧⎪=-<<⎨⎪⎩当当其他则方差DX =_____________.7.设一次试验成功的概率为p ,进行100次独立重复试验,当p =_____________时,成功次数的标准差的值最大,其最大值为____________.8.设随机变量X 的分布函数为300()0111x F x x x x <⎧⎪=≤≤⎨⎪>⎩当当当则EX=().(A )40x dx +∞⎰(B )1401x dx xdx +∞+⎰⎰(C )1203x dx ⎰(D )1303x dx ⎰9.设随机变量X Y 与独立,且21ZX Y =-+,则DZ =().(A )4DX DY -(B )4DX DY + (C )21DX DY ++(D )21DX DY -+10.设随机变量X 的密度函数为2(1)/2()xf x--=则以下()成立.(A){1}{1}P X P X<=>(B){0}{2}P X P X≤<≥(C)1EX=(D)1DX=11.如果随机变量X Y与满足D X Y D X Y+-()=(),则必须有()成立.(A)X Y与独立(B)X Y与不相关(C)0DY=(D)0DX DY⋅=12.设随机变量X服从参数为2的指数分布,随机变量22xY x e-=+,则DY=().(A)32(B)5 (C)34(D)4313.设X Y与是两个相互独立的随机变量,其概率密度分别为201()x xf x≤≤⎧=⎨⎩当其他,(5)5()ye yf y--⎧>=⎨⎩当其他则EXY=().(A)2 (B)3 (C)4 (D)514.设随机变量X Y与独立,且21~(,)X Nμσ,22~(,)Y Nμσ,则()D X Y-=().(A)22122()1σσπ⎛⎫+-⎪⎝⎭(B)2212σσ+(C)2212σσ-(D)22122()1σσπ⎛⎫--⎪⎝⎭15.设X是一个随机变量,2,EX DXμσ==,(22,0μσ>是常数),则对任意常数C,有().(A)222()E X C EX C-=-(B)22()()E X C E Xμ-=-(C)22()()E X C E Xμ-<-(D)22()()E X C E Xμ-≥-16.设随机变量12X X、的概率密度分别为2120()00x e x f x x -⎧>=⎨≤⎩当当,4240()00x e x f x x -⎧>=⎨≤⎩当当 (1)求12()E X X +和212(23)E X X -;(2)假设12X X 、相互独立,求12EX X . 17.一工厂生产的某种设备的寿命X (以年计)服从指数分布,其概率密度为410()400xe xf x x -⎧>⎪=⎨⎪≤⎩当当工厂规定,出售的设备若在售出一年之内损坏可予以调换,若工厂售出一台设备盈利100元,调换一台设备厂方需花费300元,试求厂方出售一台设备净盈利的数学期望.18.流水作业线上生产出的每个产品为不合格的概率为p ,当生产出k 个不合格品时,即停工检修一次,求在两次检修之间产品总数的数学期望与方差.19.五家商店联营,它们每两周售出的某农产品的数量(单位:kg )分别为123X X X 、、、45X X 、,已知1~(200,225)X N ,2~(240,240)X N ,3~(180,225)X N ,4~X (260,265)N ,5~(320,270)X N ,且123X X X 、、、45X X 、相互独立.(1)求五家商店两周的总销售量的均值和方差;(2)商店每隔两周进货一次,为了使新的供货到达前商店不会脱销的概率大于0.99,问商店的仓库应至少储存多少千克该产品?20.某人有一串钥匙(钥匙数量为n )其中只有一把能打开自己的家门,若他在下列情况下随意地试用这串钥匙,试求打开门时已被使用过的钥匙数的数学期望与方差:(1)把每把试用过的钥匙分开;(2)把每次试用过的钥匙再混杂在这串钥匙中.21.设一口袋中装有n 个球,每个球上标有各不相同的数字,不放回地从袋中取球,每次一个球,第k 次取到的球上的数字定义为k X (1,2,,)k n = ,对任意的j k ≠,求j k X X 和的相关系数.【答案】1.因为x a <,说明0a >,所以0()()0a a a EX x a x dx x a x dx b -⎡⎤=++-=⎢⎥⎣⎦⎰⎰502220()()6a a a a EX x a x dx x a x dx b b -⎡⎤=++-=⎢⎥⎣⎦⎰⎰ 已知22()1DXEX EX =-=,可得516a b=①又因为00()()()1a a a a f x dx a x dx a x dx b b +∞-∞-⎡⎤=++-=⎢⎥⎣⎦⎰⎰⎰,可得31a b=②联立①②,得a b ==2.22()DY D X DX αβαα=+==3.18.44.由2123~(0,6),~(0,2),~(3)X U X N X P ,可得21(60)312DX -==,24DX =,33DX =所以123123(23)493449346D X X X DX DX DX -+=++=+⨯+⨯=5.已知X 服从参数为λ的泊松分布,即EX λ=,而22[(1)(2)](32)32E X X E X X EX EX --=-+=-+ 22()3232DX EX EX λλλ=+-+=+-+ 2221λλ=-+=解得1λ=. 6.167.若X 满足二项分布,则(1)DX np p =-,1(1)(12)02dDX n p np n p p dp =--=-=⇒= 221220p d DXn dp ==-<故12p =是方差的最大值点,也是标准差的最大点.方差最大值为 (1)25DX np p =-=从而标准差最大值为25.8.由X 的分布函数可得其密度函数为2301()0x x f x ⎧≤≤=⎨⎩当其他 故1123033EXx x dx x dx =⋅=⎰⎰.因此D 项正确.9.由于X Y 与相互独立,所以(21)(2)4DZ D X Y D X DY DX DY =-+=+=+.因此B 项正确. 10.因为22(1)21()x f x --⨯=,所以~(1,1)XN .其中21,1EX DX μσ====.由于()f x 的曲线关于1x μ==对称,故{1}{1}P X P X >=<.因此,A 、C 、D 三项均正确.11.因为()2cov(,)D XY DX DY X Y +=++()2cov(,)2cov(,)D X Y DX DY X Y DX DY X Y -=++-=+-又因为()()D XY D X Y -=+所以cov(,)0X Y =,即0XY ρ=,故X Y 与不相关.因此B 项正确.12.A 13.C 14.A 15.D 16.(1)2110()2x EX xf x dx xe dx +∞+∞--∞==⎰⎰2201[]2x x xee dx +∞-+∞-=-+=⎰ 4220()4x EX xf x dx xe dx +∞+∞--∞==⎰⎰4401[]4x x xee dx +∞-+∞-=-+=⎰ 2224220()4x EX x f x dx x e dx +∞+∞--∞==⎰⎰24400[]2x x x exe dx +∞-+∞-=-+⎰4400111228x x xe e dx +∞+∞--⎡⎤=-+=⎢⎥⎣⎦⎰所以1212113()244E X X EX EX +=+=+= 221212115(23)2323288E X X EX EX -=-=⨯-⨯=(2)若12X X 、相互独立,则有1212111248EX X EX EX =⋅=⨯=17.售出一台设备的盈利函数为20001()1001x g x x -<<⎧=⎨>⎩当当则[()]()()E g x g x f x dx +∞-∞=⎰1401(200)4xe dx -=-⨯⎰ 111444401200[]100[]200200100xxe e e e----+∞=-=-+14300200e -=-18.设第1i -个不合格品出现后到第i 个不合格品出现时的产品数为iX (1,2,i =,)n ,又设两次检修之间产品总数为X ,则1ki i X X ==∑,12,,,,k X X X 独立同分布,且1{}(1)j i P X j p p -==-(1,2,,;1,2,)i k j ==由此得111(1)j i j EX j p p p∞-==-=∑22222211()i i i p pDX EX EX p p p--=-=-= 所以1ki i k EX EX p ===∑,21(1)ki i k p DX DX p =-==∑ 19.(1)设X 表示五家商店的总销售量,则51i i XX ==∑.512002401802603201200i i EX EX ===++++=∑521225240225265270122535i i DX DX ===++++==∑(2)设商店的仓库至少应储存Y kg 该产品,求使得{0}0.99P Y X -≥≥的Y ,又因为2~(1200,35)XN ,故120012001200{}0.99353535X Y Y P X Y P φ---⎧⎫⎛⎫≤=≤=≥⎨⎬ ⎪⎩⎭⎝⎭查表得12002.3335Y -≥,即120035 2.331281.55Y ≥+⨯=故至少应储存1281.55kg 该产品. 20.设X 为试用过的钥匙数. (1)12111{}121n n n k P Xk n n n k n k n---+==⋅⋅=--+-- (1,2,,)k n = 又因为1112nk n EXk n =+=⋅=∑ 2211(1)(21)6nk n n EX k n =++=⋅=∑ 所以2221()12n DX EX EX -=-=(2)111{}k n P X k n n--⎛⎫==⋅⎪⎝⎭(1,2,)k = 又因为1111k nk n EX k n n n-=-⎛⎫=⋅⋅= ⎪⎝⎭∑ 12221112k nk n EX k n n n n-=-⎛⎫=⋅⋅=- ⎪⎝⎭∑ 所以22()(1)DXEX EX n n =-=-21.设这n 个各不相同的数为12,,,n a a a ,则有1{}j i P X a n==(1,2,,)i n = 故11nj i i EX a n ==∑22112()nni i i i j n a a DX n==⋅-=∑∑(1,2,,)j n =()k j X X j k ≠和的联合分布律为1{,}(1)j i k l P X a X a n n ===-(,1,2,,)i l n =故cov(,)k j k jk j X X EX X EX EX =-⋅21121(1)i jn i j ni i a a a n n n ≤<≤=⎛⎫=- ⎪-⎝⎭∑∑2221112()()(1)n nni ii i i i a a a n n n ===-=--∑∑∑22112()(1)nni i i i a n a n n ==-=-∑∑因此cov(,)11k jX X X X nρ==-。
概率论与数理统计课后习题答案(非常全很详细)

概率论与数理统计复旦大学此答案非常详细非常全,可供大家在平时作业或考试前使用,预祝大家考试成功习题一1.略.见教材习题参考答案.2.设A,B,C为三个事件,试用A,B,C的运算关系式表示下列事件:(1)A发生,B,C都不发生;(2)A与B发生,C不发生;(3)A,B,C都发生;(4)A,B,C至少有一个发生;(5)A,B,C都不发生;(6)A,B,C不都发生;(7)A,B,C至多有2个发生;(8)A,B,C至少有2个发生.【解】(1)A BC(2)AB C(3)ABC(4)A∪B∪C=AB C∪A B C∪A BC∪A BC∪A B C∪AB C∪ABC=ABC(5) ABC=A B C(6) ABC(7) A BC∪A B C∪AB C∪AB C∪A BC∪A B C∪ABC=ABC=A∪B∪C(8) AB∪BC∪CA=AB C∪A B C∪A BC∪ABC3.略.见教材习题参考答案4.设A,B为随机事件,且P(A)=0.7,P(A-B)=0.3,求P(AB).【解】P(AB)=1-P(AB)=1-[P(A)-P(A-B)]=1-[0.7-0.3]=0.65.设A,B是两事件,且P(A)=0.6,P(B)=0.7,求:(1)在什么条件下P(AB)取到最大值?(2)在什么条件下P(AB)取到最小值?【解】(1) 当AB =A 时,P (AB )取到最大值为0.6.(2) 当A ∪B =Ω时,P (AB )取到最小值为0.3.6.设A ,B ,C 为三事件,且P (A )=P (B )=1/4,P (C )=1/3且P (AB )=P (BC )=0,P (AC )=1/12,求A ,B ,C 至少有一事件发生的概率.【解】 P (A ∪B ∪C )=P (A )+P (B )+P (C )-P (AB )-P (BC )-P (AC )+P (ABC ) =14+14+13-112=347.从52张扑克牌中任意取出13张,问有5张黑桃,3张红心,3张方块,2张梅花的概率是多少?【解】 p =5332131313131352C C C C /C8.对一个五人学习小组考虑生日问题:(1) 求五个人的生日都在星期日的概率; (2) 求五个人的生日都不在星期日的概率;(3) 求五个人的生日不都在星期日的概率.【解】(1) 设A 1={五个人的生日都在星期日},基本事件总数为75,有利事件仅1个,故 P (A 1)=517=(17)5 (亦可用独立性求解,下同) (2) 设A 2={五个人生日都不在星期日},有利事件数为65,故P (A 2)=5567=(67)5 (3) 设A 3={五个人的生日不都在星期日}P (A 3)=1-P (A 1)=1-(17)5 9.略.见教材习题参考答案.10.一批产品共N 件,其中M 件正品.从中随机地取出n 件(n <N ).试求其中恰有m 件(m ≤M )正品(记为A )的概率.如果:(1) n 件是同时取出的;(2) n 件是无放回逐件取出的;(3) n 件是有放回逐件取出的.【解】(1) P (A )=C C /C mn m n M N M N --(2) 由于是无放回逐件取出,可用排列法计算.样本点总数有P n N 种,n 次抽取中有m次为正品的组合数为C mn 种.对于固定的一种正品与次品的抽取次序,从M 件正品中取m 件的排列数有P m M 种,从N -M 件次品中取n -m 件的排列数为P n m N M --种,故P (A )=C P P P mm n m n M N M n N-- 由于无放回逐渐抽取也可以看成一次取出,故上述概率也可写成P (A )=C C C m n m M N M n N-- 可以看出,用第二种方法简便得多.(3) 由于是有放回的抽取,每次都有N 种取法,故所有可能的取法总数为N n 种,n次抽取中有m 次为正品的组合数为C m n 种,对于固定的一种正、次品的抽取次序,m 次取得正品,都有M 种取法,共有M m 种取法,n -m 次取得次品,每次都有N -M 种取法,共有(N -M )n -m 种取法,故()C ()/m m n m n nP A M N M N -=- 此题也可用贝努里概型,共做了n 重贝努里试验,每次取得正品的概率为M N,则取得m 件正品的概率为 ()C 1m n m mn M M P A N N -⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭11.略.见教材习题参考答案.12. 50只铆钉随机地取来用在10个部件上,其中有3个铆钉强度太弱.每个部件用3只铆钉.若将3只强度太弱的铆钉都装在一个部件上,则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少?【解】设A ={发生一个部件强度太弱}133103501()C C /C 1960P A == 【解】 设A i ={甲进i 球},i =0,1,2,3,B i ={乙进i 球},i =0,1,2,3,则33312123330()(0.3)(0.4)C 0.7(0.3)C 0.6(0.4)i i i P A B ==+⨯⨯+22223333C (0.7)0.3C (0.6)0.4+(0.7)(0.6)⨯=0.3207617.从5双不同的鞋子中任取4只,求这4只鞋子中至少有两只鞋子配成一双的概率.【解】 4111152222410C C C C C 131C 21p =-= 18.某地某天下雪的概率为0.3,下雨的概率为0.5,既下雪又下雨的概率为0.1,求:(1) 在下雨条件下下雪的概率;(2) 这天下雨或下雪的概率.【解】 设A ={下雨},B ={下雪}.(1) ()0.1()0.2()0.5P AB p B A P A === (2) ()()()()0.30.50.10.7p A B P A P B P AB =+-=+-=19.已知一个家庭有3个小孩,且其中一个为女孩,求至少有一个男孩的概率(小孩为男为女是等可能的).【解】 设A ={其中一个为女孩},B ={至少有一个男孩},样本点总数为23=8,故 ()6/86()()7/87P AB P B A P A === 或在缩减样本空间中求,此时样本点总数为7. 6()7P B A =20.已知5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是男人的概率(假设男人和女人各占人数的一半).【解】 设A ={此人是男人},B ={此人是色盲},则由贝叶斯公式()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.50.05200.50.050.50.002521⨯==⨯+⨯ 21.两人约定上午9∶00~10∶00在公园会面,求一人要等另一人半小时以上的概率.题21图 题22图【解】设两人到达时刻为x,y ,则0≤x ,y ≤60.事件“一人要等另一人半小时以上”等价于|x -y |>30.如图阴影部分所示.22301604P == 22.从(0,1)中随机地取两个数,求:(1) 两个数之和小于65的概率; (2) 两个数之积小于14的概率. 【解】 设两数为x ,y ,则0<x ,y <1.(1) x +y <65. 11441725510.68125p =-== (2) xy =<14. 1111244111d d ln 242x p x y ⎛⎫=-=+ ⎪⎝⎭⎰⎰ 23.设P (A )=0.3,P (B )=0.4,P (A B )=0.5,求P (B |A ∪B )【解】 ()()()()()()()()P AB P A P AB P B A B P A B P A P B P AB -==+- 0.70.510.70.60.54-==+- 24.在一个盒中装有15个乒乓球,其中有9个新球,在第一次比赛中任意取出3个球,比赛后放回原盒中;第二次比赛同样任意取出3个球,求第二次取出的3个球均为新球的概率.【解】 设A i ={第一次取出的3个球中有i 个新球},i =0,1,2,3.B ={第二次取出的3球均为新球}由全概率公式,有30()()()i i i P B P B A P A ==∑33123213336996896796333333331515151515151515C C C C C C C C C C C C C C C C C C =•+•+•+•0.089=25. 按以往概率论考试结果分析,努力学习的学生有90%的可能考试及格,不努力学习的学生有90%的可能考试不及格.据调查,学生中有80%的人是努力学习的,试问:(1)考试及格的学生有多大可能是不努力学习的人?(2)考试不及格的学生有多大可能是努力学习的人?【解】设A ={被调查学生是努力学习的},则A ={被调查学生是不努力学习的}.由题意知P(A )=0.8,P (A )=0.2,又设B ={被调查学生考试及格}.由题意知P (B |A )=0.9,P (B |A )=0.9,故由贝叶斯公式知(1)()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+0.20.110.027020.80.90.20.137⨯===⨯+⨯ 即考试及格的学生中不努力学习的学生仅占2.702% (2) ()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.80.140.30770.80.10.20.913⨯===⨯+⨯ 即考试不及格的学生中努力学习的学生占30.77%.26. 将两信息分别编码为A 和B 传递出来,接收站收到时,A 被误收作B 的概率为0.02,而B 被误收作A 的概率为0.01.信息A 与B 传递的频繁程度为2∶1.若接收站收到的信息是A ,试问原发信息是A 的概率是多少?【解】 设A ={原发信息是A },则={原发信息是B }C ={收到信息是A },则={收到信息是B }由贝叶斯公式,得()()()()()()()P A P C A P A C P A P C A P A P C A =+ 2/30.980.994922/30.981/30.01⨯==⨯+⨯ 27.在已有两个球的箱子中再放一白球,然后任意取出一球,若发现这球为白球,试求箱子中原有一白球的概率(箱中原有什么球是等可能的颜色只有黑、白两种)【解】设A i ={箱中原有i 个白球}(i =0,1,2),由题设条件知P (A i )=13,i =0,1,2.又设B ={抽出一球为白球}.由贝叶斯公式知 111120()()()()()()()i i i P B A P A P A B P A B P B P B A P A ===∑ 2/31/311/31/32/31/311/33⨯==⨯+⨯+⨯ 28.某工厂生产的产品中96%是合格品,检查产品时,一个合格品被误认为是次品的概率为0.02,一个次品被误认为是合格品的概率为0.05,求在被检查后认为是合格品产品确是合格品的概率.【解】 设A ={产品确为合格品},B ={产品被认为是合格品}由贝叶斯公式得()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.960.980.9980.960.980.040.05⨯==⨯+⨯ 29.某保险公司把被保险人分为三类:“谨慎的”,“一般的”,“冒失的”.统计资料表明,上述三种人在一年内发生事故的概率依次为0.05,0.15和0.30;如果“谨慎的”被保险人占20%,“一般的”占50%,“冒失的”占30%,现知某被保险人在一年内出了事故,则他是“谨慎的”的概率是多少?【解】 设A ={该客户是“谨慎的”},B ={该客户是“一般的”},C ={该客户是“冒失的”},D ={该客户在一年内出了事故}则由贝叶斯公式得 ()()(|)(|)()()(|)()(|)()(|)P AD P A P D A P A D P D P A P D A P B P D B P C P D C ==++ 0.20.050.0570.20.050.50.150.30.3⨯==⨯+⨯+⨯ 30.加工某一零件需要经过四道工序,设第一、二、三、四道工序的次品率分别为0.02,0.03,0.05,0.03,假定各道工序是相互独立的,求加工出来的零件的次品率.【解】设A i ={第i 道工序出次品}(i =1,2,3,4).412341()1()i i P A P A A A A ==- 12341()()()()P A P A P A P A =-10.980.970.950.970.124=-⨯⨯⨯=31.设每次射击的命中率为0.2,问至少必须进行多少次独立射击才能使至少击中一次的概率不小于0.9?【解】设必须进行n 次独立射击.1(0.8)0.9n -≥即为 (0.8)0.1n ≤故 n ≥11至少必须进行11次独立射击.32.证明:若P (A |B )=P (A |B ),则A ,B 相互独立.【证】 (|)(|)P A B P A B =即()()()()P AB P AB P B P B = 亦即 ()()()()P AB P B P AB P B =()[1()][()()]()P AB P B P A P AB P B -=-因此 ()()()P AB P A P B =故A 与B 相互独立.33.三人独立地破译一个密码,他们能破译的概率分别为15,13,14,求将此密码破译出的概率.【解】 设A i ={第i 人能破译}(i =1,2,3),则 31231231()1()1()()()i i P A P A A A P A P A P A ==-=-42310.6534=-⨯⨯= 34.甲、乙、丙三人独立地向同一飞机射击,设击中的概率分别是0.4,0.5,0.7,若只有一人击中,则飞机被击落的概率为0.2;若有两人击中,则飞机被击落的概率为0.6;若三人都击中,则飞机一定被击落,求:飞机被击落的概率.【解】设A ={飞机被击落},B i ={恰有i 人击中飞机},i =0,1,2,3由全概率公式,得30()(|)()i i i P A P A B P B ==∑=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)0.2+(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)0.6+0.4×0.5×0.7=0.45835.已知某种疾病患者的痊愈率为25%,为试验一种新药是否有效,把它给10个病人服用,且规定若10个病人中至少有四人治好则认为这种药有效,反之则认为无效,求:(1) 虽然新药有效,且把治愈率提高到35%,但通过试验被否定的概率.(2) 新药完全无效,但通过试验被认为有效的概率.【解】(1) 3101100C(0.35)(0.65)0.5138k k k k p -===∑ (2) 10102104C(0.25)(0.75)0.2241kk k k p -===∑36.一架升降机开始时有6位乘客,并等可能地停于十层楼的每一层.试求下列事件的概率:(1) A =“某指定的一层有两位乘客离开”;(2) B =“没有两位及两位以上的乘客在同一层离开”;(3) C =“恰有两位乘客在同一层离开”;(4) D =“至少有两位乘客在同一层离开”.【解】 由于每位乘客均可在10层楼中的任一层离开,故所有可能结果为106种.(1) 2466C 9()10P A =,也可由6重贝努里模型: 224619()C ()()1010P A = (2) 6个人在十层中任意六层离开,故6106P ()10P B = (3) 由于没有规定在哪一层离开,故可在十层中的任一层离开,有110C 种可能结果,再从六人中选二人在该层离开,有26C 种离开方式.其余4人中不能再有两人同时离开的情况,因此可包含以下三种离开方式:①4人中有3个人在同一层离开,另一人在其余8层中任一层离开,共有131948C C C 种可能结果;②4人同时离开,有19C 种可能结果;③4个人都不在同一层离开,有49P 种可能结果,故1213114610694899()C C (C C C C P )/10P C =++ (4) D=B .故 6106P ()1()110P D P B =-=- 37. n 个朋友随机地围绕圆桌而坐,求下列事件的概率:(1) 甲、乙两人坐在一起,且乙坐在甲的左边的概率;(2) 甲、乙、丙三人坐在一起的概率;(3) 如果n 个人并排坐在长桌的一边,求上述事件的概率.【解】 (1) 111p n =- (2) 23!(3)!,3(1)!n p n n -=>- (3) 12(1)!13!(2)!;,3!!n n p p n n n n --''===≥ 38.将线段[0,a ]任意折成三折,试求这三折线段能构成三角形的概率【解】 设这三段长分别为x ,y ,a -x -y .则基本事件集为由0<x <a ,0<y <a ,0<a -x -y <a 所构成的图形,有利事件集为由()()x y a x y x a x y y y a x y x+>--⎡⎢+-->⎢⎢+-->⎣ 构成的图形,即02022a x a y a x y a ⎡<<⎢⎢⎢<<⎢⎢⎢<+<⎢⎣ 如图阴影部分所示,故所求概率为14p =. 39. 某人有n 把钥匙,其中只有一把能开他的门.他逐个将它们去试开(抽样是无放回的).证明试开k 次(k =1,2,…,n )才能把门打开的概率与k 无关.【证】 11P 1,1,2,,P k n k n p k n n --===40.把一个表面涂有颜色的立方体等分为一千个小立方体,在这些小立方体中,随机地取出一个,试求它有i 面涂有颜色的概率P (A i )(i =0,1,2,3).【解】 设A i ={小立方体有i 面涂有颜色},i =0,1,2,3.在1千个小立方体中,只有位于原立方体的角上的小立方体是三面有色的,这样的小立方体共有8个.只有位于原立方体的棱上(除去八个角外)的小立方体是两面涂色的,这样的小立方体共有12×8=96个.同理,原立方体的六个面上(除去棱)的小立方体是一面涂色的,共有8×8×6=384个.其余1000-(8+96+384)=512个内部的小立方体是无色的,故所求概率为01512384()0.512,()0.38410001000P A P A ====, 24968()0.096,()0.00810001000P A P A ====. 41.对任意的随机事件A ,B ,C ,试证P (AB )+P (AC )-P (BC )≤P (A ).【证】 ()[()]()P A P A B C P AB AC ≥=()()()P AB P AC P ABC =+-()()()P AB P AC P BC ≥+-42.将3个球随机地放入4个杯子中去,求杯中球的最大个数分别为1,2,3的概率.【解】 设i A ={杯中球的最大个数为i },i =1,2,3.将3个球随机放入4个杯子中,全部可能放法有43种,杯中球的最大个数为1时,每个杯中最多放一球,故3413C 3!3()48P A == 而杯中球的最大个数为3,即三个球全放入一个杯中,故1433C 1()416P A == 因此 213319()1()()181616P A P A P A =--=--= 或 12143323C C C 9()416P A == 43.将一枚均匀硬币掷2n 次,求出现正面次数多于反面次数的概率.【解】掷2n 次硬币,可能出现:A ={正面次数多于反面次数},B ={正面次数少于反面次数},C ={正面次数等于反面次数},A ,B ,C 两两互斥.可用对称性来解决.由于硬币是均匀的,故P (A )=P (B ).所以1()()2P C P A -= 由2n 重贝努里试验中正面出现n 次的概率为211()()()22n n n n P C C =故 2211()[1C ]22n n n P A =- 44.掷n 次均匀硬币,求出现正面次数多于反面次数的概率.【解】设A ={出现正面次数多于反面次数},B ={出现反面次数多于正面次数},由对称性知P (A )=P (B )(1) 当n 为奇数时,正、反面次数不会相等.由P (A )+P (B )=1得P (A )=P (B )=0.5(2) 当n 为偶数时,由上题知211()[1C ()]22nn n P A =-45.设甲掷均匀硬币n +1次,乙掷n 次,求甲掷出正面次数多于乙掷出正面次数的概率.【解】 令甲正=甲掷出的正面次数,甲反=甲掷出的反面次数.乙正=乙掷出的正面次数,乙反=乙掷出的反面次数. 显然有>正正(甲乙)=(甲正≤乙正)=(n +1-甲反≤n -乙反) =(甲反≥1+乙反)=(甲反>乙反)由对称性知P (甲正>乙正)=P (甲反>乙反) 因此P (甲正>乙正)=1246.证明“确定的原则”(Sure -thing ):若P (A |C )≥P (B |C ),P (A |C )≥P (B |C ),则P (A )≥P (B ).【证】由P (A |C )≥P (B |C ),得()(),()()P AC P BC P C P C ≥即有 ()()P AC P BC ≥ 同理由 (|)(|),P A C P B C ≥ 得 ()(),P AC P BC ≥故 ()()()()()()P A P AC P AC P BC P BC P B =+≥+= 47.一列火车共有n 节车厢,有k (k ≥n )个旅客上火车并随意地选择车厢.求每一节车厢内至少有一个旅客的概率.【解】 设A i ={第i 节车厢是空的},(i =1,…,n ),则121(1)1()(1)2()(1)1()(1)n k ki kki j ki i i n P A n nP A A n n P A A A n--==-=--=-其中i 1,i 2,…,i n -1是1,2,…,n 中的任n -1个. 显然n 节车厢全空的概率是零,于是2112111122111111123111()(1)C (1)2()C (1)1()C (1)0()(1)n n nk ki ni ki j n i j nn kn i i i n i i i nn nn i ni S P A n n n S P A A n n S P A A A nS P A S S S S --=≤<≤--≤<<≤+===-=-==--==-==-+-+-∑∑∑121121C (1)C (1)(1)C (1)kkn n kn n n n nnn--=---++--故所求概率为121121()1C (1)C (1)nk i i n ni P A n n=-=--+--+111(1)C (1)n n kn n n+----48.设随机试验中,某一事件A 出现的概率为ε>0.试证明:不论ε>0如何小,只要不断地独立地重复做此试验,则A 迟早会出现的概率为1. 【证】在前n 次试验中,A 至少出现一次的概率为1(1)1()n n ε--→→∞49.袋中装有m 只正品硬币,n 只次品硬币(次品硬币的两面均印有国徽).在袋中任取一只,将它投掷r 次,已知每次都得到国徽.试问这只硬币是正品的概率是多少? 【解】设A ={投掷硬币r 次都得到国徽}B ={这只硬币为正品} 由题知 (),()m nP B P B m n m n==++ 1(|),(|)12r P A B P A B ==则由贝叶斯公式知()()(|)(|)()()(|)()(|)P AB P B P A B P B A P A P B P A B P B P A B ==+121212rrrm m m n m nm n m n m n+==++++ 50.巴拿赫(Banach )火柴盒问题:某数学家有甲、乙两盒火柴,每盒有N 根火柴,每次用火柴时他在两盒中任取一盒并从中任取一根.试求他首次发现一盒空时另一盒恰有r 根的概率是多少?第一次用完一盒火柴时(不是发现空)而另一盒恰有r 根的概率又有多少? 【解】以B 1、B 2记火柴取自不同两盒的事件,则有121()()2P B P B ==.(1)发现一盒已空,另一盒恰剩r 根,说明已取了2n -r 次,设n 次取自B 1盒(已空),n -r 次取自B 2盒,第2n -r +1次拿起B 1,发现已空。
概率论与数理统计第五章练习答案郝志峰,谢国瑞

概率论与数理统计第五章习题的联合概率分布列为即。
对应的概率为:的所有可能取值对是。
于是二维随机变量服从二项分布并的所有可能取值也是则是乙击中目标的次数,。
设分布;并服从二项的所有可能取值是则是甲击中目标的次数解:设),(.2304.06.0*8.0)2,2(P ;3072.06.0*)6.01(*8.0)1,2(P ;1024.0)6.01(*8.0)0,2(P ;1152.06.0*8.0*)8.01()2,1(P ;1536.06.0*)6.01(*8.0*)8.01()1,1(P ;0512.0)6.01(*8.0*)8.01()0,1(P ;0144.06.0*)8.01()2,0(P ;0192.06.0*)6.01(*)8.01()1,0(P ;0064.0)6.01(*)8.01()0,0(P )2,2(),1,2(),0,2(),2,1(),1,1(),0,1(),2,0(),1,0(),0,0(),().60,2(B ;,1,20).80,2(B ,1,20,.1221222221212122122212222ηξηξηξηξηξηξηξηξηξηξηξηηξξ=====-====-====-====--====--====-====--====--===C C C C C C的联合概率分布列为:即。
事件等品和二等品,不可能即抽到的产品同时是一即抽到一等品即抽到二等品即抽到三等品。
对应的概率分别为:所有可能取值对是解:),()(0)1,1();(;8.0)0,1()(;1.0)1,0();(;1.0)0,0()1,1(),0,1(),1,0(),0,0(),(.2212121212121ξξξξξξξξξξξξ============P P P P的联合概率分布列为:的边缘分布可以得到和又利用。
,得到:非负,并且和等于有可能取值对应的概率利用离散型随机变量所。
可知:解:根据),(0)1,1()1,1()1,1()1,1(11)0,1()0,1()1,0()0,0()1,0(1)0(.3212121212121212121212121ξξξξξξξξξξξξξξξξξξξξξξξξ====-====-==-=-===-=+==+==+==+-====P P P P P P P P P P的联合分布列为:所以对应的概率为:的所有可能取值为有:从而对于是的概率密度可知:解:根据),()arctan 2()1()1(P )1,1(P )1,1()arctan 21(arctan 2)1()1(P )1,1(P )0,1(arctan 2)arctan 21()1()1(P )1,1(P )1,0()arctan 21()1()1(P )1,1(P )0,0(),1,1(),0,1(),1,0(),0,0(),(.arctan 2)1(P ,arctan 21)1(P ,2,1,arctan 21)1(P arctan 2112)(2)1(P .4212212121212121212121221212121121ηηπξξξξηηππξξξξηηππξξξξηηπξξξξηηηηπξπξπξπππξξe P P e e P P ee P P e P P e e k e e de e dx e e k k xx x x =≤≤=≤≤===-=>≤=>≤===-=≤>=≤>===-=>>=>>====≤-=>=-=>=+=+=≤⎰⎰∞-∞--).1)(1()0,0()0,3()4,0()4,3()40,30()3(0y 0,00,0),1)(1(),().1)(1(12),(.12),(0,0.0),(,0),(0y 0)2(.12A 12),(1)1(.516943430)43()43(04030)43(--=+--=≤<≤<⎪⎩⎪⎨⎧≤≤>>--=--===>>==≤≤=====------+-+-∞+-∞+-∞+∞++-∞+∞-∞+∞-⎰⎰⎰⎰⎰⎰⎰⎰e e F F F F P x y x e ey x F e e dxdy e y x F e y x f y x y x F y x f x Ady e dx eA dxdy Aedxdy y x f y x y x x yy x y x y xy x ηξ时或者当时当因此:于是对应的分布函数:时,当于是对应的分布函数时,联合密度函数或者当所以解:⎪⎩⎪⎨⎧≤≤-≤≤-+=-===+-≤≤+-≤≤+===+≤≤--≤≤-==>-<⎪⎩⎪⎨⎧≤-≤-≤+≤-=⎰⎰-+-+--其他因此:于是对应的概率密度是时,)当(于是对应的概率密度是时,)当(于是对应的边缘分布时,或者)当(其他对应的概率密度是:,所以的面积为解:由于,010,101,1)(;121)(,21),(,1110iii ;121)(,21),(,1101ii ;0)(,0),(11i ,011,11,21),(),(2.61111x x x x x f x dy x f y x f x y x x x dy x f y x f x y x x x f y x f x x y x y x y x f D xx xx ξξξξηξ.48251611218141)4,4()3,3()2,2()1,1()()3(.161487481348254321;414141414321)2(.41,1161*4121*381*2)1(.7=+++===+==+==+====⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==+++ηξηξηξηξηξηξP P P P P a a 的边缘分布为:的边缘分布为:可得:根据解:.913)3(1311)()(),3arctan 2(1)3arctan 2)(22(1),()(.412)2(1211)()(),2arctan 2(1)22)(2arctan 2(1),()()3(.91416)3(131)2(1211),(),()2(.1,2,)2)(2arctan (),(0)3arctan )(2(),(0)2)(2(),(1,.822'222'222222222yy y F y f yy y F y F xx x F x f x x x F x F yx y x y x F y x y x f A C B y x C x B A x F y C B A y F C B A F y x +=+==+=++=+∞=+=+==+=++=+∞=++=++=∂∂∂====⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-∞=+-=-∞=++=+∞+∞=ππππππππππππππππππππππππηηηξξξ边缘密度函数所以边缘分布函数边缘密度函数所以边缘分布函数从而的任意性可知:利用,满足:解:对任意的.)(.1445.0)5.08413.0(21))0()1((212121)1()21()(.91212122222函数为标准正态分布的分布其中解:x dxe dx e dxdy e P x x xy Φ=--=Φ-Φ-=-=-==<⎰⎰⎰⎰---ππππξη⎪⎩⎪⎨⎧≤≤+=+==⎪⎩⎪⎨⎧≤≤+=+==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧>>≤≤>+>≤≤+≤≤≤≤+<<=+==≤≤>+==>≤≤+=+=⎥⎦⎤⎢⎣⎡+==≤≤≤≤==>>==<<==+=+=⎥⎦⎤⎢⎣⎡+==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∞+∞-∞+∞-∞-∞-∞+∞-∞+∞-∞-∞-∞+∞-∞+∞-其他的边缘密度函数为:其他的边缘密度函数为:并且并且并且并且或者因此:时并且当时并且当时并且当时并且当于是概率密度时或者当的范围分情况进行讨论下面我们对利用所以解:,020,6131)31(),()(,010,322)31(),()()3(21,1201,12131210,31322010,1213100,0),(;12131),1(),(,201)v (;3132)2,(),(,210)iv (;12131)61()31(),(),(,2010)iii (;1),(),(,21)ii (;0),(,0),(,00)i (.,,),(),()2(.31,32)22()(),(1)1(.10102220222322322322302200210210202y y dx xy x dx y x f y f x x x dy xy x dy y x f x f y x y x y y y x x x y x y x y x y x y x F y y y F y x F y x x x x F y x F y x y x y x dx xy y x dx dy xy x dxdyy x f y x F y x dxdy y x f y x F y x y x F y x f y x y x dxdy y x f y x F c c dx cx x dx dy cxy x dxdy y x f x x y x yxyηξηξ⎪⎪⎩⎪⎪⎨⎧≤≤++=++==+=≤≤==<>⎪⎪⎩⎪⎪⎨⎧≤≤++=++==+=≤≤==<>其他于是时,当没有定义;于是时或者同样,当其他于是时,当没有定义;于是时或者当,020,62332231)(),()|(,322)(10)(),()|(,0)(,01,010,226613131)(),()|(,6131)(20)(),()|(,0)(,02)4(22222y x yx x x xy x x f y x f x y f x x x f x x f y x f x y f x f x x x y xyx y xy x y f y x f y x f y y f y y f y x f y x f y f y y ξξξξηηηη⎪⎩⎪⎨⎧<≥===≥==<⎪⎩⎪⎨⎧<≥===⎪⎩⎪⎨⎧<≥===≥==<⎪⎩⎪⎨⎧<≥===--+--∞++-∞+∞---+--∞++-∞+∞-⎰⎰⎰⎰0,00,22)(),()|(0)(),()|(,0)(00,00,)2(),()(0,00,22)(),()|(0)(),()|(,0)(00,00,2)2(),()()1(.112)2(0)2(2)2(20)2(x x e e e y f y x f y x f y y f y x f y x f y f y y y e dx e dx y x f y f y y e e e x f y x f x y f x x f y x f x y f x f x x x e dy e dy y x f x f x y y x y y x yxy x x y x ηηηηξξξξηξ时,当没有定义;所以时,于是当的边缘密度函数为:时,当没有定义;所以时,于是当的边缘密度函数为:解:.12)1()1,2()1|2()2(410201)2(--+--=⎥⎦⎤⎢⎣⎡=≤≤≤=≤≤⎰⎰⎰e dyedxdy e P P P yy x ηηξηξ.2ln 11)1()3(,010),1(111),()()2(,010,11)|()(),(),(,,01,11)|(:)1,(,)10(,010,1)(:)1,0()1(:.1212110=⎥⎦⎤⎢⎣⎡-=>+⎪⎩⎪⎨⎧<<--=-==⎪⎩⎪⎨⎧<<<-==⎪⎩⎪⎨⎧<<-=<<=⎩⎨⎧<<=⎰⎰⎰⎰-∞+∞-dy dx x P y y n dx xdx y x f y f y x xx y f x f y x f y x xx y f x x x x x f y y y ηξηηξηξξηξξ其他的边缘密度为:其他的联合密度函数为:因此其他上的均匀分布,可得服从区间时又根据其他上的均匀分布,所以服从区间由于解.,:.91B ,92A )A 91(319131B A )A 91)(1819161(911B A 311819161,.13的确是独立的随机变量知代入联合分布列验证可解得::是独立的随机变量可得性质及解:根据联合分布列的ηξηξ==⎪⎪⎩⎪⎪⎨⎧+==+⇒⎪⎪⎩⎪⎪⎨⎧+++==+++++表:因此,联合分布列如下是独立随机变量:于是根据边缘分布以及的概率分布为解:设.4112131;31216111;838121;214181;1218124141;43681;416241;2418161,.3,2,1;2,1,),(),(.141332321312222112212111131212111111=-=-==--=--==-=-=====--=--========-======∙∙∙∙∙∙∙∙∙∙∙∙p p p p p p p p p p p p p p p p p p p p p p p j i p y x P ij j i ηξηξηξ.0,41,41,2121214341)0()1(.1,0;1,0,),(),(.2121*43*332143),()(.41,163;21,43,1021,43,.15010010111110001110010000011011联合分布列为解得:得:。
概率论与数理统计学1至7章课后答案

第二章作业题解:掷一颗匀称的骰子两次, 以X 表示前后两次出现的点数之和, 求X 的概率分布, 并验证其满足(2.2.2) 式.解:由表格知X 并且,361)12()2(====X P X P ;362)11()3(====X P X P ; 363)10()4(====X P X P ;364)9()5(====X P X P ; 365)8()6(====X P X P ;366)7(==X P 。
即 36|7|6)(k k X P --== (k =2,3,4,5,6,7,8,9,10,11,12)设离散型随机变量的概率分布为,2,1,}{ ===-k ae k X P k 试确定常数a .解:根据1)(0==∑∞=k k X P ,得10=∑∞=-k kae,即1111=---e ae 。
故 1-=e a甲、乙两人投篮时, 命中率分别为 和 , 今甲、乙各投篮两次, 求下列事件的概率:(1) 两人投中的次数相同; (2) 甲比乙投中的次数多. 解:分别用)2,1(,=i B A i i 表示甲乙第一、二次投中,则12121212()()0.7,()()0.3,()()0.4,()()0.6,P A P A P A P A P B P B P B P B ========两人两次都未投中的概率为:0324.06.06.03.03.0)(2121=⨯⨯⨯=B B A A P , 两人各投中一次的概率为:2016.06.04.03.07.04)()()()(1221211212212121=⨯⨯⨯⨯=+++B B A A P B B A A P B B A A P B B A A P 两人各投中两次的概率为:0784.0)(2121=B B A A P 。
所以:(1)两人投中次数相同的概率为3124.00784.02016.00324.0=++ (2) 甲比乙投中的次数多的概率为:12121221121212121212()()()()()20.490.40.60.490.3620.210.360.5628P A A B B P A A B B P A A B B P A A B B P A A B B ++++=⨯⨯⨯+⨯+⨯⨯= 设离散型随机变量X 的概率分布为5,4,3,2,1,15}{===k kk X P ,求)31()1(≤≤X P )5.25.0()2(<<X P 解:(1)52153152151)31(=++=≤≤X P (2) )2()1()5.25.0(=+==<<X P X P X P 51152151=+= 设离散型随机变量X 的概率分布为,,3,2,1,21}{ ===k k X P k ,求 };6,4,2{)1( =X P }3{)2(≥X P解:31)21211(21212121}6,4,2{)1(422642=++⨯=++== X P41}2{}1{1}3{)2(==-=-=≥X P X P X P设事件A 在每次试验中发生的概率均为 , 当A 发生3 次或3 次以上时, 指示灯发出 信号, 求下列事件的概率:(1) 进行4 次独立试验, 指示灯发出信号; (2) 进行5 次独立试验, 指示灯发出信号.解:(1))4()3()3(=+==≥X P X P X P1792.04.06.04.04334=+⨯=C (2) )5()4()3()3(=+=+==≥X P X P X P X P31744.04.06.04.06.04.054452335=+⨯+⨯=C C .某城市在长度为t (单位:小时) 的时间间隔内发生火灾的次数X 服从参数为 的泊 松分布, 且与时间间隔的起点无关, 求下列事件的概率: (1) 某天中午12 时至下午15 时未发生火灾;(2) 某天中午12 时至下午16 时至少发生两次火灾. 解:(1) ()!kP X k e k λλ-==,由题意,0.53 1.5,0k λ=⨯==,所求事件的概率为 1.5e -.(2) 0(2)110!1!P X e e e e λλλλλλλ----≥=--=--, 由题意,0.54 1.5λ=⨯=,所求事件的概率为213e --.为保证设备的正常运行, 必须配备一定数量的设备维修人员. 现有同类设备180 台, 且各台设备工作相互独立, 任一时刻发生故障的概率都是,假设一台设备的故障由一人进行修理,问至少应配备多少名修理人员, 才能保证设备发生故障后能得到及时修理的概率不小于 解:设应配备m 名设备维修人员。
概率论与数理统计 第五版 习题全解指南

概率论与数理统计第五版习题全解指南下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
此文下载后可定制随意修改,请根据实际需要进行相应的调整和使用。
并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Downloaded tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The documents can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!在概率论与数理统计领域,习题的全面解析对于学习者来说是至关重要的。
概率论与数理统计统计课后习题答案_总主编_邹庭荣_主编_程述汉_舒兴明之欧阳法创编
第一章习题解答1.解:(1) Ω={0,1,…,10};(2) Ω={=i n i|0,1,…,100n },其中n 为小班人数;(3) Ω={√,×√, ××√, ×××√,…},其中√表示击中,×表示未击中;(4) Ω={(y x ,)|22y x +<1}。
2.解:(1)事件C AB 表示该生是三年级男生,但不是运动员;(2)当全学院运动员都是三年级学生时,关系式C ⊂B 是正确的;(3)全学院运动员都是三年级的男生,ABC=C 成立;(4)当全学院女生都在三年级并且三年级学生都是女生时,A =B 成立。
3.解:(1)ABC ;(2)AB C ;(3)C B A ;(4)C B A )(⋃;(5)C B A ⋃⋃; (6)C B C A B A ⋃⋃;(7)C B A ⋃⋃;(8)BC A C B A C AB ⋃⋃4.解:因ABC ⊂AB ,则P (ABC )≤P(AB )可知P(ABC )=0所以A 、B 、C 至少有一个发生的概率为P (A∪B∪C)=P (A )+P (B )+P (C )-P (AB )-P (AC )-P (BC )+P (ABC )=3×1/4-1/8+0=5/85.解:(1)P (A∪B)= P (A )+P (B )-P (AB )=0.3+0.8-0.2=0.9)(B A P =P (A )-P (AB )=0.3-0.2=0.1(2)因为P (A∪B)= P (A )+P (B )-P (AB )≤P(A )+P (B )=α+β,所以最大值maxP (A∪B)=min(α+β,1);又P (A )≤P(A∪B),P (B )≤P(A∪B),故最小值min P (A∪B)=max(α,β)6.解:设A 表示事件“最小号码为5”,B 表示事件“最大号码为5”。
由题设可知样本点总数310C n =,2425,C k C k A ==。
概率论与数理统计学1至7章课后答案
一、第六章习题详解6.1 证明(6.2.1)和(6.2.2)式.证明: (1) ∑∑∑===+=+==ni i n i i n i i nb X a n b aX n Y n Y 111)(1)(11b X a b X n a ni i +=+=∑=1)1((2) ∑∑==+-+=--=n i i n i i Yb X a b aX n Y Y n S 12122)]()[(1)(11 2212212)(1)]([1X ni i n i i S a X X n a X X a n =-=-=∑∑==6.2设n X X X ,,,21Λ是抽自均值为μ、方差为2σ的总体的样本, X 与2S 分别为该样本均值。
证明与2(),()/E X Var X n μσ==. 证:()E X =1212111[()]()()n n E X X X E X X X n n n nμμ++=++==L L ()Var X =22121222111[()]()()n n Var X X X E X X X n n n n nσσ++=++==L L6.3 设n X X X ,,,21Λ是抽自均值为μ、方差为2σ的总体的样本,2211()1ni i S X X n ==--∑, 证明: (1) 2S =)(11212X n X n ni i --=∑= (2) 2()E S =2σ= 证:(1) ∑∑==+--=--=n i i i n i i X X X X n X X n S 122122)2(11)(11 ]2)([112112X n X X X n n i i n i i +--=∑∑== ])(2)([11212X n X n X X n n i i +--=∑= )(11212X n X n ni i --=∑=(2) )(11)(2122X n X E n S E n i i --=∑=)]()([11212X nE X E n ni i --=∑= ]})()([])()([{11212X E X Var n EX X Var n ni i i +-+-=∑= )}()({1122122μσμσ+-+-=∑=nn n ni )]()([112222μσμσn n n +-+-=222)(11σσσ=--=n n6.4 在例6.2.3 中, 设每箱装n 瓶洗净剂. 若想要n 瓶灌装量的平均阻值与标定值相差不超 过0.3毫升的概率近似为95%, 请问n 至少应该等于多少? 解:因为1)3.0(2)/3.0|/(|)3.0|(|-Φ≈<-=<-n nnX P X P σσμμ依题意有,95.01)3.0(2=-Φn ,即)96.1(975.0)3.0(Φ==Φn于是 96.13.0=n ,解之得 7.42=n 所以n 应至少等于43.6.5 假设某种类型的电阻器的阻值服从均值μ=200 欧姆, 标准差σ=10 欧姆的分布,在一个电子线路中使用了25个这样的电阻.(1) 求这25个电阻平均阻值落在199 到202 欧姆之间的概率; (2) 求这25个电阻总阻值不超过5100 欧姆的概率. 解:由抽样分布定理,知nX /σμ-近似服从标准正态分布N (0,1),因此(1) )25/10200199()25/10200202()202199(-Φ--Φ≈≤≤X P)5.0(1)1()5.0()1(Φ+-Φ=-Φ-Φ=5328.06915.018413.0=+-= (2) )204()255100()5100(≤=≤=≤X P X P X n P 9772.0)2()25/10200204(=Φ=-Φ≈6.6 假设某种设备每天停机时间服从均值μ=4 小时、标准差σ=0.8小时的分布. (1) 求一个月(30天) 中, 每天平均停机时间在1到5小时之间的概率; (2) 求一个月(30天) 中, 总的停机时间不超过115 小时的概率. 解:(1))30/8.041()30/8.045()/1()/5()51(-Φ--Φ=-Φ--Φ≈≤≤nnX P σμσμ1)54.20()85.6(≈-Φ-Φ=(2) )30115()11530(≤=≤X P X P 1271.08729.01)14.1(1)30/8.0430/115(=-=Φ-=-Φ≈6.7 设~n T t ,证明()0,2,3,.E T n ==L证:)(n t 分布的概率密度为: +∞<<-∞⎪⎪⎭⎫⎝⎛+Γ+Γ=+-t n x n n n x f n ,1)2/(]2/)1[()(212π,()()E T xf x dx +∞-∞==⎰=112222212211(1)10n n nx x x dx d n n nx n ++--+∞+∞-∞-∞-+∞-∞⎫⎫+=++⎪⎪⎭⎭⎛⎫=+=⎪⎭⎰⎰6.8 设总体X ~N(150,252), 现在从中抽取样本大小为25的样本, {140147.5}P X ≤≤. 解: 已知150=μ,25=σ,25=n ,)25/25150140()25/251505.147()5.147140(-Φ--Φ≈≤≤X P)5.0()2()2()5.0(Φ-Φ=-Φ--Φ=2857.09615.09772.0=-=6.9 设某大城市市民的年收入服从均值μ=1.5万元、标准差σ=0.5万元的正态分布. 现 随机调查了100 个人, 求他们的平均年收入落在下列范围内的概率: (1) 大于1.6万元;(2) 小于1.3万元;(3) 落在区间[1.2,1.6] 内.解:设X 为人均年收入,则)5.0,5.1(~2N X ,则)1005.0,5.1(~2N X ,得 (1) )100/5.05.16.1(1)6.1(1)6.1(-Φ-≈≤-=>X P X P0228.09772.01)2(1=-=Φ-=(2) 011)4(1)4()100/5.05.13.1()3.1(=-≈Φ-=-Φ=-Φ≈<X P(3) )100/5.05.12.1()100/5.05.16.1()6.12.1(-Φ--Φ≈<<X P9772.0)6()2(=-Φ-Φ=6.10 假设总体分布为N(12,22), 今从中抽取样本125,,,X X X L . 求 (1) 样本均值X 大于13的概率; (2) 样本的最小值小于10的概率; (3) 样本的最大值大于15的概率.解:因为 )2,12(~2N X ,所以22~(12,)5X N ,得(1) )5/21213(1)13(1)13(-Φ-≈≤-=>X P X P1314.08686.01)12.1(1=-=Φ-=(2) ?设样本的最小值为Y ,则),,,(521X X X Min Y Λ=,于是)10(1)10(≥-=<Y P Y P)10()10()10(1521≥≥≥-=X P X P X P Λ)]21210(1[1)]10(1[15151-Φ-∏-=<-∏-===i i i X P5785.0)8413.0(1)1(1)]1(1[155151=-=Φ∏-=-Φ-∏-===i i(3) ?设样本的最大值为Z ,则),,,(521X X X Max Z Λ=,于是)15(1)15(≤-=>Z P Z P)15()15()15(1521≤≤≤-=X P X P X P Λ)21215(151-Φ∏-==i 2923.0)9332.0(1)5.1(1551=-=Φ∏-==i6.11设总体),(~2σμN X ,从中抽取容量样本1216,,,X X X L , 2S 为样本方差. 计算22 2.04S P σ⎧⎫≤⎨⎬⎩⎭. 解因为),,(~2σμN X 由定理2, 得),1(~)1(21222-⎪⎪⎭⎫ ⎝⎛-=-∑=n XX S n ni i χσσ 所以,1)1(22-=⎪⎪⎭⎫ ⎝⎛-n S n E σ),1(2)1(22-=⎪⎪⎭⎫⎝⎛-n S n D σ于是,)(22σ=S E ).1/(2)(42-=n S D σ 当16=n 时, ,15/2)(42σ=S D 且2222{/ 2.04}{15/30.615}P S P S σσ≤=≤}615.30/15{122>-=σS P99.001.01=-=).578.30)15((201.0=χ第六章 《样本与统计量》定理、公式、公理小结及补充:。
《概率论与数理统计》第三版_科学出版社_课后习题答案.所有章节
第二章 随机变量 2.12.2解:根据1)(0==∑∞=k k X P ,得10=∑∞=-k kae,即1111=---e ae 。
故 1-=e a2.3解:用X 表示甲在两次投篮中所投中的次数,X~B(2,0.7) 用Y 表示乙在两次投篮中所投中的次数, Y~B(2,0.4) (1) 两人投中的次数相同P{X=Y}= P{X=0,Y=0}+ P{X=1,Y=1} +P{X=2,Y=2}=11220202111120202222220.70.30.40.60.70.30.40.60.70.30.40.60.3124C C C C C C ⨯+⨯+⨯=(2)甲比乙投中的次数多P{X >Y}= P{X=1,Y=0}+ P{X=2,Y=0} +P{X=2,Y=1}=12211102200220112222220.70.30.40.60.70.30.40.60.70.30.40.60.5628C C C C C C ⨯+⨯+⨯=2.4解:(1)P{1≤X ≤3}= P{X=1}+ P{X=2}+ P{X=3}=12321515155++= (2) P{0.5<X<2.5}=P{X=1}+ P{X=2}=12115155+= 2.5解:(1)P{X=2,4,6,…}=246211112222k +++ =11[1()]1441314k k lim →∞-=-(2)P{X ≥3}=1―P{X <3}=1―P{X=1}- P{X=2}=1111244--= 2.6解:(1)设X 表示4次独立试验中A 发生的次数,则X~B(4,0.4)34314044(3)(3)(4)0.40.60.40.60.1792P X P X P X C C ≥==+==+=X 2 3 4 5 6 7 8 9 10 11 12P 1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36(2)设Y 表示5次独立试验中A 发生的次数,则Y~B(5,0.4)345324150555(3)(3)(4)(5)0.40.60.40.60.40.60.31744P X P X P X P X C C C ≥==+=+==++=2.7 (1)X ~P(λ)=P(0.5×3)= P(1.5)0 1.51.5{0}0!P X e -=== 1.5e - (2)X ~P(λ)=P(0.5×4)= P(2)0122222{2}1{0}{1}1130!1!P X P X P X e e e ---≥=-=-==--=-2.8解:设应配备m 名设备维修人员。
概率论与数理统计学1至7章课后答案解析
第二章作业题解:2.1 掷一颗匀称的骰子两次, 以X 表示前后两次出现的点数之和, 求X 的概率分布, 并验证其满足(2.2.2) 式.解:由表格知X 的可能取值为2,3,4,5,6,7,8,9,10,11,12。
并且,361)12()2(====X P X P ;362)11()3(====X P X P ; 363)10()4(====X P X P ;364)9()5(====X P X P ; 365)8()6(====X P X P ;366)7(==X P 。
即 36|7|6)(k k X P --== (k =2,3,4,5,6,7,8,9,10,11,12)2.2 设离散型随机变量的概率分布为,2,1,}{Λ===-k ae k X P k 试确定常数a . 解:根据1)(0==∑∞=k k X P ,得10=∑∞=-k kae,即1111=---e ae 。
故 1-=e a2.3 甲、乙两人投篮时, 命中率分别为0.7 和0.4 , 今甲、乙各投篮两次, 求下列事件的概率:(1) 两人投中的次数相同; (2) 甲比乙投中的次数多. 解:分别用)2,1(,=i B A i i 表示甲乙第一、二次投中,则12121212()()0.7,()()0.3,()()0.4,()()0.6,P A P A P A P A P B P B P B P B ========两人两次都未投中的概率为:0324.06.06.03.03.0)(2121=⨯⨯⨯=B B A A P , 两人各投中一次的概率为:2016.06.04.03.07.04)()()()(1221211212212121=⨯⨯⨯⨯=+++B B A A P B B A A P B B A A P B B A A P 两人各投中两次的概率为:0784.0)(2121=B B A A P 。
所以:(1)两人投中次数相同的概率为3124.00784.02016.00324.0=++ (2) 甲比乙投中的次数多的概率为:12121221121212121212()()()()()20.490.40.60.490.3620.210.360.5628P A A B B P A A B B P A A B B P A A B B P A A B B ++++=⨯⨯⨯+⨯+⨯⨯=2.4 设离散型随机变量X 的概率分布为5,4,3,2,1,15}{===k kk X P ,求)31()1(≤≤X P )5.25.0()2(<<X P 解:(1)52153152151)31(=++=≤≤X P (2) )2()1()5.25.0(=+==<<X P X P X P 51152151=+= 2.5 设离散型随机变量X 的概率分布为,,3,2,1,21}{Λ===k k X P k,求 };6,4,2{)1(Λ=X P }3{)2(≥X P解:31)21211(21212121}6,4,2{)1(422642=++⨯=++==ΛΛΛX P41}2{}1{1}3{)2(==-=-=≥X P X P X P2.6 设事件A 在每次试验中发生的概率均为0.4 , 当A 发生3 次或3 次以上时, 指示灯发出信号, 求下列事件的概率:(1) 进行4 次独立试验, 指示灯发出信号; (2) 进行5 次独立试验, 指示灯发出信号.解:(1))4()3()3(=+==≥X P X P X P1792.04.06.04.04334=+⨯=C(2) )5()4()3()3(=+=+==≥X P X P X P X P31744.04.06.04.06.04.054452335=+⨯+⨯=C C .2.7 某城市在长度为t (单位:小时) 的时间间隔内发生火灾的次数X 服从参数为0.5t 的泊 松分布, 且与时间间隔的起点无关, 求下列事件的概率: (1) 某天中午12 时至下午15 时未发生火灾; (2) 某天中午12 时至下午16 时至少发生两次火灾. 解:(1) ()!kP X k e k λλ-==,由题意,0.53 1.5,0k λ=⨯==,所求事件的概率为 1.5e -.(2) 0(2)110!1!P X e e e e λλλλλλλ----≥=--=--, 由题意,0.54 1.5λ=⨯=,所求事件的概率为213e --.2.8 为保证设备的正常运行, 必须配备一定数量的设备维修人员. 现有同类设备180 台, 且各台设备工作相互独立, 任一时刻发生故障的概率都是0.01,假设一台设备的故障由一人进行修理,问至少应配备多少名修理人员, 才能保证设备发生故障后能得到及时修理的概率不小于0.99?解:设应配备m 名设备维修人员。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题五1.假设有10只同种电器元件,其中两只废品,从这批元件中任取一只,如果是废品,则扔掉重新取一只,如仍是废品,则扔掉再取一只,试求在取到正品之前,已取出的废品只数的数学期望和方差。
解设X为已取出的废品只数,则X的分布为X012P8184521 45即P所以,2.假设一部机器在一天解设一周所获利润为T(万元),则T的可能值为又设X为机器一周类似地可求出T的分布为(万元)X(毫米)服从正态分布所以一周3.假设自动线加工的某种零件的内径1),内径小于·55·10或大于12为不合格品,销售每件合格品获利,销售每件不合格品亏损,已知销售利润T(元)与零件的若若问平均即两边取对数得即时,平均利润最大.4.从学校到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是数学期望.解即25,设X为途中遇到红灯的次数,求随机变量X的分布律、分布函数和X~,分布律为·56 ·XP02712515412523612538 125X的分布函数为12512512512555.设随机变量服从几何分布,其分布列为,求EX与DX 解1 EX其中k由函数的幂级数展开有所以k1,1. p因为所以2,·57·解2设则(1)–(2)得(1)(2)1,所以从而,得,,22232n,,于是所以,ppp12q12q,故得X的方差为·58 ·6.设随机变量X分别具有下列概率密度,求其数学期望和方差. (1)(2)(3)1;2其他(4)其他1,(因为被积函数为奇函数)解(1)EX(2)EX212123x3x411(3)22所以,12281232(4)EX1x01331213211281211443412·59·所以7.在习题三第4题中求E解因X的分布为XP01211421831 8所以8.设随机变量X的概率密度为其他3已知,求4(1)a,b,c的值(2)随机变量Y解(1)的数学期望和方差解方程组,,12422·60 ·得1,,,(2)9.游客乘电梯从底层到电视塔顶层观光;电梯于每个整点的第5分钟,25分钟和55分钟从底层起行。
假设一游客在早八点的第分布,求该游客等候时间的数学期望.解设候梯时间为T,则X分钟到达底层候梯处,且X在[0,60]上均匀1[1210.设某种商品每周的需求量X是服从区间[10,30]上均匀分布的随机变量,而经销商店进货量为区间[10,30]中的某一个整数,商店每销售一单位商品可获利500元;若供大于求则削价处理,每处理一单位商品亏损100元;若供不应求,则从外部调剂供应,此时每一单位商品仅获利300元,为使商店所获利润期望值不少于9280元,试确定最小进货量。
解设商店获得的利润为T,进货量为y,则·61·由题意30y即解不等式得, 3即使利润的期望值不少于9280元的最少进货量为21个单位.11.设X与Y同分布,且X的概率密度为其他.和事件独立,且。
(1)已知事件(2)求E3,求常数a;41X2解(1)P(X,即有方程即可见解之得,或,故(2)12.于习题四第15题中求Z解的数学期望.X,Y的分布为(x,y)(0,1)(1,0)(1,1)(2,0)(2,1)0.100.150.250.20 0.150.1513.设的分布律为解(1)EX;yjY1 (2)111 ;23152 (3)或·63·或,先求(X的分布取值的.设离散型二维随机变量(X,Y)在点(1,1),概率均为解14,求,424244 ,5所以;8;4646443215.设(X,Y)的概率密度为其他.的数学期望.解·64 ·令r2.设二维随机变量(X,Y)的概率密度为其它.求EX,解;;;,于是故;231817.假设随机变量Y服从参数为的指数分布,随机变量若若求(1)X1,X2的联合分布,(2)解(1)(X1,X2)的分布:,,(2)·65·18.设连续型随机变量X的所有可能值在区间[a,(1)ab]之(2)证(1)因为,所以,即;(2)因为对于任意的常数C有,取,则有 219.一商店经销某种商品,每周进货量X与顾客对该种商品的需求量Y是相互独立的随机变量,且都服从区间[10,20]上的均匀分布。
商店每售出一单位商品可得利润1000元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润500元,试计算此商店经销该种商品每周所得利润的期望值。
解设T为一周其中g(x,y)f(x,y)dxdy其他.所以2·66 ·(元). 320.设X,Y是两个相互独立的随机变量,其概率密度分别为其他求E(XY),D(XY)122x,解(注:因为参数为1的指数分布的数学期望为1,而fY(y)是前指数分布向右平移了5个单位,所以)因X,Y独立,所以DXY 今求方法方法2 利用公式:当X,Y独立时21.在长为L的线段上任取两点,求两点距离的期望和方差.解以线段的左端点为原点建立坐标系,任取两点的坐标分别为X,Y,则它们均在[0,L]上服从均匀分布,且X,Y相互独立.dy 0xLL2·67·所以L2L2L222.设随机变量X与Y独立,且X服从均值为1而Y服从标准正态分布,试求随机变量的概率密度.2 解因为相互独立的正态分布的线性组合仍为正态分布,所以其中所以Z的概率密度为,N(0,1)2的随机变量,求23.设是两个相互独立的且均服从正态分布与解·68 ·t221edxdy 1122dxdy22所以re;2.注意:从上面的解题过程看,计算相当麻烦,下面给出一种简单的计算方法:解2 设Z,则Z~N(0,1)zzez22dz所以z2,2.分布,试证证1 令,,则X1,Y1仍相互独立且均服从N(0,1)24.设随机变量X与Y相互独立,且都服从于是从而·69·22y1221r2er2242r2edr4r2 2er22 dr所以r22,同理可证证2 X1,Y1如上所设,令~N(0,1) ,则Z~N(0,2) 利用23题的结果得由公式12·70 ·得25.(超几何分布的数学期望)设N件产品中有M件次品,从中任取n件进行检查,求查得的次品数X的数学期望.解设Xi第i次取到次品第i次取到正品.,则的分布为XiN1MN ,故注:(1)X的分布为,所以X的期望为,由上面的计算得MM),(2)若X表示n次有放回地抽取所得次品数,则X~B(n,此时,这与超几何分布的期望相同。
26.对三台仪器进行检验,各台仪器产生故障的概率分别为器的台数X的数学期望和方差。
·71· p1,p2,p3,求产生故障仪解1 X的分布为由此计算EX和DX相当麻繁,我们利用期望的性质进行计算。
设第i台仪器出现故障第i台仪器不出故障.的分布如下:Xi于是故;27.袋中有n张卡片,分别记有号码,从中有放回地抽取k张来,以X 表示所得号码之和,求EX,DX.,则解设Xi为第i张的号码,iXi的分布为XiP11n则,所以,28.将n只球(编号为随机地放入n只盒子(编号为1,2)中去,一只盒放一只球。
将一只球放入与球同号的盒子算作一个配对,记X为配对的个数,求EX. 解设Xi第i号球放入i号盒其他.则的分布为XinP1,nn11 n29.从10双不同的鞋子中任取8只,记X为这8只鞋子中成双的对数,求EX。
解即故X的分布为kXP012340.09150.4270.4000.080.0016730.已知,求及解31.设X,Y,Z为三个随机变量,且,,若求EW,DW. 22解·73·32.设X,Y,Z是三个两两不相关的随机变量,数学期望全为零,方差都是1,求和的相关系数.解与Y 所以的相关系数为.某箱装有100件产品,其中一、二和三等品分别为80,10和10件,现从中随机抽取一件,记若抽到i等品其他,试求:(1)随机变量X1与X2的联合分布;(2)随机变量X1与X2的相关系数. 解(1)(X1,X2)的分布所以X1,X2的相关系数为.设二维随机变量(X,Y)在矩形上服从均匀分布,记若若若若求:(1)U和V的联合分布;(2)U解(1)P(U和V的相关系数,4·74 ·,,33即(U,V)的概率分布为(2),,41611,,, 2 所以U,V的相关系数为.设X与Y为具有二阶矩的随机变量,且设使Q(a,b)达到最小值Qmin,并证明2Qmi22 解,,,求a,b解方程组得此时,[cov(X,Y)]2222 36.设随机变量X和Y在圆城上服从均匀分布,(1)求X 和Y的相关·75·系数;(2)问解X,Y是否独立?为什么?(X,Y)的密度为其他.(1)故的相关系数(2)关于X的边缘密度为关于Y的边缘密度的,所以X,Y不独立.37.设A,B是二随机事件,随机变量因为若A出现若B出现若B不出现若A不出现;A与B相互独立. 试证明随机变量X和Y不相关的充分必要条件是·76 ·[证] 若A,B独立,则X与Y独立,当然X与Y不相关,充分性得证,今证必要性设X与Y不相关,即EXYij因为,所以Y从而有故,,XA与B独立。
的概率密度为38.设随机变量不相关,也不独立,试证明X2与|X|(此乃因为是奇函数)所以,即X与|X|不相关。
今证X与|X|不独立,用反证法. 假定X与|X|独立,则对任意的正数a有证但而,所以出现矛盾,故X与|X|不独立。
39.设(X,Y)为二维正态变量,·77·,求(X,Y)的概率密度.31解(X,Y)的相关系数为,所以(X,Y)的密度为6240.设二维随机变量(X,Y)的密度函数为1,2其中和都是二维正态密度函数,且它们对应的二维随机变量的相关系数11分别为和,它们的边缘密度函数所对应的随机变量的数学期望都是零,方差都是1。
33(1)求随机变量X和Y的密度函数f1(x)和f2(y),及X和Y的相关系数(可以直接利用二维正态密度的性质)。
(2)问X,Y是否独立?为什么?解(1)2222,同理,因为,所以X和Y 的相关系数为1]dxdy2;·78 ·(2)因为(X,Y)的密度为12929222而边缘密度的乘积为所以2X,Y不独立.r41.设X为随机变量,存在,试证明:对任意有E|X|r.证若X为离散型,其概率分布为P(X则|xi|rE|x|ri|xi|r|ri12r2;若X为连续型,其概率密度为f(x),则|x|rE|x|r.42.若,利用切比雪夫不等式估计概率解由切比雪夫不等式DX0.004(0.2)20.0443.给定P(| 解,利用切比雪夫不等式估计。
