新人教版八年级数学上册总复习课件
合集下载
新人教版八年级数学上册课件:专题课堂3 有理数的混合运算 (共13张PPT)

a c 1 3 2-|-2|,求b d的值.
解:a=-1,b=-7,c=4,d=-1,
a c 则 =-1×(-1)-(-7)×4=29 b d
3.已知 a 是有理数,[a]表示不超过 a 的最大整数, 如[4.3]=4,[-1.6]=-2,[5]=5, 3 试计算:[-9.3]÷[6.9]÷[-97]×[-4.2]. 5 解:原式=-10÷6÷(-10)×(-5)=-6
类型三:有理数中的规律应用 4.(2017·日照)观察下面“品”字形中各数之间的规律, 根据观察到的规律得出 a 的值为(
B
)
A.23
B.75
C.77
D.139
5.(2017·岳阳)观察下列等式:21=2,22=4,23=8, 24=16,25=32,26=64,„,根据这个规律,则 21+22 +23+24+„+22017 的末位数字是( A.0 B.2 C.4
类型四:综合性问题 8.如图,一只蚂蚁从点 A 沿数轴向右爬了 2 个单位长度到达点 1 B,点 A 表示-12,设点 B 所表示的数为 m. (1)求 m 的值; (2)求|m-1|+(m-6)2 的值.
1 1 解:(1)m=-12+2=2 1 1 2 1 121 123 (2)|m-1|+(m-6) =|2-1|+(2-6) =2+ 4 = 4
请解答下列问题: (1)按以上规律列出第5个等式: a5=__________=____________;
1 +a1 1 (2)求a1+a1 2+a3+a4+… 100的值. 9×11 2×(9-11)
解:a1+a2+a3+a4+„+a100 1 1 1 1 1 1 1 1 =2×(1-3)+2×(3-5)+„+2×(199-201) 1 1 1 1 1 1 1 1 100 =2×(1-3+3-5+„+199-201)=2×(1-201)=201
解:a=-1,b=-7,c=4,d=-1,
a c 则 =-1×(-1)-(-7)×4=29 b d
3.已知 a 是有理数,[a]表示不超过 a 的最大整数, 如[4.3]=4,[-1.6]=-2,[5]=5, 3 试计算:[-9.3]÷[6.9]÷[-97]×[-4.2]. 5 解:原式=-10÷6÷(-10)×(-5)=-6
类型三:有理数中的规律应用 4.(2017·日照)观察下面“品”字形中各数之间的规律, 根据观察到的规律得出 a 的值为(
B
)
A.23
B.75
C.77
D.139
5.(2017·岳阳)观察下列等式:21=2,22=4,23=8, 24=16,25=32,26=64,„,根据这个规律,则 21+22 +23+24+„+22017 的末位数字是( A.0 B.2 C.4
类型四:综合性问题 8.如图,一只蚂蚁从点 A 沿数轴向右爬了 2 个单位长度到达点 1 B,点 A 表示-12,设点 B 所表示的数为 m. (1)求 m 的值; (2)求|m-1|+(m-6)2 的值.
1 1 解:(1)m=-12+2=2 1 1 2 1 121 123 (2)|m-1|+(m-6) =|2-1|+(2-6) =2+ 4 = 4
请解答下列问题: (1)按以上规律列出第5个等式: a5=__________=____________;
1 +a1 1 (2)求a1+a1 2+a3+a4+… 100的值. 9×11 2×(9-11)
解:a1+a2+a3+a4+„+a100 1 1 1 1 1 1 1 1 =2×(1-3)+2×(3-5)+„+2×(199-201) 1 1 1 1 1 1 1 1 100 =2×(1-3+3-5+„+199-201)=2×(1-201)=201
新人教版初中数学八年级上册全册精品课件(分章分课时来整理)-56.ppt

需要更完整的资源请到 新世纪教 育网 -
八年级 数学
第十一章 函数 一元函数与二元一次方程组
11.3用函数观点看方程(组)与不等式
练习
市内通话问题
全球通:月租费50元,0.4元/分 神州行:0.6元/分
如何选择计费方式更省钱?
需要更完整的资源请到 新世纪教 育网 -
需要更完整的资源请到 新世纪教 育网 -
八年级 数学
第十一章 函数 一元函数与二元一次方程组
11.3用函数观点看方程(组)与不等式
需要更完整的资源请到 新世纪教 育网 -
八年级 数学
第十一章 函数 一元函数与二元一次方程组
11.3用函数观点看方程(组)与不等式
11.3用函数观点看方程(组)与不等式
作业: P46页第6题、第9题
需要更完整的资源请到 新世纪教 育网 -
是方程组_______的解( D ) •
y 3x 6 A. 2 y x 4
x a 1.如果直线y=3x+6与y=2x-4交点坐标为(a,b),则 y b
( 11,4) .• y=-x+15和y=x-7的交点坐标是 ________ 7.已知函数y=mx-(4m-3)的图象过原点,则m 3 应取值为__________ . 4 8.直线y=2x-1与y=x+4的交点是(5,9),则当 >5 x_______ 时,直线y=2x-1• 上的点在直线y=x+4上 相应点的上方;当x_______ <5 时,直线y=2x-1上的 点在直线y=x+4上相应点的下方.
八年级 数学
第十一章 函数 一元函数与二元一次方程组
11.3用函数观点看方程(组)与不等式
最新人教版八年级数学上册《第十四章章末复习》课件

2 2 2 2 x 4 xy ( x 4 xy 4 y ) 法一:原式
2 x 2 4 xy x 2 4 xy 4 y 2 x 2 4 y 2
法二:原式 ( x 2 y ) 2 x ( x 2 y )
( x 2 y )( x 2 y ) x 2 4 y 2
0
(2)9x³-18x²+9x (4)(2a-b)²+8ab
《整式的乘法与因式分解》章末检测
0
【思路点拨】根据幂的运算性质,运用法则逐一判断. 【解题过程】 A是合并同类项,正确答案为2x; B是幂的乘方,底数不变指数相乘,正确答案为x6; C是积的乘方,正确答案为4x²;D正确
0
探究一:探索因式分解的方法——完全平方公式 例2
2 2 x ( x 2 y ) ( x 2 y ) 先化简,再求值: ,其中x=2,y=-1.
当x=2,y=-1时,x²-4y²=2²-4×(-1)²=4-4=0;
0
探究一:探索因式分解的方法——完全平方公式 例3 因式分解: (1)ab²-ac² (3)16x4-1 【解题过程】 (1)原式= a(b²-c²)= a(b+c)(b-c) (2)原式=9x(x2-2x+1)= 9x(x-1)2 (3)原式=(4x2+1)(4x2-1)=(4x2+1)(2x+1)(2x-1) (4)原式=4a²-4ab+b²+8ab= 4a²+4ab+b²=(2a+b)²
【思路点拨】 整式的化简求值通常利用整式乘法法则、乘法公式 进行运算后,再代值计算,有时也可以利用因式分解化 简整式,再代入求值.
0
探究一:探索因式分解的方法——完全平方公式 例2
2 x 2 4 xy x 2 4 xy 4 y 2 x 2 4 y 2
法二:原式 ( x 2 y ) 2 x ( x 2 y )
( x 2 y )( x 2 y ) x 2 4 y 2
0
(2)9x³-18x²+9x (4)(2a-b)²+8ab
《整式的乘法与因式分解》章末检测
0
【思路点拨】根据幂的运算性质,运用法则逐一判断. 【解题过程】 A是合并同类项,正确答案为2x; B是幂的乘方,底数不变指数相乘,正确答案为x6; C是积的乘方,正确答案为4x²;D正确
0
探究一:探索因式分解的方法——完全平方公式 例2
2 2 x ( x 2 y ) ( x 2 y ) 先化简,再求值: ,其中x=2,y=-1.
当x=2,y=-1时,x²-4y²=2²-4×(-1)²=4-4=0;
0
探究一:探索因式分解的方法——完全平方公式 例3 因式分解: (1)ab²-ac² (3)16x4-1 【解题过程】 (1)原式= a(b²-c²)= a(b+c)(b-c) (2)原式=9x(x2-2x+1)= 9x(x-1)2 (3)原式=(4x2+1)(4x2-1)=(4x2+1)(2x+1)(2x-1) (4)原式=4a²-4ab+b²+8ab= 4a²+4ab+b²=(2a+b)²
【思路点拨】 整式的化简求值通常利用整式乘法法则、乘法公式 进行运算后,再代值计算,有时也可以利用因式分解化 简整式,再代入求值.
0
探究一:探索因式分解的方法——完全平方公式 例2
人教版八年级数学上册课件:14章 整式的乘法与因式分解--知识点复习 (共53张PPT)
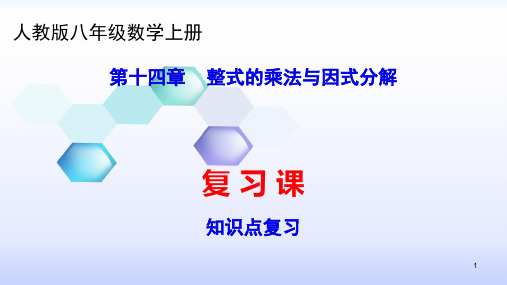
A.(6a3+3a2)÷
1 2
a=12a2+6a
B.(6a3-4a2+2a)÷2a=3a2-2a
C.(9a7-3a3)÷(﹣
1 3
a3)=﹣27a4+9
C.( 14a2+a)÷(﹣12a)=﹣12 a-2
5.一个多项式与﹣2x2的积为﹣2x5+4x3﹣x2,则这个多项式
为
.
6.计算:⑴
(9x2y-6xy2)÷3xy;
2.已知M= a-1,N=a2- a(a为任意实数),则M,N的
大小关系为( A ) A. M<N B. M=N C. M>N D.不能确定
3.若x2+y2+ =2x+y,则y-x= .
3、am﹣n=am ÷ an(a≠0,m,n都
是正整数,并且m>n).
10
知识点一:幂的运算性质
巩固练习
1.(易错题)若(1-x)1-3x=1,则x的取值有( C )个.
A.0 B.1 C.2 D.3 4
2.若3x=4,9y=7,则3x-2y的值为 7 . 3.已知am=3,an=2,则a2m-n的值为 4.5 .
为( B ) A M<N
B M>N
C M=N D.不能确定
10.计算:(1)(x+1)(x+4); (2)(y-5)(y-6); (3)(m-3)(m+4)
(x+p)(x+q)
18
知识点二:整式的运算
知识回顾
单项式的除法法则: 系数、同底数幂分别相除 只在被除式里含有的字母
19Βιβλιοθήκη 知识点二:整式的运算2
重点难点
重点:运用整式的乘法法则和除法法则进行运算;因式分 解. 难点:应用整式的乘法和因式分解决问题.
人教版初中八年级上册数学-期末复习 第12章全等三角形 课件(共48张PPT)
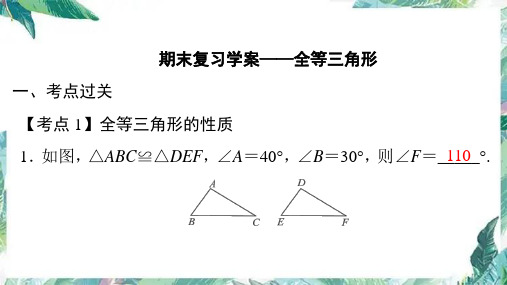
的依据是_H__L_.
第3题
4.如图,AO=BO,下列条件不能判定△AOD≌△BOC 的是( B )
A.OC=OD C. ∠A=∠B
第4题 B.AD=BC D.∠C=∠D
【考点 3】角平分线的性质和判定 5.如图,在△ABC 中,∠C=90°,AD 平分∠BAC,AB=6,CD
=2,则点 D 到 AB 的距离是_2_,△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A=∠D, 从而 AB∥DE.
10.如图,在△ABC 和△DEF 中,下面有四个条件,请你在其中 选 3 个作为题设,余下的 1 个作为结论,写一个真命题,并加 以证明. ① AB=DE;②AC=DF;③∠ABC=∠DEF;④BE =CF.
题设:①③④;结论:② 证明提示:BC=BE+EC=CF+EC=EF. 用 SAS 证明△ABC≌△DEF,从而 AC=DF.
证明:(1)如图,连接 AF, ∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE, ∵∠ACB=∠AEF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF, ∴CF=EF.∴BF+EF=BF+CF=BC, ∴BF+EF=DE;
(2)如图,DE=BF-EF,理由是: 连接 AF,∵Rt△ABC≌Rt△ADE, ∴AC=AE,BC=DE, ∵∠E=∠ACF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF,∴CF=EF, ∴DE=BC=BF-FC=BF-EF,即 DE=BF-EF.
24.已知 Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°. (1)将这两个三角形按图①方式摆放,使点 E 落在 AB 上,DE 的延长线交 BC 于点 F.求证:BE+EF=DE; (2)改变△ADE 的位置,使 DE 交 BC 的延长线于点 F(如图②), 写出此时 BF、EF 与 DE 之间的等量关系,并说明理由.
第3题
4.如图,AO=BO,下列条件不能判定△AOD≌△BOC 的是( B )
A.OC=OD C. ∠A=∠B
第4题 B.AD=BC D.∠C=∠D
【考点 3】角平分线的性质和判定 5.如图,在△ABC 中,∠C=90°,AD 平分∠BAC,AB=6,CD
=2,则点 D 到 AB 的距离是_2_,△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A=∠D, 从而 AB∥DE.
10.如图,在△ABC 和△DEF 中,下面有四个条件,请你在其中 选 3 个作为题设,余下的 1 个作为结论,写一个真命题,并加 以证明. ① AB=DE;②AC=DF;③∠ABC=∠DEF;④BE =CF.
题设:①③④;结论:② 证明提示:BC=BE+EC=CF+EC=EF. 用 SAS 证明△ABC≌△DEF,从而 AC=DF.
证明:(1)如图,连接 AF, ∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE, ∵∠ACB=∠AEF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF, ∴CF=EF.∴BF+EF=BF+CF=BC, ∴BF+EF=DE;
(2)如图,DE=BF-EF,理由是: 连接 AF,∵Rt△ABC≌Rt△ADE, ∴AC=AE,BC=DE, ∵∠E=∠ACF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF,∴CF=EF, ∴DE=BC=BF-FC=BF-EF,即 DE=BF-EF.
24.已知 Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°. (1)将这两个三角形按图①方式摆放,使点 E 落在 AB 上,DE 的延长线交 BC 于点 F.求证:BE+EF=DE; (2)改变△ADE 的位置,使 DE 交 BC 的延长线于点 F(如图②), 写出此时 BF、EF 与 DE 之间的等量关系,并说明理由.
人教版八年级数学上册整式的乘法与因式分解《乘法公式:平方差公式》示范教学课件

相反数 相同
平方差
(a+b)(a-b)=a2-b2.
平方差公式的特征:
两个数的和 这两个数的差 这两数的平方差
1.左边是两个二项式相乘,并且这两个二项式中有一项完全相同,
另一项互为相反数.
2.右边是乘式中两项的平方差(相同项的平方减去相反项的平方)
3.公式中的a,b既可代表具体的数,还可代表单项式或多项式.
解:原式=4x2-y2-(4y2-x2) =4x2-y2-4y2+x2 =5x2-5y2.
当x=1,y=3时, 原式=5×12-5×32=-40.
课堂小结 平方差公式: (a+b)(a-b)=a2-b2. 即:两数和与这两数差的积等于这两个数的平方差. 平方差公式的逆用: a2-b2 = (a+b)(a-b)
互动新授
(a+b)(a-b)= a2-ab+ab-b2= a2-b2 . 平方差公式: (a+b)(a-b)=a2-b2.
即:两个数的和与这两个数的差的积,等于这两个 数的平方差.
公式变形: 1.(a-b)(a+b)=a2-b2 2.(b+a)(-b+a )=a2-b2
归纳总结 平方差公式的特征:
= y2-22-y2-5y+y+5 =-4y+1
(2) 102×98 000-4 =9996
小试牛刀
1.下列多项式乘法中,能用平方差公式计算的是
( (2)(5)(6) ) (1)(x+1)(1+x);
(2)(a+b)(b-a);
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
归纳总结 填一填:
人教版数学八年级上册第十二章 全等三角形复习课件-课件
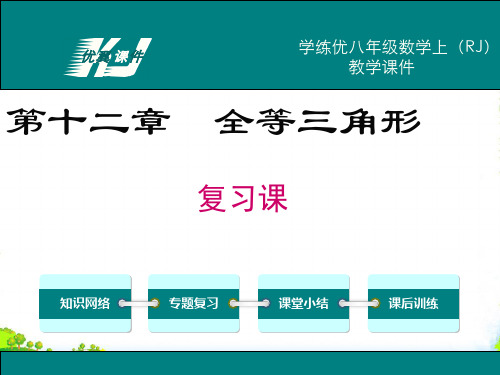
求证: ∠ABC=∠DCB.
A
D
B
C
【证明】 取AD,BC的中点N,M,
连接BN,CN,MN,则有AN=DN,BM=CM.
A ND
在△ABN和△DCN中,
AN=DN,
∠A= ∠D, AB=CD,
B
C
M
∴ △ABN ≌ △DCN(SAS).∴ ∠ABN = ∠ DCN, NB=NC.
在△NBM和△NCM中,
•
【证明】 ∵CE⊥AD, ∴ ∠AGE=∠AGC=90 °.
在△AGE和△AGC中,
∠AGE=∠AGC, AG=AG, ∠EAG=∠CAG, ∴ △AGE ≌ △AGC(ASA), ∴ GE =GC. 在△DGE和△DGC中,
D
C
EG=CG, ∠ EGD= ∠ CGD=90 °,
DG=DG. ∴ △DGE ≌ △DGC(SAS). ∴ ∠DEG = ∠ DCG.
【证明】 ∵AO平分∠BAC,CD⊥AB于点D,
A
BE⊥AC于点E, ∴OD=OE, ∠ODB=
∠OEC=90 °. 在△BOD和△COE中, ∠ODB= ∠OEC=90 °,
D
E
O
OD=OE, ∠DOB= ∠EOC,
B
C
∴ △BOD ≌ △COE(ASA),∴OB=OC.
专题二 证明角相等
【例2】如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交
判 定 一般三角形 SSS,SAS,ASA,AAS
直角三角形 除上述判定方法之外,还
有“HL”
角平分线的性质定理
角平分线的判定定理
专题复习
专题一 证明线段相等
【例1】如图,点D、E分别在线段AB、AC上,已知AD=AE, ∠B= ∠C,H为线段BE、CD的交点,求证:BH=CH.
人教版八年级数学上册 12.2 复习小专题(二)构造全等三角形常见辅助线的添法 课件(共20张

9
知识点二:利用“截补法”构造全等三角形
归纳总结
不管是截长法还是补短法,往往都需要连接 其他线段,构造全等三角形,利用全等三角形的性 质解决问题.
10
知识点三:利用“倍长中线法”构造全等三角形
典例分析
例3:如图,在△ABC中,AD是BC边上的中线,
求证:AD< (AB+AC)
A
通过添加辅助线,构造全等三角形,将
AD AB ,AC转化到同一个三角形中来求解. B D
C
E
11
知识点三:利用“倍长中线法”构造全等三角形
典例分析
A
例3:如图,在△ABC中,AD是BC边上的中线,
求证:AD< (AB+AC)
B
2
DC
证明:延长AD至点E,使得DE = AD,连接BE.
E
∵AD是BC边上的中线, ∴点D为BC的中点,∴BD=CD.
∴∠F=∠4.
6
知识点二:利用“截补法”构造全等三角形
大显身手
1.如图,AD为△ABC的角平分线,AB >AC,
A
求证:AB﹣AC> BD﹣DC.
E
B
DC
7
知识点二:利用“截补法”构造全等三角形
大显身手
2.如图,在△ABC中, B=2∠C,AD是BC边上的高.
求证:CD=AB+BD.
A
∟
E
BD
C
B
从结论出发,把较长的线段AB截成与 AC,BD分别相等的两条线段,或延长较短的线段AC, 使延长后的线段的长等于线段AB的长,再利用三角 形全等即可证明.
4
知识点二:
解:如图,在线段AB上截取AF=AC连接EF C ∵AE,BE分别平分∠CAB和∠DBA
知识点二:利用“截补法”构造全等三角形
归纳总结
不管是截长法还是补短法,往往都需要连接 其他线段,构造全等三角形,利用全等三角形的性 质解决问题.
10
知识点三:利用“倍长中线法”构造全等三角形
典例分析
例3:如图,在△ABC中,AD是BC边上的中线,
求证:AD< (AB+AC)
A
通过添加辅助线,构造全等三角形,将
AD AB ,AC转化到同一个三角形中来求解. B D
C
E
11
知识点三:利用“倍长中线法”构造全等三角形
典例分析
A
例3:如图,在△ABC中,AD是BC边上的中线,
求证:AD< (AB+AC)
B
2
DC
证明:延长AD至点E,使得DE = AD,连接BE.
E
∵AD是BC边上的中线, ∴点D为BC的中点,∴BD=CD.
∴∠F=∠4.
6
知识点二:利用“截补法”构造全等三角形
大显身手
1.如图,AD为△ABC的角平分线,AB >AC,
A
求证:AB﹣AC> BD﹣DC.
E
B
DC
7
知识点二:利用“截补法”构造全等三角形
大显身手
2.如图,在△ABC中, B=2∠C,AD是BC边上的高.
求证:CD=AB+BD.
A
∟
E
BD
C
B
从结论出发,把较长的线段AB截成与 AC,BD分别相等的两条线段,或延长较短的线段AC, 使延长后的线段的长等于线段AB的长,再利用三角 形全等即可证明.
4
知识点二:
解:如图,在线段AB上截取AF=AC连接EF C ∵AE,BE分别平分∠CAB和∠DBA
