极大极小法
高等数学-第七版-课件-3-6 函数的极值与最大值最小值

o
x
定义 设函数f(x)在点x0的某邻域U(x0)内有定义, 如果对于去心邻域U0(x0)内的任一x,有 y f(x)<f(x0)(或f(x)>f(x0)) 称f(x0)为函数f(x)的一个极大值(极小值) 函数的极大值与极小值统称为函数的极值, 使函数取得极值的点称为极值点 注 极值是一个局部的概念
海岸位于A点南侧40km,是一条东西走向的笔直长堤. 演习中部队先从A出发陆上行军到达海堤,再从海堤处乘舰艇 到达海岛B. 已知陆上行军速度为每小时36km,舰艇速度为
每小时12km.问演习部队在海堤的何处乘舰艇才能使登岛用 y 时最少? 分析 陆上行军耗时 o 海上行军耗时 A
(0,40)
? R(x,0) B
x
(140,-60)
三、最大值最小值问题
(一)最大值最小值求法
(二)最值应用问题
三、最大值最小值问题
(一)最大值最小值求法
(二)最值应用问题
例4 从边长为a的一张正方形薄铁皮的四角切去 边长为x的四个小正方形,折转四边,作一 个盒子,问x为何值时盒子的容积最大?
例5 某企业以钢材为主要生产材料。设该厂每天的钢材需求量为 R吨,每次订货费为C1元,每天每吨钢材的存贮费为C2元 (其中R、 C1、 C2为常数),并设当存贮量降为零时,能 立即得到补充(在一个订货周期内每天的平均存贮量为订货 量的二分之一)求一个最佳的订货周期,使每天的平均费用 最小? q(t) Q o T C C0
o
x
定义 设函数f(x)在区间I上有定义,如果存在x0∈I,使得对于区间I内 的任一x,有 f(x)≤f(x0)(或f(x)≥f(x0)),则称f(x0)为函数f(x) 在区间I上的最大值(或最小值).
投资组合选择极大极小模型的方程组法

投资组合选择极大极小模型 的方程组法
引、 杰 ( 海理工大学 世 上 管理学院)
摘要: 以极大极小投资组合选择原理 , 建立 了完美市场下的一种新 的极 用 文 献【】 【】 2和 3中的 K T最 优性 条件 , ( ) 可 转化 为 { P 问题 大极小投资组合选择模型。着重讨论了极大极小模型 的方程组法, 利用非光
s 一 X + ta ∑ ∑ [x m E ( " t
一Leabharlann 1 0 : s ( ,= l : ) 、
《, P)
Ii x mi la n
, +
’∑
1
x
t
∑xt —i …
该模型等价于 ( P) 之
( 4 P ) 的解 ,f 贝 转 化 为 l 4 P ) 光 滑 方程 组 (
.
1 = 【 t 12 1 l 二 .. _
, ( 三 } . 、 『, )/ -
i
0
o 7 1二 . 二 . . .7 1
根 据 【】 知道 5我们
O l x ( ) ox fx‘x=Ix ) c( aC ) l m x =cn{ i) () I fx} ’ , (I V 1 ( a
非线性互补问题
(
w
~
_ } ( _』 二 }
‘
中 图分 类 号 :8 0 5 : 2 F 3 .4 02 4 文 献标 识 码 : A
0 引 言
Makwi ro t 1 5 z于 9 2年发表 了著名 的论文 “ otoo S l — P r l ee fi c t n, i ” o 标志着华尔街第一次数学 革命的开始. 该论文创立的均值 一方 差证券组合投资模 型, 了现代投资理论 的基础 , 奠定 该模型是用均值 来度量投资组合 的收益, 方差来度量风 险, 用 前提是假设资产 的收 益符合正态分布。然而 , 资产的实际收益并 不一定符合正态分布 , 投 资者对风险的理解也不同 ,有些人认为收益的不确定性就是风险 , 也有人认为只有当未来的收益低于预期收益时 才存在风险 , 因此人
函数的极值与最大值最小值

x1 x2 x3 x4 x5
定理1(必要条件) 设函数f(x)在点x0处可导, 且在x0处取得极值, 那么f ′(x0)=0. •驻点 使导数f ′(x)为零的点(方程f ′(x)=0的实根)称为函数 f(x)的驻点. 观察与思考: (1) 观察曲线的升降与极值
x1 x2
x3 x4 x5
定理2(第一充分条件)
设函数f(x)在x0处连续, 且在(a, x0)∪(x0, b)内可导. (1)如果在(a, x0)内f ′(x)>0, 在(x0, b)内f ′(x)<0, 那么函数f(x) 在x0处取得极大值; (2)如果在(a, x0)内f ′(x)<0, 在(x0, b)内f ′(x)>0, 那么函数f(x) 在x0处取得极小值; (3)如果在(a, x0)及(x0, b)内 f ′(x)的符号相同, 那么函数f(x) 在x0处没有极值.
1 2 所以当b= d 时, 抗弯截面模量 W 最大, 这时 h = d . 3 3
讨论:
函数f(x)=x4, g(x)=x3在点x=0是否有极值? >>>
例2 求函数f(x)=(x2−1)3+1的极值. 解 f ′(x)=6x(x2−1)2. 令f ′(x)=0, 求得驻点x1=−1, x2=0, x3=1. f ′′(x)=6(x2−1)(5x2−1). 因为f ′′(0)=6>0, 所以f (x)在x=0处取得极小值, 极小值为f(0)=0. 因为f ′′(−1)=f ′′(1)=0, 所以用定理3无法判别. 因为在−1的左右邻域内f ′(x)<0, 所以f(x)在−1处没有极值. 同理, f(x)在1处也没有极值.
求极值的三种方法
求极值的三种方法一、直接法。
先判断函数的单调性,若函数在定义域内为单调函数,则最大值为极大值,最小值为极小值二、导数法(1)、求导数f'(x);(2)、求方程f'(x)=0的根;(3)、检查f'(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
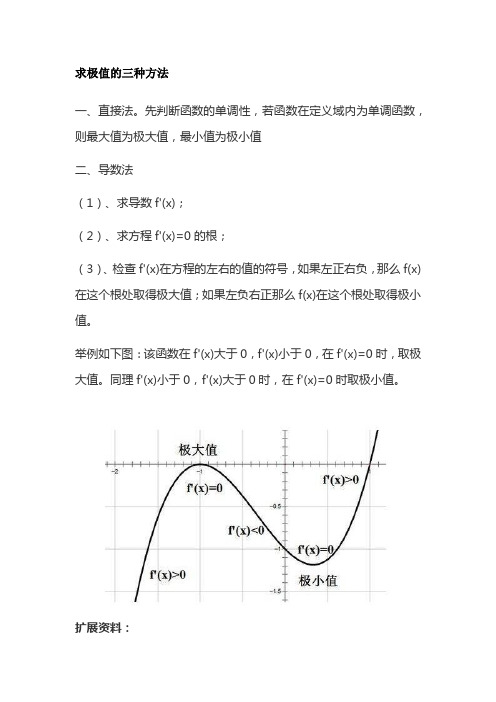
举例如下图:该函数在f'(x)大于0,f'(x)小于0,在f'(x)=0时,取极大值。
同理f'(x)小于0,f'(x)大于0时,在f'(x)=0时取极小值。
扩展资料:寻求函数整个定义域上的最大值和最小值是数学优化的目标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最大值和最小值。
此外,整个定义域上最大值(或最小值)必须是域内部的局部最大值(或最小值),或必须位于域的边界上。
因此,寻找整个定义域上最大值(或最小值)的方法是查看内部的所有局部最大值(或最小值),并且还查看边界上的点的最大值(或最小值),并且取最大值或最小的)一个。
1、求极大极小值步骤:求导数f'(x);求方程f'(x)=0的根;检查f'(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
f'(x)无意义的点也要讨论。
即可先求出f'(x)=0的根和f'(x)无意义的点,再按定义去判别。
2、求极值点步骤:求出f'(x)=0,f"(x)≠0的x值;用极值的定义(半径无限小的邻域f(x)值比该点都小或都大的点为极值点),讨论f(x)的间断点。
上述所有点的集合即为极值点集合。
扩展资料:定义:若函数f(x)在x₀的一个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x₀),则称f(x₀)是函数f(x)的一个极大值。
摩擦市场投资组合选择的极大极小方法

Ab ta t sr c .A e p rfl ee t nmo e i p o o e n t eb s fan w rfl ee t nt e r , n w o toi slci d l s r p sdo h a i o e p toi slci h o y o o s o o o
Ke od : ss m pr sw?n e to y y w r s yt .o t a i e mi o ot l e ci f o l o nma rbe Y c tr nrp ; t i ̄ a
t a a to o t r ns c i n c s
Z Qa-u G O Y n i y . A a n
( ol e fMa a e e t nvri h n h i o Si c n e nl y t nh i 0 0 3,Cz a C l g e o ngm n ,U iesyo a ga f r c ne dT c o g ,S ̄ ga 2 0 9 t fS e a h o z ln ) i
尽管如此 , 出新 的更加有 效的模 型仍 然是 一个 提
即构成投资组合 . 现代投资组合理论是 19 年 由诺 90
贝尔经济学奖得主马柯维茨( ro i ) 2 世纪 Makw t 于 0 z 5 年代创 立的 , 由他发 表 的“ 资组合 的选择 ” 0 即 投 (ot l e co ) P ro o l t n 论文奠定 了现代投资组合理论 fiS e i 基础. 自从这一投资组合选择的均值一 方差理论被创
文章编号 :0 7 7 5 2 0 ) 1 0 7 4 10 —6 3 (0 6 0 —0 2 —0
摩 擦 市 场 投 资 组 合选 择 的极 大极 小 方 法
张乾 宇, 高 岩
机械优化设计PPT

二、离散变量优化的主要方法及其特点、思路和步骤
表7-3 离散变量优化的主要方法及其特点和步骤
图7-8 两个目标函数的等值线和约束边界
三、协调曲线法
图7-9 协调曲线
四、分层序列法及宽容分层序列法
四、分层序列法及宽容分层序列法
采用分层序列法,在求解过程中可能会出现中断现象,使求解过程 无法继续进行下去。当求解到第k个目标函数的最优解是惟一时, 则再往后求第(k+1),(k+2),…,l个目标函数的解就完全没有意义 了。这时可供选用的设计方案只是这一个,而它仅仅是由第一个至 第k个目标函数通过分层序列求得的,没有把第k个以后的目标函数 考虑进去。尤其是当求得的第一个目标函数的最优解是唯一时,则 更失去了多目标优化的意义了。为此引入“宽容分层序列法”。这 种方法就是对各目标函数的最优值放宽要求,可以事先对各目标函 数的最优值取给定的宽容量,即ε1>0,ε2>0,…。这样,在求后一 个目标函数的最优值时,对前一目标函数不严格限制在最优解内, 而是在前一些目标函数最优值附近的某一范围内进行优化,因而避 免了计算过程的中断。
5.组合型算法终止准则
6.组合型算法的辅助功能
(1) 直线加速与二次曲线加速 当目标函数严重非线性时,即若
函数具有尖峰脊线,即存在“谷”时,则希望能沿着脊线方向进 行搜索,可迅速提高算法的寻优效率,该算法称为具有脊线加速 能力。 (2) 网格搜索法技术 将离散空间视为一网格空间,每个离散点 就是一个网格节点。 (3) 变量分解策略 将目标函数中的变量分成若干个子集合,若
离散复合形,重新进行调优搜索,直到前后两次离散复合形运算
的优化点重合,算法才最终结束。
6.组合型算法的辅助功能
图7-24 有脊线目标函数 寻优过程示意图
极值判断方法

极值判断方法是一种用于确定函数的最大值和最小值的数学方法。
以下是两种常见的极值判断方法:
1. 导数法(一阶导数法):该方法基于函数在极值点处的导数为零的性质。
首先,求函数的导数,并找出导数为零的点,这些点可能是函数的极值点。
然后,通过求取导数的二阶导数来确定这些点的极值类型。
若二阶导数为正,则该点为函数的极小值点;若二阶导数为负,则该点为函数的极大值点。
2. 边界点法:该方法适用于在给定的闭区间内寻找函数的最大值和最小值。
首先,计算函数在区间的端点处的函数值,然后计算函数在区间内的临界点处的函数值。
最后,比较所有这些函数值,找出最大值和最小值。
这个方法适用于函数在闭区间上是连续的情况。
需要注意的是,极值判断方法可以用于一元函数和多元函数。
在多元函数的情况下,需要对每个自变量求偏导数,并解出偏导数为零的方程组,以确定极值点。
这些方法是常用的极值判断方法,但在具体应用时还需要考虑函数的性质和特点,并结合具体问题进行分析和判断。
高中物理求极值方法与常用结论总结

高中物理求极值方法与常用结论总结高中物理中,求极值是一个重要的数学应用问题。
很多物理问题都需要通过求极值来进行分析和解决,因此掌握求极值方法和常用结论是十分重要的。
下面将为你总结高中物理求极值的方法和常用结论。
一、求极值的方法1.寻找最值法:通过寻找物理问题的最大值或最小值来求出极值。
2.解析法:通过建立数学模型,对其求导或使用其他数学方法得出极值。
3.几何方法:通过几何图形的性质和分析来求出极值。
二、常用结论1.极大值与极小值:对于一元函数f(x),若在x=a处,f'(a)=0,并且在a点左侧由正变负,在a点右侧由负变正,则a称为f(x)的极大值点;若在x=b处,f'(b)=0,并且在b点左侧由负变正,在b点右侧由正变负,则b称为f(x)的极小值点。
2.拐点与拐点性质:对于函数f(x),若在x=c处f''(c)=0,并且在c点左侧由负变正,在c点右侧由正变负,则c称为f(x)的拐点。
拐点的性质为:由凹变凸的拐点称为极小值点,由凸变凹的拐点称为极大值点。
3.一元二次函数的最值结论:一元二次函数y=ax^2+bx+c(其中a≠0)的最值点可以通过如下结论求得:当a>0时,最小值为:y_min=c-b^2/(4a)当a<0时,最大值为:y_max=c-b^2/(4a)4.相对速度最小值结论:当两个运动着的物体相对于一些静止参考系运动时,它们的相对速度最小值出现在它们的运动方向夹角为0°或者180°时。
5.成千上万法:在解决物理问题中,当数据较多时,可以通过逐个数值代入进行计算。
6.速度为零但加速度不为零时的移动物体:当一个物体在其中一时刻速度为零(静止),但加速度不为零时,可以通过如下结论求出物体在这一时刻的位置:位移s = (1/2)at^2,其中a为加速度,t为时间。
7.物体自由落体的最高点:自由落体的物体在竖直上抛运动中,最高点时速度为零,也就是物体停止上升,准备掉下来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、建立目标函数 由于优化设计中存在四个目标函数, 属于多目标优化 问题。 运用多目标优化问题中的 “统一目标法中的极大 极小法”,该方法的主要思想是考虑对各个目标最不利情 况来表示各个目标函数重要程度。 建立总体目标式独立悬架 极大极小法的优化研究
简介:
在给定工况下,车轮定位参数和轮 距都会相应地发生改变,若变化量太大, 会导致轮胎的严重磨损。采用统一目标 法中极大极小法对前轮定位参数进行了 优化分析 , 优化结果表明取得了良好的 优化结果,进一步改善悬架运动学性能。
优化计算步骤:
3 、确定约束条件
根据独立悬架导向机构的设计空间布置的要求,可以确定如下约束条件: 上横臂外点:
下横臂外点:
转向节内点:
minKnuckle_ inner_ x Knuckle_ inner_ y max Knuckle_ inner_ x
minKnuckle_ inner _ x Knuckle_ inner _ y max Knuckle_ inner _ y minKnuckle_ inner_ x Knuckle_ inner_ y max Knuckle_ inner_ z
4、优化分析计算
选取三个硬点共 9 个坐标值作为优化变量,进行计算分析
将优化后的硬点坐标值替代原模型中的相应硬 点值,再次进行仿真分析可得出优化效果良好,能 够进一步改善悬架运动学性能。
min U(f(x)) min max {Wifi ( x)}
xD xD 1i 4
W i 为加权系数, W i 的数值根据各目标重要程度确定。 参 考《汽车工程手册》上的推荐值, 综合权衡后确定各车轮定 位参数加权因子分别是主销内倾角为 4 ,主销后倾角为 11 , 前轮外倾角为 4 ,前轮前束为 25 。 即所求目标函数为: minU(f(x))=4×f 1 +11×f 2 +4×f 3 +11×f 4 其中 (f 1 , f 2 , f 3 , f 4 ) 分别为相应加权系数的对应定位 参数。
极大极小法
---唐成吉
对于多目标函数最优化问题,考虑对各个目标
最不利情况下求出最有利的解。就是对多目标极小
化问题采用各个目标fi(i=1,2,3,4…l)中的最大
值作为评价函数。
对各目标函数作出极大值选择后,再在可 行域内进行极小化,故称为极大极法。
即 minU f ( X ) minmax fi ( X ) 或 minU f ( X ) minmax Wi fi ( X ) 或 min s.t. Wi fi ( X )
