结构力学6静定结构位移计算
合集下载
静定结构的位移计算
第4章
二、单位荷载法
1、定义：应用虚力原理，通过加单位力求实际位移的方法。 2、计算结构位移的一般公式
PK=1 RK
1
RK RK3
2
( a , a , a , Ca )
位移状态
RK
4
(M K ,Q K , N K , RK )
虚力状态
对上述两种状态应用虚功原理：
1 Ka R K 1 C a1 R K 2 C a 2 M K a ds Q K a ds N K a ds
P/2
P/2
c
c
CV
4、结构的动力计算和稳定分析中，都常需计算结 构的位移。
第4章
三、计算位移的有关假定
2、小变形假设。变形前后荷载作用位臵不变。 3、结构各部分之间为理想联结，不计摩擦阻力。 4、当杆件同时承受轴力与横向力作用时， 不考虑由于杆 弯曲所引起的杆端轴力对弯矩及弯曲变形的影响。
ω1
ω2
MP图
1 Δ (ω1 y1 ω2 y2 ) EI
第4章
3、当杆件为变截面时亦应分段计算； y1
EI1
y2
EI 2
MK图
ω1
EI1
ω2
EI 2
MP图
1 1 Δ ω1 y1 ω2 y2 EI1 EI 2
第4章
4、图乘有正负之分：弯矩图在杆轴线同侧时，取正号； 异侧时，取负号。
13860 0.0924m( ) EI
第4章
例题 试求左图所示刚架C点的竖向位移AV和转角C。 EI 1.5 105 KN m 2 各杆材料相同，截面抗弯模量为:
MB A
力状态(状态1)
结构力学 静定结构的位移计算
情景一 引起结构位移的原因及位移计算的目的
能力拓展 如图 2 – 61a 所示屋架，通过对比左右两图，运用结构位移的相关知识 ，可以解释制作时为何通常将各下弦杆的实际下料长度做得比设计长度
要短些，这样可以使屋架拼装后，结点 C 位于 C′的位置（图 2 – 61b）
， 工程上将这种做法称为建筑起拱。那么预先应知道哪些位移量？
情景二 虚功原理及单位荷载法
项目表述
静定结构位移计算是演算结构刚度和计算超静定结构所必需的。变形 体虚功原理是结构力学中的重要理论。通过本项目学习，同学们重点理 解变形体的虚功原理、单位荷载法及位移计算一般公式。对变形体的虚 功原理的推导过程的理解是本项目的难点内容。
情景二 虚功原理及单位荷载法 学习进程
情景一 引起结构位移的原因及位移计算的目的 知识链接
情景一 引起结构位移的原因及位移计算的目的
知识链接
2．引起位移的原因 众所周知，引起位移的原因主要是荷载作用。除此之外，温度改变使材料膨胀 或收缩、结构构件的尺寸在制造过程中产生误差、基础的沉陷或结构支座产生 移动等因素，均会引起结构的位移。如图 2 – 56a、图 2 – 57a 所示，由荷载作 用产生的位移。如图 2 – 57b 所示，因温度改变或材料胀缩产生的位移。如图 2 – 57c 所示，因制造误差或支座移动产生的位移。
情景一 引起结构位移的原因及位移计算的目的
知识链接
1．结构位移的概念 建筑结构在施工和使用过程中常会发生变形，由于结构变形，其上各点或截面 位置会发生改变，这称为结构的位移。如图 2 – 56a 所示的刚架，在荷载作用 下，结构产生变形如图中虚线所示，使截面的形心 A 点沿某一方向移到 A′点， 线段 AA′称为 A 点的线位移，一般用符号 ΔA 表示。 它也可用竖向线位移 ΔAy 和水平线位移 ΔAx 两个位移分量来表示，如图 2 – 56b 所示。
结构力学——静定结构位移计算 ppt课件
刚体位移变形力状态满足平衡条件位移状态满足约束条件第二节变形体虚功原理按外力虚功和内力虚功计算微段虚功总和微段内力虚功所以由于变形连续及相邻截面内力是作用力和反作用力的关系第二节变形体虚功原理可编辑课件ppt按刚体虚功和变形虚功计算微段虚功总和微段变形虚功所以基于平衡状态的刚体虚功原理第二节变形体虚功原理可编辑课件ppt对于直杆体系由于变形互不耦连有
要求： 领会变形体虚功原理和互等定理。 掌握实功、虚功、广义力、广义位移的概念。 熟练荷载产生的结构位移计算。 熟练掌握图乘法求位移。
第一节 位移计算概述
1、结构的位移
杆系结构在外界因素作用下会产生变形和位移。
• 变形 是指结构原有形状和尺寸的改变； • 位移 是指结构上各点位置产生的变化
线位移（位置移动） 角位移（截面转动）。
5
G0.4E
则：
ΔAV85qE4lI171501150
第三节 位移计算公式
各类结构的位移计算公式
荷载引起的位
1、梁和刚架：
ΔiP
MMPds EI
移与杆件的绝 对刚度值有关
2、桁
架： ΔiP
FNFNdPs FNFNlP
EA
EA
3、组合结构：
Δ kP
M M Pds EI
F N F Nd Ps EA
任何一个处于平衡状态的变形体，当发生任意一个虚位移 时，变形体所受外力在虚位移上所作的总虚功 We恒等于 变形体各微段外力在微段变形上作的虚功之和 Wi。
也即恒有如下虚功方程成立：
We = Wi
第二节 变形体虚功原理 变形体虚功原理的必要性证明:
力状态
位移状态
（满足平衡条件）
（满足约束条件）
刚体位移
4、拱结构：
要求： 领会变形体虚功原理和互等定理。 掌握实功、虚功、广义力、广义位移的概念。 熟练荷载产生的结构位移计算。 熟练掌握图乘法求位移。
第一节 位移计算概述
1、结构的位移
杆系结构在外界因素作用下会产生变形和位移。
• 变形 是指结构原有形状和尺寸的改变； • 位移 是指结构上各点位置产生的变化
线位移（位置移动） 角位移（截面转动）。
5
G0.4E
则：
ΔAV85qE4lI171501150
第三节 位移计算公式
各类结构的位移计算公式
荷载引起的位
1、梁和刚架：
ΔiP
MMPds EI
移与杆件的绝 对刚度值有关
2、桁
架： ΔiP
FNFNdPs FNFNlP
EA
EA
3、组合结构：
Δ kP
M M Pds EI
F N F Nd Ps EA
任何一个处于平衡状态的变形体，当发生任意一个虚位移 时，变形体所受外力在虚位移上所作的总虚功 We恒等于 变形体各微段外力在微段变形上作的虚功之和 Wi。
也即恒有如下虚功方程成立：
We = Wi
第二节 变形体虚功原理 变形体虚功原理的必要性证明:
力状态
位移状态
（满足平衡条件）
（满足约束条件）
刚体位移
4、拱结构：
结构力学5-6静定结构在非荷载因素作用下的位移计算
F
N
图
⑵作单位荷载作用下的轴力图和弯矩图。 ⑶求D点竖向位移。
yD
10
2
2
20
2a 10
1 2 a a 2
1 2
a
20 0 .1 5 a
0 .1 5 a
1 2
a
2
M 图
2 5 a ( )
Kt
t0 A
F
N
பைடு நூலகம்
t
§5-6 静定结构在非荷载因素作用下的位移计算
5-6-1 由于温度变化、制造误差等引起的位移
中 性 轴 处 温 度 变 化 ： t0 h1 t 2 h 2 t 1 h
截 面 对 称 于 中 性 轴 时 ： t0
t1 t 2 2
杆 件 上 下 侧 温 度 变 化 之 差 ： t t 2 t1
F P i ii
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
1
ij
1
ji
5-7-3 反力互等定理
r ji r ij
rii 0 r ji 1 rij 1 r jj 0
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
5-7-3 反力互等定理 5-7-4 反力与位移互等定理
r ji r ij r ji ij
r ji 1 1 ij 0
N
图
⑵作单位荷载作用下的轴力图和弯矩图。 ⑶求D点竖向位移。
yD
10
2
2
20
2a 10
1 2 a a 2
1 2
a
20 0 .1 5 a
0 .1 5 a
1 2
a
2
M 图
2 5 a ( )
Kt
t0 A
F
N
பைடு நூலகம்
t
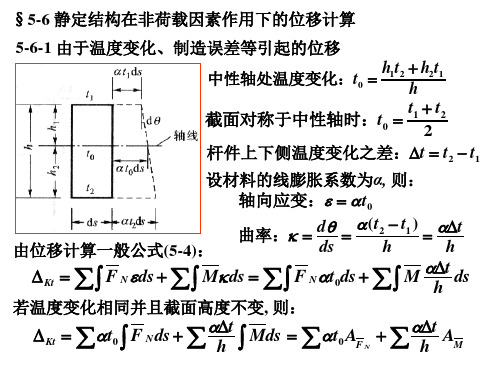
§5-6 静定结构在非荷载因素作用下的位移计算
5-6-1 由于温度变化、制造误差等引起的位移
中 性 轴 处 温 度 变 化 ： t0 h1 t 2 h 2 t 1 h
截 面 对 称 于 中 性 轴 时 ： t0
t1 t 2 2
杆 件 上 下 侧 温 度 变 化 之 差 ： t t 2 t1
F P i ii
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
1
ij
1
ji
5-7-3 反力互等定理
r ji r ij
rii 0 r ji 1 rij 1 r jj 0
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
5-7-3 反力互等定理 5-7-4 反力与位移互等定理
r ji r ij r ji ij
r ji 1 1 ij 0
《结构力学》静定结构的位移计算
A
x
C
x
C
∆AV
l 2 l 2
(a) 实际状态 1）列出两种状态的内力方程： ）列出两种状态的内力方程：
AC段 0 ≤ x ≤ 段 l 2
B
l 2
l 2
(b) 虚设状态
N =0 M = −x Q = −1
NP = 0 MP = 0 Q =0 P
2
2
∆Q ∆Q h 1 h 1 当 = 时, = 1.83%;当 = 时, = 7.32% l 10 ∆M l 5 ∆M
计算屋架顶点的竖向位移。 例2 计算屋架顶点的竖向位移。
q(N/m )
1 1 1
4.5
3.0
1.5
P 2
P
D
C
ql P= 4 P
F G 0.25l
NP
1
1.5
P 2
B 0 1.5 0.5 0
二、利用虚功原理，用单位荷载法求结构位移一般公式： 利用虚功原理，用单位荷载法求结构位移一般公式：
K
K′
实际状态 （位移状态） 外虚功： 外虚功：W
e
∆
t1 t2
c2 c1
1
R 1
虚拟状态 （力状态） 内虚功： 内虚功：W
i
R2
= 1 ⋅ ∆ + ∑ Rk ⋅ ck
1 ⋅ ∆ + ∑ R k ck = ∑ ∫ (Mκ + N ε + Q γ )d s
第4章 静定结构的位移计算
Calculation of Statically Displacement Structures
目
录
§4-1 结构位移和虚功的概念 §4-2 变形体系的虚功原理和单位荷载法 §4-3 静定结构由荷载所引起的位移 §4-4 图乘法 §4-5 互等定理
结构力学-静定结构位移计算
↓↓↓↓↓↓↓↓↓↓↓↓↓
80
32
3m
求图示刚架C铰左右两截面的 相对转动。EI=5×104kN.m
1
m=1
5/8
5m
MP
16
16
M
4m
4m
H
=
M0 C
= 1682
=16kN
f 88
1/8
1/8
H
=
M0 C
=
1m
f8
D
C
=
2 5104
580 2
2 3
5 8
+
580 2
2 3
5 8
+
1 3
-
2532 3
（1）同一结构可用不同的方式撤除多余约束但其超静定次数相同。
X1
X1
X3
X1
X2
X3
X3
X2
X1
X2
X3
（2）撤除一个支座约束用一个多余未知力代替， 撤除一个内部约束用一对作用力和反作用力代替。
（3）内外多余约束都要撤除。 （4）不要把原结构撤成几何
可变或几何瞬变体系
4
3
5 1
外部一次，内部六次 共七次超静定
1
2
不撤能除作支为杆1多后余体系约成束为的瞬变是杆1、2、 5
§9.2 力法的基本概念
1、超静定结构计算的总原则: 欲求超静定结构先取一个基本体系,然后让基本体系在受力方
面和变形方面与原结构完全一样。 力法的特点： 基本未知量——多余未知力； 基本体系——静定结构； 基本方程——位移条件——变形协调条件。
ql 2 8
5 8
l 4
2
+
l－x
80
32
3m
求图示刚架C铰左右两截面的 相对转动。EI=5×104kN.m
1
m=1
5/8
5m
MP
16
16
M
4m
4m
H
=
M0 C
= 1682
=16kN
f 88
1/8
1/8
H
=
M0 C
=
1m
f8
D
C
=
2 5104
580 2
2 3
5 8
+
580 2
2 3
5 8
+
1 3
-
2532 3
（1）同一结构可用不同的方式撤除多余约束但其超静定次数相同。
X1
X1
X3
X1
X2
X3
X3
X2
X1
X2
X3
（2）撤除一个支座约束用一个多余未知力代替， 撤除一个内部约束用一对作用力和反作用力代替。
（3）内外多余约束都要撤除。 （4）不要把原结构撤成几何
可变或几何瞬变体系
4
3
5 1
外部一次，内部六次 共七次超静定
1
2
不撤能除作支为杆1多后余体系约成束为的瞬变是杆1、2、 5
§9.2 力法的基本概念
1、超静定结构计算的总原则: 欲求超静定结构先取一个基本体系,然后让基本体系在受力方
面和变形方面与原结构完全一样。 力法的特点： 基本未知量——多余未知力； 基本体系——静定结构； 基本方程——位移条件——变形协调条件。
ql 2 8
5 8
l 4
2
+
l－x
结构力学——静定结构位移计算
结构力学——静定结构位移计算在工程和建筑领域中，结构力学作为一门重要的学科，主要研究了结构的受力、变形、破坏机理等问题。
其中，静定结构位移计算是结构力学中的一个重要内容。
静定结构所谓静定结构，是指能够通过静力学方程求解出所有节点的受力、反力和变形的结构。
这种结构是不需要知道材料的物理性质和荷载的实际情况的。
在静定结构中，结构的支座固定方式和荷载情况是已知的，因此能够通过解决一组静力学方程，求解出结构中节点的受力和变形。
静定结构位移计算静定结构位移计算是静定结构的重要计算方法之一。
在结构分析中，位移是一种常见的形变量，它反映了物体在载荷作用下发生的形变情况。
在静定结构中，位移是结构的重要参数之一。
它可以通过求解一组线性方程组得到。
具体来说，就是通过应变—位移—节点力关系，将结构各节点位移用系数矩阵和加载节点力表示出来，再通过求解一个线性方程组，就可以得到各节点的位移值。
静定结构位移计算的步骤静定结构位移计算中的步骤包括：1.列出节点位移方程节点位移与内力之间有一定的关系，可以通过位移方程和内力方程来表示。
这些方程可以根据物理实际条件进行建立。
2.确定支座反力支座反力是从位移计算中得到的结果之一。
支座反力是指结构上所有支点所承受的力，在位移计算时是必须考虑的。
3.形成节点位移方程组形成节点位移方程组时，需要考虑杆件的个数、受力条件、材料特性、支座情况等因素。
4.解出节点位移通过解一个线性方程组，我们可以根据已知的节点力和位移方程，求出每个节点的位移值。
静定结构位移计算的应用静定结构位移计算在现代工程设计中具有广泛的应用。
它能够在保证结构稳定的前提下，可以对结构进行优化设计，提高结构的安全性、稳定性、经济性等方面的性能。
除此之外，静定结构位移计算还可以应用于建筑设计、桥梁设计、机械设计、工业生产等领域中。
它可以提供结构设计的数据支持，为结构工程的实施提供参考。
静定结构位移计算是结构力学中的一个重要方向，其计算方法基于静力学方程进行，其特点是简单、可靠和实用。
结构力学 静定结构的位移
仅发生支座移动
FR i ci
N
无支座移动
M d F
d FQ d
虚功原理求位移的关键：
虚设相应的力系
1. C点竖向线位移
2. D点水平线位移
3.铰C左右截面的相对角位移
D
C
l
A b
l 2 l 2
B
a
B
P
C
l
A D
1.求D点的水平、竖向 位移
C
0
A
0 l
D
0
A
0 l
D 1/l
0
l
-1/l
l
CD
P EA
本章重点： 图乘法求梁和 刚架的位移
D
l
A C B
l
l
已知：每根杆的抗拉刚度均为EA， 1.求D点的水平、竖向位移 0.207 P 2.求BD杆的角位移 EA
梁和刚架在荷载下的位移计算
M MP ds EI
E
Pl
l
求：1. B点的水平位移和角位移
2. D点的水平位移
ql ql
2
q
B
C
EI=常数
D
l
A
l l
求：１.
２.
ql2
C、D两点的相对水平位移
A、D两点的相对角位移
B
C
EI
q
l
A
l
D
q ql
2
已知：EI=常数．求： 1．C点的竖向位移和
l
D
C
E
铰C左右截面的相对角位移
２．D点的水平位移和角位移
已知：
C 梁式杆的EI=常数，
FR i ci
N
无支座移动
M d F
d FQ d
虚功原理求位移的关键：
虚设相应的力系
1. C点竖向线位移
2. D点水平线位移
3.铰C左右截面的相对角位移
D
C
l
A b
l 2 l 2
B
a
B
P
C
l
A D
1.求D点的水平、竖向 位移
C
0
A
0 l
D
0
A
0 l
D 1/l
0
l
-1/l
l
CD
P EA
本章重点： 图乘法求梁和 刚架的位移
D
l
A C B
l
l
已知：每根杆的抗拉刚度均为EA， 1.求D点的水平、竖向位移 0.207 P 2.求BD杆的角位移 EA
梁和刚架在荷载下的位移计算
M MP ds EI
E
Pl
l
求：1. B点的水平位移和角位移
2. D点的水平位移
ql ql
2
q
B
C
EI=常数
D
l
A
l l
求：１.
２.
ql2
C、D两点的相对水平位移
A、D两点的相对角位移
B
C
EI
q
l
A
l
D
q ql
2
已知：EI=常数．求： 1．C点的竖向位移和
l
D
C
E
铰C左右截面的相对角位移
２．D点的水平位移和角位移
已知：
C 梁式杆的EI=常数，
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
a
BA
B
§6-4 制造误差产生的位移计算
利用虚功方程有： 1 CH 2 2 0
得： CH 2 2cm
例：图示悬臂梁C点由于制造误差有一转角 ，求由
此引起的B点竖向位移 BV 。
α
Mc=a Fp=1
A
b
Ca
BA
C
B
解：虚设一力状态：在B点加一竖向单位力，求出C点 的弯矩，并把C点的抗弯连系去掉，用弯矩 M C 表示。
§6-4 制造误差产生的位移计算
例：图示桁架DC杆短了2cm,FE杆短长了3cm,求C点的
竖向位移。
D
F
D
F
-2
+3
4m
A
CE
B
C
E
B
3×4=12m
A
Fp=1
解：在C点作用一竖向单位力，求出DC杆、FE杆的
轴力：
1 FNDC 4
FNFE
5 16
运用位移计算公式有：
C
12 5 3 7 4 16 16
§6-4 制造误差产生的位移计算
制造误差产生的位移采用刚体的虚力原理计算。
例：图示桁架AC杆比要求的短了2cm,求由此产生的C
点水平位移 。
解：在C点作用一水平单位力，方向朝左，求出AC杆的
内力，令虚设的力到真实的位移上去做功，由虚功
方程有 ：
C
C Fp=1
真实的位 移状态
-2cm
b
2
虚设的力 状态
制造误差产生的位移——刚体位移 温度改变产生的位移——变形体位移 显然支座移动产生的位移、制造误差产生的位移应 该用刚体的虚力原理计算。荷载作用产生的位移、温 度改变产生的位移应该用变形菜体的虚力原理计算。
§6-2 支座移动产生的位移计算
支座移动产生的位移应采用刚体的虚力原理来计算。
例：图示简支梁B支座往下位移了 ，求由此产生的A
§6-3 力的虚设方法
Fp=1
C
Fp=1 B
M=1 C
求C点竖向位移 A
Fp=1
求B点水平位移
Fp=1 B
A Fp=1
求C点转角位移 B
Fp=1
求A、B两点 相对竖向位移
求A、B两点 相对水平位移
§6-3 力的虚设方法
M=1 C
C Fp=1/L
求C点相对转角位移
D Fp=1/L 求CD杆相对转角位移
CV
( 1 b 1 a) 24
b 2
a 4
A
B
（2）求C点的相对转角 C
虚设的力状态
在C点作用一对力矩，求出 FYA 和 FXB 。
§6-2 支座移动产生的位移计算
M=1
C
C
b
L
A
L/2
B L/2 a
A
B
真实的位移状态
虚设的力状态
FYA 0
1 FXB L
1
a
C
( L
a)
L
§6-3 力的虚设方法
复习一下以下概念： ▲ 虚功——力在由其它原因产生的位移上所做的功。
1 Fp1 2 Fp2
A △11 △12
B
△22
其中：T FP1 12 ——虚功
▲ 虚功原理
刚体虚功原理 变形体虚功原理
§6-1 概述
刚体虚功原理：
所有外力所做的虚功等于零，即：W外 0
变形体虚功原理：
所有外力做的虚功=所有内力做的虚功，即：W外 W内
虚功原理
虚力原理 虚位移原理
虚力原理——位移是真的，力是虚设的。用虚设力的 办法来求真实的位移。
虚位移原理——力是真的，位移是虚设的。用虚设位 移的办法来求真实的力。
§6-1 概述
很显然求位移用的是虚功原理中的虚力原理 。 2）静定结构位移的类型
支座移动产生的位移——刚体位移
荷载作用产生的位移——变形体位移
§6-5 温度作用时的计算
温度作用产生的位移采用变形体的虚力原理计算 。
计算公式推导：
图示简支梁上下温度不一样 ，t1 t2 求由此起的A
点转角 A。
t1
取出一微段，研究一下 A
t2
B
温度所引起的变形。
微段发生的转角为：
d t1ds t2ds tds
h
h
h1 h
h2
L αt1 ds
+t1
+t0
dθ αt0ds
+t2
ds αt2ds
§6-5 温度作用时的计算
微段发生的轴向变形为： d t0ds
其中： t t1 t2 — 杆件上下边缘的温度差值
t0 — 杆件轴线处的温度变化值
温度变化不会产生剪切变形。
t1
M=1
A
t2
BA
B
L
L
真实的位移状态
虚设的力状态
运用变形体的虚功原理，所有外力所做的虚功等
力的大小— 一般虚设单位力 。 力的位置— 作用在所求位移的点及方向上。
力的方向— 随意假设，若求出的位移是正的，说 明位移与假设的方向一致。若是负的， 说明与假设的方向相反 。
力的性质— 求线位移加单位集中力；求转角加单位 力矩；求二点的相对水平或竖向位移加 一对相反的单位集中力；求二点相对转 角要加一对单位力矩。
例：图示三铰刚架A支座往下位移了b，B支座往右位移
了a，求C点的竖向位移 CV , 和C点的相对转角 C 。
C
（1）求C点的竖向位移 CV
真实的位移状态
A
L/2
B L/2 a
b
L
§6-2 支座移动产生的位移计算
在C点作用一个竖向单位力，求出 FYA和 FXB 。
FYA
1 2
FXB
1 4
Fp=1 C
§6-4 制造误差产生的位移计算
利用虚功方程有： 1 BV MC 0 得： BV M C
由制造误差引起的位移计算公式如下：
F
N
M
F
Q其中：Biblioteka F N M FQ —虚设单位力作用下产生的轴力、
剪力和弯矩。
—制造产生的轴向变形、弯曲变
形和剪切变形。
正负号规定：虚内力与变形方向一致为正，方向相反为负。
于内力所做的虚功：
§6-5 温度作用时的计算
有：
F N d Md
F
N
t0ds
M
t ds
h
若是结构，则公式为：
F d N
Md
F
N
t0ds
M
t
h
ds
若温度沿杆长变化相同，且截面高度不变，则上式
可写成：
F
N
t0
ds
M
t
h
ds
t0 N
t
h
M
其中： N
— 由虚设单位力产生的轴力图面积
第6章 静定结构位移计算
主要内容
§6-1 概述 §6-2 支座移动产生的位移计算 §6-3 力的虚设方法 §6-4 制造误差产生的位移计算 §6-5 温度作用时的计算 §6-6 荷载作用下的位移计算 §6-7 图乘法 §6-8 线性变形体系的互等定理
§6-1 概述
1）计算所采用的理论——虚功原理
点转角 A 。
A
B
运用刚体的虚功原理， 虚设的力状态上的所有外
Δ
L
力在真实的位移状态上所
真实的位移状态
做的虚功应该等于零，有：
1
A
1 L
0
得：
A
L
M=1 虚设的力状态
§6-2 支座移动产生的位移计算
可以得出由支座移动引起的位移计算公式如下：
R c
其中：R —由虚设力产生的在有支座位移处的支座反力 c —真实的支座位移