球面渐开线弧齿锥齿轮参数化建模
基于UG的球面渐开线弧齿锥齿轮参数化建模

基于 UG 的球面渐开线弧齿锥齿轮参数化建模王占富【摘要】摘要:阐述了球面渐开线弧齿锥齿轮齿廓的形成机理,并以弧齿锥齿轮数学模型理论为基础,提出了一种利用UG 表达式功能和参数化建模思想,精确生成锥齿轮的球面渐开线的方法,用变换、扫掠及回转等操作,建立了完整的球面渐开线弧齿锥齿轮三维造型。
为弧齿锥齿轮设计与制造研究提供了设计思想及方法,同时也为其它具有复杂表面形体的参数化建模提供了参考。
【期刊名称】矿山机械【年(卷),期】2010(038)022【总页数】4【关键词】球面渐开线;弧齿锥齿轮;UG;参数化建模弧齿锥齿轮因其具有承载能力大、运转平稳、传动效率高及噪声小等诸多优点,而广泛应用于航空、航天、工程机械和矿山机械等高速或重载的机械产品中。
由于圆锥齿轮的齿廓为球面渐开线[1],而球面是不可展曲面,因此不利于设计、制造和检测,所以一般采用将球面渐开线的齿廓在背锥(辅助圆锥)上投影展开(如格里森制齿轮),即以直代曲的近似分析和设计方法。
这种近似方法必然会影响弧齿锥齿轮的设计精度,在一定程度上影响了弧齿锥齿轮的特有优点,降低了其使用性能。
为了解决上述问题,笔者利用UG 表达式优异精确的建模功能,设计出以线接触共轭展成机理为基础的球面渐开线弧齿锥齿轮。
1 球面渐开线弧齿锥齿轮齿廓形成[2-3]如图1 所示,设一圆平面与一基圆锥相切,基圆锥的母线OA1 等于圆平面的半径 Rb,且圆锥的顶点 O始终与圆平面的圆心 O 相重合。
当圆平面在这个基圆锥上作纯滚动时,该圆平面上任一通过圆心O 的直径OA1 在空间展出一锥曲面OA1A2。
由于曲线A1A2 上任一点离顶点O 的距离不变(等于圆平面的半径Rb),所以其轨迹A1A2 为一球面曲线。
根据其形成原理可知,该球面曲线为一球面渐开线。
因球面渐开线位于OA1A2 上,所以该锥曲面就是球面渐开线齿廓曲面。
当球面的半径增至无穷大时(即锥顶移至无穷远时),该球面渐开线便成为平面渐开线,该平面渐开线就是圆柱齿轮的齿廓曲线。
球面渐开线螺旋锥齿轮精确模型设计

关键词 : 螺旋锥齿轮 ; 齿廓 曲线 ; 球面渐开线 ; 齿线 ; 模型设计
中图分类号 : T H1 6 ; T H1 3 2 . 4 2 1 文献标识码 : A 文章编号 : 1 0 0 1 — 3 9 9 7 ( 2 0 1 4 ) 0 3 — 0 0 2 3 — 0 4
Ac c u r a t e Mo d e l i n g f o r t h e Sp h e r i c a l I n v o l u t e Sp i r a l Be v e l Ge a r s
DI NG Ha n,ADAYI 。 Xi e e r y a z i d a n, W ANG Yo n g - s h e n g
A b s t r a c t : I n v i e w o f p r e v i o u s s t u d i e s o n t h e m o d e l i n g a n d t h e b a s i c c o m p o n e n t s o ft h e t o o t h p r o il f e c u r v e s f o r t h e s p i r a ! b e v e l g e a r s , i t m a d e f u l l e o fc h ra a c t e r i s t i c s a n d a d v a n t a g e s ft o h e s p h e r i c a l i n v o l u t e t h e o r y , a n d a mo d e l i n g s c h e m a ft o h e s p i r a l b e v e l ea g r s w i t h t h e s p h e r i c a l i v o l u t e t o o t h p r o il f e i s p r o p o s e d . F i r s t l y , b a s i n g o n t h e t h e o r y o f f o r m i n g t h e s p h e r i c l a i n v o l u t e nd a b u i l d i n g a s p h e r i c a l c o o r d i n a t e s y s t e m, e q u ti a o n e x p r e s s i o n fe o ch a p a r t ft o o o t h p r o i f l e s c u ve r ft o h e t o e a n d h e e l re a l a l
基于Pro_E的渐开线弧齿锥齿轮的三维建模_冉兆波

机械 2007年第1期 总第34卷 计算机应用技术 ·35·——————————————— 收稿日期:2006-08-22作者简介:冉兆波,在读研究生,研究方向为机械CAD/CAE ;万朝燕,教授,硕士生导师。
基于Pro/E 的渐开线弧齿锥齿轮的三维建模冉兆波,万朝燕(大连交通大学 机械工程学院,辽宁 大连 116028)摘要:介绍了在Pro/E 环境下,实现标准渐开线弧齿锥齿轮的造型方法和步骤,从原理出发,利用方程建立渐开线,从而保证齿形的准确性。
通过建立齿轮中各变量与模数m 、齿数z 等基本参数的关系,实现了不同模数、齿数齿轮的快速造型,提高了设计效率。
关键词:渐开线;弧齿锥齿轮;Pro/E中图分类号:TH122 文献标识码:A 文章编号:1006-0316(2007)01-0035-03Study on the method of molding for the standard involute spiral cone gear based on Pro/EngineerRAN Zhao-bo ,WAN Chao-yan(Dalian Jiaotong University ,Dalian 116028,China )Abstract :Introduces the methodologies and steps of exact modeling for the standard involute spiral cone gear in environment of Pro/ Engineer. Based on principle, using equation build up the involute .Consequently we can ensure the accuracy of the involute gear shape. Carry out quick modeling of various modulus and teeth number by set up relations between variable and basic parameters. t raised the design efficiency. Key words :Involute ;spiral cone gear ;Pro/E弧齿锥齿轮作为基础传动件,用于传递相交轴之间的运动和动力,广泛应用于航空、航海、汽车、拖拉机、机床等行业中。
弧齿锥齿轮几何全参数设计
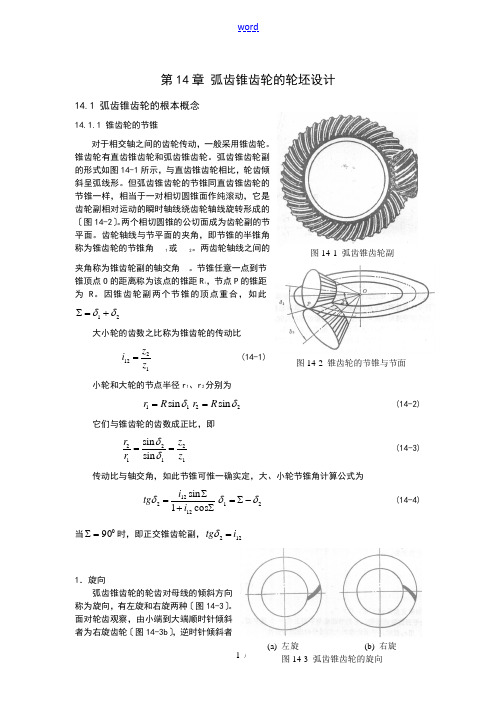
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的根本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的〔图14-2〕。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角1或2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,如此21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r =22sin δR r = (14-2)它们与锥齿轮的齿数成正比,即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角,如此节锥可惟一确实定,大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ21δδ-∑= (14-4)当090=∑时,即正交锥齿轮副,122i tg =δ1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种〔图14-3〕。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮〔图14-3b 〕,逆时针倾斜者图14-2 锥齿轮的节锥与节面图14-1 弧齿锥齿轮副如此为左旋齿〔图14-3a 〕。
大小轮的旋向相反时,才能啮合。
一般情况下,工作面为顺时针旋转的〔从主动轮背后看,或正对被动轮观察〕,主动锥齿轮的螺旋方向为左旋,被动轮为右旋〔图14-1〕;工作面为逆时针旋转的,情况相反。
这样可保证大小轮在传动时具有相互推开的轴向力,从而使主被动轮互相推开以防止齿轮承载过热而咬合。
基于SolidWorks的渐开线斜齿轮_锥齿轮参数化设计

2010第4期总第197期现代制造技术与装备SolidWorks提供了几百个API函数,这些API函数是SolidWorks的OLE或COM接口,用户可以使用VB\C++\Delphi等高级语言对SolidWorks进行二次开发,建立适合用户需要的、专用的SolidWorks功能模块。
渐开线齿轮机构是机械产品中应用最广泛的一种传动机构,本文在SolidWorks平台上利用VB6.0进行二次开发,实现了渐开线斜齿轮、直齿圆锥齿轮的参数化设计,使齿轮三维实体建模的过程变得方便、快捷。
1渐开线斜齿轮参数化设计1.1斜齿轮齿形的绘制渐开线斜齿轮齿形由两部分组成:工作部分和非工作部分。
工作部分的齿形为渐开线,而非工部分采用过渡圆弧。
齿形的绘制一般采用描点法,根据渐开线齿廓公式计算求得多个齿形坐标点的值后,利用SolidWorks样条曲线API函数CreateSpline,来绘制光滑渐开线曲线。
渐开线部分的齿形建立坐标系如图1所示。
渐开线齿廓上任意M点的坐标:x=r x sinw xy=r xcoswx!式中:w x 为渐开线任意M点的齿间中心半角,r x 为M点的半径。
w x 按下式计算:wx=w0+θx=w0+invαx=Pb2-Sb2rb+tanαx-αx=π2z-tanα+α+tan(arccosrbrx)-arccosrbrx式中:w0为基圆齿间中心半角,θx为渐开线任意M点的展角,αx为渐开线任意M点的压力角,Pb为基圆齿距,Sb为基圆齿厚,α为分度圆上的压力角,z为齿轮齿数,rb为基圆半径。
1.2斜齿轮斜齿造型斜齿轮齿面为渐开线螺旋面,不同截面上齿形不同,斜齿轮的端面渐开线齿廓可参照上述方法建立。
渐开线斜齿轮三维造型中齿廓是按照螺旋线方向扫描的,螺旋线的螺距是需要求出的。
本文中采用求分度圆的螺距在SolidWorks构建螺旋线。
螺距Pz按下式计算:Pz=πdtanβ式中:β为斜齿轮分度圆柱面上的螺旋角,d为分度圆直径。
基于SolidWorks的渐开线斜齿轮_锥齿轮参数化设计

基于SolidWorks的渐开线斜齿轮_锥齿轮参数化设计渐开线斜齿轮是一种常见的齿轮传动装置,其特点是传动平稳、噪音小、传动效率高等。
而基于SolidWorks的渐开线斜齿轮参数化设计可以实现对齿轮的灵活设计和快速制造。
首先,我们需要了解渐开线斜齿轮的基本参数。
渐开线斜齿轮由齿数、模数、压力角、齿轮宽度等参数来决定。
其中,齿数是指齿轮上齿的数量,模数是指齿轮模具的大小,压力角是指齿轮齿面与齿轮轴线之间的夹角,齿轮宽度是指齿轮的厚度。
在SolidWorks中,我们可以通过创建宽度为0的圆柱体来建立齿轮的基本几何形状。
然后,通过参数化设计功能,我们可以将齿数、模数、压力角等参数作为输入变量,实现对齿轮形状的自动调整。
例如,我们可以通过创建一个方程来计算齿轮的齿数和模数之间的关系。
然后,我们可以将齿数和模数作为输入变量,在方程中进行计算,并将计算结果应用到齿轮的几何形状上。
这样,当我们改变齿数或模数时,齿轮的形状会自动更新,实现对齿轮的灵活设计。
此外,我们还可以通过创建一个参数表来管理齿轮的参数。
在参数表中,我们可以定义齿数、模数、压力角等参数,并将它们与齿轮的几何形状关联起来。
这样,当我们需要修改齿轮的参数时,只需要修改参数表中的数值,齿轮的形状就会自动更新。
在实际应用中,我们还可以通过添加其他功能来完善渐开线斜齿轮的设计。
例如,我们可以添加齿轮的轴承孔、键槽等特征,以满足实际使用的需求。
同时,我们还可以进行齿轮的装配设计,将齿轮与其他零件组装在一起,完成整个传动系统的设计。
总之,基于SolidWorks的渐开线斜齿轮参数化设计可以实现对齿轮的灵活设计和快速制造。
通过参数化设计功能和其他功能的结合,我们可以实现对齿轮的自动调整和快速更新,提高设计效率和制造质量。
这对于齿轮传动装置的设计和制造具有重要意义。
UG GRIP的弧齿锥齿轮参数化建模方法
资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载UG GRIP的弧齿锥齿轮参数化建模方法地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容UG GRIP的弧齿锥齿轮参数化建模方法基于UG GRIP,本文针对弧齿锥齿轮建模方法进行了深入细致的研究。
首先介绍了弧齿锥齿轮建模的总体方案。
其次详细说明了大轮的展成法建模原理;对于小轮的造型,基于共轭理论,提出了一种用工具大轮与小轮坯体进行展成布尔运算的实体建模的创新方法,从而得到小轮模型。
采用此方法造型弧齿锥齿轮小轮比其它造型方法简便,是弧齿锥齿轮参数化建模和加工的一种实用的新方法。
接着以一对齿数为21-35、模数为13的齿轮副为例,详细图解说明了整个建模过程。
最终还对建立的模型进行了数控加工试验以验证上述方法的正确性。
1 前言弧齿锥齿轮是一种节锥齿线为曲线、用来传递在一个平面内的两相交轴之间的定传动比回转运动的齿轮[1]。
由于其承载能力大、传动平稳、噪声小、结构紧凑等优点,是航空、造船、汽车、能源、装备、国防等部门产品的关键零件,因此弧齿锥齿轮生产在现代化机械制造业中占有十分重要的地位 [1-3]。
其制造主要使用专用的齿轮加工机床。
目前国内使用的齿轮加工机床主要有美国格里森公司生产的No.116铣齿机、No.609拉齿机、No.463磨齿机和国产的Y2280铣齿机等[1]。
随着科技的进步、技术的创新,数控化的切齿加工机床纷纷涌现。
但是由于机床结构、机床尺寸等因素的制约,每一种机床都有对应的技术规格,如最大加工模数、最大加工锥距、最大加工直径等,因此无法加工一些尺寸超过其技术规格的齿轮副(如大模数的油田、煤矿机械使用的大型弧齿锥齿轮副)。
而且弧齿锥齿轮加工中仍然存在着众多问题,如:加工过程烦琐、加工周期长、人力和资金投入大等[4]。
弧齿锥齿轮建模
弧齿锥齿轮建模
弧齿锥齿轮建模是一种常见的机械零件设计方法,它广泛应用于工业
机械、航空航天和军事等领域。
对于如何进行弧齿锥齿轮建模,除了
需要一定的机械设计基础知识之外,还需要掌握一些相关的设计软件。
下面是一个简单的弧齿锥齿轮建模步骤的列表:
1. 建立基础形状:首先要确定弧齿锥齿轮的基础形状,也就是锥齿轮
和齿轮的齿数、模数、分度圆直径等参数,然后根据这些参数建立基
础形状。
2. 切割齿形:再根据齿形参数,通过“齿形滚轮”的原理来切割齿形。
3. 修整齿形:切割完齿形后,还需要进行一些修整操作,以达到更好
的齿形质量。
4. 分离齿轮:注意到弧齿锥齿轮的构造是由两个齿轮垂直组成的,所
以在建模时需要将两个齿轮进行分离。
5. 添加轴孔:生成轴孔用于齿轮的安装和传动。
6. 细节调整:检查齿轮的细节问题,比如齿轮毂的高度、齿根和齿顶
的半径等,并进行必要的调整。
在进行弧齿锥齿轮建模时,需要掌握一些相关的软件技能。
目前比较
流行的建模软件包括Solidworks、Creo、CATIA等,这些软件都提供
了强大的建模功能和用户友好的界面设计,使得建模过程更加快捷、
高效。
当然,掌握一种建模软件并不能替代实际的机械设计经验和技能,需要不断学习和探索,才能不断提升弧齿锥齿轮建模的水平。
基于UG弧齿锥齿轮参数化建模及动力学仿真
基于UG弧齿锥齿轮参数化建模及动力学仿真史朋真;王春燕;贾廷臣【摘要】根据弧齿锥齿轮的形成原理和加工方法,推导弧齿锥齿轮的齿廓方程和齿面节线方程.在UG三维建模环境下,通过对弧齿锥齿轮基本参数的输入,实现对弧齿锥齿轮的参数化建模,并对建好的模型进行虚拟装配和动力学仿真分析.检验模型是否存在干涉以及齿轮的啮合特性质量,以此来提高机械设计人员在虚拟环境下对弧齿锥齿轮的设计和使用效率.【期刊名称】《太原科技大学学报》【年(卷),期】2019(040)001【总页数】5页(P68-72)【关键词】弧齿锥齿轮;参数化建模;动力学仿真【作者】史朋真;王春燕;贾廷臣【作者单位】太原科技大学机械工程学院,太原030024;太原科技大学机械工程学院,太原030024;太原科技大学机械工程学院,太原030024【正文语种】中文弧齿锥齿轮是一种重要的传动零件,由于它具有传动平稳、噪声低、承载能力大等特点。
被广泛应用于汽车、船舶、机床、飞机等机械领域中,因此人们更加重视对弧齿锥齿轮的设计和制造领域的研究。
弧齿锥齿轮复杂的空间齿面和不规则的空间曲线给人们建模带来了困难。
传统的设计建模方法是将弧齿锥齿轮的球面渐开线近似为基锥平面上的平面渐开线,以螺旋线代替齿轮啮合节线,这样的建模方法影响了弧齿锥齿轮的建模精度,建立出来的弧齿锥齿轮齿面在啮合传动中容易产生干涉的现象。
本文根据推导的齿轮啮合传动节线和球面渐开线的数学表达式,通过球面渐开线形成原理和弧齿锥齿轮的加工方法,建立弧齿锥齿轮的齿廓曲线,在UG建模模块环境下以传动节线作为齿面线来扫掠出弧齿锥齿轮的轮齿齿面,从而保证一对轮齿齿面是共轭的。
在UG装配模块环境下对一对弧齿锥齿轮进行虚拟装配,在动力学模块环境下对一对弧齿锥齿轮的进行动力学仿真,以此来提高弧齿锥齿轮建模和装配的高效性和准确性[1]。
1 弧齿锥齿轮齿廓形成原理在推导弧齿锥齿轮的轮齿齿廓前,我们需要知道弧齿锥齿轮的基本参数和这些参数之间对应的关系,如表(1)所示给出了弧齿锥齿轮的模数、齿数、压力角、螺旋角和根据这些参数所查到的齿高系数、径向、切向变位系数、名义刀盘半径等。
基于Pro_E的弧齿锥齿轮参数化精确建模-武理
第32卷 第10期2010年5月武 汉 理 工 大 学 学 报JOURNAL OF WUHAN UNIVERSITY OF TECHNOLOGY Vo l.32 N o.10 M ay.2010DOI:10.3963/j.issn.1671 4431.2010.10.023基于Pro/E 的弧齿锥齿轮参数化精确建模王,华 林(武汉理工大学材料科学与工程学院,武汉430070)摘 要: 以啮合原理为基础,在Pro/E 环境下研究了弧齿锥齿轮三维精确设计方法。
通过齿轮曲线方程生成齿槽大、小端球面渐开线以及齿根、齿顶处的齿形曲线,并沿齿宽方向插入若干辅助球面渐开线;利用边界混合功能沿各渐开线及齿形曲线扫描建立齿槽齿面片体,由其切割齿形坯得到齿槽实体;将齿槽实体和齿形坯进行布尔减运算并环形阵列,最后添加轮毂实体,从而实现了弧齿锥齿轮的参数化精确建模。
经虚拟装配检验,齿轮副啮合过程中无干涉现象发生。
文中的参数化精确建模方法为弧齿锥齿轮三维设计与分析提供了有效途径。
关键词: 弧齿锥齿轮; 球面渐开线; 曲线方程; 参数化精确建模中图分类号: TH 132.4文献标识码: A 文章编号:1671 4431(2010)10 0099 05Accurate Parametric Modeling of Spiral Bevel Gear Basedon CAD Software Pro/EWAN G Ben ,H UA Lin(School of M aterials Science and Eng ineering,W uhan U niversity of T echnology ,Wuhan 430070,China)Abstract: An accurate 3D design method of the spher ical involute spiral bevel gear was researched based on the engaging pr inciple and CAD software Pro/E.T he spherical invo lutes for the heel and toe ends of the gear gr oove,t he tooth cur ves for the dedendum and addendum,as well as the aux iliary spherical involutes along the direction of tooth w idth w ere gener ated from the functio n of curvilinear equation.T he profile surfaces of the g ear g roove which w er e used to obtain the gr oo ve entity by cutting tooth blank w ere formed t hrough boundar y blend along both the spherical involutes and the too th curves.Finally ,after subtr act Boolean oper ation betw een the groov e entity and tooth blank,polar ar ray and adding the hub entity,the accurate par ametric modeling of spiral bevel g ear w as r ealized.After vir tual assembly inspection,there was no interference during the eng agement.So,the accurate parametr ic modeling metho d is an effect ive approach to 3D design and analysis of spher ical involute spiral bevel gear.Key words: spiral bevel gear; spher ical involute; curv ilinear equation; accurate parametric modeling收稿日期:2009 12 08.基金项目:国家杰出青年科学基金(50725517)和国家科技支撑计划资助项目(2006BAF04B06).作者简介:王 (1985 ),男,硕士生.E mail:w angben1017@弧齿锥齿轮因具有传动平稳、效率高、承载能力强、噪声低等优点,已在汽车、航空航天、石油、化工等诸多领域中代替直齿锥齿轮来实现相交轴间的运动传递。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9期2018年9月组合机床与自动化加工技术ModularMachineTool&AutomaticManufacturingTechniqueNo.9Sep.2018文章编号:1001-2265(2018)09-0037-04㊀㊀㊀㊀DOI:10.13462/j.cnki.mmtamt.2018.09.011收稿日期:2017-12-07ꎻ修回日期:2018-03-12㊀∗基金项目:湖北高校2015年省级大学生创新创业训练计划项目(201510488019)作者简介:倪胜利(1993 )男ꎬ湖北黄冈人ꎬ武汉科技大学学生ꎬ(E-mail)nsl_wust@163.comꎻ通讯作者:陈霞(1972 )ꎬ男ꎬ湖北黄冈人ꎬ武汉科技大学副教授ꎬ博士ꎬ研究方向为数字化制造技术㊁制造工艺设计ꎬ(E-mail)dmcad@126.comꎮ球面渐开线弧齿锥齿轮参数化建模∗倪胜利ꎬ陈㊀霞ꎬ邹艳龙ꎬ刘㊀芳ꎬ李文凯(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室ꎬ武汉㊀430081)摘要:基于球面渐开线形成原理ꎬ推导出了球面渐开线的参数化方程ꎮ根据纵向齿形是弧齿锥齿轮的齿面与节锥交线的性质ꎬ建立了齿向曲线参数化方程ꎮ齿根曲线和齿顶曲线分别是齿根圆弧和齿顶圆弧ꎬ由此分别建立了齿根参数化曲线和齿顶参数化曲线方程ꎮ齿面和齿根的过渡圆角部分ꎬ通过倒角圆方法进行优化处理ꎮ针对弧齿锥齿轮轮齿端面特征ꎬ给出了精确划分轮齿有限元网格的方法ꎮ对某弧齿锥齿轮副ꎬ在MATLAB环境下获得了含齿根过渡曲面的精确轮齿有限元模型ꎬ为齿轮啮合的应力分析和修形提供了精确的数字模型ꎮ关键词:弧齿锥齿轮ꎻ参数化精确建模ꎻ球面渐开线ꎻ有限元模型中图分类号:TH132ꎻTG506㊀㊀㊀文献标识码:AParametricModelingofSpiralBevelGearwithSphericalInvoluteNISheng ̄liꎬCHENXiaꎬZOUYan ̄longꎬLIUFangꎬLIWen ̄kai(KeyLaboratoryforFerrousMetallurgyandResourcesUtilizationofMinistryofEducationꎬWuhanUniversityofScienceandTechnologyꎬWuhan430081ꎬChina)Abstract:Theparametricequationofthespiralinvoluteisintroducedwiththebasicprincipleofformingsphericalinvolutetoothsurface.Thelongitudinaltoothprofileisestablishedwithitscharacteroftheinter ̄sectionofthetoothsurfaceandtheconeofthespiralbevelgear.Addendumcircleandrootcircleareusedtogeneratedtherootfillerandthetipfillerofthespiralbevelgearrespectively.Thepartofthetransitionroundangleofthetoothsurfaceandtherootofthetoothisoptimizedbythemethodofchamferingcircle.Inviewofthecharacteristicsofthetoothtransverseshapeofspiralbevelgearteethꎬafiniteelementmeshmethodforaccuratedivisionofgearteethisgiven.Forapairofspiralbevelgearsꎬtheprecisefiniteele ̄mentmodelswithfillerareformedinMATLABsoftwaretolaythefacilitationforthedesignꎬthemodifi ̄cationandthetoothcontactanalysisofsphericalinvolutespiralbevelgears.Keywords:spiralbevelgearsꎻaccurateparametricmodelingꎻsphericalinvoluteꎻfiniteelementmodel0㊀引言弧齿锥齿轮为一种局部点接触的不完全共轭的齿轮副ꎬ几何模型相当复杂ꎬ使用UG等三维建模软件却无法建立其精确的三维模型ꎮ对一些高端精密应用的弧齿锥齿轮ꎬ齿根过渡曲面对轮齿的强度和使用寿命有重要的影响ꎮ李兆文等[1]利用展成法的原理ꎬ用VB编程获得弧齿锥齿轮的齿面点ꎬ借助于Pro/E软件建立弧齿锥齿轮实体模型ꎮ张武刚等[2]用切齿原理和实际切齿过程建立几何仿真模型ꎮ任燕[3]和杨宏斌[4]用展成法原理推导弧齿球面渐开线方程ꎬ结合MATLAB和Solid ̄Works软件建立了弧齿锥齿轮模型ꎮLitvin[5]推导出刀具外侧方程和刀尖圆角方程及齿面展成原理ꎬ却没有给出齿根过渡曲面的推导过程ꎮ唐进元[6]运用啮合方程和切齿原理推导出弧齿锥齿轮工作齿面和过渡曲面方程ꎬ在MATLAB中计算出齿面的数据点ꎬ再导入到Pro/E中建立了含有过渡曲面的弧齿锥齿轮ꎮ刘光磊[7]根据齿轮加工的展成法ꎬ通过坐标转换顺序ꎬ从刀具方程得到了齿轮的齿面方程和齿根过渡曲面方程ꎮ以上所述主要是以近似球面渐开线齿形的设计与加工研究为主ꎬ而球面渐开线理论在弧齿锥齿轮设计中却起步比较晚ꎮ传统方式加工的齿轮难以获得理想的球面渐开线齿形ꎬ该齿轮传动体系属于局部点接触ꎬ它采用了一种近似球面渐开线的齿形ꎬ接近于共轭传动ꎬ造成了齿轮啮合不理想的现实问题ꎮ正因为如此ꎬ李丹红[8]用球面渐开线理论应用于建模中ꎬ借助CAD曲面设计功能为主进行建模ꎬ但其中没有设计到齿根过渡曲面的设计ꎮ为了得到理想啮合的弧齿锥齿轮模型ꎬ本文基于球面渐开线理论ꎬ推导出弧齿锥齿轮的参数化方程ꎬ不仅给出了球面渐开线方程ꎬ还推导出了齿形方程ꎬ最后还给出了齿根过渡曲面方程ꎮ整个模型的设计都在MATLAB环境中实现ꎬ不存在数据丢失等问题ꎮ轮齿由端面㊁齿廓面㊁齿顶面和齿根面组成ꎬ齿廓面分成齿面㊁齿根圆锥面㊁齿根过渡曲面3部分ꎬ轮齿的齿面由球面渐开线和齿向曲线组成ꎮ轮齿端面分成6个子区域ꎬ每个区域通过球面渐开线㊁齿顶㊁齿根㊁齿根过渡等部分的网格数目协调地连接起来ꎮ1㊀弧齿锥齿轮啮合原理弧齿锥齿轮齿形理论上为球面渐开线ꎬ为便于制造ꎬ在实际生产中将弧齿锥齿轮大端齿形展成平面ꎬ把大端球面渐开线转化成平面渐开线ꎬ从而得到近似的齿形ꎬ精确的弧齿锥齿轮模型必须使用球面渐开线ꎮ当平面在基圆锥上滚动时ꎬ平面上的一点运动轨迹称为球面渐开线ꎮ如图1所示ꎬ圆平面T与基圆锥OKoO1相切并在锥面上作纯滚动ꎬ圆平面上的动点K在空间的运动轨迹为渐开线ꎮ由于动点K在球面渐开线上任意位置到基圆锥顶点O的距离始终相等ꎬ故该渐开线是以O点为球心的球面上ꎮ当圆平面由初始OK位置滚动到ON位置时ꎬ动点K的轨迹为球面渐开线K0Kꎮ图1㊀球面渐开线的形成原理过点K作轴线OO1垂直的平面ꎬ交轴线OO1于Q点ꎬ交母线OK0于P点ꎮ在直角三角形OKQ㊁OKP㊁OPN中ꎬ存在如下关系:cosγ=OPOK=OQcosδbOQcosδk=cosδkcosδb(1)通过渐开线的性质可知:KoK(=KoN(=γOK=OKarccoscosδkcosδb(2)øK0O1N=K0K(OKsinδb(3)由上述方程可推导出:øK0O1N=arccoscosδkcosδbsinδb(4)由球面三角学和边角关系可得出:øK0O1N=arccostanδbtanδk(5)球面渐开线上任意一点K的偏角可求出:βk=øK0O1N-øK0O1K=arccoscosδkcosδbsinδbsinδb-arccostanδbtanδk(6)在图1中的球面坐标系中ꎬ可表示为:K=K(ρꎬθꎬφ)=K(Rꎬδkꎬβk)(7)式中ꎬδk为球面渐开线上任意点所对应锥角ꎬδb为基圆锥角ꎮ在产形线K0Kt上分别取等分点Kn(n=0ꎬ1ꎬ...ꎬt)ꎬ当大端面上的点Kn=0每次旋转θ角度ꎬ就完成一条球面渐开线曲线ꎬ线段OK0作为纯滚动时的切线就自动转过一定的角度θnꎬ以下一点Kn=1再作空间球面渐开线运动形成一条球面渐开线曲线ꎬ循环上述操作ꎬ直到产形线起点K0指向末点Ktꎬ则所有球面渐开线曲线构成了整个齿面ꎬ如图2所示ꎮ当球面半径R和旋转角度θ变化时ꎬ曲线K0Kt点Kn(n=0ꎬ1ꎬ...ꎬt)所形成的曲线便可形成球面渐开线齿面ꎮ图2㊀球面渐开线齿面形成原理图2㊀弧齿锥齿轮齿面的基本组成2.1㊀弧齿锥齿轮球面渐开线如图3所示ꎬ节平面为产形面ꎬ所绘制的圆为齿宽的中点圆ꎻO1为刀盘中心位置ꎬ刀盘半径是RDꎬO是锥顶ꎬ螺旋角为LXJꎮ通过余弦定理可求得:L1=LM2+RD2-2ˑLMˑRDˑsin(LXJ)(8)对于外锥距为Rꎬ齿宽为B的弧齿锥齿轮ꎬ弧齿锥齿轮中的任意一条球面渐开线所对应的球面半径如下式表示:Rbi=R-(i-1)B/(n-1)(9)弧齿锥齿轮球面渐开线上点Si角度为:Si=180-arccosL21+RD2-R2bi2ˑL1ˑRD(10)图3㊀刀盘位置及几何关系球面渐开线中的点所对应的偏角ZJi为:ZJi=arccosL1+RDcosSi(RDsinSi)2+(L1+RDsinSi)2(11)83 组合机床与自动化加工技术㊀第9期ρ=Rbiθ=δk=δf+(δa-δf)tϕi=(ZJi-ZJ1)/sinδ{(12)在坐标系中从大端到任意一条齿形曲线所转过角度为ϕiꎬδ为齿轮分度圆锥角ꎬδa为齿顶角ꎮ与其对称一侧球面渐开线如式(13)所示:ϕi=(ZJi-ZJ1)/sinδ-(360z-ϕb)(13)其它参数与式(12)相同ꎮ上面公式是根锥角大于基锥角的情况ꎻ当根锥角小于基锥角时ꎬ根锥角到基锥角这段曲线用公式表示如下:θ=δk=δf+(δb-δf)t(14)式中ꎬδb为基锥角ꎮ基锥角到齿顶角的这段曲线用式(15)表示:θ=δk=δf+(δa-δb)t(15)式中ꎬδa为齿顶角ꎮ2.2㊀齿根曲线和齿顶曲线公式齿根曲线是齿根圆上的一段圆弧ꎬ公式如下:ρ=Rθ=δk=δfϕ=βk+δfst{(16)另一侧齿根曲线表示:ϕ=βk-(360z-ϕf)(17)其它参数与上相同ꎮ而齿顶的求解与齿根类似ꎬ只需将根锥角换成顶锥角ꎬ将根锥齿厚角换成顶锥齿厚角ꎮ2.3㊀齿形曲线弧齿锥齿轮的齿面与节锥的交线称之为节线ꎬ所有节线是齿轮的纵向齿形ꎮ齿面上沿纵向分成h等分ꎬ这样齿面上有h条齿形曲线ꎬ每条齿形曲线分成t等分ꎬ则每条齿形曲线上的i等分的点的偏角为:Si=S1+(i-1)(Sn-S1)/t(18)式中ꎬi从1~tꎬS1㊁Sn分别是式(10)中i=1和i=n的取值ꎮZJi=arccosL1+RDcosSi(RDsinSi)2+(L1+RDsinSi)2(19)R=(L1+RDcosSi)/cos(ZJi)θ=δfi=δf+(δa-δf)(i-1)/(h-1)ϕi=βi-(Q1-ZJ(i)/sin(δ)){(20)另一侧的齿形曲线可表示为:DYi=FYCHJ+2(β-βi)(21)ϕi=βi-(Q1-ZJ(i)/sin(δ))+DYi(22)FYCHJ为分度圆齿厚角ꎬβ为分度圆偏角ꎬ其它参数与式(20)相同ꎮ上述是根锥角大于基锥角情况ꎬ当根锥角小于基锥角ꎬ则根锥角到基锥角这段曲线公式为:θ=δfi=δb+(δa-δb)(i-1)/(h-1)(23)基锥角到齿顶角的这段曲线公式与根锥角大于基锥角相同ꎮ2.4㊀齿根过渡曲面连接齿面和齿根的过渡曲面部分ꎬ可以通过倒角圆方法进行优化处理:(1)当基锥角小于根锥角时ꎬ球面渐开线是与齿根曲线相交ꎬ则齿根过渡曲面可以采用变半径倒圆角[10]的方法来处理ꎮRf=0.3mne(24)式中ꎬmne为法向模数ꎮ(2)当基锥角大于根锥角时ꎬ弧齿锥齿轮在基圆内没有球面渐开线ꎬ则弧齿锥齿轮过渡部分圆角曲线的起点为基圆与球面球面渐开线的交点ꎬ终点为基圆与齿根曲线的交点ꎮ3㊀轮齿有限元网格划分方法根据轮齿的端面齿廓形状ꎬ可以将整个端面划分为6大子块ꎬ网格划分的方法如下所述:B点和I点是齿面和齿根过渡曲面分界点ꎬ先连接齿顶和齿根的中点K点和L点ꎬ然后根据端面的形状确定KL线段中的O点ꎬ最后确定轮毂上的侧面的D点和G点的位图4㊀弧齿锥齿轮的轮齿端面㊀㊀分块图置ꎬB点和I点是齿面和齿根过渡曲面分界点ꎬ分别连接OB㊁OI㊁OG㊁OD㊁OL㊁OKꎬ如图4所示ꎮ根据齿廓上渐开线分成的n等分ꎬ可将KO分成相应的n等分ꎻ齿轮啮合时齿根过渡部分应力集中ꎬ这时齿根过渡部分网格划分相对比较密集ꎬOG㊁DO㊁EL㊁LF划分数目与齿根以及齿根过渡部分BC和IH数目相同ꎻ将BO㊁OI㊁CD㊁HG划分的等分与齿顶AK与KJ所划分数目相同ꎮ4㊀实例以表1中 小轮左旋㊁大轮右旋 的弧齿锥齿轮副为例ꎬ在MATLAB环境下按照上述方法参数化地建立起了弧齿锥齿轮网格模型ꎮ表1㊀齿轮副的基本参数基本参数小轮大轮齿数z1㊁z2637旋向右左轴交角(o)90模数(mm)7.95压力角(o)22.5高度变位系数0.38切向变位系数0.25中点螺旋角(o)35.7齿高系数0.85顶隙系数0.188齿宽b(mm)45刀盘直径D(mm)304.8Step1:绘出弧齿锥齿轮一个齿面ꎮ齿面上沿齿廓93 2018年9月㊀㊀倪胜利ꎬ等:球面渐开线弧齿锥齿轮参数化建模方向球面渐开线划分n等分ꎬ沿齿向方向划分h等分ꎬ本文中n取11ꎬh取9ꎮ在MATLAB中根据公式(8)~公式(15)编写参数化程序ꎬ将表1中的数据齿数z1㊁z2等参数代入到上述公式画出11条球面渐开线ꎮ在MATLAB中根据公式(18)~公式(23)编写参数化程序ꎬ将表1中的数据代入到上述公式画出9条齿形曲线ꎮ由11条球面渐开线和9条齿形曲线画出的一个齿面如图5所示ꎮStep2:确定齿根的过渡曲面ꎮ根据公式(24)可以将齿根的过渡曲面画出来ꎮ齿面和齿根的过渡曲面如图6所示ꎮ㊀㊀㊀㊀图5㊀弧齿锥齿轮的㊀㊀㊀㊀㊀㊀㊀工作齿面㊀㊀㊀图6㊀弧齿锥齿轮的工作㊀㊀㊀㊀齿面与齿根的过渡曲面Step3:对应的齿面与齿根圆角部分如图7所示ꎮ球面渐开线与对应一侧球面渐开线公式区别在于转过角度ϕi不同ꎬ齿形曲线与对应一侧齿形曲线公式区别在于转过角度ϕi不同ꎬ通过公式(8)~公式(15)与公式(18)~公式(23)可以对应的齿面ꎮ㊀㊀图7㊀一对弧齿锥齿轮的㊀㊀㊀㊀齿面与齿根的过渡曲面㊀㊀图8㊀齿面㊁齿根的过渡㊀㊀㊀㊀㊀曲面与齿顶面Step4:确定齿顶面ꎮ将表1中的参数代入到公式(16)㊁公式(17)中ꎬ绘出齿顶面ꎬ如图8所示ꎮStep5:确定齿根面ꎮ将表1中的参数代入到公式(16)㊁公式(17)中ꎬ绘出齿根面ꎬ如图9所示ꎮ图9㊀齿面㊁过渡曲面㊁齿顶面㊁齿根面和侧面Step6:确定齿轮的体网格ꎮ弧齿锥齿轮的齿顶面㊁齿根面㊁齿面与倒圆角部分划分网格如图9所示ꎬ齿轮大小端面的网格可以按照图4确定ꎬ最后由齿向方向所划分的数目可以将齿轮的体网格参数化划分ꎬ如图10所示ꎮ图10㊀弧齿锥齿轮的网格划分由图10看出ꎬ齿根过渡曲面与齿根曲面以及齿面光滑地连接起来ꎬ不存在干涉问题ꎮ5㊀结论本文提出的球面渐开线形成理论ꎬ易于编程ꎬ实用性强ꎮ本模型完全可以在MATLAB环境中进行编程建模ꎬ减少了以前复杂绘图的时间ꎮ只需输入齿轮副的基本参数程序自动绘制出弧齿锥齿轮模型ꎮ(1)用MATLAB参数化建模能得出弧齿锥齿轮的空间点的坐标ꎬ为齿轮设计和加工提供了便利ꎮ(2)其精确地参数化齿轮模型能提供有效的齿面信息ꎬ为进一步TCA等分析打下基础ꎮ(3)该程序能为有限元分析提供前处理网格信息ꎬ对弧齿锥齿轮进行加载啮合分析ꎬ计算出齿轮啮合时的应力和应变大小ꎮ(4)根据齿轮啮合噪声的大小对齿面进行修形ꎬ在MATLAB环境里修改齿面空间点的坐标ꎬ即在齿廓方向上对齿顶和齿根进行修形ꎬ在齿向上对大端和小端进行修形ꎮ[参考文献][1]李兆文ꎬ王勇ꎬ万金领.基于实际切齿方法的弧齿锥齿轮建模与仿真[J].组合机床与自动化加工技术ꎬ2008(6):26-30.[2]张武刚ꎬ赵栓峰ꎬ张传伟.弧齿锥齿轮半滚切法与滚动检验仿真[J].组合机床与自动化加工技术ꎬ2013(9):121-124.[3]任燕ꎬ贾育秦ꎬ张帅ꎬ等.基于MATLAB和SolidWorks的弧齿锥齿轮三维精确建模[J].机械工程与自动化ꎬ2014(4):220-223.[4]杨宏斌ꎬ王强ꎬ王鸿昌.基于Solidworks的弧齿锥齿轮齿面三维精确建模[J].中国农机化学报ꎬ2015ꎬ36(1):74-77.[5]LitvinFLꎬFuentesAꎬHayasakaK.Designꎬmanufactureꎬstressꎬandexperimentaltestsoflow ̄noisehighendurancespiralbevelgears[J].MechanismandMachineTheoryꎬ2006ꎬ41:83-118.[6]唐进元ꎬ曹康ꎬ杜晋ꎬ等.含过渡曲面的弧齿锥齿轮齿面精确建模[J].机械科学与技术ꎬ2009ꎬ28(3):317-321.[7]刘光磊ꎬ樊红卫.含齿根过渡曲面的弧齿锥齿轮有限元精确建模[J].机械科学与技术ꎬ2010ꎬ29(12):1595-1600.[8]李丹红ꎬ阿达依.谢尔亚孜旦ꎬ丁撼ꎬ等.球面渐开线齿形的弧齿锥齿轮建模及优化[J].组合机床与自动化加工技术ꎬ2015(1):9-12.[9]董慧敏.基于柔轮变形函数的谐波齿轮传动几何学及其啮合性能研究[D].大连:大连理工大学ꎬ2008.(编辑㊀李秀敏)04 组合机床与自动化加工技术㊀第9期。
