2013届高三北师大版文科数学一轮复习课时作业(33)数列的综合应用B)

合集下载

【走向高考】高三数学一轮总复习 6-5数列的综合应用课件北师大版

课前自主预习
知识梳理 1．数列在实际生活中有着广泛的应用，其解题的基本步骤，可用图表示如下：审题，找出题意 ――→ 实际应用题构建数列模型与结论间的数学关系
与数列有关的数学问题
数学问题的解
2．数列应用题常见模型： (1)等差模型：如果增加(或减少)的量是一个固定量时，该模型是等差模型，增加(或减少)的量就是公差． (2)等比模型：如果后一个量与前一个量的比是一个固定的数时，该模型是等比模型，这个固定的数就是公比． (3)递推数列模型：如果题目中给出的前后两项之间的关系不固定，随项的变化而变化时，应考虑是 an 与 an＋1 的递推关系，还是前 n 项和 Sn 与 Sn＋1 之间的递推关系．
[答案] B
)
B．7s D．9s
[解析]
设至少需要 ns，则
1＋21＋22＋…＋2n－1≥100， 1－2n ∴ ≥100，∴n≥7.故选 B. 1－2
5．(2012· 合肥模拟)秋末冬初，流感盛行，某医院近 30 天每天入院治疗流感的人数依次构成数列{an}，已知 a1＝1，a2 ＝2，且 an＋2－an＝1＋(－1)n(n∈N＋)，则该医院 30 天入院治疗流感的人数共有________．
课堂典例讲练
等差数列与等比数列的综合应用
[例 1]
设数列{an}的前 n 项和为 Sn，且(3－m)Sn＋2man
＝m＋3(n∈N＋)，其中 m 为常数，m≠－3，且 m≠0. (1)求证：{an}是等比数列； 3 (2)若数列{an}的公比满足 q＝f(m)且 b1＝a1，bn＝2f(bn－
[答案] 2n2＋6n
[解析]
令 n＝1 得 a1＝4，即 a1＝16，
当 n≥2 时， an＝(n2＋3n)－[(n－1)2＋3(n－1)]＝2n＋2，所以 an＝4(n＋1)2，当 n＝1 也适合，所以 an＝4(n＋1)2(n∈N＋)． an a1 a2 an 于是＝4(n＋1)，故 2 ＋ 3 ＋…＋＝2n2＋6n. n＋1 n＋1

高三一轮复习北师大版5.5 数列的综合应用

[难点正本
疑点清源]
1．用函数的观点理解等差数列、等比数列 (1)对于等差数列，由an＝a1＋(n－1)d＝dn＋(a1－d)，当 d≠0时，an是关于n的一次函数，对应的点(n，an)是位于直线上的若干个离散的点．当d>0时，函数是增函数，对应的数列是递增数列；同理，d＝0时，函数是常函数，对应的数列是常数列；d<0时，函数是减函数，对应的数列是递减数列．若等差数列的前n项和为Sn，则Sn＝pn2＋qn (p、q∈R)．当 p＝0时，{an}为常数列；当p≠0时，可用二次函数的方法解决等差数列问题．
要点梳理
1．等比数列与等差数列比较
不同点 (1)强调从第二项起每一等差数列项与前一项的差； (2)a1 和 d 可以为零； (3)等差中项唯一 (1)强调从第二项起每一等比数列项与前一项的比； (2)a1 与 q 均不为零； (3)等比中项有两个值相同点 (1)都强调从第二项起每一项与前一项的关系； (2)结果都必须是同一个常数； (3)数列都可由 a1， d 或 a1，q 确定
3 2 45 d 5a1 d 50, 3a1 2 2 2 (a1 3d ) a1 (a1 12d ),
a1 3, 解得 d 2,
∴an=a1+(n-1)d=3+2×(n-1)=2n+1,即an=2n+1.
a2 =2×2n+1=2n+1+1, (2)由已知得,bn=
5.5 数列的综合应用
考 1
点
考纲解读以数列知识为载体考查数学建模和运用数列知识解决实际问题的能力.
运用数列的概念、公式、性质解决简单的实际问题
数列的综合应用问题既能考查潜能,又具有较强的区分度,创新应用问题选材也可以用数列为背景,在近几年的高考试题解答题中,有关数列的试题出现的频率较高,不仅可与函数、方程、不等式相关联,还可与三角、几何、复数等知识相结合,题目新颖,难度较大,对数学思想方法的运用和各种数学能力的要求较高. 在复习中要重视紧扣等差、等比数列的性质和定义,做到合理地分析,灵巧

北师版高考总复习一轮文科数学精品课件第6章数列解答题专项三数列

整理可得a1=b1,得证.
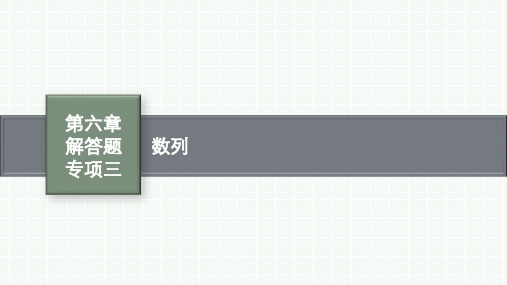
(2)解:由(1)知d=2b1=2a1,由bk=am+a1,可得b1·
2k-1=a1+(m-1)d+a1,即b1·
2k-1
=b1+(m-1)·
2b1+b1,得2k-1=2m.
∵1≤m≤500,∴2≤2k-1≤1 000.
∴2≤k≤10.
又k∈Z,故集合{k|bk=am+a1,1≤m≤500}中元素的个数为9.
所以 − -1 =1(n≥2),
所以数列{ }是以 1 = 1 =1 为首项,公差为 1 的等差数列,
所以 =1+(n-1)×1=n,则 Sn=n2,
当 n≥2 时,an= + -1 =n+n-1=2n-1,又 a1=1 满足上式,
所以{an}的通项公式为 an=2n-1.
(1)求{an}的公比q;
(2)对于任意
- 1
2 17
2
例1(2022全国甲,文17)设Sn为数列{an}的前n项和.已知
+n=2an+1.

(1)证明:{an}是等差数列;
(2)若a4,a7,a9成等比数列,求Sn的最小值.
2
(1)证明:由 +n=2an+1,变形为2Sn=2nan+n-n2,记为①式,又当n≥2时,有

2Sn-1=2(n-1)an-1+n-1-(n-1)2,记为②式,①-②并整理可得(2n-2)an-(2n-2)an-1
13-5 ≤ 0,
即实数 k 的取值范围是
13 11
,
5 4
.
Байду номын сангаас
规律方法 1.新定义数列问题的特点

3-3 等比数列-2013届高考文科数学第一轮考点总复习课件

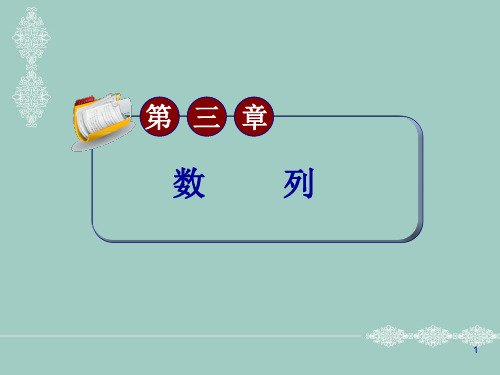
ac 五、若a，c同号，则a，c的等
比中项为11 ________ .
六、等比数列中的解题技巧与
经验
等差数列
5
2.三个数成等比数列可设这三
个aq 数a,a为q 13 __________，四个正数成等
比数列a可3q , aq设a这q,a四q3 个数为14
____________. an1 q
na1(q 1)
a1 - anq 1- q
(q
1)
则Sn=⑥___________=⑦
=
___________.
4
2.等比数列{an}中，Sn为其前n
项和，q为公比，当n为偶数q 时，S偶=S
奇·⑨___.
3.公比成不等比为数1的列等比数列{an}中，
Sk，S2k-Sk，S3k-S2k⑩_____________.
35p)，
解得p=3或p=2.
16
(2)要证{cn}不是等比数列只需证
c22≠c1·c3. 事实上，c22=(22+32)2=169,
c1·c3=(2+3)(23+33)=175, 因此，c22≠c1·c3,故{cn}不是等比数
列.
点评：判断一个数列是等比数
列或处理相关问题,基本解法是定义法
得p=2或p=3.
cn - pcn-1
解法2：因为{cn+1-pcn}是等比数
列故，存94--32在pp--32非qq零ppqq常00, 数q使得
对 15
解法3：cn+1-pcn=2n+1+3n+1-p·2n-
p·3n，
故c2-pc1=13-5p， c3-pc2=35-13p，

2013高考数学一轮同步训练(文科) 5.5数列的综合应用

2013高考数学一轮强化训练 5.5数列的综合应用文新人教A 版1.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )A.5B.4C.3D.2答案:C解析: 115201552530a d a d +=⎧⎨+=⎩ 3d ⇒=,故选C. 2.等比数列{n a }中1824a a ,=,=,函数12()()()f x x x a x a =--…8()x a -,则 f′(0) 等于( )A.62B.92 C .122 D.152答案:C解析:f′(x 12)()()x a x a =--…8()x a x -+⋅ 12[()()x a x a --… 8()]x a -′, ∴f′12(0)a a =…8a .∵{n a }为等比数列1824a a ,=,=,∴f′12(0)a a =…4412818()82a a a ===.3.在直角坐标系中,O 是坐标原点111()P x y ,,、222()P x y ,是第一象限的两个点,若1214x x ,,,依次成等差数列,而1218y y ,,,依次成等比数列,则△12OPP 的面积是 .答案:1解析:由1214x x ,,,依次成等差数列得1212215x x x x =+,+=,解得1223x x =,=.又由1218y y ,,,依次成等比数列,得212128y y y y =,=,解得1224y y =,=,∴12(22)(34)P P ,,,.∴12(22)(34)OP OP =,,=, .∴126814OP OP ⋅=+=, |1OP|=|2OP |=5, ∴cos 121212OP OP POP OP OP ⋅∠===|||| ∴sin 12POP ∠=∴1212OP P S = |1OP ||2OP|sin 121512POP ∠=⨯=.4.在△ABC 中,三边a,b,c 成等差数列也成等差数列,求证:△ABC 为正三角形.证明:由题设,2b=a+c 且=∴4b a c =++.∴a c +=即20=.从而a=c,∴b=a=c.∴△ABC 是正三角形.题组一等差、等比数列综合问题1.已知等差数列{n a }的公差为2,若134a a a ,,成等比数列,则2a 等于( )A.-4B.-6C.-8D.-10答案:B 解析:∵2143a a a =,∴2222(2)(4)(2)a a a -+=+.∴2212a =-.∴26a =-.2.若一等差数列{n a }的首项15a =-,其前11项的平均值为5,又若从中抽取一项,余下的10项的平均值为4,则抽去的是( )A.8aB.9a C .10a D.11a 答案:D解析:1111110111152S a d ⨯=+=⨯, 可得d=2.由1140n S a -=,得15n a =.即1(1)n a a n d =+-=15.∴n=11.故选D.3.已知数列{n a }是等差数列,若471045617a a a a a a ++=,+++…12131477a a a +++=且13k a =,则k= .答案:18解析:∵779917317117773a a a a =,=,=,=, ∴23d =. 又∵9(9)k a a k d -=-.∴13-72(9)3k =-⨯. ∴k=18.4.已知a,b,a+b 成等差数列,a,b,ab 成等比数列,且0<log ()1m ab <,则m 的取值范围是 .答案:(8),+∞5.设等差数列{n a }的前n 项和为n S ,已知312a =, 121300S S >,< .求公差d 的取值范围.解:依题意有 311211312121211120213121302a a d S a d S a d ⎧=+=,⎪⎪⨯=+>,⎨⎪⨯⎪=+<.⎩ 解之得公差d 的取值范围为2437d -<<-. 题组二数列与函数知识的综合应用6.等比数列{n a }的各项均为正数,且564718a a a a +=,则log 31a +log 32a +…+log 310a 等于( )A.12B.10C.1+log 35D.2+log 35答案:B解析:log 31a +log 32a +…+log 310a =log 312(a a …10)a =log 5356()a a =log 103(3)10=.7.已知等差数列{n a }的前n 项和为n S ,若m>1,且21121038m m m m a a a S -+-+-=,=,则m 等于 ( )A.38B.20C.10D.9答案:C 解析:∵2110m m m a a a -++-=,又112m m m a a a -++=,∴(2)0m m a a -=.∴2m a =.又∵2112121()(21)382m m m m S a a m a ---=+=-=, ∴2m-1=19.∴m=10.8.在△ABC 中,tanA 是以-4为第三项,4为第七项的等差数列的公差,tanB 是以13为第三项,9为第六项的等比数列的公比,则这个三角形是( )A.钝角三角形B.锐角三角形C.等腰直角三角形D.以上都不对答案:B9.等差数列中,若()m n S S m n =≠,则m n S += .答案:0题组三数列在实际问题中的应用10.已知镭经过100年剩留原来质量的95.76%,设质量为1的镭经过x 年后剩留量为y,那么y和x 之间的关系是( ) A.y=0.957 1006xB.y=0.957 1006xC.09576()100x y .= D.y=1-0.042 1004x答案:A11.根据市场调查结果,预测某种家用商品从年初的n 个月内累积的需求量(n S 万件)近似地满足n S =(2190n n -25)(1n n -=,2,…,12).按此预测,在本年度内,需求量超过1.5万件的月份是( )A.5月、6月B.6月、7月C.7月、8月D.8月、9月答案:C解析:当n=1时1116a S ,==; 当2n ≥时12330210n n n n n a S S -,=-=-+-, 即2330210n n n a =-+-. 当n=7或n=8时1n a ,>.5.12.成等差数列的三个正数的和等于15,并且这三个数分别加上2 、5、13后成为等比数列{n b }中的3b 、b 4、,b 5 .(1)求数列{n b }的通项公式;(2)数列{n b }的前n 项和为n S ,求证:数列{54n S +}是等比数列. 解:(1)设成等差数列的三个正数分别为a-d,a, a+d . 依题意,得a-d+a+a+d=15,解得a=5.所以{n b }中的345b b b ,,依次为7-d,10,18+d,依题意,有(7-d)(18+d)=100,解得d=2或d=-13(舍去). 故{n b }的第3项为5,公比为2,由2312b b =⋅,即2152b =⋅,解得154b =. 所以{n b }是以54为首项,2为公比的等比数列,其通项公式为 n b = 1352524n n --⋅=⋅. (2)证明:数列{n b }的前n 项和5(12)412n n S -==- 25524n -⋅-,即54n S += 252n -.⋅ 所以15115552424252524Sn n S n S n +-+⋅+=,==-+⋅. 因此{54n S +}是以52为首项,公比为2的等比数列.。

[精]高三第一轮复习全套课件3数列：数列的综合应用

新疆源头学子小屋特级教师王新敞
wxckt@ /wxc/
新疆源头学子小屋特级教师王新敞
wxckt@
/wxc/
证明：①根据 S n a n
a 1 , ( n 1) 得 an=a+(n─1) 2b, S n S n 1 , ( n 2 )
新疆源头学子小屋特级教师王新敞
wxckt@ /wxc/
新疆源头学子小屋特级教师王新敞
wxckt@
/wxc/
例 6 数列{an}的前 n 项和 Sn=na+(n─1)nb,(n=1,2,…),a,b 是常数，且 b≠0, ①求证{an}是等差数列； ②求证以(an,Sn/n─1)为坐标的点 Pn 都落在同一直线上，并求出直线方程； ③设 a=1,b=1/2,C 是以(r,r)为圆心，r 为半径的圆(r>0),求使得点 P1,P2,P3 都落在圆外的 r 的取值范围
新疆源头学子小屋特级教师王新敞
wxckt@
/wxc/
解：①依题意，由{an}是等差数列，有 ar+ar+2=2ar+1 (r∈N),即 x=─1 时，方程成立，因此方程恒有实数根 x=─1; ②设公差为 d(化归思想),先解出方程的另一根 mr=─ar+2/ar, ∴ 1/(mr+1)=ar/(ar─ar+2)=─ar/(2d), ∴ 1/(mr+1+1)─1/(mr+1)= 〔─ar+1/(2d)〕─〔─ar/(2d)〕=─1/2, ∴ {1/(mr+1)}是等差数列
∴{an}是等差数列，首项为 a,公比为 2b
②由 x=an=a+(n─1)2b, y=Sn/n─1=a+(n─1)b 两式中消去 n,得：x─2y+a─2=0, （另外算斜率也是一种办法）

高三大一轮复习讲义数学文课时作业：数列的综合应用北师大含解析

课时作业(三十二)数列的综合应用1. (2012.聊城模拟)已知数列｛如的前川项和为S”过点Pm Sd 和β(n+b S n ÷ι)(n∈N*) 的直线的斜率为3/1 — 2»则①+心+心+①的值等于()已知数列｛色｝, ｛仇｝都是公差为1的等差数列，其首项分别为g » 且m+Z η=5, ⑷，⅛I ∈N÷(H ∈N+),则数列“如的前10项的和等于()已知数列｛a n ｝, ｛%｝满足如=1且如如】是函数J(X)=X 2~b n x+2n的两个零点,则仞U 等于((2011.上海卷)设仏｝是各项为正数的无穷数列，人是边长为如“小的矩形的而积(= 1,2,…),则｛∕⅛｝为等比数列的充要条件为()蓄起来，每月初存入银行“元，存期1年(存12次)，到期取出本金和利息.假设一年期零存整取的月利率为儿每期存款按单利计息.那么，小王存款到期利息为.6. (2012.济南模拟)若数列｛⑷｝满足一一7=4H ∈N∣, 〃为常数)，则称数列伽｝为“调和数列”・已知数列｛召为“调和数列”，且X 1+X 2+-→X20=200,则X 3X 18的最大值是7・在等比数列仏｝中，亦＞0("∈N) 公比q∈(0,l),且5心+2“3"5+"2血=25,又心与 “5的等比中项为2.(1) 求数列｛“”｝的通项公式：(2) 设b”=IOg 2如，数列｛切的前"项和为S”当半+多+…+存取最大值时，求”的值.A. 52B. 40C. 26D ・202. a ∖>b ∖^ A. 65 B. 75 C. 85D ・953・ A. 24B. 32C. 48D ・644. A. ｛心｝是等比数列B ・ a↑9 "3，…,^2∕∣-ι> …或心C ・ a ∖, "3，…，^2π-l> …和G2, 知…，U2jnD ・ ait "3,…,t∕2∏-ι>…和G2, Ol,…，<∕2∕rt5.小王每月除去所有日常开支，大约结余"7…均是等比数列，且公比相同・小王决左采用零存整取的方式把余钱积…是等比数列 …均是等比数列利r + "("为奇数> 7? ∈ N ♦) 8. (2012∙湛江模拟)C知数列｛如｝满足“1 = 1,t∕∏+ι=xM n-2n(n为偶数，n∈N ♦)(1)求"2，"3；(2)设%=如一2, "∈N+,求证：数列｛b”｝是等比数列，并求其通项公式:(3)已知 C=Iogl1几1,求证：——-K-—-1 1-—-—<1.°2C]C2 C2C3 c n-∖c nB级1.祖国大陆允许台湾农民到大陆创业以来，在11个省区设立了海峡两岸农业合作试验区和台湾农民创业园，台湾农民在那里申办个体工商户可以享受“绿色通道”的申请、受理、审批一站式服务，某台商到大陆一创业园投资72万美元建起一座蔬菜加工厂，第一年各种经费12万美元，以后每年增加4万美元，每年销售蔬菜收入50万美元，设_/0?)表示前"年的纯收入.(/(”)=前∏年的总收入一前n年的总支出一投资额)(1)从第几年开始获取纯利润？(2)若干年后，该台商为开发新项目，有两种处理方案：①年平均利润最大时以48万美元岀售该厂：②纯利润总和最大时，以16万美元岀售该厂，问哪种方案最合算？2.(2012∙Γ州市调研)已知数列仏｝中,αι=b 血=3,且‰÷ι=αn+2α∏-ι(n≥2).⑴设b“=如］+肋”，是否存在实数2,使数列｛九｝为等比数列.若存在,求岀2的值，若不存在，请说明理由；(2)求数列伽｝的前几项和Sm课时作业(三十二)A 级S H + 1 - Sn1. B由题R %十―严"J.β.S π+ ]・ S n = 3π - 2 t 即 αn ÷ι = 3n - 2 t ：.Un = 3?? - 5 , 因此数列｛⑷｝是等差数列^/5=IO f.∙."2 +"4 +"5 +49 = 2(心十"7)= 4么5 = 40. 2.C 应用等差数列的通项公式得Un=a ∖^∏ -1» b∏=b ∖^∏-1,A UhI X =a↑^b n -1 ="ι + (Z η+n- I)-1=Cι∖ +b] + 办―2=5+〃 — 2=打 + 3,6∕∏÷23・D 依题意有“伽+】二2" •所以<θ!÷κ∕∕1÷2 = 2υ+l■两式相除得一^二2.所以“1山3 t as ，… 成等比数歹U , ιi2 , U4 I U(I ,…也成等比数歹I 」，而"1二1 , in = !所以t∕ιo = 2∙24= 32 , <∕u 二1∙25= 32.又因为 Un 十 απ+1 = b n r 所以 bio = UIO + a∏ = 64.4. D ∙.∙An,若｛A”｝为等比数列，贝厂孚=丝4=宁为常数，即牛=半，Y=Λ∣ι U n a n \ 1 Un Λ∖ a ∖ Ai "4— • • • "2‘.∙."1, CI3, "5，…，…和“2，"4，…，CllJi>…成等比数列，且公比相等.反之，若奇数项和偶数项分别成等比数列，且公比相等，设为⑴则学I=罟=q,从而｛/V ｝为等比数列.12(12+1)5. 解析：由题意知/小王存款到期利息为12"+ 1 h∕r+ l‰r+…十2ar + Ur = ~Ur = 7答案：78"6. 解析：因为数列｛三：为“调和数列”，所以X" + ∣-X" = c∕G∈N+ , d 为常数)，答案•••数列｛心｝也是等差数列, 且前10项和为10×(4÷13)=85.即数列20(A∣ + .¥20) 20(x3 + Xjg)仇｝为等差数歹∣J ,由 Xi +X2+…十X20 = 200 得 --- 5 ----- 二-- = 200 r即 X3+XIS = 20I易知X3 r和都为正数时，心18取得最大值，所以A^I8≤丄占2=I OO r即心W的最大值为∖ L ) 100.答案：1007・解析：(1)因为a↑U5 + 2如"5十"2心=25 r所以aj + IayaS十加=25 ,又Un>O f所以“3 + as = 5.又(13与"5的等比中项为2 ,所以U3U5 = 4.而gW(OJ),所以心>心/所以心二4 ,5二1 ,所以 g = * , "1 = 16 ,所以""二 16x(g"-1 =25^fl.(2)bn -10g2<∕H = 5 - 7? f所以/λ∕÷ 1 - /?;I=-I l故血｝是以仞二4为首项，-I为公差的等差数列，当π≤8时，存>0 ；当”二9时，中二O ；当“>9时，中<0 ；所以当/? = 8或9时，¥十丰十¥ +…+弓1取最大值•3 58.解析：⑴由数列｛如的递推关系易知：宀二扌r "3二运⑵证明：∕λ∣÷ι = am 2 -2 = y<∕2∕r÷] + ⑵】+ 1) - 2=如加 +1 + (2H - 1)=去2n - 4n) + (2n - 1)=Jt - 1 二如2厂 2) = *b rh… 1 仇+1 1又仞二"2 - 2二--t .∖b ll≠0 t :Γ-^-=-,即数列｛如是公比为+,首项为-土的等比数列,亠二丄丄心2). (n - 1)/? n - 1 n= IlII +I =I _1<L2 23 H _ J H H1・解析：由题意，知每年的经费是以12为首项，4为公差的等差数列・设纯利:闰与年贝0/(«) = 50?! - 12n + - X 4 ■ 72 = - 2n 2+ 40/? - 72.（1）获取巒IJ 润就是要求和）> O ,故有・2τr + 40n ・72 > 0『解得2 S V 18・又n∈N + r 知从第三年开始获利・ ⑵①平均利润为豊2二40 - 2（”十普）W16 ,当且仅当”二6时取等号•故此方案获利6× 16 + 48= 144（万美元）/此时H = 6.@f(n) = - 2n 2 + 40n - 72 = - 2(n - IO)2+ 128 ,当办二 10 时 z J(H)I n dX = 12&故此方案共获禾IJ 128 + 16= 144（万美元）・比较两种方案，第①种方案只需6年r 第②种方案需要10年，故选择第①种方案・ 2・解析：（1）假设存在实数2 ,使数列｛b n ｝为等I ：匕数列，即 U n +1 + λa n = q(a n + λa n .i ) I 得 U n ÷ι = (</ - λ)a,t + qλa n .∖.q - λ=∖t 解得2二1或2二-2.6二 2 所以存在实数R ■使数列伽｝为等比数列■当2二1时，"二2肠二4 ,则数列血｝是首项为4 ,公比为2的等t 缴列；当2二・2时,q 二 m ■则数列｛%｝是首项为1 r 公比为・1的等比数列・1 1 .∙. + + •••十 g C2C36•心 11十…十--------+ ------- "1X2 2X3](n - 1)/?h∏ 设応T2）.与已知1二ChI 十2心-1比较I 令中τ÷市τs ÷ 駆T .+能⅛⅛⅛+τT R 昴h '-N +邑∙ΓE⅛、(爪ΓA ∙。

2013届高三人教B版文科数学一轮复习课时作业(33)数列的综合应用A

课时作业(三十三)A [第33讲数列的综合应用][时间：45分钟分值：100分]基础热身1．数列{a n }中，a 1＝1，对所有的n ≥2都有a 1·a 2·a 3·…·a n ＝n 2，则a 3＝( ) A.32 B.94 C.259 D.2516 2．[2011·东北三校一模] ( )A ．求数列⎩⎨⎧⎭⎬⎫1n 的前10项和 B ．求数列⎩⎨⎧⎭⎬⎫12n 的前10项和C ．求数列⎩⎨⎧⎭⎬⎫1n 的前11项和D ．求数列⎩⎨⎧⎭⎬⎫12n 的前11项和3．一条信息，若一人得知后用一小时将信息传给两个人，这两个人又用一小时各传给未知信息的另外两个人，如此继续下去，要传遍100万人口的城市，所需的时间大约为( )A ．三个月B ．一个月C ．10天D ．20小时4．已知数列{a n }的首项a 1＝1，且点A n (a n ，a n ＋1)在函数y ＝xx ＋1的图象上．则该数列{a n }的通项公式是a n ＝________.能力提升 5．[2011·济南二模] 数列{a n }的前n 项和为S n ，若S n ＝2n 2－17n ，则当S n 取得最小值时n 的值为( ) A ．4或5 B ．5或6 C ．4 D ．5 6．[2011·天津卷] 已知{a n }为等差数列，其公差为－2，且a 7是a 3与a 9的等比中项，S n 为{a n }的前n 项和，n ∈N *，则S 10的值为( )A ．－110B ．－90C ．90D ．110 7．[2011·衡水模拟] 设等比数列的公比为q ，前n 项和为S n ，若S n ，S n ＋1，S n ＋2成等差数列，则公比q ( )A ．等于－2B ．等于1C ．等于1或－2D ．不存在8．[2011·合肥一中月考] 各项均为正数的等比数列{a n }的公比q ≠1，a 2，12a 3，a 1成等差数列，则a 3a 4＋a 2a 6a 2a 6＋a 4a 5＝( )A.5＋12B.5－12C.3－52D.2＋529．[2011·陕西卷] 植树节某班20名同学在一段直线公路一侧植树，每人植一棵，相邻两棵树相距10米，开始时需将树苗集中放置在某一树坑旁边，现将树坑从1到20依次编号，为使各位同学从各自树坑前来领取树苗所走的路程总和最小，树苗可以放置的两个最佳坑位的编号为( )A ．①和⑳B ．⑨和⑩C ．⑨和⑪D ．⑩和⑪ 10．数列{a n }中，a 1＝2，点(log 3a n ，a n ＋1)在函数y ＝2×3x 的图象上，则{a n }的通项公式为a n ＝________.11．[2011·虹口区质检] 数列{a n }的前n 项和S n ＝n 2＋n －3，则通项公式a n ＝________.12．[2011·广东六校联考] 已知数列{a n }满足a 1＝23，且对任意的正整数m 、n 都有a m ＋n ＝a m ·a n .若数列{a n }的前n 项和为S n ，则S n ＝________.13．[2011·菏泽二模] 已知a n ＝2n －1(n ∈N ＋)，把数列{a n }的各项排成如图K33－2所示的三角数阵．记S (m ，n )表示该数阵中第m 行中从左到右的第n 个数，则S (10,6)对应数阵中的数是________．1 3 5 7 9 11 13 15 17 19… 图K33－214．(10分)[2012·惠州模拟] 当p 1，p 2，…，p n 均为正数时，称np 1＋p 2＋…＋p n为p 1，p 2，…，p n 的“均倒数”．已知数列{a n }的各项均为正数，且其前n 项的“均倒数”为12n ＋1.(1)求数列{a n }的通项公式；(2)设c n ＝a n2n ＋1(n ∈N *)，试比较c n ＋1与c n 的大小．15．(13分)已知数列{a n }中，a 1＝1，a n ＋1＝a n2a n ＋1(n ∈N *)．(1)求数列{a n }的通项公式a n ；(2)设：2b n ＝1a n＋1，求数列{b n b n ＋1}的前n 项和T n .难点突破16．(12分)设数列{b n }满足：b 1＝12，b n ＋1＝b 2n ＋b n . (1)求证：1b n ＋1＝1b n －1b n ＋1；(2)若T n ＝1b 1＋1＋1b 2＋1＋…＋1b n ＋1，对任意的正整数n,3T n －log 2m －5>0恒成立．求m 的取值范围．课时作业(三十三)A【基础热身】1．B [解析] a 2＝22a 1＝4，a 3＝32a 1a 2＝94.故选B.2．B [解析] 可知S ＝12＋14＋…＋120，所以其描述的是数列⎩⎨⎧⎭⎬⎫12n 的前10项和．3．D [解析] 每小时传递人数构成数列2,4,8，…，所以n 小时共传递人数S n ＝1－2n 1－2＝2n－1≈106，所以n ≈20小时．4.1n [解析] 因为a n ＋1＝a n a n ＋1且a 1＝1，所以1a n ＋1＝1＋1a n ，所以1a n ＋1－1a n＝1. 所以⎩⎨⎧⎭⎬⎫1a n 是以1为首项，1为公差的等差数列.1a n ＝1＋(n －1)×1＝n ，所以a n ＝1n .【能力提升】5．C [解析] 二次函数f (x )＝2x 2－17x 的对称轴为直线x ＝174，因为n ∈N ＋，所以当n ＝4时，S n ＝2n 2－17n 有最小值．故选C.6．D [解析] 由a 27＝a 3·a 9，d ＝－2，得(a 1－12)2＝(a 1－4)(a 1－16)，解之得a 1＝20，∴S 10＝10×20＋10×92(－2)＝110. 7．B [解析] 依题意有2S n ＋1＝S n ＋S n ＋2，当q ≠1时，有2a 1(1－q n ＋1)＝a 1(1－q n )＋a 1(1－q n ＋2)，解得q ＝1，但q ≠1，所以方程无解；当q ＝1时，满足条件．故选B.8．B [解析] 依题意，有a 3＝a 1＋a 2，设公比为q ，则有q 2－q －1＝0，所以q ＝1＋52(舍去负值).a 3a 4＋a 2a 6a 2a 6＋a 4a 5＝a 2a 4(q ＋q 2)a 2a 4(q 2＋q 3)＝1q ＝21＋5＝5－12.故选B. 9．D [解析] 从实际问题中考虑将树苗放在最中间的坑旁边，则每个人所走的路程和最小，一共20个坑，为偶数，在中间的有两个坑为10和11号坑，故答案选D.10．2n [解析] 由已知得a n ＋1＝2×3log 3a n ＝2a n ，显然{a n }的各项不为零，所以a n ＋1a n＝2，数列{a n }是首项为2，公比为2的等比数列，a n ＝2×2n －1＝2n .11.⎩⎪⎨⎪⎧－1(n ＝1)，2n (n ≥2)[解析] n ＝1时，a n ＝－1；n ≥2时，a n ＝S n －S n －1＝2n ，所以a n ＝⎩⎪⎨⎪⎧－1(n ＝1)，2n (n ≥2).12．2－2n ＋13n [解析] 令m ＝1，得a n ＋1＝a 1·a n ，即a n ＋1a n ＝a 1＝23，可知数列{a n }是首项为a 1＝23，公比为q ＝23的等比数列，于是S n ＝a 1(1－q n)1－q＝23×⎣⎡⎦⎤1－⎝⎛⎭⎫23n 1－23，＝2⎣⎡⎦⎤1－⎝⎛⎭⎫23n ＝2－2n ＋13n .13．101 [解析] 观察知每一行的第1个数构成数列：1,3,7,13,21，…，相邻两项构成递推关系：a n ＋1＝a n ＋2n ，所以a 10＝a 9＋18＝a 8＋16＋18＝a 7＋14＋34＝a 6＋12＋48＝a 5＋10＋60＝a 4＋8＋70＝13＋78＝91，即第10行的第1个数为91，所以第10行第6个数为101. 14．[解答] (1)由已知有a 1＋a 2＋…＋a n －1＋a n ＝n (2n ＋1)，则a 1＋a 2＋…＋a n －1＝(n －1)(2n －1)，两式相减，得a n ＝4n －1(n ≥2)．又1a 1＝12×1＋1，解得a 1＝3＝4×1－1， ∴a n ＝4n －1(n ∈N *)．(2)∵c n ＝a n 2n ＋1＝4n －12n ＋1＝2－32n ＋1，c n ＋1＝a n ＋12n ＋3＝2－32n ＋3，∴c n ＋1－c n ＝32n ＋1－32n ＋3＞0，即c n ＋1＞c n .15．[解答] (1)由a n ＋1＝a n 2a n ＋1得1a n ＋1－1a n＝2且1a 1＝1，所以数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项，以2为公差的等差数列，所以1a n ＝1＋2(n －1)＝2n －1，得a n ＝12n －1.(2)由2b n ＝1a n ＋1得2b n ＝2n －1＋1＝2n ，∴b n ＝1n，从而b n b n ＋1＝1n (n ＋1)，则T n ＝b 1b 2＋b 2b 3＋…＋b n b n ＋1＝11×2＋12×3＋…＋1n (n ＋1)＝⎝⎛⎭⎫11－12＋⎝⎛⎭⎫12－13＋⎝⎛⎭⎫13－14＋…＋⎝⎛⎭⎫1n －1n ＋1 ＝1－1n ＋1＝nn ＋1.【难点突破】16．[解答] (1)因为b 1＝12，b n ＋1＝b 2n ＋b n ＝b n (b n ＋1)，所以对任意的n ∈N *，b n >0. 所以1b n ＋1＝1b n (b n ＋1)＝1b n －1b n ＋1，即1b n ＋1＝1b n －1b n ＋1. (2)T n ＝⎝⎛⎭⎫1b 1－1b 2＋⎝⎛⎭⎫1b 2－1b 3＋…＋⎝⎛⎭⎫1b n －1b n ＋1＝1b 1－1b n ＋1＝2－1b n ＋1. 因为b n ＋1－b n ＝b 2n >0， ∴b n ＋1>b n ，所以数列{b n }是单调递增数列．所以数列{T n }关于n 递增．所以T n ≥T 1.因为b 1＝12，所以b 2＝b 1(b 1＋1)＝34，所以T 1＝2－1b 2＝23，所以T n ≥23.因为3T n －log 2m －5>0恒成立，所以log 2m <3T n －5恒成立，所以log 2m <－3，所以0<m <18.。

【北师大版】高三数学一轮课时作业【32】(含答案)

课时作业32 数列的综合应用一、选择题(每小题5分，共40分)1．已知{a n }为等比数列．下面结论中正确的是( )A ．a 1＋a 3≥2a 2B ．a 21＋a 23≥2a 22C ．若a 1＝a 3，则a 1＝a 2D ．若a 3>a 1，则a 4>a 2解析：设公比为q ，对于选项A ，当a 1<0，q ≠1时不正确；选项C ，当q ＝－1时不正确；选项D ，当a 1＝1，q ＝－2时不正确；选项B 正确，因为a 21＋a 23≥2a 1a 3＝2a 22.答案：B2．(2014·威海期中)某化工厂打算投入一条新的生产线，但需要经环保部门审批同意方可投入生产．已知该生产线连续生产n 年的累计产量为f (n )＝12n (n ＋1)(2n ＋1)吨，但如果年产量超过150吨，将会给环境造成危害．为保护环境，环保部门应给该厂这条生产线拟定最长的生产期限是( )A ．5年B ．6年C ．7年D ．8年解析：由已知可得第n 年的产量a n ＝f (n )－f (n －1)＝3n 2.当n ＝1时也适合，据题意令a n ≥150⇒n ≥52，即数列从第8项开始超过150，即这条生产线最多生产7年．答案：C3．(2013·福州模拟)在等差数列{a n }中，满足3a 4＝7a 7，且a 1>0，S n 是数列{a n }前n 项的和，若S n 取得最大值，则n ＝( )A ．7B ．8C ．9D ．10解析：设公差为d ，由题设3(a 1＋3d )＝7(a 1＋6d )，所以d ＝－433a 1<0.解不等式a n >0，即a 1＋(n －1)(－433a 1)>0，所以n <374，则n ≤9，当n ≤9时，a n >0，同理可得n ≥10时，a n <0. 故当n ＝9时，S n 取得最大值．答案：C4．黑白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案，则第n 个图案中有白色地砖的块数是( )A ．4n ＋2B ．4n －2C ．2n ＋4D ．3n ＋3解析：白色地砖的块数成等差数列，其公差为4，即得通项为4n ＋2.故选A.答案：A5．(2014·湖南十二校联考)设f (x )是定义在R 上恒不为零的函数，对任意x ，y ∈R ，都有f (x )·f (y )＝f (x ＋y )，若a 1＝12，a n ＝f (n )(n ∈N ＋)，则数列{a n }的前n 项和S n 的取值范围是( )A.12≤S n <2B.12≤S n ≤2C.12≤S n ≤1 D.12≤S n <1解析：由条件得：f (n )·f (1)＝f (n ＋1)，即a n ＋1＝a n ·12，所以数列{a n }是首项与公比均为12的等比数列，求和得S n ＝1－(12)n ，所以12≤S n <1.答案：D6．设函数f (x )＝x m＋ax 的导函数f ′(x )＝2x ＋1，则数列{1f (n )}(n∈N ＋)的前n 项和是( )A.n n ＋1B.n ＋2n ＋1C.n n －1D.n ＋1n解析：f ′(x )＝mx m －1＋a ＝2x ＋1，∴a ＝1，m ＝2， ∴f (x )＝x (x ＋1)，1f (n )＝1n (n ＋1)＝1n －1n ＋1，∴S n ＝⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎫1n －1n ＋1＝nn ＋1.答案：A7．(2014·浙江金华一中月考)已知等差数列{a n }的前n 项和为S n ，a 2＝4，S 10＝110，则S n ＋64a n的最小值为( )A ．7B ．8 C.152D.172解析：由题意知⎩⎪⎨⎪⎧ a 1＋d ＝4，10a 1＋45d ＝110.∴⎩⎪⎨⎪⎧a 1＝2，d ＝2.∴S n ＝n 2＋n ，a n ＝2n .∴S n ＋64a n＝n 2＋n ＋642n ＝n 2＋12＋32n ≥12＋2n 2·32n ＝172.等号成立时，n 2＝32n ，∴n ＝8，故选D.答案：D8．(2013·辽宁理，4)下面是关于公差d >0的等差数列{a n }的四个命题：p 1：数列{a n }是递增数列； p 2：数列{na n }是递增数列； p 3：数列{a nn }是递增数列； p 4：数列{a n ＋3nd }是递增数列．其中的真命题为( ) A ．p 1，p 2 B ．p 3，p 4 C ．p 2，p 3D ．p 1，p 4解析：对于p 1，数列{a n }的公差d >0，所以数列是递增数列；对于p 4，因为(a n ＋1＋3(n ＋1)d )－(a n ＋3nd )＝d ＋3(n ＋1)d －3nd ＝4d >0，是递增数列．对于p 2，因为(n ＋1)a n ＋1－na n ＝(n ＋1)a n ＋(n ＋1)d －na n ＝a 1＋2nd ，a 1不知道正负，不一定大于零，所以不一定是递增数列；同理，对于p 3，也不一定是递增数列，选D.答案：D二、填空题(每小题5分，共15分)9．(2014·赣州模拟)设关于x 的不等式x 2－x <2nx (n ∈N ＋)的解集中整数的个数为a n ，数列{a n }的前n 项和为S n ，则S 100的值为________．解析：由x 2－x <2nx (n ∈N ＋)，得0<x <2n ＋1，因此知a n ＝2n . ∴S 100＝100(2＋200)2＝10 100.答案：10 10010．(2014·南通模拟)已知a ，b ，c 成等比数列，如果a ，x ，b 和b ，y ，c 都成等差数列，则a x ＋cy ＝________.解析：赋值法．如令a ，b ，c 分别为2,4,8，可求出x ＝a ＋b2＝3，y ＝b ＋c 2＝6，a x ＋c y ＝2.答案：211．已知α∈(0，π2)∪(π2，π)，且sin α，sin2α，sin4α成等比数列，则α的值为________．解析：由题意，sin 22α＝sin α·sin4α， ∴sin 22α＝2sin α·sin2α·cos2α，即sin2α＝2sin α·cos2α，∴2sin αcos α＝2sin α·cos2α，即cos α＝cos2α， ∴2cos 2α－1＝cos α，∴(2cos α＋1)(cos α－1)＝0. 解得cos α＝1(舍去)或cos α＝－12，∴α＝2π3. 答案：2π3三、解答题(共3小题，每小题15分，共45分．解答写出必要的文字说明，证明过程或演算步骤)12．从4月1日开始，有一新款服装投入某商场销售，4月1日该款销售出10件，第二天销售出25件，第三天销售出40件，以后，每天售出的件数分别递增15件，直到4月12号日销售量达到最大，然后，每天销售的件数分别递减10件．(1)记该款服装四月份日销售量与销售天数n 的关系为a n ，求a n ；(2)求四月份的总销售量．解：(1)依题意，数列a 1，a 2，…，a 12是首项为10，公差为15的等差数列．∴a n ＝15n －5(1≤n ≤12)，a 13，a 14，a 15，…，a 30是首项为a 13＝a 12－10＝165，公差为－10的等差数列．∴a n ＝165＋(n －13)(－10)＝－10n ＋295(13≤n ≤30)，∴a n ＝⎩⎪⎨⎪⎧15n －5，1≤n ≤12，n ∈N ＋－10n ＋295，13≤n ≤30，n ∈N ＋.(2)四月份的总销售量为12(10＋175)2＋18×165＋18×17×(－10)2＝2 550(件)． 13．祖国大陆允许台湾农民到大陆创业以来，在11个省区设立了海峡两岸农业合作试验区和台湾农民创业园，台湾农民在那里申办个体工商户可以享受“绿色通道”的申请、受理、审批一站式服务，某台商到大陆一创业园投资72万美元建起一座蔬菜加工厂，第一年各种经费12万美元，以后每年增加4万美元，每年销售蔬菜收入50万美元，设f (n )表示前n 年的纯收入．(f (n )＝前n 年的总收入－前n 年的总支出－投资额)(1)从第几年开始获取纯利润？(2)若干年后，该台商为开发新项目，有两种处理方案：①年平均利润最大时以48万美元出售该厂；②纯利润总和最大时，以16万美元出售该厂，问哪种方案最合算？解：由题意，知每年的经费是以12为首项，4为公差的等差数列．设纯利润与年数的关系为f (n )，则f (n )＝50n －[12n ＋n (n －1)2×4]－72＝－2n 2＋40n －72. (1)获取纯利润就是要求f (n )>0，故有－2n 2＋40n －72>0，解得2<n <18.又n ∈N ＋，知从第三年开始获利．(2)①平均利润为f (n )n ＝40－2(n ＋36n )≤16，当且仅当n ＝6时取等号．故此方案获利6×16＋48＝144(万美元)，此时n ＝6. ②f (n )＝－2n 2＋40n －72＝－2(n －10)2＋128，当n ＝10时，f (n )max ＝128.故此方案共获利128＋16＝144(万美元)．比较两种方案，第①种方案只需6年，第②种方案需要10年，故选择第①种方案．14．(2013·安徽理，20)设函数f n (x )＝－1＋x ＋x 222＋x 332＋…＋x nn 2(x ∈R ，n ∈N ＋)，证明：(1)对每个n ∈N ＋，存在唯一的x n ∈[23，1]，满足f n (x n )＝0 (2)对任意p ∈N ＋，由(Ⅰ)中x n 构成的数列{x n }满足0<x n －x n ＋p <1n . 解：(1)对每个n ∈N ＋，当x >0时，f ′n (x )＝1＋x2＋…＋x n －1n >0，故f n (x )在(0，＋∞)内单调递增．由于f 1(1)＝0，当n ≥2时，f n (1)＝122＋132＋…＋1n 2>0，故f n (1)≥0. 又f n (23)＝－1＋23＋∑k ＝2n (23)k k 2≤－13＋14∑k ＝2n (23)k＝－13＋14·(23)2[1－(23)n －1]1－23 ＝－13·(23)n －1<0，所以存在唯一的x n ∈[23，1]，满足f n (x n )＝0. (2)当x >0时，f n ＋1(x )＝f n (x )＋x n ＋1(n ＋1)2>f n (x )，故f n ＋1(x n )>f n (x n )＝f n ＋1(x n ＋1)＝0.由f n ＋1(x )在(0，＋∞)内单调递增知，x n ＋1<x n . 故{x n }为单调递减数列，从而对任意n ，p ∈N ＋，x n ＋p <x n . 对任意p ∈N ＋，由于f n (x n )＝－1＋x n ＋x 2n 22＋…＋x n nn 2＝0，①f n ＋p (x n ＋p )＝－1＋x n ＋p ＋x 2n ＋p 22＋…＋x n n ＋p n 2＋x n ＋1n ＋p(n ＋1)2＋…＋x n ＋pn ＋p (n ＋p )2＝0.②①式减去②式并移项，利用0<x n ＋p <x n ≤1，得x n －x n ＋p ＝∑k ＝2nx k n ＋p －x k n k 2＋∑k ＝n ＋1n ＋p x k n ＋p k 2≤∑k ＝n ＋1n ＋p x k n ＋pk 2≤∑k ＝n ＋1n ＋p1k 2<∑k ＝n ＋1n ＋p 1k (k －1)＝1n －1n ＋p <1n .因此，对任意p ∈N ＋，都有0<x n －x n ＋p <1n .。

高考数学一轮复习同步训练第33讲《数列的综合应用》B 文北师大版必修5

[时间：45分钟分值：100分]基础热身1．一张报纸厚度为a ，对折(沿一组对边的中点连线折叠)7次后，报纸的厚度为( ) A ．8a B ．64a C ．128a D ．256a2．某放射性物质的质量每天衰减3%，若此物质衰减到其质量的一半以下，则至少需要的天数是(参考数据lg0.97＝－0.0132，lg0.5＝－0.3010)( )A ．22B ．23C ．24D ．253．[2011·杭州二中模拟] 在数列{a n }中，a 1＝2，当n 为正奇数时，a n ＋1＝a n ＋2，当n 为正偶数时，a n ＋1＝2a n ，则a 6＝( )A ．11B ．17C ．22D ．234．夏季高山上的气温从山脚起每升高100米降低0.7 ℃，已知山脚气温为26 ℃，山顶气温为14.1 ℃，那么此山相对山脚的高度为________米．能力提升5．已知数列{a n }中，a 1＝－1，a n ＋1·a n ＝a n ＋1－a n ，则数列通项a n ＝( ) A.1n B.2nC ．－1nD ．－2n6．[2011·丰台二模] 已知数列{a n }中，a 1＝35，a n ＝1－1a n －1(n ≥2)，则a 2011＝( )A ．－12B ．－23C.35D.527．[2011·江西八校联考] 设数列{a n }为等差数列，其前n 项和为S n ，a 1＋a 4＋a 7＝99，a 2＋a 5＋a 8＝93.若对任意n ∈N *，都有S n ≤S k 成立，则k 的值为( )A ．22B ．21C ．20D ．198．[2011·湖北卷] 《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为( )A ．1升 B.6766升 C.4744升 D.3733升9．已知等差数列{a n }的首项a 1及公差d 都是整数，前n 项和为S n ，若a 1>1，a 4>3，S 3≤9，设b n ＝1na n ，则使b 1＋b 2＋…＋b n <99100成立的最大n 值为( )A ．97B ．98C ．99D ．10010．某厂在2011年底制订生产计划，要使2021年底的总产量在原有基础上翻两番，则年平均增长率为________．11．[2011·江西重点中学三模] 已知数列{a n }中，a 201＝2，a n ＋a n ＋1＝0(n ∈N ＋)，则a 2011＝________.12．[2011·江西鹰潭一中模拟] 在数列{a n }中，若a 1＝2，且对任意的正整数p ，q 都有a p ＋q ＝a p a q ，则a 8的值为________．13．已知a n ＝3n，把数列{a n }的各项排列成如下的三角形状：a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 ………………记A (m ，n )表示第m 行的第n 个数，则A (11,12)＝________.14．(10分)[2011·揭阳一模] 已知数列{a n }是首项为2，公比为12的等比数列，S n 为{a n }的前n 项和．(1)求数列{a n }的通项a n 及S n ；(2)设数列{b n ＋a n }是首项为－2，公差为2的等差数列，求数列{b n }的通项公式及其前n 项和T n .15．(13分)张先生2011年底购买了一辆排量1.6 L 的小轿车，为积极响应政府发展“森林碳汇”的号召(森林碳汇是指森林植物吸收大气中的二氧化碳并将其固定在植被或土壤中)，买车的同时出资1万元向中国绿色碳基金购买了2亩荒山用于植树造林．科学研究表明：轿车每行驶3000公里就要排放1吨二氧化碳，林木每生长1立方米，平均可吸收1.8吨二氧化碳．(1)张先生估计第一年(即2012年)会用车1.2万公里，以后逐年会增加1000公里，若轿车使用10年，则共要排放二氧化碳多少吨？(2)若种植的林木第一年生长了1立方米，以后每年以10%的生长速度递增，问林木至少生长多少年吸收的二氧化碳相当于轿车10年间排出的二氧化碳？难点突破16．(12分)[2011·广东卷] 设b ＞0，数列{a n }满足a 1＝b ，a n ＝nba n －1a n －1＋n －1(n ≥2)．(1)求数列{a n }的通项公式；(2)证明：对于一切正整数n,2a n ≤b n ＋1＋1.课时作业(三十三)B【基础热身】1．C [解析] 报纸的厚度为27a ＝128a .故选C.2．B [解析] 依题意有(1－3%)n<0.5，所以n >lg0.5lg0.97≈22.8.故选B.3．C [解析] 逐项计算得该数列的前6项依次为：2,4,8,10,20,22，故选C.4．1700 [解析] 从山脚到山顶气温的变化成等差数列，首项为26，末项为14.1，公差为－0.7，设数列的项数为n ，则14.1＝26＋(n －1)×(－0.7)，解得n ＝18，所以山的高度为h ＝(18－1)×100＝1700(米)．【能力提升】5．C [解析] 已知变形为1a n ＋1－1a n ＝－1，设b n ＝1a n，则{b n }是等差数列，b 1＝－1，b n ＝－1＋(n －1)×(－1)＝－n ，所以a n ＝－1n.故选C.6．C [解析] 由递推公式得a 2＝－23，a 3＝52，a 4＝35，a 5＝－23，…，所以数列{a n }是周期数列，周期为3，于是a 2011＝a 2010＋1＝a 1＝35.故选C.7．C [解析] 依题意即求S n 最大时的项数n .将两已知等式相减，可得公差d ＝－2，所以3a 1＋9d ＝99，解得a 1＝39，所以a n ＝39－2(n －1)＝41－2n .当a n >0时，S n 取得最大值，所以41－2n >0，得n <20.5，所以k ＝n ＝20.故选C.8．B [解析] 从上到下各节记为a 1，a 2，…，a 9，公差为d ，则有⎩⎪⎨⎪⎧a 1＋a 2＋a 3＋a 4＝3，a 9＋a 8＋a 7＝4，即⎩⎪⎨⎪⎧4a 1＋6d ＝3，3a 1＋21d ＝4，解得⎩⎪⎨⎪⎧d ＝766，a 1＝1322，所以a 5＝a 1＋4d ＝1322＋4×766＝6766.故选B.9．B [解析] 因为S 3＝3a 2≤9，即a 2≤3，且a 1>1，a 4>3，首项及公差d 为整数，所以可得a 1＝2，d ＝1，所以a n ＝n ＋1，所以b n ＝1n n ＋1＝1n －1n ＋1，b 1＋b 2＋…＋b n ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1，所以n n ＋1<99100成立的最大n 值为98.故选B.10.104－1 [解析] 令2011年底的产量为1，则2021年底的产量为4，则(1＋x )10＝4，所以x ＝104－1.11．2 [解析] 由已知得a n ＋1＝－a n ，所以a 202＝－2，a 203＝2，a 204＝－2，…，可以看出，奇数项为2，偶数项为－2，所以a 2011＝2.12．256 [解析] 令p ＝q ＝1，则a 2＝4，令p ＝q ＝2，则a 4＝16，令p ＝q ＝4，则a 8＝256.13．3112[解析] 由图形知，各行数字的个数构成首项为1，公差为2的等差数列，所以前10行数字个数的和为10×1＋10×92×2＝100，故A (11,12)为{a n }的第112项，所以A (11,12)＝a 112＝3112.14．[解答] (1)因为数列{a n }是首项a 1＝2，公比q ＝12的等比数列，所以a n ＝2·⎝ ⎛⎭⎪⎫12n －1＝22－n，S n ＝2⎝ ⎛⎭⎪⎫1－12n 1－12＝4⎝ ⎛⎭⎪⎫1－12n .(2)依题意得：b n ＋a n ＝－2＋2(n －1)＝2n －4，所以b n ＝2n －4－a n ＝2n －4－22－n. 设数列{b n ＋a n }的前n 项和为P n ，则P n ＝n －2＋2n －42＝n (n －3)，所以T n ＝P n －S n ＝n (n －3)－41－12n ＝n 2－3n －4＋22－n.15．[解答] (1)该市逐年投入的电力型公交车的数量组成等比数列{a n }，其中a 1＝128，q ＝1.5，则在2018年应该投入的电力型公交车为 a 7＝a 1q 6＝128×1.56＝1458(辆)． (2)记S n ＝a 1＋a 2＋…＋a n ，依据题意，得S n 10000＋S n >13，即S n >5000，于是S n ＝1281－1.5n1－1.5>5000，即1.5n >65732，则有n >lg 65732lg1.5≈7.5，因此n ≥8.所以，到2019年底，电力型公交车的数量开始超过该市公交车总量的13.【难点突破】16．[解答] (1)由a 1＝b >0，知a n ＝nba n －1a n －1＋n －1>0，n a n ＝1b ＋1b ·n －1a n －1. 令A n ＝n a n ，A 1＝1b，当n ≥2时，A n ＝1b ＋1bA n －1＝1b ＋…＋1b n －1＋1b n －1A 1＝1b＋ (1)n －1＋1bn .①当b ≠1时，A n ＝1b ⎝ ⎛⎭⎪⎫1－1b n 1－1b＝b n －1b n b －1，②当b ＝1时，A n ＝n . ∴a n ＝⎩⎪⎨⎪⎧nb nb －1b n－1，b ≠1，1， b ＝1.(2)证明：当b ≠1时，欲证2a n ＝2nbnb －1b n －1≤b n ＋1＋1，只需证2nb n≤(b n ＋1＋1)b n －1b －1.∵(b n ＋1＋1)b n －1b －1＝b 2n ＋b 2n －1＋…＋b n ＋1＋b n －1＋b n －2＋…＋1＝b n ⎝⎛⎭⎪⎫b n＋1b n ＋b n －1＋1bn －1＋…＋b ＋1b>b n(2＋2＋ (2)＝2nb n，∴2a n ＝2nb nb －1b n－1<1＋b n ＋1. 当b ＝1时，2a n ＝2＝b n ＋1＋1.综上所述2a n ≤b n ＋1＋1.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课时作业(三十三)B [第33讲数列的综合应用][时间：45分钟分值：100分]基础热身1．一张报纸厚度为a ，对折(沿一组对边的中点连线折叠)7次后，报纸的厚度为( ) A ．8a B ．64a C ．128a D ．256a2．某放射性物质的质量每天衰减3%，若此物质衰减到其质量的一半以下，则至少需要的天数是(参考数据lg0.97＝－0.0132，lg0.5＝－0.3010)( )A ．22B ．23C ．24D ．25 3．[2011·杭州二中模拟] 在数列{a n }中，a 1＝2，当n 为正奇数时，a n ＋1＝a n ＋2，当n 为正偶数时，a n ＋1＝2a n ，则a 6＝( )A ．11B ．17C ．22D ．234．夏季高山上的气温从山脚起每升高100米降低0.7 ℃，已知山脚气温为26 ℃，山顶气温为14.1 ℃，那么此山相对山脚的高度为________米．能力提升5．已知数列{a n }中，a 1＝－1，a n ＋1·a n ＝a n ＋1－a n ，则数列通项a n ＝( ) A.1n B.2nC ．－1nD ．－2n6．[2011·丰台二模] 已知数列{a n }中，a 1＝35，a n ＝1－1a n －1(n ≥2)，则a 2011＝( )A ．－12B ．－23C.35D.52 7．[2011·江西八校联考] 设数列{a n }为等差数列，其前n 项和为S n ，a 1＋a 4＋a 7＝99，a 2＋a 5＋a 8＝93.若对任意n ∈N *，都有S n ≤S k 成立，则k 的值为( )A ．22B ．21C ．20D ．19 8．[2011·湖北卷] 《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为( )A ．1升 B.6766升 C.4744升 D.3733升9．已知等差数列{a n }的首项a 1及公差d 都是整数，前n 项和为S n ，若a 1>1，a 4>3，S 3≤9，设b n ＝1na n ，则使b 1＋b 2＋…＋b n <99100成立的最大n 值为( )A ．97B ．98C ．99D ．10010．某厂在2011年底制订生产计划，要使2021年底的总产量在原有基础上翻两番，则年平均增长率为________．11．[2011·江西重点中学三模] 已知数列{a n }中，a 201＝2，a n ＋a n ＋1＝0(n ∈N ＋)，则a 2011＝________.12．[2011·江西鹰潭一中模拟] 在数列{a n }中，若a 1＝2，且对任意的正整数p ，q 都有a p ＋q ＝a p a q ，则a 8的值为________．13．已知a n ＝3n ，把数列{a n }的各项排列成如下的三角形状：a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 ………………记A (m ，n )表示第m 行的第n 个数，则A (11,12)＝________.14．(10分)[2011·揭阳一模] 已知数列{a n }是首项为2，公比为12的等比数列，S n 为{a n }的前n 项和．(1)求数列{a n }的通项a n 及S n ；(2)设数列{b n ＋a n }是首项为－2，公差为2的等差数列，求数列{b n }的通项公式及其前n 项和T n .15．(13分)张先生2011年底购买了一辆排量1.6 L 的小轿车，为积极响应政府发展“森林碳汇”的号召(森林碳汇是指森林植物吸收大气中的二氧化碳并将其固定在植被或土壤中)，买车的同时出资1万元向中国绿色碳基金购买了2亩荒山用于植树造林．科学研究表明：轿车每行驶3000公里就要排放1吨二氧化碳，林木每生长1立方米，平均可吸收1.8吨二氧化碳．(1)张先生估计第一年(即2012年)会用车1.2万公里，以后逐年会增加1000公里，若轿车使用10年，则共要排放二氧化碳多少吨？(2)若种植的林木第一年生长了1立方米，以后每年以10%的生长速度递增，问林木至少生长多少年吸收的二氧化碳相当于轿车10年间排出的二氧化碳？难点突破16．(12分)[2011·广东卷] 设b ＞0，数列{a n }满足a 1＝b ，a n ＝nba n －1a n －1＋n －1(n ≥2)．(1)求数列{a n }的通项公式；(2)证明：对于一切正整数n,2a n ≤b n ＋1＋1.课时作业(三十三)B【基础热身】1．C [解析] 报纸的厚度为27a ＝128a .故选C.2．B [解析] 依题意有(1－3%)n <0.5，所以n >lg0.5lg0.97≈22.8.故选B.3．C [解析] 逐项计算得该数列的前6项依次为：2,4,8,10,20,22，故选C.4．1700 [解析] 从山脚到山顶气温的变化成等差数列，首项为26，末项为14.1，公差为－0.7，设数列的项数为n ，则14.1＝26＋(n －1)×(－0.7)，解得n ＝18，所以山的高度为h ＝(18－1)×100＝1700(米)．【能力提升】5．C [解析] 已知变形为1a n ＋1－1a n＝－1，设b n ＝1a n ，则{b n }是等差数列，b 1＝－1，b n＝－1＋(n －1)×(－1)＝－n ，所以a n ＝－1n .故选C.6．C [解析] 由递推公式得a 2＝－23，a 3＝52，a 4＝35，a 5＝－23，…，所以数列{a n }是周期数列，周期为3，于是a 2011＝a 2010＋1＝a 1＝35.故选C.7．C [解析] 依题意即求S n 最大时的项数n .将两已知等式相减，可得公差d ＝－2，所以3a 1＋9d ＝99，解得a 1＝39，所以a n ＝39－2(n －1)＝41－2n .当a n >0时，S n 取得最大值，所以41－2n >0，得n <20.5，所以k ＝n ＝20.故选C.8．B [解析] 从上到下各节记为a 1，a 2，…，a 9，公差为d ，则有⎩⎪⎨⎪⎧a 1＋a 2＋a 3＋a 4＝3，a 9＋a 8＋a 7＝4，即⎩⎪⎨⎪⎧4a 1＋6d ＝3，3a 1＋21d ＝4，解得⎩⎨⎧d ＝766，a 1＝1322，所以a 5＝a 1＋4d ＝1322＋4×766＝6766.故选B.9．B [解析] 因为S 3＝3a 2≤9，即a 2≤3，且a 1>1，a 4>3，首项及公差d 为整数，所以可得a 1＝2，d ＝1，所以a n ＝n ＋1，所以b n ＝1n (n ＋1)＝1n －1n ＋1，b 1＋b 2＋…＋b n ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1，所以n n ＋1<99100成立的最大n 值为98.故选B. 10.104－1 [解析] 令2011年底的产量为1，则2021年底的产量为4，则(1＋x )10＝4，所以x ＝104－1.11．2 [解析] 由已知得a n ＋1＝－a n ，所以a 202＝－2，a 203＝2，a 204＝－2，…，可以看出，奇数项为2，偶数项为－2，所以a 2011＝2.12．256 [解析] 令p ＝q ＝1，则a 2＝4，令p ＝q ＝2，则a 4＝16，令p ＝q ＝4，则a 8＝256.13．3112 [解析] 由图形知，各行数字的个数构成首项为1，公差为2的等差数列，所以前10行数字个数的和为10×1＋10×92×2＝100，故A (11,12)为{a n }的第112项，所以A (11,12)＝a 112＝3112.14．[解答] (1)因为数列{a n }是首项a 1＝2，公比q ＝12的等比数列，所以a n ＝2·⎝⎛⎭⎫12n －1＝22－n ，S n ＝2⎝⎛⎭⎫1－12n 1－12＝4⎝⎛⎭⎫1－12n .(2)依题意得：b n ＋a n ＝－2＋2(n －1)＝2n －4，所以b n ＝2n －4－a n ＝2n －4－22－n . 设数列{b n ＋a n }的前n 项和为P n ，则P n ＝n (－2＋2n －4)2＝n (n －3)，所以T n ＝P n －S n ＝n (n －3)－41－12n ＝n 2－3n －4＋22－n .15．[解答] (1)该市逐年投入的电力型公交车的数量组成等比数列{a n }，其中a 1＝128，q ＝1.5，则在2018年应该投入的电力型公交车为 a 7＝a 1q 6＝128×1.56＝1458(辆)． (2)记S n ＝a 1＋a 2＋…＋a n ，依据题意，得S n 10000＋S n >13，即S n >5000，于是S n ＝128(1－1.5n )1－1.5>5000，即1.5n >65732，则有n >lg 65732lg1.5≈7.5，因此n ≥8.所以，到2019年底，电力型公交车的数量开始超过该市公交车总量的13.【难点突破】16．[解答] (1)由a 1＝b >0，知a n ＝nba n －1a n －1＋n －1>0，n a n ＝1b ＋1b ·n －1a n －1. 令A n ＝n a n ，A 1＝1b，当n ≥2时，A n ＝1b ＋1bA n －1＝1b ＋...＋1b n －1＋1b n －1A 1 ＝1b ＋ (1)n －1＋1b n . ①当b ≠1时，A n ＝1b ⎝⎛⎭⎫1－1b n 1－1b＝b n －1b n (b －1)，②当b ＝1时，A n ＝n . ∴a n ＝⎩⎪⎨⎪⎧nb n(b －1)b n －1，b ≠1，1， b ＝1.(2)证明：当b ≠1时，欲证2a n ＝2nb n (b －1)b n －1≤b n ＋1＋1，只需证2nb n ≤(b n ＋1＋1)b n －1b －1.∵(b n ＋1＋1)b n －1b －1＝b 2n ＋b 2n －1＋…＋b n ＋1＋b n －1＋b n －2＋…＋1＝b n ⎝⎛⎭⎫b n ＋1b n ＋b n －1＋1b n 1＋…＋b ＋1b>b n (2＋2＋…＋2) ＝2nb n ，∴2a n ＝2nb n (b －1)b n－1<1＋b n ＋1. 当b ＝1时，2a n ＝2＝b n ＋1＋1.综上所述2a n ≤b n ＋1＋1.。