正态分布及其经典习题和答案整理

合集下载

正态分布练习含答案【范本模板】

正态分布一。

选择题：1。

正态分布有两个参数μ与σ,（）相应的正态曲线的形状越扁平。

A ．μ越大B ．μ越小C ．σ越大D ．σ越小答案: C 。

解析：由正态密度曲线图象的特征知。

2。

已知随机变量X 服从正态分布N （3，σ2）则P （X 〈3)等于 ( ）A 。

错误! B.错误! C 。

错误! D.错误!解析：由正态分布图象知，μ＝3为该图象的对称轴，P （X 〈3)＝P （X >3）＝错误!.答案:D3．设两个正态分布N (μ1，σ错误!）(σ1〉0)和N （μ2,σ错误!)(σ2>0）的密度函数图象如图所示，则有（）A ．μ1<μ2，σ1<σ2B ．μ1〈μ2,σ1>σ2C ．μ1〉μ2，σ1〈σ2D ．μ1〉μ2，σ1〉σ2解析：由图可知，μ2〉μ1，且σ2>σ1. 答案：A4。

设随机变量ξ服从正态分布)1,0(N ，则下列结论不正确的是 .A ．)0)(|(|)|(|)|(|>=+<=<a a P a P a P ξξξB 。

)0(1)(2)|(|>-<=<a a P a P ξξC 。

)0)((21)|(|><-=<a a P a P ξξD. )0)(|(|1)|(|>>-=<a a P a P ξξ答案：C 解析:(||)0P a ξ==。

5. 某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布，其密度函数为f （x ）＝错误!e 2(80)200x e -- （x ∈R )，则下列命题不正确的是（ )A ．该市这次考试的数学平均成绩为80分B ．分数在120分以上的人数与分数在60分以下的人数相同C ．分数在110分以上的人数与分数在50分以下的人数相同D ．该市这次考试的数学成绩标准差为10解析：由密度函数知，均值（期望)μ＝80，标准差σ＝10，又曲线关于直线x ＝80对称,故分数在100分以上的人数与分数在60分以下的人数相同，所以B 是错误的．答案：B6. 已知随机变量X ～N (3，22)，若X ＝2η＋3，则Dη等于 ( ）A ．0B ．1C ．2D ．4解析：由X ＝2η＋3,得DX ＝4Dη，而DX ＝σ2＝4，∴D η＝1.答案：B7。

正态分布习题与详解(1)

1.若x〜N(0,1), 求(I) P<x<; (2) P(x>2).解：⑴ P<x<=-=-[1- ]==.(2)Rx>2)=1- P(x<2)=1- (2)==.亍2利用标准正态分布表，求标准正态总体(1)在 N(1,4)下，求F(3).2 ,(2)在 N(^,b )下，求F (卩一6,卩+6)3 1解：(1) F (3) = (— -)= Q( 1)=2(2)F(y+b)= ( ------- ) =0( 1)=F(y—b) )=0(—1 )=1 —①(1)=1— =F(y — c,a+b)=F(a+b) — F(y — cr)3某正态总体函数的概率密度函数是偶函数，而且该函数的最大值为1=，求总体落入区间(一，)之间的概率 40() =, 0()=]解：正态分布的概率密度函数是f(x) (x )22 2,x)，它是偶函数,1说明”。

，f(x)的最大值为f()=石，所以c= 1,这个正态分布就是标准正态分布+4.某县农民年平均收入服从 =500 入在500：520元间人数的百分比；内的概率不少于，则a至少有多大？元，(2)[O=200元的正态分布.(1)求此县农民年平均收如果要使此县农民年平均收入在( a, a )()=,0()=]解：设表示此县农民年平均收入, ~N(500,2002).P(500 520) (520 500200 ) P( a) 500 500( )(0.1) (0) 0.5398 0.5 0.0398 ( 2 )200a a0.95,查表知: —1.962003921设随机变量(3,1), 若沪以："昭:-.松”则P(2<X<4)=(B)l C. l-2p【答案】C 因为垃3；厂□恳飞签Cf：所以 P(2<X<4)=——「二 T"；：：；：一丄匸,选 C.2. （2010新课标全国理）某种种子每粒发芽的概率都为，现播种了 1 000粒，对于没有发芽的种子，每粒需再补种 2粒，补种的种子数记为X,则X 的数学期望为（）［答案］C［解析］由条件知 3B （n, P ）,np= 4 np 1 — p = 2A. 100B . 200C. 300D . 400［答案］B［解析］记“不发芽的种子数为了 , 则严 B(1 000,,所以 E( 3= 1 000X = 100,而 X=2 3 故 E(X)= E(2 3 = 2E( 3 = 200,故选 B.3.设随机变量3的分布列如下:其中a, b, c 成等差数列，若 E （ 3 = 3则D （3 =（3B.- 1 ［答案］D［解析］由条件a, b, c 成等差数列知，2b= a + c, 由分布列的性质知 a+ b+ c= 1,又1 111 1E(3 = — a+ c= 3,解得 a=6, b = 3, c= 3,「. D(3 =—1 —1 2+10 —1 2+11 —-3 丁 3 0 3 丁 2 13 4. （2010上海松江区模考）设口袋中有黑球、白球共 7个，从中任取 2个球，已知取到白球个数的数学期望值为 7，则口袋中白球的个数为（)A . 3 B . 4C. 5D. 2［答案］A［解析］设白球x 个，则黑球7 — x 个，取出的2个球中所含白球个数为 3贝U 3取值0,1,2 , C 7-x? 7— x 6— x P( =0)= "CTT =42 x - 7— x x 7— xP( 3= 1) = C 2~ 21 ,C x 2x x — 1P(3= 2)=尹,...7-x 6-x + 1 X x7^ 4221+ 2X 红二16427'二 x= 3.5.小明每次射击的命中率都为 p ，他连续射击 n 次，各次是否命中相互独立，已知命中次数3的期望值为4,方差为2,则 p( 31)=(解之得，p = 2, n = 8,1 1 1••• P （ = o ）= C80x 2 °x 18= 2 8, 1 1 1 P （ = 1）= C81x 2 1x 2 7= 2 5， • p（>1）= 1 — P （ = o ）- P （ = 1）1 8— 1 5= 2472 2 256.A . d < d= d, 01= d2> d3 B. d > d=d, o=d < o C. d= d <d, d 1< o= 03 D. d < d= d, o= o < 03 ［答案］D［解析］正态分布密度函数$2（x ）和g （x ）的图象都是关于同一条直线对称，所以其平均数相同，故d= d ，又屉（X ）的对称轴的横坐标值比也（X ）的对称轴的横坐标值大，故有 d < d=d .又d 越大，曲线越“矮胖”，0越小，曲线越“瘦高”，由图象可知，正态分布密度函数咖（X ）和$2（x ）的图象一样"瘦高”，艇（X ）明显"矮胖”，从而可知01= d < 03.6①命题"卫匚小:；：：.-I ； ”的否定是:"二丫匚―常.T 二卄”； ②若:■: ■;,则叮:■-;：•?的最大值为 4;③ 定义在R 上的奇函数满足c ,则的值为0;④ 已知随机变量服从正态分布，则:Sr - ” ；■. i> ;其中真命题的序号是 _________ （请把所有真命题的序号都填上）.【答案】①③④ ①命题"讥■匕迂:”的否定是：“ mm j ” ;所以① 正确•② 若；：—.芒*、二加―：:、:,则題:牡=谄幕“专,即 '.心* ―二.•杠.所以L.-- —:—厂,即（./ - . JI - ■ ■ I. " /■:,解得b '.4 ,则 L- I ■' 的最小值为 4；*2*所以②错误.③定义在 R 上的奇函数满足...m,：；； - -：d ,贝U= 且 2」；C ：,即函数的周期是4.所以「；学二门.•： == 3 ;所5已知三个正态分布密度函数则（）机X）= 2n 厂x — d 22^（x € R ,i= 1,2,3）的图象如图所以③正确.④已知随机变量服从正态分布空匕二、—匸:匚,则■■■■..- 旷「,_丨所以i：」，；所以④正确，所以真命题的序号是①③④.7、在区间| 上任取两数 m和n,则关于x的方程f - :?有两不相等实根的概率为___________ .【答案】由题意知]■- ...? ■要使方程/ m - 1 - u有两不相等4实根,则、：； I ,即::訂 gu二::'：:；-::.作出对应的可行域,如图直线厂--f11 ，拦：,当身I 时，；；，「，：-,所以—1I | 1< J -',所以方程于--m、- J有两不相等实根的概率为j_ ―■ 2 2=】2S 22X n ]8、下列命题：(2)不等式.v-；-i|-!- - ；■ |>农恒成立,则；(3)随机变量X服从正态分布 N(1,2),贝U 厂吒门=逍.即、/■；：:2 |(4)已知a.b e R\2a + b =1,则一■—>吕.其中正确命题的序号为_________________ .a b【答案】⑵(3) ⑴ 「丄扛二1口工；=1n2 ,所以(1)错误.(2)不等式X| - | ..:的最小值为4,所以要使不等式|> 成立，则，所以(2) 正确.(3) 正确.(4) | ' 」「 I ' ' ,所以⑷错误，所以正a b a b a b - a b确的为3).2已知某篮球运动员2012年度参加了 40场比赛，现从中抽取5场,用茎叶图统计该运动员 5 场中的得分如图所示，则该样本的方差为B. 25C. 23D. 18【答案】D 样本的平均数为 23,所以样本方差为: ?T - .：?<■-： ■:- f 2?- / U' - i < - / | .；■,选 D•3有一个容量为的样本,其频率分布直方图如图所示,据图估计,样本数据在'>.|n 内的【答案】C 样本数据在之外的频率为匸「匸心 J 7 I g :: c ■■-所以样本数据在内的频率为［『珀龙二二:疥，所以样本数据在的频数为038x200=^76,选 C.【答案】【答案】B 根据积分的应用可知所求阴影部分的面积为^x-x^ = (~x 2-~x的概率为,选B.5从集合1,2,3,4,5中随机选取3个不同的数,这个数可以构成等差数列的概率为,所以由几何概型公式可得点P恰好取自阴影部分频数为OABC 中4.【答案】25从集合1,2,3,4,5中随机选取3个不同的数有C55 10种.则3个数能构成等差数列的有，1,2,3;2,3, 4;3,4,5;1,3,5;有4种，所以这个数可以构成等差数列的概率为4 2 10 5。

正态分布综合测试题(附答案)

正态分布综合测试题（附答案）选修2-32.4正态分布一、选择题1．下列函数中，可以作为正态分布密度函数的是()A．f(x)＝12πe－(x－1)22B．f(x)＝12π•σe(x－2)22σ2C．f(x)＝12πσe－(x－μ)22σ2D．f(x)＝12πe－(x－μ)22π答案]A2．已知ξ～N(0,62)，且P(－2≤ξ≤0)＝0.4，则P(ξ>2)等于()A．0.1B．0.2C．0.6D．0.8答案]A解析]由正态分布曲线的性质知P(0≤ξ≤2)＝0.4，∴P(－2≤ξ≤2)＝0.8，∴P(ξ>2)＝12(1－0.8)＝0.1，故选A.3．若随机变量ξ～N(2,100)，若ξ落在区间(－∞，k)和(k，＋∞)内的概率是相等的，则k等于()A．2B．10C.2D．可以是任意实数答案]A解析]由于ξ的取值落在(－∞，k)和(k，＋∞)内的概率是相等的，所以正态曲线在直线x＝k的左侧和右侧与x轴围成的面积应该相等，于是正态曲线关于直线x＝k对称，即μ＝k，而μ＝2.∴k＝2.4．已知一次考试共有60名同学参加，考生的成绩X～N(110,52)，据此估计，大约应有57人的分数在下列哪个区间内()A．(90,110]B．(95,125]C．(100,120]D．(105,115]答案]C解析]由于X～N(110,52)，∴μ＝110，σ＝5.因此考试成绩在区间(105,115]，(100,120]，(95,125]上的概率分别应是0.6826,0.9544,0.9974.由于一共有60人参加考试，∴成绩位于上述三个区间的人数分别是：60×0.6826≈41人，60×0.9544≈57人，60×0.9974≈60人．5．(2010•山东理，5)已知随机变量ξ服从正态分布N(0，σ2)，P(ξ>2)＝0.023，则P(－2≤ξ≤2)＝()A．0.477B．0.628C．0.954D．0.977答案]C解析]∴P(ξ>2)＝0.023，∴P(ξ故P(－2≤ξ≤2)＝1－P(ξ>2)－P(ξ6．以φ(x)表示标准正态总体在区间(－∞，x)内取值的概率，若随机变量ξ服从正态分布(μ，σ2)，则概率P(|ξ－μ|A．φ(μ＋σ)－φ(μ－σ)B．φ(1)－φ(－1)C．φ1－μσD．2φ(μ＋σ)答案]B解析]设η＝|ξ－μ|σ，则P(|ξ－μ|＝φ(1)－φ(－1)．点评]一般正态分布N(μ，σ2)向标准正态分布N(0,1)转化．7．给出下列函数：①f(x)＝12πσe－(x＋μ)22σ2；②f(x)＝12πe－(x－μ)24；③f(x)＝12•2πe－x24；④f(x)＝1πe－(x－μ)2，其中μ∴(－∞，＋∞)，σ＞0，则可以作为正态分布密度函数的个数有()A．1B．2C．3D．4答案]C解析]对于①，f(x)＝12πσe－(x＋μ)22σ2.由于μ∴(－∞，＋∞)，所以－μ∴(－∞，＋∞)，故它可以作为正态分布密度函数；对于②，若σ＝1，则应为f(x)＝12πe－(x－μ)22.若σ＝2，则应为f(x)＝12π•2e－(x－μ)24，均与所给函数不相符，故它不能作为正态分布密度函数；对于③，它就是当σ＝2，μ＝0时的正态分布密度函数；对于④，它是当σ＝22时的正态分布密度函数．所以一共有3个函数可以作为正态分布密度函数．8．(2008•安徽)设两个正态分布N(μ1，σ21)(σ1>0)和N(μ2，σ22)(σ2>0)的密度函数图象如图所示，则有()A．μ1B．μ1σ2C．μ1>μ2，σ1D．μ1>μ2，σ1>σ2答案]A解析]根据正态分布的性质：对称轴方程x＝μ，σ表示总体分布的分散与集中．由图可得，故选A.二、填空题9．正态变量的概率密度函数f(x)＝12πe－(x－3)22，x∴R的图象关于直线________对称，f(x)的最大值为________．答案]x＝312π10．已知正态总体的数据落在区间(－3，－1)里的概率和落在区间(3,5)里的概率相等，那么这个正态总体的数学期望为________．答案]1解析]正态总体的数据落在这两个区间里的概率相等，说明在这两个区间上位于正态曲线下方的面积相等．另外，因为区间(－3，－1)和区间(3,5)的长度相等，说明正态曲线在这两个区间上是对称的．∴区间(－3，－1)和区间(3,5)关于直线x＝1对称，所以正态分布的数学期望就是1.11．在某项测量中，测量结果ξ服从正态分布N(1，σ2)(σ>0)，若ξ在(0,1)内取值的概率为0.4，则ξ在(0,2)内取值的概率为____________．答案]0.8解析]∴μ＝1，∴正态曲线关于直线x＝1对称．∴在(0,1)与(1,2)内取值的概率相等．12．(2010•福安)某厂生产的零件尺寸服从正态分布N(25,0.032)，为使该厂生产的产品有95%以上的合格率，则该厂生产的零件尺寸允许值范围为________．答案](24.94,25.06)解析]正态总体N(25,0.032)在区间(25－2×0.03，25＋2×0.03)取值的概率在95%以上，故该厂生产的零件尺寸允许值范围为(24.94,25.06)．三、解答题13．若一个正态分布的概率密度函数是一个偶函数，且该函数的最大值等于142π.求该正态分布的概率密度函数的解析式．解析]由于该正态分布的概率密度函数是一个偶函数，所以其图象即正态曲线关于y轴对称，即μ＝0.而正态密度函数的最大值是12π•σ，所以12π•σ＝12π•4，因此σ＝4，故该正态分布的概率密度函数的解析式是φμ，σ(x)＝142πe－x232，x∴(－∞，＋∞)．14．(2010•邯郸高二检测)设随机变量ξ～N(2,9)，若P(ξ>c＋1)＝P(ξ分析]由题目可获取以下主要信息：①ξ～N(2,9)，②P(ξ>c＋1)＝P(ξ解答本题可利用正态曲线的对称性来求解．解析]由ξ～N(2,9)可知，密度函数关于直线x＝2对称(如图所示)，又P(ξ>c＋1)＝P(ξ故有2－(c－1)＝(c＋1)－2，∴c＝2.点评]解答此类问题要注意以下知识的应用：(1)充分利用正态曲线的对称性和曲线与x轴之间面积为1；(2)正态曲线关于直线x＝μ对称，从而在关于x＝μ对称的区间上概率相等．(3)P(xP(x若b15．某个工厂的工人月收入服从正态分布N(500,202)，该工厂共有1200名工人，试估计月收入在440元以下和560元以上的工人大约有多少？解析]设该工厂工人的月收入为ξ，则ξ～N(500,202)，所以μ＝500，σ＝20，所以月收入在区间(500－3×20,500＋3×20)内取值的概率是0.9974，该区间即(440,560)．因此月收入在440元以下和560元以上的工人大约有1200×(1－0.9974)＝1200×0.0026≈3(人)．16．已知某种零件的尺寸ξ(单位：mm)服从正态分布，其正态曲线在(0,80)上是增函数，在(80，＋∞)上是减函数，且f(80)＝182π.(1)求概率密度函数；(2)估计尺寸在72mm～88mm间的零件大约占总数的百分之几？解析](1)由于正态曲线在(0,80)上是增函数，在(80，＋∞)上是减函数，所以正态曲线关于直线x＝80对称，且在x＝80处取得最大值，因此得μ＝80.12π•σ＝182π，所以σ＝8.故概率密度函数解析式是φμ，σ(x)＝182πe－(x－80)2128.(2)尺寸在72mm～88mm之间的零件的百分率，即在(80－8,80＋8)之间的概率为68.28%.。

医学统计学正态分布习题及答案

1.96
二、是非题
1．对于偏态分布资料， 1.96
范围内也包含了95%的变量值（）
答案：错
2．正态分布在横轴上的位置由均数决定（）
答案：对
3．任何一个正态分布都可以通过标准化变换转化为标准正态分布（）
答案：对
4．设随机变量的值在(0，+)范围中，从该变量值的总体中抽样，若样本的标准差大于样本均数，则可推断不服从正态分布（）
4．在排放的工业废水中规定有害物质含量不能超过0.005。现从某企业排出的废水中抽取10份水样，测出有害物质的平均含量为：0.0053，标准差为：0.0004。
假设某企业排出的废水符合标准，从该企业排出的废水中抽到的含量为10的样本是否小概率事件？
5．某医院要求除内科之外的各科室住院病人的平均住院日均不超过20天。该院某科对科室全部病人计算出平均住院日为15天。科主任认为：该科室目前已达到了医院的要求。这个看法是否正确？
10．某市500名10岁正常男孩中，有95% 的人体重在 18～30kg范围内，由此可知此500名男孩体重的标准差等于（） kg
A 2.000
B 2.326
C 6.122
D 3.061
E 6.000 答案：D
11．对于服从标准正态分布的变量，有（）
A 的概率是0.10 B 的概率是0.025 C 的概率是0.05 D 的概率是0.01 E 的概率是0.005 答案：B
二、是非判断题
1．对于一个含量为n样本，为了推断该样本是否取自均数为μ0的总体，需要对该样本的均数与μ0之间的差别是否是抽样误差进行假设检验（）
2．从均数为μ0的总体中抽取一个含量为 n样本，必须对样本均数与μ0之间的差别是否是抽样误差进行假设检验（）

2023年新教材人教A版高中数学选择性必修第三册7.5正态分布同步课时练习题含答案解析

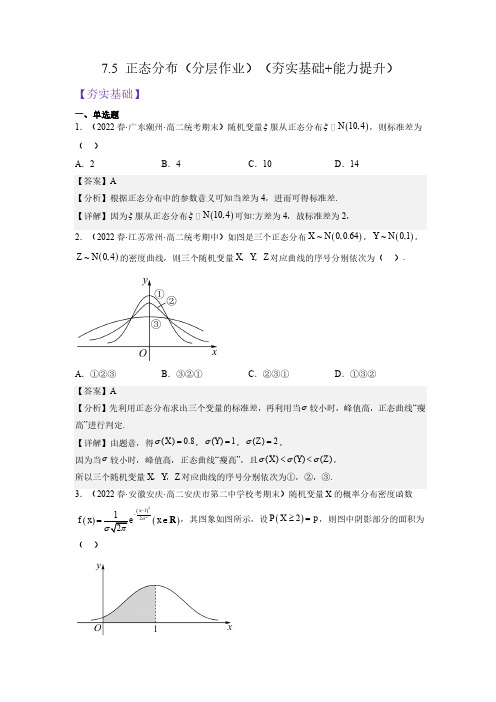
7.5 正态分布（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题 1．（2022春·广东潮州·高二统考期末）随机变量ξ服从正态分布()10,4N ξ，则标准差为（） A ．2 B ．4C ．10D ．14【答案】A【分析】根据正态分布中的参数意义可知当差为4，进而可得标准差. 【详解】因为ξ服从正态分布()10,4N ξ可知:方差为4，故标准差为2，2．（2022春·江苏常州·高二统考期中）如图是三个正态分布()~0,0.64X N ，()~0,1Y N ，()~0,4Z N 的密度曲线，则三个随机变量X ，Y ，Z 对应曲线的序号分别依次为（）.A ．①②③B ．③②①C ．②③①D ．①③②【答案】A【分析】先利用正态分布求出三个变量的标准差，再利用当σ较小时，峰值高，正态曲线“瘦高”进行判定.【详解】由题意，得()0.8X σ=，()1Y σ=，()2Z σ=，因为当σ较小时，峰值高，正态曲线“瘦高”，且()()()X Y Z σσσ<<，所以三个随机变量X ，Y ，Z 对应曲线的序号分别依次为①，②，③.3．（2022春·安徽安庆·高二安庆市第二中学校考期末）随机变量X 的概率分布密度函数()()()2212x f x x σ--=∈R ，其图象如图所示，设()2P X p ≥=，则图中阴影部分的面积为（）A ．pB ．2pC ．12p -D ．12p -A ．两个随机变量的线性相关性越强，则相关系数r 的绝对值越接近于0B ．若X 是随机变量，则()()()()2121,2141E X E X D X D X +=++=+.C ．已知随机变量()0,1N ξ，若(1)P p ξ>=，则(1)12P p ξ>-=-D ．设随机变量ξ表示发生概率为p 的事件在一次随机实验中发生的次数，则()14D ξ≤某中学参加网课的100名同学每天的学习时间（小时）服从正态分布()29,1N ，则这些同学中每天学习时间超过10小时的人数估计为（）. 附：随机变量ξ服从正态分布()2,N μσ，则()0.6826P μσξμσ-<<+=，()220.9544P μσξμσ-<<+=. A ．12 B ．16C ．30D ．32所以每天学习时间超过10小时的人数为1000.158716⨯≈，6．（2023秋·辽宁营口·高二统考期末）正常情况下，某厂生产的零件尺寸X 服从正态分布()22,N σ（单位：m ），()1.90.1P X <=，则()2.1P X <=（）A ．0.1B ．0.4C ．0.5D ．0.9【答案】D【分析】根据正态分布概率的对称性求解. 【详解】因为()()1.9 2.10.1P X P X <=>=，所以()1.9 2.110.10.10.8P X <<=--=，所以()()()2.1 1.9 2.1 1.90.9P X P X P X <=<<+<=，7．（2022·高二课时练习）4月23日为世界读书日，已知某高校学生每周阅读时间（单位：h ）()8,4XN ，则下列说法错误的是（）A ．该校学生每周平均阅读时间为8hB ．该校学生每周阅读时间的标准差为2C ．若该校有10000名学生，则每周阅读时间在46h 的人数约为2718D ．该校学生每周阅读时间低于4h 的人数约占2.28% ()8,4N 知)100.6826≤≈46h 的人数约占(62P X -≤，所以C 错误；0.95442.28%=从N （90，2σ），若()90950.3P c ≤≤=，则可估计该班体能测试成绩低于85分的人数为（）A ．5B ．10C ．15D ．30则可估计该班体能测试成绩低于85分的人数为500.210⨯=人， 9．（2022春·山西忻州·高二统考期末）随机变量X 服从正态分布()2,N μσ，且(1)(5)P X P X >-=<，则下列说法一定正确的是（）A ．3μ=B ．2μ=C ．3σ=D ．2σ=分）服从正态分布()285,N σ，且(8387)0.3,(7883)0.26P P ξξ<≤=<≤=，则(78)P ξ≤=（）A ．0.03B ．0.05C ．0.07D ．0.0911．（2022春·江苏苏州·高二校考期末）在网课期间，为了掌握学生们的学习状态，某省级示范学校对高二一段时间的教学成果进行测试．高二有1 000名学生，某学科的期中考试成绩(百分制且卷面成绩均为整数)Z 服从正态分布()282.5,5.4N ，则(人数保留整数) （）参考数据：若20.682 7220.954 5()()()Z N P Z P Z μσμσμσμσμσ<≤≈<≤≈～，，则－＋，－＋，330.997 3()P Z μσμσ<≤≈－＋．A ．年级平均成绩为82.5分B ．成绩在95分以上(含95分)人数和70分以下(含70分)人数相等C ．成绩不超过77分的人数少于150D ．超过98分的人数为1 【答案】ABD【分析】根据正态分布的概念可知A 对，根据对称性可知B 对，根据3σ原则和曲线的对称性即可求解C,D.【详解】由()282.5,5.4N Z ～，可知82.5, 5.4μσ==，所以平均分为82.5μ=，故A 对.12．（2022春·重庆沙坪坝·高二重庆八中校考期末）已知121,X N σ~，220,Y N σ~，则下列结论中正确的是（）A ．若12σσ=，则()()10P X P Y >>>B ．若12σσ=，则()()101P X P Y >+>=C ．若12σσ>，则()()0211P X P Y ≤≤<-≤≤D ．若12σσ>，则()()0101P X P Y ≤≤>≤≤13．（2022春·云南昭通·高二校联考期末）设随机变量()2,X N μσ，X 的正态密度函数为()22x f x -，则μ=______.14．（2023秋·河南南阳·高二统考期末）已知随机变量ξ服从正态分布()210,N σ，若()310.5P a ξ≤+=，则实数=a ______．【答案】3【分析】由正态分布曲线的特点可知，得正态曲线关于10x =对称，且100.5PX ≤=（），结合题意得到a 的值．【详解】随机变量ξ服从正态分布()210,N σ，正态曲线关于10x =对称，且100.5PX ≤=（），由()310.5P a ξ≤+=，可知3110a +=，解得3a =．15．（2022春·重庆·高二校联考阶段练习）已知随机变量X 服从正态分布()2,N μσ，若()260.6P X <<=，()60.2P X ≥=，则μ=______．【答案】4【分析】先求出()2P X ≤的概率，然后根据正态分布的特征求解即可. 【详解】解：由题意得：∵()()()()2162610.60.20.26P X P X P X P X ≤=-≥-<<=--==≥ ∴2与6关于x μ=对称 ∴4μ=．16．（2023秋·安徽宿州·高二安徽省泗县第一中学校考期末）某学校高二年级有1500名同学，一次数学考试的成绩X 服从正态分布()2110,10N ．已知(100110)0.34P X <≤=，估计高二年级学生数学成绩在120分以上的有__________人．17．（2023秋·辽宁葫芦岛·高二葫芦岛第一高级中学校考期末）随机变量X 服从正态分布，即()10,9X N ~，随机变量23Y X =-，则()E Y =__________，()D Y =__________．【答案】 17 36【分析】首先根据正态分布的知识得()(),E X D X ，然后可得答案. 【详解】因为()10,9X N ~，所以()()10,9E X D X ==，因为23Y X =-，所以()()2320317E Y E X =-=-=，()()436D Y D X ==，五、解答题18．（2023秋·河南南阳·高二统考期末）某车间生产一批零件，现从中随机抽取10个，测量其内径的数据如下（单位：mm ）：192，192，193，197，200，202，203，204，208，209．设这10个数据的均值为μ，标准差为σ． (1)求μ和σ；(2)已知这批零件的内径X （单位：mm ）服从正态分布()2,N μσ，若该车间又新购一台设备，安装调试后，试生产了5个零件，测量其内径（单位：mm ）分别为：181，190，198，204，213，如果你是该车间的负责人，以原设备生产性能为标准，试根据3σ原则判断这台设备是否需要进一步调试？并说明你的理由．参考数据：若()2,XN μσ，则：()0.6826P X μσμσ-<≤+≈，()220.9544P X μσμσ-<≤+≈，()330.9974P X μσμσ-<≤+≈，40.99740.99≈． (200,36N )200180.9974+≈所以五个零件的内径中恰有1态分布()2N 500,5（单位：g ）．(1)求正常情况下，任意抽取一包白糖，质量小于485g 的概率约为多少？。

渐进正态分布习题及答案

渐进正态分布习题及答案在统计学中，正态分布是一种连续概率分布，其形状呈现为对称的钟形曲线，也被称为高斯分布。

当样本量足够大时，许多不同的分布都会趋向于正态分布，这被称为中心极限定理。

下面，我们通过一些习题来加深对渐进正态分布的理解，并给出相应的答案。

习题1：假设一个总体的均值μ=100，标准差σ=15。

如果从这个总体中随机抽取一个容量为36的样本，求样本均值的分布。

答案：根据中心极限定理，当样本容量足够大时（通常n>30），样本均值的分布将接近正态分布。

样本均值的分布的均值等于总体均值，即100，标准误差（标准差）为总体标准差除以根号下的样本容量，即15/√36。

习题2：如果一个正态分布的样本容量为100，样本均值为120，样本标准差为20，求样本均值的95%置信区间。

答案：样本均值的95%置信区间可以通过以下公式计算：\[ \text{CI} = \bar{x} \pm z \times \frac{\sigma}{\sqrt{n}} \] 其中，$\bar{x}$ 是样本均值，$z$ 是标准正态分布的分位数（对于95%置信区间，$z$ 约为1.96），$\sigma$ 是样本标准差，$n$ 是样本容量。

代入数值：\[ \text{CI} = 120 \pm 1.96 \times \frac{20}{\sqrt{100}} \]\[ \text{CI} = 120 \pm 1.96 \times 2 \]\[ \text{CI} = (116.12, 123.88) \]习题3：一个工厂生产的产品重量服从正态分布，总体均值为500克，总体标准差为50克。

如果从该总体中随机抽取一个容量为16的样本，求样本均值的分布。

答案：样本均值的分布将接近正态分布，其均值等于总体均值500克，标准误差为50克除以根号下的16，即：\[ \text{SE} = \frac{50}{\sqrt{16}} \approx 15.81 \]习题4：如果一个正态分布的样本容量为64，样本均值为150，样本标准差为30，求样本均值的99%置信区间。

高二数学正态分布试题答案及解析

高二数学正态分布试题答案及解析1.设随机变量X服从正态分布N（3，4），若P（X＜2a+3）=P（X＞a﹣2），则a的值为（）.A．B．3C．5D．【答案】A.【解析】因为随机变量X服从正态分布N（3，4），且P（X＜2a+3）=P（X＞a﹣2），所以与关于对称，即，所以，即.【考点】正态分布.2.设随机变量X服从正态分布N（0,1），P（X>1）＝p，则P（－1<X<0）等于A．p B．1－p C．1－2p D．－p【答案】D【解析】由于随机变量X服从正态分布N（0,1）,图象关于对称，，因此.【考点】正态分布的应用.3.设随机变量服从正态分布,若,则( ).A．3B．C．5D．【答案】D【解析】由题意，得与关于对称，则，所以.【考点】正态分布的对称性.4.已知随机变量X服从正态分布N(3．1)，且=0．6826，则p（X>4）=（）A．0．1588B．0．1587C．0．1586D．0．1585【答案】B【解析】正态分布曲线关于对称，因为,故选B．【考点】正态分布5.均值为2，方差为2π的正态分布的概率密度函数为________．【答案】f(x)＝【解析】在密度函数f(x)＝中，μ＝2，σ＝，故f(x)＝.6.已知X～N(0,1)，则P(－1＜X＜2)＝________.【答案】0.818 5【解析】∵P(－1＜X＜1)＝0.682 6，P(－2＜X＜2)＝0.954 4，∴P(1＜X＜2)＝ (0.954 4－0.682 6)＝0.135 9.∴P(－1＜X＜2)＝0.682 6＋0.135 9＝0.818 5.7.设随机变量X服从正态分布N(2,9)若P(X＞c＋1)＝P(X＜c－1)，则c等于________．【答案】2【解析】∵μ＝2，由正态分布的定义知其图象关于直线x＝2对称，于是＝2，∴c＝2.8.已知X～N(0，σ2)且P(－2≤X≤0)＝0.4，则P(X＞2)＝________.【答案】0.1【解析】∵P(0≤X≤2)＝P(－2≤X≤0)＝0.4，∴P(X＞2)＝(1－2×0.4)＝0.1.9.已知正态总体落在区间(0.2，＋∞)内的概率是0.5，那么相应的正态曲线f(x)在x＝________时达到最高点．【答案】0.2【解析】由正态曲线的性质知：μ＝0.2，故x＝0.2时，正态曲线f(x)达到最高点．10.如图是当σ取三个不同值σ1、σ2、σ3时的三种正态曲线N(0，σ2)的图象，那么σ1、σ2、σ3的大小关系是________．【答案】0＜σ1＜σ2＝1＜σ3【解析】由已知得＝，∴σ2＝1.由正态曲线的性质知，当μ一定时，曲线的形状由σ确定，σ越小，曲线越“瘦高”，所以0＜σ1＜σ2＝1＜σ3.11.已知随机变量服从正态分布，且，则= .【答案】0.3【解析】随机变量ξ服从正态分布，∴曲线关于x=2对称，∴P（ξ＜0）=P（ξ＞4）=1－0.8=0.2，∴=0.5－0.2=0.3，故答案为0.3.【考点】正态分布点评：简单题，随机变量ξ服从正态分布，得到曲线关于x=2对称，根据曲线的对称性得到小于0的和大于4的概率是相等的，从而做出大于2的数据的概率，根据概率的性质得到结果．12.已知随机变量X服从正态分布，且=0.6826，则=（）A．0.1588B．0.1587C．0.1586D．0.1585【答案】B【解析】因为随机变量X服从正态分布，所以正态曲线关于对称，又因为=0.6826，所以【考点】本小题主要考查正态分布的概率求解.点评：求解正态分布的概率问题，关键是利用正态曲线的图象.13.某市对10000名中学生的数学成绩（满分100分）进行抽样统计，发现他们近似服从正态分布N～（70，102），若90分以上者有230人，则这10000名学生中分数在50分到90分之间的人数约有（）A．7140人B．230人C．9540人D．4770人【答案】C【解析】解：因为利用正态分布的对称性可知，某市对10000名中学生的数学成绩（满分100分）进行抽样统计，发现他们近似服从正态分布N～（70，102），因为90分以上者有230人，则这10000名学生中分数在50分到90分之间的人数约有10000-460=9540人，选C14.设随机变量服从正态分布N(0,1)，若P(>1)= ，则P(-1<<0)=（）。

正态分布习题与详解非常有用必考点

1. 若x ～N 0,1,求l P <x <；2Px >2. 解：1P <x <=- =-1-==.2Px >2=1-Px <2=1-2==. 2利用标准正态分布表,求标准正态总体1在N1,4下,求)3(F 2在N μ,σ2下,求Ｆμ－σ,μ＋σ；解：１)3(F ＝)213(-Φ＝Φ1＝２Ｆμ＋σ＝)(σμσμ-+Φ＝Φ1＝Ｆμ－σ＝)(σμσμ--Φ＝Φ－1＝１－Φ1＝１－＝Ｆμ－σ,μ＋σ＝Ｆμ＋σ－Ｆμ－σ＝－＝3某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间－,之间的概率 =, Φ=解：正态分布的概率密度函数是),(,21)(222)(+∞-∞∈=--x ex f x σμσπ,它是偶函数,说明μ＝0,)(x f 的最大值为)(μf ＝σπ21,所以σ＝1,这个正态分布就是标准正态分布 4.某县农民年平均收入服从μ=500元,σ=200元的正态分布求此县农民年平均收入在500520元间人数的百分比；2如果要使此县农民年平均收入在a a +-μμ,内的概率不少于,则a 至少有多大Φ=, Φ=解：设ξ表示此县农民年平均收入,则)200,500(~2N ξ 520500500500(500520)()()(0.1)(0)0.53980.50.0398200200P ξ--<<=Φ-Φ=Φ-Φ=-=2∵()()()2()10.95200200200a a aP a a μξμ-<<+=Φ-Φ-=Φ-≥,查表知： 1.96392200aa ≥⇒≥ 1设随机变量3,1,若,,则P2<X<4= ABl —p C ．l-2pD ．答案C因为,所以P2<X<4=,选 C ．2．2010·新课标全国理某种种子每粒发芽的概率都为,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为A．100B．200C．300D．400答案 B解析记“不发芽的种子数为ξ”,则ξ～B1 000,,所以Eξ＝1 000×＝100,而X＝2ξ,故EX ＝E2ξ＝2Eξ＝200,故选B.3．设随机变量ξ的分布列如下：其中a,b,c成等差数列,若EξB．－错误!答案 D解析由条件a,b,c成等差数列知,2b＝a＋c,由分布列的性质知a＋b＋c＝1,又Eξ＝－a ＋c＝错误!,解得a＝错误!,b＝错误!,c＝错误!,∴Dξ＝错误!×错误!2＋错误!错误!2＋错误!错误!2＝错误!.4．2010·上海松江区模考设口袋中有黑球、白球共7个,从中任取2个球,已知取到白球个数的数学期望值为错误!,则口袋中白球的个数为A．3 B．4 C．5 D．2 答案 A解析设白球x个,则黑球7－x个,取出的2个球中所含白球个数为ξ,则ξ取值0,1,2, Pξ＝0＝错误!＝错误!,Pξ＝1＝错误!＝错误!,Pξ＝2＝错误!＝错误!,∴0×错误!＋1×错误!＋2×错误!＝错误!,∴x＝3.5．小明每次射击的命中率都为p,他连续射击n次,各次是否命中相互独立,已知命中次数ξ的期望值为4,方差为2,则pξ>1＝答案 C解析由条件知ξ～Bn,P,∵错误!,∴错误!,解之得,p＝错误!,n＝8,∴Pξ＝0＝C80×错误!0×错误!8＝错误!8,Pξ＝1＝C81×错误!1×错误!7＝错误!5,∴Pξ>1＝1－Pξ＝0－Pξ＝1＝1－错误!8－错误!5＝错误!.5已知三个正态分布密度函数φi x＝错误!e－错误!x∈R,i＝1,2,3的图象如图所示,则A．μ1<μ2＝μ3,σ1＝σ2>σ3B．μ1>μ2＝μ3,σ1＝σ2<σ3C．μ1＝μ2<μ3,σ1<σ2＝σ3D．μ1<μ2＝μ3,σ1＝σ2<σ3答案 D解析正态分布密度函数φ2x和φ3x的图象都是关于同一条直线对称,所以其平均数相同,故μ2＝μ3,又φ2x的对称轴的横坐标值比φ1x的对称轴的横坐标值大,故有μ1<μ2＝μ3.又σ越大,曲线越“矮胖”,σ越小,曲线越“瘦高”,由图象可知,正态分布密度函数φ1x和φ2x的图象一样“瘦高”,φ3x明显“矮胖”,从而可知σ1＝σ2<σ3.6①命题“”的否定是:“”;②若,则的最大值为4;③定义在R上的奇函数满足,则的值为0;④已知随机变量服从正态分布,则;其中真命题的序号是________请把所有真命题的序号都填上.答案①③④ ①命题“”的否定是:“”;所以①正确.②若,则,即.所以,即,解得,则的最小值为4;所以②错误.③定义在R上的奇函数满足,则,且,即函数的周期是4.所以;所以③正确.④已知随机变量服从正态分布,则,所以;所以④正确,所以真命题的序号是①③④.7、在区间上任取两数m和n,则关于x的方程有两不相等实根的概率为___________.答案由题意知要使方程有两不相等实根,则,即.作出对应的可行域,如图直线,,当时,,所以,所以方程有两不相等实根的概率为.8、下列命题:` 1;2不等式恒成立,则;3随机变量X服从正态分布N1,2,则4已知则.其中正确命题的序号为____________.答案23 1,所以1错误.2不等式的最小值为4,所以要使不等式成立,则,所以2正确.3正确.4,所以4错误,所以正确的为23.2已知某篮球运动员2012年度参加了40场比赛,现从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为A．26 B．25 C．23 D．18答案D样本的平均数为23,所以样本方差为,选D．3有一个容量为的样本,其频率分布直方图如图所示,据图估计,样本数据在内的频数为A ．B ．C ．D ．答案C 样本数据在之外的频率为,所以样本数据在内的频率为,所以样本数据在的频数为,选 C ．4．2013年临沂市高三教学质量检测考试理科数学如图所示,在边长为l 的正方形OABC 中任取一点P,则点P 恰好取自阴影部分的概率为A ．B ．C ．D ．答案答案B 根据积分的应用可知所求阴影部分的面积为,所以由几何概型公式可得点P 恰好取自阴影部分的概率为,选 B ．5从集合{}1,2,3,4,5中随机选取3个不同的数,这个数可以构成等差数列的概率为______.答案25从集合{}1,2,3,4,5中随机选取3个不同的数有3510C =种.则3个数能构成等差数列的有,1,2,3;2,3,4;3,4,5;1,3,5;有4种,所以这个数可以构成等差数列的概率为42105=.。

高中数学教案学案正态分布含习题答案与解析

高中数学教案学案正态分布学习目标：利用实际问题的直方图，了解正态分布曲线的特点及曲线所表示的意义.1. 正态分布密度曲线及性质（1）正态曲线的定义函数叩M ）=（其中实数〃和a 0>0）为参数）的图象为正态分布密度曲线.（2）正态分布密度曲线的特点① 曲线位于x 轴,与x 轴不相交；② 曲线是单峰的，它关于直线对称；③ 曲线在________处达到峰值____________；④ 曲线与x 轴之间的面积为；⑤ 当o ■一定时，曲线随着的变化而沿x 轴移动；⑥ 当么一定时，曲线的形状由<7确定.O ,曲线越“高瘦"，表示总体的分布越集中；G ________,曲线越“矮胖”，表示总体的分布越分散.2. 正态分布（1）正态分布的定义及表示如果对于任何实数a,b （a 〈b ）,随机变量X 满足P （a<XWb ）=, 则称随机变量X 服从正态分布，记作.（2）正态分布的三个常用数据— O<X + <7）=；② P （JJ-2<7<X 寻+2<7）=；③ - 3技寻+3<t ）=.1. （2011•大连模拟）下列说法不正确的是（）A. 若X 〜N （0,9），则其正态曲线的对称轴为y 轴B. 正态分布阳，导）的图象位于*轴上方C. 所有的随机现象都服从或近似服从正态分布2.巳知随机变量4服从正态分布M3, °2）,则p （g<3）等于（）3. （2011•湖北）已知随机变量彳服从正态分布N （2, <t 2）,且P （<f<4）=0.8,则P （0<<f<2）等于（）A. 0.6B. 0.4C. 0.3D. 0.2]—4. 某随机变量4服从正态分布，其正态分布密度函数为9（x ）=^=e 8 ,则4的期望和标准差分别是（）A. 0 和 8B. 0 和 4C. 0 和SD.。

【高中】正态分布经典练习题(可编辑修改word版)

正态分布一、选择题1.已知随机变量服从正态分布N (2,9) ，若P (>c +1) =P (<c -1) ，则c 等于（）A.1B.2C.3D.42.已知随机变量服从正态分N (2,2) ，且P (< 4) = 0.8 ，则P(0 << 2) 等于（）A.0.6B.0.4C.0.3D.0.23.已知随机变量服从正态分布N (2,2) ，P (≤4)=0.84，则P (≤0)等于（）A. 0.16B. 0.32C. 0.68D. 0.844.已知随机变量X 服从正态分布N (2,2)，P(0 <X < 4) = 0.8 ，则P( X > 4) 等于（）A．0.1 B.0.2 C.0.4 D.0.65.已知随机变量服从正态分布N (3,2) ，且P (< 2) = 0.3 ，则P(2 << 4) 等于（）A.0.5B.0.2C.0.3D.0.46.已知随机变量服从正态分布N (3,2) ，P (≤4)=0.842，则P (≤2)等于（）A.0.842B.0.158C.0.421D.0.3167.已知随机变量X 服从正态分布N (3,1) ，且P(2 <X < 4) = 0.6826 ，则P( X > 4) 等于（）A.0.1588B.0.158C.0.1586D.0.15858.已知随机变量X 服从正态分布N (0,2) ，若P( X > 2) = 0.023，则P(-2 ≤X ≤2) 等于（）A.0.477B.0.628C.0.954D.0.9779.在某次联考数学测试中，学生成绩服从正态分布(100, 2) (> 0) ，若在（80,120）内的概率为0.8，则落在（0,80）内的概率为（）A.0.05B.0.1C.0.15D.0.210.已知随机变量X 服从正态分布N (,2) ，且P (- 2<X <+ 2) = 0.9544 ，P (-<X <+) =0.6826 ，若=4,=1, 则P(5 <X <6) =（）A.0.1358B.0.1359C.0.2716D.0.271811.某商场经营的一种袋装的大米的质量服从正态分布N (10, 0.12 ) （单位kg）,任选一袋这种大米，其质量在9.8~10.2kg 的概率为（）A.0.0456B.0.6826C.0.9544D.0.997412.一批电池的使用时间X （单位：小时）服从正态分布N (36,42 ) ，在这批灯泡中任取一个第1 页共 2 页“使用时间不小于40 小时”的概率是（）A.0.9544B.0.6826C. 0.3174D. 0.1587二、填空题13.某校在本学期期中考试中，理科数学考试成绩~ N (90,2) ,统计结果显示P(60≤≤120)=0.8，该校参加此次考试的理科学生共420 人，试估计该校成绩高于120 分的理科学生数为.14.某班有50 名学生，一次考试的成绩服从正态分布N (100,2) , 已知P(90 ≤≤ 100) = 0.3 ,估计该班数学成绩在110分以上的人数为.15.某中学200 名考生的高考数学成绩近似服从正态分布N (120,102 ) ，则此校数学成绩在140 分以上的考生人数约为.16.某市高二理科学生数学考试的成绩x 服从正态分布，其密度曲线如图，已知该市理科学生总数是10000 人，则成绩位于(65,85] 的人数约.17.在某项测量中，测量结果服从正态分布N (1,2) (>0) ，若在(0,1) 内取值的概率为0.4，则在(0,2)内取值的概率为.18.假设每天从甲地去乙地的旅客人数X 是服从正态分布N (800,502) 的随机变量．记一天中从甲地去乙地的旅客人数不超过900 的概率为.19.一批电阻的阻值X 服从正态分布N (1000,52 ) (单位Ω).今从甲乙两箱成品中各随机抽取一个电阻，测得阻值分别为1011 Ω和982 Ω，可以认为. (填写正确序号)①甲乙两箱电阻均可出厂；②甲乙两箱电阻均不可出厂；③甲箱电阻可出厂，乙箱电阻不可出厂；④甲箱电阻不可出厂，乙箱电阻可出厂.20.某一部件由三个电子元件按下图方式连接而成，元件1 或元件2 正常工作，且元件3 正常工作，则部件正常工作．设三个电子元件的使用寿命(单位：小时)均服从正态分布N (1000,502 ) ，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000 小时的概率为.16 题图第2 页共 2 页20 题图15 2O75 x。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题：正态分布【知识网络】 1、取有限值的离散型随机变量均值、方差的概念； 2、能计算简单离散型随机变量的均值、方差，并能解决一些实际问题； 3、通过实际问题，借助直观（如实际问题的直观图），认识正态分布、曲线的特点及曲线所表示的意义。

【典型例题】例1：（1）已知随机变量X服从二项分布，且E（X）=2.4，V（X）=1.44，则二项分布的参数n，p的值为（）

A．n=4，p=0.6 B．n=6,p=0.4 C．n=8，p=0.3 D．n=24，p=0.1 答案：B。解析：4.2npXE，44.1)1(pnpXV。（2）正态曲线下、横轴上，从均数到的面积为( )。 A．95% B．50% C．97.5% D．不能确定（与标准差的大小有关）

答案：B。解析：由正态曲线的特点知。 21

（3）某班有48名同学，一次考试后的数学成绩服从正态分布，平均分为80，标准差为10，理论上说在80分到90分的人数是（）

A 32 B 16 C 8 D 20 答案：B。解析:数学成绩是X—N(80,102)， 80809080(8090)(01)0.3413,480.3413161010PXPZPZ





。

（4）从1，2，3，4，5这五个数中任取两个数，这两个数之积的数学期望为___________ 。

答案：8.5。解析：设两数之积为X， X 2 3 4 5 6 8 10 12 15 20

P 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ∴E(X)=8.5. （5）如图，两个正态分布曲线图： 1为)(1,1x，2为)(22x，则1 2，1 2（填大于，小于）答案：＜，＞。解析：由正态密度曲线图象的特征知。例2：甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格.

（Ⅰ）求甲答对试题数ξ的概率分布及数学期望；

（Ⅱ）求甲、乙两人至少有一人考试合格的概率.

答案：解：（Ⅰ）依题意，甲答对试题数ξ的概率分布如下：

甲答对试题数ξ的数学期望 Eξ=5961321210313010. （Ⅱ）设甲、乙两人考试合格的事件分别为A、B，则 P(A)=310361426CCCC=321202060，P(B)=15141205656310381228CCCC.

因为事件A、B相互独立，方法一： ∴甲、乙两人考试均不合格的概率为 4511514132

1BPAPBAP

ξ 0 1 2 3 P ∴甲、乙两人至少有一人考试合格的概率为 4544451

11BAPP

答：甲、乙两人至少有一人考试合格的概率为4544．方法二： ∴甲、乙两人至少有一个考试合格的概率为答：甲、乙两人至少有一人考试合格的概率为4544.

例3：甲、乙两名射手在一次射击中得分为两个相互独立的随机变量X和Y，其分布列如下：

（1）求a,b的值；

（2）比较两名射手的水平.

答案：（1）a=0.3,b=0.4;

（2）23.034.023.01,3.26.031.023.01EYEX

所以说甲射手平均水平比乙好，但甲不如乙稳定.．

例4：一种赌博游戏：一个布袋内装有6个白球和6个红球，除颜色不同外，6个小球完全一样，每次从袋中取出6个球，输赢规则为：6个全红，赢得100元；5红1白，赢得50元；4红2白，赢得20元；3红3白，输掉100元；2红4白，赢得20元；1红5白，赢得50元；6全白，赢得100元.而且游戏是免费的.很多人

Ｘ１２３Ｐａ 0.1 0.6 Y 1 2 3 P 0.3 b 0.3 认为这种游戏非常令人心动，现在，请利用我们学过的概率知识解释我们是否该“心动”.。

答案：设取出的红球数为X，则X—H（6，6，12），666612()kkCCPXkC，其中k=0,1,2,…,6

设赢得的钱数为Y，则Y的分布列为 X 100 50 20 —100

P ∴1675100()100502010029.4446277154231EY，故我们不该“心动”。【课内练习】 1．标准正态分布的均数与标准差分别为( )。 A．0与1 B．1与0 C．0与0 D．1与1 答案：A。解析：由标准正态分布的定义知。 2．正态分布有两个参数与，( )相应的正态曲线的形状越扁平。 A．越大 B．越小 C．越大 D．越小答案： C。解析：由正态密度曲线图象的特征知。 3．已在n个数据nxxx,,,21，那么niixxn121是指 A． B． C．2 D．2（）答案：C。解析：由方差的统计定义知。 4．设),(~pnB，12E，4V，则n的值是。答案：4。解析：12npE，4)1(pnpV

5．对某个数学题，甲解出的概率为23，乙解出的概率为34，两人独立解题。记X为解出该题的人数，则E（X）= 。

答案：1712。解析：11121145(0),(1),3412343412PXPX231(2)342PX。 ∴15117()012212212EX。 6．设随机变量服从正态分布)1,0(N，则下列结论正确的是。 (1))0)(|(|)|(|)|(|aaPaPaP (2))0(1)(2)|(|aaPaP

(3))0)((21)|(|aaPaP

(4))0)(|(|1)|(|aaPaP

答案：(1),(2),(4)。解析：(||)0Pa。 7．抛掷一颗骰子，设所得点数为X，则V（X）= 。答案：3512。解析：1(),1,2,,66PXkk，按定义计算得735(),()212EXVX。 8．有甲乙两个单位都想聘任你，你能获得的相应的职位的工资及可能性如下表所示：

根据工资待遇的差异情况，你愿意选择哪家单位并说明理由。

答案：由于E（甲）=E（乙），V（甲）选择甲单位。

解析：E（甲）=E（乙）=1400，V（甲）=40000，V（乙）=160000。

9．交5元钱，可以参加一次摸奖。一袋中有同样大小的球10个，其中有8个标有1元钱，2个标有5元钱，摸奖者只能从中任取2个球，他所得奖励是所抽2球的钱数之和（设为），求抽奖人获利的数学期望。

答案：解：因为为抽到的2球的钱数之和，则可能取的值为2，6，10.

4528)2(21028CCP，4516)6(2101218CCCP，451)10(21022CCP

甲单位 1200 1400 1600 1800 概率 0.4 0.3 0.2 0.1 乙单位 1000 1400 1800 2200 概率 0.4 0.3 0.2 0.1 设为抽奖者获利的可能值，则5，抽奖者获利的数学期望为故，抽奖人获利的期望为-75。

10．甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92.

（1）求该题被乙独立解出的概率；（2）求解出该题的人数的数学期望和方差. 答案：解：（1）记甲、乙分别解出此题的事件记为A、B. 设甲独立解出此题的概率为P1，乙为P2. 则P（A）=P1=0.6, P(B)=P2

0 1 2 P 0.08 0.44 0.48 00.0810.4420.480.440.961.4E， 222()(01.4)0.08(11.4)0.44(21.4)0.480.15680.07040.17280.4V

，

或利用22()()()2.361.960.4VEE。【作业本】 A组 1．袋中装有5只球，编号为1，2，3，4，5，从中任取3球，以X表示取出球的最大号码，则E（X）等于（）

A、4 B、5 C、4.5 D、4.75 答案：C。解析：X的分布列为

X 3 4 5 P 0.1 0.3 0.6 故E（X）=30.1+40.3+50.6=4.5。 2．下列函数是正态分布密度函数的是（）

A．2221)(rxexf B．2

)(xexf



C．412221)(xexf D．2

)(xexf

答案：B。解析：选项B是标准正态分布密度函数。 3．正态总体为1,0概率密度函数)(xf是