插值与拟合例题
插值与拟合

且 f(1.5) ≈L1(1.5) = 0.885。
Lagrange插值法的缺点
• 多数情况下,Lagrange插值法效果是不错的, 但随着节点数n的增大,Lagrange多项式的次 (Runge)现象。
• 例:在[-5,5]上用n+1个等距节点作插值多项 式Ln(x),使得它在节点处的值与函数y = 1/(1+25x2)在对应节点的值相等,当n增大时, 插值多项式在区间的中间部分趋于y(x),但 对于满足条件0.728<|x|<1的x, Ln(x)并不趋 于y(x)在对应点的值,而是发生突变,产生 剧烈震荡,即Runge现象。
总结
• 拉格朗日插值:其插值函数在整个区间 上是一个解析表达式;曲线光滑;收敛 性不能保证,用于理论分析,实际意义 不大。
• 分段线性插值和三次样条插值:曲线不 光滑(三次样条已有很大改进);收敛 性有保证;简单实用,应用广泛。
1.2 二维插值
• 二维插值是基于一维插值同样的思想, 但是它是对两个变量的函数Z=f(x,y)进 行插值。
• n=5; • x0=-1:1/(n-1):1;y0=1./(1+25*x0.^2);y1=lagr(x0,y0,x); • subplot(2,2,2), • plot(x,z,'r-',x,y,'m-'),hold on %原曲线 • plot(x,y1,'b'),gtext('L8(x)','FontSize',12),pause %Lagrange曲线
基函数为
l0 (x)
x x1 x0 x1
x2 1 2
2
x
l1(x)
线性插值函数为
第二章 插值与拟合

第二章 插值与拟合2.1 插值与拟合的基本概念2.1.1 插值与插值函数已知由()g x (可能未知或非常复杂)产生的一批离散数据 (,),0,1,,i i x y i n =,且n+1个互异插值节点011n n a x x x x b -=<<<<=,在插值区间内寻找一个相对简单的函数 ()f x ,使其满足下列插值条件:再利用已求得的()f x 计算任一非插值节点*x 的近似值**()y f x =,这就是插值。
其中()f x 称为插值函数, ()g x 称为被插函数。
下面介绍几种常用的而且有现成MATLAB 命令的插值方法的数学原理。
1. 分段线性插值将两个相邻节点用直线连起来,如此形成的一条折线就是分段线性插值函数,记作()n I x ,它满足()n j j I x y =,且()n I x 在每个小区间1[,],0,1,,j j x x j n +=,上是线性函数。
()n I x 可以表示为()()nn j j j I x y l x ==∑111111,,0(),,,j j j j j j j j j jj x x x x x j x x x x l x x x x j n x x ---+++-⎧≤≤=⎪-⎪⎪-⎪=≤≤=⎨-⎪⎪⎪⎪⎩舍去,舍去,0 其他()n I x 有良好的收敛性,即对于[,]x a b ∈时,有lim ()()n n I x g x →∞=。
用()n I x 计算x 点的插值时,只用到x 左右的两个节点,计算量与节点个数n 无关。
但是n 越大,分段越多,插值误差越小。
MATLAB 中有现成的分段线性插值命令: y=interp1(x0,y0,x)其中x0,y0为节点数组(同长度),x 为插值点数组,y 为插值数组。
2. 三次样条插值三次样条函数记作()()S x a x b ≤≤,要求它满足以下条件: (1)在每个小区间1[,](1,,)i i x x i n -=上是三次多项式;(2)在a x b ≤≤上二阶导数连续; (3)(),(0,1,,)i i S x y i n ==。
第2章 计算方法插值与拟合

n
( xi ) ( xi x0 )(xi x1 )( xi xi 1 )(xi xi1 )( xi xn )
' n1
Ln( x)
n1 ( x) yi ' i 0 ( x xi )n 1 ( xi )
n
特例:n=1时,根据式(2-9)和(2-10)得出
如果选简单函数 ( x) 作为 y f ( x) 的近似表达式,并要 求满足以下条件:
( xi ) yi ,
i 0,1,..., n
(2 1)
这样的函数近似问题就称为插值问题。 (2-1)式称为插值条件,满足插值条件(2-1)的近 似函数 ( x) 称为插值函数,而 f ( x) 称为被插值函数, 互异点 x0 , x1, , xn 称为插值节点(简称节点),而 x 称 为插值点,区间[a, b]称为插值区间。
插值多项式 Pn ( x) 只是 y f ( x) 的近似值,其误差叫做 插值多项式的余项或截断误差,记作:
Rn ( x) f ( x) Pn ( x)
(2-5)
记 I 为包含 x0 , x1, , xn 的最小闭区间,I 为包含于 I 中的最大开区间,又记:
n1 ( x) ( x xi )
证明: 当 x为某个节点时定理显然成立。
设 x 异于所有的节点,构造辅助函数:
f ( x) Pn ( x) (t ) f (t ) P n (t ) n1 (t ) n1 ( x)
显然, ( x) ( x0 ) ( x1 ) L ( xn ) 0 xn 根据罗尔定理:在n+2个点 x, x0 , x1 ,L ,之间存在n+1 (0 ) (1 ) L ( n ) 0 个 0 , 使得 n , 1 ,L , 在这n+1个点之间存在n个点,使得 n 个点处 0 在这n个点之间存在n-1个点,使得 0 依次类推,在这些点之间存在一点 ,使得 ( n 1) ( ) 0 即: f ( n 1) ( ) P ( n 1) ( ) f ( x) pn ( x) ( n 1) ( ) 0 n n 1 n 1 ( x)
【精品】学号_姓名_专业_插值拟合练习题.docx
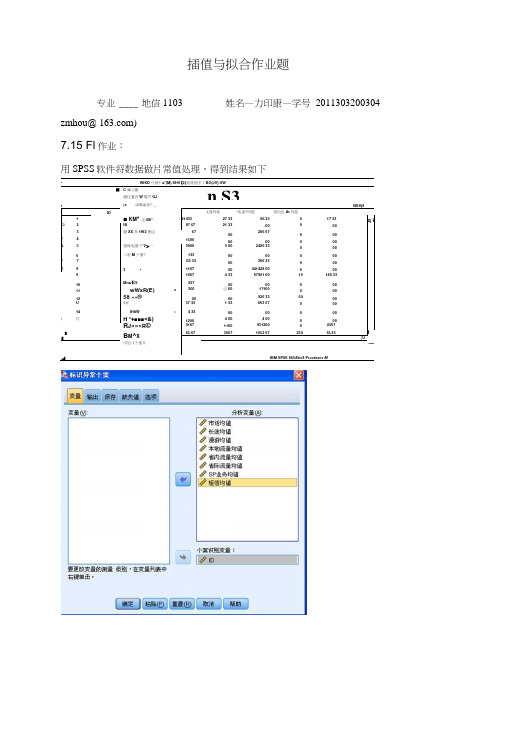
插值与拟合作业题专业____ 地信1103 _______ 姓名—力印康—学号_2011303200304 zmhou@ )7.15 Fl作业:用SPSS软件将数据做片常值处理,得到结果如下LWIKD 介併® a*(M) SHV(2)気网祝序3 BO(JV) UW■C庫乂置超住豪齐W娶巧GJ n S3r|s 审事备件© _9Xlff)9 ID£淺均值*电虑*均值省内氏At均值1■ KM*疋.Bfi*2143327 3396.33017 33q i Ci 2IB87 6721 33.00900r 3囲XX多1W2集凶6700286 67000F 415000000000 & 5罢林电夏个*2>一3900 3 002406 330006二和M个累©1330000000F 7G5 3300306 33000E 8 3 •116700441428 0000091067 4 3367901 0019149 3310Mna(£93670000000 11wWxR(E) •300引0017100000 1258 »«®0000926 336400U%弁57 33 1 33663 6700014IHltW » 4 330000000| 巧H *♦■■■<&)1200 4 00 4 00000R J»»«R©9167110095120004567J B M^X65.6730671052 672546L33t I|U 中加《个密0—1IBM SP8S 8Uh$tic$ Proctssor M异常个案原因列表3252 3252 短信均値 .936 863 100.07 4017 4017 省内流量均値 .663 60975 918.64 2337 2337 短信均値 .938 852 100.07 1611 1611 短信均値 .884 824 100.07 3&5& 3656 短信均値 .958 855 100.07 940 940 短信均値 .716 747 100.07 183& 1836 短信均値 .821 785 100.07 820 820 漫游均値 .503 46.00 3.6738 2735 2735 短信均値 .951 835 100.07 1887 1887 短信均値 .751 746 100.07 41484148 短信均値.859790100.07葡萄酒样品检验同样可以利用相同方法进行异常值检测。
3实验任务-插值和拟合,数值积分

0 0
3 1.2
5 1.7
7 2.0
9 2.1
11 2.0
12 1.8
13 1.2
14 1.0
15 1.6
3.弹簧在力F的作用下伸长x,一定范围内服从胡克定律:F与x成正比, 即F=kx,现在得到下面一组F,x数据,并在(x,F)坐标下作图,可以看到 当F大到一定数据值后,就不服从这个定律了。试由数据确定k,并给出 不服从胡克定律时的近似公式。
在1点~12点的12小时内,每隔1小时测量一次温度,温度依次是: 5,8,9,15,25,29,31,30,22,25,27,24. (1)试估计在3.2h,6.5h,7.1h,11.7h时的温度值(线性、三次样条、拉格朗日); (2)试估计每隔1/10h的温度值,用图形表示。 1.
2.已知某精密仪器的某部件轮廓线的数据如下表所列,求x每改变0.1时的 Y值。 x y
x F
1
2
4
7
9
12
13
15
17
1.5 3.9
6.6 11.7 15.6 18.8 19.6 20.6 21.1
4.用matlab计算
L = 4∫
π /2
0
(a2 sin2 (t) + b2 cos2 (t))1/2dt
注:其中a=7782.5 ,b=7721.5.要求分别用梯形公式,辛普森公式计算
5、以以下积分为例,利用复化梯形法计算pi的值, 将误差控制在1e-5以内
π =∫
1
4 1+ x
2
0
dx
数值分析—插值拟合复习题

nk-1 由差分定义递推,查 n=k-1,k-2,…
(3f) ok!
(6). (c10 分)设 g(x)和 h(x)分别是 f(x)关于互异节点 x1,…, xn-1 以及互异
节点 x2,…, xn 的插值多项式,试用 g(x)和 h(x)表示 f(x)关于互异节 点 x1,…, xn 的插值多项式. 解:令 q(x)=Ag(x)(x-xn)+Bh(x)(x-x1)
方法与 Newton 插值方法所得多项式 相等 (相等, 不相等)
§2. 计算题
(1). (a10 分)依据下列函数值表,建立不超过 3 次的 lagrange 插值多项 式 L3(x).
x 012 3 f(x) 1 9 23 3 解:基函数分别为
l0(x)=-
1 8
x3+
7 8
x2-
7 4
x+1
l1(x)= 1 x 3 2x 2 8 x
2. 方程的根
(1). 用 Newton 法求方程 f(x)=x3+10x-20=0 的根,取初值 x0= 1.5, 则
x1= (3)
【 x1=1.5970149】
(2). 迭代公式 xk+1=xk (xk2+3a)/(3xk2+a)是求 a1/2 的 (12) 阶方法
3. 方程组直接解法
4. 迭代解法
f (x)
P1( x)
(b a)2 8
max
a xb
f
( x)
x [a, b]
证明:利用插值余项结果可得线性插值多项式 P1(x)在子区间[a,b]上的
余项估计式,再估计最值 ok!
f ( x) P1( x)
实验六拟合与插值问题PPT课件

2021/8/17
插值问题实例1
机翼下 轮廓线
y
x
19
第19页/共47页
插值问题的提法 已知 n+1个节点 (xj,yj)(j 0 ,1 ,L n ,其中 x j
互不相同,不妨设 a x 0 x 1 L x n b ) , 求任一插值点 x*( xj )处的插值 y * .
节点可视为由
y* y1
2[a1
xi
a2)
yi ]xi
0
i1
2[a1xi
a2 )
yi
]
0
a1,a2
2021/8/17
13
第13页/共47页
用MATLAB作线性最小二乘拟合 1. 作多项式f(x)=a1xm+ …+amx+am+1拟合,可利用已有程序:
a=polyfit(x,y,m)
输出拟合多项式系数 a=[a1, …,am , am+1] (数组)
1200
1000
800
600
400
200
0
0
2
4
6
8
10
12
14
2021/8/17
17
第17页/共47页
二、插 值
1. 插值的基本原理;三种插值方法:拉格朗日 插值,分段线性插值,三次样条插值。
2. 面 对 一 个 实 际 问 题,应 该 用 插 值,还 是 拟 合。
2021/8/17
18
第18页/共47页
y* y1
y0 •
• •
• •
x0 x1 x*
xn
2021/8/17
21
第21页/共47页
数值计算04-插值与拟合

二维插值的定义
第一种(网格节点):
y
O
x
已知 mn个节点 其中 互不相同,不妨设
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
第二种(散乱节点):
y
0
x
已知n个节点
其中 互不相同,
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
最邻近插值
y
( x1 , y2 ) ( x2 , y2 )
( x1 , y1 ) ( x2 , y1 )
x
O
注意:最邻近插值一般不连续。具有连续性的最简单 的插值是分片线性插值。
分片线性插值
速度最快,但平滑性差
linear
占有的内存较邻近点插值方法多,运算时间 也稍长,与邻近点插值不同,其结果是连续 的,但在顶点处的斜率会改变 运算时间长,但内存的占有较立方插值方法 要少,三次样条插值的平滑性很好,但如果 输入的数据不一致或数据点过近,可能出现 很差的插值结果 需要较多的内存和运算时间,平滑性很好 二维插值函数独有。插值点处的值和该点值 的导数都连续
x=0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 y=0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
海拔高度数据为: z=89 90 87 85 92 91 96 93 90 87 82 92 96 98 99 95 91 89 86 84 82 84 96 98 95 92 90 88 85 84 83 81 85 80 81 82 89 95 96 93 92 89 86 86 82 85 87 98 99 96 97 88 85 82 83 82 85 89 94 95 93 92 91 86 84 88 88 92 93 94 95 89 87 86 83 81 92 92 96 97 98 96 93 95 84 82 81 84 85 85 81 82 80 80 81 85 90 93 95 84 86 81 98 99 98 97 96 95 84 87 80 81 85 82 83 84 87 90 95 86 88 80 82 81 84 85 86 83 82 81 80 82 87 88 89 98 99 97 96 98 94 92 87
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 山区地貌:在某山区测得一些地点的高程如下表:(平面区域
1200<=x<=4000,1200<=y<=3600),试作出该山区的地貌图和等高线图,并对几种插值方法
进行比较。
3600 3200 2800 2400 2000 1600 1200 1480 1500 1550 1510 1430 1300 1200 980
1500 1550 1600 1550 1600 1600 1600 1550
1500 1200 1100 1550 1600 1550 1380 1070
1500 1200 1100 1350 1450 1200 1150 1010
1390 1500 1500 1400 900 1100 1060 950
1320 1450 1420 1400 1300 700 900 850
1130 1250 1280 1230 1040 900 500 700
Y/x
1200 1600 2000 2400 2800 3200 3600 4000
2 用给定的多项式,如y=x3-6x2+5x-3,产生一组数据(xi,yi,i=1,2,…,n),再在yi上添加随
机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数),然后用xi
和添加了随机干扰的yi作的3次多项式拟合,与原系数比较。如果作2或4次多项式拟合,
结果如何?
3 用电压V=10伏的电池给电容器充电,电容器上t时刻的电压
为 ,其中V0是电容器的初始电压, 是充电常数。
试由下面一组t,V数据确定V0, 。
2用给定的多项式,如y=x3-6x2+5x-3,产生一组数据(xi,yi,i=1,2,…,n),再在
yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分
布随机数),然后用xi和添加了随机干扰的yi作的3次多项式拟合,与原系数比
较。
分别作1、2、4、6次多项式拟合,比较结果,体会欠拟合、过拟合现象。
解:程序如下:
x=1:0.5:10;
y=x.^3-6*x.^2+5*x-3;
y0=y+rand;
f1=polyfit(x,y0,1)%输出多项式系数
y1=polyval(f1,x);%计算各x点的拟合值
plot(x,y,'+',x,y1)
grid on
title('一次拟合曲线');
figure(2);
f2=polyfit(x,y0,2)%2次多项式拟合
y2=polyval(f2,x);
plot(x,y,'+',x,y2);
grid on
title('二次拟合曲线');
figure(3);
f4=polyfit(x,y0,4)%4次多项式拟合
y3=polyval(f4,x);
plot(x,y,'+',x,y3)
grid on
title('四次拟合曲线');
figure(4);
f6=polyfit(x,y0,6)%6次多项式拟合
y4=polyval(f6,x);
plot(x,y,'+',x,y4)
grid on
title('六次拟合曲线');
运行结果如下:依次为各个拟合曲线的系数(按降幂排列)
f1 =43.2000 -149.0663
f2 = 10.5000 -72.3000 89.8087
f4 =0.0000 1.0000 -6.0000 5.0000 -2.5913
f6 = 0.0000 -0.0000 0.0000 1.0000 -6.0000 5.0000
-2.4199
运行后,比较拟合后多项式和原式的系数,发现四次多项式系数与原系数比较接
近,四次多项式的四次项系数很小。作图后,发现一次和二次多项式的图形与原
函数的差别比较大,属于欠拟合的情况,而四次多项式和六次多项式符合得比较
好。作图如下:
3.解:据题意分析如下:电容器充电的数学模型已经建立。
0
()()exp(/)vtVVVt
(已知V=10)可见,v(t)与τ成指数变化关系,所以在
通过曲线拟合的时候,使用指数曲线y=a1ea2x。(非线性拟合)。首先进行变量
代换在程序中用v1代替v(t),t0代替τ,v2是拟合后的曲线方程:
对0()10(10)exp(/)vtvt变形后取对数,有0ln(10())ln(10)(/)vtvt
令y=ln(10-)(tv) ,f1=ln(10-0) ,f2= -1/t0,则
v0=10-exp(f(2)), t0= -1/ f(1)。
编写程序如下:
t=[0.5 1 2 3 4 5 7 9];
v1=[6.36 6.48 7.26 8.22 8.66 8.99 9.43 9.63];
y=log(10- v1);
f=polyfit(t,y,1)
t0=-1/f(1)
v0=10-exp(f(2))
v2=10-(10-v0)*exp(-t/t0);
plot(t,v1,'rx',t,v2,'k:')
grid on
xlabel('时间t(s)'),ylabel('充电电压(V)');
title('电容器充电电压与时间t的曲线');
程序运行输出结果如下:
f =-0.2835 1.4766
t0 = 3.5269 v0 =5.6221
即电容器的初始电压为 v0 =5.6221,τ=3.5629。
4.某年美国旧车价格的调查资料如下表其中xi表示轿车的使用年数,yi表示相应的平均价
格。试分析用什么形式的曲线来拟合上述的数据,并预测使用4.5年后轿车的平均价格大致
为多少?
x
i
1 2 3 4 5 6 7 8 9 10
y
i
2615 1943 1494 1087 765 538 484 290 226 204
5 汽车制造厂生产的某种轿车的外形数据如下表所示
试找出最佳的拟合曲线拟合以上数据
6
