高考数学三角函数知识点及典型例题讲解

――概念、方法、题型、易误点及应试技巧总结
三角函数
1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。
2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。
3. 终边相同的角的表示:
(1)α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k k αθπ=+∈Z ,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角ο1825-的终边相同,且绝对
值最小的角的度数是___,合___弧度。
(答:25-o ;5
36
π-)
(2)α终边与θ终边共线(α的终边在θ终边所在直线上) ?()k k αθπ=+∈Z . (3)α终边与θ终边关于x 轴对称?2()k k αθπ=-+∈Z . (4)α终边与θ终边关于y 轴对称?2()k k απθπ=-+∈Z . (5)α终边与θ终边关于原点对称?2()k k απθπ=++∈Z .
(6)α终边在x 轴上的角可表示为:,k k Z απ=∈;α终边在y 轴上的角可表示为:
,2k k Z παπ=+∈;α终边在坐标轴上的角可表示为:,2k k Z πα=∈.如α的终边与6
π
的终
边关于直线x y =对称,则α=____________。
(答:Z k k ∈+
,3
2π
π)
4、α与2
α的终边关系:由“两等分各象限、一二三四”确定.如若α是第二象限角,则
2
α
是第_____象限角 (答:一、三)
5.弧长公式:||l R α=,扇形面积公式:211||22
S lR R α==,1弧度(1rad)57.3≈o . 如
已知扇形AOB 的周长是6cm ,该扇形的中心角是1弧度,求该扇形的面积。
(答:22cm )
6、任意角的三角函数的定义:设α是任意一个角,P (,)x y 是α的终边上的任意一点
(异于原点),它与原点的距离是0r =>,那么sin ,cos y x
r r
αα==,
()tan ,0y x x α=≠,cot x y α=(0)y ≠,sec r
x
α=()0x ≠,()csc 0r y y α=≠。三角函数值只
与角的大小有关,而与终边上点P 的位置无关。如
(1)已知角α的终边经过点P(5,-12),则ααcos sin +的值为__。
(答:7
13
-);
(2)设α是第三、四象限角,m
m --=
43
2sin α,则m 的取值范围是_______ (答:(-1,)2
3
);
(3)若
0|
cos |cos sin |sin |=+αα
αα,试判断)tan(cos )cot(sin αα?的符号 (答:负)
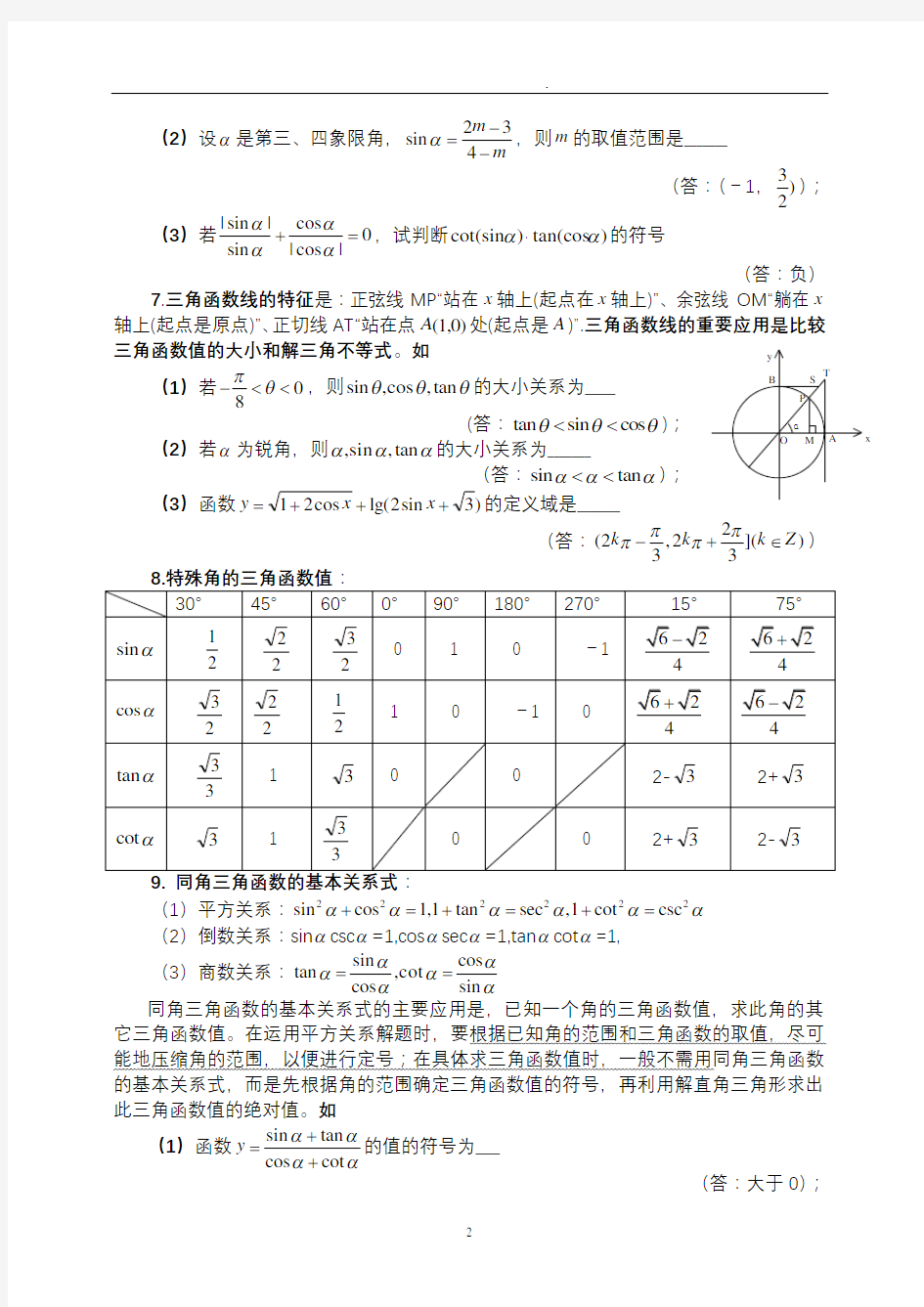
7.三角函数线的特征是:正弦线MP “站在x 轴上(起点在x 轴上)”、余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “站在点(1,0)A 处(起点是A )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如 (1)若08
π
θ-
<<,则sin ,cos ,tan θθθ的大小关系为_____
(答:tan sin cos θθθ<<);
(2)若α为锐角,则,sin ,tan ααα的大小关系为_______
(答:sin tan ααα<<); (3)函数)3sin 2lg(cos 21+++=x x y 的定义域是_______
(答:2(2,2]()3
3
k k k Z π
π
ππ-
+
∈)
(1)平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= (2)倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1,
(3)商数关系:sin cos tan ,cot cos sin αα
αααα
==
同角三角函数的基本关系式的主要应用是,已知一个角的三角函数值,求此角的其它三角函数值。在运用平方关系解题时,要根据已知角的范围和三角函数的取值,尽可能地压缩角的范围,以便进行定号;在具体求三角函数值时,一般不需用同角三角函数的基本关系式,而是先根据角的范围确定三角函数值的符号,再利用解直角三角形求出此三角函数值的绝对值。如
(1)函数sin tan cos cot y αα
αα
+=+的值的符号为____
(答:大于0);
y
T
A x
α B S
O M P
(2)若π220≤≤x ,则使x x 2cos 2sin 12=-成立的x 的取值范围是____
(答:[0,
]4π
U ],4
3
[ππ)
; (3)已知53sin +-=
m m θ,)2
(524cos πθπ
θ<<+-=m m ,则θtan =____ (答:12
5
-
); (4)已知
11tan tan -=-αα,则
α
αα
αcos sin cos 3sin +-=___;2cos sin sin 2++ααα=____ (答:35-;5
13
);
(5)已知a =ο200sin ,则ο160tan 等于
A 、21a a --
B 、21a
a
- C 、a a 21-- D 、a a 2
1-
(答:B );
(6)已知x x f 3cos )(cos =,则)30(sin οf 的值为______
(答:-1)。
10.三角函数诱导公式(2
k
πα+)的本质是:奇变偶不变(对k 而言,指k 取奇数或
偶数),符号看象限(看原函数,同时可把α看成是锐角).诱导公式的应用是求任意角的三角函数值,其一般步骤:(1)负角变正角,再写成2k π+α,02απ≤<;(2)转化为锐角三角函数。如
(1)97cos tan()sin 2146
ππ
π+-+的值为________
); (2)已知5
4
)540sin(-=+αο,则=-)270cos(οα______,若α为第二象限角,则
=+-+-)
180tan()]360cos()180[sin(2
αααο
οο________。 (答:5
4-;1003
-)
11、两角和与差的正弦、余弦、正切公式及倍角公式:
()sin sin cos cos sin sin 22sin cos 令αβ
αβαβαβααα=±=±???→= ()()2222222cos cos cos sin sin cos 2cos sin 2cos 112sin tan tan 1+cos2tan cos 1tan tan 2
1cos2sin 2
2tan tan 21tan 令 =
=
αβαβαβαβααα
αααβα
αβααβα
αα
αα=±=???→=-↓=-=-±±=
?-↓=
-m m
如(1)下列各式中,值为
1
2
的是 A 、1515sin cos o o B 、2
2
12
cos sin π
π
-
C 、22251225tan .tan .-o o
D (答:C );
(2)命题P :0tan(A B )+=,命题Q :0tan A tan B +=,则P 是Q 的 A 、充要条件 B 、充分不必要条件
C 、必要不充分条件
D 、既不充分也不必要条件
(答:C );
(3)已知3
5
sin()cos cos()sin αβααβα---=,那么2cos β的值为____
(答:7
25
);
(4)110sin o 的值是______ (答:4);
(5)已知0tan110a =,求0tan 50的值(用a
,乙求得的
结果是2
12a a
-,对甲、乙求得的结果的正确性你的判断是______
(答:甲、乙都对)
12. 三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。基本的技巧有:
(1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如()()ααββαββ=+-=-+,2()()ααβαβ=++-,
2()()αβαβα=+--,22
αβαβ++=?,()(
)
222αββ
ααβ+=---等)
,如 (1)已知2tan()5αβ+=,1tan()44πβ-=,那么tan()4
π
α+的值是_____
(答:3
22
);
(2)已知02πβαπ<<<<,且129cos()βα-=-,2
23
sin()αβ-=,求cos()αβ+的
值
(答:490
729
);
(3)已知,αβ为锐角,sin ,cos x y αβ==,3
cos()5
αβ+=-,则y 与x 的函数关系
为______
(答:43
(1)55
y x x =<<) (2)三角函数名互化(切割化弦),如 (1)
求值sin 50(1)o o
(答:1);
(2)已知
sin cos 2
1,tan()1cos 23
αααβα=-=--,求tan(2)βα-的值
(答:1
8
)
(3)公式变形使用(tan tan αβ±()()tan 1tan tan αβαβ=±m 。如
(1)已知A 、B 为锐角,且满足tan tan tan tan 1A B A B =++,则cos()A B +=_____
(答:2
-
); (2)设ABC ?
中,tan A tan B Atan B +=
,4
sin Acos A =,则此三角形是____三角形
(答:等边)
(4)三角函数次数的降升(降幂公式:21cos 2cos 2αα+=,21cos 2sin 2
α
α-=与升幂公
式:21cos 22cos αα+=,21cos 22sin αα-=)。如
(1)若32(,)αππ∈
为_____
(答:sin
2
α);
(2)
函数25f (x )sin x cos x x =
-x R )∈的单调递增区间为____ (答:51212
[k ,k ](k Z )ππ
ππ-+∈)
(5)式子结构的转化(对角、函数名、式子结构化同)。如
(1)tan (cos sin )ααα- sin tan cot csc αα
αα
+++
(答:sin α);
(2)求证:
2
1tan 1sin 212sin 1tan 2
2
ααα
α
++=--;
(3)化简:
4221
2cos 2cos 22tan()sin ()
44
x x x x ππ-+
-+ (答:1
cos 22
x )
(6)常值变换主要指“1”的变换(221sin cos x x =+22sec tan tan cot x x x x =-=?
tan sin 42ππ===L 等),如已知tan 2α=,求22sin sin cos 3cos αααα+-(答:3
5).
(7)正余弦“三兄妹—sin cos sin cos x x x x ±、”的内存联系――“知一求二”,如 (1)若 sin cos x x t ±=,则sin cos x x = __
(答:21
2
t -±),特别提醒:这里[t ∈;
(2)若1(0,),sin cos 2
απαα∈+=,求tan α的值。
(答:43
-
); (3)已知
2sin 22sin 1tan k ααα+=+()42
ππ
α<<,试用k 表示sin cos αα-的值
。
13、辅助角公式中辅助角的确定:()sin cos a x b x x θ+=+(其中θ角所在的象限由a , b 的符号确定,θ角的值由tan b
a
θ=确定)在求最值、化简时起着重要作用。如
(1)若方程sin x x c =有实数解,则c 的取值范围是___________.
(答:[-2,2]);
(2)当函数23y cos x sin x =-取得最大值时,tanx 的值是______
(答:3
2
-);
(3)如果()()sin 2cos()f x x x ??=+++是奇函数,则tan ?=
(答:-2);
(4)求值:
=?+?
-?20sin 6420cos 120sin 32
2
2________ (答:32)
14、正弦函数和余弦函数的图象:正弦函数sin y x =和余弦函数cos y x =图象的作图
方法:五点法:先取横坐标分别为0,3,,,222
ππ
ππ的五点,再用光滑的曲线把这五点连
接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。
15、正弦函数sin ()y x x R =∈、余弦函数cos ()y x x R =∈的性质: (1)定义域:都是R 。
(2)值域:都是[]1,1-,对sin y x =,当()22
x k k Z π
π=+
∈时,y 取最大值
1;当
()322
x k k Z π
π=+
∈时,y 取最小值-1;对cos y x =,当()2x k k Z π=∈时,y 取最大值1,当()2x k k Z ππ=+∈时,y 取最小值-1。如
(1)若函数sin(3)6y a b x π=-+的最大值为23,最小值为2
1
-,则=a __,=b _
(答:1
,12
a b ==或1b =-);
(2)函数x x x f cos 3sin )(+=(]2,
2[π
π-
∈x )的值域是____
(答:[-1, 2]);
(3)若2αβπ+=,则6y cos sin βα=-的最大值和最小值分别是____ 、_____
(答:7;-5);
(4)函数2()2cos sin()3
f x x x x π
=+sin cos x x +的最小值是_____,此时x =
__________
(答:2;()12
k k Z π
π+
∈)
; (5)己知2
1
cos sin =
βα,求αβcos sin =t 的变化范围 (答:1
[0,]2
);
(6)若αβαcos 2sin 2sin 22=+,求βα2
2sin sin +=y 的最大、最小值
(答:1max =y ,222min -=y )
。特别提醒:在解含有正余弦函数的问题时,你深入挖掘正余弦函数的有界性了吗? (3)周期性:①sin y x =、cos y x =的最小正周期都是2π;②()sin()f x A x ω?=+和
()cos()f x A x ω?=+的最小正周期都是2||
T π
ω=。如 (1)若3
sin )(x
x f π=,则(1)(2)(3)(2003)f f f f ++++L =___
(答:0);
(2) 函数4()cos f x x =2sin cos x x -4sin x -的最小正周期为____
(答:π); (3) 设函数)5
2sin(2)(π
π+=x x f ,若对任意R x ∈都有)()()(21x f x f x f ≤≤成立,则
||21x x -的最小值为____
(答:2)
(4)奇偶性与对称性:正弦函数sin ()y x x R =∈是奇函数,对称中心是()(),0k k Z π∈,对称轴是直线()2
x k k Z π
π=+
∈;余弦函数cos ()y x x R =∈是偶函数,对称中心是
(),02k k Z ππ??+∈
??
?,对称轴是直线()x k k Z π=∈(正(余)弦型函数的对称轴为过最高点或最低点且垂直于x 轴的直线,对称中心为图象与x 轴的交点)。如
(1)函数522y sin x π??
=- ???
的奇偶性是______、 (答:偶函数);
(2)已知函数31f (x )ax b sin x (a,b =++为常数),且57f ()=,则5f ()-=______
(答:-5);
(3)函数)cos (sin cos 2x x x y +=的图象的对称中心和对称轴分别是_______、_______
(答:128k (,)(k Z )ππ-∈、28
k x (k Z )ππ=+∈);
(4)
已知f (x )sin(x )x )θθ=++为偶函数,求θ的值。
(答:6
k (k Z )π
θπ=+
∈)
(5)单调性:()sin 2,222y x k k k Z ππππ?
?=-+∈???
?在上单调递增,在
()32,222k k k Z ππππ??++∈????
单调递减;cos y x =在[]()2,2k k k Z πππ+∈上单调递减,在[]()2,22k k k Z ππππ++∈上单调递增。特别提醒,别忘了k Z ∈!
16、形如sin()y A x ω?=+的函数:
(1)几个物理量:A ―振幅;1
f T
=―频率(周期的倒数);x ω?+―相位;?―初
相;
(2)函数sin()y A x ω?=+表达式的确定:A 由最值确定;ω由周期确定;?由图象上的特殊点确定,
如()sin()(0,0f x A x A ω?ω=+>>,||)2
π
?<
=_____(答:15()2sin()23
f x x π
=+);
(3)函数sin()y A x ω?=+图象的画法:①“五点法”――设X 令X =0,3,,,222
ππ
ππ求出相应的x 值,计算得出五点的坐标,描点后得出图象;②图
象变换法:这是作函数简图常用方法。
(4)函数sin()y A x k ω?=++的图象与sin y x =图象间的关系:①函数sin y x =的图象纵坐标不变,横坐标向左(?>0)或向右(?<0)平移||?个单位得()sin y x ?=+的图象;②函数()sin y x ?=+图象的纵坐标不变,横坐标变为原来的
1
ω
,得到函数()sin y x ω?=+的图象;③函数()sin y x ω?=+图象的横坐标不变,纵坐标变为原来的A
倍,得到函数sin()y A x ω?=+的图象;④函数sin()y A x ω?=+图象的横坐标不变,纵坐标向上(0k >)或向下(0k <),得到()sin y A x k ω?=++的图象。要特别注意,若由
()sin y x ω=得到()sin y x ω?=+的图象,则向左或向右平移应平移|
|?
ω
个单位,如 (1)函数2sin(2)14y x π
=--的图象经过怎样的变换才能得到sin y x =的图象?
(答:2sin(2)14y x π=--向上平移1个单位得2sin(2)4
y x π
=-的图象,再向左平移
8
π
个单位得2sin 2y x =的图象,横坐标扩大到原来的2倍得2sin y x =的图象,最后将纵坐标缩小到原来的1
2
即得sin y x =的图象);
(2) 要得到函数cos()24x y π=-的图象,只需把函数sin 2
x
y =的图象向___平移____个
单位
(答:左;
2
π); (3)将函数72sin(2)13y x π
=-
+图像,
按向量a r 平移后得到的函数图像关于原点对称,这样的向量是否唯一?若唯一,求出a r
;若不唯一,求出模最小的向量
(答:存在但不唯一,模最小的向量(,1)6
a π=--r
);
(4)若函数()[]()cos sin 0,2f x x x x π=+∈的图象与直线y k =有且仅有四个不同的交点,则k 的取值范围是
(答:)
(5)研究函数sin()y A x ω?=+性质的方法:类比于研究sin y x =的性质,只需将
sin()y A x ω?=+中的x ω?+看成sin y x =中的x ,
但在求sin()y A x ω?=+的单调区间时,要特别注意A 和ω的符号,通过诱导公式先将ω化正。如
(1)函数23
y sin(x )π
=-+
的递减区间是______
(答:51212
[k ,k ](k Z )π
πππ-
+∈)
; (2)12
34
x y log cos(
)π
=+的递减区间是_______ (答:336644
[k ,k ](k Z )π
πππ-+∈)
; (3)设函数)2
2
,0,0)(sin()(π?πω?ω<<->≠+=A x A x f 的图象关于直线3
2π=x 对称,它
的周期是π,则
A 、)21,0()(的图象过点x f
B 、()f x 在区间52[,]123
ππ
上是减函数
C 、)0,12
5()(π是的图象的一个对称中心x f D 、()f x 的最大值是A
(答:C );
(4)对于函数()2sin 23f x x π?
?=+ ??
?给出下列结论:
①图象关于原点成中心对称;
②图象关于直线12
x π
=
成轴对称;
③图象可由函数2sin 2y x =的图像向左平移3
π
个单位得到; ④图像向左平移
12
π
个单位,即得到函数2cos 2y x =的图像。 其中正确结论是_______
(答:②④);
(5)已知函数()2sin()f x x ω?=+图象与直线1y =的交点中,距离最近两点间的距离为3
π
,那么此函数的周期是_______
(答:π)
17、正切函数tan y x =的图象和性质: (1)定义域:{|,}2
x x k k Z π
π≠
+∈。遇到有关正切函数问题时,你注意到正切函数
的定义域了吗?
(2)值域是R ,在上面定义域上无最大值也无最小值;
(3)周期性:是周期函数且周期是π,它与直线y a =的两个相邻交点之间的距离是一个周期π。绝对值或平方对三角函数周期性的影响:一般说来,某一周期函数解析式加绝对值或平方,其周期性是:弦减半、切不变.既为周期函数又是偶函数的函数自变量加绝对值,其周期性不变,其它不定。 如x y x y sin ,sin 2==的周期都是π, 但sin y x =
cos x +的周期为
2
π
,而1|2sin(3)|,|2sin(3)2|626y x y x ππ=-+=-+,|tan |y x =的周期不变;
(4)奇偶性与对称性:是奇函数,对称中心是,02k π??
???
()k Z ∈,特别提醒:正(余)切型函数的对称中心有两类:一类是图象与x 轴的交点,另一类是渐近线与x 轴的交点,但无对称轴,这是与正弦、余弦函数的不同之处。
(5)单调性:正切函数在开区间
,k k k Z ππππ??
-++∈内都是增函数。但要注意在整个定
18. 三角形中的有关公式:
(1)内角和定理:三角形三角和为π,这是三角形中三角函数问题的特殊性,解题可不能忘记!任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形?三内角都是锐角?三内角的余弦值为正值?任两角和都是钝角?任意两边
的平方和大于第三边的平方.
(2)正弦定理:2sin sin sin a b c R A B C
===(R 为三角形外接圆的半径).注意:①正弦定理
的一些变式:()sin sin sin i a b c A B C ::=::;()sin ,sin ,sin 22a b ii A B C R R
== 2c R
=;()2sin ,2sin ,2sin iii a R A b R B b R C ===;②已知三角形两边一对角,求解三角形时,若运用正弦定理,则务必注意可能有两解.
(3)余弦定理:2222
2
2
2cos ,cos 2b c a a b c bc A A bc
+-=+-=等,常选用余弦定理鉴定三
角形的形状.
(4)面积公式:111sin ()222
a S ah a
b C r a b
c ===++(其中r 为三角形内切圆半径).
如ABC ?中,若C B A B A 22222sin sin cos cos sin =-,判断ABC ?的形状(答:直角三角形)。
特别提醒:(1)求解三角形中的问题时,一定要注意A B C π++=这个特殊性:
,sin()sin ,sin cos 22
A B C
A B C A B C π++=-+==;
(2)求解三角形中含有边角混合关系的问题时,常运用正弦定理、余弦定理实现边角互化。如
(1)ABC ?中,A 、B 的对边分别是 a b 、,且A=60 4,a b ==o ,那么满足条件的ABC ? A 、 有一个解 B 、有两个解 C 、无解 D 、不能确定
(答:C );
(2)在ABC ?中,A >B 是sin A sin B >成立的_____条件
(答:充要);
(3)在ABC ?中, 112(tan A)(tan B )++=,则2log sinC =_____
(答:1
2
-);
(4)在ABC ?中,a,b,c 分别是角A 、B 、C 所对的边,若(a b c )(sin A sin B +++3sinC )a sin B -=,则C ∠=____
(答:60o );
(5)在ABC ?中,若其面积222
S =,则C ∠=____
(答:30o );
(6)在ABC ?中,60 1A ,b ==o ,则ABC ?外接圆的直径
是_______
(答:
3
);
(7)在△ABC 中,a 、b 、c 是角A 、B 、C 的对边,21,cos 32
B C
a A +==则= ,
22b c +的最大值为
(答:19
32
;);
(8)在△ABC 中AB=1,BC=2,则角C 的取值范围是
(答:06
C π
<≤
); (9)设O 是锐角三角形ABC 的外心,若75C ∠=o ,且,,AOB BOC COA ???的面积满
足关系式AOB BOC COA S S ???+=,求A ∠(
答:45o ).
19.反三角函数:(1)反三角函数的定义(以反正弦函数为例):arcsin a 表示一个角,
这个角的正弦值为a ,且这个角在,22ππ??
-????
内(11)a -≤≤。(2)反正弦arcsin x 、反余弦
arccos x 、反正切arctan x 的取值范围分别是)2
,2(],,0[],2
,2[πππππ--.
在用反三角表示两异面直线所成的角、直线与平面所成的角、二面角的平面角、直
线的倾斜角、1l 到2l 的角、1l 与2l 的夹角以及两向量的夹角时,你是否注意到了它们的范围?(0,],[0,],[0,]22πππ,[)π,0, [0,),[0,),[0,]2
π
ππ.
20、求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值)。如
(1)若,(0,)αβπ∈,且tan α、tan β是方程2560x x -+=的两根,则求αβ+的值______
(答:34
π
);
(2)ABC ?中,3sin 4cos 6,4sin 3cos 1A B B A +=+=,则C ∠=_______
(答:3
π
);
(3)若02αβγπ≤<<<且0sin sin sin αβγ++=,0cos cos cos αβγ++=,求βα-的值
(答:23
π
).
三角函数知识点及题型归纳
三角函数高考题型分类总结 一.求值 1.若4sin ,tan 05 θθ=->,则cos θ= . 2.α是第三象限角,2 1)sin(= -πα,则αcos = )25cos(απ+= 3.若角α的终边经过点(12)P -,,则αcos = tan 2α= 4.下列各式中,值为 2 3 的是 ( ) (A )2sin15cos15?? (B )?-?15sin 15cos 22(C )115sin 22-?(D )?+?15cos 15sin 22 5.若02,sin 3cos απαα≤≤> ,则α的取值范围是: ( ) (A),32ππ?? ??? (B),3ππ?? ??? (C)4,33ππ?? ??? (D)3,32 ππ ?? ??? 二.最值 1.函数()sin cos f x x x =最小值是 。 2.若函数()(13tan )cos f x x x =+,02 x π ≤< ,则()f x 的最大值为 3.函数()cos 22sin f x x x =+的最小值为 最大值为 。 4.已知函数()2sin (0)f x x ωω=>在区间,34ππ?? - ??? ?上的最小值是2-,则ω的最小值等于 5.设02x π?? ∈ ??? ,,则函数22sin 1sin 2x y x +=的最小值为 . 6.将函数x x y cos 3sin -=的图像向右平移了n 个单位,所得图像关于y 轴对称,则n 的最小正值是 A . 6π7 B .3π C .6π D .2 π 7.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( ) A .1 B .2 C .3 D .2 8.函数2 ()sin 3sin cos f x x x x =+在区间,42ππ?? ? ??? 上的最大值是 ( ) A.1 B. 13 2 + C. 3 2 D.1+3 三.单调性 1.函数]),0[()26 sin(2ππ ∈-=x x y 为增函数的区间是 ( ).
三角函数,反三角函数公式大全
三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1 cotAcotB -+ 倍角公式 tan2A = A tan 12tanA 2 - Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3 π -a) 半角公式 sin( 2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2 A )= A A cos 1cos 1-+ tan(2 A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cos b = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2 b a - tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB 积化和差 sinasinb = - 21[cos(a+b)-cos(a-b)] cosacosb = 2 1 [cos(a+b)+cos(a-b)]
中考数学压轴题专题锐角三角函数的经典综合题
一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.某地是国家AAAA 级旅游景区,以“奇山奇水奇石景,古賨古洞古部落”享誉巴渠,被誉为 “小九寨”.端坐在观音崖旁的一块奇石似一只“啸天犬”,昂首向天,望穿古今.一个周末,某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离.他们把蹲着的“啸天犬”抽象成四边形ABCD ,想法测出了尾部C 看头顶B 的仰角为40,从前脚落地点D 看上嘴尖A 的仰角刚好60,5CB m =, 2.7CD m =.景区管理员告诉同学们,上嘴尖到地面的距离是3m .于是,他们很快就算出了AB 的长.你也算算?(结果精确到0.1m .参考数据:400.64400.77400.84sin cos tan ?≈?≈?≈,,.2 1.41,3 1.73≈≈) 【答案】AB 的长约为0.6m . 【解析】 【分析】 作BF CE ⊥于F ,根据正弦的定义求出BF ,利用余弦的定义求出CF ,利用正切的定义求出DE ,结合图形计算即可. 【详解】 解:作BF CE ⊥于F , 在Rt BFC ?中, 3.20BF BC sin BCF ?∠≈=, 3.85CF BC cos BCF ?∠≈=, 在Rt ADE ?E 中,3 1.73tan 3 AB DE ADE ===≈∠, 0.200.58BH BF HF AH EF CD DE CF ∴+=﹣=,==﹣= 由勾股定理得,22BH AH 0.6(m)AB =+≈, 答:AB 的长约为0.6m .
【点睛】 考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键. 2.如图,某无人机于空中A 处探测到目标B D 、的俯角分别是30、60??,此时无人机的飞行高度AC 为60m ,随后无人机从A 处继续水平飞行303m 到达'A 处. (1)求之间的距离 (2)求从无人机'A 上看目标的俯角的正切值. 【答案】(1)120米;(223. 【解析】 【分析】 (1)解直角三角形即可得到结论; (2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D ,于是得到'60A E AC ==, '30CE AA ==3Rt △ABC 中,求得33,然后根据三角函数的定义即可得到结论. 【详解】 解:(1)由题意得:∠ABD=30°,∠ADC=60°, 在Rt △ABC 中,AC=60m , ∴AB=sin 30AC ?=6012 =120(m ) (2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D , 则'60A E AC ==, '30 CE AA ==3 在Rt △ABC 中, AC=60m ,∠ADC=60°, ∴33∴3 ∴tan ∠A 'A D= tan ∠'A DC='A E DE 503235
高中文科数学三角函数知识点总结
三角函数知识点 一.考纲要求 考试内容3 要求层次 A B C 三角函数、 三角恒等 变换、 解三角形 三角函数 任意角的概念和弧度制 √ △ 弧度与角度的互化◇ √ 任意角的正弦、余弦、正切的定义 √ 用单位圆中的三角函数线表示正弦、余弦和正切 √ 诱导公式 √ △ 同角三角函数的基本关系式 √ 周期函数的定义、三角函数的周期性 √ 函数sin y x =,cos y x =,tan y x =的图象 和性质 √ 函数sin()y A x ω?=+的图象 √ 用三角函数解决一些简单的实际问题◇ √ 三角 恒等 变换 两角和与差的正弦、余弦、正切公式 √ 二倍角的正弦、余弦、正切公式 √ 简单的恒等变换 √ 解三角形 正弦定理、余弦定理 √ △ 解三角形 √ △ 二.知识点 1.角度制与弧度制的互化:,23600π= ,1800π= 1rad =π 180°≈57.30°=57°18ˊ. 1°= 180 π≈0.01745(rad ) 2.弧长及扇形面积公式 弧长公式:r l .α= 扇形面积公式:S=r l .2 1 α----是圆心角且为弧度制。 r-----是扇形半径 3.任意角的三角函数 设α是一个任意角,它的终边上一点p (x,y ), r=22y x +
(1)正弦sin α= r y 余弦cos α=r x 正切tan α=x y (2)各象限的符号: sin α cos α tan α 4、三角函数线 正弦线:MP; 余弦线:OM; 正切线: AT. 5.同角三角函数的基本关系: (1)平方关系:sin 2α+ cos 2α=1。 (2)商数关系: ααcos sin =tan α(z k k ∈+≠,2 ππ α) 6.诱导公式:奇变偶不变,符号看象限 ()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-. ()5sin cos 2π αα??-= ???,cos sin 2παα?? -= ??? . ()6sin cos 2παα??+= ???,cos sin 2παα??+=- ??? . x y +O — — + x y O — + + — + y O — + + — (3) 若 o
三角函数知识点及典型例题
三角函数知识点及典型例题 §1.1.1、任意角 1、 正角、负角、零角、象限角的概念. 2、 与角α终边相同的角的集合:{} |360,S k k Z ββα==+?∈ . §1.1.2、弧度制 1、 把长度等于半径长的弧所对的圆心角叫做1弧度的角. 2、 r l =α. 3、弧长公式: R 4、扇形面积公式: S=21 lr=2 1αr 2. §1.2.1、任意角的三角函数 1、 设α是一个任意角,它的终边与单位圆交于点()y x P ,,那么: x y x y = ==αααtan ,cos ,sin . 2、 设点()00,y x A 为角α终边上任意一点,那么:(设2020y x r +=) _______ sin r y =α,________cos r x =α,_____tan x y =α. 3、 αsin ,αcos ,αtan 在四个象限的符号一正二正弦三切四余 和三角函数线的画法. 4、 诱导公式一: ()()()_tan _2tan _cos _2cos _sin _2sin απααπααπα=+=+=+k k k (Z k ∈) 5、 特殊角0°,30°,45°,60°, 90°,180°,270°的三角函数值. §1.2.2、同角三角函数的基本关系式 1、 平方关系:2 2 sin cos 1αα+=.2、 商数关系:sin tan cos α αα =. §1.3、三角函数的诱导公式 1、 诱导公式二:()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ=+-=+-=+ 2、诱导公式三:()()()._tan _tan _____,cos _cos _,sin _sin αααααα-=-=--=- 3、诱导公式四: ()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ-=--=-=- 4、诱导公式五:._sin _2cos _,cos _2sin ααπααπ=?? ? ??-=??? ??-
高中数学常用反三角函数公式
反三角函数公式 arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x = 2 arc tanx = cos (n arc cos x) = .
反三角函数图像与特征 反正弦曲线图像与特征反余弦曲线图像与特征 拐点(同曲线对称中心):,该点切线斜率为1 拐点(同曲线对称中心): ,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征 拐点(同曲线对称中心):,该点切线斜率 为1 拐点: ,该点切线斜率为-1 渐近线: 渐近线: .
名称 反正割曲线反余割曲线 方程 图像 顶点 渐近线 反三角函数的定义域与主值范围 函数主值记号定义域主值范围 反正弦若,则 反余弦若,则 反正切若,则 反余切若,则 反正割若,则 反余割若,则 式中n为任意整数. .
反三角函数的相互关系 arc sin x = arc cos x = arc tan x = arc cot x = sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞
初三锐角三角函数知识点与典型例题
锐角三角函数: 知识点一:锐角三角函数的定义: 一、 锐角三角函数定义: 在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA= ∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数 【特别提醒:1、sinA 、∠cosA 、tanA 表示的是一个整体,是两条线段的比,没有,这些比值只与 有关,与直角三角形的 无关 2、取值范围
1.已知Rt △ABC 中,,12,43 tan ,90==?=∠BC A C 求AC 、AB 和cos B . 2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?= ∠4 3sin AOC 求:AB 及OC 的长. 3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,?=∠5 3 sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4. 已知A ∠是锐角,17 8 sin =A ,求A cos ,A tan 的值 对应训练: (西城北)3.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为 A . 55 B .255 C .12 D .2 (房山)5.在△ABC 中,∠C =90°,sin A=5 3 ,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 类型二. 利用角度转化求值: 1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2. 求:sin B 、cos B 、tan B .
高中数学三角函数知识点归纳总结
《三角函数》 【知识网络】 一、任意角的概念与弧度制 1、将沿x 轴正向的射线,围绕原点旋转所形成的图形称作角. 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角 2、同终边的角可表示为 {}()360k k Z ααβ? =+∈g x 轴上角:{}()180k k Z αα=∈o g y 轴上角:{}()90180k k Z αα=+∈o o g 3、第一象限角:{}()036090360k k k Z αα? ?+<<+∈o g g 第二象限角:{}()90 360180360k k k Z αα??+<<+∈o o g g 第三象限角:{}()180360270360k k k Z αα? ?+<<+∈o o g g 第四象限角: {}()270 360360360k k k Z αα??+<<+∈o o g g 4、区分第一象限角、锐角以及小于90o 的角 第一象限角:{}()0360 90360k k k Z αα? ?+<<+∈o g g 锐角: {}090αα< ,2 4 , 0π απ ≤ ≤=k ,2 345, 1παπ≤≤=k 所以 2 α 在第一、三象限 6、弧度制:弧长等于半径时,所对的圆心角为1弧度的圆心角,记作1rad . 7、角度与弧度的转化:01745.0180 1≈=?π 815730.571801'?=?≈? = π 9、弧长与面积计算公式 弧长:l R α=?;面积:211 22 S l R R α=?=?,注意:这里的α均为弧度制. 二、任意角的三角函数 1、正弦:sin y r α=;余弦cos x r α=;正切tan y x α= 其中(),x y 为角α终边上任意点坐标,r = 2、三角函数值对应表: 3、三角函数在各象限中的符号 高中数学必修4三角函数知识点总结 一、角的概念和弧度制: (1)在直角坐标系内讨论角: 注意:若角的终边在坐标轴上,就说这个角不属于任何象限,它叫象限界角。 (2)①与α角终边相同的角的集合:},2|{},360|{0Z k k Z k k ∈+=∈+=απββαββ或 与α角终边在同一条直线上的角的集合: ; 与α角终边关于x 轴对称的角的集合: ; 与α角终边关于y 轴对称的角的集合: ; 与α角终边关于x y =轴对称的角的集合: (3)区间角的表示: ①象限角:第一象限角: ; 第四象限角: ; 第一、三象限角: ; ②写出图中所表示的区间角: (4)由α的终边所在的象限, 来判断2α所在的象限,来判断3 α所在的象限 (5)弧度制:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零; 任一角α的弧度数的绝对值r l =||α,其中l 为以角α为圆心角时所对圆弧的长。 (6)弧长公式: ;半径公式: ;扇形面积公式: ; 练习:已知扇形AOB 的周长是6cm ,该扇形的中心角是1弧度,求该扇形的面积。(22cm ) 二、任意角的三角函数: (1)任意角的三角函数定义: 以角α的顶点为坐标原点,始边为x 轴正半轴建立直角坐标系 I )在角α的终边上任取一个异于原点的点),(y x P ,点P 到原点的距离记为r ,则=αsin ;=αcos ;=αtan (注意r>0) 练习:已知角α的终边经过点P(5,-12),则ααcos sin +的值为__。 角α的终边上一点)3,(a a -,则=+ααsin 2cos 。 II )作单位元交角α的终边上点),(y x P ,则=αsin ;=αcos ;=αtan (2)在图中画出 角α的正弦线、 余弦线、正切 线; 练习: (1)若α为锐角,则,sin ,tan ααα的大小关系为_____ (sin tan ααα<<) (2)函数)3sin 2lg(cos 21+++=x x y 的定义域是______222,33x k x k k Z ππππ??∣- <≤+∈???? (3)特殊角的三角函数值: 三、同角三角函数的关系与诱导公式: (1)同角三角函数的关系 反三角函数公式 反三角函数图像与特征 1 : 反三角函数的定义域与主值范围 式中n为任意整数. 反三角函数的相互关系 sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞ If x > 0.5 And x <= 1 Then ArcSin = -Atn(Sqr(1 - x * x) / x) + 2 * Atn(1) End Function ArcCos(x) 函数 功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double。 语法:ArcCos(x)。 说明:其中,x的取值范围为[-1,1],x的数据类型为Double。 程序代码: Function ArcCos(x As Double) As Double If x >= -1 And x < -0.5 Then ArcCos = Atn(Sqr(1 - x *x) / x) + 4 * Atn(1) If x >= -0.5 And x <= 0.5 Then ArcCos = -Atn(x/ Sqr(1 - x * x)) + 2 * Atn(1) If x> 0.5 And x <= 1 Then ArcCos = Atn(Sqr(1 - x*x) / x) End Function 一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG =FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米. 【答案】553 【解析】 【分析】 如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可. 【详解】 解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J. ∵AM⊥CD, ∴∠QMP=∠MPO=∠OQM=90°, ∴四边形OQMP是矩形, ∴QM=OP, ∵OC=OD=10,∠COD=60°, ∴△COD是等边三角形, ∵OP⊥CD, ∠COD=30°, ∴∠COP=1 2 ∴QM=OP=OC?cos30°=3 ∵∠AOC=∠QOP=90°, ∴∠AOQ=∠COP=30°, ∴AQ=1 OA=5(分米), 2 ∴AM=AQ+MQ=5+3 ∵OB∥CD, ∴∠BOD=∠ODC=60° 在Rt△OFK中,KO=OF?cos60°=2(分米),FK=OF?sin60°=23(分米), 在Rt△PKE中,EK=22 -=26(分米), EF FK ∴BE=10?2?26=(8?26)(分米), 在Rt△OFJ中,OJ=OF?cos60°=2(分米),FJ=23(分米), 在Rt△FJE′中,E′J=22 -(2)=26, 63 ∴B′E′=10?(26?2)=12?26, ∴B′E′?BE=4. 故答案为:5+53,4. 【点睛】 本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型. 2.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系; (2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由 (3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长. 【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP62 23 . 【解析】 【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再 初中三角函数知识点总结(中考复习) 锐角三角函数知识点总结 1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。 2、如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。 4、任意锐角的正切值等于它的余角的余切值;任意锐角的余 A 90 B 90 ∠ - ? = ∠ ? = ∠ + ∠ 得 由B A C 切值等于它的余角的正切值。 5、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 6、正弦、余弦的增减性: 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。 7、正切、余切的增减性: 当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。 1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。 依据:①边的关系:2 2 2 c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法) 2、应用举例: (1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。 仰角铅垂线 水平线 视线 视线俯角 (2)坡面的铅直高度h 和水平宽度l 的比叫做坡度 (坡比)。用字 母i 表示,即h i l =。坡度一般写成1:m 的形式,如1:5i =等。 把坡面与水平面的夹角记作α(叫做坡角),那么tan h i l α==。 3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。 4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。 反比例函数知识点整理 一、 反比例函数的概念 :i h l =h l α 三角函数知识点 1.特殊角的三角函数值: (1)平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= (2)倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, (3)商数关系:sin cos tan ,cot cos sin αα αααα == ) 3、两角和与差的正弦、余弦、正切公式及倍角公式: ()sin sin cos cos sin sin 22sin cos 令αβ αβαβαβααα=±=±???→= ()()2222222cos cos cos sin sin cos 2cos sin 2cos 112sin tan tan 1+cos2tan cos 1tan tan 2 1cos2sin 2 2tan tan 21tan 令 = = αβ αβαβαβααα αα αβα αβααβα αα αα =±=???→=-↓=-=-±±= ?-↓= - (1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、 两角与其和差角的变换. 如()()ααββαββ=+-=-+,2()()ααβαβ=++-, 2()()αβαβα=+--,22 αβαβ++=?,()( ) 222αββ ααβ+=---等), (2)三角函数次数的降升(降幂公式:21cos 2cos 2αα+=,21cos 2sin 2 α α-=与升幂公 式:21cos 22cos αα+=,21cos 22sin αα-=)。如 (; (3)常值变换主要指“1”的变换(221sin cos x x =+22sec tan tan cot x x x x =-=? tan sin 42 ππ=== 等),. 。 (4)周期性:①sin y x =、cos y x =的最小正周期都是2π;②()sin()f x A x ω?=+和 ()cos()f x A x ω?=+的最小正周期都是2||T π ω=。如 (5)单调性:()sin 2,222y x k k k Z ππππ? ?=-+∈??? ?在上单调递增,在 ()32,222k k k Z ππππ??++∈??? ?单调递减;cos y x =在[]()2,2k k k Z πππ+∈上单调递减,在[]()2,22k k k Z ππππ++∈上单调递增。特别提醒,别忘了k Z ∈! (6)、形如sin()y A x ω?=+的函数: 1几个物理量:A ―振幅;1 f T =―频率(周期的倒数); x ω?+― 相位;?―初相; 2函数sin()y A x ω?=+表达式的确定:A 由周 期确定;?由图象上的特殊点确()sin()(0,0f x A x A ω?ω=+>>,||)2 π?<()f x =_____(答:15()2sin()23 f x x π =+); 3函数sin()y A x ω?=+图象的画法:①“五点法”――设X x ω?=+,令X =0,3,,,222 ππ ππ求出相应的x 值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法。 4函数sin()y A x k ω?=++的图象与sin y x =图象间的关系:①函数sin y x =的图象纵坐标不变,横坐标向左(?>0)或向右(?<0)平移||?个单位得()sin y x ?=+的图象;②函数()si n y x ?=+图象的纵坐标不变,横坐标变为原来的 1 ω ,得到函数 ()sin y x ω?=+的图象;③函数()sin y x ω?=+图象的横坐标不变,纵坐标变为原来的A 倍,得到函数sin()y A x ω?=+的图象;④函数sin()y A x ω?=+图象的横坐标不变,纵坐标向上(0k >)或向下(0k <),得到()sin y A x k ω?=++的图象。要特别注意,若由 ()sin y x ω=得到()sin y x ω?=+的图象,则向左或向右平移应平移| |? ω 个单位,如 (1)函数2sin(2)14 y x π =--的图象经过怎样的变换才能得到sin y x =的图象? sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 2、倍角公式 tan2A =A tan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 3、半角公式 sin(2A )=2cos 1A - cos(2 A )=2cos 1A + tan( 2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式 sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a a cos sin 5、万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2 )2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) = a sin 1 sec(a) =a cos 1 7、(a +b )的三次方,(a -b )的三次方公式 高中数学三角函数知识点总结 1.特殊角的三角函数值: 2.角度制与弧度制的互化: ,23600π= ,1800 π= 1rad =π 180°≈57.30°=57°18ˊ 1°= 180 π≈0.01745(rad ) 3.弧长及扇形面积公式 (1)弧长公式:r l .α= α----是圆心角且为弧度制 (2)扇形面积公式:S=r l .2 1 r-----是扇形半径 4.任意角的三角函数 设α是一个任意角,它的终边上一点p (x,y ), r=22y x + (1)正弦sin α= r y 余弦cos α=r x 正切tan α=x y (2)各象限的符号: 记忆口诀:一全正,二正弦,三两切,四余弦 sin α cos α tan α 5.同角三角函数的基本关系: (1)平方关系:s in 2α+ cos 2α=1 (2)商数关系:ααcos sin =tan α(z k k ∈+≠,2 ππ α) 6.诱导公式: 记忆口诀:把2 k π α±的三角函数化为α的三角函数,概括为:奇变偶不变,符号看象限。 ()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-. 口诀:函数名称不变,符号看象限. ()5sin cos 2π αα??-= ???,cos sin 2παα?? -= ??? . ()6sin cos 2π αα??+= ???,cos sin 2παα?? +=- ??? . 口诀:正弦与余弦互换,符号看象限. x y O — + + — + y O — + + — 1、两角和公式 sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinB cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB tan(A+B)=tanAtanB -1tanB tanA +tan(A-B)=tanAtanB 1tanB tanA +- cot(A+B)=cotA cotB 1-cotAcotB +cot(A-B)=cotA cotB 1cotAcotB -+ 2、倍角公式 tan2A=A tan 12tanA 2-Sin2A=2SinA?CosA Cos2A=Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 3、半角公式 sin(2A )=2cos 1A -cos(2 A )=2cos 1A + tan( 2A )=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式 sin(-a)=-sinacos(-a)=cosa sin(2π-a)=cosacos(2π-a)=sinasin(2π+a)=cosacos(2 π+a)=-sina sin(π-a)=sinacos(π-a)=-cosasin(π+a)=-sinacos(π+a)=-cosa tgA=tanA=a a cos sin 5、万能公式 sina=2)2(tan 12tan 2a a +cosa=22)2(tan 1)2(tan 1a a +-tana=2 )2 (tan 12tan 2a a - 6、其他非重点三角函数 csc(a)=a sin 1sec(a)=a cos 1 7、(a +b )的三次方,(a -b )的三次方公式 (a+b)^3=a^3+3a^2b+3ab^2+b^3 (a-b)^3=a^3-3a^2b+3ab^2-b^3 a^3+b^3=(a+b)(a^2-ab+b^2) a^3-b^3=(a-b)(a^2+ab+b^2) 8、反三角函数公式 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanx arccot(-x)=π-arccotx 锐角三角函数 1 .把 Rt △ABC 各边的长度都扩大 3 倍得 Rt △A′B′C′,那么锐角 A , A ′的余弦值的关系为() A .cosA=cosA ′B. cosA=3cosA ′C. 3cosA=cosA ′ D .不能确定 2 .如图 1 ,已知 P 是射线 OB 上的任意一点, PM ⊥ OA 于 M ,且 PM :OM= 3 : 4 ,则 cos α的值等于() A .3 B. 4 C. 4 D . 3 4 3 5 5 图 1 图 2 图 3 图 4 图 5 3 .在△ABC 中,∠C=90 °,∠A ,∠B,∠C 的对边分别是a, b , c,则下列各项中正确的是() A .a=c ·sin B B. a=c ·cosB C.a=c ·tanB D.以上均不正确 4 .在 Rt △ABC 中,∠C=90 °,cosA= 2 ,则 tanB 等于()3 A .3 B. 5 C. 2 5 D . 5 5 3 5 2 5 .在 Rt △ABC 中,∠C=90 °,AC=5 ,AB=13 ,则 sinA=______ , cosA=______ , ?tanA=_______ . 6 .如图 2 ,在△ABC 中,∠C=90 °,BC: AC=1 : 2 ,则 sinA=_______ ,cosA=______ , tanB=______ . 7 .如图 3 ,在 Rt △ABC 中,∠C=90 °,b=20 , c=20 2 ,则∠B 的度数为 _______. 8 .如图 4 ,在△CDE 中,∠E=90 °,DE=6 , CD=10 ,求∠D 的三个三角函数值. 9 7 .已知:α是锐角, tan α=,则sinα=_____,cosα=_______. 24 10 .在 Rt △ABC 中,两边的长分别为 3 和 4 ,求最小角的正弦值为 10 .如图 5 ,角α的顶点在直角坐标系的原点,一边在x 轴上, ?另一边经过点 P( 2 ,2 3),求角α的三个三角 函数值. 12 .如图,在△ ABC 中,∠ABC=90 °,BD ⊥ AC 于 D,∠CBD= α,AB=3 ,?BC=4 ,?求 sin α,cos α,tan α的值. 解直角三角形 一、填空题 3 1.已知 cosA=,且∠B=900-∠A,则sinB=__________. 2三角函数知识点总结及练习题
常用反三角函数公式表
人教中考数学锐角三角函数-经典压轴题附详细答案
初中三角函数知识点总结(中考复习)
三角函数知识点及例题讲解
三角函数_反三角函数_积分公式_求导公式
高中数学三角函数知识点总结(珍藏版)
角函数反三角函数积分公式求导公式
完整版锐角三角函数练习题及答案.doc
