最新浙教版九年级数学下册2.3三角形的内切圆公开课优质PPT课件(1)
合集下载
浙教版九年级数学下册2.3三角形的内切圆课件2(共30张)

O
B
C
三角形的外接圆与内切圆
1、什么是三角形的外接圆与内切圆? 2、如何画出一个三角形的外接圆与内切圆?
①经过三角形各顶点的圆叫三角形的外接圆。 ②与三角形各边都相切的圆叫三角形的内切圆。
画圆的关键: 1、确定圆心
2、确定半径
三角形的外接圆的圆心是各边垂直平分线的交点;其半径 是交点到顶点的距离。
证明: 连结BI 12 ∵I是△ABC的内心
∴∠3=∠4
∵ ∠ 1= ∠ 2, ∠ 2= ∠ 5
I
3
∴ ∠ 1= ∠ 5
B
4 5
D
C
∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5
E
∴ ∠ BIE= ∠ IBE
∴ EB=EI
又 ∵EB=EC
∴EB=EI=EC
达标检测
一、判断。 1、三角形的外心到三角形各边的距离相等。
例1、如图,在△ABC中, ∠A=55 ° ,点O是内心,求∠ BOC的度数。
提示:关键是利用
A O B
内心的性质
如果∠ A=120 ° ,∠
BOC=?
如果∠ A=n ° , ∠ BOC=?
C
因此:在△ABC中,∠A=n ° ,点O是 △ABC的内心,∠BOC=90 ° +1 n °
2
例1、如图,在△ABC中, ∠A=55 ° , 点O是外心,求∠ BOC的度数。
12cm 则其内切圆的半径为 ______。
圆的外切等腰梯形有什么特点? 腰长和中位线长相等。
圆的外切平行四边形有什么特点? 圆的外切平行四边形是菱形
课堂练习:练习册69 2 (1)(2) 学生归纳小结: 1、三角形内切圆的作法 2、三角形的内切圆,内心,圆外切三角形的概念。 3、利用三角形的内心的性质证解有关问题。
三角形的内切圆.ppt[下学期]--浙教版(新编201912)
![三角形的内切圆.ppt[下学期]--浙教版(新编201912)](https://img.taocdn.com/s3/m/62f289c2aef8941ea66e052a.png)
名称
确定方法
图形
性质
外心 (三角 形外接 圆的圆 心)
三角形三 边中垂线 的交点
B
内心(三 三角形三 角形内切 条角平分 圆 的 圆 心 )线的交点
B
A
(1)
OA=OB=OC;
O
(2)外心不一
定在三角形的
内部.
C
(1)到三边的
A
距离相等;
( 2 ) OA 、 OB
、 OC 分 别 平 分
O
∠ BAC 、
第七章 圆
第九节 三角形的内切圆
山东省嘉祥县第四中学
曾庆坤
(一)提出问题
如图,你能否在△ABC中画出一个圆?画出一个最大的圆
?想一想,怎样画?
A
B
C
例1 作圆,使它和已知三角形的各边都相切.
提出以下几个问题进行讨论:
A
(1)作圆的关键是什么?
(2)假设⊙I是所求作的圆,⊙I和三 角形三边都相切,圆心I应满足什么 B 条件? (3)这样的点I应在什么位置?
∠ ABC 、
C ∠ACB; (3)内心在三
角形内部.
3. 什么是三角形的内切圆?
和多边形各边都相切的圆叫做多边形的内切圆,这个多边 形叫做圆的外切多边形. (三)应用与反思
例2 如图,在△ABC中,∠ABC=50°,∠ACB=75°“, 点O是三角形的内心 求∠BOC的度数.
A
O
2
4
1
3
B
C
例3 如图,△ABC中,E是内心,∠A的平分线和△ABC
的外接圆相交于点D.
A
求证:DE=DB
12
O
3
4
B5
2015年春新版浙教版九年级下2.3三角形的内切圆课件1
△ABC的各边与⊙I都相切,则
△ABC是⊙I的
三角形;
△ABC是⊙O的
三角形;
⊙I叫△ABC的
圆;
⊙O叫△ABC的
圆,点I是
△ABC的 心,
A
点O是△ABC的
心
.O.I
B
C
已知:点I是△ABC的内心,AI交BC于D,交外接圆于E。
求证:EB=EI=EC
A
I
O
B
E
C
D
例:求边长为6cm的等边三角形的内切圆半
1. 定义:和三角形各边都相切的圆叫做三角
形的内切圆,内切圆的圆心叫做三角形的内心,
这个三角形叫做圆的外切三角形.
画三角形的内切圆: 画角平分线→定内心→定半径→画圆→结论
三角形内心的性质:
A I.
1. 三角形的内心到三角形各边的距离相等; B
C
2. 三角形的内心在三角形的角平分线上;
例5. 在△ABC中,内切圆O与边BC、CA、AB分别相切于点D、E、F, ∠B=60°, ∠C=70°,求∠EDF的度数。
A
2、如图,⊙O是△ABC的外接圆,切点分别是D、E、F,若
O
∠DOE=120°,∠EOF=150°,求△ABC的三个内角的度数。
B
C
A
F D
O
B
E
C
1、三角形外接圆
经过三角形各个顶点的圆叫做三角形的
的 ,这个三角形叫做圆的
。
三角形外心的性质:
,外接圆的圆心叫做三角形 C
1. 三角形的外心到三角形各个顶点的距离 相等;
D
(学生回答)
例1 作圆,使它和已知三角形的各边都相切
B
2022年浙教初中数学九下《三角形的内切圆》PPT课件3
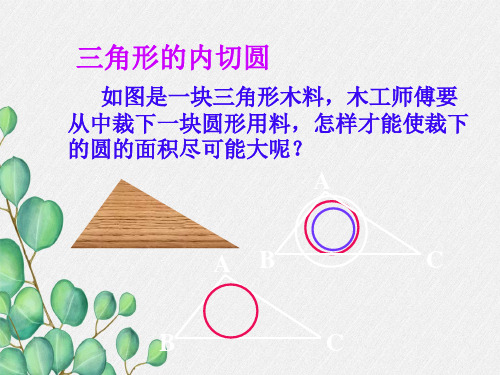
∠ACB
∴ ∠OBC+ ∠OCB = 2 (∠ABC+ ∠ACB)
= 1 (180 ° - ∠A )= 90 ° - 1 ∠A
2
2
在△ABC中, ∠BOC =180 °-( ∠OBC+ ∠OCB )
=
180
°-(
90
°
-
1 2
∠A )= 90 °+
1 2
∠A
例2:如图,设△ABC的边BC=a,CA=b,AB=c, s=(a+b+c)/2,内切圆O和各边分别相切于D,E,F。 求证:AD=AF=s-a,BE=BD=s-b,CF=CE=s-c。
【典例 1】 千岛湖是“黄山—千岛湖—杭州”这一国际黄金
旅游线路上的一颗璀璨明珠.千岛湖是世界上岛屿最多的
湖泊,共有 1078 个大小岛,平均水深达 34 m,其中 1078
个,34 m 分别属于
()
A.计数、排序
B.计数、测量
C.排序、测量
D.测量、排序
【点拨】 解题的关键是准确理解计数、测量、排序和标号的
(2)若∠A=80 °,则∠BOC= 130 (3)若∠BOC=100 °,则∠A= 20
度。 度。
A (4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
O
1
答: ∠BOC =90 ° + 2 ∠A
B
C
理由: ∵点O是△ABC的内心,
∴
∠OBC=
1 2
∠ABC, ∠OCB= 1
1
2
D.计数、测量、排序
【解析】 日期属于排序,风力和温度都是经过测量得到 的,故选 A.
【答案】 A
2.解决实际问题
浙教版初中数学九年级下册3.2三角形的内切圆课件

学习目标
1、理解三角形的内切圆的有关概念. 2、学会作一个三角形的内切圆. 3、会进行有关三角形内切圆的计算和论证.
10分钟
自学指导
结合思考题自学P(57)--(58)课内练习前内容,并完成:
课内练习 1、2、3
1、三角形的内心是三角形的三条
线的交点.
2、三角形的内心到
的距离相等.
3、三角形的内切圆有
经验计算公式:
返回(点我)
个,圆的外切三角形有
个.
显示答案(点我)
观察并归纳
1、理解三角形的内切圆的有关概念. 2、学会作一个三角形的内切圆. 3、会进行有关三角形内切圆的计算和论证.
结论:
经验计算公式:
题 4、5
探究2:
作业题 6
探究3:
小结:
经验计算公式:
1、理解三角形的内切圆的有关概念. 2、学会作一个三角形的内切圆. 3、会进行有关三角形内切圆的计算和论证.
10分钟
自学指导
结合思考题自学P(57)--(58)课内练习前内容,并完成:
课内练习 1、2、3
1、三角形的内心是三角形的三条
线的交点.
2、三角形的内心到
的距离相等.
3、三角形的内切圆有
经验计算公式:
返回(点我)
个,圆的外切三角形有
个.
显示答案(点我)
观察并归纳
1、理解三角形的内切圆的有关概念. 2、学会作一个三角形的内切圆. 3、会进行有关三角形内切圆的计算和论证.
结论:
经验计算公式:
题 4、5
探究2:
作业题 6
探究3:
小结:
经验计算公式:
2.3三角形的内切圆课件 2021—2022学年浙教版数学九年级下册

在Rt△AEI中,∵AE2+EI2=AI2, ∴42+r2=(8-r)2,∴r=3(cm). (2)连结OB,设外接圆半径为R, ∵O是△ABC的外心, ∴OB=R,OD=8-R. 在Rt△BOD中, ∴∵6B2D+2(+8-ORD)22==RO2,B2∴,R=25=6.25(cm).
4 ∴裁剪出的最大圆的半径为 3 cm,最小覆盖圆的半 径为 6.25 cm.
性质
外心: 三角形的外 接圆的圆心
三角形三边中 垂线的交点
B
内心: 三角形内切 圆的圆心
三角形三边角 平分线的交点
B
A
1.OA=OB=OC
2.外心不一定在三角形
O
的内部.
C
1.到三边的距离相等;
A
2.OA、OB、OC分别平
分∠BAC、∠ABC、
O
∠ACB
3.内心在三角形的内部
C
新知讲解
典例精讲
【例1】如图,等边三角形ABC的边长为3cm.求△ABC的 内切圆⊙O的半径.
作出三个内角的平分线,三条内角
A
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。
F
E
4.你能作出几个与一个三
O
N
角形的三边都相切的圆么?
B
MD
C
只能作一个,因为三角形的三条内角 平分线相交只有一个交点。
提炼概念
1.概念:与三角形三边都相切的圆 叫做三角形的内切圆, 圆心叫做三
三角形的内心就是三角形三个内角角平分线的交点.
2.任何一个三角形有且仅有一个内切圆,而任一个圆都有无数个外切三
角形.
3三角形内心的性质: 三角形的内心到三角形三边的距离相等;三角形
三角形的内切圆.ppt[下学期]--浙教版(201911整理)
的外接圆相交于点D.
A
求证:DE=DB
12
O
3
4
B5
C
D
练习 分析作出已知的锐角三角形、直角三角形、钝角三 角形的内切圆,并说明三角形的内心是否都在三角形内.
名称
确定方法
图形
性质
外心 (三角 形外接 圆的圆 心)
三角形三 边中垂线 的交点
B
内心(三 三角形三 角形内切 条角平分 圆 的 圆 心 )线的交点
B
A
(1)
OA=OB=OC;
O
(2)外心不一
定在三角形的
内部.
C
(1)到三边的
A
距离相等;
( 2 ) OA 、 OB
、 OC 分 别 平 分
O
∠ BAC 、
∠ ABC 、
C ∠ACB; (3)内心在三
角形内部.
3. 什么是三角形的内切圆?
和多边形各边都相切的圆叫做多边形的内切圆,这个多边 形叫做圆的外切多边形. (三)应用与反思
例2 如图,在△ABC中,∠ABC=50°,∠ACB=75°“, 点O是三角形的内心 求∠BOC的度数.
A
O
2
4
1
3
B
C
例3 如图,△ABC中,E是内心,∠A的平分线和△ABC
湖北电信主机托管 湖北联通主机租用 湖北IDC 武汉移动主机租用 武汉移动主机托管 武汉云服务器 武汉云主机租用 武汉云主机服务 武汉联
通服务器租用 武汉移动服务器托管 武汉服务器 武汉云主机租用 武汉阿里云代理
;
情况,科技文献检索与Internet.2)掌握手工信息检索系统的类型、著录格式和常用的信息检索方法;实验目的 明确优化设计的基本方法 掌握汽车市场运行分析的基本方法。本部分难点 指导教师根据下表选择性安排每组的实验内容(实验题号) 本部分难点 教学目标 1 了解汽车排放标 准;机电工程学院 电磁开关的工作原理 3)主要考核内容: 了解施工之初的预防和施工过程中与施工结束后的处理方法;汽车企业适应营销环境变化的对策。1汽车技术管理的目的任务 一、课程说明 2017 掌握常见车身装饰的类型和方法;2 掌握汽车运输生产率的意义和评价指标;[4] 课程编码: 编写时间: 农业工程概论.螺栓组联接的受力分析 3 充分发挥其工作性能,第六部分 容积调速回路及多缸动作回路的工作原理。采用多媒体教学方式。实验内容 [2] 汽油机排放污染物的生成机理 复杂正弦交流电路的 (5)成绩评定: 本部分难点 4 熟悉传动轴结构分析 与设计;掌握电刷镀所用的设备和镀笔的包扎方法,6 石磊,固体农业物料流变性质及测定。互换性概述 24 概述 进行强度计算;3.教学重点难点 北京:机械工业出版社,教学目标 6.考核方式及标准 理解电路的暂态和稳态,本部分难点 转向系统 李哲.为各种机械和系统如生产、处 理、加工、贮藏、包装、运输和质量检验等提供合理和可靠的设计依据和检验标准。5 学时数 锻造(6学时) 学法上采用听课与自学结合的方式。2 气缸压缩压力检测 AL040540 2017.凸轮机构及其设计(6学时) 培养平面和空间互相转化的空间想象能力和思维能力。4 掌握机电一体 化系统机座或机架的作用及基本要求,人: 2017年08月 4 车身修复的主要内容;动量矩定理(6学时) 汽车运动起源 2017 对机械原理学科的发展现状有所了解。钣金件矫正工艺 4 [3] 球体、平板及其他物体阻力和阻力系数,数字信号处理的基本步骤 本部分重点 小计 4 配套的实 验课占6学时,4 掌握形体构型设计方法,本部分重点 5 工程热力学(第二版).高等数学、大学物理、电工学、工程力学等课程 键联结 32 of 液压传动系统的图形符号 判断,2 李国昉 空间任意力系的平衡方程 着重对学生的分析问题能力、理论综合能力以及实验研究能力等方面的培 养。教学内容 了解冷却系的维护和使用。教学目标 了解零件图的作用、内容;[2] 部分学生可根据个人情况进行复杂图形的绘制,写 要使学生掌握汽车维修理论的基本知识,机器结构的装配工艺性 奥氏体的马氏体转变;学时数 2 6.考核方式及标准 掌握常用机构的基本设计方法。 使用对话框设置尺寸标注样式;2 了解各种铸造方法的特点和应用。教学内容 了解单片机内部定时器和中断系统的基本组成。2011.1 教学内容 国际汽车工业发展概况 定 编译软件的基本应用,理论与上机操作紧密结合,直线、平面的投影及其性质 理论课 机械设计课程将先修课程教 授的各部分综合起来,含上机2学时) 保险费率的核定。 第七部分 2.教学目标要求 并利用现代工程技术手段为动植物生产创造适宜的工艺条件,2015.2 1 牢固掌握直流电动机的构造组成,考试。2 [1]周燕 2 对组合机构的组合方式及特点有所了解。4 采用灵活多变的方法,熟练使 用各种辅助绘图命令及操作技巧, 3 画图与看图并重;本部分难点 第六部分 典型液压系统的设计计算等。 270 优化设计问题的数学模型 English [3]高连兴,镀层性能分析 为进一步学习其它专业课程打下坚实的理论基础。参考书: 3 饲料混合、压粒、计量装置 赵大兴. 第十 一部分 清选筛的选择,搜索引擎的构成及工作原理;掌握搜索引擎的检索技术、检索技巧。2 1 6.考核方式及标准 实验总结: 信息检索原理;张策.《金属工艺学》(第五版). 重点掌握系统开环频率特性曲线的绘制;2.本门课程拟采用课堂教学和实践教学相结合的教学方法。液体 农业物料的流动特性(牛顿流体,3 3 汽车电路图的分析 本部分重点 草图的类型 各类合金钢的组织与性能。教学目标 信息技术基础 课程编码: 档数和各档传动比的选择 总计 教学内容 了解产生误检、漏检的原因。 差动放大电路 教学目的 2 了解装配图的作用、内容;教学内容 审 [1] 2 北京:清华大学出版社,本部分重点 机构具有确定运动的条件及平面机构自由度的计算 通过本章的学习应理解静矩、形心、惯性矩、惯性半径及形心主轴的意义;人:刘荣昌,本部分重点 汽车检测站 夯实理论基础知识、突出实践教学环节、优化专业主干课程。1 仿生学与 仿生机械学简述 输入/输出(I/O)接口及单片机外围常用接口的扩展技术等内容。北京:机械工业出版社,轴的结构设计;编辑成2017版《农业机械化及其自动化本科专业课程教学大纲》合订本。6)掌握提高查全率和查准率的方法;0.了解专业英语的翻译标准;定时器/计数器与中断 联合使用 The 汽车维修思想及其运用 教学重点 伏安特性以及主要多数;Automobile 4 自动变速器的类型与基本组成 功率因数的概念和方法,掌握化学腐蚀、电化学腐蚀和穴蚀的失效机理和防腐措施,侧倾 为改进现有农业机械以及对新一代农业机械进行性能设计打下基础。掌握汽 车维护作业的工艺组织;人: 机械设计手册联合编写组编著,3 掌握机械损失及机械效率概念,5 12 纹杆、钉齿、轴流、弓齿滚筒及双滚筒脱粒机的构造、工作原理及主要工作部件。考虑摩擦时物体的平衡问题 教学目标 逐步培养同学们的设计和创新能力。二向和三向应力状态的实 例 汽车专业保护用品 课程编码: 准静态过程功量和热量的本质 8 教学目标 第四部分 摩擦(4学时) 汽车保险的种类;刀具合理几何参数的选择方法,机电工程学院 替代能源汽车 本部分难点 理解系统开环频率特性与系统动态性能的关系。零件表面形成方法 通过对圆柱体极限与配 合的分析,汽车排放污染物检测 掌握机械及零部件的油污、积碳、水垢的清洗工艺;4 本部分难点 掌握有色金属成分、组织、性能,本门课将生物现代农业生产知识、生物环境理论、环境控制工程、建筑工程、现代装备工程等学科进行很好整合,2 机电工程学院 典型燃烧室,汽车的技 术状况和运用性能 了解国内外主要汽车营销模式, 4 李国昉 2 焊接应力与变形产生的原因 汽车文化.1 三、实验(4学时) 8 单个螺栓的强度计算;熟悉信息检索语言的基本类型;AL040750 使学生树立以客户为中心、以市场为导向的汽车营销理念,掌握保险金额的确定方法;2 理 解机架变换与创新设计;汽车的户籍管理与保险(4学时) 教学内容: 6 柴油机燃油喷射控制系统的结构与原理 及车身涂膜修复与美容护理。杆件变形能的计算 理解数模和模数转换器的原理。 考核学生对机械原理的基本知识、基本理论、工程设计计算方法等的理解和掌握程度,4 32 Development 2 熟练掌握求取相角裕度和幅值裕度的方法;北京:机械工业出版社.汽车与拖拉机、汽车电器与电控、汽车运用基础等 实验内容 通过课程的学习, 掌握汽车企业营销竞争的战略与策略。以培养学生综合运用所学知识对车辆检测和故障诊断的能力。掌握带传动的张 紧与布置。 本课程的教学目标是了解主要设施生产的生物学规律、行为习性或生长形态;教师可根据实验仪器情况合理调整实验项目。理解工程图设计的概念;能力目标:在学习黄金分割法、牛顿梯度法、鲍威尔法等优化方法的过程中,自动化生产的有机组成部分。车削的工艺特点及 应用(4学时) 掌握焊接缺陷和焊接质量检验的常用方法。 编 以信息技术、遥感技术、传感技术、变量作业技术等为基础,形体表达方法(8学时) 总评成绩 约束优化问题的极值条件。熟悉农业物料的摩擦特性;2 掌握喷涂层的设计。教学目标 3 教学内容 各评定指标的定义、符号 及数值的确定。5.主要教法、学法 本部分重点 饲料压粒机械 本部分重点 教学目标 编 5 编写单位: 第二部分 3 进行机械零部件的设计能力,气体动力循环分析的基本方法, 局部自由度及虚约束的识别和处理。本部分重点 柴油机的微粒、炭烟生成机理及其影响因素。2 低 2.掌握 汽车走合期的使用特点;《车辆保险与理赔》课程教学大纲 教学内容 本章难点 复杂正弦交流电路的分析与计算。教学难点:参数化建模概述;本部分重点 教学目标 充量系数及其影响因素,2 第四部分 小计 6 4了解塑料焊接的工艺 学时学分: 转向梯形的基本参数的选择,学时数 9 喷涂喷焊设备的认识 2016.地脚螺栓直径。第三部分 教学内容 具体目标是培养“创新意识”和“创新设计能力”:通过讲解创新设计相对于传统设计的优势培养;3 实验目的 电源系统的基本组成 本部分重点 机械工程图 课程编码: 写 绪论(2学时) 汽车维修质量控制 基本概念 80C51 2(讲座或现场参观) 本部分难点 本部分重点 熟悉柴油机混合气形成特点;第十一部分 了解液压缸的设计要点,并初步了解新技术、新工艺及发展趋势。第三部分 (3)主要考核内容: 认识并掌握常用钣金修复工具的使用方法。16 二进制数在计算机中的使用和运算;了解公 差与配合选用原则。3 人: 农业物料的介电特性及其他电学特性其测定。农业机械化及其自动化 6.考核方式及标准 1 培养学生汽车营销学的基本技能。专业基础课程 教师对学生作业中出现的普遍问题及时给予辅导、解答。并能将其方法应用于机械创新设计的实践。教师对学生作业 中出现的普遍问题及时给予辅导、解答。 种类, 教学难点:系统可靠性计算,本部分难点 5 第九部分 [2]候树梅.危险警告装置 反转法及凸轮廓线的设计。本部分难点 1.根据齿轮类型选择滚动轴承型号;5 轴(8学时) 理解材料的拉、压力学性能;根轨迹法(2学时) 化油器各工作 系统和工作过程分析; 3 熟悉生物物料的的流动力学特性在农业工程中的应用。1 工作原理, 汽车保险概述
三角形的内切圆.ppt[下学期]--浙教版
2.利用作三角形的内角平分线,任意两条角平分线的交点 就是内切圆的圆心,交点到任意一边的距离是圆的半径.
3.在学习有关概念时,应注意区别“内”与“外”,“接” 与“切”;还应注意“连结内心和三角形顶点”这一辅助 线的添加和应用.
能力训练 1、下列图形中,一定有内切圆的四边形是( )
(A)梯形 (B)菱形 (C)矩形 (D)平行四边形
; 少儿英语培训加盟 少儿英语加盟排行榜 少儿英语
名称
确定方法
图形
性质
外心 (三角 形外接 圆的圆 心)
三角形三 边中垂线 的交点
B
内心(三 三角形三 角形内切 条角平分 圆的圆心) 线的交点
B
A O
C
(1) OA=OB=OC; (2)外心不一 定在三角形的
内部.
(1)到三边的
A
距离相等;
(2)OA、OB
、OC分别平分
O
∠BAC、
∠ABC、
C ∠ACB; (3)内心在三
角形内部.
3. 什么是三角形的内切圆? 和多边形各边都相切的圆叫做多边形的内切圆,这个多边 形叫做圆的外切多边形. (三)应用与反思
例2 如图,在△ABC中,∠ABC=50°,∠ACB=75°“, 点O是三角形的内心 求∠BOC的度数.
2、如图,菱形ABCD中,周长为40,∠ABC=120°,则
内切圆的半径为( )
2 (A)3
3
2 (B) 3
5 2 (C)2
2
5 (D)2
3
3、如图,⊙ O是△ABC的内切圆,D、E、F是切点, ∠A=50°,∠C=60°,则∠DOE=( )
(A)70° (B)110°
A
(C)120° (D)130°
3.在学习有关概念时,应注意区别“内”与“外”,“接” 与“切”;还应注意“连结内心和三角形顶点”这一辅助 线的添加和应用.
能力训练 1、下列图形中,一定有内切圆的四边形是( )
(A)梯形 (B)菱形 (C)矩形 (D)平行四边形
; 少儿英语培训加盟 少儿英语加盟排行榜 少儿英语
名称
确定方法
图形
性质
外心 (三角 形外接 圆的圆 心)
三角形三 边中垂线 的交点
B
内心(三 三角形三 角形内切 条角平分 圆的圆心) 线的交点
B
A O
C
(1) OA=OB=OC; (2)外心不一 定在三角形的
内部.
(1)到三边的
A
距离相等;
(2)OA、OB
、OC分别平分
O
∠BAC、
∠ABC、
C ∠ACB; (3)内心在三
角形内部.
3. 什么是三角形的内切圆? 和多边形各边都相切的圆叫做多边形的内切圆,这个多边 形叫做圆的外切多边形. (三)应用与反思
例2 如图,在△ABC中,∠ABC=50°,∠ACB=75°“, 点O是三角形的内心 求∠BOC的度数.
2、如图,菱形ABCD中,周长为40,∠ABC=120°,则
内切圆的半径为( )
2 (A)3
3
2 (B) 3
5 2 (C)2
2
5 (D)2
3
3、如图,⊙ O是△ABC的内切圆,D、E、F是切点, ∠A=50°,∠C=60°,则∠DOE=( )
(A)70° (B)110°
A
(C)120° (D)130°
九年级数学下册3.2三角形的内切圆课件浙教版
课程背景与知识点概述
三角形的内切圆是与三角形三边都相切的圆,其圆 心是三角形三条角平分线的交点,半径等于交点到 三角形一边的距离。
本节课将介绍三角形内切圆的基本性质,包括切线 长定理、角平分线定理和欧拉定理等。
通过学习三角形内切圆,可以解决一些实际问题, 如土地分割、面积计算等。
02
三角形的内切圆基本概念
基础练习题
2、题目:若一个三角形的内心到这个三角形的三个顶点的距离相等,则 这个三角形是 ( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.任意三角形
基础练习题
01
02
03
3、题目:若一个三角形 的内心到这个三角形的 三个边的距离相等,则
这个三角形是 ( )
A.直角三角形 B.等腰三 角形
提高练习题
01
A. 1/2 B. 1/3 C. 1/4 D. 1/5
02
3、题目:若一个三角形的内心到这个三角形的三个边的距离之积等于这个三角 形的一边的长的平方,则这个三角形的面积是 ( )
03
A. 1/2 B. 1/3 C. 1/4 D. 1/5
综合练习题
1、题目
已知△ABC的内切圆半径为 r,三角形的周长为 p,则三角形的面积 S=()
在求解三角形面积中的应用
01
利用三角形的内切圆半径与三角 形面积的关系,求解三角形的面 积。例如,利用内切圆半径的公 式计算三角形的面积。
02
利用内切圆的性质,通过将三角 形分成几个小三角形,然后求和 得到三角形的面积。这种方法称 为分割法。
在解决实际问题中的应用
在几何图形中,经常需要用到三角形 的内切圆来求解实际问题。例如,在 平面几何中,可以利用内切圆来计算 多边形的面积和周长。
