钢筋混凝土受压构件承载力计算
混凝土局部承压计算公式

混凝土局部承压计算公式
1.标准公式:
P=Pc+Pb
其中,P为混凝土局部承压载荷,Pc为混凝土压力,Pb为附加荷载。
混凝土压力Pc的计算可以使用以下公式:
Pc=fcd×(α1×β×γ×δ×μ)
其中,fcd为混凝土设计抗压强度,α1为荷载系数,β为尺寸系数,γ为激活系数,δ为荷载概论系数,μ为其他修正系数。
附加荷载Pb可以根据具体的设计要求和施工条件来确定。
2.配筋面积的计算公式:
A=s×t
其中,A为配筋面积,s为配筋率,t为构件厚度。
在计算配筋面积时,需要根据混凝土的设计强度和结构的要求来确定
合理的配筋率。
3.局部承压强度的计算公式:
σ=σc+σs
其中,σ为混凝土局部承压强度,σc为混凝土的标准强度,σs为
混凝土配筋钢筋的强度。
4.等效混凝土面积的计算公式:
Ae=A1+A2-0.5b
其中,Ae为等效混凝土面积,A1为混凝土面积,A2为钢筋面积,b 为受压区域宽度。
等效混凝土面积的计算是根据钢筋与混凝土的相互作用来确定的,这有助于更准确地评估混凝土局部承压的能力。
5.极限承载力的计算公式:
Pult=σ×Ae
其中,Pult为混凝土局部承压的极限承载力,σ为混凝土的极限承受应力,Ae为等效混凝土面积。
极限承载力的计算可根据混凝土的极限应力和等效混凝土面积来确定混凝土局部承压的能力。
以上是一些常用的混凝土局部承压计算公式,根据具体设计和施工的要求,还可以结合其他因素进行进一步的修正和计算。
钢筋混凝土受压构件和受拉构件—偏心受压柱计算
① 当同一主轴方向的杆端弯矩比: M1 0.9
M2
② 轴压比:
N 0.9
fc A
③ 构件的长细比满足要求: l0 34 12( M1 )
i
M2
M1、M2:分别为已考虑侧移影响的偏心受压构件两端截面按结构弹性
分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为M2,绝对值较小 端为 M1;当构件按单曲率弯曲时, M1/M2取正值,否则取负值。
α1fc
α1fcbx x=ξh0
f 'yA's A's
b
h0用平面的受压承载力计算
可能垂直弯矩作用平面先破坏,按非偏心方向的轴心受 压承载力计算
N Nu 0.9 ( fc A f yAs )
2.对称配筋矩形截面小偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
Ne f y As (h0 as ')
e
ei
h 2
as
e ei
N e’
fyAs As
α1fcbx x
α1fc
f 'yA's A's
b
as
h0
a's
h
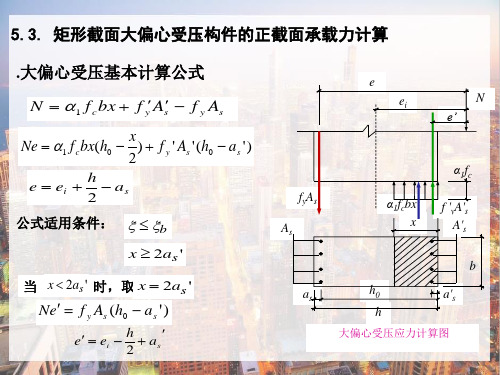
大偏心受压应力计算图
2.对称配筋矩形截面大偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
5.3. 矩形截面大偏心受压构件的正截面承载力计算
.大偏心受压基本计算公式
N 1 f cbx f y As f y As
混凝土受压构件的承载力计算

0 受剪承载力计算
1
1 砌体沿体水平缝的抗剪能力为沿通缝的抗剪承载能力及作用在截面上的压力所产生的摩擦力总和。
VVAf 1.4N o d u
vd
fk
0 式中: Vd—剪力设计值
2
A—受剪截面面积 ○ fvd—抗剪强度设计值 ○ μf—摩擦系数,对实心砖砌体,μf=0.7
Nk—与受剪截面垂直的压力标准值
§17.2受压构件的承载力计算 砌体受压短构件受力状态(图17-2)
特点: (1)构件承受轴心压力时,截面上产生均匀的压应力;
(17-2a) (2)构件承受偏心压力时,压应力分布随偏心距的变化
而变化,砌体表现出弹塑性性能。 (17-2b)
(3)随着偏心距的增大,在远离偏心压力作用的截面边 缘,由受压过渡到受拉,直至破坏,仍会全截面受力。 (17-2c)
φ—轴向受压弯曲系数
拱的承载力计算
1)拱的截面承载力验算
(1)砌体拱圈截面 (2)混凝土拱圈截面 各符号意义同前。
oNdNuAfcd oNdNuAcfcd
2)拱的整体承载力(强度—稳定)验算
近似模拟直杆方法,全拱取一个轴向力和一个偏心距。
(1)砌体拱圈
oN dN u Afcd
(2)混凝土拱圈 oN dN uA cfcd
单击添加副标题
§17 圬 土结构构 件的承载
力计算
2 0 2 3
17.1 计算原则
○ 极限状态设计法设计原则是使荷载效应不利组合的设计值要小于或等于结构抗力
效应的设计值 oSRfd,ad
○ 即: ○ 式中:γo —桥梁结构重要系数
S—作用效应组合值
R(·)—构件承载力设计值函数
○ fd—材料强度设计值 ○ ad—几何参数设计值,可采用几何参数标准值 ak
钢筋混凝土受弯构件正截面承载力计算

由相对界限受压区高度b可推出最大配筋率 b及单筋矩形截面的最大受弯承载力Mumax。
As bh0
b
1
f
fc
y
4.3.5 适筋和少筋破坏的界限条件
min.h/h0 b min —— 最小配筋率, 根据钢筋混凝土梁的破坏弯
矩等于同样截面尺寸素砼梁的开裂弯矩 确定的。
确定的理论依据为:
Mu = Mcr
《规范》对min作出如下规定:
(1)受弯构件、偏心受拉、轴心受拉构件其 一侧纵向受拉钢筋的配筋百分率不 应小于0.2%和0.45ft/fy中的较大值 ;
梁的宽度和高度
宽度 :b = 120、150、(180)、200、(220)、 250、300、350、…(mm)
高度:h=250、300、350、400、……、750、800、 900、…(mm)。
二、 截面尺寸和配筋构造
2. 板
c15mm d
分布钢筋
h0
h
d 6 ~ 12mm
h0 h 20
(2)卧置于地基上的混凝土板,板的受拉钢 筋的最小配筋百分率可适当降低, 但不应小于0.15%。
4.4 单筋矩形截面的承载力计算
4.4.1 基本计算公式及适用条件
1fc
x
Mu
C=1fc bx
Ts = fyAs
1. 基本计算公式
N 0
M 0
1 fcbx fyAs (3 - 20)
架立
箍筋
弯矩引起的 垂直裂缝
钢筋混凝土受弯构件正截面承载力计算

为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能,钢筋的混凝土保护层厚
5度、一配般筋不率小于2A 5msm% ; ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义:
As为受拉钢筋截面面积; b为梁宽;h0为梁的有效 高度,h0=h-as;as为所有受拉钢筋重心到梁底面 的距离,单排钢筋as= 35mm ,双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩-曲率关系
说明:
对于配筋合适的梁,在III
阶段,其承载力基本保持不 变而变形可以很大,在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力,破坏预兆明显,我们把
0.8 My
通常采用两点对称集中加荷,加载点位于梁跨度 的1/3处,如下图所示。这样,在两个对称集中荷载间 的区段(称“纯弯段”)上,不仅可以基本上排除剪力的 影响(忽略自重),同时也有利于在这一较长的区段上(L /3)布置仪表,以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内,沿梁高两侧布置多排测 点,用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小, Mcr -Mu的差值越大; 越大(但仍在少筋梁范围内), Mcr -Mu的差值越小。
当Mcr -Mu =0时,它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。
3、钢筋混凝土受压构件的强度计算

3、钢筋混凝土受压构件的强度计算第三章钢筋混凝土受压构件的强度计算桥梁结构中的桥墩、桩、主拱圈、斜拉桥的索塔,以及单层厂房柱、拱、屋架上弦杆,多层和高层建筑中的框架柱、剪力墙、筒体,烟囱的筒壁等均属于受压构件。
受压构件按受力情况分为轴心受压构件和偏心受压构件两类。
第一节配有纵向钢筋和普通箍筋的轴心受压构件当构件受到位于截面形心的轴向压力时,为轴心受压构件。
钢筋混凝土轴心受压构件按箍筋的作用及配置方式可分为普通箍筋柱和螺旋箍筋柱两种,本节介绍配有纵向钢筋和普通箍筋的轴心受压构件。
3.1.1 一般构造要求1、混凝土标号轴心受压构件的正截面承载力,主要由混凝土提供,一般多采用C20~C30混凝土,或者采用更高标号的混凝土。
2、截面尺寸轴心受压构件截面尺寸不宜过小,因长细比越大,承载力越小,不能充分利用材料强度。
矩形截面的最小尺寸不宜小于250mm。
3、纵向钢筋纵向受力钢筋一般选R235、HRB335级钢筋,有特殊要求时,可用HRB400级钢筋。
钢筋的直径不应小于12mm,净距不应小于5Omm 且不应大于35Omm。
在构件截面上,纵向受力钢筋至少应有4根并且在截面每一角隅处必须布置一根。
柱内设置纵向钢筋的目的是:a、提高柱的承载力,以减小构件的截面尺寸;b、防止因偶然偏心产生的破坏;c、改善构件破坏时的延性;d、减小混凝土的徐变。
为此,《公桥规》规定:构件全部纵向钢筋的配筋百分率不应小于0.5%(当混凝土强度等级在C50及以上时,不应小于0.6%);同时,一侧钢筋的配筋百分率不应小于0.2%。
轴心受压构件在加载后荷载维持不变的条件下,由于混凝土徐变,随着荷载作用时间的增加,混凝土的压应力逐渐变小,钢筋的压力逐渐变大,初期变化比较快,经过一定时间后趋于稳定。
在荷载突然卸载时,构件回弹,由于混凝土徐变变形的大部分不可恢复,故当荷载为零时,会使柱中钢筋受压而混凝土受拉,若柱的配筋率过大,还可能将混凝土拉裂;若柱中纵筋和混凝土之间有很强的粘应力时,则可能同时产生纵向裂缝。
混凝土梁受弯承载能力计算方法

混凝土梁受弯承载能力计算方法一、前言混凝土梁是一种常见的结构构件,用于支撑和传递荷载。
在设计混凝土梁时,需要计算其承载能力,以确保其安全可靠。
本文将介绍混凝土梁受弯承载能力的计算方法。
二、承载能力计算方法混凝土梁受弯的承载能力主要由混凝土和钢筋的受拉能力共同决定。
因此,混凝土梁的承载能力计算可以分为混凝土受压区的计算和钢筋的计算两个部分。
(一)混凝土受压区的计算1. 受压区高度的确定受压区高度的确定需要考虑以下几个方面:(1)混凝土的强度等级和变形能力;(2)钢筋的布置方式、直径和数量;(3)截面的几何形状。
根据混凝土的强度等级和变形能力以及钢筋的布置方式、直径和数量,可以确定混凝土受压区的高度。
对于矩形截面,混凝土受压区的高度一般为截面高度减去钢筋直径的一半;对于T形截面,混凝土受压区的高度一般为T形翼缘高度减去钢筋直径的一半。
2. 混凝土受压区受压应力的计算混凝土受压区受压应力的计算需要考虑以下几个因素:(1)混凝土的强度等级和变形能力;(2)钢筋的布置方式、直径和数量;(3)截面的几何形状。
混凝土受压区的受压应力一般按照受压区高度的平均值计算。
若混凝土的强度等级为C30,则受压区的极限受压应力为0.446fcu,其中fcu为混凝土的抗压强度。
若混凝土的强度等级为C40,则受压区的极限受压应力为0.536fcu。
3. 混凝土受压区的承载力计算混凝土受压区的承载力主要由混凝土的强度和受压区的面积共同决定。
混凝土受压区的承载力计算公式为:Nc = 0.85fcuAb其中,Nc为混凝土受压区的承载力,fcu为混凝土的抗压强度,Ab为混凝土受压区的面积。
(二)钢筋的计算钢筋的计算需要考虑以下几个因素:(1)钢筋的抗拉强度和屈服强度;(2)钢筋的数量、直径和布置方式;(3)混凝土受压区的受压应力。
1. 钢筋的受拉应力的计算钢筋受拉应力的计算需要考虑以下几个因素:(1)钢筋的抗拉强度和屈服强度;(2)钢筋的数量、直径和布置方式;(3)混凝土受压区的受压应力。
钢筋混凝土梁的承载力分析

钢筋混凝土梁的承载力分析钢筋混凝土梁是建筑结构中常见的构件,承载力分析对于工程设计和结构安全至关重要。
本文将对钢筋混凝土梁的承载力进行分析,并探讨影响承载力的主要因素。
一、钢筋混凝土梁的基本构造钢筋混凝土梁一般由混凝土和钢筋组成。
混凝土负责承载压力,而钢筋则用来承载拉力。
在构造中,钢筋通常布置在混凝土的底部,以增强梁的抗拉能力。
梁的形状可以是矩形、T形、L形等,根据设计要求确定。
二、钢筋混凝土梁的承载力计算钢筋混凝土梁的承载力计算是根据结构力学和材料力学原理进行的。
主要考虑以下几个因素:1. 弯矩的影响:钢筋混凝土梁在承受外力作用时会产生弯矩,该弯矩对梁的截面产生压力和拉力,从而影响承载力。
根据弯矩的大小和位置,可以计算出梁截面的最大受压区和最大受拉区。
2. 混凝土和钢筋的材料特性:混凝土和钢筋的强度是决定承载力的重要因素。
混凝土的强度可以通过抗压强度来衡量,钢筋的强度则通过抗拉强度来衡量。
在计算承载力时,需要根据材料的特性确定其强度参数。
3. 截面形状和尺寸:梁的截面形状和尺寸对其承载力有直接影响。
常见的梁截面形状有矩形、T形、L形等,设计中需根据实际要求选择合适的截面形状和尺寸。
截面尺寸的选择与受力分析密切相关。
4. 预应力和配筋设计:在一些要求较高的工程中,钢筋混凝土梁常采用预应力设计和配筋设计来增强其承载力。
预应力设计通过在混凝土中引入预应力钢筋来抵消荷载产生的应力,从而减小梁的变形和裂缝。
配筋设计则根据荷载和构件几何尺寸来确定钢筋的布置。
三、影响钢筋混凝土梁承载力的因素除了上述提及的弯矩、材料特性、截面形状和尺寸等因素外,还有其他影响钢筋混凝土梁承载力的因素,如环境荷载、温度变化、锚固和支座条件等。
1. 环境荷载:钢筋混凝土梁所承受的环境荷载包括恒载(如自重、设备重量)、可变活载(如人员、设备动载)和附加活载(如雪、风载等)。
这些环境荷载对梁的承载能力产生影响,需在设计中考虑。
2. 温度变化:温度变化会导致钢筋混凝土梁产生热胀冷缩和变形,从而影响其承载能力。
