第05讲 自适应线性元件_1
自适应滤波器原理 ppt课件

课程的评语范文1、教学重难点突出,板书条理清晰。
教学步骤设计合理,由浅入深,循序渐进。
2、教师基本功扎实,知识讲解准确,教学设计合理,始终以学生为主体,自主学习,小组交流讨论,上台交流展示等形式,师生配合默契,取得了较好的学习效果。
3、教师教态自然,语调亲切,并不断鼓励学生,充分发挥学生的主体作用。
使学生在和谐融洽的课堂氛围中学习,推进了知识的掌握和智力的发展,达到了良好的教学效果。
4、教师准确的把握了设疑的方向,调动了学生学习的兴趣,使学生进入积极的的思维状态。
5、教师组织课堂教学效果好,语言清晰,能注重学法指导,培养学生的创新能力,问题设计富有启发性。
6、教学环节设计安排清晰明了,过渡自然。
7、老师以渊博的知识,青春的激昂,璀璨的语言,悦耳的语音,扮演者精典式的演讲,令人心悦诚服,耳目一新,有身临其境之感,真是众妙毕绝啊。
本节课引经据典,恰如其分,启发深思,事半功倍,旁敲侧击,循循善诱。
无粉饰之患,无喧宾夺主之影。
x老师注重读,读是语文教学的`根,抓住了读,就抓住了整个语;书读百遍,其义自见,这是睿智的选择。
9、教师语言语调抑扬顿挫,普通话过硬,板书优美,基本功扎实,能循循善诱,逐步引导学生思考问题及分析事件与人物,解决讨论要点有成效。
并注重学生的诵读能力口头表达能力的培养,学生的学习习惯较好。
10、该专题内容丰富多彩,一定程度上积淀了学生的文学素养,学生参与多,课件精美,涉及知识范围广,开阔学生眼界,点面结合加练笔,让学生对鸟的认识逐步深入,效果较好。
11、语言富有情趣,给人的感觉很亲切教态恩好,同时在课堂中让学生了解到数学与生活息息相关,使学生对数学产生了求知欲,对数学的知识也产生了兴趣,从而这样的课堂效果会很好,该老师的提问也很到位,在同学产生疑问的时候也引导的很到位,课件做的也非常好,很吸引小朋友的眼球,那么这样的教学就会避免小朋友做与课堂其它的事情,而是去仔细的观察课件,思考问题,唯有一点点不足的地方就是课件有点小小的问题。
自适应信号控制课件

g ld P= = xmin xmin
2
DERIVATIVE MEASUREMENT AND PERFORMANCE PENALTIES WITH MULTIPLE WEIGHTS
A two-dimensional gradient
x = xmin + V RV 骣 v 0÷ ç = xmin + (v0 , v1 ) R ç ÷ ÷ ç v1 ÷ 桫
Hence,
The result is
1 ˆr )= 2 var (a N 2 a 2r - a r = N
2 2 2 轾 N a 2 r + ( N - N )a r - a r 犏 臌
a4 - a a 2 = x , so, var (x ) = N
2 2
The values of α depend on how εk is distributed. For example, suppose that εk is distributed normally with zero mean and with a variance 2 . The mean fourth moment is 4
2 r
1 r 2 轾 = 2 邋 E犏 ek el ) - a r ( N k = 1 l= 1 臌
2r ì 轾 ï E犏 e = a k = l k 2 r ï r 臌 ï 轾 E犏 ek el ) = í ( r r 2 臌 ï 轾 轾 E犏 e E e = a k ? l ï k l r 犏 ï î 臌 臌
GRADIENT COMPONENT ESTIMATION BY DERIVATVE MEASUREMENT
x = xmin + l v
《自适应滤波器原理》课件

自适应滤波器原理:通过调整滤波 器的参数,使滤波器的输出接近期 望输出
减小稳态误差的方法:调整滤波器 的参数,使其更接近期望输出
添加标题
添加标题
添加标题
添加标题
稳态误差:滤波器在稳态条件下的 输出误差
性能优化:通过减小稳态误差,提 高自适应滤波器的性能
调整滤波器参数,如调整滤波 器阶数、调整滤波器系数等
军事领域:用于 雷达信号处理, 提高探测精度
工业领域:用于 机器故障诊断, 提高生产效率
深度学习算法:利用神经网络进行自适应滤波 强化学习算法:通过强化学习实现自适应滤波器的优化 遗传算法:利用遗传算法进行自适应滤波器的参数优化 模糊逻辑算法:利用模糊逻辑进行自适应滤波器的决策和控制
FPGA实现:利用FPGA的灵活性和并行性,实现自适应滤波器 ASIC实现:利用ASIC的高性能和低功耗,实现自适应滤波器 专用芯片实现:设计专用芯片,实现自适应滤波器 云计算实现:利用云计算平台的计算资源,实现自适应滤波器
特点:全局搜索能力强,收 敛速度快
原理:通过模拟鸟群觅食行 为,寻找最优解
应用:广泛应用于自适应滤 波器、神经网络等领域
优缺点:优点是简单易实现, 缺点是容易陷入局部最优解
采用快速傅里叶变 换(FFT)算法, 减少计算量
利用并行计算技术, 提高计算速度
采用稀疏矩阵算法 ,减少存储需求
采用低复杂度算法 ,如LMS算法,减 少计算量
挑战:如何提高自适应滤波器的性能和稳定性,降低成本,提高可靠性,以及如何应对新的应 用场景和需求。
汇报人:
,
汇报人:
01
02
03
04
05
06
添加标题
自适应滤波器:一种能够根据输入信号的变化自动调整滤波器参数 的滤波器
自适应控制讲义(模型参考部分)2013-v1
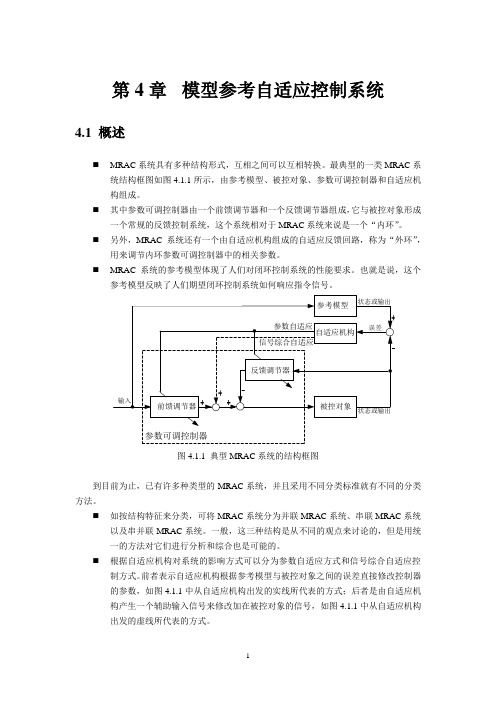
第4章模型参考自适应控制系统4.1 概述⏹MRAC系统具有多种结构形式,互相之间可以互相转换。
最典型的一类MRAC系统结构框图如图4.1.1所示,由参考模型、被控对象、参数可调控制器和自适应机构组成。
⏹其中参数可调控制器由一个前馈调节器和一个反馈调节器组成,它与被控对象形成一个常规的反馈控制系统,这个系统相对于MRAC系统来说是一个“内环”。
⏹另外,MRAC系统还有一个由自适应机构组成的自适应反馈回路,称为“外环”,用来调节内环参数可调控制器中的相关参数。
⏹MRAC系统的参考模型体现了人们对闭环控制系统的性能要求。
也就是说,这个参考模型反映了人们期望闭环控制系统如何响应指令信号。
图4.1.1 典型MRAC系统的结构框图到目前为止,已有许多种类型的MRAC系统,并且采用不同分类标准就有不同的分类方法。
⏹如按结构特征来分类,可将MRAC系统分为并联MRAC系统、串联MRAC系统以及串并联MRAC系统。
一般,这三种结构是从不同的观点来讨论的,但是用统一的方法对它们进行分析和综合也是可能的。
⏹根据自适应机构对系统的影响方式可以分为参数自适应方式和信号综合自适应控制方式。
前者表示自适应机构根据参考模型与被控对象之间的误差直接修改控制器的参数,如图4.1.1中从自适应机构出发的实线所代表的方式;后者是由自适应机构产生一个辅助输入信号来修改加在被控对象的信号,如图4.1.1中从自适应机构出发的虚线所代表的方式。
根据MRAC系统的设计方法可以分为如下三类:基于局部参数最优化的方法、基于Lyapunov稳定性理论的方法以及基于Popov超稳定性理论的方法。
⏹基于局部参数最优化的方法是最早采用的MRAC系统设计方法,通常称为MIT律。
⏹基于Lyapunov稳定性理论的方法是Butcharty及Parks于六十年代中期相继提出的,这种方法与局部参数最优化方法相比,不仅可保证系统的稳定性,还具有自适应速度快的优点。
⏹由法国学者Landau于1969年提出的基于Popov超稳定性理论的方法,主要是以Popov超稳定性理论为基础,由于不需要选择Lyapunov函数,并且能给出一族自适应规律,从而该方法有利于设计者结合实际系统灵活地选择合适的自适应规律。
中文第三章自适应滤波器

• 1. 自适应滤波器原理 • 2. 自适应线性组合器 • 3. 均方误差性能曲面 • 4. 最陡下降算法 • 5. LMS算法 • 6. RLS算法 • 7. 典型应用:噪声消除
理论分析 自适应算法
1。 自适应滤波原理
1. 学习和跟踪(时变信号) 2. 带有可调参数的最优线性滤波器
两输入两输出Two inputs and two outputs; FIR,IIR, and 格形(Lattice) 最小均方误差和最小平方误差准则
Tmse mse N
1 fs
,
sec
where mse iteration number
N (data samples for each iteration)
fs (sample frequency)
注意
• 最陡下降法具有更多的理论分析意义, 实际操作时我们必须对其做很多近似。
5. LMS 方法
1
陡
下
0.5
降
0
-0.5 0 20 40 60 80 100 120 140 160 180 200
1.5
1
LMS 0.5 单次 0
-0.5 0 20 40 60 80 100 120 140 160 180 200
1.5
最1 陡 下 0.5 降0
-0.5 0 20 40 60 80 100 120 140 160 180 200
确性 (7) 鲁棒性:对噪声干扰不敏感,小能量干扰只能造成小估
计误差
本章主要讨论自适应线性组合器(其分析和实现简单,在大多数 自适应滤波系统中广泛应用)。
2。 自适应线性组合器
一类具有自适应参数的FIR数字滤波器。--》一般形式
第6章神经网络-感知器与自适应元件

请画出感知器网络结构图,并编写MATLAB程序解 该分类问题。
2019/2/15 20
• 感知器的局限性
由于感知器的激活函数采用的是阀值函数,输出
矢量只能取0或1,所以只能用它来解决简单的分 类问题;
感知器仅能够线性地将输入矢量进行分类。
感知器还有另外一个问题,当输入矢量中有一个
数比其他数都大或小得很多时,可能导致较慢的 收敛速度。
2019/2/15 33
在随机初始值为:W0=—0.9309;B0=—0.8931的 情况下,经过12次循环训练后,网络的输出误差平方 和达到0.000949,网络的最终权值为: W=-0.2354;B=0.7066
实际上,对于上面这个简单的例题,它存在一个 精确解,且可以用解二元一次方程的方式将P和T值分 别对应地代入方程T=W*P十B得:
2019/2/15
11
如果第i个神经元的输出是正确的,即有:ai=ti,那么
与第i个神经元联接的权值wij和偏差值bi保持不变;
如果第i个神经元的输出是0,但期望输出为1,即有ai
=0,而ti=1,此时权值修正算法为:新的权值wij为旧 的权值wij加上输人矢量pj;类似的,新的偏差bi为旧偏 差bi加上它的输入1;
由感知器的网络结构,我们可以看出感知器的基 本功能是将输入矢量转化成0或1的输出。这一功能可 以通过在输人矢量空间里的作图来加以解释。
感知器权值参数的设计目的,就是根据学习法 则设计一条W*P+b=0的轨迹,使其对输入矢量能够 达到期望位置的划分。
2019/2/15 8
以输入矢量r=2为例,对于选定的权值w1、w2和b, 可以在以p1和p2分别作为横、纵坐标的输入平面内画 出W*P+b=w1 p1十w2 p2十b=0的轨迹,它是一条直线, 此直线以上部分的所有p1、p2值均使w1 p1十w2 p2十b >0,这些点若通过由w1、w2和b构成的感知器则使其 输出为1;该直线以下部分的点则使感知器的输出为0。 所以当采用感知器对不同的输入矢量进行期望输 出为0或1的分类时,其问题可转化为:对于已知输入 矢量在输入空间形成的不同点的位置,设计感知器的 权值W和b,将由W*P+b=0的直线放置在适当的位置 上使输入矢量按期望输出值进行上下分类。
自适应控制基本原理
School of Automation Engineering
3. 修正实现的一般方式
自适应控制一般原理
参数修正法
直接调整被控系统的相关参数;
通过修正控制器或补偿网络的参数到达调整可调系统 参数的目的。
信号综合法
根据性能指标要求,综合出加到对象上去的控制信 号。
t
∫ fi( e,τ ,t ) = fi1(e,τ ,t)dτ + fi2( e,t ) 0
t
∫ gi( e,τ ,t ) = gi1( e,τ ,t )dτ + gi2( e,t ) 0
t
μ( e,τ ,t ) = ∫ μ1( e,τ ,t )dτ + μ2( e,t )
Intelligent Vision Technology Lab0
i=0
i=0
e = yp −r
Intelligent Vision Technology Lab
School of Automation Engineering
四 自校正调节器原理和数学模型
1. 自校正调节器基本原理
在线递推参数估计 最小方差控制 校正控制器参数
Intelligent Vision Technology Lab
School of Automation Engineering
三 MRACS 基本原理与数学模型
1. 并联MRACS的基本原理
根据被控系统性能要求,设计一个与对象同阶的定常 参考模型,并与被控对象并联;
根据模型与对象之间的广义误差e(t) ,通过自适应机 构,调节对象的参数或产生一个辅助控制量,以最终 使e(t)→0。
线性元件和非线性元件
线性元件和非线性元件山东省邹平县第一中学李进在金属导体中,电流跟电压成正比,伏安特性曲线是通过坐标原点的直线,具有这种伏安特性的电学元件叫做线性元件。
对欧姆定律不适用的导体和器件,电流和电压不成正比的电学元件叫做非线性元件。
非线性元件是一种通过它的电流与加在它两端电压不成正比的电工材料,即它的阻值随外界情况的变化而改变.1.只有在其它外界参量(如温度)一定的情况下,线性元件的伏安特性曲线才是通过坐标原点的直线。
实际情况下由于温度的变化,线性元件的伏安曲线仍为过原点的曲线。
学生实验中描绘的小灯泡的伏安曲线就是这样的。
2.线性与非线性的实质:R =是电阻的定义式,是普适的,非线性并不是这个关系不成立了,而是在温度等外界参数不变的情况下,电流不随电压同比变化。
3.非线性的原因:设载流子在与正离子(或空穴)的两次碰撞之间是由静止做匀加速直线运动的,载流子定向移动的速率为v==l为电阻的长度λ为载流子的平均自由程,v热为载流子热运动平均速率对于线性元件,在温度一定的情况下,载流子体密度n,载流子热运动平均速率v热,载流子的平均自由程λ均为定值,ρ、R为定值,因此I与U的正比关系成立。
对于非线性元件,影响载流子体密度n的因素不仅仅是温度,外加电场的强度也会影响载流子的数量(如气体导电过程,随着电压的增大,越来越多的空气分子被电场力“撕裂”成离子,成为载流子),因此即便在温度一定的情况下,I与U的正比关系也是不成立的。
公式也可以用来解释半导体与金属导体的导电特性的差异。
对金属导体,温度升高后,λ减小(正离子运动加剧)、v热增大,n几乎不变(由于金属正离子结构稳定,自由电子浓度受电场影响极小),电阻率升高,电阻增大。
自适应滤波器原理精品PPT课件
3、ADF实现
•可以由FIR DF或IIR DF实现。
但由于收敛性及稳定性,目前用得多为FIR DF 实现。
•FIR滤波器结构有:
横向型结构(直接型)(Transveral Structure)
对称横向型结构(Symmetric Transveral Structure)
格形结构(Lattice Structure)
电子发烧友 电子技术论坛
4、FIR ADF实现
若FIR DF的单位脉冲响应长度为,则其输出为
自适应算法
组成.
若设x1j, x2j , x3j …… xNj ,为同一信号的不同延 时组成的延时线抽头形式,即所谓横向FIR结构。 它是最常见的一种自电适子发应烧友D电F子结技术构论坛形式。
6、横向FIR ADF的结构
x(j) x(j-1) x(j-N+1) w1 w2 ... wN
简化符号为
y(j)
第二节 最小均方误差 (LMS)自适应DF
的基本原理
电子发烧友 电子技术论坛
一、均方误差
用统计方法,大量数求平均,提出均方误差 最小准则,即输出信号与进行信号之间误差最小。 其定义为:
E 2 (n) E (s(n) sˆ(n))2
测量数据越多,则越准确。
x(n)=s(n)+w(n) h(n)
y(n) sˆ(n) 其中s(n)信号(可以是随 机信号或规则信号。
N 1
输出:y(n) h(n) x(电n子)发烧友 电h子(技n术)论x坛(n m) m0
自适应第一章预备知识
& 李雅普诺夫意义下: x
李雅普诺夫稳定性示意图
PDF 檔案使用 "pdfFactory Pro" 試用版本建立
渐进稳定: x0
x (t ) = 0 。 < δ ,恒有 lim t →∞
n
即 t → ∞, x (t ) → xe 全局渐进稳定:对所有 x0 ∈ R ,恒有 lim
t →∞
x (t ) = 0 。
一致稳定:δ 的选择不依赖于 t0 ,稳定性和时间初值无关。
− α ( t − t0 ) x ( t ) ≤ me x0 指数稳定性: m、α > 0 有
f (t ), 0,
t≤s t>s
PDF 檔案使用 "pdfFactory Pro" 試用版本建立
二、矩阵的范数 定义: A
p
= max Ax
x p =1
p
其中A为m*n矩阵,x为任意n*1向量
基本性质(充分必要条件) ①非负性:若 A ≠ 0,则 A > 0; 0 = 0 ②奇次性:对任何实数α,有 α A = α A ③三角不等式:对任意A和B,恒有 A + B ≤ A + B 矩阵范数相容性:若某矩阵范数对任意m*n矩阵A和n*l 矩阵B恒有 A • B p ≤ A p • B p ,则称该矩阵范数是相 容的。
PDF 檔案使用 "pdfFactory Pro" 試用版本建立
线性: f ( x, t ) = A(t ) • x (t ) 非线性:
系统的平衡点:
& = f ( x, t ) x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由此可得零误差的唯一精确解为:
[例5.3]设计训练一个线性网络实现下列从 输人矢量到目标矢量的变换:
所给出的输入矢量元素之间是线性相关的:第三组元 素等于第二组元素的两倍减去第一组:P3=2P2-P1。 由于输入矢量的奇异性,用函数solvelin.m来设计时 网络会产生问题。只有在能够线性地解出问题的情 况下,用函数solvelin.m才比较准确。
η为学习速率。在一般的实际运用中,实践表明, η通常取一接近1的数,或取值为:
(5.5) 学习速率的这一取法在神经网络工具箱中用函数 maxlinlr.m来实现。(5.5)式可实现为:
W—H学习规则的函数为:learnwh.m来实现,加上线性 自适应网络输出函数purelin.m,可以写出W—H学习规 则的计算公式为: A=purelin(W*P); E=T—A; [dW,dB]=learnwh(P,E,h); W=W十dW; B=B十dB;
5.4例题与分析
[例5.1]设计自适应线性网络实现从输入矢 量到输出矢量的变换关系。其输入矢量 和输出矢量分别为: P=[1.0 -1.2] T=[0.5 1.0]
%wf1.m % P=[1 -1.2]; T=[0.5 1]; [R,Q]=size(P); [S,Q]=size(T); [W,B]=rands(S,R); max_epoch=20; %最大循环次数 err_goal=0.001; %期望误差 1r=0.4*maxlinlr(P); %最佳学习速率 disp_freq=1; %设置显示频率 TP=[disp_freq max_epoch err_goal lr]; %设置参数变量TP [W,B,epochs,error]=trainwh(W,B,P,T,TP) %进行线性网 络权值训练
以例5.1 为样本,
1)对于第一个尝试,学习速率lr取: 1r=1.7*maxlinlr(P); 2)第二个尝试是选用更大学习速率: 1r=2.5*maxlinlr(P);
5.5对比与分析
感知器和自适应线性网络 (1)网络模型结构上
感知器和自适应线性网络而言,结构上的主要区 别在于激活函数:一个是二值型的,一个线性 的。 当把偏差与权值考虑成一体时,自适应线性网络 的输入与输出之间的关系可以写成A=W*P。如 果P是满秩的话,则可以写成AP-1=W,或 W=A/P。
只要将前面已编写的wf2.m程序中的输入与目标矢量改 变一下,并给出(—l,1)之间的随机初始值,即可运行 看到本例的结果。 其最终误差在1.04左右,这就是本例题下的最小误差 平方和,
而当采用完全线性函数的设计solvelin.m去求解网络权 值时,所得到的误差是4.25。
采用W—H算法训练出的误差是它的1/4,由此可见其 算法的优越性。
%训练网络 flops(0) tp=[disp_freq max_epoch err_goal lr]; %设置参数变量tp [W, B, epochs,errors]=trainwh(W, B, P, T, tp); %进行线性网络权值训 练 W %显示最终训练权矢量 B %显示最终训练偏差矢量 SSE=sumsqr(T-purelin(W*P, B)); %最终误差 %显示结果并给出结论 ploterr(errors), fprintf (‘\n After%.0f epochs,sum squared e error=%g. \n\n’, SSE), fprintf (‘Training took %.0f flops. \n’, flops), fprintf (‘ Trained network operates:’); if SSE<err_goal disp(‘Adequately.’) else disp(‘Inadequately.’) end end
作业
设计一个有三个输入的单层线性网络: P={2 3 2.4 -0.6; -2 4 6 -1; 4 2 -3.2 1.8} T={1 6 -4.4 2.8; 2.2 -2.4 3.4 -0.8; 6 0.4 -3.6 -0.8; -2 0.2 -2 1.2}
5.6 本章小结
1)自适应线性网络仅可以学习输入输出矢量之间的线性关 系,可用于模式联想及函数的线性逼近。网络结构的 设计完全由所要解决的问题所限制,网络的输入数目 和输出层中神经元数目,由问题所限制; 2)多层线性网络不产生更强大的功能,从这个观点上看, 单层线性网络不比多层线性网络有局限性; 3)输入和输出之间的非线性关系不能用一个线性网络精确 地设计出,但线性网络可以产生一个具有误差平方和 最小的线性逼近。
[例5.4]现在假定在[例5.1]的输入/输出矢量中增加两 组元素,使其变为 P=[1.0 1.5 3.0 -1.2] T=[0.5 1.1 3.0 -1.0] 本例题的目的是在于了解自适应线性网络的线性逼近求 解的能力。
图5.4给出了输入输出对的位置以及网络求解的结果。 对于所设置的err_goal=0.001, 在循环训练了50次后所得 的误差平方和仍然为:SSE=0.289。这个值即是本题所 能达到的最小误差平方和的值。
采用W—H规则训练自适应线性元件使其能够得以收敛 的必要条件是被训练的输入矢量必须是线性独立的, 且应适当地选择学习速率以防止产生振荡现象。
5.3 网络训练
自适应线性元件的网络训练过程可以归纳为以下 三个步骤:
1)表达:计算训练的输出矢量A=W*P十B,以及 与期望输出之间的误差E=T—A; 2)检查:将网络输出误差的平方和与期望误差相 比较,如果其值小于期望误差,或训练已达到 事先设定的最大训练次数,则停止训练;否则 继续; 3)学习:采用W—H学习规则计算新的权值和偏 差,并返回到1)。
训练后的网络权值为:
网络训练过程中的误差记录
对于存在零误差的精确权值网络,若用函数solvelin.m来 求解,则更加简单如下: %wf3.m % P=[1 1.5 1.2 –0.3; -1 2 3 –0.5; 2 1 –1.6 0.9]; T=[0.5 3 –2.2 1.4; 1.1 –1.2 1.7 –0.4; 3 0.2 –1.8 -0.4; -1 0.1 – 1.0 0.6]; [W,B]=solvelin(P,T); A=simulin (P, W, B); SSE=sumsqr (T-A) W B end
在随机初始值为:W0=—0.9309;B0=—0.8931 的情况下,经过12次循环训练后,网络的输出 误差平方和达到0.000949,网络的最终权值为: W=-0.2354;B=0.7066
实际上,对于[例5.1]这个简单的例题,它存在一 个精确解,且可以用解二元一次方程的方式将 P和T值分别对应地代入方程T=W*P十B得:
我们的目的是通过调节权矢量,使E(W,B)达到最小值。
所以在给定E(W,B)后,利用W—H学习规则修正权矢量 和偏差矢量,使E(W,B)从误差空间的某一点开始,沿 着E(W,B)的斜面向下滑行。
根据梯度下降法,权矢量的修正值正比于当前位 置上E(W,B)的梯度,对于第i个输出节点有:
或表示为:
(5. 3)
[例5.2]现在来考虑一个较大的多神经元网络的 模式联想的设计问题。输入矢量和目标矢量分 别为:
解: 由输入矢量和目标输出矢量可得:r=3,s=4,q =4。所以网络的结构如图5.2所示。
这个问题的求解同样可以采用线性方程组求出,即对每 一个输出节点写出输入和输出之间的关系等式。
实际上要求出这16个方程的解是需要花费一定的 时间的,甚至是不太容易的。 对于一些实际问题,常常并不需要求出其完美的 零误差时的解。也就是说允许存在一定的误差。 在这种情况下,采用自适应线性网络求解就显示 出它的优越性:因为它可以很快地训练出满足 一定要求的网络权值。
采用Matlab进行自适应线性元件网络的训练过程如下: trainwh.m
%表达式 A=purelin(W*P,B); E=T-A; SSE=sumsqr(E); %求误差平方和 for epoch=1: max_epoch %循环训练 if SSE<err_goal %比较误差 epoch=epoch—1; break %若满足期望误差要求,结束训练 end [dW,dB]=1earnwh(P,E,lr);%修正权值 W=W十dW; B=B十dB; A=purelin(W*P,B); %网络输出 E=T-A; SSE=sumsqr(E); %计算网络误差平方和 end
当采用线性自适应线性网络求解问题所得到的误差特别 大时,可以认为此问题不适宜用线性网络来解决。
图5. 4网络训练结果图
自适应线性网络还有另一个潜在的困难,当学习速率取 得较大时,可导致训练过程的不稳定。 [例5.5]输入/目标矢量与[例5.1]相同。我们将以不同 的学习速率训练两次网络以展现两种不希望的学习速率 带来的影响。
%wf2.m % P=[1 1.5 1.2 –0.3; -1 2 3 –0.5; 2 1 –1.6 0.9]; T=[0.5 3 –2.2 1.4; 1.1 –1.2 1.7 –0.4; 3 0.2 –1.8 –0.4; -1 0.1 –1.0 0.6]; disp_freq=400; %中间不显示结果 max_epoch=400; err_goal=0.001; lr=0.9*maxlinlr(P); W=[1.9978 –0.5959 –0.3517; 1.5543 0.05331 1.3660; %初始权值 1.0672 0.3645 –0.9227; -0.7747 1.3839 –0.3384]; B=[0.0746; -0.0642; -0.4256; -0.6433]; SSE=sumsqr(T-purelin(W*P,B)); %未训练前误差 fprintf(‘Before trainihg, sum squared error=%g. \n’, SSE)
5.1自适应线性神经元模型和 结构
图5. 1 自适应线性神经网络的结构
