轴向运动弦线横向振动的控制_能量方法
《轴系扭转振动》课件

固有频率
01
轴系在无外部激励下的自振频率,是扭振特性的重要参数。
模态分析
02
分析轴系的模态形状、模态刚度和模态阻尼等特性,了解轴系
的振动特性。
稳定性分析
03
分析轴系在不同工况下的稳定性,判断轴系是否会发生失稳。
扭振的稳定性分析
稳定性判据
根据不同的稳定性判据,如能量判据、Lyapunov指数等,判 断轴系的稳定性。
《轴系扭转振动》ppt课件
contents
目录
• 轴系扭转振动概述 • 轴系扭转振动的原理 • 轴系扭转振动的应用 • 轴系扭转振动的控制与优化 • 轴系扭转振动的研究展望
01
轴系扭转振动概述
定义与特点
Hale Waihona Puke 定义轴系扭转振动是指轴系在受到扭矩作 用时发生的周期性振动现象。
特点
轴系扭转振动具有特定的频率、振幅 和相位,与轴系的几何形状、转动惯 量、阻尼等参数有关。
常用的主动控制技术包括电磁 阻尼控制、液压阻尼控制和电 动马达控制等。
主动控制技术能够提供快速的 响应和精确的控制,但需要额 外的能量输入和复杂的控制系 统。
扭振的被动控制技术
被动控制技术是通过吸收或隔 离系统中的能量来抑制扭振的
方法。
常用的被动控制技术包括橡 胶隔振器、阻尼材料和减震
器等。
被动控制技术具有结构简单、 可靠性高和成本低等优点,但 响应速度较慢,对低频振动控
发展
近年来,随着计算机技术和数值模拟方法的进步,轴系扭转振动的理论研究和 实践应用得到了快速发展。未来,随着智能化和绿色化技术的发展,轴系扭转 振动的研究将更加深入,应用将更加广泛。
02
轴系扭转振动的原理
振动控制原理

振动控制原理
振动控制原理指的是通过对振动系统进行控制,降低或消除系统的振动,并使系统能够稳定工作的技术原理。
在振动控制中,一般会采用控制器和执行器来实现振动的监测和抑制。
振动控制的基本原理是通过合适的控制算法,根据振动系统的输入输出关系,对系统进行有针对性的控制,从而达到减小系统振动幅度和频率,提高系统的稳定性和运行效率的目的。
振动控制的核心思想是通过调节系统的力、位置或速度等参数,使系统的振动能量减小或分散到其他影响较小的频段中。
常见的振动控制方法包括被动控制和主动控制。
被动控制是指通过连接阻尼器、减振器等被动元件来消耗和分散振动能量,从而减小系统振动的幅度。
被动控制通常适用于频率固定的振动问题,而对于频率变化较大或需要更加精确的控制问题,主动控制则是更为有效的方法。
主动控制是指通过对系统输入信号进行实时调整和控制,实现对系统振动的主动抑制。
主动控制通常需要使用传感器来监测系统的振动状态,然后通过控制器对执行器进行控制,对系统进行实时调整。
主动控制方法通常包括PID控制、自适应控制、模糊控制等。
振动控制的应用领域非常广泛,包括工程结构防振、车辆振动控制、航空航天、机器人、医疗设备等。
振动控制可以降低噪声、提高系统的稳定性和寿命,同时也可以提高系统的运行效率和精度。
尽管振动控制领域存在一些挑战,如控制算法的设
计、系统模型的准确性、实时性等问题,但随着技术的不断进步,振动控制技术在各个领域的应用前景仍然非常广阔。
果园货运链索横向振动非线性控制

弦振动的工作原理及应用

弦振动的工作原理及应用1. 引言弦振动是指当一个弦线或绳子在两端受到固定的约束条件下,产生一种沿弦线传播的波动现象。
弦振动具有重要的理论和实际应用价值,广泛应用于乐器制作、声学研究、医学成像等领域。
本文将介绍弦振动的工作原理及其在不同领域的应用。
2. 弦振动的工作原理弦振动的工作原理可以通过以下几个方面来描述:2.1 弦线的特性弦线的振动受到弦线的特性影响,包括弦线的材质、长度、密度和张力等因素。
不同的弦线会产生不同的振动频率和波形。
2.2 初始条件弦线振动的初始条件包括弦线的初位移、初速度和初加速度。
这些初始条件将决定弦线振动的形式和特征。
2.3 波动方程弦线振动的行为可以通过波动方程来描述。
波动方程是一个偏微分方程,可以用来描述弦线上的振动行为。
一般而言,波动方程包含时间和空间两个变量。
2.4 边界条件弦线振动的边界条件包括弦线两端的约束条件。
常见的约束条件有自由端和固定端。
不同的约束条件将会导致不同的振动模式和频率。
3. 弦振动的应用3.1 乐器制作弦乐器是应用弦振动原理制作的乐器,包括吉他、小提琴、钢琴等。
乐器的音质和音色取决于弦线振动的特性和乐器的结构。
通过改变乐器的弦线材质、长度、密度和张力等参数,可以实现不同的音效。
3.2 声学研究弦振动在声学研究中有着重要的应用。
通过研究弦线振动的频率、波长和波形等特性,可以了解声音的产生与传播机制,进一步研究声音的品质和效果。
3.3 医学成像弦振动在医学成像中也有非常广泛的应用。
例如,超声波成像利用声波在组织中的传播特性来生成图像,通过观察弦线在组织中的振动情况,可以获取详细的组织结构信息,从而实现医学诊断。
3.4 工程应用弦振动在工程领域也有重要的应用。
例如,通过利用弦线的振动特性,可以研究桥梁、建筑物和机械结构的稳定性和安全性。
此外,弦振动还可以应用于振动传感器、纤维光纤通信等领域。
4. 结论弦振动作为一种重要的波动现象,在乐器制作、声学研究、医学成像和工程应用等领域发挥着重要作用。
等速驱动轴横摆振动的研究及解决

12710.16638/ki.1671-7988.2019.23.044等速驱动轴横摆振动的研究及解决朱钊,黄巨成,张海源,滕杰(奇瑞商用车(安徽)有限公司 工程研究院底盘部,安徽 芜湖 241006)摘 要:针对某电动汽车在40km/h 到60km/h 速度下,全油门加速产生的整车振动问题,运用噪声阶次和振动分析,确定为驱动轴三阶振动,产生原因为全油门加速时,驱动扭矩增大产生的轴向派生力(GAF),使整车产生Y 向振动,即横摆振动。
根据驱动轴轴向派生力的影响因素,通过采用无震颤式万向节(AAR),降低轴向派生力,解决整车横摆振动。
关键词:驱动轴;振动;横摆;轴向派生力中图分类号:U463 文献标识码:A 文章编号:1671-7988(2019)23-127-03Research And Solution Of Swing Vibration Of Drive ShaftZhu Zhao, Huang Ju Cheng, Zhang Haiyuan, Teng Jie( Chery Commercial Vehicle ( Anhui ) Co., Ltd., Engineerring Research Institute Chassis, Anhui Wuhu 241006 ) Abstract: Aiming at the vibration problem of a electric vehicle caused by acceleration offull throttle at speeds ranging from 40 km/h to 60 km/h, the third-order vibration of driving shaft is determined by noise order and vibration analysis. The reason is that when acceleration of fullthrottle, increased driving torque has generated axial force(GAF), which makes the whole vehicle produce Y-direction vibration, i.e. yaw. Vibration. According to the influencing factors of the generated axial force of the drive axle, the generated axial force is reduced and the yaw vibration of the vehicle is solved by using the non-vibration universal joint.Keywords: Drive shaft; Vibration; Yaw; Generated axial forceCLC NO.: U463 Document Code: A Article ID: 1671-7988(2019)23-127-03前言某前驱电动车型,在40km/h-60km/h 加速时,整车Y 向横摆严重,主观评价无法接受,而相同型号燃油车型,未发现有此问题。
振动控制 PPT课件

绪 论
振源
受控对象
吸振
3. 吸振:又称动力吸振。在受控对象上附加一个子系 统称之为动力吸振器,用它产生吸振力以减小受控 对象对振源激励的响应。
– 从能量的角度,使激励能量分配到受控对象和子系统上,并 使分配到受控对象上的能量最小,以达到减振目的。
2019/10/17
南京航空航天大学 振动工程研究所
17
– 作业:迟交或缺一次作业扣10分,两次取消考试资格 – 缺席处理:无故缺席一次扣10分,三次取消考试资格
推荐两个论坛:
SIMWE仿真论坛:/ 振动论坛:/forum/index.php
课件交流邮箱: vc_nuaa@, 密码:vc666888
振动控制 Vibration Control
振动控制 Vibration Control
2019/10/17
南京航空航天大学 振动工程研究所
1
振动控制 Vibration Control
课程在学科体系中的位置
• 振动控制是联系振动理论和控制理论的一门交叉 学科。
• 结构动力学 • 振动数值分析(有限元计算) • 振动测试与分析、模态分析理论
4
振动控制 Vibration Control
参考书籍
• 顾仲权, 振动主动控制 • 张阿舟, 振动控制工程 • 张阿舟, 实用振动工程2 -- 振动控制与设计 • Richard C. Dorf, 现代控制系统(第八版中译
版)
• Wodek K. Gawronshi, Advanced Structural Dynamics and Active Control of Structures
• 主动控制(Active Control):除外界振动源或干扰外,有 其他外部能量输入或交换的振动系统;
船舶推进轴系的扭转振动与控制
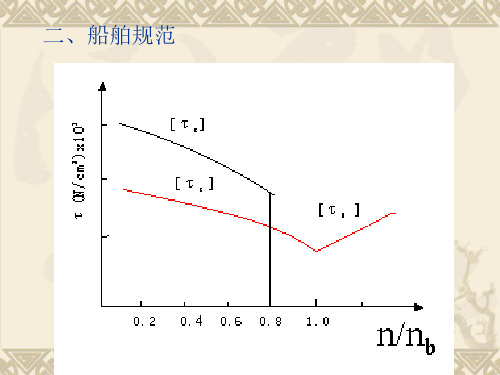
当量轴段长 6)轴系中有弹性联轴器或气胎离合器时,应把它们的主、从动
部分分为两集中质量 7)轴系中有液力偶合器时为界,分成两个独立的扭振系统 8)被发动机拖动的机械,转动惯量大的也要作一集中质量
二、多质量系统无阻尼简谐振动计算
等,振幅不同,惯量大的振幅小,惯量小 的振幅大,且振动方向永远相反。
振型图
A1
e12 O
A1
单结 A2
e12
e23
单结
A1
A2
双结
取A1=1,A2=-I1/I2, O为结点,振幅为0, 应力最大,双质量 只有一个结点。
A2
三质量系统有两个
自振频率,单结或
双结,即两个结点。
A3 A3
n个质量就有n-1个 振型,n-1个自振 频率。
(
2 n
2)2
4n 2 2
2 n
2
Asin(t )
A
h
h
1
(
2 n
2)2
4n 2
2
2 n
[1 ( n
)2 ]2
n2
4
2 n
(
n
)2
h
பைடு நூலகம்
2 n
M I
Ie
Me
Ast
静振幅
放大系数
m A Ast
1
f ( , )
[1 ( )2 ]2 ( )2
n
n
n
讨论:
1)
0
n
m 1
有因
IK
次
eK,K+1
AK
n2
Uk,,k+1=(AK+1-AK)/ eK,K+1
振动控制的方法

振动控制的方法
振动控制是指对机械系统或结构中的振动进行控制或降低,以达到减小噪声、提高系统稳定性和可靠性等目的。
常见的振动控制方法包括以下几种:
1. 被动振动控制:通过结构设计和材料选择来实现振动控制。
常见的被动振动控制技术包括质量阻尼、弹簧阻尼、隔振器等。
2. 主动振动控制:通过在系统中引入反馈控制回路来主动控制振动。
常见的主动振动控制技术包括主动振动控制装置、电磁作动器、压电陶瓷等。
3. 半主动振动控制:介于被动振动控制和主动振动控制之间,通过改变系统的参数或边界条件来控制振动。
常见的半主动振动控制技术包括可调节质量阻尼、可调节隔振器等。
4. 智能振动控制:利用人工智能和机器学习技术,对振动进行智能识别和控制。
常见的智能振动控制技术包括神经网络控制、模糊控制、遗传算法等。
振动控制方法多种多样,可以根据具体情况选择适合的方法进行控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i( ∃t- % x )
和
2
分别为张紧器两侧的弦线在
+ Bu e
i( ∃ t+ % x )
u
l1 # x # 1
+
平衡位置 X = L 1 处和张紧器间的夹角。 引入无量纲变量 x = X W ,w= ,t= T L L ie = P 2, c = V L P , l1 = L1 , L
( 11)
4
最佳控制参数选择
为了抑制运动弦线受初始激励扰动而引起的横向 达到控制弦线 ( 12)
I B L L 3, b = L , k = K P , me = Me P L
2
振动, 可通过调整张紧器的旋转角度 振动的目的。 为此, 控制力矩 m e 取为 m e = k f w t( l 1 , t ) b
[9] [ 10] [ 4] [ 8] [ 6]
轴向运动弦线的横向振动控制是多个技术领域的 重要工程目标, 如动力传送带、 空中缆车索道、 高楼升 降机缆绳、 单索架空索等。尽管这些工程系统元件具 有重要应用前景 , 由于轴向运动而引起的横向振动却 限制了它们在一些工程领域中的应用。因此 , 有必要 引进控制手段来抑制轴向运动弦线的振动
[ 12 ]
( 0) = #
其中 ! 为张紧器 与铅垂线 间的夹 角,
为张紧 器在
x = l1 处的位移。 从方程 ( 3) ~ ( 5) 可知 , 弦线动力学 方程 ( 3) 和张紧器的动力学方程( 4) 通过边界条件( 5) 相耦合, 形成一个耦合振动系统。
可
3
波的反射和透射分析
对于一无限长的沿轴向运动的弦线 , 其横向振动
203
图2
轴向运动弦线的纵向振动位移 ( 1) 图 ( a) 、 ( c) 、 ( e) 为末控弦线 ; ( 2) 图 ( b) 、 ( d) 、 ( f) 为已控弦线 Fig. 2 Transverse vibrat ion displacement of the axially moving string ( 1) Fig. ( a) , ( c) , ( e) for un control led st ing; ( 2) Fig. ( b) , ( d) , ( e) for controlled st ing
图1 轴向运动弦线受控系统模型
关系 ∃= % d ( 1+ c ) = % u ( 1- c ) Aie
i( ∃ t- % x )
d
Fig. 1 A model of t he axially moving st ring syst em
( 9)
i( ∃ t+ % x )
u
弦线动力学方程 ( WTT + 2 VWXT + V WXX ) - PWXX = 0 X [ 0, L 1 ]
202
机
械
强
度
2006 年
向运动弦线耦合振动模型。为控制弦线的纵向振动, 引入作用在张紧器上的作动器 , 控制张紧器的转动角, 通过张紧器和弦线的耦合关系进而达到控制弦线纵向 振动的目的。分 析中采用能量方法得到 最优控制参 数, 使得系统的能量耗散最大 , 有效降低了弦线的横向 振动。最后用有限差分法进行数值模拟 , 证实此方法 的有效性。
分析了轴向运动弦线的振动和能量传输问题。通过引 [ 11] 入一个非 线性反馈边界 控制器, Fung 等 用 Lypunov 方法证明了控制器的渐近稳定性和指数稳定性。 本文在分析轴向运动弦线纵向振动时采用新的轴
将频域分
20040527 收到初稿 , 20040928 收到修改稿。国家自然科学基金资助项目 ( 10472060) 、 上 海市自然科学基 金 ( 04ZR14058) 和 上海市重 点学科建 设 项目 ( Y0103) 。 张 伟 , 男 1971 年 10 月生 , 吉林长春市人 , 汉族。博士研究生 , 研究方向为机械振动及其控制。 E mail: wzhangfz@ eyou. com
2
若在 弦 线 中 的 某 一 处 存 在 一 个 限 制 点, 入 射 波
+
[L1 , L]
T !0 ( 1)
在此限制点处将产生反射波 A r e
d
和透
射波 A t e
i( ∃t- % x )
, A t 为透射波的幅值。 相应的反射系数 Ar Ai At Ai
和透射系数定义为 r= t= ( 10)
1
引言
析与行波消去法相结合 , 提出轴向运动弦线一种新的 控制方法 , 从波的传播角度分析, 控制器使通过传感器 的波在边界作动器处全部消除。Ying 和 Tan 用传递 函数和行波消去法研究了作动器和传感器不在边界的 轴向运动弦线横向振动控制。自适应控制是处理参数 不确 定系统 的有 效方法。通过 引入 两个 控制输 入, [ 7] Queiroz 等建立了自适应控制律 , 并给出渐近稳定的 控制条件。 Fung 等设计了用于弦线纵向振动控制的 鲁棒自适应控制器。Wicket 和 Mote 、 Lee 和 Mote
摘要 基于行波能量的传输原理 , 研究轴向运动弦线 耦合系统的 纵向振动控 制。通过使系 统的能 量耗散 最大而 获
得的 控制器最优控制参数 , 使系统的能量达到最小值 , 从而达到控制弦线横向振动的目的。采用有限差分 法进行数值 模 拟的结果证实此方法的有效性。 关键词 Abstract 轴向运动弦线 横向振动 耦合系统 振动控制 能量 中图分类号 O328 In order to understand the mechanism of energy transfer in an axially moving string with a tensioner and to develop a control strategy for the system, transverse vibration control of an axially moving string is investigated based on the energy transfer princi ple of traveling waves. The energy of the system is minimized via choosing the optimal control coefficient, determined by maximizing the total energy dissipation. Hence the transverse vibration of the string is minimized as well. The finite difference method is employed to solve the governing equation numerically. The simulation results demonstrate the effectiveness of the control approach. Key words Axially moving string; Transverse vibration; Coupled system; Vibration control; Energy Corresponding author : CH EN LiQun , E mail : lqchen @ staff . shu . edu . cn , Tel : + 86 2166134972, Fax : + 86 21 56553692 The project supported by the National Natural Science Foundation of China ( No. 10472060) , the Natural Science Foundation of Shanghai Municipality( No. 04ZR14058) , and Shanghai Leading Academic Discipline Project( No. Y0103) . Manuscript received 20040527, in revised form 20040928.
张 伟
1, 2
陈立群
1,3
( 1. 上海市应用数学和力学研究所 , 上海 200072) ( 2. 福州大学 机械系, 福州 350002) ( 3. 上海大学 力学系, 上海 200436) ZHANG Wei
1, 2
CHEN LiQun
1, 3
( 1. Shanghai Institute o f Applied Mathematics and Mechanics , Shanghai 200072, China ) ( 2. Department o f Mechanics , Fuzhou University , Fuzhou 350002, China ) ( 3. Department of Mechanics , Shanghai University , Shanghai 200436, China )
( t ) sin !
( 5)
2
运动方程
轴向运动弦线受控系统的模型如图 1 所示。 此模
w t ( x , 0) = v 0 ( x )
t
( 6) ( 7)
型包括一根弦线和一个张紧器。 考虑长度为 L 、 单位密 度为 、 轴向张力为 P , 以均匀运动通过相距为 L 的两 个固定孔座的均匀弦线横向振动。 为简化系统模型 , 假 设( 1) 忽略系统元件相互间的阻尼影响 ; ( 2) 忽略弦线 的抗弯刚度 ; ( 3) 忽略张紧器的张紧轮相对其质心的 惯性矩。 在上述假设条件下, 运用 Hamilton 原理 推导出弦线和张紧器的动力学方程。
张紧器动力学方程 I∀ = ( P V )( W
