等节距圆锥螺旋压缩弹簧计算机辅助设计
弹簧设计参数

计算公式
备注
压缩弹簧
拉伸弹簧
中径D2
D2=Cd
按表4取标准值
内径D1
D1=D2-d
外径D
D=D2+d
旋绕比C
C=D2/d
压缩弹簧长细比b
b=H0/D2
b在1~5.3的ቤተ መጻሕፍቲ ባይዱ围内选取
自由高度或长度H0
H0≈pn+(1.5~2)d
(两端并紧,磨平)
H0≈pn+(3~3.5)d
(两端并紧,不磨平)
一、普通圆柱螺旋弹簧的主要参数和尺寸
1)外径D、中径D2、内径D1和簧丝直径d;
2)旋绕比C:C=D2/d。也称弹簧指数,是弹簧最重要的性能参数之一,取值见表1;
2)节距p;
3)螺旋升角α: 。对圆柱螺旋压缩弹簧一般应在5°~9°范围内选取。
弹簧的旋向可以是右旋或左旋,无特殊要求时,一般都用右旋。
二、普通圆柱螺旋压缩及拉伸弹簧的结构尺寸
p=(0.28~0.5)D2
p=d
轴向间距δ
δ=p-d
展开长度L
L=πD2n1/cosα
L≈πD2n+钩环展开长度
螺旋角α
α=arctg(p/πD2)
对压缩螺旋弹簧,推荐α=5°~9°
质量ms
ms=
γ为材料的密度,对各种钢,γ=7700kg/ ;对铍青铜,γ=8100kg/
H0=nd+钩环轴向长度
工作高度或长度
H1,H2,…,Hn
Hn=H0-λn
Hn=H0+λn
λn--工作变形量
有效圈数n
根据所要求的变形量计算
n≥2
总圈数n1
n1=n+(2~2.5)(冷卷)
弹簧设计
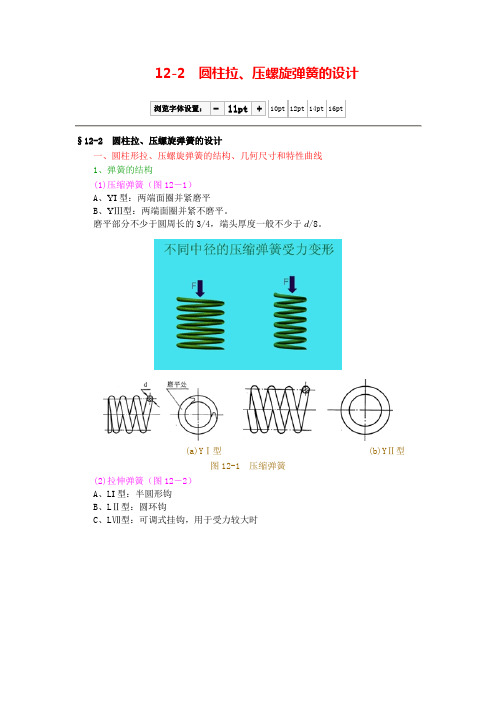
12-2 圆柱拉、压螺旋弹簧的设计浏览字体设置:- 11pt + 10pt 12pt 14pt 16pt§12-2 圆柱拉、压螺旋弹簧的设计一、圆柱形拉、压螺旋弹簧的结构、几何尺寸和特性曲线1、弹簧的结构(1)压缩弹簧(图12-1)A、YI型:两端面圈并紧磨平B、YⅢ型:两端面圈并紧不磨平。
磨平部分不少于圆周长的3/4,端头厚度一般不少于d/8。
(a)YⅠ型(b)YⅡ型图12-1 压缩弹簧(2)拉伸弹簧(图12-2)A、L I型:半圆形钩B、LⅡ型:圆环钩C、LⅦ型:可调式挂钩,用于受力较大时图12-2 拉伸弹簧2、主要几何尺寸弹簧丝直径d、外径D、内径、中径、节距p、螺旋升角 、自由高度(压缩弹簧)或长度(拉伸弹簧),如图12-3。
此外还有有限圈数n,总圈数,几何尺寸计算公式见表12-1。
(a) (b)图12-3 圆柱形拉、压螺旋弹簧的参数弹簧指数C:弹簧中径D2和簧丝直径d的比值即:C=D2/d。
弹簧丝直径d相同时,C值小则弹簧中径D2也小,其刚度较大。
反之则刚度较小。
通常C值在4~16范围内,可按表12-2选取。
表12-2 圆柱螺旋弹簧常用弹簧指数C弹簧直径d/mm0.2~0.40.5~1 1.1~2.2 2.5~67~1618~42C7~145~125~104~104~84~63、特性曲线弹簧所受载荷与其变形之间的关系曲线称为弹簧的特性曲线。
(1)压缩弹簧其特性曲线如图12-4所示。
图中H0为弹簧未受载时的自由高度。
F min为最小工作载荷,它是使弹簧处于安装位置的初始载荷。
在F min的作用下,弹簧从自由高度H0被压缩到H1,相应的弹簧压缩变形量为λmin。
在弹簧的最大工作载荷F max作用下,弹簧的压缩变形量增至λmax。
图中F lim为弹簧的极限载荷,在其作用下,弹簧高度为H lim,变形量为λlim,弹簧丝应力达到了材料的弹性极限。
此外,图中的h=λmax-λmin,称为弹簧的工作行程。
圆柱螺旋弹簧的参数

圆柱螺旋弹簧的参数(原创版)目录一、圆柱螺旋弹簧的基本几何参数二、圆柱螺旋弹簧的设计参数三、圆柱螺旋弹簧的应用范围四、圆柱螺旋弹簧的选用与安装正文一、圆柱螺旋弹簧的基本几何参数圆柱螺旋弹簧是一种常见的弹簧类型,广泛应用于各种工程机械、仪器仪表等领域。
它的基本几何参数包括以下几个方面:1.弹簧线径(d):即弹簧线的直径,是圆柱螺旋弹簧的主要尺寸参数之一。
2.心轴最大直径(s):工业应用中弹簧轴的最大直径,通常公差为 2%。
3.内径(di):即簧圈的内直径,通常公差为 2%。
4.外径(de):即簧圈的外直径,dedi2d,通常公差为 2%。
5.最小孔径(h):弹簧正常工作状态下所需通过的最小孔径。
二、圆柱螺旋弹簧的设计参数在设计圆柱螺旋弹簧时,需要考虑以下几个参数:1.钢丝的抗剪切模量(G):这是设计弹簧的重要参数,决定了弹簧的刚度。
2.弹簧中径(D):弹簧的工作直径,直接影响弹簧的承载能力。
3.弹簧有效圈数(n):决定弹簧的长度和弹性。
4.节距(t):除两端支承圈外,相邻两圈的轴向距离。
5.支承圈数(n2)和总圈数(n1):为使压缩弹簧工作时放置平稳、受力均匀,制造时会将弹簧两端并紧且磨平。
三、圆柱螺旋弹簧的应用范围圆柱螺旋弹簧广泛应用于各种工程机械、仪器仪表、汽车、摩托车等领域,主要用于减震、调节、支撑等作用。
四、圆柱螺旋弹簧的选用与安装在选用圆柱螺旋弹簧时,需要根据实际工作条件选择合适的弹簧材料、线径、中径等参数。
在安装时,要注意弹簧的压缩量、安装高度、工作环境等因素,确保弹簧能正常工作。
总之,圆柱螺旋弹簧是一种重要的弹性元件,在工程应用中具有广泛的应用前景。
变节距弹簧的设计

变节距弹簧弹簧节距,即是弹簧圈与圈之间的中心距离,如下图:图中标注的“t”即代表节距,左图是我们在生活中常见的等节距圆柱形压缩弹簧。
而与此不同的另一种圆柱形压缩弹簧——变节距弹簧,就是弹簧的每圈的节距不是相等的,常见的有节距递增型和多节距组合型。
1.节距递增型:每圈节距由小到大,呈递增趋势,如图:2.多节距组合型:由两种或两种以上的节距组合的弹簧,如图:变节距圆柱压簧大致分为这两大类,也可以根据不同需要做小的调整。
如何准确地设计一款变节距圆柱压簧,首先得知道它的刚度曲线,即弹性系数,它的弹性系数不是一个定值,而且伴随弹簧压缩行程的增加而增加(刚度曲线图见下)因为变节距圆柱压簧的刚度会随着压缩行程的增加而增加,所以在设计这种弹簧时,计算方法不能用常规的公式计算载荷。
我们常用的弹簧计算公式为K=Gd 4/8D 3n (K 为弹性系数、G 为弹性模量、D 为中径、n 为有效圈数)但变节距弹簧的刚度是不断变化的,所以我们在计算时需要用一个约数的概念来计算,就像一个圆可以分解为m 个正多边形一个概念。
以下我举例说明一下比较简单的‘多节距组合型’的变节距压缩弹簧的计算方法。
例如:一个装配空间为直径小于25mm ,高度小于80mm 的空间,所需要的载荷是压缩20mm 时承重150牛顿;压缩45mm 时承重440牛顿,我们该如何设计?载荷 压缩行程小节距 大节距分析一下:压缩20mm时承重15KG,粗计其刚度K1=150N/20mm=7.5N/mm;同样粗计压缩45mm刚度K2=9.8N/mm,所以弹簧的刚度是递增型,符合设计为变节距弹簧。
如果我们设计为两段节距组合的弹簧,则我们可以把弹簧看成是两个等节距的小弹簧组合而成;如图,弹簧可以看成是由小节距和大节距组合而成;按照我们的设计思路,弹簧在压缩到20mm内刚度为K1,在压缩20mm以后弹簧的刚度会增加为K2;现在我们分段计算,根据刚度计算公式:K=Gd4/8D3n 知K1= Gd4/8D3n1 (n1为整个弹簧的有效圈数)K2= Gd4/8D3n2(n2为有效总圈-小节距的圈数)根据K1,我们假设弹簧线径为2.8mm,中径为20.2mm,则得Gd4/8D3n1=7.5N/mm,推出n1≈10圈,而弹簧必须能压缩45mm,所以行程需大于45mm,代入假设的线径和圈数,弹簧总行程=80mm-2.8mm×(10+2)圈=46.4mm,符合大于45mm,即假设成立;而K2由小节距圈数决定大小,但小节距的圈数会影响弹簧由K1转折到K2的转折点位置;所以我们在确定小节距圈数的时候,需要考虑弹簧的应力大小和刚度转折点位置;此款弹簧的第一压缩量是20mm,那么刚度肯定是在20mm以后开始变化,所以我们假定弹簧刚度在25mm时开始变化(当然,你也可以取其它大于20mm的值,具体还要运算一下弹簧的内应力,并不是值越大越好),根据转折点的值,我们可以通过以下公式计算转折点值=(小节距-线径)×总的有效圈数=25mm代入前面有效圈为10圈,线径为2.8mm,得出小节距为5.3mm;所以,通过关系式:第二压缩量承重载荷=K1×25mm+K2×(45mm-25mm)=440牛顿,得出K2=12.625N/mm;而同时K2= Gd4/8D3n2(n2为小节距的圈数)由此得出Gd4/8D3n2 =12.625N/mm,结果算出n2=5.8圈综上所述,经过一系列推算,满足命题条件的弹簧规格为:线径2.8mm,外径23mm(中径20.2mm),总圈数12圈(有效圈10圈,其中小节距4.2圈),自由长度为80mm,其第一刚度K1=7.5N/mm,第二刚度K2=12.625N/mm。
拉伸弹簧的设计计算

发生在弹簧丝内侧,其
值为:
max
K8 C dF 2
式弹中簧:丝K—直曲径度d系: 数
max =K
=F+T
F
T
BB
m
n
K d 441C C.6 1 4K0F .C 62C 15
C —弹簧指数(旋绕比)。
C D2
卷绕困难,且工作时弹簧内侧应力
d
C
2、弹簧的许用应力
弹簧材料的许用应力与弹簧的受载循环次数有关.
§15—3 圆柱螺旋压缩(拉伸)弹簧的设计计算
一、弹簧特性线(压缩弹簧)
dd
p
D1 D2 D
弹簧特性线——表示弹簧载荷 与变形量之间的关系曲线.
预紧力F1称为弹簧的最 小载荷。Fmax(F2)为弹簧所承
H0 H1 H2
受的最大工作载荷,此时,
3.熟悉圆柱螺旋压缩、拉伸弹簧的设计 计算,主要包括强度和刚度计算、基 本参数和几何尺寸计算、结构设计、 特性曲线等。
§15—1 概述
一、弹簧的功用
弹簧是一种弹性的元件,它具有刚度小、变 形大、在载荷作用下易产生较大弹性变形等特 点,在各类机械中应用十分广泛。
弹簧的主要功用有:
(1)控制机构的位置和运动; (2)缓冲及吸振; (3)储存能量; (4)测量力和力矩 。
思考题与习题
5.已知圆柱螺旋压缩弹簧中径D2=16mm,弹 簧丝直径d=3mm,材料为碳素弹簧钢丝C级,Ⅲ 类弹簧,承受静载荷,弹簧工作圈数n=4,支 承端部并紧磨平。 试计算: 1)弹簧所能承受的最大载荷Fmax及最大载荷下 的变形量λmax 2)弹簧节距t,自由高度Ho及弹簧工作圈数n; 3)计算弹簧所需钢丝长度;
圆柱螺旋拉伸、压缩弹簧的设计计算
圆锥弹簧

各物理参数
d (弹簧线径) :该参数描述了弹簧线的直径。
S (心轴最大直径)该参数描述的是工业应用中弹簧轴的最大
直径,公差±2%。
De (大底外径):弹簧最宽端的外径,公差±2%。
De (小底外径):弹簧最窄端的外径,公差±2%。
H (最小孔径): 这是弹簧正常工作所需的最小空间的直径,
公差±2%。
Lc (压并长度):弹簧压至各线圈接触时的理论长度。
对于
大部分塔簧,该值等于线径的两陪,公差±2%。
L0 (自然长度):弹簧在压并过一次后,自然状态下的长度,
公差±2%。
R 弹簧刚度:这个参数表示弹簧每单位变形时的负荷变化。
单
位计算:1 DaN/mm = 10 N/mm (牛顿/毫米),公差
±15%。
L1 & F1 (弹簧在负荷F1作用下的长度L1):负荷F1与长
度L1可用这个公式计算:F1 = (L0-L1)* R, 然后算出长
度L1: L1 = L0 - F1/R
材料
I (不锈钢): 18/8 不锈钢,标注Z10 CN 18.09。
弹簧特性

弹簧特性曲线
表征弹簧轴向载荷F(或扭矩T)与其压缩或伸长变形量λ(或扭转角)之间的关系曲线称为弹簧特性曲线。
1)等节距圆柱螺旋压缩弹簧的特性曲线
图中的H
是压缩弹簧在没有承受外力时的自由长度。
弹簧在安装时,通常预加一个压力 F
min ,使它可靠地稳定在安装位置上。
F
min
称为弹簧的最小载荷(安装载荷)。
在它的作用下,弹簧的长度被压缩到H
1
其压
缩变形量为λ
min。
F
max 为弹簧承受的最大工作载荷。
在F
max
作用下,弹簧长度减到H
2
,其压缩变
形量增到λ
max 。
λ
max
与λ
min
的差即为弹簧的工作行程h,h=λ
max
-λ
min。
F
lim
为弹簧的极限载荷。
在该力的作用下,弹簧丝内的应力达到了材料的弹
性极限。
与F
lim 对应的弹簧长度为H
3
,压缩变形量为λ
lim。
弹簧的最大工作载荷
Fmax,由弹簧在机构中的工作条件决定。
但不应到达它的极限载荷,通常应保持Fmax ≤0.8Flim。
不等节距压缩弹簧

不等节距压缩弹簧
不等节距圆柱压缩螺旋弹簧,它的节距大小不等,这种弹簧在受载后,当载荷达到一定程度时,随着载荷的增加,从小节距开始到大节距依次逐渐并紧,刚度也逐渐增大。
特性线由线性关系变为非线性关系(渐增型).从而,有利于防止弹簧共振和颤振现象的发生。
弹簧节距的大小,可以是各个圈之问取成不同的节距,也可以几圈为一组取成几种不同的节距。
弹簧节距可以由小到大单向排列,也可以按两端小中间大双向排列。
不等节距压缩弹簧设计计算
不等节距圆柱螺旋压缩弹的设计计算方法有多种,根据使用的要求,一种是给出载荷与变形的特性曲线方程,根据
特性线设计弹簧;另一种是只给几个载荷,使设计的弹簧在给定的变形下满足这些载栽荷的要求。
不等节距螺旋弹簧的设计计算与普通弹簧相同,需要计算的主要是变形和刚度。
不等节距圆柱螺旋压缩弹簧相当于多个不同节距弹簧的直列组合。
