矩形截面圆柱螺旋压缩弹簧计算书
圆柱螺旋压缩弹簧计算公式
圆柱螺旋压缩弹簧计算
公式
-CAL-FENGHAI.-(YICAI)-Company One1
普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式
参数名称及代号计算公式备注
压缩弹簧拉伸弹簧
中径D2 D2=Cd 按普通圆柱螺旋弹簧尺寸系列表取标准值
内径D1 D1=D2-d
外径D D=D2+d
旋绕比C C=D2/d压缩弹簧长细比b b=H0/D2 b在1～的范围内选取自由高度或长度H0 H0≈pn+～2)d（两端并紧，磨平）H0≈pn+(3～d（两端并紧，不磨平） H0=nd+钩环轴向长度工作高度或长度H1,H2,…,Hn Hn=H0-λn Hn= H0+λn λn--工作变形量有效圈数n 根据要求变形量按式（16-11）计算n≥2总圈数n1 n1=n+(2～（冷卷）n1=n+～2) （YII型热卷） n1=n 拉伸弹簧n1尾数为1/4,1/2,3/4整圈。
推荐用1/2圈节距p p=～D2 p=d 轴向间距δ δ=p
-d 展开长度L L=πD2n1/cosα L≈πD2n+钩环展开长度螺旋角α α=arctg(p/πD 2) 对压缩螺旋弹簧，推荐α=5°～9°质量ms ms= γ为材料的密度，对各种钢，γ=7700kg/ ；对铍青铜，γ=8100kg/。
圆柱螺旋弹簧设计计算
圆柱螺旋弹簧设计计算
圆柱螺旋弹簧设计计算：
1. 理论背景：
a) 圆柱螺旋弹簧的原理：圆柱螺旋弹簧，也叫圆柱形螺旋弹簧，是由一组相互
交错的螺旋体和螺母组成的。
当加载时，弹簧体得到延伸，而螺母围绕弹簧体旋转，除把压缩和拉伸联结在一起发挥缓冲作用外，还具有润滑作用。
b) 圆柱螺旋弹簧设计原则：圆柱螺旋弹簧的设计应遵循计算公式、材料要求、
可行性等原则。
计算公式需要仔细考虑，其结果取决于弹簧的存在位置，构造形状和材料等因素，都受常规制造工艺条件的制约。
2. 设计流程：
a) 需求确定：确定所使用的圆柱螺旋弹簧的类型、材料、构造形状、尺寸和其
他设计要求。
b) 计算设计：根据设计要求和原则，运用有关计算公式，计算出所需弹簧的中
心周长和绕线转折处周长等参数。
c) 设计校核：根据实际使用情况及要求，综合分析由计算设计结果确定的弹簧
尺寸，进行结构安全性分析和性能验证，设计完善。
3. 成品检测：
a) 符合要求：圆柱螺旋弹簧成品检查，校验其各尺寸参数是否符合要求，确保
图纸尺寸的准确性。
b) 功能测试：检查弹簧的功能是否正常，测试弹簧的位移、压缩、伸出和伸长
量是否符合要求。
c) 耐久性测试：测试圆柱螺旋弹簧的耐久性，检测其在一定环境条件下的使用
寿命和安全性。
4. 总结：
圆柱螺旋弹簧的设计计算是一个复杂的过程，在设计计算前要确定需求，根据
设计原则完成计算设计流程，确保设计质量，对成品进行检测，及时发现存在的质量问题，提高质量水平。
矩形截面圆柱螺旋压缩弹簧计算书
85.07
螺旋角
°
α
5.46
展开长度
mm
L 1732.33
kg kg
合格 1.12
n
11.79
总圈数
n1
13.79
弹簧刚度
N/mm P'
49.0
工作极限载荷
N
Pj
2016.2 查表 11-2-36
极限载荷变形
mm
Fj
41.1
最小工作载荷
N
P1
672.1
最小载荷变形
mm
F1
13.7
工作行程
mm
h
27.4
节距
mm
t
12.00间距mmδ来自5.60自由高度
mm
H0
151.11
压并高度
mm
Hb
材料 65Mn
MPa
G
79000 查表 11-2-2
许用应力
MPa
τP
570
查表 11-2-6
选择旋绕比
C
5
边长
mm
a
8
选择
a＞b
边长
mm
b
6.4
a/b
1.25
弹簧中径
mm
D
40
弹簧内径
mm
D1
32
验算切应力
MPa
β τ
2.9 465.4
查图 11-2-12
＜
570
有效圈数
γ
5.6
查图 11-2-11
原始条 件
计算 项目
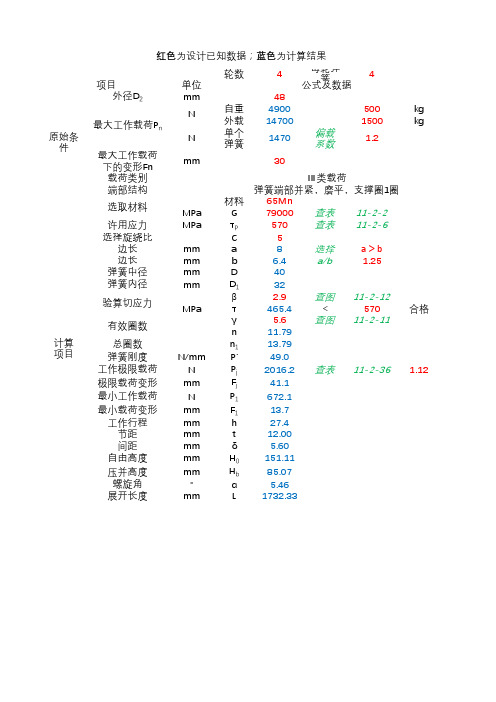
红色为设计已知数据；蓝色为计算结果
项目
单位
轮数
4
每轮弹 公式簧及数据
圆柱螺旋压缩弹簧的设计计算
圆柱螺旋压缩弹簧的设计计算圆柱螺旋压缩弹簧是一种常见的弹簧结构，具有重要的弹簧特性，广泛应用于机械设备、汽车、航空航天等领域。
设计计算圆柱螺旋压缩弹簧需要考虑材料的特性、工作环境、载荷条件等因素。
下面将详细介绍圆柱螺旋压缩弹簧的设计计算方法。
1.第一步：确定设计参数设计圆柱螺旋压缩弹簧的第一步是确定设计参数，包括弹簧材料、弹簧直径、弹簧长度、扭矩、载荷等。
根据实际使用需求和弹簧的工作环境，选择合适的弹簧材料，一般常用的材料有弹簧钢、钢丝，也可以根据具体需要选择其他材料。
2.第二步：计算细节参数根据设计参数，可以计算得到弹簧的一些细节参数。
首先，通过弹簧的自由长度、线径和扭转角等参数，计算得到螺旋压缩弹簧的几何特性，包括平均直径、圈数、绕制长度等。
其次，根据材料的特性和载荷条件，计算得到弹簧的刚度系数和承载能力。
3.第三步：弹簧的受力分析弹簧在工作中受到载荷的作用，需要进行受力分析。
根据载荷的大小和方向，计算得到弹簧的最大应力、变形量和弹簧应变能等参数。
在弹簧的受力分析中，需要考虑弹簧的静态刚度和动态刚度，以及载荷的周期性变化对弹簧的影响。
4.第四步：校核设计根据计算得到的参数，进行弹簧设计的校核。
首先，根据弹簧材料的强度和安全系数，判断设计的合理性。
其次，根据弹簧的尺寸和载荷条件，进行弹簧的参数调整，优化设计方案。
最后，进行弹簧的模拟试验或实验验证，确保设计的可靠性和安全性。
以上是圆柱螺旋压缩弹簧的设计计算方法，需要综合考虑弹簧的几何特性、材料特性和载荷条件等因素，进行详细的设计计算，以满足具体需求。
整个设计过程需要严谨的计算和校核，确保弹簧设计的准确性和可靠性。
圆柱螺旋压缩弹簧计算公式
圆柱螺旋压缩弹簧计算公式
弹簧常量（Spring Constant）是指单位压缩或拉伸长度下所储存的能量。
它是衡量弹簧刚性和柔性的重要指标。
圆柱螺旋压缩弹簧的弹簧常量可以通过以下公式计算：
k=(Gd^4)/(8D^3n)
其中，k为弹簧常量，G为弹簧材料的剪切模量，d为弹簧线圈的直径，D为弹簧线圈的平均直径，n为弹簧线圈的总数。
F = kx
其中，F为受到的力，k为弹簧常量，x为弹簧的位移。
Fmax = kxmax
其中，Fmax为最大力，k为弹簧常量，xmax为允许的最大位移。
Lmax = Ln - (D/2 + d/2 + c)
其中，Lmax为最大压缩长度，Ln为弹簧线圈的总长度，D为弹簧线圈的平均直径，d为弹簧线圈的直径，c为线圈间的缝隙。
x_max = (Ln - L0) / n
其中，x_max为最大位移，Ln为弹簧线圈的总长度，L0为弹簧的初始长度，n为弹簧线圈的总数。
S=F/x
其中，S为刚度，F为受到的力，x为位移。
E = (1/2)kx^2
其中，E为弹性能量，k为弹簧常量，x为位移。
以上就是关于圆柱螺旋压缩弹簧的计算公式。
通过这些公式，我们可以准确地计算弹簧的性能参数，为机械设计提供依据，并确保弹簧在实际使用中能够正常工作。
当然，在实际设计中，还需要考虑许多其他因素，如疲劳寿命、可靠性和安全系数等，并结合实际应用需求进行综合设计。
矩形截面压缩弹簧
矩形截面压缩弹簧
矩形截面压缩弹簧，简称矩形弹簧，又称模具弹簧，因其制作材料截面为矩形而得名。
矩形弹簧通常选用合金材质，在同样空间条件下，矩形截面螺旋压缩弹簧比圆形截面圆柱螺旋压缩弹簧的刚度更大。
它具有体积小、能够承受高速振幅、稳定性和耐疲劳强度良好等特点。
常见的矩形弹簧颜色有紫色、黄色、蓝色、红色、绿色、棕色、橙色、象牙色、浅蓝色、淡绿色。
矩形弹簧广泛应用于冲压模具、金属压铸模具、塑胶模具以及其他弹性运动精密机械设备、汽车等领域。
圆柱螺旋压缩弹簧计算示例
圆柱螺旋压缩弹簧计算示例
圆柱螺旋压缩弹簧计算示例之一
项目
单位
公式及数据
最小工作载荷Pl
N
P仁60
原
最大工作载荷Pn
N
Pn=240
始
工作行程h
mm
h=36±1
条
弹簧外径D2
mm
D2<45
件
弹簧类别
N=10
3~106次
端部结构
端部并紧、磨平，支承圈数为1
圈
弹黄材料
碳素弹簧钢丝C级
初算弹簧刚度P/
高度比b
b虫
D
-902.37V2.6
38
bv2.6不必进行稳定性验算
精选文档
技术要求：
1•总圈数ni=7.5
2•旋向为右旋
3.展开长度L=902mm
4•硬度HRC45~50
N/m
p/
PnP 240
60匚
P
h
367
m
工作极限载荷Pj
N
因是II类载荷：PjA1.25Pn
顾Pj=1.25
X210=300
弹簧材料直径d及弹簧中径
根据Pj与D条件从表11-2-19得：
参
d
D
Pj
fj
Pd/
D与有关参数
3.5
38
306.97
11.37
27
数
有效圈数n
圈
Pd
27
n~i
5.4
P/
5
计
按照表11-2-10取标准值n=5.5
总圈数ni
圈
n1= n+2=5.5+2=7.5
算
弹簧刚度P/
圆柱螺旋压缩(拉伸)弹簧的设计计算
圆柱螺旋压缩（拉伸）弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。
由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。
弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。
圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。
普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青•(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。
因此在设计弹簧时，务必使其工作应力在弹性极限范围内。
在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。
为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系(右图b)。
这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。
对拉伸弹簧，如图<圆柱螺旋拉伸弹簧的特性曲线>所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。
右图a中的H0是压缩弹簧在没有承受外力时的自由长度。
弹簧在安装时，通常预加一个压力F min，使它可靠地稳定在安装位置上。
F min称为弹簧的最小载荷(安装载荷)。
在它的作用下，弹簧的长度被压缩到H1其压缩变形量为λmin。
F max为弹簧承受的最大工作载荷。
在F max作用下，弹簧长度减到H2，其压缩变形量增到λmax。
λmax与λmin的差即为弹簧的工作行程圆柱螺旋压缩弹簧的特性曲线h,h=λmax-λmin。
F lim为弹簧的极限载荷。
在该力的作用下，弹簧丝内的应力达到了材料的弹性极限。
圆柱螺旋扭转弹簧计算表
mm
工 作 图
略
1.有效圈数n= 2.旋向为右旋 3.展开长度L= 4.硬度
算公式
公式及数据 14142 77616 80 N<103 外臂扭转 120
入数值，粉色为公式自动计算值
8～10 1471 1471 1176.8 5 1.1875 9.276144715 10 1471 安全 50 44 4.4 206000 16.09154535 16 797.9646478 97.26746694 17.26746694 13778.82817 1177 919.375 1176.8 97257.36842 121.881801 13 218 5.375351329
2220.314257 0.960999674 正确 16 2220.314257
总长度值再加L0
旋向为右旋 总长度值再加L0
3 b
mm Mpa Mpa Mpa
mm mm Mpa mm mm Mpa 圈 圈 N·mm/(°) (°) (°) N·mm Mpa Mpa Mpa N·mm (°)osα +L0 最小稳定性指标nmin=(φj/123.1)4 检查最小稳定性指标是否小于n
圆柱螺旋扭转弹簧计算公式
注：对应机械设计手册第四版扭簧计算过程，黄色手动输入数值，粉色为公式自动计算值
项目 最小工作扭矩T1 原 最大工作扭矩Tn 始 工作扭转角φ 条 弹簧类别 件 端部结构 自由角度 选择材料及许用弯曲应力σ
单位 N·mm N·mm (°)
(°)
Bp
根据设计要求选择弹簧类型、材料、等级 假设钢丝直径 d（XX-XXmm） 根据表11-2-3 查得σ b=（XX-XXMpa） 取中间值σ b= 根据表11-2-6 许用弯曲应力σ Bp=0.8 ·σ b 初选旋绕比 C 为使结构紧凑，暂定C=6（5-8） 曲度系数K1 =（4C-1）/(4C-4） 钢丝直径d=（32Tn·K1/π σ Bp）1/3 取标准值d 对照表11-2-3查σ b数值 对照表11-2-3看σ b数值是否大于原暂定值 弹簧中径D=CХ d 取标准值D （表11-2-9） 旋转比C=D/d 根据表11-2-2 查得弹簧材料弹性模量E 弹簧圈数n=Ed4φ/(3667·D·(Tn-T1)) n取整数 弹簧刚度T'=Ed4/（3667·D·n） 最大工作扭矩时的扭转角φn=Tn/T' 最小工作扭矩时的扭转角φ1=φn-φ 实际最小工作扭矩T1=/T'φ1 根据弹簧类型计算工作极限弯曲应力σ j Ⅱ类 工作极限弯曲应力σ j=0.625Х σ b Ⅲ类 工作极限弯曲应力σ j=0.8Х σ 工作极限扭矩Tj=π d σ j/32K1 工作极限扭转角φj=Tj/T' 弹簧节距t=d+δ 无特殊要求δ =0.5 自由长度H0=nt+d 螺旋角α =arctan t/π D
圆柱螺旋压缩弹簧计算示例
圆柱螺旋压缩弹簧计算示例假设我们要设计一个圆柱螺旋压缩弹簧，用于悬挂汽车底盘的悬挂系统。
首先，我们需要确定弹簧的材料。
常用的弹簧材料有碳钢、合金钢、不锈钢等。
在这个示例中，我们选择使用碳钢材料，其具有良好的机械性能和耐磨性。
接下来，我们需要确定弹簧的几何尺寸和刚度。
弹簧的外径、内径、线径、圈数等参数都会影响其刚度和负载能力。
为了简化计算，我们假设弹簧材料为线弹簧，并且线径为0.5厘米，圈数为10。
在计算弹簧刚度时，我们可以使用胡克定律。
胡克定律表示弹簧的位移与受力之间的线性关系。
根据胡克定律，弹簧刚度（K）等于弹簧受力（F）与位移（x）之比。
在这个示例中，我们假设弹簧的刚度为100牛顿/米。
接下来，我们需要计算弹簧的自由长度。
弹簧的自由长度是指在未受外力作用时，弹簧处于松弛状态的长度。
我们可以使用公式Lf=(D+d)*n，其中Lf表示自由长度，D表示弹簧的外径，d表示弹簧的线径，n表示圈数。
在这个示例中，我们假设D为10厘米，d为0.5厘米，n为10，则弹簧的自由长度为100厘米。
接下来，我们需要计算弹簧的变形和负载能力。
弹簧的变形可以使用胡克定律来计算。
根据胡克定律，弹簧的变形等于外力除以刚度。
在这个示例中，我们假设外力为500牛顿，则弹簧的变形为500/100=5厘米。
最后，我们需要进行弹簧的可变速率计算。
可变速率是指弹簧在受力变化过程中的刚度变化程度。
为了简化计算，我们可以使用一个可变速率系数（Kv）来表示弹簧的可变速率。
在这个示例中，我们假设可变速率系数为1、则弹簧在受力变化过程中的刚度不变。
以上是一个圆柱螺旋压缩弹簧计算的示例。
实际应用中，需要考虑更多的因素，如材料的疲劳性能、应力分布等，以确保弹簧的安全可靠性。
圆柱螺旋压缩弹簧的设计计算
圆柱螺旋压缩（拉伸）弹簧的设计计算（一）几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D中径D2内径D1、节距P、螺旋升角a及弹簧丝直径d。
由下图圆柱螺旋弹簧P a= arctg的几何尺寸参数图可知，它们的关系为：’〔式中弹簧的螺旋升角a，对圆柱螺旋压缩弹簧一般应在5°〜9范围内选取。
弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。
r—D——-1「Di —*1圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表（［color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm计算公式）。
丫为材料的密度，质量m s对各种钢，m s= 4丫=7700kg/m ;对铍青（二）特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。
因此在设计弹簧时，务必使其工作应力在弹性极限范围内。
在这个范围内工作的压缩弹簧，当承受轴向载荷P时, 弹簧将产生相应的弹性变形，如右图a所示。
为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系（右图b）。
这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。
对拉伸弹簧，如图< 圆柱螺旋拉伸弹簧的特性曲线> 所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。
右图a中的H0是压缩弹簧在没有承受外力时的自由长度。
弹簧在安装时，通常预加一个压力F min，使它可靠地稳定在安装位置上。
F min称为弹簧的最小载荷（安装载荷）。
在它的作用下，弹簧的长度被压缩到H1其压缩变形量为入min。
F max为弹簧承受的最大工作载荷。
在F max作用下，弹簧长度减到H2, 其压缩变形量增到入max。
入max 与入min的差即为弹簧的工作行程圆柱螺旋压缩弹簧的特性曲线騒二险” u 常数 AminArux圆柱螺旋拉伸弹簧的特性曲线h, h= X max-入 min 。
圆柱螺旋压缩弹簧设计计算
% 圆柱螺旋压缩弹簧设计计算% M文件中的表16-3和表16-5见参考文献[1]% 已知条件：最小和最大弹簧载荷、工作行程、剪切弹性模量、许用应力、最小内径F1=500;F2=1200;h=60;G=7.85e4;sigma=1420;D1_min=50;% 1-按照强度条件确定弹簧丝直径% 由于弹簧丝材料强度与它的直径相关，需要采用试算法ds=input(' 试选弹簧丝直径(mm) ds = ');sigma_b=input(' 按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = ');tau_p=0.45*sigma_b;fprintf(' 许用剪切应力tau_p = %3.4f MPa \n',tau_p);Cj=D1_min/ds+1;fprintf(' 计算弹簧指数Cj = %3.4f \n',Cj);C=input(' 按照表16-5，选择弹簧指数C = ');Kq=(4*C-1)/(4*C-4)+0.615/C;fprintf(' 计算曲度系数Kq = %3.4f \n',Kq);dj=sqrt(8*Kq*F2*C/(pi*tau_p));fprintf(' 计算簧丝直径dj = %3.4f mm \n',dj);if dj>dsdisp ' 不安全，需要重选弹簧丝直径'elsedisp ' 安全'd=ds; % 确定弹簧丝直径end第1次试算：试选弹簧丝直径(mm) ds = 6按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = 1420许用剪切应力tau_p = 639.0000 MPa计算弹簧指数Cj = 9.3333按照表16-5，选择弹簧指数C = 9计算曲度系数Kq = 1.1621计算簧丝直径dj = 7.0721 mm不安全，需要重选弹簧丝直径第2次试算：试选弹簧丝直径(mm) ds = 7按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = 1370许用剪切应力tau_p = 616.5000 MPa计算弹簧指数Cj = 8.1429按照表16-5，选择弹簧指数C = 8计算曲度系数Kq = 1.1840计算簧丝直径dx = 6.8520 mm安全% 2-按照刚度条件确定弹簧工作圈数Kj=(F2-F1)/h;fprintf(' 计算弹簧刚度Kj = %3.4f N/mm \n',Kj);nj=G*d/(8*C^3*Kj);fprintf(' 计算弹簧圈数nj = %3.4f \n',nj);n=input(' 选取弹簧工作圈数n = ');n2=input(' 选取弹簧支承圈数n2 = ');n1=n+n2;fprintf(' 弹簧总圈数n1 = %3.4f \n',n1);% 计算弹簧的刚度和变形量Kp=G*d/(8*C^3*n);f1=F1/Kp;f2=F2/Kp;fprintf(' 弹簧实际刚度Kp = %3.4f N/mm \n',Kp);fprintf(' 弹簧最小变形量f1 = %3.4f mm \n',f1);fprintf(' 弹簧最大变形量f2 = %3.4f mm \n',f2);计算结果：计算弹簧刚度Kj = 11.6667 N/mm计算弹簧圈数nj = 11.4990选取弹簧工作圈数n = 12选取弹簧支承圈数n2 = 2弹簧总圈数n1 = 14.0000弹簧实际刚度Kp = 11.1796 N/mm弹簧最小变形量f1 = 44.7243 mm弹簧最大变形量f2 = 107.3383 mm% 3-弹簧稳定性校核D2=C*d;fprintf(' 弹簧中径D2 = %3.4f mm \n',D2);delta=input(' 选取相邻两圈弹簧丝间隙系数delta = ');t=(1+delta)*d+f2/n; % 圆柱螺旋压缩弹簧fprintf(' 弹簧节距t = %3.4f mm \n',t);Y=input(' 选取弹簧端部结构类型Y = '); % 弹簧端部结构类型:1或是2if Y==1H0=n*t+(n2-0.5)*d;elseif Y==2H0=n*t+(n2+1)*d;endfprintf(' 弹簧自由高度H0 = %3.4f mm \n',H0);b=H0/D2;fprintf(' 弹簧高径比 b = %3.4f \n',b);% 采用3次样条插值确定圆柱螺旋弹簧不稳定系数CbDBZC=input(' 选取弹簧端部支承类型DBZC = '); % 弹簧端部支承类型:1、2、3 switch DBZCcase 1 % 1-弹簧两端固定支承bx=[5.3 5.4 5.5 5.75 6 6.5 7 7.5 8 8.5 9 10];Cby=[0.80 0.65 0.60 0.45 0.40 0.325 0.265 0.225 0.19 0.165 0.145 0.125];case 2 % 2-弹簧一端固定、一端自由支承bx=[3.7 3.85 4 4.5 5 5.5 6 6.5 7 8 9 10];Cby=[0.80 0.60 0.50 0.31 0.24 0.20 0.17 0.15 0.13 0.105 0.08 0.075];case 3 % 3-弹簧两端自由支承bx=[2.6 2.8 3 3.5 4 4.5 5 5.5 6 7 8 9 10];Cby=[0.8 0.5 0.4 0.27 0.21 0.15 0.12 0.09 0.075 0.05 0.04 0.03 0.025]; endCb=interp1(bx,Cby,b,'spline'); % 3次样条插值fprintf(' 弹簧不稳定系数Cb = %3.4f \n',Cb);% 绘制圆柱螺旋弹簧不稳定系数Cb线图plot(bx,Cby,'ro',bx,Cby);grid on;xlabel('\bf\it b');ylabel('\bf\it Cb');title('\bf 弹簧不稳定系数线图');switch DBZCcase 1gtext('\bf 1-弹簧两端固定支承')case 2gtext('\bf 2-弹簧一端固定、一端自由支承')case 3gtext('\bf 3-弹簧两端自由支承')endFc=Cb*Kp*H0;fprintf(' 弹簧稳定临界载荷Fc = %3.4f N \n',Fc);if Fc<F2disp ' 弹簧工作不稳定，需要改变参数或是加装导向装置'elsedisp ' 弹簧工作稳定'end计算结果：弹簧中径D2 = 56.0000 mm选取相邻两圈弹簧丝间隙系数delta = 0.15弹簧节距t = 16.9949 mm选取弹簧端部结构类型Y = 1弹簧自由高度H0 = 214.4383 mm弹簧高径比 b = 3.8293选取弹簧端部支承类型DBZC = 3弹簧不稳定系数Cb = 0.2278弹簧稳定临界载荷Fc = 546.0792 N弹簧工作不稳定，需要改变参数或是加装导向装置。
圆柱螺旋压缩弹簧设计计算
圆柱螺旋压缩弹簧设计计算
对于圆柱螺旋压缩弹簧的设计计算，首先需要确定压缩弹簧的基本
参数，包括弹簧的长度、弹簧的外径、弹簧的内径、弹簧的压缩高度、弹簧的圈数和弹簧的负荷。
同时还需要确定使用材料、计算等级设定
及拉伸曲线等参数。
其次，在设计确定基本参数后，根据几何原则和
结构分析相关理论，建立并编制圆柱螺旋压缩弹簧的数据库，并利用
数据库，结合实际需求和使用条件，根据弹簧的形状调整所需的参数值，计算所需的特定压缩量。
然后根据已建立的弹性平面曲线及弹簧
的拉伸性能，做好拉伸及压缩弹簧计算，并绘制出压缩弹簧的荷载-位
移曲线。
最后，对于一些特殊形状的压缩弹簧，像外面添加一组悬挂
环等，需要根据实际情况另行计算，确保压缩弹簧正确行使其作用。
综上所述，圆柱螺旋压缩弹簧设计计算主要需要确定压缩弹簧的基本
参数，建立并编制弹簧的数据库，根据弹簧的拉伸性能进行计算，并
绘制压缩弹簧的荷载-位移曲线，最后，对边添加了特殊结构的压缩弹簧，也要另行计算，以确保压缩弹簧正确执行其功能。
圆柱螺旋压缩弹簧计算
圆柱螺旋压缩弹簧计算圆柱螺旋压缩弹簧计算是设计和制造压缩弹簧的重要步骤。
压缩弹簧广泛应用于各种机械设备和工具中，例如汽车悬挂系统、工业机械、家电等。
在进行圆柱螺旋压缩弹簧计算时，需要考虑到材料的性质、几何参数和应力分析等因素。
首先，进行圆柱螺旋压缩弹簧计算之前需要了解弹簧的工作条件和设计要求。
这包括弹簧所受的力、位移和弹簧的寿命要求等。
根据这些要求，可以确定弹簧的材质、弹簧线直径、绕制方向等。
传统的圆柱螺旋压缩弹簧计算方法是根据胡克定律来进行的。
胡克定律表明，弹簧的弹性应变与所受的应力成正比。
根据弹簧的线性弹性行为，可以得到以下的胡克定律方程：F=k·δ式中，F表示所受的力，k表示弹簧的刚度，δ表示弹簧的压缩位移。
根据胡克定律，我们可以获得刚度k的计算公式：k=Gd^4/(8NαD^3)式中，G表示弹簧材料的剪切模量，d表示弹簧线直径，N表示弹簧的总匝数，D表示弹簧的平均直径，α表示绕制角度。
通过这些参数的计算，可以得到弹簧的刚度。
然后，我们需要计算弹簧的自由长度。
自由长度是指在没有外力作用下，弹簧的长度。
自由长度的计算公式如下：L0=N·P式中，L0表示自由长度，N表示弹簧的总匝数，P表示弹簧线的间距。
除了刚度和自由长度，还需要计算弹簧的压缩长度。
压缩长度是指弹簧在受到外力压缩后的长度。
压缩长度的计算公式如下：d=L0-δ式中，d表示弹簧的压缩长度，L0表示自由长度，δ表示弹簧的压缩位移。
弹簧的应力分析也是圆柱螺旋压缩弹簧计算的关键。
弹簧在受到外力作用时，会发生应力的变化。
这些应力会直接影响到弹簧的性能和寿命。
因此，在计算中需要考虑到弹簧的应力分布情况。
弹簧的应力分布可以通过以下公式计算得到：σ=F/A式中，σ表示弹簧的应力，F表示所受的力，A表示弹簧的截面积。
除了弹簧的应力分布，还需要计算弹簧的最大应力。
弹簧的最大应力是指弹簧所能承受的最大应力。
计算弹簧的最大应力可以通过以下公式得到：σmax = Kn · σ式中，σmax表示弹簧的最大应力，Kn表示安全系数。
螺旋弹簧的设计计算资料
弹簧设计资料
计算公式
本文中使用的主要记号如表1所示。
表1
(ⅰ)非接触性卷簧
a. 卷数太多外端固定支持的情况
図1
图1那样卷数很多的非接触性卷簧，外端被固定，内端固定在卷芯上，计算公式如下。
(1)
(2)
(3)
b.卷数多外端自由支持的情况
同时外端为铰接等自由支持的情况下，计算公式如下。
(4)
(5)
(6)
自由支持外端为了不产生力矩，与外端固定支持的情况相比偏转角大约增大20%。
另外弯曲应力，弹簧全体并不相同，在外端附近的弯曲应力最大，相同扭矩的情况下，是外端固定支持的2倍。
(10)
(11)
耐久性大约15000回。
* 像卷簧那样长方形断面的宽度比厚度大的情况，用EI/（1－ν2）代替EI得到的结果更加正确。
* 根据本公司的数据，⊿σ≒600 MPa、耐久性105。
弹簧的设计用记号如下记表1所示。
另外，纵弹性系数E的值如表2所示。
表１. 计算用记号及单位
表2.纵弹性系数：E（N/m㎡）
设计用基本计算公式
卷入时求弹簧定数的基本公式如下。
另外，发生任意力矩时，应力的公式如下。
数值代入计算公式的话，求得下次的扭矩和应力。
E：2.06×105(N/mm2)b：10 (mm)
t：1.0 (mm)l：1200 (mm)的时候，弹簧定数K如下公式
因此，转一回(360°)的时候扭矩M，360°用2π代入，如下这个时候的应力σ为，如下。
矩形截面圆柱螺旋压缩弹簧计算书
材料 65Mn
MPa
G
79000 查表 11-2-2
许用应力
MPa
τP
570
查表 11-2-6
选择旋绕比
C
5
边长
mm
a
8
选择
a＞b
边长
mm
b
6.4
a/b
1.25
弹簧中径
mm
D
40
弹簧内径
mmLeabharlann D132验算切应力
MPa
β τ
2.9 465.4
查图 11-2-12
＜
570
有效圈数
γ
5.6
查图 11-2-11
n
11.79
总圈数
n1
13.79
弹簧刚度
N/mm P'
49.0
工作极限载荷
N
Pj
2016.2 查表 11-2-36
极限载荷变形
mm
Fj
41.1
最小工作载荷
N
P1
672.1
最小载荷变形
mm
F1
13.7
工作行程
mm
h
27.4
节距
mm
t
12.00
间距
mm
δ
5.60
自由高度
mm
H0
151.11
压并高度
mm
Hb
85.07
螺旋角
°
α
5.46
展开长度
mm
L 1732.33
kg kg
合格 1.12
原始条 件
计算 项目
红色为设计已知数据；蓝色为计算结果
项目
单位
圆柱螺旋扭转弹簧计算公式
变形范围
工作圈数nFra bibliotek所需的最少圈数
各圈间的间距
无间距的制造容易，有间距的特性线精度高
节距
t
螺旋角
α
自由长度
H0
簧丝长度
L
注：对矩形截面弹簧，表中的d应相应地改用a或b。
圆柱螺旋扭转弹簧计算公式
簧丝截面形状
抗弯截面系数Zm
惯性距l
扭转变形角
弯曲应力σ
簧丝直径d/mm
圈数n
注:Kt、K′t为扭转弹簧的曲度因子，Kt=（4C-1）/（4C-4）；K′t=（3C-1）/（3C-3）。
参数名称
符号
关系式
说明
工作扭矩
Ti
安装时必须预加扭矩T1
试验扭矩
Ts
对应于最大试验弯曲应力 的扭矩。对应的扭转变形角为 。
圆柱螺旋弹簧设计计算
圆柱螺旋弹簧设计计算一．弹簧的参数名称及代号 GB/T 1239.6-93二．基本计算公式弹簧的强度和变形的基本计算公式1．材料切应力：P dck P d D 2388ππτ==. 2.弹簧变形量：P Gd n c P Gd n D F 34388==3.弹簧的刚度：n c GD n D Gd F P P 434'88=== 4.弹簧变形量：222'F D PF U ==5．弹簧材料直径：][6.1τKPCd = 6.弹簧的中径：D=Cd 7.弹簧的有效圈数：P c GD P D F Gd n 43488== 8.曲度系数：cc c K 615.04414+--= 9．弹簧特性：为了保证指定的负荷，弹簧变形量应在试验负荷下变形量Fs 的20%~80%之间： 0.2Fs ≤F 1，2，3~n ≤0.8Fs10.在特殊需要保证刚度时，其刚度按试验负荷下变形量Fs 的30%~70%之间，由两负荷点的负荷差之比来确定：1212F F P P P ，--=11．试验负荷Ps 为测定弹簧特性时，弹簧允许承受的最大负荷，其值可按其曲度系数K=1，导出： s Dd Ps τπ83=式中τs 为试验切应力，其最大值取表3和表4中的Ⅲ类负荷下的许用切应力值。
12．压并负荷Pb 为弹簧压并时的理论负荷，对应的压并变量为Fb 。
切变模量G 值按弹簧常用材料表查取，当工作温度超过60度时，就对常温下的G 值进行修正：Gt=KtG 。
Kt 温度修正系数表13.弹簧中径：2)(21D D D += 14弹簧内径：D 1=D －d 15.弹簧外径：D 2=D+da ．当弹簧两端固定时，从自由高度到并紧时，中径增大为：D D d t D )05.0(222-=∆b ．当弹簧与支承座可以自由回转而摩擦力比较小时，中径增大为：D D d td t D )2.08.001.0(222--=∆ 16．弹簧的旋绕比：c=D/d=4~22,其荐用值根据材料直径在表中选取；17．总圈数：n1=n+n2 。