现代信号处理方法1_2解析
现代信号处理方法2-2

2.2 Radon-Wignel 变换2.2.1 Wigner-Ville 分布的时频聚集性时变信号中,线性调频(LFM )信号特别引人关注:首先, LFM 信号广泛用于各种信息系统,如通信、雷达和地震勘探等;其次,探测系统的目标多普勒频率与目标速度近似成正比,当目标作等加速运动时,回波即为线性调频;再次,复杂运动目标回波在一段短的时间里,常可用线性调频作为其一阶近似;另外,对于空间线性阵列,若信号源位于近场,则沿阵列分布的信号也近似为线性调频。
因此深入研究线性调频信号具有重大的理论价值与实际应用价值。
用Ville Wigner -分布研究单分量LFM 信号是十分有效的:现考虑幅度为1的单分量信号)5.0(220)(m t t f j et z +=π (2.2.1) 因为 τπττπττπττ)(2])2(21)2([2])2(21)2([2*02020)2()2(mt f j t m t f j t m t f j e e et z t z +-+--+++=⋅=-+ (2.2.2) 故根据(1.3.32)可求得其Ville Wigner -分布为⎰∞∞--+⋅=τπττπd e e f t W f j mt f j LFM 2)(20),()]([0mt f f +-=δ (2.2.3) 从(2.2.3)说明单分量LFM 信号的Ville Wigner -分布是沿直线mt f f +=0分布的冲激线谱,即分布的幅值集中出现在表示信号的瞬时频率变化率的直线上,因此,从最佳展现LFM 信号的频率调制率这一意义上讲Ville Wigner -分布具有理想的时频聚集性。
在实际中由于LFM 信号的长度有限,其Ville Wigner -分布往往显示为背鳍状如图2.2.1所示,能够看出信号的能量集中于瞬时频率附近。
图2.2.1 实际LFM 信号的Ville Wigner -分布呈背鳍状 若所研究的LFM 信号是多分量的,那么信号各分量之间的交叉项就会使时-频平面变得模糊不清,尤其是在信噪比不高的情况下,甚至难于区分各个LFM 信号分量。
现代信号处理-现代谱

4. AR模型谱估计的性能 均值: ˆ ( )] P ( ) E[ P
方差:
4 p 2 P ( ), 0, ˆ ( )} N ar{P 2p 2 P ( ) , else N
7.3 功率谱估计的AR模型法
5. 确定AR模型阶数的几种方法 实验方法:观察拟合误差法 算出取各种模型阶数时的白噪声方差2, 以能使2值显著减小的模型阶数的最大值 作为选定的结果。
7.1 引言
AR
(Auto Regressive)系统:
a p 0且 bi 0, i 1,q
ARMA系统:
y( n) x ( n) a i y( n i )
i 1
p
a p 0且bq 0
7.2 ARMA模型
Y ( z ) X ( z )B( z ) [ A( z ) 1] Y ( z )
7.3 功率谱估计的AR模型法
令
R( 1) R(1 p) R( 0 ) R R ( p 1 ) R ( p 2 ) R ( 0 )
R(0) R( 1) R( p) 1 2 R(1) a R ( 0 ) R ( 1 p ) 1 0 R ( p ) R ( p 1 ) R ( 0 ) a p 0
2 * a R ( m i ) a h i x i (k )h(k m i ) i 0 i 0 k 0
p
p
2 h* (k ) ai h(k m i )
k 0 i 0
p
2 * a R ( m i ) h i x (k )bk m i 0 k 0
现代信号处理方法1-3
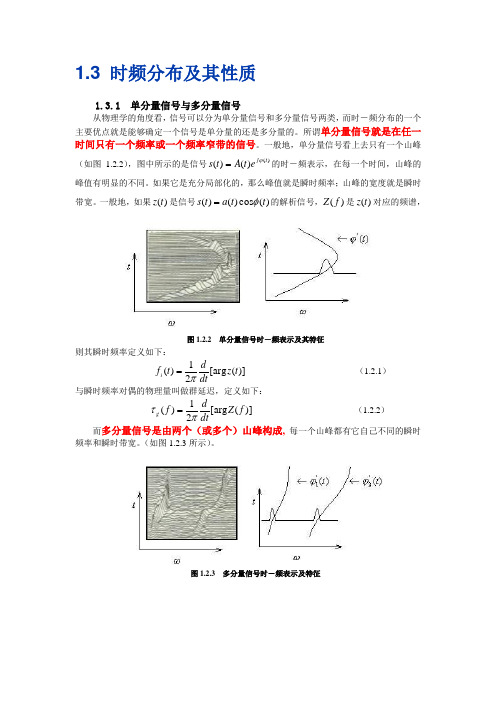
1.3 时频分布及其性质1.3.1 单分量信号与多分量信号从物理学的角度看,信号可以分为单分量信号和多分量信号两类,而时-频分布的一个主要优点就是能够确定一个信号是单分量的还是多分量的。
所谓单分量信号就是在任一时间只有一个频率或一个频率窄带的信号。
一般地,单分量信号看上去只有一个山峰(如图 1.2.2),图中所示的是信号)()()(t j e t A t s ϕ=的时-频表示,在每一个时间,山峰的峰值有明显的不同。
如果它是充分局部化的,那么峰值就是瞬时频率;山峰的宽度就是瞬时带宽。
一般地,如果)(t z 是信号)(cos )()(t t a t s φ=的解析信号,)(f Z 是)(t z 对应的频谱,图1.2.2 单分量信号时-频表示及其特征则其瞬时频率定义如下:)]([arg 21)(t z dtdt f i π=(1.2.1) 与瞬时频率对偶的物理量叫做群延迟,定义如下: )]([arg 21)(f Z dtdf g πτ=(1.2.2) 而多分量信号是由两个(或多个)山峰构成, 每一个山峰都有它自己不同的瞬时频率和瞬时带宽。
(如图1.2.3所示)。
图1.2.3 多分量信号时-频表示及特征1.3.2 时-频分布定义Fourier 变换的另一种形式⎰∞∞--=dt e t s f S ft j π2)()(⎰∞∞-=dfe f S t s tf j π2)()(Cohen 指出,尽管信号)(t z 的时-频分布有许多形式,但不同的时-频分布只是体现在积分变换核的函数形式上,而对于时-频分布各种性质的要求则反映在对核函数的约束条件上,因此它可以用一个统一形式来表示,通常把它叫做Cohen 类时-频分布,连续时间信号)(t z ()(t z 为连续时间信号)(t s 的解析信号)的Cohen 类时-频分布定义为ττφτττπdudvd e v u z u z f t P vu f vt j )(2*),()21()21(),(-+-∞∞-∞∞-∞∞--+=⎰⎰⎰(1.3.1) 式中),(v τφ称为核函数。
6章现代无线通信信号处理技术解析PPT课件

• (1)地波传播——无线电波沿地球表面的传 播。
• 主要用于低频及甚低频远距离无线电导航 、标准频率和时间信号的广播、对潜通信 等业务。
• 传播特点:
• 传输损耗小、作用距离远;受电离层扰动 影响小,传播情况稳定;有较强的穿透海 水及土壤的能力;但大气噪声电平高,工 作频带窄
电磁场与电磁波—6章现代无线 通信信号处理技术
仍可保持通信。
电磁场与电磁波—6章现代无线 通信信号处理技术
• 3)流星电离余迹散射传播。利用发生在80~120km处流星电离 余迹对电波的散射作用,实现2000km内的远距离传播。常用 频段为30~70MHz。由于流星电离余迹持续时间短,但出现频 繁,可利用它建立瞬间通信,在军事上应用较多。
• (4)地-电离层波导传播。电波在以地球表面及电离层下缘为 界的地壳形空间内传播。
• 根据不同频段的电波在媒质中传播的物理过程,可将电波 传播方式分类为:
• (1)地波传播 • (2)对流层电波传播(视距、散射传播) • (3)电离层电波传播(反射、散射、流星电离余迹散射传播
)
• (4)地—电离层波导传播 • (5)外大气层及行星际空间电波传播
电磁场与电磁波—6章现代无线 通信信号处理技术
。其主要传播特点是:传播距离限于视线 距离以内,一般为10 ~50km;频率愈高受
电磁场与电磁波—6章现代无线 通信信号处理技术
•
2)散射传播。利用对流层中介质的不
均匀性对电波的散射作用,实现超视距传
播,常用频段为200MHz~5GHz。由于散射
波相当微弱,传输损耗大,需使用大功率
发射机、高灵敏度接收机及高增益天线等
短波远距离广播、通信,船岸间航海移动通信,飞机地面问
中科院课件---《现代信号处理的理论与方法》课程回顾祥解

, xk t xt k1
mkx 1, ,k1 Ext xt 1 xt k1
随机信号 x(t)的k阶累积量:
ckx 1, ,k1 cumxt, xt 1, , xt k1
矩和累积量的估计
矩的估计:
mˆ k1
累积量的估计:
谱、双谱和三谱的BBR公式:
Py
2 x
H
H
*
2 x
H 2
By 1,2 3xH 1 H 2 H * 1 2
Ty 1,2,3 4xH 1 H 2 H 3 H * 1 2 3
FIR系统辨识
n
L1
2
2
2
30 1
1
4
6
Lm
5
1
2 c3y n1, n2 3x h k h k n1 h k n2
二次叠加原理
设
z(t) c1z1(t) c2 z2 (t)
则
Pz (t,) | c1 |2 Pz1 (t,) | c2 |2 Pz2 (t,) c1c2*Pz1,z2 (t,) c1*c2Pz2,z1 (t,)
式中: Pz1 Pz2
z1(t)和z2(t)的自时频分布;
P 和 分 z1,z2
幅值和相位分别为:
at s2 t sˆ2 t
t
arctan
sˆt st
瞬时频率
❖ 瞬时频率:表征了信号在局部时间点上的瞬态频 率特性,整个持续期上的瞬时频率反映了信号频 率的时变规律。
fi
t
1
2
d dt
arg
zt
1
0 E
'(t) | x(t) |2 dt
➢ 信号的中心频率是其瞬时频率在整个时间轴上的加 权平均。
信号的处理与分析

信号的处理与分析作者:周箭宇花卉来源:《科学与财富》2015年第16期摘要:随着现代科技日新月异的进步,无线电子产品已遍布人们的日常生活,人们用手机跟远方的人进行沟通交流,或是人们使用电脑上网浏览听音乐,使用GPS导航仪找寻目的地的时候,广播发出声音,正在不断地进行发射信号与接收信号,这些信号充斥着世界的每个角落,这些信号的交互其实它的处理方法都大同小异。
信号处理的方法其实有很多种,本文将详细地进行描述。
关键词:信号;处理;分析1 信号的调制1.1进行信号调制的意义因为在某些场合,如需要对信号本身精密地测量或者我们为了满足某一方面的需求,只想获得模拟的电信号,然而这些信号本身很微弱,很容易与电噪声一起混合,对我们所需的信号或者测量信号进行调制后,就赋予了它一定的特性,便于区分出噪声信号和我们需要的信号。
另一个原因就是信号接收端距离信号发射源很远,需要将信号本身进行长距离的传输,而低频信号的信号传输过程容易受到其他低频信号的干扰而导致失真,如人说话声音的频率一般在300—700Hz,属于一种低频的信号,结合自己的日常生活想象一下,当两个人在交谈的时候只要站在二三十米的地方就听不到了,这说明低频信号在传呼过程中很容受其他低频信号影响,但是低频信号可以进行调制,就是用我们所需要的低频信号加载到一个高频的载波信号上,让低频需求信号区控制载波信号上的某一种参数比如幅度,频率,相位。
由电磁波波长*电磁波频率的公式可知,当电磁波频率越高时,电磁波波长越短,此时的电磁波由于波长短,能量大,能够远距离传输,而且抗干扰能力非常强,况且在我们的地球外有一层等离层,非常有利于短波的反射,因而原因显而易见,高频信号在传输中有着明显的优势。
1.2信号的调制方式信号的调制方法有四种。
一是调幅调,用一个低频的需求信号a去控制高频传输信号b的幅度。
他的优点是电路简洁容易设计和使用,缺点是只能控制信号强度,却无法区分电信号的正负。
第5讲 现代信号处理方法(2+2)
缺乏时频分析能力、多分辨率分析能力,难以分析非平稳信号
6
第5讲现代信号处理方法
5-1 5-2 5-3 5-4 5-5 傅里叶变换存在的问题 短时傅里叶变换 连续小波 离散小波与小波包 故障诊断中的应用
机械动态信号分析与处理
第5讲现代信号处理方法
5-2 短时傅里叶变换
FT
STFT
x( f ) x(t) e
机械动态信号分析与处理
第5讲现代信号处理方法
分析的时间位置,也即时间中心。
5-3 连续小波
函数 f (t ) 的连续小波变换定义为:
1 WT (a, b) a
x(t ) (
t b t b )dt x(t ), ( ) b是时移 a a
待分析序列 基函数
a是尺度因子
把基本小波作伸缩。 思考:时域伸缩,频域?
- 2jft
dt
x(t, f) [x(t) h(t - t' )] e-2jft dt
矩形窗
h(t )
高斯窗
h(t )
三角窗
h(t )
8
机械动态信号分析与处理
短时傅里叶变换
第5讲现代信号处理方法
非平稳信号
20Hz 80Hz 120Hz
h(t )
利用高斯窗STFT对非平稳信号进行分析
×
x(t)
X
0 a 1
35
机械动态信号分析与处理
连续小波---运算过程示意图
第5讲现代信号处理方法
(s,t)
Inner product
×
x(t)
X
50
a 1
36
现代信号处理讲义讲义
子空间:向量组 a1, ,ap 的线性组合的集合,称为 a1, ,ap 张成的空间。
p
span a1, ,a p close a1, ,a p ja j , j C
j1
信号子空间: span s1, ,sp span u1, ,up 噪声子空间: span g1, ,g p span up1, ,um
J (w) 0
w*
wopt Rxx1a(k )
又
wH opt
a(k
)
1
aH
(k
)wopt
,代入上式
aH
(k
1
)R xx1a( k
)
wopt
Rxx1a(k ) aH (k )Rxx1a(k )
最佳滤波器
由Capon提出,称为最小方差无畸变(MVDR)波束形成器
MVDR: minimum variance distortionless response
期望信号 干扰信号 加性噪声
E z(n) 2 lim 1 N z(n) 2 wH E x(n)xH (n) w
N N
n1
E sk (n) 2 wH a(k ) 2 p E si (n) 2 wH a(i ) 2 2 w 2 i 1,i k
wH a(k ) 1
(波束形成条件)
现代信号处理讲义
3.5 MUSIC方法
1. 阵列信号处理问题 2. 最优波束形成器 3. 子空间方法 4. MUSIC方法 5. 改进的MUSIC方法
3.5 MUSIC方法
MUSIC: Multiple Signal Classification 1. 阵列信号处理问题 (array signal processing)
现代信号处理
4.信号的函数表达式为:()()()()sin(2100) 1.5sin(2300)sin(2200)x t t t A t t dn t n t πππ=++++,其中,()A t 为一随时间变化的随机过程,()dn t 为经过390—410Hz 带通滤波器后的高斯白噪声,()n t 为高斯白噪声,采样频率为1kHz ,采样时间为2.048s 。
(1)利用现代信号处理的知识进行信号谱估计;(2)利用现代信号处理知识进行信号的频率提取; (3)分别利用Winner 滤波和Kalman 滤波进行去噪; (4)利用Wigner-Ville 分布分析信号的时频特性。
(1):利用现代信号处理的知识进行信号谱估计:经典谱估计中两种主要的方法为直接法和间接法,其中间接法则先根据N 个样本数据()x n 的样本自相关函数()()()1*01,01N x n R k x n k x n k M N-==+=⋅⋅⋅∑,,,(4.1)其中1M N ≤<,且()()*x x R k R k -=。
计算样本自相关函数的Fourier 变换,得到功率谱()()Mjk x x k MP R k e ωω-=-=∑(4.2)周期图方法估计的功率谱为有偏估计,可通过加窗来减少其偏差。
定义为 ()()()2101N jn x n P x n c n e NWωω--==∑ (4.3)式中()()122112N n W c n C d NNππωωπ--===∑⎰(4.4)式中,()C ω是窗函数()c n 的Fourier 变换。
功率谱估计程序为: clear clcclose all hidden sf=1000;nfft=2048; t=0:1/1000:2.047;A=normrnd(0,1,1,2048); N=wgn(1,2048,1); f1=390;f2=410;wc1=2*f1/sf; wc2=2*f2/sf; %归一化频率f0=[0 wc1-0.05 wc1 wc2 wc2+0.05 1]; B=[0 0 1 1 0 0];%设置带通和带阻 weigh=[1 1 1 ];%设置带通和带阻权重 b=remez(50,f0,B,weigh);%传函分子 D=filter(b,1,N);y=sin(2*pi*t*100)+1.5*sin(2*pi*t*300)+A.*sin(2*pi*t*200)+D+N; a(1,:)=y;a(2,:)=y.*sin(y); x=a(1,:);y=a(2,:)-a(1,:);f=0:sf/nfft:sf/2-sf/nfft;w=boxcar(nfft);%加矩形窗 z=psd(y,nfft,sf,w,nfft/2); nn=1:nfft/2;plot(f(nn),abs(z(nn))); xlabel('频率(Hz)'); ylabel('幅值'); grid on;图4.1 功率谱估计结果图(2).信号频率的提取用离散傅立叶算法离散傅立叶算法程序 clear clcclose all hidden sf=1000;nfft=2048; t=0:1/1000:2.047;A=normrnd(0,1,1,2048); N=wgn(1,2048,1); f1=390;f2=410; wc1=2*f1/sf; wc2=2*f2/sf;050100150200250300350400450500200400600800频率(Hz)幅值%归一化频率f0=[0 wc1-0.05 wc1 wc2 wc2+0.05 1];B=[0 0 1 1 0 0];%设置带通和带阻weigh=[1 1 1 ];%设置带通和带阻权重b=remez(50,f0,B,weigh);%传函分子D=filter(b,1,N);y=sin(2*pi*t*100)+1.5*sin(2*pi*t*300)+A.*sin(2*pi*t*200)+D+N; t2=(0:nfft-1)/sf;f=(0:nfft-1)*sf/nfft;y1=abs(fft(y));f=f(1:nfft/2);y1=y1(1:nfft/2);plot(t,y);title('原始信号');axis([0 2.047 -6 8]);plot(f,y1);title('fft频率提取');axis([0 500 0 1000]);xlabel('f/Hz');grid on;原信号时间(t)图4.2 原始信号时域图图4.3 信号频谱(3)分别利用Winner 滤波和Kalman 滤波进行去噪;clear all close allM=100;%维纳滤波器阶数 sf=1000;nfft=2048; L=nfft;t=0:1/1000:2.047;A=normrnd(0,1,1,2048); N=wgn(1,2048,1); f1=390;f2=410; wc1=2*f1/sf; wc2=2*f2/sf; %归一化频率f0f0=[0 wc1-0.05 wc1 wc2 wc2+0.05 1]; B=[0 0 1 1 0 0];%设置带通和带阻 weigh=[1 1 1 ];%设置带通和带阻权重 b=remez(50,f0,B,weigh);%传函分子 D=filter(b,1,N);y=sin(2*pi*t*100)+1.5*sin(2*pi*t*300)+A.*sin(2*pi*t*200)+D+N; phixx=xcorr(y,y); for i=1:M for j=1:MRxx(i,j)=phixx(i-j+L); end ends=sin(2*pi*t*100)+1.5*sin(2*pi*t*300)+A.*sin(2*pi*t*200); phixs=xcorr(y,s); for i=1:Mrxs(i)=phixs(i+L); endh1=(inv(Rxx))*rxs';2004006008001000fft 频率提取f/Hz%获得理想FIR滤波器系数h1AA=sin(2*pi*t*100)+1.5*sin(2*pi*t*300)+A.*sin(2*pi*t*200); for i=1:Mh(i)=AA(i);end%绘图比较估计滤波器与实际滤波器figurek=1:M;plot(k,h(k),'r',k,h1(k),'b');title('Ideal h(n) & Calculated h(n)');legend('Ideal h(n)',' Calculated h(n)');xlabel('n');ylabel('h(n)');%比较理想输出与实际输出v=D+N;S=conv(h,v);SI(1)=S(1);LL1=sin(2*pi*t*100)+1.5*sin(2*pi*t*300)+A.*sin(2*pi*t*200); for i=2:LSI(i)=LL1(i);endfigurek=1:L;plot(k,s(k),'r',k,SI(k),'b');title('s(n) VS. SI(n)');legend('s(n)','SI(n)',0);xlabel('n');ylabel('Ideal Output');hold onSR=conv(h1,y);figurek=1:L;plot(k,s(k),'r',k,SR(k),'b');title('s(n)VS. SR(n)');legend('s(n)去噪前','SR(n)去噪后',0);xlabel('n');ylabel('Actual Output');图4.4 Winner 滤波去噪图Kalman 滤波程序 clear; clc;Fs=1000; nfft=2048;t1=0:1/Fs:2.047;A=normrnd(0,1,1,2048); N=wgn(1,2048,2); f1=390;f2=410; wc1=2*f1/Fs; wc2=2*f2/Fs; wc2=2*f2/sf; %归一化频率f0f0=[0 wc1-0.05 wc1 wc2 wc2+0.05 1]; B=[0 0 1 1 0 0];%设置带通和带阻 weigh=[1 1 1 ];%设置带通和带阻权重 b=remez(50,f0,B,weigh);%传函分子 D=filter(b,1,N);x=sin(2*pi*t1*100)+1.5*sin(2*pi*t1*300)+A.*sin(2*pi*t1*200)+D+N; x1=sin(2*pi*t1*100)+1.5*sin(2*pi*t1*300)+A.*sin(2*pi*t1*200); a1=-1.352;a2=1.338;a3=-0.662;a4=0.240;A=[-a1 -a2 -a3 -a4;1 0 0 0;0 1 0 0;0 0 1 0];%状态转移矩阵 H=[1 0 0 0];%观测矩阵Q=[1 0 0 0;0 0 0 0;0 0 0 0;0 0 0 0];%状态噪声方差 R=1;%观测噪声方差阵X(:,1)=[x(4);x(3);x(2);x(1)];p(:,:,1)=[10 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];%一步预测误差方针 %开始滤波 for k=2:nfftp1(:,:,k)=A*p(:,:,k-1)*A'+Q;%p1(:,:,k)即是一步预测误差的自相关矩阵,它是4*4的矩阵,取不同的k 值就构成了一个三维矩阵K(:,k)=p1(:,:,k)*H'/(H*p1(:,:,k)*H'+R); %K(:,:,k)是增益矩阵,对于固定的k 值它是4*1矩阵,取不同的k 值就是三维矩阵s(n)VS. SR(n)nA c t u a l O u t p u tX(:,k)=A*X(:,k-1)+K(:,k)*[x(k)-H*A*X(:,k-1)]; %X(:,k)是估计值,4*1矩阵p(:,:,k)=p1(:,:,k)-K(:,k)*H*p1(:,:,k);%p(:,:,k)是估计误差的自相关矩阵,4*4矩阵的三维矩阵end%结束一次滤波%绘图t=1:nfft;figure(2);plot(t,x1,'k-',t,x,'r-',t,X(1,:),'b-.');title('卡曼滤波去噪')legend('真实轨迹','观测样本','估计轨迹');grid on;卡曼滤波去噪n图5 Kalman滤波去噪图(4) 利用Wigner-Ville分布分析信号的时频特性MATLAB程序clear;clc;Fs=1000;nfft=2049;t1=0:1/Fs:2.048;A=normrnd(0,1,1,2049);N=wgn(1,2049,2);f1=390;f2=410;wc1=2*f1/Fs;wc2=2*f2/Fs;%归一化频率f0f0=[0 wc1-0.05 wc1 wc2 wc2+0.05 1];B=[0 0 1 1 0 0];%设置带通或带阻,1为带通,0为带阻weigh=[1 1 1 ];%设置通带和阻带的权重b=remez(50,f0,B,weigh);%传函分子D=filter(b,1,N);x=sin(2*pi*t1*100)+1.5*sin(2*pi*t1*300)+A.*sin(2*pi*t1*200)+D+N; figure(8)tfrwv(x');xlabel('时间t');ylabel('频率f');0.50.450.40.350.30.250.20.150.10.05图6 幅频特性图。
现代测试技术 信号处理与分析-1
本数为若干个因子之积时,该序列可以分解成比较小的序
列,对这些小序列可以用较少的计算就能得到其变换,而
9
5.3.4 有限化和泄漏问题
信号有限化(即突然截断)相当于时域内采 样函数乘一矩形窗W(t)(高为1,宽为T0 ),它会 使信号的频域能量散布(泄漏)到整个频域轴上。
x (f)
x(f) xω (f-f0)
xω (f-f1)
-
1 T
1 T
f
f
f0
f1
泄漏现象示意图
10
• 解决泄漏问题的办法
增大T0(矩形窗的长度),使旁瓣向主 瓣靠近,但T0 增大要受到其它条件限 制;
2, ⋅⋅⋅, N-1) 做下式计算:
Yk
=
N −1 −
n
∑ =
0
yn
e
j( 2π N
)kn
k=0, 1, 2, ⋅⋅⋅, N-1
FFT算法:FFT是使一个序列的DFT所要求的计 算能得以加快实现的各种算法的总称,称为
快速付立叶变换。
33
FFT快速计算的原理
在计算时间上能做到大大减少的原因是:当序列的样
X(f)
栅栏效应使得频率抽样 间隔之间的频谱无法反 映出来,克服的办法是 采用频率细化技术,该
f
技术将在5.4.5中介绍。
X(f)
12
2
5.3.6 量化和量化误差
对模拟信号的连续值离散化称为量化,离散
间隔称为量化单位,量化后原先光滑的波形成为
阶梯形,相当于叠加了“毛刺”,称为量化误差。
近代信号处理机
14
——稳态信号分析——
稳态信号的特点是其频率结构不随时间变 化。稳态信号的分析方法已经很成熟。常用的 稳态信号分析方法可分为时域分析方法和频域 分析方法两大类。
