精选新版2019高考数学《导数及其应用》专题完整版考核题(含答案)
精选新版2019高考数学《导数及其应用》专题考试题(含标准答案)

2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.设a>0,b>0,e 是自然对数的底数( )A .若e a+2a=e b+3b,则a>b B .若e a+2a=e b+3b,则a<bC .若e a-2a=e b-3b,则a>b D .若e a-2a=e b-3b,则a<b (2012浙江文)二、填空题2.函数()ln f x x =的图象在点()e ,(e)f 处的切线方程是 3.函数()2x f x x e =-的单调减区间是 ▲4.已知2(),()(1),xf x xeg x x a ==-++若12,,x x R ∃∈使得21()()f x g x ≤成立,则实数a 的取值范围是 ▲5.(文科)已知存在实数a ,满足对任意的实数b ,直线y=﹣x+b 都不是曲线y=x 3﹣3ax 的切线,则实数a 的取值范围是 .6.设()2sin f x x x =-,若0()0f x '=且0(0,)x π∈,则0x =____▲____.7. 函数y =x 2(x >0)的图象在点(a k ,a k 2)处的切线与x 轴的交点的横坐标为a k +1,其中k ∈N *.若a 1=16,则a 1+a 3+a 5的值是________.8.已知存在实数a ,满足对任意的实数b ,直线y x b =-+都不是曲线33y x ax =-的切线,则实数a 的取值范围是 ▲ .9.直线b x y +=21是曲线)0(ln >=x x y 的一条切线,则实数b= ▲10.已知函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别 为,M m ,则M m -= .答案 3211.已知函数()y f x =的图象在点(1(1))M f ,处的切线方程是122y x =+,则(1)(1)f f '+=12.曲线x y ln =在点(,1)M e 处的切线的斜率是_________,切线的方程为______________.三、解答题13.已知函数2()(21)ln(21)(21)(0)f x x x a x x a =++-+->. (1)若函数()f x 在0x =处取极值,求a 的值;(2)如图,设直线1,2x y x =-=-将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数()y f x =的图象恰好位于其中一个区域内,判断其所在的区域并求对应的a 的取值范围;(3)比较23420113452012⨯⨯⨯⋅⋅⋅⨯与34520122342011⨯⨯⨯⋅⋅⋅⨯的大小,并说明理由.14.已知函数432()2f x x a x x b =+++(x R ∈),其中R b a ∈,.(Ⅰ)当103a =-时,讨论函数()f x 的单调性;(Ⅱ)若函数()f x 仅在0x =处有极值,求a 的取值范围;(Ⅲ)若对于任意的[2,2]a ∈-,不等式()1f x ≤在[1,1]-上恒成立,求b 的取值范围.(天津卷21)本小题主要考查利用导数研究函数的单调性、函数的最大值、解不等式等基础知识,考查综合分析和解决问题的能力.满分14分. (Ⅰ)15.已知函数21()kx f x x c+=+(0c >且1c ≠,k ∈R )恰有一个极大值点和一个极小值点,其中一个是x c =-.(第23题)(Ⅰ)求函数()f x 的另一个极值点;(Ⅱ)求函数()f x 的极大值M 和极小值m ,并求1M m -≥时k 的取值范围.(陕西卷21)16.已知cx bx ax x f ++=23)(在区间[0,1]上是增函数,在区间),1(),0,(+∞-∞上是减函数,又.23)21(='f (Ⅰ)求)(x f 的解析式;(Ⅱ)若在区间],0[m (m >0)上恒有)(x f ≤x 成立,求m 的取值范围. (陕西文 本小题满分12分)17.两个二次函数2()f x x bx c =++与2()2g x x x d =-++的图象有唯一的公共点(1,2)P -,(1)求,,b c d 的值;(2)设()(())()F x f x m g x '=+⋅,若()F x 在R 上是单调函数,求m 的范围,并指出是单调递增函数,还是单调递减函数。
精选最新2019高考数学《导数及其应用》专题完整题(含标准答案)

2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.函数13)(3+-=x x x f 在闭区间[-3,0]上的最大值、最小值分别是 ( )(A)1,-1 (B)1,-17 (C)3,-17 (D)9,-19(2004江苏)2.已知函数32()39f x x x x a =-+++(a 为常数),在区间[2,2]-上有最大值20,那么此函数在区间[2,2]-上的最小值为( )A . 37-B . 7-C . 5-D . 11-答案 B二、填空题3.已知定义在上偶函数且当时有则不等式解集为▲ .4.点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-5.曲线32242y x x x =--+在点(13)-,处的切线方程是 .(浙江文)6.函数f (x )=x 3–3bx +3b 在(0,1)内有极小值,则b 的取值范围是 .0<b <7.已知曲线 x e y =在点P 处的切线经过原点,则此切线的方程为8.给出下列命题:①函数)(x f y =的图象与函数3)2(+-=x f y 的图象一定不会重合; ②函数)32(log 221++-=x x y 的单调区间为),1(∞+;③ππ---=+⎰e dx e x x 1)(cos 0;④双曲线的渐近线方程是x y 43±=,则该双曲线的离心率是45. 其中正确命题的序号是 (把你认为正确命题的序号都填上).答案 ③9.若曲线 y=lnx+1的一条切线方程为 y=x+b,则b= .10.如图,函数()f x 的图象是折线段ABC ,其中A B C ,,的坐标分别为(04)(20)(6,,,,,,则((0))f f = 2 ;0(1)(1)limx f x f x∆→+∆-=∆ -2 .(用数字作答)(北京卷12) 11.若0,0a b >>,且函数32()422f x x ax bx =--+在1x =处有极值,则ab 的最大值等于_________12.下列关于函数2()(2)x f x x x e =-的判断正确的是________①()0f x >的解集是{}|02x x <<; ②(f 是极小值,f 是极大值; ③()f x 既没有最小值,也没有最大值.13.已知函数()322f x x ax bx a =+++在1x =处有极值10,则a b += .14.设函数ln ,0()21,0x x f x x x >⎧=⎨--≤⎩,D 是由x 轴和曲线()y f x =及该曲线在点(1,0)处的切线所围成的封闭区域,则2z x y =-在D 上的最大值为 .15.已知可导函数)(x f )(R x ∈的导函数)(x f '满足)(x f '>)(x f ,则不等式()(1)x ef x f e >的解集是 ▲ .16.已知曲线y=ax 2在x=1处切线的斜率是﹣4,则实数a 的值为17.定义在R 上的函数()f x ,其导函数()'fx 满足()'1f x >,且()23f =,则关于x的不等式()1f x x <+的解集为 ▲ . 18.设函数21()ln .2f x x ax bx =--若x =1是()f x 的极大值点,则实数a 的取值范围是 .19.已知三次函数32()()32a b f x x x cx d a b =+++<在R 上单调递增,则a b c b a++-的最小 值为 ▲ . 关键字:多项式函数;含多参;已知单调性;求最值;整体换元;分式函数三、解答题20.函数()()1ln f x x a x a R =--∈(I )求函数()f x 的极值(II )若0a <,对于任意(]12,0,1x x ∈,且12x x ≠,都有()()1212114f x f x x x -<-,求实数a 的取值范围(16分)21.设函数x x f ln )(=,xb ax x g +=)(,函数f (x )的图像与x 轴的交点也在函数g (x )的图像上,且在此点处)(x f 与)(x g 有公切线. ⑵求a ,b 的值; ⑵ 设0x >,试比较)(x f 与)(x g 的大小.(本题满分16分)22.设函数ax x x f -=ln )(,ax e x g x-=)(,其中a 为实数.(1)若)(x f 在),1(+∞上是单调减函数,且)(x g 在),1(+∞上有最小值,求a 的取值范围;(2)若)(x g 在),1(+∞-上是单调增函数,试求)(x f 的零点个数,并证明你的结论.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分16分.23.已知函数2()sin cos f x x x x x =++.(Ⅰ)若曲线()y f x =在点(,())a f a )处与直线y b =相切,求a 与b 的值.(Ⅱ)若曲线()y f x =与直线y b = 有两个不同的交点,求b 的取值范围. (2013年高考北京卷(文))24. 已知函数3211()(1)132f x x ax a x =-+-+. (1)求()f x 的单调区间;(2)若()f x 在区间(1,4)上是减函数,求a 的取值范围.25.设函数ax x x f -=ln )(,ax e x g x-=)(,其中a 为实数.(1)若)(x f 在),1(+∞上是单调减函数,且)(x g 在),1(+∞上有最小值,求a 的取值范围;(2)若)(x g 在),1(+∞-上是单调增函数,试求)(x f 的零点个数,并证明你的结论.(本小题满分16分)26.已知函数f (x)=(m -3)x3 + 9x.(1)若函数f (x)在区间(-∞,+∞)上是单调函数,求m 的取值范围;(2)若函数f (x)在区间[1,2]上的最大值为4,求m 的值.(本小题满分16分)27.已知函数()322f x x bx cx =+++. (1)若()f x 在1x =时,有极值1-,求b 、c 的值.(2)当b 为非零实数时,()f x 是否存在与直线()210b c x y -++=平行的切线,如果存在,求出切线的方程,如果不存在,说明理由.(3)设函数()f x 的导函数为()'f x ,记函数()()'11f x x -≤≤的最大值为M ,求证32M ≥.(2010陕西省第五次适应性考试)关键字:已知极值点;求参数的值;已知切线;28.请你设计一个包装盒,如图所示,ABCD 是边长为60cm 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD 四个点重合于图中的点P ,正好形成一个正四棱柱形状的包装盒,E 、F 在AB 上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm(1)若广告商要求包装盒侧面积S (cm 2)最大,试问x (2)若广告商要求包装盒容积V (cm 3)最大,试问x 应取何值?并求出此时包装盒的高与底面边长的比值。
最新2019高考数学《导数及其应用》专题考核题(含参考答案)
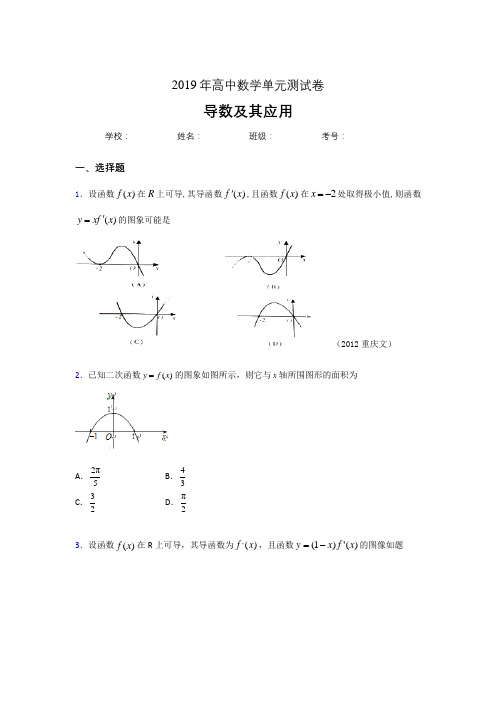
2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.设函数()f x 在R 上可导,其导函数()f x ',且函数()f x 在2x =-处取得极小值,则函数()y xf x '=的图象可能是(2012重庆文)2.已知二次函数()y f x =的图象如图所示,则它与x 轴所围图形的面积为A .2π5 B .43C .32D .π23.设函数()f x 在R 上可导,其导函数为,()f x ,且函数)(')1(x f x y -=的图像如题(8)图所示,则下列结论中一定成立的是(A )函数()f x 有极大值(2)f 和极小值(1)f (B )函数()f x 有极大值(2)f -和极小值(1)f (C )函数()f x 有极大值(2)f 和极小值(2)f - (D )函数()f x 有极大值(2)f -和极小值(2)f4. 设函数()f x 是R 上以5为周期的可导偶函数,则曲线()y f x =在5x = 处的切线的斜率为( ) A .15- B .0C .15D .5二、填空题5.已知三次函数3221()(41)(1527)23f x x m x m m x =--+--+在()x ∈-+,∞∞上是增函数,则m 的取值范围为.6.已知定义在R 上的函数()f x ,其导函数为()'1f x x =+,则函数()f x 的单调增区间为 ()1,-+∞7.记函数f (x )=x +1x 的导函数为f '(x ),则 f '(1)的值为 ▲ .8.设奇函数()f x 定义在(,0)(0,)ππ-U 上,其导函数为()f x ',且()02f π=,当0x π<<时, ()sin ()cos 0f x x f x x '-<,则关于x 的不等式()2()sin 6f x f x π<的解集为 ▲ .9.若直线3y x b =-+是曲线3232y x x =-+的一条切线,则实数b 的值是 ▲10.已知函数ln (),()xf x kxg x x==,若不等式()()f x g x ≥在区间(0,)+∞上恒成立,则实数k 的取值范围是 .11.若函数()4ln f x x =,点(,)P x y 在曲线'()y f x =上运动,作PM x ⊥轴,垂足为M ,则△POM (O 为坐标原点)的周长的最小值为___▲___ .12. 直线12y x b =+能作为下列函数()y f x =的切线有 ▲ .(写出所有正确....的函数的序号) ①1()f x x=②()ln f x x = ③()sin f x x = ④()x f x e =- 13.已知函数()c x x x x f +--=22123,若对任意[]2,1-∈x 都有()2c x f <,则c 的取值范围是 .[来14.不过原点的直线l 是曲线x y ln =的切线,且直线l 与x 轴、y 轴的截距之和为0,则直线l 的方程为 .15.cos y x x =在3x π=处的导数值是___________.16.已知函数32()6f x x ax x =--+在(0,1)内单调递减,则a 的取值范围为 .三、解答题17.已知函数2()ln f x a x x =-。
(完整)最新版精选2019高考数学《导数及其应用》专题完整考试题(含参考答案)

2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、填空题1.曲线32242y x x x =--+在点(13)-,处的切线方程是 . 答案 520x y +-=2.若函数f (x )=ax 4+bx 2+c 满足(1) 2f '=,则(1)f '-= . 3.函数f (x )=12x -sin x 在区间[0,π]上的最小值为 .4.已知A 、B 、C 是直线l 上的三点,向量,,OA OB OC u u u r u u u r u u u r满足()[2'(1)]ln OA f x f x OB x OC =+-⋅u u u r u u u r u u u r,则函数()y f x =的表达式为 ▲ .5.设函数()2ln f x x x =+,若曲线()y f x =在点()()1,1f 处的切线方程为y ax b =+,则a b += .6.给出下列命题:①函数)(x f y =的图象与函数3)2(+-=x f y 的图象一定不会重合; ②函数)32(log 221++-=x x y 的单调区间为),1(∞+;③ππ---=+⎰edx e x x 1)(cos 0;④双曲线的渐近线方程是x y 43±=,则该双曲线的离心率是45.其中正确命题的序号是 (把你认为正确命题的序号都填上). 答案 ③7.已知函数f(x)= ()2f π'sinx+cosx ,则()4f π= .8.函数()sin ln f x x x =+的导函数()f x '= ▲ .二、解答题9.已知函数()f x 的导函数()f x '是二次函数,且()0f x '=的两根为1±.若()f x 的极大值与极小值之和为0,(2)2f -=. (1)求函数()f x 的解析式;(2)若函数在开区间(99)m m --, 上存在最大值与最小值,求实数m 的取值范围. (3)设函数()()f x x g x =⋅,正实数a ,b ,c 满足()()()0ag b bg c cg a ==>,证明:a b c ==.10.已知函数21()2,()log 2a f x x x g x x ==-(a >0,且a ≠1),其中为常数.如果()()()h x f x g x =+ 是增函数,且()h x '存在零点(()h x '为()h x 的导函数).(Ⅰ)求a 的值;(Ⅱ)设A (x 1,y 1)、B (x 2,y 2)(x 1<x 2)是函数y =g (x )的图象上两点,21021()y y g x x x -'=-(()g'x 为()g x 的导函数),证明:102x x x <<.11.过点A (2,1)作曲线()f x =l . (Ⅰ)求切线l 的方程;(Ⅱ)求切线l ,x 轴及曲线所围成的封闭图形的面积S .12.设函数()32221f x x mx m x m =---+-(其中2m >-)的图象在2x =处的切线与直线512y x =-+平行。
精选最新版2019高考数学《导数及其应用》专题考核题(含答案)

2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、填空题1.函数y =x 3-3x 2+1的单调递减区间为 ▲ .2.若函数2()1x af x x +=+在1x =处取极值,则a =【解析】f ’(x)=222(1)()(1)x x x a x +-++f ’(1)=34a-=0 ⇒ a =33.已知定义在R 上的函数2()(3)f x x ax =-,函数()()()([0,2])g x f x f x x '=+∈,若()g x 在0x =处取得最大值,则正数a 的取值范围是 ▲ .4.若函数b bx x x f 36)(3+-=在(0,1)内有极小值,则实数b 的取值范围是 ▲ .5.设函数()2ln f x x x =+,若曲线()y f x =在点()()1,1f 处的切线方程为y ax b =+,则a b += .6.函数32)21()(+-=x x x f 的单调减区间为 ),21(+∞ .7.给出下列图象其中可能为函数f (x )=x 4+ax 3+bx 2+cx +d (a ,b ,c ,d ∈R)的图象的是_____.8. 已知函数2()xf x e ax ex =+-,a R ∈.,若曲线()y f x =在点(1,(1))f 处的切线平行于x 轴,则函数()f x 的单调区间为 .9.已知函数210()0x x f x a x ⎧+>⎪=≤ 在点(1,2)处的切线与()f x 的图像有三个公共点,则a 的取值范围是 ;10.若3()3f x ax x =-在R 上是单调函数,则a 的取值范围为_____▲ __11.曲线sin y x =在点(3π12.已知2(),()(1),x f x xe g x x a ==-++若12,,x x R ∃∈使得21()()f x g x ≤成立,则实数a 的取值范围是 ▲13.设曲线y =e ax 有点(0,1)处的切线与直线x +2y +1=0垂直,则a =_________. 2 14.已知f (x )=x 3,g (x )=-x 2+x -29a ,若存在x 0∈[-1,a3](a >0),使得f (x 0)<g (x 0),则实数a 的取值范围是 ▲ .(0,-3+212)15.设直线y=a分别与曲线2y x =和xy e =交于点M 、N ,则当线段MN 取得最小值时a的值为___________.16.曲线()ln f x x x =在点1x =处的切线方程为 ▲ .二、解答题17.已知函数()2ln f x ax x =-(a 为常数).(1)当12a =时,求()f x 的单调递减区间; (2)若0a <,且对任意的[]1,x e ∈,()()2f x a x >-恒成立,求实数a 的取值范围.试题18.已知函数),0,(ln )1(2)(2>∈∈--=*a R a N k x a x x f k 且 (1)讨论函数)(x f 的单调性;(2)若2014=k 时,关于x 的方程ax x f 2)(=有唯一解,求a 的值; (3)当2013=k 时,证明: 对一切),0(+∞∈x ,都有)21(2)(2exe a x xf x ->-成立.(本小题满分16分)19.如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线AE 排水管1l ,在路南侧沿直线CF 排水管2l ,现要在矩形区域ABCD 内沿直线EF 将1l 与2l 接通.已知AB = 60 m ,BC = 80 m ,公路两侧排管费用为每米1万元,穿过公路的EF 部分的排管费用为每米2万元,设EF 与AB 所成角为α.矩形区域ABCD 内的排管费用为W . (1)求W 关于α的函数关系式;(2)求W 的最小值及相应的角α.(本小题满分14分)l 2l 120.已知函数)ln()(m x e x f x +-=.(Ⅰ)设0x =是()f x 的极值点,求m ,并讨论()f x 的单调性;(Ⅱ)当2m ≤时,证明()0f x >.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))21.已知函数2()ln (,)f x ax bx x a b R =+-∈ (Ⅰ)设0a ≥,求)(x f 的单调区间(Ⅱ) 设0a >,且对于任意0x >,()(1)f x f ≥.试比较ln a 与2b -的大小(2013年高考山东卷(文))22.设函数b ax x x f n n ++-=3)((*N n ∈,R b a ∈,)。
精编新版2019高考数学《导数及其应用》专题考核题(含参考答案)

2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.设函数)(x f 的定义域为R ,)0(00≠x x 是)(x f 的极大值点,以下结论一定正确的是( )A .)()(,0x f x f R x ≤∈∀B .0x -是)(x f -的极小值点C .0x -是)(x f -的极小值点D .0x -是)(x f --的极小值点(2013年高考福建卷(文))2.32()32f x x x =-+在区间[]1,1-上的最大值是( )(A)-2 (B)0 (C)2 (D)4(2006浙江文)3.若曲线12y x -=在点12,a a -⎛⎫ ⎪⎝⎭处的切线与两个坐标围成的三角形的面积为18,则a =( )(A )64 (B )32 (C )16 (D )8 (2010全国2理10)4.设函数()x f x xe =,则( )A. 1x =为()f x 的极大值点B.1x =为()f x 的极小值点C. 1x =-为()f x 的极大值点D. 1x =-为()f x 的极小值点[学5.已知函数y =f (x ),y =g (x )的导函数的图象如下图,那么y =f (x ),y =g (x )的图象可能是( )(2008福建理)二、填空题6.函数x x y cos 2+=在(0,)π上的单调递减区间为 .7.已知函数23221()1(0)()31,()2(3)1(0)x x f x x x g x x x ⎧-+>⎪=-+=⎨⎪-++≤⎩,则方程[()]0g f x a -=(a 为正实数)的实数根最多有 ▲ 个8. 如果函数y =f (x )的导函数的图象如图所示,给出下列判断:①函数y =f (x )在区间⎝⎛⎭⎫-3,-12内单调递增; ②函数y =f (x )在区间⎝⎛⎭⎫-12,3内单调递减; ③函数y =f (x )在区间(4,5)内单调递增;④当x =2时,函数y =f (x )有极小值;⑤当x =-12时,函数y =f (x )有极大值. 则上述判断中正确的是__________.9.曲线x x y C In :=在点)e e,(M 处的切线方程为___________.10.函数ln(1)y x x =-+的单调递减区间为 ▲ .11. 曲边梯形由曲线,0,1,5x y e y x x ====所围成,过曲线,[1,5]x y e x =∈上一点P 作切线,使得此切线从曲边梯形上切出一个面积最大的普通梯形,这时点P 的坐标是____________.12.设函数21()ln(1)3,[,](0)2x f x x e x x t t t =+-+∈->,若函数()f x 的最大值是M ,最小值是m ,则M m +=______13.给出下列图象其中可能为函数f (x )=x 4+ax 3+bx 2+cx +d (a ,b ,c ,d ∈R)的图象的是_____.14.设曲线axy e =在点(01),处的切线与直线210x y ++=垂直,则a = .2(全国二14) 三、解答题15.设常数0a ≥,函数2()ln 2ln 1f x x x a x =-+-((0,))x ∈+∞.(Ⅰ)令()()g x xf x '=(0)x >,求()g x 的最小值,并比较()g x 的最小值与零的大小; (Ⅱ)求证:()f x 在(0,)+∞上是增函数;(Ⅲ)求证:当1x >时,恒有2ln 2ln 1x x a x >-+.16.已知函数.32)(2x x e x f x -+=(I )求曲线))1(,1()(f x f y 在点=处的切线方程;(Ⅱ)求证函数)(x f 在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x 的近似值(误差不超过0.2);(参考数据e ≈2.7,e ≈1.6,e 0.3≈1.3) (III )当,1)3(25)(,212恒成立的不等式若关于时+-+≥≥x a x x f x x 试求实数a 的取值范围。
精选新版2019高考数学《导数及其应用》专题测试版题(含参考答案)
2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.已知某生产厂家的年利润y (单位:万元)与年产量x (单位:万件)的函数关系式为31812343y x x =-+-,则使该生产厂家获得最大年利润的年产量为( )(A )13万件 (B)11万件 (C) 9万件 (D)7万件(2010山东文8) 2.22(1cos )x dx ππ-+⎰等于( )A .πB . 2C . π-2D . π+2(2009福建理)3.已知函数)(()(x f x f x y ''=其中的图象如右图所示))(的导函数是函数x f ,下面四个图象中)(x f y =的图象大致是( )(2005江西理)4.曲线12e x y =在点2(4e ),处的切线与坐标轴所围三角形的面积为______________二、填空题5.函数2()l n 1f x a x x=++在[,)e +∞上是减函数,则实数a 的取值范围是 .6. 曲线y=2lnx 在点(e,2)处的切线与y 轴交点的坐标为_________.7.已知点(1,1)A 和点(1,3)B --在曲线C :32(,,y ax bx d a b d =++为常数)上,若曲线在点A 和点B 处的切线互相平行,则32a b d ++= ▲ .【考点定位】此题考查的是曲线的切线问题和导数的运算,紧扣切点是本题的关键。
8.已知3()f x x ax =-在区间[1,+∞)上是单调增函数,则实数a 的最大值是 。
9.已知函数3221()(21)13f x x x a x a a =++-+-+,若()0f x '=在(1,3]上有解,则实数a 的取值范围为 ▲ .10.已知函数1)2(33)(23++++=x a ax x x f 既有极大值又有极小值,则实数a 的取值范围是 .三、解答题11.已知函数2ln )(x x a x f += (a 为实常数) .(1)当4-=a 时,求函数)(x f 在[]1,e 上的最大值及相应的x 值; (2)当[]e x ,1∈时,讨论方程()0=x f 根的个数.(3)若0>a ,且对任意的[]12,1,x x e ∈,都有()()212111x x x f x f -≤-,求实数a 的取值范围.(本小题满分16分)12.函数32()2()f x x ax x x R =+++∈(1)若()(,)f x x ∈-∞+∞在上是增函数,求实数a 的取值范围;(2)0a =时,曲线3()2f x xx =++的切线斜率的取值范围记为集合A ,曲线3()2f x x x =++上不同两点1122(,),(,)P x y Q x y ,连线斜率取值范围记为集合B ,你认为集合A 、B 之间有怎样的关系,(真子集、相等)并证明你的结论;(3)3=a 时,32()2f x x ax x =+++的导函数()f x '是二次函数,()f x '的图象具有对称性,由此你能判断三次函数32()2f x x ax x =+++的图象是否具有某种对称性,试证明你的结论.13.已知函数32()33(0)3x f x x x a a =-++-<. (1)如果1a =-,点P 为曲线()y f x =上一个动点,求以P 为切点的切线斜率取最大值时的切线方程;(2)若[3,]x a a ∈时,()0f x ≥恒成立,求实数a 的取值范围.14.设函数32()2338f x x ax bx c =+++在1x =及2x =时取得极值. (Ⅰ)求a 、b 的值;(Ⅱ)若对于任意的[03]x ∈,,都有2()f x c <成立,求c 的取值范围. 关键字:多项式;已知极值;求参数的值;恒成立问题;15.已知直线k x y +=2被抛物线y x 42=截得的弦长AB 为20,O 为坐标原点. (1)求实数k 的值;(2)问点C 位于抛物线弧AOB 上何处时,△ABC 面积最大?16.已知函数1)(+=x ax ϕ,a 为正常数. ⑴若)(ln )(x x x f ϕ+=,且a 29=,求函数)(x f 的单调增区间;⑵在⑴中当0=a 时,函数)(x f y =的图象上任意不同的两点()11,y x A ,()22,y x B ,线段AB 的中点为),(00y x C ,记直线AB 的斜率为k ,试证明:)(0x f k '>.⑶若)(ln )(x x x g ϕ+=,且对任意的(]2,0,21∈x x ,21x x ≠,都有1)()(1212-<--x x x g x g ,求a 的取值范围.17.已知函数1()ln 1af x x ax x-=-+-()a R ∈. (1)1=a 时,求函数)(x f 的极大值。
最新版精选2019高考数学《导数及其应用》专题完整版考核题(含答案)
2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、填空题1.曲线12ex y =在点2(4e ),处的切线与坐标轴所围三角形的面积为2. 曲线21()cos 3f x x x =-在0x =处的切线的斜率为 ▲ . 3. 过坐标原点作函数ln y x =图像的切线,则切线斜率为 .4. 设()ln ,()()()f x x g x f x f x '==+.则()g x 的单调减区间为 ▲ . 5.函数=x3-15x2-33x +6的单调减区间为________6.函数2|32|y x x =-+的极大值为 .7. 已知函数()a f x x =在1x =处的导数为2-,则实数a 的值是 ▲ .8.已知()f x 是定义在(,0)(0,)ππ- 上的奇函数,其导函数为'()f x ,当0x π<<时,'()cos sin ()0f x x x f x -> ,则不等式()cos 0f x x > 的解集为______________9.设0a >,函数32()91f x x ax x =+--,若曲线()y f x =的切线中斜率最小的切线与直线120x y -=垂直,则实数a 的值为 .10.已知曲线 xe y =在点P 处的切线经过原点,则此切线的方程为二、解答题11.已知函数2()()xf x ax x e =+,其中e是自然数的底数,a R ∈。
(1) 当0a <时,解不等式()0f x >;(2) 若()f x 在[-1,1]上是单调增函数,求a 的取值范围;(3) 当0a =时,求整数k的所有值,使方程()2f x x =+在[k,k+1]上有解。
12.已知函数2()ln (,0)2x f x a x a R x =+∈>.(1)若()0f x >对0x ∀>恒成立,求常数a 的取值范围;(2)设1a e <≤,()()(1)H x f x a x =-+的两个极值点为,()αβαβ<,是证明:对12,[,]x x αβ∀∈,恒有12|()()|1H x H x -<.13.已知函数1()ln(1),01xf x ax x x-=++≥+,其中0a > ()I 若()f x 在x=1处取得极值,求a 的值; ()II 求()f x 的单调区间;(Ⅲ)若()f x 的最小值为1,求a 的取值范围。
精选新版2019高考数学《导数及其应用》专题完整题(含标准答案)
2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.函数y =x cos x -sin x 在下面哪个区间内是增函数( )(A )(2π,23π) (B )(π,2π) (C )(23π,25π) (D )(2π,3π)(2004全国2理)(10) 2.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =________二、填空题3.用铁皮制作一个无盖的圆锥形容器,已知该圆锥的高为10cm ,体积为31000cm 3π.则制作该容器需要铁皮面积为 2cm 取1.414,π取3.14,结果保留整数)4. 点P 在曲线73+-=x x y 上移动,设点P 处切线的倾斜角为α,则角α的取值范围是 .5.若曲线()2f x ax Inx =+存在垂直于y 轴的切线,则实数a 的取值范围是 . 解析6.已知函数2()ln f x a x x =-,若对区间(0,1)内任取两个实数p ,q ,且p ≠q ,不等式(1)(1)1f p f q p q+-+>-恒成立,则实数a 的取值范围是 . 7.曲线C :()sin e 2x f x x =++在x=0处的切线方程为8.已知函数32()(6)1f x x ax a x =++++有三个单调区间,则实数a 的取值范围是______________9.曲线42x y =上一点到直线1--=x y 的距离的最小值为 . 答案 162510.曲线13++=x x y 在点(1,3)处的切线方程是 。
11.对函数()sin f x x x =,现有下列命题:①函数()f x 是偶函数②函数()f x 的最小正周期是2π③点(,0)π是函数()f x 的图象的一个对称中学; ④函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递增,在区间,02π⎡⎤-⎢⎥⎣⎦上单调递减。
精选最新2019高考数学《导数及其应用》专题完整考试题(含标准答案)
2019年高中数学单元测试卷 导数及其应用 学校:__________ 姓名:__________ 班级:__________ 考号:__________ 一、选择题 1.已知直线y=x+1与曲线yln()xa相切,则α的值为( B ) (A)1 (B)2 (C) -1 (D)-2 (2009全国卷Ⅰ理) 二、填空题 2. 设()fx是定义在R上的可导函数,且满足()()0fxxfx,则不等式
2(1)1(1)fxxfx的解集为 .
3. 已知函数()yfx在定义域[4,6]内可导,其图象如图,记()yfx的导函数为'()yfx,则不等式'()0fx的解集为_____ 411[4,][1,]33 ___.
4.函数f (x)=12x-sinx在区间[0,π]上的最小值是 . 5.已知函数223)(abxaxxxf在1x处有极值为10,则)2(f= 6.已知函数)(xf是定义在正实数集上的单调函数,且满足对任意x > 0,都有[()ln]1effxx,则(1)f= ________.
7.若函数f(x)= x3+ax-2在区间(1,+∞)上是增函数,则实数a的取值范围为__________ 8.已知直线2xy与曲线axyln相切,则a的值为 ▲ . 9.已知函数()sinfxxx,则()fx ▲ . 10.已知定义在R上的函数()yfx的导函数为()fx,且满足()()fxfx,则不等式24(23)(1)xfxef≥解集为 .
11.曲线xyln在点(,1)Me处的切线的斜率是_________,切线的方程为______________.
12.设函数)(xf在定义域内可导,)(xfy的图象如右图所示,则导函数y=f (x)可能为 .
13.若函数f(x)=ax3-x2+ x-5在R上单调递增,则a的范围是 . 三、解答题 14.设函数axxxfln)(,axexgx)(,其中a为实数. (1)若)(xf在),1(上是单调减函数,且)(xg在),1(上有最小值,求a的取值范围; (2)若)(xg在),1(上是单调增函数,试求)(xf的零点个数,并证明你的结论.(本小题满分16分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年高中数学单元测试卷导数及其应用学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.已知函数y =x ²-3x+c 的图像与x 恰有两个公共点,则c = (A )-2或2 (B )-9或3 (C )-1或1 (D )-3或12.(2009湖南卷文)若函数()y f x =的导函数...在区间[,]a b 上是增函数, 则函数()y f x =在区间[,]a b 上的图象可能是【 A 】A .B .C .D .二、填空题3.若对任意的x D ∈,均有()()()12f x f x f x ≤≤成立,则称函数()f x 为函数()1f x 到函数()2f x 在区间D 上的“折中函数”.已知函数()()()11,0,f x k x g x =--= ()()1ln h x x x =+,且()f x 是()g x 到()h x 在区间[]1,2e 上的“折中函数”,则实数k 的取值为 ▲4. 若存在实常数k 和b ,使函数()f x 和()g x 对其定义域上的任意实数x 恒有:()f x kx b ≥+和()g x kx b ≤+,则称直线:l y kx b =+为()f x 和()g x 的“隔离直线”.已知2(),()2ln h x x x e x ϕ==,则可推知(),()h x x ϕ的“隔离直线”方程为 ▲ . 5.在实数集R 上定义运算:()().(),xx y x a y a f x e ⊗=-=为实常数若(),xg x ex -=+令()()().F x f x g x =⊗若函数))0(,0()(F P x F 在点处的切线斜率为1,则此切线方程为ab ab ao b a b________________.6.当h 无限趋近于0时,22(2)2h h+-无限趋近于常数A ,则常数A 的值为 。
17.函数()(1)sin π1(13)f x x x x =---<<的所有零点之和为 ▲ .8.已知存在实数a ,满足对任意的实数b ,直线y x b =-+都不是曲线33y x ax =-的切线,则实数a 的取值范围是 ▲ .9.在平面直角坐标系xOy 中,点P 是第一象限内曲线y = - x 3 + 1上的一个动点,以点P 为切点作切线与两个坐标轴交于A ,B 两点,则△AOB 的面积的最小值为 .10.函数()f x 在定义域R 内可导,若()(2)f x f x =-,且当(,1)x ∈-∞时,(1)'()0x f x -<,设1(0),(),(3)2a fb fc f ===,则,,a b c 的大小关系为c <a<b.提示:依题意得,当1x <时,有'()0f x >,()f x 为增函数; 又(3)(1)f f =-,且11012-<<<,因此有1(1)(0)()2f f f -<<, 即有1(3)(0)()2f f f <<,c a b <<. 11.点()00,y x P 是曲线C :xy 1=(x >0)上的一个动点,曲线C 在点P 处的切线与x 轴、y 周分别交与B A ,两点,点O 是坐标原点。
给出三个命题:①PB PA =;②OAB ∆的面积为定值;③ 曲线C 上存在两点N M ,,使得OMN ∆为等腰直角三角形。
其中真命题的个数是 。
12.已知定义在上偶函数且当时有则不等式解集为▲ .13.已知函数)(ln )(R a ax x x f ∈-=(1)若1=a ,求函数)(x f 的单调区间(2)当0>a 时,求函数)(x f 在]2,1[上的最大14.已知函数()c x x x x f +--=22123,若对任意[]2,1-∈x 都有()2c x f <,则c 的取值范围是 .[来15.设()sin (,)44f x x x x ππ⎡⎤=+∈-⎢⎥⎣⎦, ()f x 的最大值为 。
16.如果质点A 的位移S 与时间t 满足方程32S t =(位移单位:米,时间单位:秒),则质点在3t =时的瞬时速度为 ▲ 米/秒.17.由曲线2613y x x =-+与直线3y x =+所围成的封闭区域的面积为 .三、解答题18.已知关于的方程两根为,试求的极值。
19.某商场从生产厂家以每件20元购进一批商品。
若该商品零售价定为P 元,则销售量Q (单位:件)与零售价P (单位:元)有如下关系:Q=8300-170P-P 2,问该商品零售价定为多少时毛利润L 最大,并求出最大毛利润。
(毛利润=销售收入-进货支出)(本题满分15分)20.已知2x =是函数2()ln 12f x a x x x =+-的一个极值点. (Ⅰ)求实数a 的值;(Ⅱ)求函数()f x 的单调区间. (13分)21.已知函数()f x 的导函数为'()f x ,且满足2'()32(1)f x x xf =+. (1)求'(1)f 的值;(2)求函数()y f x =在点(1,(1))f 处的切线方程.22.已知函数32()f x ax x ax =+-,x R ∈,a R ∈.(1) 当0a <时,若函数()f x 在区间(1,2)上是单调增函数,试求a 的取值范围; (2) 当0a >时,直接写出(不需给出演算步骤)函数()()ln f x g x x x =- (12x >)的单调增区间;(3) 如果存在实数(,1]a ∈-∞-,使函数()()'()h x f x f x =+,[1,]x b ∈-(1b >-) 在1x =- 处取得最小值,试求实数b 的最大值. (本小题满分16分) 23.已知函数f (x )=e x+ax 2-ex ,a ∈R.(Ⅰ)若曲线y=f (x )在点(1,f (1))处的切线平行于x 轴,求函数f (x )的单调区间;(Ⅱ)试确定a 的取值范围,使得曲线y=f (x )上存在唯一的点P ,曲线在该点处的切线与曲线只有一个公共点P. 【2012高考真题福建理20】(本小题满分14分)24.已知函数()f x 的导函数()f x '是二次函数,且()0f x '=的两根为1±.若()f x 的极大值与极小值之和为0,(2)2f -=. (1)求函数()f x 的解析式;(2)若函数在开区间(99)m m --, 上存在最大值与最小值,求实数m 的取值范围. (3)设函数()()f x x g x =⋅,正实数a ,b ,c 满足()()()0ag b bg c cg a ==>,证明:a b c ==.25.已知函数()1ax x ϕ=+,a 为正常数. (1)若()ln ()f x x x ϕ=+,且92a =,求函数()f x 的单调增区间;(2)若()|l n |g x x x ϕ=+,且对任意12,(0,2]x x ∈,12x x ≠,都有2121()()1g x g x x x -<--,求a 的的取值范围.26.已知函数()322f x x bx cx =+++.(1)若()f x 在1x =时,有极值1-,求b 、c 的值.(2)当b 为非零实数时,()f x 是否存在与直线()210b c x y -++=平行的切线,如果存在,求出切线的方程,如果不存在,说明理由.(3)设函数()f x 的导函数为()'f x ,记函数()()'11f x x -≤≤的最大值为M ,求证32M ≥.(2010陕西省第五次适应性考试)关键字:已知极值点;求参数的值;已知切线;27.已知函数222121451()ln ,()ln ,()2,6392f x ax x f x x x x f x x ax a R =+=++=+∈ (1)求证:函数()f x 在点(,())e f e 处的切线横过定点,并求出定点的坐标; (2)若2()()f x f x <在区间(1,)+∞上恒成立,求a 的取值范围; (3)当23a =时,求证:在区间(1,)+∞上,满足12()()()f x g x f x <<恒成立的函数()g x 有无穷多个。
28.已知函数f (x )=ln x +1-xax ,其中a 为大于零的常数.(1)若函数f (x )在区间[1,+∞)内不是单调函数,求a 的取值范围; (2)求函数f (x )在区间[e ,e 2]上的最小值.29.某种产品每件成本为6元,每件售价为x 元(x >6),年销量为u 万件,若已知u-8585与2)421(-x 成正比,且售价为10元时,年销量为28万件.(1)求年销售利润y 关于x 的函数关系式;(2)求售价为多少时,年利润最大,并求出最大年利润.30.设函数1()(01)ln f x x x x x=>≠且 (Ⅰ)求函数()f x 的单调区间;(Ⅱ)已知12axx >对任意(0,1)x ∈成立,求实数a 的取值范围。
(安徽卷20).解 (1) '22ln 1(),ln x f x x x +=-若 '()0,f x = 则 1x e= 列表如下(2) 在 12axx > 两边取对数, 得1ln 2ln a x x>,由于01,x <<所以 1ln 2ln a x x>(1) 由(1)的结果可知,当(0,1)x ∈时, 1()()f x f e e≤=-, 为使(1)式对所有(0,1)x ∈成立,当且仅当ln 2ae >-,即ln 2a e >-。
