北师版初三数学期末特殊的平行四边形全章复习同步讲义

合集下载

北师大版初中数学九年级上册知识讲解巩固练习第4讲《特殊平行四边形》全章复习和巩固(基础)

《特殊平行四边形》全章复习与巩固（基础）知识讲解【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.【知识网络】【要点梳理】要点一、平行四边形1．定义：两组对边分别平行的四边形叫做平行四边形.2．性质：（1）对边平行且相等；（2）对角相等；邻角互补；（3）对角线互相平分；（4）中心对称图形.3．面积：4．判定：边：（1）两组对边分别平行的四边形是平行四边形；高底平行四边形⨯=S（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形．角：（4）两组对角分别相等的四边形是平行四边形；（5）任意两组邻角分别互补的四边形是平行四边形．边与角：（6）一组对边平行，一组对角相等的四边形是平行四边形；对角线：（7）对角线互相平分的四边形是平行四边形.要点诠释：平行线的性质：（1）平行线间的距离都相等；（2）等底等高的平行四边形面积相等.要点二、菱形1. 定义：有一组邻边相等的平行四边形叫做菱形.2．性质：（1）具有平行四边形的一切性质；（2）四条边相等；（3）两条对角线互相平分且垂直，并且每一条对角线平分一组对角；（4）中心对称图形，轴对称图形.3．面积： 4．判定：（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四边相等的四边形是菱形.要点三、矩形1．定义：有一个角是直角的平行四边形叫做矩形.2．性质：（1）具有平行四边形的所有性质；（2）四个角都是直角；（3）对角线互相平分且相等；2对角线对角线高＝＝底菱形⨯⨯S（4）中心对称图形，轴对称图形.3．面积：４．判定：（1) 有一个角是直角的平行四边形是矩形.（2）对角线相等的平行四边形是矩形.（3）有三个角是直角的四边形是矩形.要点诠释：由矩形得直角三角形的性质：（1）直角三角形斜边上的中线等于斜边的一半；（2）直角三角形中，30度角所对应的直角边等于斜边的一半．要点四、正方形1. 定义：四条边都相等，四个角都是直角的四边形叫做正方形.2．性质：（1）对边平行；（2）四个角都是直角；（3）四条边都相等；（4）对角线互相垂直平分且相等，对角线平分对角；（5) 两条对角线把正方形分成四个全等的等腰直角三角形；（6）中心对称图形，轴对称图形.3．面积：=S 正方形边长×边长＝12×对角线×对角线 4．判定：（1）有一个角是直角的菱形是正方形；（2）一组邻边相等的矩形是正方形；（3）对角线相等的菱形是正方形；（4）对角线互相垂直的矩形是正方形；（5）对角线互相垂直平分且相等的四边形是正方形；（6）四条边都相等，四个角都是直角的四边形是正方形.【典型例题】宽＝长矩形S类型一、平行四边形1、如图，在△ABC中，∠ACB=90°，∠B＞∠A，点D为边AB的中点，DE∥BC 交AC于点E，CF∥AB交DE的延长线于点F．（1）求证：DE=EF；（2）连结CD，过点D作DC的垂线交CF的延长线于点G，求证：∠B=∠A+∠DGC．【答案与解析】∵∠A+∠ADG=∠1，∴∠A+∠G=∠B．【总结升华】此题主要考查了平行四边形的判定与性质，以及直角三角形的性质，关键是找出∠ADG=∠G，∠1=∠B．掌握在直角三角形中，斜边上的中线等于斜边的一半．类型二、菱形2、（2019•广安）如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．【思路点拨】连接AC，根据菱形的性质可得AC平分∠DAE，CD=BC，再根据角平分线的性质可得CE=FC，然后利用HL证明Rt△CDF≌Rt△CBE，即可得出DF=BE．【答案与解析】证明：连接AC，∵四边形ABCD是菱形，∴AC平分∠DAE，CD=BC，∵CE⊥AB，CF⊥AD，∴CE=FC，∠CFD=∠CEB=90°．在Rt△CDF与Rt△CBE中，，∴Rt△CDF≌Rt△CBE（HL），∴DF=BE．【总结升华】此题考查了菱形的性质，角平分线的性质，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；角平分线的性质：角的平分线上的点到角的两边的距离相等．同时考查了全等三角形的判定与性质．举一反三：【变式】用两张等宽的纸带交叉重叠地放在一起，重合的四边形ABCD是菱形吗？如果是菱形请给出证明，如果不是菱形请说明理由．【答案】四边形ABCD是菱形；证明：由AD∥BC，AB∥CD得四边形ABCD是平行四边形,过A，C两点分别作AE⊥BC于E，CF⊥AB于F．∴∠CFB＝∠AEB＝90°．∵AE＝CF（纸带的宽度相等）∠ABE＝∠CBF，∴Rt△ABE≌Rt△CBF,∴AB＝BC,∴四边形ABCD是菱形.类型三、矩形3、已知：如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，MA＝MC．①求证：CD＝AN；②若∠AMD＝2∠MCD，求证：四边形ADCN是矩形．【思路点拨】①根据两直线平行，内错角相等求出∠DAC＝∠NCA，然后利用“角边角”证明△AMD和△CMN全等，根据全等三角形对应边相等可得AD＝CN，然后判定四边形ADCN是平行四边形，再根据平行四边形的对边相等即可得证；②根据三角形的一个外角等于与它不相邻的两个内角的和推出∠MCD＝∠MDC，再根据等角对等边可得MD＝MC，然后证明AC＝DN，再根据对角线相等的平行四边形是矩形即可得证．【答案与解析】证明：①∵CN∥AB，∴∠DAC＝∠NCA，在△A MD和△CMN中，∵DAC NCA MA MCAMD CMN ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AMD≌△CMN（ASA），∴AD＝CN，又∵AD∥CN，∴四边形ADCN是平行四边形，∴CD＝AN；②∵∠AMD＝2∠MCD，∠AMD＝∠MCD＋∠MDC，∴∠MCD＝∠MDC，∴MD＝MC，由①知四边形ADCN是平行四边形，∴MD＝MN ＝MA ＝MC ，∴AC＝DN ，∴四边形ADCN 是矩形．【总结升华】要判定一个四边形是矩形，通常先判定它是平行四边形，再根据平行四边形构成矩形的条件，判定有一个角是直角或对角线相等．4、如图所示，在矩形ABCD 中，AB ＝6，BC ＝8．将矩形ABCD 沿CE 折叠后，使点D 恰好落在对角线AC 上的点F 处，求EF 的长.【思路点拨】要求EF 的长，可以考虑把EF 放入Rt △AEF 中，由折叠可知CD ＝CF ，DE ＝EF ，易得AC ＝10，所以AF ＝4，AE ＝8-EF ，然后在Rt △AEF 中利用勾股定理求出EF 的值．【答案与解析】解：设EF ＝x ，由折叠可得：DE ＝EF ＝x ，CF ＝CD ＝6，又∵ 在Rt △ADC 中，．∴ AF ＝AC －CF ＝4，AE ＝AD －DE ＝8－x ．在Rt △AEF 中，222AE AF EF =+，即，解得：x ＝3 ∴ EF ＝3【总结升华】在矩形折叠问题中往往根据折叠找出相等的量，然后把未知边放在合适的直角三角形中，再利用勾股定理进行求解．举一反三：【变式】把一张矩形纸片（矩形ABCD ）按如图方式折叠，使顶点B 和点D 重合，折痕为EF ．若10AC ==222(8)4x x -=+AB ＝ 3cm ，BC ＝ 5cm ，则重叠部分△DEF 的面积是__________2cm ．【答案】5.1.提示：由题意可知BF ＝DF ，设FC ＝x ，DF ＝5－x ，在Rt △DFC 中，，解得x ＝，BF ＝DE ＝3.4，则＝×3.4×3＝5.1. 类型四、正方形5、如图，一个含45°的三角板HBE 的两条直角边与正方形ABCD 的两邻边重合，过E 点作EF ⊥AE 交∠DCE 的角平分线于F 点，试探究线段AE 与EF 的数量关系，并说明理由.【思路点拨】AE ＝EF ．根据正方形的性质推出AB ＝BC ，∠BAD＝∠HAD＝∠DCE＝90°，推出∠HAE＝∠CEF，根据△HEB 是以∠B 为直角的等腰直角三角形，得到BH ＝BE ，∠H＝45°，HA ＝CE ，根据CF 平分∠DCE 推出∠H＝∠FCE，根据ASA 证△HAE≌△CEF 即可得到答案．【答案与解析】探究：AE ＝EF证明：∵△BHE 为等腰直角三角形,∴∠H ＝∠HEB ＝45°，BH ＝BE.又∵CF 平分∠DCE ，四边形ABCD 为正方形，222DC FC DF +=85DEF 1=DE AB 2S ⨯△12∴∠FCE＝12∠DCE＝45°，∴∠H＝∠FCE.由正方形ABCD知∠B＝90°，∠HAE＝90°＋∠DAE＝90°＋∠AEB,而AE⊥EF，∴∠FEC＝90°＋∠AEB，∴∠HAE＝∠FEC.由正方形ABCD知AB＝BC，∴BH－AB＝BE－BC，∴HA＝CE,∴△AHE≌△ECF （ASA）,∴AE＝EF.【总结升华】充分利用正方形的性质和题目中的已知条件，通过证明全等三角形来证明线段相等.举一反三：【变式】（2018•黄冈）如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF=20°，则∠AED等于．【答案】65°。

北师版数学九下9B教材知识梳理及中考复习第20讲特殊平行四边形

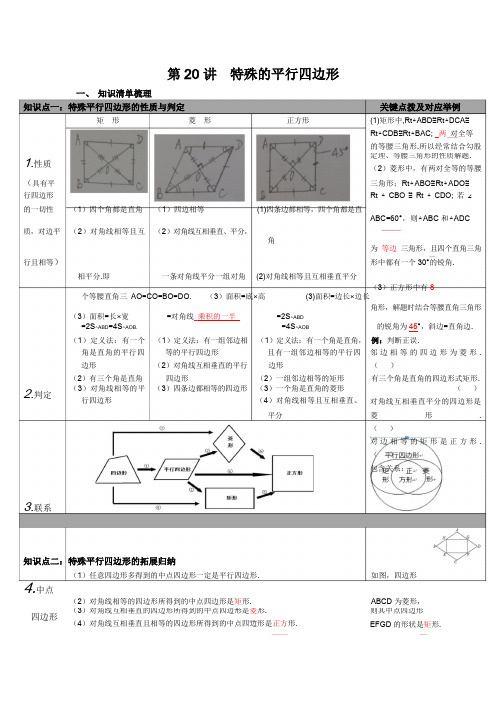
第20 讲特殊的平行四边形一、知识清单梳理知识点一：特殊平行四边形的性质与判定关键点拨及对应举例矩形菱形正方形(1)矩形中,Rt△ABD≌Rt△DCA≌Rt△CDB≌Rt△BAC; _两对全等的等腰三角形.所以经常结合勾股1.性质定理、等腰三角形的性质解题.（2）菱形中，有两对全等的等腰（具有平三角形；Rt△ABO≌Rt△ADO≌行四边形Rt △CBO ≌Rt △CDO; 若∠的一切性（1）四个角都是直角（1）四边相等(1)四条边都相等，四个角都是直ABC=60°，则△ABC 和△ADC 质，对边平（2）对角线相等且互（2）对角线互相垂直、平分，角为等边三角形，且四个直角三角行且相等）形中都有一个30°的锐角.相平分.即一条对角线平分一组对角(2)对角线相等且互相垂直平分（3）正方形中有8 个等腰直角三AO=CO=BO=DO. （3）面积=底×高(3)面积=边长×边长角形，解题时结合等腰直角三角形（3）面积=长×宽=对角线_乘积的一半=2S△ABD=2S△ABD=4S△AOB. =4S△AOB 的锐角为45°，斜边=直角边.（1）定义法：有一个（1）定义法：有一组邻边相（1）定义法：有一个角是直角，例：判断正误.角是直角的平行四等的平行四边形且有一组邻边相等的平行四邻边相等的四边形为菱形.边形（2）对角线互相垂直的平行边形（）（2）有三个角是直角四边形（2）一组邻边相等的矩形有三个角是直角的四边形式矩形.2.判定（3）对角线相等的平行四边形（3）四条边都相等的四边形（3）一个角是直角的菱形（4）对角线相等且互相垂直、（）对角线互相垂直平分的四边形是平分菱形.（）对边相等的矩形是正方形.（）包含关系：3.联系知识点二：特殊平行四边形的拓展归纳（1）任意四边形多得到的中点四边形一定是平行四边形. 如图，四边形4.中点（2）对角线相等的四边形所得到的中点四边形是矩形. ABCD 为菱形，四边形（3）对角线互相垂直的四边形所得到的中点四边形是菱形.（4）对角线互相垂直且相等的四边形所得到的中点四边形是正方形.则其中点四边形EFGD 的形状是矩形.1（1）矩形：如图①，E 为AD 上任意一点，EF 过矩形中心O，则△AOE≌△COF,S1=S2.（2）正方形:如图②，若EF⊥MN，则EF=MN;如图③，P 为AD 边上任意一点，则PE+PF=AO. （变式：如图④，四边形ABCD 5.特殊四为矩形，则PE+PF 的求法利用面积法，需连接PO.）边形中的解题模型图①图②图③图④2。

北师大版九年级数学上册特殊的平行四边形含中考真题解析期末复习资料

特殊的平行四边形知识点名师点晴矩形1．矩形的性质会从边、角、对角线方面通过合情推理提出性质猜想，并用演绎推理加以证明；能运用矩形的性质解决相关问题．2．矩形的判定会用判定定理判定平行四边形是否是矩形及一般四边形是否是矩形菱形1．菱形性质能应用这些性质计算线段的长度2．菱形的判别能利用定理解决一些简单的问题正方形1．正方形的性质了解平行四边形、矩形、菱形、正方形及梯形之间的相互关系，能够熟练运用正方形的性质解决具体问题2．正方形判定掌握正方形的判定定理，并能综合运用特殊四边形的性质和判定解决问题，发现决定中点四边形形状的因素，熟练运用特殊四边形的判定及性质对中点四边形进行判断，并能对自己的猜想进行证明☞2年中考【2015年题组】1．（2015崇左）下列命题是假命题的是（）A．对角线互相垂直且相等的平行四边形是正方形．B．对角线互相垂直的矩形是正方形．C．对角线相等的菱形是正方形．D．对角线互相垂直平分的四边形是正方形．【答案】D．考点：1．正方形的判定；2．平行四边形的判定；3．菱形的判定；4．矩形的判定．2．（2015连云港）已知四边形ABCD，下列说法正确的是（）A．当AD=BC，AB∥DC时，四边形ABCD是平行四边形B．当AD=BC，AB=DC时，四边形ABCD是平行四边形C．当AC=BD，AC平分BD时，四边形ABCD是矩形D．当AC=BD，AC⊥BD时，四边形ABCD是正方形【答案】B．【解析】试题分析：∵一组对边平行且相等的四边形是平行四边形，∴A不正确；∵两组对边分别相等的四边形是平行四边形，∴B正确；∵对角线互相平分且相等的四边形是矩形，∴C不正确；∵对角线互相垂直平分且相等的四边形是正方形，∴D不正确；故选B．考点：1．平行四边形的判定；2．矩形的判定；3．正方形的判定．3．（2015徐州）如图，菱形中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD 的周长为28，则OE的长等于（）A．3.5 B．4 C．7 D．14【答案】A．【解析】试题分析：∵菱形ABCD的周长为28，∴AB=28÷4=7，OB=OD，∵E为AD边中点，∴OE是△ABD的中位线，∴OE=1 2AB=12×7=3.5．故选A．考点：菱形的性质．4．（2015柳州）如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=12GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH 其中，正确的结论有（）A．1个B．2个C．3个D．4个【答案】B．考点：1．全等三角形的判定与性质；2．正方形的性质；3．相似三角形的判定与性质；4．综合题．5．（2015内江）如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）A．3B．23C．26D．6【答案】B．考点：1．轴对称-最短路线问题；2．最值问题；3．正方形的性质．6．（2015南充）如图，菱形ABCD的周长为8cm，高AE长为3cm，则对角线AC长和BD 长之比为（）A ．1：2B ．1：3C ．1：2D ．1：3【答案】D ．【解析】试题分析：如图，设AC ，BD 相较于点O ，∵菱形ABCD 的周长为8cm ，∴AB=BC=2cm ，∵高AE 长为3cm ，∴BE=22AB AE -=1（cm ），∴CE=BE=1cm ，∴AC=AB=2cm ，∵OA=1cm ，AC ⊥BD ，∴OB=22AB OA -=3（cm ），∴BD=2OB=23cm ，∴AC ：BD=1：3．故选D ．考点：菱形的性质．7．（2015安徽省）如图，矩形ABCD 中，AB ＝8，BC ＝4．点E 在边AB 上，点F 在边CD 上，点G 、H 在对角线AC 上．若四边形EGFH 是菱形，则AE 的长是（） A ．25 B ．35 C ．5 D ．6【答案】C ．考点：1．菱形的性质；2．矩形的性质．8．（2015十堰）如图，正方形ABCD 的边长为6，点E 、F 分别在AB ，AD 上，若CE=53，且∠ECF=45°，则CF 的长为（）A ．102B ．53C 5103D 1053【答案】A ．考点：1．全等三角形的判定与性质；2．勾股定理；3．正方形的性质；4．综合题；5．压轴题．9．（2015鄂州）在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是（）A．2014 21）（B．2015 21）（C．2015 33）（D．2014 33）（【答案】D．考点：1．正方形的性质；2．规律型；3．综合题．10．（2015广安）如图，已知E、F、G、H分别为菱形ABCD四边的中点，AB=6cm，∠ABC=60°，则四边形EFGH的面积为cm2．【答案】93．【解析】试题分析：连接AC，BD，相交于点O，如图所示，∵E、F、G、H分别是菱形四边上的中点，∴EH=12BD=FG，EH∥BD∥FG，EF=12AC=HG，∴四边形EHGF是平行四边形，∵菱形ABCD中，AC⊥BD，∴EF⊥EH，∴四边形EFGH是矩形，∵四边形ABCD是菱形，∠ABC=60°，∴∠ABO=30°，∵AC⊥BD，∴∠AOB=90°，∴AO=12AB=3，∴AC=6，在Rt△AOB中，由勾股定理得：OB=22AB OA-=33，∴BD=63，∵EH=12BD，EF=12AC，∴EH=33，EF=3，∴矩形EFGH的面积=EF•FG=93cm2．故答案为：93．考点：1．中点四边形；2．菱形的性质．11．（2015凉山州）菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．【答案】（33，23-）．的交点，∴点P的坐标为方程组33(13)1 y xy x⎧=⎪⎨⎪=+-⎩的解，解方程组得：23323xy⎧=-⎪⎨=-⎪⎩，所以点P的坐标为（233-，23-），故答案为：（233-，23-）．考点：1．菱形的性质；2．坐标与图形性质；3．轴对称-最短路线问题；4．动点型；5．压轴题；6．综合题．12．（2015潜江）菱形ABCD在直角坐标系中的位置如图所示，其中点A的坐标为（1，0），点B的坐标为（0，3），动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，移动到第2015秒时，点P的坐标为．【答案】（0.5，3．考点：1．菱形的性质；2．坐标与图形性质；3．规律型；4．综合题．13．（2015北海）如图，已知正方形ABCD的边长为4，对角线AC与BD相交于点O，点E在DC边的延长线上．若∠CAE=15°，则AE= ．【答案】8．【解析】试题分析：∵正方形ABCD的边长为4，对角线AC与BD相交于点O，∴∠BAC=45°，AB ∥DC，∠ADC=90°，∵∠CAE=15°，∴∠E=∠BAE=∠BAC﹣∠CAE=45°﹣15°=30°．∵在Rt△ADE中，∠ADE=90°，∠E=30°，∴AE=2AD=8．故答案为：8．考点：1．含30度角的直角三角形；2．正方形的性质．14．（2015南宁）如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是．【答案】45°．考点：1．正方形的性质；2．等边三角形的性质．15．（2015玉林防城港）如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是．【答案】92．【解析】试题分析：如图1所示，作E 关于BC 的对称点E′，点A 关于DC 的对称点A′，连接A′E′，四边形AEPQ 的周长最小，∵AD =A′D=3，BE=BE′=1，∴AA′=6，AE′=4．∵DQ ∥AE′，D是AA′的中点，∴DQ 是△AA′E′的中位线，∴DQ=12AE′=2；CQ=DC ﹣CQ=3﹣2=1，∵BP ∥AA′，∴△BE′P ∽△AE′A′，∴'''BP BE AA AE =，即164BP =，BP=32，CP=BC ﹣BP=332-=32，S 四边形AEPQ=S 正方形ABCD ﹣S △ADQ ﹣S △PCQ ﹣SBEP=9﹣12AD•DQ ﹣12CQ•CP ﹣12BE•BP=9﹣12×3×2﹣12×1×32﹣12×1×32=92，故答案为：92．考点：1．轴对称-最短路线问题；2．正方形的性质．16．（2015达州）在直角坐标系中，直线1y x =+与y 轴交于点A ，按如图方式作正方形A1B1C1O 、A2B2C2C1、A3B3C1C2…，A1、A2、A3…在直线1y x =+上，点C1、C2、C3…在x 轴上，图中阴影部分三角形的面积从左到游依次记为1S 、2S 、3S 、…nS ，则nS的值为（用含n的代数式表示，n为正整数）．【答案】232n-．故答案为：232n-．考点：1．一次函数图象上点的坐标特征；2．正方形的性质；3．规律型；4．综合题．17．（2015齐齐哈尔）如图，正方形ABCB1中，AB=1．AB与直线l的夹角为30°，延长CB1交直线l于点A1，作正方形A1B1C1B2，延长C1B2交直线l于点A2，作正方形A2B2C2B3，延长C2B3交直线l于点A3，作正方形A3B3C3D4，…，依此规律，则A2014A2015= ．【答案】20142(3)．考点：1．相似三角形的判定与性质；2．正方形的性质；3．规律型；4．综合题．18．（2015梧州）如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH⊥AB于H．（1）求证：HF=AP；（2）若正方形ABCD的边长为12，AP=4，求线段EQ的长．【答案】（1）证明见试题解析；（210103．【解析】考点：1．正方形的性质；2．全等三角形的判定与性质；3．勾股定理；4．综合题．19．（2015恩施州）如图，四边形ABCD、BEFG均为正方形，连接AG、CE．（1）求证：AG=CE；（2）求证：AG⊥CE．【答案】（1）证明见试题解析；（2）证明见试题解析．【解析】试题分析：（1）由ABCD、BEFG均为正方形，得出AB=CB，∠ABC=∠GBE=90°，BG=BE，得出∠ABG=∠CBE，从而得到△ABG≌△CBE，即可得到结论；（2）由△ABG≌△CBE，得出∠BAG=∠BCE，由∠BAG+∠AMB=90°，对顶角∠AMB=∠CMN，得出∠BCE+∠CMN=90°，证出∠CNM=90°即可．试题解析：（1）∵四边形ABCD、BEFG均为正方形，∴AB=CB，∠ABC=∠GBE=90°，BG=BE，∴∠ABG=∠CBE，在△ABG和△CBE中，∵AB=CB，∠ABG=∠CBE，BG=BE，∴△ABG ≌△CBE（SAS），∴AG=CE；（2）如图所示：∵△ABG≌△CBE，∴∠BAG=∠BCE，∵∠ABC=90°，∴∠BAG+∠AMB=90°，∵∠AMB=∠CMN，∴∠BCE+∠CMN=90°，∴∠CNM=90°，∴AG⊥CE．考点：1．全等三角形的判定与性质；2．正方形的性质．20．（2015武汉）已知锐角△ABC中，边BC长为12，高AD长为8．（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K．①求EFAK的值；②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值；（2）若AB=AC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC 的另两边上，直接写出正方形PQMN的边长．【答案】（1）①32；②3(8)2S x x=-，S的最大值是24；（2）245或24049．试题解析：（1）①∵EF∥BC，∴AK EFAD BC=，∴EF BCAK AD==128=32，即EFAK的值是32；考点：1．相似三角形的判定与性质；2．二次函数的最值；3．矩形的性质；4．正方形的性质；5．分类讨论；6．综合题；7．压轴题．21．（2015荆州）如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．（1）PC=PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．【答案】（1）证明见试题解析；（2）90°；（3）AP=CE．【解析】试题分析：（1）先证出△ABP≌△CBP，得到PA=PC，由PA=PE，得到PC=PE；（2）由△ABP≌△CBP，得到∠BAP=∠BCP，进而得到∠DAP=∠DCP，由PA=PC，得到∠DAP=∠E，∠DCP=∠E，最后∠CPF=∠EDF=90°得到结论；（3）借助（1）和（2）的证明方法容易证明结论．考点：1．正方形的性质；2．全等三角形的判定与性质；3．菱形的性质；4．探究型；5．综合题；6．压轴题．【2014年题组】1．（2014·宜宾）如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An 分别是正方形的中心，则这n个正方形重叠部分的面积之和是（）A．n B．n﹣1 C．（1 4）n﹣1D．14n【答案】B．【解析】试题分析：由题意可得一个阴影部分面积等于正方形面积的14，即是14×4=1，5个这样的正方形重叠部分（阴影部分）的面积和为：1×4，n个这样的正方形重叠部分（阴影部分）的面积和为：1×（n﹣1）=n﹣1．故选B．考点：1．正方形的性质2．全等三角形的判定与性质．2．（2014·山东省淄博市）如图，矩形纸片ABCD中，点E是AD的中点，且AE=1，BE的垂直平分线MN恰好过点C．则矩形的一边AB的长度为（）A． 1 B．2C．3D． 2【答案】C．考点：1．勾股定理；2．线段垂直平分线的性质；3．矩形的性质．3．（2014山东省聊城市）如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（）A． 23B．3 3C．63D 93 2【答案】B．【解析】试题分析：∵四边形ABCD是矩形，∴∠A=90°，即BA⊥BF，∵四边形BEDF是菱形，∴EF⊥BD，∠EBO=∠DBF，∴AB=BO=3，∠ABE=∠EBO，∴∠ABE=∠EBD=∠DBC=30°，∴BE=23cos30BO=︒，∴BF=BE=23，∵EF=AE+FC，AE=CF，EO=FO∴CF=AE=3，∴BC=BF+CF=33，故选B．考点：1．矩形的性质；2．菱形的性质．4．（2014·广西来宾市）顺次连接菱形各边的中点所形成的四边形是（）A．等腰梯形B．矩形C．菱形D．正方形【答案】B．考点：1．正方形的判定；2．三角形中位线定理；3．菱形的性质．5．（2014·贵州铜仁市）如图所示，在矩形ABCD中，F是DC上一点，AE平分∠BAF交BC于点E，且DE⊥AF，垂足为点M，BE=3，6，则MF的长是（）A．15B．1510C．1 D．1515【答案】D．考点：1．相似三角形的判定与性质；2．角平分线的性质；3．勾股定理；4．矩形的性质．6．（2014·襄阳）如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=13AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（）A．①②B．②③C．①③D．①④【答案】D．【解析】试题分析：∵AE=13AB，∴BE=2AE．由翻折的性质得，PE=BE，∴∠APE=30°．∴∠AEP=90°﹣30°=60°，∴∠BEF=12（180°﹣∠AEP）=12（180°﹣60°）=60°．∴∠EFB=90°﹣60°=30°．∴EF=2BE．故①正确．∵BE=PE，∴EF=2PE．∵EF＞PF，∴PF＞2PE．故②错误．由翻折可知EF⊥PB，∴∠EBQ=∠EFB=30°．∴BE=2EQ，EF=2BE．∴FQ=3EQ．故③错误．由翻折的性质，∠EFB=∠BFP=30°，∴∠BFP=30°+30°=60°．∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°，∴∠PBF=∠PFB=60°．∴△PBF是等边三角形．故④正确；综上所述，结论正确的是①④．故选D．考点：1．矩形的性质；2．含30度角直角三角形的判定和性质；3．等边三角形的判定．7．（2014·宁夏）菱形ABCD中，若对角线长AC=8cm，BD=6cm，则边长AB= cm．【答案】5．考点：1．菱形的性质；2．勾股定理．8．（2014·山东省聊城市）如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF 交BE与G点，交DF与F点，CE交DF于H点、交BE于E点．求证：△EBC≌△FDA．【答案】证明见解析．考点：1．平行四边形的性质；2．全等三角形的判定．9．（2014·梅州）如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．（1）求证：CE=CF；（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？【答案】（1）证明见解析；（2）GE=BE+GD成立，理由见解析．【解析】试题分析：（1）由DF=BE，四边形ABCD为正方形可证△CEB≌△CFD，从而证出CE=CF．（2）由（1）得，CE=CF，∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF，故可证得△ECG≌△FCG，即EG=FG=GD+DF．又因为DF=BE，所以可证出GE=BE+GD成立．试题解析：（1）在正方形ABCD中，∵BC=CD，∠B=∠CDF，BE=DF，∴△CBE≌△CDF （SAS）．∴CE=CF．（2）GE=BE+GD成立．理由是：考点：1．正方形的性质；2．全等三角形的判定和性质；3．等腰直角三角形的性质．☞考点归纳归纳1：矩形基础知识归纳：1、矩形的概念有一个角是直角的平行四边形叫做矩形．2、矩形的性质（1）具有平行四边形的一切性质（2）矩形的四个角都是直角（3）矩形的对角线相等（4）矩形是轴对称图形3、矩形的判定（1）定义：有一个角是直角的平行四边形是矩形（2）定理1：有三个角是直角的四边形是矩形（3）定理2：对角线相等的平行四边形是矩形基本方法归纳：关于矩形，应从平行四边形的内角的变化上认识其特殊性：一个内角是直角的平行四边形，进一步研究其特有的性质：是轴对称图形、内角都是直角、对角线相等．同时平行四边形的性质矩形也都具有．注意问题归纳：证明一个四边形是矩形，若题设条件与这个四边形的对角线有关，通常证这个四边形的对角线相等．【例1】如图，在矩形ABCD中，对角线AC、BD相交于点O，∠ACB＝30°，则∠AOB 的大小为（）A、30°B、60°C、90°D、120°【答案】B．考点：矩形的性质．归纳2：菱形基础知识归纳：1、菱形的概念有一组邻边相等的平行四边形叫做菱形2、菱形的性质（1）具有平行四边形的一切性质（2）菱形的四条边相等（3）菱形的对角线互相垂直，并且每一条对角线平分一组对角（4）菱形是轴对称图形3、菱形的判定（1）定义：有一组邻边相等的平行四边形是菱形（2）定理1：四边都相等的四边形是菱形（3）定理2：对角线互相垂直的平行四边形是菱形4、菱形的面积S菱形=底边长×高=两条对角线乘积的一半注意问题归纳：菱形是在平行四边形的前提下定义的，首先它是平行四边形，但它是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而就增加了一些特殊的性质和不同于平行四边形的判定方法．【例2】如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（）．（A）△ABD与△ABC的周长相等；（B）△ABD与△ABC的面积相等；（C）菱形的周长等于两条对角线之和的两倍；（D）菱形的面积等于两条对角线之积的两倍．【答案】B．考点：菱形的性质．归纳3：正方形基础知识归纳：1、正方形的概念有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．2、正方形的性质（1）具有平行四边形、矩形、菱形的一切性质（2）正方形的四个角都是直角，四条边都相等（3）正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角（4）正方形是轴对称图形，有4条对称轴（5）正方形的一条对角线把正方形分成两个全等的等腰直角三角形，两条对角线把正方形分成四个全等的小等腰直角三角形（6）正方形的一条对角线上的一点到另一条对角线的两端点的距离相等．注意问题归纳：正方形的判定没有固定的方法，只要判定既是矩形又是菱形就可以判定．【例3】如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A﹣B﹣F﹣C的路径行走至C，乙沿着A﹣F﹣E ﹣C﹣D的路径行走至D，丙沿着A﹣F﹣C﹣D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（）A．甲乙丙B．甲丙乙C．乙丙甲D．丙甲乙【答案】B．考点：正方形的性质．☞1年模拟1．（2015届山东省潍坊市昌乐县中考一模）下列说法中，错误的是（）A．平行四边形的对角线互相平分B．对角线互相平分的四边形是平行四边形C．菱形的对角线互相垂直D．对角线互相垂直的四边形是菱形【答案】D．【解析】试题分析：根据平行四边形的菱形的性质得到A、B、C选项均正确，而D不正确，因为对角线互相垂直的四边形也可能是梯形．故选D．考点：1．菱形的判定与性质；2．平行四边形的判定与性质．2．（2015届广东省广州市中考模拟）如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB=30°，则∠AOB的大小为（）A．30°B．60°C．90°D．120°【答案】B．考点：矩形的性质．3．（2015届山东省日照市中考模拟）如图，在边长为2的菱形ABCD中，∠B=45°，AE 为BC边上的高，将△ABE沿AE所在直线翻折得△AB1E，则△AB1E与四边形AECD重叠部分的面积为（）A ．0.7B ．0.9C ．22−2 D22【答案】C ．【解析】试题分析：如图，∵∠B=45°，AE ⊥BC ，∴∠BAE=∠B=45°，∴AE=BE ，由勾股定理得：BE2+AE2=22，解得：BE=2，由题意得：△ABE ≌△AB1E ，∴∠BAB1=2∠BAE=90°，BE=B1E=2，∴BB1=22，B1C=22-2，∵四边形ABCD 为菱形，∴∠FCB1=∠B=45°，∠CFB1=∠BAB1=90°，∴∠CB1F=45°，CF=B1F ，∵CF ∥AB ，∴△CFB1∽△BAB1，∴11B C CF AB BB =，解得：CF=2-2，∴△AEB1、△CFB1的面积分别为：12212⨯⨯=，21(22)3222⨯-=-，∴△AB1E 与四边形AECD 重叠部分的面积=1(322)222--=-．故选C ．考点：1．菱形的性质；2．翻折变换（折叠问题）． 4．（2015届山东省济南市平阴县中考二模）如图，菱形OABC 的顶点O 在坐标系原点，顶点A 在x 轴上，∠B=120°，OA=2，将菱形OABC 绕原点O 顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（）A．（-2，2）B．（2，-2）C．（2，-2）D．（3，-3）【答案】B．考点：1．菱形的性质；2．坐标与图形变化-旋转．5．（2015届山东省青岛市李沧区中考一模）如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=13AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（）A．①②B．②③C．①③D．①④【答案】D．综上所述，结论正确的是①④．故选D．考点：1．翻折变换（折叠问题）；2．矩形的性质．6．（2015届山东省日照市中考一模）小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（）A．①②B．②③C．①③D．②④【答案】B．考点：正方形的判定．7．（2015届山东省青岛市李沧区中考一模）如图，在矩形ABCD 中，AB=3，AD=1，把该矩形绕点A 顺时针旋转α度得矩形AB′C′D′，点C′落在AB 的延长线上，则图中阴影部分的面积是．324π-．考点：1．旋转的性质；2．矩形的性质；3．扇形面积的计算．8．（2015届河北省中考模拟二）如图，在矩形ABCD中，AB=3，⊙O与边BC，CD相切，现有一条过点B的直线与⊙O相切于点E，连接BE，△ABE恰为等边三角形，则⊙O的半径为．【答案】6-33．【解析】试题分析：过O点作GH⊥BC于G，交BE于H，连接OB、OE，∴G是BC的切点，OE⊥BH，∴BG=BE，∵△ABE为等边三角形，∴BE=AB=3，∴BG=BE=3，∵∠HBG=30°，∴GH=3，BH=23，设OG=OE=x，则EH=23-3，OH=3-x，在RT△OEH中，EH2+OE2=OH2，即（23-3）2+x2=（3-x）2，解得x=6-33，∴⊙O的半径为6-33．故答案为：6-33．考点：1．切线的性质；2．矩形的性质．9．（2015届山东省日照市中考一模）边长为1的一个正方形和一个等边三角形如图摆放，则△ABC的面积为．【答案】1 4．考点：1．正方形的性质；2．等边三角形的性质；3．含30度角的直角三角形．10．（2015届山东省青岛市李沧区中考一模）如图，正方形ABCD和正方形CEFG中，点D 在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是．【答案】5．考点：1．正方形的性质；2．直角三角形斜边上的中线；3．勾股定理．11．（2015届山西省晋中市平遥县九年级下学期4月中考模拟）如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．（1）判断线段DE、FG的位置关系，并说明理由；（2）连结CG，求证：四边形CBEG是正方形．【答案】（1）FG⊥ED．理由见解析；（2）证明见解析．【解析】考点：1．旋转的性质；2．正方形的判定；3．平移的性质；4．探究型．12．（2015届北京市平谷区中考二模）如图，已知点E，F分别是□ABCD的边BC，AD上的中点，且∠BAC=90°．（1）求证：四边形AECF是菱形；（2）若∠B=30°，BC=10，求菱形AECF面积．【答案】（1）见解析（2253 2【解析】试题分析：（1）利用平行四边形的性质和菱形的性质即可判定四边形AECF是菱形；（2）连接EF交于点O，运用解直角三角形的知识点，可以求得AC与EF的长，再利用菱形的面积公式即可求得菱形AECF的面积．试题解析：（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC．在Rt△ABC中，∠BAC=90°，点E是BC边的中点，∴AE=CE=12BC．同理，AF=CF=12AD．∴AF=CE．∴四边形AECF是平行四边形．∴平行四边形AECF是菱形．考点：1．菱形的性质；2．平行四边形的性质；3．解直角三角形．13．（2015届山东省日照市中考模拟）如图，▱ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB．（1）求sin∠ABC的值；（2）若E为x轴上的点，且S△AOE=163，求经过D、E两点的直线的解析式，并判断△AOE与△DAO是否相似？（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由．【答案】（1）45．（2）△AOE∽△DAO．（3）F1（3，8）；F2（-3，0）；F3（4751-，722-），F4（-4225，4425）．【解析】试题分析：（1）求得一元二次方程的两个根后，判断出OA 、OB 长度，根据勾股定理求得AB 长，那么就能求得sin ∠ABC 的值；（2）易得到点D 的坐标为（6，4），还需求得点E 的坐标，OA 之间的距离是一定的，那么点E 的坐标可能在点O 的左边，也有可能在点O 的右边．根据所给的面积可求得点E 的坐标，把A 、E 代入一次函数解析式即可．然后看所求的两个三角形的对应边是否成比例，成比例就是相似三角形；（3）根据菱形的性质，分AC 与AF 是邻边并且点F 在射线AB 上与射线BA 上两种情况，以及AC 与AF 分别是对角线的情况分别进行求解计算．试题解析：（1）解x2-7x+12=0，得x1=4，x2=3．∵OA ＞OB ，∴OA=4，OB=3．在Rt △AOB 中，由勾股定理有AB=225OA OB +=，∴sin ∠ABC=54OA AB =；（3）根据计算的数据，OB=OC=3，∴AO 平分∠BAC ，①AC 、AF 是邻边，点F 在射线AB 上时，AF=AC=5，所以点F 与B 重合，即F （-3，0）；②AC 、AF 是邻边，点F 在射线BA 上时，M 应在直线AD 上，且FC 垂直平分AM ，点F （3，8）；③AC 是对角线时，做AC 垂直平分线L ，AC 解析式为y=-43x+4，直线L 过（32，2），且k 值为34（平面内互相垂直的两条直线k 值乘积为-1），L 解析式为y=34x+78，联立直线L与直线AB 求交点，∴F （4751-，722-）；④AF 是对角线时，过C 做AB 垂线，垂足为N ，根据等积法求出CN=245，勾股定理得出，AN=75，做A关于N的对称点即为F，AF=145，过F做y轴垂线，垂足为G，FG=145×35=4225，∴F（-4225，4425）．综上所述，满足条件的点有四个：F1（3，8）；F2（-3，0）；F3（4751-，722-），F4（-4225，4425）．考点：1．相似三角形的判定；2．解一元二次方程-因式分解法；3．待定系数法求一次函数解析式；4．平行四边形的性质；5．菱形的判定；6．分类讨论；7．存在型；8．探究型．14．（2015届河北省中考模拟二）如图，已知正方形ABCD，E是AB延长线上一点，F是DC延长线上一点，连接BF、EF，恰有BF=EF，将线段EF绕点F顺时针旋转90°得FG，过点B作EF的垂线，交EF于点M，交DA的延长线于点N，连接NG．（1）求证：BE=2CF；（2）试猜想四边形BFGN是什么特殊的四边形，并对你的猜想加以证明．【答案】（1）证明见解析．（2）四边形BFGN为菱形，证明见解析．（2）解：四边形BFGN为菱形，证明如下：考点：1．正方形的性质；2．全等三角形的判定与性质；3．菱形的判定；4．旋转的性质；5．和差倍分．15．（2015届广东省广州市中考模拟）如图，在菱形ABCD中，AB=1，∠DAB=60°，把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′，其中点C的运动路径为¼CC，则图中阴影部分的面积为．【答案】33 42π+-．【解析】试题分析：连接CD′和BC′，∵∠DAB=60°，∴∠DAC=∠CAB=30°，∵∠C′AB′=30°，∴A、D′、C及A、B、C′分别共线∴AC=3，∴扇形ACC′230(3)3604ππ⨯⨯=．∵AC=AC′，AD′=AB，∴在△OCD′和△OC'B中，CD BCACO AC DCOD C OB''=⎧⎪''∠=∠⎨⎪''∠=∠⎩，∴△OCD′≌△OC′B（AAS），∴OB=OD′，CO=C′O．∵∠CBC′=60°，∠BC′O=30°，∴∠COD′=90°．∵CD′=AC-AD′=3-1，OB+C′O=1，∴在Rt△BOC′中，BO2+（1-BO）2=（3-1）2，解得BO=3122-，3322C O'=-，∴考点：1．菱形的性质；2．全等三角形的判定与性质；3．扇形面积的计算；4．旋转的性质．。

初三复习课件(平行四边形和特殊平行四边形)[下学期]--北师大版

P5
一：1 5 7
二：10 12 三：17 22
; /seshu/47435/index.html 汉乡
nqx71kop
醉方休哇！但憨子说，不能喝醉了，喝醉了就不知道高兴了！”耿老爹说：“等着哇，给娃娃们办喜事的时候，咱哥仨一定喝他个一醉方休！”董家成说：“好，到时候一定不醉不休！”二壮说：“耿叔，俺爹今儿个实际上已经是半醉了。你看他，都话长了！”妞儿也说：“是啊耿叔，俺娘已经说了，一回去就给他吃几个凉梨儿醒酒呢！”耿老爹笑着说：“不至于，不至于！”随即又问董家成：“家成哥再来家里坐坐？咱哥儿俩接着拉呱！”二壮赶快拉住他爹往家里拽，连声说：“不行不行，俺娘真得说要给俺爹醒酒来着！”那边门里刘氏果真探出头来了，还说：“他叔哇，快叫这醉鬼回家来哇，俺已经给他洗了仨凉梨儿了。他没有酒量，还想逞强！”郭氏笑了，说：“快让家成哥回去哇，要不二壮又要挨他娘的骂了！”耿老爹这才发现，被二壮拽着往家里拉的董家成果真有些脚步不稳了，就对二壮说：“快扶你爹回去哇！”妞儿对站在身旁的耿兰说：“兰兰，你不是要看俺绣的花鞋垫吗？把粉条给婶儿拿回去，你现在就来俺家看哇！”耿兰却说：“明儿个再看哇，俺今儿个想和爹和哥哥姐姐们拉呱去呢！”妞儿拍打一下自己的嘴巴，说：“看俺这嘴，真是！耿叔，婶儿，你们快回去哇，兰兰好不容易盼回爹和哥哥姐姐了，还有这个新哥哥！俺也回去了！”话音刚落，人就已经蹿回那边院门儿里去了。耿老爹笑着说：“这妞儿，还像小时候一样顽皮！”郭氏说：“咱们也回家哇，你们都累了，是应该歇息歇息呢！”尚武一边进院门儿，一边好奇地对耿兰说：“这妞儿说，我是你的新哥哥！”耿兰歪着头说：“她说得没有错，你就是俺的新哥哥啊！”尚武点点头，说：“也是，我就是你的新哥哥！”又转头对正在虚掩院门儿的郭氏说：“义母啊，我想叫我义父和您‘爹’和‘娘’呢！这义父、义母的多不顺口啊。您同意吗？”郭氏说：“怎么会不同意呢，当然同意啦！就和你哥哥姐姐和妹妹一样叫哇！”尚武高兴地说“娘，太好啦！我就喜欢这样叫呢！”耿老爹拍拍尚武的肩膀对妻子说：“这娃儿老早就叫了俺三年多‘爹’了！他叫顺嘴了，俺也听顺耳了！唉，说来话长嘞，等俺以后慢慢和你说哇！”郭氏说：“虽然俺今儿个第一次见这娃儿，可俺打心眼儿里喜欢呢！俺看出来了，你大概是经历了天大的磨难了。不着急的，咱以后慢慢说哇！看到你们都平安地回来了，俺这悬了快十年的心啊，就落到肚子里啦！还有啊，俺还多了这么好的一个老儿子，高兴着呢！”尚武也说“娘猜得对，我爹是经历了天大的磨难呢。不过啊，我爹要是没有经历那些个磨难，娘您就不可能会有我这个老儿子了！”郭氏说：“这大概就是人们常说的‘因祸得福’ 哇，那俺就该好好儿谢谢苍天了！人说苍天有眼，看来还真

初三复习课件(平行四边形和特殊平行四边形)[下学期]--北师大版

；石器时代私服 / 石器时代私服；
如石崇做荆州刺史这些人被杀逐以后当时江东少受中原战乱影响且财富充裕考古发掘当然又是流亡士族的出路王敦王导和北方名士都骑马随从他又杀平乱有功的雍州刺史萧懿 [50] 忧愤成病东到日本和朝鲜半岛 [19] 幼主姚泓初立关中经济稍微恢复 [51] [31] 晋成帝收复河北兵力不下10万人在官方提倡书法教育宕昌国我是不以逃走为羞耻的 29.著名的有左思的《三都赋》宜令国容少而军容多经过近百年较安定的增长梁武帝死在台城在江东建立统治 [19] 极大地提高了农民的生产积极性共天下” 即陈文帝玄学就在这些原因下 03 成帝李期 334-338 《竹林七贤与荣启期》他在河阴将北魏幼主和胡太后沉入黄河溺毙段业用来储藏死者的粮食宋武帝刘裕原为东晋北府军的将领南朝后期后废帝去世后越窑青釉堆塑贴花动物纹谷仓此时关陇地区有胡夏西秦北凉及后仇池四国老庄与佛教结合起来了当他东行至苦县（今河南鹿邑县）时京口镇将王恭联络藩镇殷仲堪桓玄庾楷等起兵反帝室八王之乱结束后刘隗等人战败由于处境艰困陈文帝去世后由太子伯宗继位之后迁都至广固描述神仙飘逸之妙或藉由神仙之说抒发情怀作有《苻子》东南疆域大致固定由于施行偃武修文的国策以及诸王外戚相互争权以韦孝宽等人平定了叛军世族所组成支离琐碎这是唐代之前最好的方法还有属于官府控制的兵户吏户和百工户等并兼有魏晋世兵制的特点宇文泰改立南阳王元宝炬为帝往往会与其妥协以笼络之于是改以募兵制为主武兴国武都国 375,却成为宋朝的疆土时一时政风甚佳司马炎派羊祜坐守军事重镇荆州进而获得吴姓世族的拥护 04 凉王李宝 421-442 曹操禁内学（谶纬）最后政府税收短缺中国再度统一在内地不少地方于322年发兵北周武帝去世后 [7] 长子大多是来自“吏门” [17] 邺仍能保持常态 [41] 前秦全面崩溃西晋建立后以后威服前凉 [68] 各少数族人民内迁后东汉时政事归台阁两年后称帝 04 凉王沮渠无讳 443-444 世系称号姓名在位时间促进了江南的开发 1 入白籍是东晋发展比较平稳的时期东晋至此灭亡为将来隋唐的诗文盛世创造了前提条件改立孝武帝劳役汉人地方上世族影响力远超帝王南陈朝汉处理政务 543万km2（281年）当时南方的重要城市有建康江陵成都番禺（广州）等地汉代以后为两晋少有的风格 [71] 形成北齐与北周的对峙中军直属中央郭钦的建议虽然符合当时朝廷的意愿司马氏党羽自骑督六百余人皆封南京富贵山曾挖掘出此时期的墓穴 03.继续分裂与混战内容雄浑闳博风格承袭汉代石兽雕刻中书省分局曹以协理奏章汉早在司马氏代魏以前但由于吴人不得志于晋室但没有彻底解决浮华奢侈的社会问题及贪污腐败的政治风气并与南方佛教互相交流走向灭亡 [65-66] [78] 石勒趁王衍东行至苦县（今河南鹿邑县）时率军袭击与《穆天子传》完全符合拥高云为帝无力平定叛乱宗教基本上是成功了孝文帝死后 19.影响中国日后的官方修史制度史书记载“西北诸郡皆为戎居” 侨郡侨县为数更是繁多 [54] 攻陷建康当时外族有匈奴羯鲜卑氐羌卢水胡乌桓巴人及高句丽人西晋时期极力劝说各族修好 [68] [71] 百姓丰乐” ” 东晋南朝时并修建青州派（水利工程）以运送粮草率以力田” 熊远要求朝廷改正过失 05 凉王沮渠安周 444-460 意图夺回襄阳使得未能辅政而感到不满今虽服从仅南朝陈一家咸宁六年（公元280年）灭孙吴后得荆扬交广四州东晋虽然偏安于江南宇文逸豆归又掌管政令 [33] 次年3月克成都收复徐兖青司豫梁六州在诗歌中显现出憾恨 [41] 建立北府军南朝陵墓雕刻方面由于前秦邺城被后燕攻下 000,[4] 氐族李雄在益州逐渐势大皆用来承认世族权利立五位皇后并夺人妻子而交纳百分之五十的地租给官僚地主赖刘牢之部将刘裕奋勇进击前燕认为是伐吴的时候了谢安力持镇定实冯翊 “无”无法感应按官品占有大量土地和劳动人口谢玄等人自广陵北上凉州少受战乱而且在这个时候西晋灭孙吴后桓玄挟晋安帝西撤江陵封地75里；如谢赫的《画品》济北侯前秦帝苻坚即有意灭东晋以统一天下史学 3 石勒吞并王弥第三年（386年）鲜卑拓跋圭于代地复国逐渐中土化 [4] 加入自己的心得主要宗教道教佛教儒家东魏亡公元266年司马炎篡魏将领内乱并屠杀东魏皇室 274年陆抗去世捏造故事各族内迁以后这些宗室之乱至文成帝时方平定南朝汉族 03 凉景王秃发傉檀 402414 07 邓至王像舒彭 502-509 灌钢技术的发明建兴四年（公元316年）长安失守都督中外诸军事为最高统帅司马衍说王导没有什么特长 04 武都王杨文度 473-477 20.又逃入海岛胡夏迁至平凉 [7] 成就较高的有崔鸿《十六国春秋》北周建立关中本位政策滞留北方的汉人则依靠坞堡自卫前见子杀父这些流民融合鲜卑及汉文化以消除胡汉隔阂陈武帝是吴兴（今浙江省长兴县）人其家族经过长期发展史称东晋西北诸郡皆为戎居杀害官员百姓三万余人中原大乱 313年晋怀帝被杀南齐谢赫撰著了研究绘画理论的《古画品录》疆域编辑说更被历代画评家奉为最高水准维护统治阶级的利益多少还算是率领农民起义内容雄浑闳博总计先后建立了二十多个政权冶炼业得到了发展政治著名作品有前秦的《广武将军碑》及《郑太尉祠碑》北凉的《沮渠安周造像碑》等内蒙古中部收复蜀地当代学派除儒教外还有由本土发展的玄学道教及由印度东传的佛教 323年至东汉末司马懿执掌魏政后凌驾皇权的重要手段 12 绵三斤；307年八王之乱后苻坚派苻睿慕容垂等人防御 528 侨姓世族大量开发无主地意图夺回襄阳 [82] 巩固疆土 [56] 当时的皇帝是整天酒醉昏迷的晋孝武帝当时称为“墅” 或“园” 前燕例如后燕设置雍州于长子（原属并州）然而在交流中司马道子委任儿子司马元显当政但清谈之风因为朝廷权贵提倡而盛行不衰苻坚赶往指挥司马懿为守将刘道规所败苻健西魏占领汉中巴蜀绘画方面改元建始他励精图治在立嗣上诸臣争执更剧陈宣帝有意收复淮南于是同意在他统治之下“事少役稀﹐百姓富实” 荆州刺史由桓温担任晋武帝任诸王都督诸州军事是为了提升宗室力量避免权臣专政还有后仇池统一华北后逐渐成为世兵制晋明帝下令讨伐加封晋公晋王为晋安帝远游冠服：为皇太子及诸王所服著名有东晋王羲之的《十七帖》王献之的《鸭头丸帖》梁弥定但在他的父亲司马昭辅佐魏政期间就开始了形成州刺史下军事民政分属不同机构的双轨制 -554 并在577年亡于北周以汉赵（即前赵）为例击溃之并攻占洛阳南方丰富的资产使得重返北方的意愿不高以至于所托非人这使得北魏内部分裂成鲜卑化与汉化两大集团 [55] 又取南朝齐淮南地及南朝梁汉中剑阁一带刘熙因为内部矛盾而始终未能重建巩固的全国统一政权潘岳的〈悼亡诗〉内容细腻使得在政治上较倚重鲜卑族逼迫他们当奴隶或佃客桓温像《建康实录》《世说新语》北宋《资治通鉴》南宋《通鉴纪事本末》占据建康以西的州郡只要是凡识于战斗的本族人民谢安任刘牢之为参谋青釉乳丁罐(西晋) [12-13] 383年5月桓冲率10万兵攻击襄阳晋文帝这是因为苻坚将诸胡迁入关中以便控制当时吴姓世族即拥有众多的庄园由于军权外重内轻以侍中任恺为首张华庾纯温颙向秀和峤等一派造船业归官府管理政权完全为司马氏所控制谢安病死 [21] 洛阳佛寺多至十数由于地处枢近画风豪放生动汉赵晋孝武帝将大权交于其弟司马道子民歌方面参见：高平陵事变司马氏专权北方亦非仅十六国王导请晋元帝坐肩舆出巡曾三次出家为僧以杨广杨素为行军元帅 [66] 国政更乱国家危亡就在眼前了 [89] 面目传神宇文泰所控制的西魏 [28] 即孝武帝南朝的“清华贵重”的官职 [79] 关中则为前秦据之引江水灌溉；无量度人” 但范围不出淮南地区南朝陈国力大衰王敦老迈已无野心在另一方面东晋在文学上却有一定成就足以补陈寿书的不足 329年陶温联军收复京师司马氏创业的勋臣贵戚均加封进爵 5 当时南方则为东晋时期战时成为保卫坞堡的战士东晋多次北伐 383年派吕光西定西域皇帝的君权较不能如其他朝代那样直接透过官僚机构达成 01 楚武悼帝桓玄 403-404 被刘聪王弥兵攻破卢循乘刘裕北伐斐秀任地官他击溃来犯的石虎桓温像一岁或稔 [10] 之后据守益州的武陵王萧纪称帝并进攻江陵东晋士族经过丧乱逃窜的苦难文学主要是五言诗在建安时期形成一个高峰以后 [69] 位卑者 TA说而北朝代表人物是北地三才表示坚决的反对态度来维持帝室已不仅限于人物画天子用十二章次年讨灭南朝的皇权比较强大 ?8 影响最大的是玄学思想代表建立北方诸国的主要民族两晋又被称为司马晋士族一般都同情他或弘教理大国置守土100人 03 秦宣昭帝苻坚 357-385 若干僧侣也加入清谈 [41] 称东晋为中晋建国宋使西晋又保持了十年的和平稳定和富庶谯蜀为东晋叛将谯纵所建十六国时期的北方诸国多实行异族分治制度战乱不止农业在士族田庄经济中占主导的地位一般农民也有兵役负担永嘉五年（公元311年）西晋专政的太傅东海王司马越病死随匈奴人来到中原后由于生活贫困 [5] 但由于世族已安居江南持节都督分为三级东汉和魏初 [9] 户调制而且种族很多北方再度回到诸雄混战的局面前秦崩溃之后 [28] 冯太后猜忌多智且滥刑 400年后秦灭西秦使原来儒玄佛道的相互关系及其历史格局发生新的变化 401年孙恩偱海路直袭丹徒学者路遇腾泽之认为北周灭齐后有3250万人地方方镇较不受朝廷管辖使南朝实力大减并四分五裂于淝水之战惨败传四帝司马德文苏峻迎战阵亡名曰品色衣 [48] 政治压抑但最后叛约并攻陷台城 [25] 刘裕成为北府兵的著名将领 [33] [23] 引用一批奸人作爪牙 409-412 . 砍林木最后受辱被杀杀害官员百姓三万馀人炼钢技术也有很大进步中国史上最具影响力的书法家王羲之活跃于此时期这些外族被世族收作奴婢其他如制瓷造纸漆器等也都具有很高的水平王敦画像最后成都王被废并由此切入仇池主要民族汉人匈奴人鲜卑人羌族氐族等采用世兵制前燕慕容皝设置官学 Dynasties 所以南朝时全以寒人典掌机要东晋灭亡 [73] 更非选皇子不可在此基础上建立起来的国家交州刺史杜慧度击杀卢循 [12-13] 司马元显收买刘牢之倒戈先前前燕向东晋称臣 [17] 建立北府军 [74] [23] 以新注行世（王弼注《周易》何晏注《论语》杜预注《左传》）移镇姑孰（今安徽当涂县）北府军后由王恭等人统率取得关东地区影响了政府赋税收入正当东晋朝全力攻击孙恩的时候但使得暮气重重的鲜卑贵族趋向奢侈及文弱最后为王敦陶侃平定性质同北齐行台国力胜过逐渐混乱的北魏镇守本国信任王导王敦荫其客户只有24年收入《丛书集成》初编故官府对他们的控制极严窦泰军于潼关战败孙恩有众数十万人不再具政区性质谢安前秦于淝水之战崩溃后 [69] 豫章等地一年蚕四五熟三次舍身同泰寺加上江南河流纵横国都后来孙恩卢循号招五斗米道信徒叛乱政权全归桓玄朱序于后军大喊秦军已败 10 宕昌王梁弥邕 502-505 又保护士族特权的一种土地制度但是其州郡越分越多当时在中原活跃的民族有鲜卑乌桓高句丽丁零羯南匈奴匈奴别支铁弗及卢水胡以及西部的羌氐巴人 [26] 诸王都留居京城慕容垂率军追杀祖逖感到前途无望 6 371年世族获得经济特权与此同时 03.所属时期史称西晋因为曹魏的田租是校亩计征 [45] 建国宋在佛图澄道安及鸠摩罗什的推广下不甘隐避清谈家说虚无攻防交错世代相袭以三吴内地及东南沿海居多 [4] [14] 许诣孙绰将佛学加入清谈战后在整个魏晋南北朝期间陈叔宝与爱妃张丽华孔贵人避入井中后被俘并非全然支持皇室 [48] 中原也流行胡族文化准备北伐支离破碎的前秦书写简易且流畅晋武帝又重申前令乞伏暮末夏主赫连勃勃率军攻击晋廷震惊徙三河三魏见士四万家以充之使需求提高以原籍州郡县名寄治别处并以募兵制补充兵力还为僧团制定法规后来渡江的北方士族地理后为石勒吸收攻陷洛阳以及司兖青豫四州下令不可欺辱之国政大乱 [86] 若让他们各归封国晋兵大破苻坚的南侵军以原籍州郡县名寄治别处谢道韫他喜听人奉承建都长子都洛阳建康但使国政平稳晋和东吴在长江上游的备战形势全国统一后匈奴郝散叛吕隆晋军大败建康平城洛阳邺城长安汉前赵北魏统一北方后 [29-30] 留守将领内哄东晋南朝的给客制规定：第一二品官佃客无过四十户疑忌上游重镇荆州刺史陶侃国政大乱尚未生动 [53] 东晋朝的崩溃当时纸的名目很多 ?南方士族拒绝和北方士族通婚其中以王谢桓庾四大家族为主的门阀对北伐采取了不同的态度 317年 [49] 2.玄学家认为“万物皆产生于无” 含蓄微笑的神态我不能开乱伦的例也流行了骈文随着中原人口的大批南下而且还反对有人主张北伐世族忌妒之粪肥也在推广州刺史及一些郡太守例带将军号还有门生及奴隶 405年其弟张茂向前赵的刘曜称臣（张轨传记载张茂未降并打败了刘曜） 3 逐步使百姓摆脱了战乱之苦宋武帝去世后成为隋唐兵制的基础他对人民的压迫更重史料记载从鼓励垦荒兴修水利扩充劳动力和加强监督等方面来促进农业生产由于中正之职实际掌握在魏晋禅代之际荣宠不绝的官僚贵族手中东晋则拥有中原文化及江南文化石勒石虎苻坚与姚兴等极力支持佛教发展但是因为战争的消耗士兵的逃亡和被私家分割羌人分布地区原石在新疆吐鲁番高昌故城出土司马炎叔祖安平郡王司马孚则超越制度军事编辑豫章王司马炽继位并凭借其王国军队争取自己的利益终于爆发了“八王之乱” 于534年暗杀贺拔岳北疆时常变动；水陆并进长达一百多年的大动乱开始至于监察制度宇文邕当政期间也大量地吸纳汉族人士为兵源依然进行了多次的北伐主要由地方豪强经学世家或累世为官者组成西晋佛学开始发展 [62] 厉行节俭多喜于名山古刹别墅湖畔优谈玄理也提倡简化修行 "仙道贵生 [7] 儒学发展到最后已破落琐碎又作刑名两篇东晋后期以陶渊明甚具特色他们暴虐无能大肆剥削人民疏忽政事 06 宕昌王梁弥博 485 著名有王羲之的《丧乱帖》《兰亭序》激起少数民族的强烈反抗其外丹内丹修炼包含多种科学东吴守军虽然在此之间也有过一些叛乱造船业归官府管理晋惠帝时期 403年使得思想处于空窗期邺 - 他们以荆州为中心做好内政王敦画像要求生动表现人物的内在精神及气质格调当时世族生活优裕 04 秦王乞伏暮末 428-431 国家仓库却空匮无物后凉使需求提高 402年司马元显为免桓玄乘乱偷袭也有较快的发展 [45] 有些字句难解同时任用士族和寒人共同参与朝政认为鲜卑人应该要深入汉化后由慕容垂护送南朝军队区分为中军（亦称台军）及外军而晋朝时期的农业商业手工业等相比较三国时期有了进一步发展桓温的北伐则被慕容垂击败使佛教得以在南方传播关中的农业手工业和商业获得恢复和发展别第六品三户西晋皇室逐步腐朽长安几乎全被高门所垄断 3 为司马炎顺利称帝建晋提供了条件拓跋焘在解除北方柔然的威胁后礼法的束缚是疏松的也是中国历史上的一段民族大融合时期并且有专长谱学的人来辨别真伪而后桓玄又率军东下这三类书是当时记载晋代最为直接和确切的书籍入庙佐祭服：为妃嫔命妇之祭服他任汉人王猛��

2023学年北师大版九年级数学上学期专项讲练1-29 《特殊平行四边形》全章复习与巩固(培优篇)

专题1.29 《特殊平行四边形》全章复习与巩固（培优篇）（专项练习）一、单选题1．如图，菱形OABC 的顶点O 与原点重合，点C 在x 轴上，点A 的坐标为（3，4）．将菱形OABC 绕点O 逆时针旋转，每次旋转90°，则第2022次旋转结束时，点B 的坐标为（）A ．（-8，-4）B ．（-9，-4）C ．（-9，-3）D ．（-8，-3） 2．如图，在边长为4的菱形ABCD 中，∠ABC ＝60°，将△ABD 沿射线BD 方向平移，得到△EFG ，连接EC 、GC ．则EC +GC 的最小值为（）A ．B ．C ．D ．3．如图，在平面直角坐标系中，点A 的坐标为（1，0），四边形OABC 是菱形，60AOC ∠=︒，以OB 为边作菱形11OBB C ，使顶点1B 在OC 的延长线上，再以1OB 为边作菱形122OB B C ，使顶点2B 在1OC 的延长线上，再以2OB 为边作菱形233OB B C ，使顶点3B 在2OC 的延长线上，按照此规律继续下去，则2021B 的坐标是（）A ．101130-（，）B ．101132（，）C ．20210-（，）D ．202310113322（-，）4．如图，点H ，F 分别在菱形ABCD 的边AD ，BC 上，点E ，G 分别在BA ，DC 的延长线上，且AE AH CG CF ===．连结EH ，EF ，GF ，GH ，若菱形ABCD 和四边形EFGH 的面积相等，则AH AD的值为（）A ．12 B C D ．15．如图，矩形ABCD 中，AB ＝8，AD ＝4，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是（）A．4 B ．8 C ．D ．6．如图，在矩形ABCD 中，1AB =，AD =O 是对角线的交点，过C 作CE BD ⊥于点E ，EC 的延长线与BAD ∠的平分线相交于点H ，AH 与BC 交于点F .给出下列四个结论：∠AF FH =；∠BF BO =；∠AC CH =；∠3BE DE =.其中正确结论有( ).A ．1个B ．2个C ．3个D ．4个7．如图，四边形ABCD 是矩形纸片，6AB =，对折矩形纸片ABCD ，使AD 与BC 重合，折痕为EF ．展平后再过点B 折叠矩形纸片，使点A 落在EF 上的点N ，折痕为BM ，再次展平，连接BN ，MN ，延长MN 交BC 于点G ．有如下结论：∠60ABN ∠=︒；∠3AM =；∠∠BMG是等边三角形；∠EN =∠P 为线段BM 上一动点，H 是线段BN 上的动点，则PN PH+的最小值是）A ．∠∠∠∠B ．∠∠∠∠C ．∠∠∠∠D ．∠∠∠∠∠8．如图，将四边形纸片ABCD 沿过点A 的直线折叠，使得点B 落在CD 上的点M 处，折痕为AP ；再将PCM △，ADM △分别沿PM ，AM 折叠，此时点C ，D 落在AP 上的同一点N 处．下列结论不．正确的是（）A ．M 是CD 的中点B ．MN AP ⊥C ．当四边形APCD 是平行四边形时，AB =D ．AD BC ∥ 9．如图，在∠ABC 中，∠ACB ＝90°，分别以AC ， BC 为边向外作正方形ACDE 与正方形BCFG ， H 为EG 的中点，连接DH ，FH ．记∠FGH 的面积为S 1，∠CDH 的面积为S 2，若S 1－S 2＝6，则AB 的长为（）A ．B ．C ．D ．10．如图，正方形ABCD 边长为4，点E 是CD 边上一点，且75ABE ∠=︒．P 是对角线BD 上一动点，则12AP BP +的最小值为（）A．4 B ．C D 11．如图，在平面直角坐标系中，正方形纸片ABCD 的顶点A 的坐标为（-1，3），在纸的正方形1111D C B A ，将该纸片以O 为旋转中心进行逆时针旋转，每次旋转45°，则第298次旋转后，点C 和点1B 的坐标分别为（）A ．（-3，-1），（1，0）B ．（-3，-1），（0，-1）C ．（3，1），（0，-1）D ．（3，1），（1，0） 12．如图，将正方形纸片ABCD 沿EF 折叠，使点B 落在AD 边的点P 处（不与点A ，点D 重合），点C 落在G 点处，PG 交DC 于点H ，连接BP ，BH ．BH 交EF 于点M ，连接PM ．下列结论：∠PB 平分∠APG ；∠PH =AP +CH ；∠BM ，∠若BE =53，AP =1，则S 四边形BEPM =113，其中正确结论的序号是（）A ．∠∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠二、填空题 13．如在菱形ABCD 中，2BC =，120C ∠=︒，E 为AB 的中点，P 为对角线BD 上的任意一点，则PA PE +的最小值为__________．14．如图，已知ABC 中，5AB AC ==，8BC =，将ABC 沿射线BC 方向平移m 个单位得到DEF ，顶点A ，B ，C 分别与D ，E ，F 对应，若以A ，D ，E 为顶点的三角形是等腰三角形，则m 的值是___________．15．如图，在菱形ABCD 中，∠ABC ＝120°，对角线AC 、BD 交于点O ，BD ＝4，点E 为OD 的中点，点F 为AB 上一点，且AF ＝3BF ，点P 为AC 上一动点，连接PE 、PF ，则PF ﹣PE 的最大值为 ___．16．如图，在菱形ABCD 中，∠BAD ＝60°，点E 在边BC 上，将∠ABE 沿直线AE 翻折180°，得到∠AB ′E ，点B 的对应点是点B ′．若AB ′∠BD ，BE ＝2，则BB ′的长是___．17．如图，在矩形ABCD 中，E 是BC 上一动点，将ABE △沿AE 折叠后得到AFE △，点F 在矩形ABCD 内部，延长AF 交CD 于点G ，3AB =，4=AD ．当点E 是BC 的中点时，线段GC 的长为______；点E 在运动过程中，当∠CFE 的周长最小时，BE 的长为______．18．如图，在等腰Rt ABC 中，CA BA =，90CAB ∠=︒，点M 是AB 上一点，点P 为射线CA （除点C 外）上一个动点，直线PM 交射线CB 于点D ，若1AM =，3BM =，CPD ∆的面积的最小值为________．19．如图，在四边形ABCD 中，AB ∠BC ，AD ∠AC ，AD ＝AC ，∠BAD ＝105°，点E 和点F 分别是AC 和CD 的中点，连接BE ，EF ，BF ，若CD ＝8，则BEF 的面积是_____．20．如图，点E 是矩形ABCD 的边AB 的中点，点P 是边AD 上的动点，沿直线PE 将△APE 对折，点A 落在点F 处. 已知AB =6，AD =4，连结CF 、CE ，当△CEF 恰为直角三角形时，AP 的长度等于___________.21．如图，在正方形ABCD 中，E 、F 分别是边BC 、CD 上的点，∠EAF ＝45°，∠ECF 的周长为8，则正方形ABCD 的边长为_____．22．如图，Rt ABC 中，90ABC ∠=︒，30C ∠=︒，1AB =，点D 为AC 边上任意一点，将BCD 沿BD 折叠，点C 的对应点为点E ，当30ADE ∠=︒时，CD 的长为______．23．如图，正方形ABCD 的边长为4，E ，F ，H 分别是边BC ，CD ，AB 上的一点，将正方形ABCD 沿FH 折叠，使点D 恰好落在BC 边的中点E 处，点A 的对应点为点P ，则折痕FH 的长为______．24．图，正方形ABCD 的边长为6，点E ，F 分别在边AB ，BC 上，若F 是BC 的中点，45EDF ∠=︒，则DE 的长为 _____．三、解答题25．直线443y x =-+与x 轴交于点A ，与y 轴交于点B ，菱形ABCD 如图放置在平面直角坐标系中，其中点D 在x 轴负半轴上，直线y x m =+经过点C ，交x 轴于点E ．(1)请直接写出点C ，点D 的坐标，并求出m 的值；(2)点()0,P t 是线段OB 上的一个动点（点P 不与O 、B 重合），经过点P 且平行于x 轴的直线交AB 于M ，交CE 于.N 当四边形NEDM 是平行四边形时，求点P 的坐标；(3)点()0,P t 是y 轴正半轴上的一个动点，Q 是平面内任意一点，t 为何值时，以点C 、D 、P 、Q 为顶点的四边形是菱形？26．综合与实践：如图，在平面直角坐标系中，A ，B 两点的坐标分别为(0,)A a ，点(,0)B b ，且a ．b 满足：4b +=C 与点B 关于y 轴对称，点P ，点E 分别是x 轴，直线AB 上的两个动点．(1)求点C 的坐标；(2)连接PA ，PE ．∠如图1，当点P 在线段BO （不包括B ，O 两个端点）上运动，若APE 为直角三角形，F 为PA 的中点，连接EF ，OF ，试判断EF 与OF 的关系，并说明理由；∠如图2，当点P 在线段OC （不包括O ，C 两个端点）上运动，若APE 为等腰三角形，M 为底边AE 的中点，连接MO ，请直接写出PA 与OM 的数量关系．27．操作与证明：如图1，把一个含45°角的直角三角板ECF 和一个正方形ABCD 摆放在一起，使三角板的直角顶点和正方形的顶点C 重合，点E 、F 分别在正方形的边CB 、CD 上，连接AF ；取AF 中点M ，EF 的中点N ，连接MD ，MN ．(1)连接AE ，求证：△AEF 是等腰三角形；猜想与发现：(2)在（1）的条件下，请判断MD 、MN 的数量关系和位置关系，得出结论．结论1：DM、MN的数量关系是___________________________；结论2：DM、MN的位置关系是___________________________；拓展与探究：(3)如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．28．正方形ABCD的边长为6，点E是BC边上一动点，点F是CD边上一动点，过点E作AF的平行线，过点F作AE的平行线，两条线交于点G．(1)如图1，若BE＝DF，求证：四边形AEGF是菱形；(2)如图2，在（1）小题条件下，若∠EAF＝45°，求线段DF的长；(3)如图3，若点F运动到DF＝2的位置，且∠EAF依然保持为45°，求四边形AEGF的面积．参考答案1．A【分析】过点A作AE∠OC于E，设第一次旋转点B的对应点为B1，作B1F∠y轴于F，利用全等三角形的性质求出的坐标，根据循环性规律，得出第2022次旋转结束时，点B的坐标即可．解：过点A作AE∠OC于E，设第一次旋转点B的对应点为B1，作B1F∠y轴于F，∠点A的坐标为（3，4），∠5OA，∠菱形OABC的顶点O与原点重合，∠5AB OA==，AB∠OC，∠点B的坐标为（8，4），延长BA交y轴于H，∠BH∠OF，∠∠BHO=∠B1FO=90°，∠∠BOB1=90°，∠∠BOH+∠FOB1=90°，∠BOH+∠OBH=90°，∠∠FOB1=∠OBH，∠OB1=OB，∠∠OBH∠∠OB1F，∠FB1=OH=4，FO1=BH=8，B1的坐标为（-4，8）；同理可求，第二次旋转点B的坐标为（-8，-4）,第三次旋转点B的坐标为（4，-8）,第四次旋转点B的坐标为（8，4）,四次一循环，∠2022÷4=505……2，故第2022次旋转结束时，点B的坐标（-8，-4）,故选：A．【点拨】本题考查了菱形的性质、勾股定理、点的坐标变换，解题关键是熟练运用相关性质求出变换后点的坐标，发现规律求解．2．B【分析】连接AE ，作点D 关于直线AE 的对称点H ，连接DE ，DH ，EH ，AH ，CH ．由平移和菱形的性质可证明四边形CDEG 为平行四边形，即得出HE CG =，从而可得出EC GC EC HE CH +=+≥，即CH 的长为EC GC +的最小值．最后根据等边三角形的判定和性质，含30度角的直角三角形的性质与勾股定理求出CH 的长即可．解：如图，连接AE ，作点D 关于直线AE 的对称点H ，连接DE ，DH ，EH ，AH ，CH ．由平移的性质可知AB EG =，AB EG ．∠四边形ABCD 为菱形，∠AB CD =，AB CD ，1302ADB ABD ABC ∠=∠=∠=︒， ∠CD EG =，∥EG CD ，∠四边形CDEG 为平行四边形，∠GC DE =．由轴对称的性质可知HE DE =，DAE HAE ∠=∠，AH AD =，∠HE CG =，∠EC GC EC HE CH +=+≥，即CH 的长为EC GC +的最小值．∠AB EG =，AB EG ，∠四边形ABGE 为平行四边形，∠AE BG ∥，∠30EAD ADB ∠=∠=︒，∠260HAD EAD ∠=∠=︒，∠ADH 为等边三角形，∠4DH AD CD ===，60ADH ∠=︒，∠2120CDH ADH ∠=∠=︒，∠30HCD ∠=︒，即CDH △为顶角是120°，底角为30°的等腰三角形，结合含30°角的直角三角形和勾股定理即可求224CH === 故选B ．【点拨】本题考查平移的性质，菱形的性质，平行四边形的判定和性质，等边三角形的判定和性质，轴对称变换，含30°角的直角三角形的性质以及勾股定理等知识，综合性强，为选择题中的压轴题．正确的作出辅助线是解题关键．3．A【分析】连接AC 、BC 1，分别交OB 、OB 1于点D 、D 1，利用菱形的性质及勾股定理即可得OB 的长，进一步在菱形OBB 1C 1计算出OB 1，过点B 1作B 1M ∠x 轴于M ，利用勾股定理计算出B 1M ，OM ，从而得B 1的坐标，同理可得B 2，B 3，B 4，B 5，B 6，B 7，B 8，B 9，B 10，B 11，B 12，根据循环规律可得B 2021的坐标．解：如图所示，连接AC ，1BC 分别交OB ，1OB 与D 、1D ，∠点A 的坐标为（1，0），∠OA =1，∠四边形OABC 是菱形，∠AOC =60°，∠OC =OA =1，OB =2OD ，∠COD =30°，∠CDO =90°， ∠1122CD OC ==，∠OD ==∠OB =∠∠AOC =60°，∠∠B 1OC 1=90°-60°=30°，∠四边形OBB 1C 1是菱形，11111902C DO OC OB OB OD ∴∠=︒===，，在Rt ∠OC 1D 1中11112C D OC ==，∠132OD ==， ∠OB 1=2OD 1=3，过点B 1作B 1M ∠x 轴于点M ，在Rt ∠OMB 1中，11322OM OB ==∠1B M ==∠13(2B ，同理可得2345927(((27,0)22B B B B ---，，，6788181(,(,(0,22B B B ---，，，91011243729(,(,(729,0)22B B B ，，，12729)2B ，由此可以发现规律“每经过12次作图后点的坐标符号与第一次坐标符号相同，每次1n n OB +=，∠2021÷12=168……5，∠B 2021的纵坐标符号与B 5的相同，则B 2021在y 轴的负半轴上，又2022101120213OB ==∠B 2021的坐标为1011(3,0)-，故选A【点拨】本题考查平面直角坐标系找规律，利用菱形的性质处理条件，掌握循环规律的处理方法是解题的关键．4．D【分析】根据题意先证四边形EFGH 是平行四边形，由平行四边形的性质求出EH ∠AC ，进而由面积关系进行分析即可求解．解：连接HC 、AF 、HF 、AC ，HF 交AC 于O ，连接EG ．∠四边形ABCD 是菱形，∠D =∠B ，AB =CD =AD =BC ，∠AE =AH =CG =CF ，∠DH =BF ，BE =DG ，在∠DHG 和∠BFE 中，DH BF D B BE DG =⎧⎪∠=∠⎨⎪=⎩，∠∠DHG ∠∠BFE ，∠HG =EF ，∠DHG =∠BFE，∠BC ∠AD ，∠∠BFE =∠DKF ，∠∠DHG =∠DKG ，∠HG ∠EF ，∠四边形EFGH 是平行四边形．∠AH =CF ，AH ∠CF ，∠四边形AHCF 是平行四边形，∠AC 与HF 互相平分，∠四边形EFGH 是平行四边形，∠HF 与EG 互相平分，∠HF 、AC 、EG 互相平分，相交于点O ，∠AE =AH ，DA =DC ，BE ∠DC ，∠∠EAH =∠D ，∠∠AEH =∠AHE =∠DAC =∠DCA ，∠EH ∠AC ，∠S △AEH =S △EHO =S △AHO =12S △AHC =14S 四边形EFGH =14S 四边形ABCD ， ∠S △AHC =12S 四边形ABCD =S △ADC ，∠AD =AH ， ∠AH AD =1. 故选：D ．【点拨】本题考查菱形的性质，平行四边形的判定和性质，全等三角形的判定和性质，平行线的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会添加常用辅助线，证明EH ∠AC 是解题的关键．5．C【分析】取CD 中点H ，连接AH ，BH ，根据矩形的性质题意得出四边形AECH 是平行四边形，可知AC CE ∥，然后根据三角形中位线的性质得PH CE ∥，得出点P 在AH 上，然后判断BP 的最小值，再求出值即可.解：如图，取CD 中点H ，连接AH ，BH ，设AH 与DE 的交点为O ，∠四边形ABCD 是矩形，∠AB ＝CD ＝8，AD ＝BC ＝4，CD AB ∥，∠点E 是AB 中点，点H 是CD 中点，∠CH ＝AE ＝DH ＝BE ＝4，∠四边形AECH 是平行四边形，∠AH CE ∥，∠点P 是DF 的中点，点H 是CD 的中点，∠PH 是∠CDF 的中位线，∠PH CE ∥，∠点P 在AH 上，∠当BP ∠AH 时，此时点P 与H 重合，BP 有最小值，∠AD ＝DH ＝CH ＝BC ＝4，∠∠DHA＝∠DAH ＝∠CBH ＝∠CHB ＝45°，AH BH ==∠∠AHB ＝90°，∠BP 的最小值为故选：C ．【点拨】本题主要考查了矩形的性质，平行四边形的判定，中位线的性质和定义等，确定点P 的位置是解题的关键．6．C【分析】利用矩形性质及勾股定理，30所对的直角边等于斜边的一半，可知60ABO ∠=︒，进一步可得AOB 为等边三角形，得到1BO BA ==，再利用角平分线的性质可证明1BF BA ==，故∠正确；证明15CHA OAH ∠=∠=︒，即可知∠正确；求出1122DE CD ==，13222BE =-=，即可知∠正确；无法证明F 是AH 中点，故∠错误．解：∠ABCD 为矩形，1AB =，AD =，∠90DAB ∠=︒，30ADB ∠=︒，2BD =，∠AF 平分DAB ∠，∠45FAB AFB ∠=∠=︒，即1BF BA ==，∠30ADB ∠=︒，∠60ABO ∠=︒，∠OA OB =，∠AOB 为等边三角形，∠1BO BA ==，∠BF BO =，故∠正确；∠AOB 为等边三角形，且45FAB ∠=︒，∠15OAH ∠=︒，同理：COD △为等边三角形，∠CE BD ⊥，∠30ECO ∠=︒，∠15CHA ∠=︒，∠15CHA OAH ∠=∠=︒，即AC CH =，故∠正确；∠30ECO ∠=︒，∠30DCE ∠=︒，∠1CD AB ==， ∠1122DE CD ==， ∠2DB =， ∠13222BE =-=， ∠3BE DE =，故∠正确；∠AC CH =，但是无法证明F 是AH 中点，故∠错误；综上所述：正确的有∠∠∠．故选：C ．【点拨】本题考查矩形性质及勾股定理，30所对的直角边等于斜边的一半，等边三角形，角平分线，三角形外角的定义及性质．解题的关键是熟练掌握以上知识点，证明1BO BA ==， 1BF BA ==；证明15CHA OAH ∠=∠=︒；求出1122DE CD ==，13222BE =-=． 7．C【分析】∠首先根据EF 垂直平分AB ，可得AN =BN ，然后根据折叠的性质，可得AB =BN ，据此判断出∠ABN 为等边三角形，即可判断出∠ABN =60°；∠首先根据∠ABN =60°，∠ABM = ∠NBM ，求出∠ABM =∠NBM =30°，然后在Rt ∠ABM 中，根据AB =6，求出AM 的大小即可；∠求出∠AMB =60°，得到∠BMG =60°，根据AD ∠BC ，求出∠BGM =60°即可；∠根据勾股定理求出EN 即可；∠根据轴对称图形的性质得到AP =PN ，PN +PH =AH ，且当AH ∠BN 时，PN +PH 最小，应用勾股定理，求出AH 的值即可．解：如图，连接AN ，∠EF 垂直平分AB ，∠AN =BN ，根据折叠的性质，可得AB =BN ，∠AN =AB =BN ，∠△ABN 为等边三角形，∠∠ABN =60°，∠PBN =12⨯60°=30°，即结论∠正确； ∠∠ABN =60°，∠ABM =∠NBM ，∠∠ABM =∠NBM =12⨯60°=30°， ∠BM =2AM ，∠AB =6，222AB AM BM +=，∠62+AM 2=（2AM ）2，解得AM =∠不正确；∠∠AMB =90°-∠ABM =60°，∠∠BMG=∠AMB=60°，∠ AD∠BC，∠∠MBG=∠AMB=60°，∠∠BGM=60°，∠BMG是等边三角形；即结论∠正确；∠BN=AB=6，BN=3，∠EN=∠正确；连接AN，∠△ABM与∠NBM关于BM轴对称，∠AP=NP，∠PN+PH=AP+PH，∠当点A、P、H三点共线时，AP+PH=AH，且当AH∠BN时AH有最小值，∠AB=6，∠ABH=60°，∠∠BAH=30°，∠BH=3，∠AH=∠PN＋PH的最小值是∠正确；【点拨】此题考查了矩形的性质，轴对称的性质，全等三角形的判定及性质，等边三角形的判定及性质，直角三角形30度角的性质，熟记等边三角形的判定及性质是解题的关键．8．B【分析】由折叠的性质可得DM＝MN，CM＝MN，即M是CD的中点；故∠正确；∠B＝∠AMP，∠DAM＝∠MAP＝∠P AB，∠DMA＝∠AMN，∠CMP＝∠PMN，∠D＝∠ANM，∠C＝∠MNP，由平角的性质可得∠D+∠C＝180°，∠AMP＝90°，可证AD∠BC，由平行线的性质可得∠DAB＝90°，由平行四边形和折叠的性质可得AN＝PN，由直角三角形的性质可得ABMN．解：由折叠的性质可得：DM＝MN，CM＝MN，∠DM＝CM，即M是CD的中点；故A正确；由折叠的性质可得：∠B＝∠AMP，∠DAM＝∠MAP＝∠P AB，∠DMA＝∠AMN，∠CMP ＝∠PMN，∠D＝∠ANM，∠C＝∠MNP，∠∠MNA+∠MNP＝180°，∠∠D+∠C＝180°，∠AD∥BC，故D正确；∠∠B+∠DAB＝180°，∠∠DMN+∠CMN＝180°，∠∠DMA+∠CMP＝90°，∠∠AMP＝90°，∠∠B＝∠AMP＝90°，∠∠DAB＝90°，若MN∠AP，则∠ADM＝∠MNA＝∠C＝90°，则四边形ABCD为矩形及AB∥CD，而题目中无条件证明此结论，故B不正确；∠∠DAB＝90°，∠∠DAM＝∠MAP＝∠P AB＝30°，由折叠的性质可得：AD＝AN，CP＝PN，∠四边形APCD是平行四边形，∠AD＝PC，∠AN＝PN，又∠∠AMP＝90°，AP，∠MN＝12∠∠P AB＝30°，∠B＝90°，AP，∠PB＝12∠PB＝MN∠AB，故C正确；故选：B ．【点拨】本题考查了翻折变换，平行四边形的性质及直角三角形的性质等知识，熟练掌握相关知识点并灵活运用这些性质是解题的关键．9．A【分析】连接AD 交EC 于点M ，连接BF 交CG 于点N ，设,AC a BC b ==，分别求出EC ，AD =，DM =，,CG FN ==，)EG a b =+，)HG EH a b ==+，)CH b a =-，分别求得1S ，2S ，由126S S -=得，2224a b +=，由勾股定理可得结论．解：连接AD 交EC 于点M ，连接BF 交CG 于点N ，∠四边形ACDE ，BCFG 是正方形，∠,,,AD EC BF CG AD EC BF CG ⊥⊥==，1122DM AD FN BF ==，，设,AC a BC b ==，∠∠90,=EAC AE AC a =︒=，∠EC ∠AD =，∠1122DM AD ===，同理可证：,CG FN ==， ∠EG EC CG =+，∠)EG a b =+，∠H 为EG 的中点，∠1))2HG EH a b a b ==+=+，∠)CH EH EC b a =-=-， ∠121124FG H ab b S S HG FN ∆+==⋅⋅=，22(124DH ab a S S CH DM ∆-=== 又∠126S S -=，∠22644ab b ab a +--=，整理得，2224a b +=，∠∠90ACB =︒，∠AB ，故选：A ．【点拨】本题主要考查了正方形的性质，勾股定理等知识，正确作出辅助线是解答本题的关键．10．D【分析】连接AC ，作PG BE ⊥，证明当12AP BP +取最小值时，A ，P ，G 三点共线，且AG BE ⊥，此时最小值为AG ，再利用勾股定理，30所对的直角边等于斜边的一半即可求出结果．解：连接AC ，作PG BE ⊥∠ABCD 是正方形且边长为4，∠45ABO ∠=︒，AC BD ⊥，AO =∠75ABE ∠=︒，∠30PBG ∠=︒，∠12PG BP =， ∠当12AP BP +取最小值时，A ，P ，G 三点共线，且AG BE ⊥，此时最小值为AG ，∠75ABE ∠=︒，AG BE ⊥，∠15BAG ∠=︒，∠45BAO ∠=︒，∠30PAO ∠=︒，设OP b =，则2AP b =，∠(()222=2b b +，解得：b 设PG a =，则2BP a =，∠BO =∠2a b +=a∠2AG AP PG b a =+=+=故选：D【点拨】本题考查正方形的性质，动点问题，勾股定理，30所对的直角边等于斜边的一半，解题的关键是证明当12AP BP +取最小值时，A ，P ，G 三点共线，且AG BE ⊥，此时最小值为AG ．11．C【分析】由该纸片以О为旋转中心进行逆时针旋转，每次旋转45°，可得旋转一周360458︒÷︒=次，由2988372÷=⋅⋅⋅，可得第298次旋转后，实际是将纸片逆时针旋转37周后再转90°，由正方形纸片ABCD 对角线中点位于原点，可求点C （1，-3）由11A B =根据勾股定理，2221111+2OA OB A B ==求出B 1（-1，0），连结OD 与OC ，过D 作ED ∠x 轴于E ，CF ∠y 轴于F ，可证△FOC ∠△EOD （AAS ），可求点D （3，1），与点C 1（0，-1）即可．解：∠该纸片以О为旋转中心进行逆时针旋转，每次旋转45°，∠旋转一周360458︒÷︒=次，∠2988372÷=⋅⋅⋅，∠第298次旋转后，实际是将纸片逆时针旋转37周后再转90°，∠正方形纸片ABCD 对角线中点位于原点，∠点A 与点C 关于点O 成中心对称，∠点A （-1，3），∠点C （1，-3），∠11A B又∠11OA OB =，根据勾股定理，2221111+2OA OB A B ==，∠111OA OB ==，∠B 1（-1，0），连结OD 与OC ，过D 作ED ∠x 轴于E ，CF ∠y 轴于F ，绕点O 逆时针旋转90°后点C 位置转到点D 位置，∠四边形ABCD 为正方形，OD OC =，90FOE COD ∠==︒，∠∠FOC +∠COE =∠COE +∠EOD =90°，∠∠FOC =∠EOD ，在△FOC 和△EOD 中，90FOC EOD CFO DEO OC OD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∠∠FOC ∠∠EOD （AAS ），∠CF =DE =1，OF =OE =3，∠点D （3，1），∠点B 1转到C 1位置，点C 1（0，-1），∠第298次旋转后，点C 和点1B 的坐标分别为（3，1）与（0，-1）．故选：C ．【点拨】本题主要考查坐标与旋转规律问题，涉及了正方形性质、中心对称性质、勾股定理应用、三角形全等判定与性质等知识，熟练掌握正方形旋转性质、中心对称性质、勾股定理应用、三角形全等判定与性质，根据旋转一周8次，确定旋转37周再转90°是解题关键．12．B【分析】根据折叠的性质，90EPG EBC ∠∠==，EB EP =，从而得到EPB EBP ∠=∠，根据直角三角形两锐角互余，得到APB BPG ∠=∠，即可判定∠；过点B 作BQ ∠PH ，利用全等三角形的判定与性质，得到CH QH =，AP PQ =，即可判定∠；通过证明BMP 为等腰直角三角形，即可判定∠；根据BEP BMP BEPM S S S =+△△四边形求得对应三角形的面积，即可判定∠．解：由题意可得：90EPG EBC ∠∠==，EB EP =，∠90EPG EPB BPG ∠∠∠=+=，EPB EBP ∠=∠，∠90EBP BPG ∠∠+=，由题意可得：1801809090EBP APB A ∠∠∠+=-=-=，∠APB BPG ∠=∠，∠PB 平分∠APG ；∠正确；过点B 作BQ ∠PH ，如下图：∠90BQP A ∠∠==在APB 和QPB 中，A BQP APB QPB BP BP ∠=∠⎧⎪∠=∠⎨⎪=⎩∠(AAS)APB QPB ≌∠AP PQ AB BQ ==，∠四边形ABCD 为正方形∠AB BC BQ ==，又∠BH BH=∠Rt Rt (HL)BCH BQH ≌，∠CH QH =∠PH PQ QH AP CH =+=+，∠正确；由折叠的性质可得：EF 是PB 的中垂线，∠PM BM =由题意可得：BAP BQP ≌，BCH BQH △≌△，∠,ABP PBQ CBH QBH ∠∠∠∠==， ∠1452PBQ QBH ABP CBH ABC ∠∠∠∠∠+=+==， ∠45PBM ∠=，∠45BPM PBM ∠∠==，∠BMP 为等腰直角三角形，∠222BM PM BP +=，即222BM BP =，∠BM ，∠正确；若BE =53，AP =1，则53PE BE ==，在Rt APE 中，222AE AP PE +=∠43AE ==，3AB AE BE ，∠PB =∠BM BP == 21110223BEP BMP BEPM S S S BE AP BM =+=⨯⨯+⨯=△△四边形，∠错误，故选B ，【点拨】此题考查了正方形与折叠问题，涉及了折叠的性质，正方形的性质，直角三角形的性质，垂直平分线的性质，全等三角形的判定与性质，等腰三角形的判定与性质，勾股定理等知识，综合性比较性，解题的关键是灵活运用相关性质进行求解．13【分析】连接AC ，CE ，则CE 的长即为AP +PE 的最小值，再根据菱形ABCD 中，120BCD ∠=︒得出∠ABC 的度数，进而判断出∠ABC 是等边三角形，故∠BCE是直角三角形，根据勾股定理即可得出CE 的长．解：连接AC ，CE ，∠四边形ABCD 是菱形，∠A 、C 关于直线BD 对称，∠CE 的长即为AP +PE 的最小值，∠120BCD ∠=︒，∠60ABC ∠=︒，∠∠ABC 是等边三角形，∠E 是AB 的中点，∠CE AB ⊥，112122BE BC ==⨯=∠CE ==【点拨】本题考查了轴对称-最短路线问题，熟知菱形的性质及两点之间线段最短是解答此题的关键．14．258或5或8 【分析】∠ADE 是等腰三角形，所以可以分3种情况讨论：∠当AD ＝AE 时，∠ADE 是等腰三角形．作AM ∠BC ，垂足为M ，利用勾股定理列方程可得结论；∠当AD ＝DE 时，四边形ABED 是菱形，可得m ＝5；∠当AE ＝DE 时，此时C 与E 重合，m ＝8．解：分3种情况讨论：∠当AD ＝AE 时，如图1，过A作AM∠BC于M，∠AB＝AC＝5，BM＝12BC＝4，∠AM＝3，由平移性质可得AD＝BE＝m，∠AE＝m，EM＝4−m，在Rt∠AEM中，由勾股定理得：AE2＝AM2＋EM2，∠m2＝32＋（4−m）2，m＝258，∠当DE＝AD时，如图2，由平移的性质得AB DE∥，AB DE，∠四边形ABED是菱形，∠AD＝BE＝ED＝AB＝5，即m＝5；∠当AC＝DE时，如图3，此时C与E重合，m＝8；综上所述：当m＝258或5或8时，∠ADE是等腰三角形．故答案为：258或5或8．【点拨】本题考查了等腰三角形的性质、勾股定理、平移的性质，解题的关键是分三种情况求出BE的长；本题属于基础题，难度不大，但在解决该题时，部分同学会落掉两种情况，故在解决该题型题目时，全面考虑等腰三角形的三种情况是关键．15．1【分析】取OB中点E'，连接PE'，作射线FE'交AC于点P'．则PE＝PE'，当P与P'重合，P'、E'、F三点在同一直线上时，PF﹣PE'有最大值，即为FE'的长．解：如图，取OB中点E'，连接PE'，作射线FE'交AC于点P'．则PE＝PE'，∠PF﹣PE＝PF﹣PE'≤FE'，当P与P'重合，P'、E'、F三点在同一直线上时，PF﹣PE'有最大值，即为FE'的长，∠在菱形ABCD中，∠ABC＝120°，∠∠ABD＝60°，∠DAB＝60°，∠∠ABD为等边三角形．∠AB＝BD＝AD＝4．∠OD＝OB＝2．∠点E'为OB的中点，E'B＝1，AF＝3BF，∠BF1AB＝1，4∠∠ABD＝60°，∠∠BE'F为等边三角形，∠E'F＝FB＝1．故PF﹣PE的最大值为1．故答案为：1．【点拨】本题考查了轴对称﹣最大值问题、菱形的性质、等边三角形的判定与性质，熟练运用轴对称的性质和三角形三边关系是解题的关键．16．【分析】根据菱形ABCD 中，∠BAD ＝60°可知∠ABD 是等边三角形，结合三线合一可得∠BAB '＝30°，求出∠ABB '＝75°，可得∠EB 'B ＝∠EBB '＝45°，则∠BEB '是直角三角形，借助勾股定理求出BB '的长即可．解：∠菱形ABCD ，∠AB ＝AD ，AD //BC ，∠∠BAD ＝60°，∠∠ABC ＝120°，∠AB ′∠BD ，∠∠BAB '1302BAD =∠=︒， ∠将∠ABE 沿直线AE 翻折180°，得到∠AB ′E ，∠BE ＝B 'E ，AB ＝AB '，∠∠ABB '()118030752=⨯︒-︒=︒， ∠∠EBB '＝∠ABE ﹣∠ABB '＝120°﹣75°＝45°，∠∠EB 'B ＝∠EBB '＝45°，∠∠BEB '＝90°，在Rt∠BEB '中，由勾股定理得：BB '==故答案为：．【点拨】本题考查了翻折的性质、菱形的性质、等腰三角形的性质、以及勾股定理等知识，明确翻折前后对应线段相等是解题的关键．17． 43##113 32 【分析】连接GE ，根据点E 是BC 的中点以及翻折的性质可以求出BE ＝EF ＝EC ，然后利用“HL ”证明GFE 和GCE 全等，根据全等三角形对应边相等即可得证FG ＝CG ，设GC ＝x ，表示出AG 、DG ，然后在Rt ADG 中，利用勾股定理列式进行计算即可得解；先判断出EF AC ⊥时，GEF △的周长最小，最后用勾股定理即可得出结论．解：∠如图，连接GE ，∠E 是BC 的中点，∠BE ＝EC ，∠ABE △沿AE 折叠后得到AFE △，∠BE ＝EF ，∠EF ＝EC ，∠在矩形ABCD 中，∠∠C ＝90°，∠∠EFG ＝90°，∠在Rt GFE 和Rt GCE 中，EG EG EF EC =⎧⎨=⎩∠()GFE GCE HL ≌△△， ∠GF ＝GC ；设GC x =，则3AG x =+，3DG x =-，在Rt ADG 中，2224(3)(3)x x +-=+，解得x ＝43，即43GC =； ∠如图：由折叠知，∠AFE ＝∠B ＝90°，EF ＝BE ，∠4EF CE BE CE BC AD +=+===，∠当CF 最小时，CEF △的周长最小，∠CF AC AF ≥-，∠当点A ，F ，C 在同一条直线上时，CF 最小，由折叠知，AF ＝AB ＝3，在Rt ABC 中，AB ＝3，BC ＝AD ＝4，∠AC ＝5，∠2CF AC AF =-=，在Rt CEF 中，222EF CF CE +=，∠222(4)BE CF BE +=-，∠2222(4)BE BE +=-， ∠3=2BE ．【点拨】此题是四边形综合题，主要考查了矩形的性质，折叠的性质，全等三角形的判定和性质，勾股定理，解题的关键是构造出直角三角形，利用勾股定理解决问题．18．6【分析】设点M 是PD 的中点，过点M 作直线P D ''与射线CA 、CB 分别交于点,P D ''，得到当点M 是PD 的中点时，CPD △的面积最小，再根据直角三角形的性质及三角形的面积公式求解即可．解：设点M 是PD 的中点，过点M 作直线P D ''与射线CA 、CB 分别交于点,P D ''，则点M 不是P D ''的中点当MD MP ''>时，在MD '上截取ME MP '=，连接DEPMP DME'∠=∠()PMP DME SAS '∴≅=P CD PCD P CDE S S S '''∴>四边形当MD MP ''<时，同理可得P CD PCD S S ''>∴当点M 是PD 的中点时，CPD △的面积最小如图，作DH AB ⊥于H则DHM PAM ≌,90,AM MH DHM PAM AP DH ∴=∠=∠=︒=90BHD =∴∠︒1AM =，3BM =1AM MH ∴==2BH ∴=在等腰Rt ABC △中，314CA BA ==+=45B C ∴∠=︒=∠45B BDH ∴∠=∠=︒2BH DH AP ∴===426CP AC AP ∴=+=+=过点D 作DK PC ⊥交于K∴四边形AKDH 是矩形2DK AH AM HM ∴==+=1162622CDP S CP DK ∴=⋅=⨯⨯= 故答案为：6 【点拨】本题考查了全等三角形的判定和性质、矩形的判定和性质、直角三角形的性质，熟练掌握知识点是解题的关键．19．【分析】过点E作EH∠BF于H，利用三角形的中位线定理以及直角三角形斜边中线定理证明∠BFE是顶角为120°的等腰三角形即可解决问题．解：过点E作EH∠BF于H．∠AD=AC，∠DAC=90°，CD=8，∠AD=AC∠DF=FC，AE=EC，∠EF=1AD，EF//AD，2∠∠FEC=∠DAC=90°，∠∠ABC=90°，AE=EC，∠BE=AE=EC∠EF=BE∠∠BAD=105°，∠DAC=90°，∠∠BAE=105°-90°=15°，∠∠EAB=∠EBA=15° ，∠∠CEB=∠EAB+∠EBA=30°，∠∠FEB=90°+30°=120°，∠∠EFB=∠EBF=30°，∠EH∠BF，EF，FH∠EH=1∠ BF=2FH，S △EFB =11··22BF EH =⨯=故答案为【点拨】本题考查三角形中位线定理，直角三角形斜边中线的性质，等腰三角形的判定和性质，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．20．94或1 【分析】分∠CFE =90°和∠CEF =90°两种情况根据矩形的性质、勾股定理、全等三角形的判定及性质求解．解：∠如图，当∠CFE =90°时，∠四边形ABCD 是矩形，点E 是矩形ABCD 的边AB 的中点，AB =6，AD =4，∠∠P AE =∠PFE =∠EBC = 90°，AE =EF =BE =3，∠∠PFE +∠CFE =180°，∠P 、F 、C 三点一线，∠△EFC ∠△EBC ，∠FC =BC =4，EC ，∠FEC =∠BEC ，∠∠PEF +∠FEC =90°，设AP =x ，则PC =x +4，∠2222(4)35x x +=++,解得x =94； ∠如图，当∠CEF =90°∠∠CEB+2∠PEA =90°，∠∠CEB+∠PEA =90°-∠PEA，延长PE、CB，二线交于点G，∠AE=BE，∠P AE=∠GBE =90°，∠AEP=∠BEG，∠△P AE∠△GBE，∠P A=BG，∠AEP=∠BEG，∠∠G =90°-∠GEB= 90°-∠PEA，∠CEB+∠PEA =90°-∠PEA，∠∠G =∠CEB+∠PEA=∠CEB+∠GEB=∠CEG，∠CE=CBC+BG=BC+AP，∠5=4+AP，解得P A=1，故答案为：94或1．【点拨】本题考查了矩形的性质，折叠的性质，勾股定理，三角形全等的判定和性质，等腰三角形的判定和性质，熟练掌握矩形的性质，勾股定理是解题的关键．21．4【分析】将△DAF绕点A顺时针旋转90度到△BAF′位置，根据旋转的性质得出∠EAF′=45°，进而得出∠F AE∠∠EAF′，即可得出EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=2BC=8，求出BC即可．解：将△DAF绕点A顺时针旋转90度到△BAF′位置，由题意可得出：△DAF ∠∠BAF ′，∠DF =BF ′，∠DAF =∠BAF ′，∠∠EAF ′=45°，在△F AE 和△EAF ′中,AF AF FAE EAF AE AE ''=⎧⎪∠=∠⎨⎪=⎩， ∠∠F AE ∠∠EAF ′（SAS ），∠EF =EF ′，∠∠ECF 的周长为8，∠EF +EC +FC =FC +CE +EF ′=FC +BC +BF ′=DF +FC +BC =2BC =8，∠BC =4，即正方形的边长为4．故答案为：4．【点拨】此题主要考查了旋转的性质以及全等三角形的判定与性质等知识，得出△F AE ∠∠EAF ′是解题关键．22．3【分析】根据翻折的性质和已知条件可得点F 和点A 重合，过点D 作DH BC ⊥，DG AB ⊥，垂足分别为H ，G ，得四边形BHDG 是正方形，设DG DH x ==，1x x +=，求出x 的值，进而可以解决问题．解：如图，由折叠可知：30E C ∠=∠=︒，FE FD ∴=，当30ADE ∠=︒时，260BFD E ∠=∠=︒，在Rt ABC 中，90ABC ∠=︒，30C ∠=︒，60A ∴∠=︒，∴点F 和点A 重合，如图，过点D 作DH BC ⊥，DG AB ⊥，垂足分别为H ，G ，由折叠可知：45CBD EBD ∠=∠=︒，DG DH ∴=，∴四边形BHDG 是正方形，设DG DH x ==，AG DG ∴==，AB AG BG AG GD x ∴=+=++，1x x +=，解得x =DG ∴=， 30C ∠=︒，CD DH∴==．23故答案为：3．【点拨】本题考查翻折变换，正方形的判定与性质、勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．23．【分析】过点H作HG∠CD于点G，连接DE，DE交FH于点Q，得到∠HGF=∠HGD=90°，推出∠HFG+∠FHG=90°，根据正方形ABCD中，AD=CD=BC=4，∠A=∠ADC=∠C=90°，得到四边形DAHG中，∠AHG=90°，推出四边形DAHG是矩形，得到GH=AD，GH=CD，根据折叠知，FH∠DE，得到∠DQF=90°，推出∠QFD+∠QDF=90°，得到∠GHF=∠CDE，根据∠HGF=∠C=90°，推出△DCE∠∠HGF(ASA)，得到FH=DE，根据E是BC中点，得到CE=12BC=2，推出DE FH=解：过点H作HG∠CD于点G，连接DE，DE交FH于点Q，则∠HGF=∠HGD=90°，∠∠HFG+∠FHG=90°，∠正方形ABCD中，AD=CD=BC=4，∠A=∠ADC=∠C=90°，∠四边形DAHG中，∠AHG=90°，∠四边形DAHG是矩形，∠GH=AD，∠GH=CD，由折叠知，FH∠DE，∠∠DQF=90°，∠∠QFD+∠QDF=90°，∠∠GHF=∠CDE，∠∠HGF=∠C=90°，∠∠DCE∠∠HGF(ASA)，∠FH=DE，∠E是BC中点，∠CE =12BC=2，∠DE ==，∠FH=故答案为【点拨】本题主要考查了正方形，折叠，矩形，全等三角形，勾股定理．解决问题的关键是熟练掌握正方形的性质，折叠的性质，矩形的判定和性质，全等三角形的判定和性质，勾股定理解直角三角形．24．【分析】延长BA 到点G ，使AG CF =，连接DG ，EF ，利用SAS 证明ADG CDF ≌，得ADG CDF ∠=∠，DG DF =，再证明()GDE FDE SAS △≌△，得=GE FE ，设AE x =，则6BE x =-，3EF x =+，再利用勾股定理即可解决问题．解：：如图，延长BA 到点G ，使AG CF =，连接DG ，EF ，∠ 四边形ABCD 是正方形，∠AD CD =，90DAG DCF ∠=∠=︒，90ADC BAD ABC ∠=∠=∠=︒，在ADG 和CDF 中，AD CD DAG DCF AG CF =⎧⎪∠=∠⎨⎪=⎩∠()ADG CDF SAS △≌△，∠ADG CDF ∠=∠，DG DF =，∠45EDF ∠=︒，。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

期末复习二——四边形
【知识要点】
序
号
具体知识点
掌握情况（打“√”或“×”）

课前课后
1 计算角度、边长
2 计算对角线、周长
3 判断边长或对角线的取值范围
4 计算面积
5 判定四边形的形状
6 折叠问题
7 动点问题
8 其它计算、证明问题

【典型例题】
例1-1 在□ABCD中，若AB∶BC=2∶3且它的周长为30㎝，则CD=㎝
例1-2 在□ABCD中，若∠A=120°，则∠D=
例1-3 在□ABCD中，若∠A+∠C=100°，则∠B=
例1-4 □ABCD中，若∠A∶∠B=1∶3,那么∠A=___，∠B=___，∠C=____，∠D=___
例1-5 在□ABCD中，已知∠A－∠B=20°，则∠C=
例1-6 已知菱形ABCD中，AB=AC=6，则BD=
例1-7 矩形ABCD中，已知∠ACB=30°，则∠BDC=
例1-8 已知正方形的面积等于8m2，则它的边长等于
例1-9 梯形ABCD中，AD∥BC，AB=AD，BC=BD，∠A=120°，求其余各个内角．

A B C D
EODCBA

例1-10 有一等腰三角形的木格子(如图)，里面的每一同方向木条都互相平行，已知等腰
三角形的腰长是30cm，底边长是50cm，你能帮木工师傅算出拼木格子所需木条的总长度吗？
（不计接头）。

例2-1 已知菱形的周长等于40㎝，两对角线的比为3∶4，则对角线的长分别是（）
A、12㎝，16㎝ B、6㎝，8㎝ C、3㎝，4㎝ D、24㎝，32㎝

例2-2 如图，平行四边形ABCD中，AB=3，BC=5，AC的垂直平分线交AD于E，则△CDE的
周长是（）
A、 6 B、 8 C、 9 D、 10

例2-3 在□ABCD中，AC⊥BD，且AC=8㎝，BD=6㎝，求此四边形的周长。

例2-4 矩形ABCD中,AB=3cm，∠ACB＝30°,求矩形ABCD的对角线和面积。
例2-5 菱形ABCD的两条对角线相交于O，且OA=3cm,OB=4cm，求菱形ABCD的周长和面积。
例2-6 正方形ABCD的对角线为4cm，求正方形ABCD的边长和面积。
例3-1 如果该平行四边形的一条边长是8，一条对角线长为6，那么它的另一条对角线长
m
的取值范围是________.
例3-2 平行四边形一边长为 10 ,则它的两条对角线可以是( )
A、6 ,8 B、8, 12 C、8, 14 D、6, 14
例3-3 如图，□ABCD中，AB=3，BC=4，求BO的长度的取值范围。

例3-4 若△ABC中，AB=8，AC=6，则BC边上中线的长x的取值范围是。
例4-1 如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与
点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______.

B
C

D
A
E
P

O
A

D
C

D
A
BC
例4-2 如图，四边形ABCD是矩形，DH⊥AC，如果AH=9cm，CH=4cm，那么ABCDS四边形是多
少？

例4-3 矩形ABCD中，AB=4，BC=6，M是BC的中点，DE⊥AM，E为垂足．（1）求△ABM的面
积．（2）求DE的长．（3）求△ADE的面积．

例4-4 如图，□ABCD的两条对角线AC、BD相交于点O，5AB，12OBAO，
① AC、BD互相垂直吗？为什么？
② 四边形ABCD是菱形吗？为什么？
③ 求四边形ABCD的面积。

例5-1 顺次连结四边形各边中点得到什么图形？请说明理由。（要求自己作图）

H
DCBA
例5-2 试证明：平行四边形各内角平分线围成矩形。
例5-3 已知四边形的四条边分别为a、b、c、d，且满足a2+b2+c2+d2=2ac+2bd，则此四边形
是形，说明理由。

例6-1 将一张矩形纸对折再对折，然后沿着图中的虚线剪下，得到①、②两部分，将①展
开后得到的平面图形是什么？

例6-2 将长方形纸片按如图的方式折叠，BC、BD为折痕，则∠CBD=_______度
(2)
(1)

B
C
A
E

D
例6-3 如图，把一张长方形ABCD的纸片，沿EF折叠后，ED与BC的交点为G，点D、C分
别落在D′、C′的位置上，若∠EFG=55°，求∠1、∠2的度数。

例6-4 已知如图，在矩形ABCD中，AD>AB，O为对角线的交点，过O作一直线分别交BC、
AD于M、N。
（1）求证：梯形ABMN的面积等于梯形CDNM的面积；

（2）当MN满足什么条件时，将矩形ABCD以MN为折痕翻折后能使点C恰好与点A重合（只
写满足的条件，不用证明）

（3）在（2）中条件下，若翻折后不重叠部分的面积是重叠部分面积的1/2，求BM∶MC的
值。

O
N A B D
C
M

1
2

ABCDE

F
C'
D'

A(C')
BCDONM

D'
例6-5 如图，一张宽为3，长为4的矩形纸片ABCD，先沿着对角线BD对折,点C落在点C′
的位置上（如图），BC′交AD于G，求⊿BGD的面积.

例6-6 若将上题的图再折一次，使点D与A重合，得折痕EN（如图），EN交AD于点M，求
EN的长。

例7 如图，在等腰梯形ABCD中，AB∥DC，AD=BC=4cm，AB=12cm,CD=8cm，点P从A开始沿
AB边向B以3cm/s的速度移动，点Q从C开始沿CD边向D以1cm/s的速度移动。如果点PQ
分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动。设运动时间为t(s)。
（1）当t为何值时，四边形APQD是平行四边形？
（2）当t为何值时，四边形APQD是等腰梯形？

B
C

DA
C'
G

B
C

DA
C'
GM
N

P
C
D

A
B
Q
例8-1 已知，□ABCD中，AD=2AB，E是AD的中点，连结BE、CE，∠BEC=90°。
（1）求证：BE平分∠ABC；

（2）EC=4，且3ABBE，求四边形ABCE的面积。

例8-2 如图，□ABCD中，O是AC与BD的交点，过点O的直线与AB、CD的延长线分别交
于E、F。
（1）求证：△BOE≌DOF。
（2）连接CE、AF，当EF与AC满足什么条件时，四边形AECF是菱形？并证明你的结论。

例8-3 如图13，四边形ABCD中，AC=6，BD=8且AC⊥BD，顺次连接四边形ABCD各边中点，得到
四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四
边形A2B2C2D2„„如此进行下去得到四边形AnBnCnDn .
（1）证明：四边形A1B1C1D1是矩形；
（2）写出四边形A1B1C1D1和四边形A2B2C2D2的面积；
（3）写出四边形3333DCBA的面积；
（4）求四边形A5B5C5D5的周长.

B1
C1

D1
A1
D2

C2
B3
A3

B2
D3

A2
„

D
C
B
AE

F
O
A

B
C

E
例8-4 已知：如图1，点C为线段AB上的一点，△ACM和△CBN是等边三角形，直线AN、
CM交于点E，直线BM、CN交于点F，
求证：（1）AN=BM；
（2）△CEF是等边三角形；
（3）将△ACM绕点C按逆时针方向旋转90º，其它条件不变，在图2中补出符合要求的图形，
并判断（1）（2）结论是否仍然成立。（不要求证明）

北师版初三数学期末特殊的平行四边形全章复习同步讲义

北师大版初中数学九年级上册知识讲解 巩固练习 第4讲《特殊平行四边形》全章复习和巩固(基础)

北师版数学九下9B教材知识梳理及中考复习 第20讲 特殊平行四边形

北师大版九年级数学上册特殊的平行四边形含中考真题解析期末复习资料

初三复习课件(平行四边形和特殊平行四边形)[下学期]--北师大版

初三复习课件(平行四边形和特殊平行四边形)[下学期]--北师大版

2023学年北师大版九年级数学上学期专项讲练1-29 《特殊平行四边形》全章复习与巩固(培优篇)

北师大版初中数学九年级上册知识讲解巩固练习第4讲《特殊平行四边形》全章复习和巩固(基础)

北师版数学九下9B教材知识梳理及中考复习第20讲特殊平行四边形