小学六年级数学小升初珍藏版复习资料第5讲 比和比例(解析)
六年级下册数学小升初复习课件-比和比例(共15张PPT)-人教新课标(2014秋)

正比例和反比例的意义,也可以用字母表示:
_y x
=k
(一定)
xy =k (一定)
二、例4:
(1)写出李阿姨平时和节日期间剪纸 张数及相应工作时间的比。
李阿姨平时剪纸张数与工作时间的比是:72:6=12:1 节日期间剪纸张数与工作时间的比是: 96:8=12:1
(2)上面两个比能组成比例吗?
这两个比成比例,因为这两个比是相等的,所以这 两个比成比例。
▪ 这两种方法的区别在于解比例 只用到一个关系式:工作量÷工作 时间=工作效率,思路简捷;而列 算式解答,除了用到上面这个关系 式,还要用到:工作量÷工作效率 =工作时间,思路转折多一些。请 大家以后在解题时,用自己理解的 方法解答。
三、比例尺.
(1)什么叫做比例尺?
图上距离 ————
=比例尺
实际距离
一、回顾与交流
1、回忆一下,在比和比例的知识 中,我们研究了哪 些内容?
在比和比例的知识中,我们研究了:比和 比例的意义;比和比例的各部分名称;比和比 例的基本性质等。
(1)什么是比?什么是比例?
两个数相除又叫做两个数的比。
表示两个比相等的式子叫做比例。
(2)比、比例各部分的名称是什么? (3)比和比例的基本性质是怎样的?
不成比例。全班人数一定,也就是出勤人数和缺勤人数的和一定, 所以不成比例。
(2)分数的大小一定,它的分子和分母。
成正比例关系。分数的大小一定,也就是分子和分母的比值一定, 所以成正比例。。
(3)三角形的面积一定,它的底和高。
成反比例关系。三角形的面积一定,也就是它的底和高的乘积一定, 所以成反比例。
比的前项相当于分数中的分子,比号相当于分数 中的分数线,比的后项相当于分数中的分母,比值 相当于分数中分数值;比的前项相当于除法中的被 除数,比号相当于除法中的除号,比的后项相当于 除法中的除数,比值相当于除法中的商。
六年级下册数学素材-小升初《确定位置》-《比和比例》知识点总结--全国通用

【一】确定位置一、利用有序数对确定位置常考题型:理解什么是有序数对1、会写有序数对2、会根据有序数对描述物体位置3、会根据有序数对画出物体位置二、利用方向和距离确定位置常考题型:1、根据已知图,确定物体的位置信息2、根据已知的文字信息,画出物体的位置(注意作图步骤)3、描述路线4、会分析雷达图【二】比和比例知识提要:1、比和比例的意义2、求比值和化简比3、比例尺图上距离和实际距离的比,叫做这幅图的比例尺。
用式子表示:比例尺=图上距离:实际距离或比例尺=图上距离实际距离4、正比例和反比例(1)两种相关联的量,一种量(x )变化,另一种量(y )也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
用式子表示:y=k(一定)。
x(2)两种相关联的量,一种量(x )变化,另一种量(y )也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的=k(一定)。
关系叫做反比例关系。
用式子表示:x y(3)规律:正比例两种量同时扩大,同时缩小,它们的比值不变反比例一种量扩大,另一种量就缩小;一种量缩小,另一种量就扩大,它们的积不变5、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“1”。
题中如果有几个不同的单位“1”,必须根据具体情况,将不同的单位“1”,转化成统一的单位“1”,使数量关系简单化,达到解决问题的效果。
在解答分数应用题时,要注意以下几点:(1)题中有几种数量相比较时,要选择与各个已知条件关系密切、便于直接解答的数量为单位“1”。
(2)若题中数量发生变化的,一般要选择不变量为单位“1”。
(3)应用正、反比例性质解答应用题时要注意题中某一数量是否一定,然后再确定是成正比例,还是成反比例。
找出这些具体数量相对应的分率与其他具体数量之间的正、反比例关系,就能找到更好、更巧的解法。
(4)题中有明显的等量关系,也可以用方程的方法去解。
小升初数学专项复习第五讲《 比和比例》名师教学课件

比的前项和比的后项同时乘或除以相同的数(0除外),比值不变。
应用:化简比
2.比例的基本性质:
在比例里,两个外项的积等于两个内项的积。
注:在分数比例中求比例的两外项的积、两内项的积,交叉相乘即可。
应用:解比例
一、知识梳理
(三)化简比,求比值
方法:前项÷后项,把结果写成最简分数。
15 3
A. 16
B. 18
C.24
D.27
③实际距离一定,比例尺扩大10倍,图上距离( B )。
A.缩小10倍
B. 扩大10倍
C. 不变
D.无法确定
④长方形的周长是40厘米,长与宽的比是5:3,面积是( C )平方厘米。
A. 375
B. 15
C. 93.75
D.45
三、基础训练
2.填空题
①小明要调制1.8升的果汁,纯果汁和水的体积比是7:2,需要纯果汁( 1.4)升,水
( 3x=84×1
)。
三、基础训练
3.在一个书架上装有两层的书,上层书的数量与下层书的数量比是5:6,从上层拿出30
本书到下层后,上、下两层书的数量之比是3:4,上、下两层书原来各有多少本?
书的总本书:
30÷(
4
6
- )=1155(本)
3+4 5+6
5
原来上层的本数是:1155× =525(本)
5+6
小升初专项复习数与代数
比和比例
目录
CONTENTS
01 知识梳理
02 典例精讲
03 基础训练
04 拓展提升
1
Part One
知 识 梳 理
一、知识梳理
苏教版六年级下册数学讲义及试题小升初总复习资料:比和比例(含答案)

比和比例⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧→→⎭⎬⎫→→⎪⎩⎪⎨⎧⎩⎨⎧⎭⎬⎫→⎪⎭⎪⎬⎫→⎩⎨⎧→→→应用意义正、反比例解比例性质意义比例比例尺按比例分配求未知数化简比性质求未知数求比值比与除法、分数的关系意义比比和比例一、本章概念: 比:比的意义:两个数相除,又叫做两个数的比。
比值:比的前项除以后项所得的商,叫作比值。
比值相等的两个比相等。
比、分数、除法的关系:)0(:≠÷==b b a bab a比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
按比例分配:在工农业生产和日常生活中,常常需要把一个数量按照一定的比例进行分配。
比例:比例的意义:表示两个比相等的式子叫作比例。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
解比例:根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另一个未知项。
求比例中的未知项,叫做解比例。
比例尺:图上距离和实际距离的比,叫做这幅图的比例尺。
比例尺分为数值比例尺和线段比例尺。
正比例的意义:两种相关联的量,一种量变化,另一种也随着变化,如果这两种量中相对应的两个量的比值(也就是商)一定,这两种量叫做成正比例的量,它们的关系叫作正比例关系。
如果用字母x 和y 分别表示两种相关联的量,用k 表示它们的比值,正比例关系的式子可表示为:(一定)k xy =。
反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量对应的两个量积一定,这两种量就叫作反比例的量,它们的关系叫作反比例关系。
如果用字母x 和y 分别表示两种相关联的量,用k 表示它们的积,反比例关系可以用式子表示为:(一定)k xy =。
二、先关概念的比较1.比和比例的意义、形式、组成和基本性质的区别意义 形式 各部分名称 组成 基本性质比两个数相除由两项组成(前项、后项)项后号比:项前↓↓↓7149任意两个数都可以组成比(同类量或不同类量) 比的前项和后项同时乘以或除以相同 的数(0除外),比值不变比例两个比相等的式子由四项组成(内项、外项各两个)任意四个数不一定能组成比例 在比例里,两个外项的积等于两个内项的积2.比、分数和除法的区别和联系相当部分区别比(bab a 或:) 前项 比号(:) 后项 比值 两个数的倍比关系分数(ba ) 分子 分数线(—) 分母 分数值 一个数值 除法(b a ÷)被除数除号(÷)除数商一种运算3.求比值和化简的区别意义一般方法结果求比值 前项除以后项所得的商根据比值的意义,用前项除以后项是一个商,可以是整数、小数或分数化简比把两个数的比化成最简单的整数比 根据比的基本性质,比的前项和后项同时乘以或除以相同的数(0除外);有时也可以用求比值的方法来化简比 是一个比,它的前项和后项都是整数,而且公因数只有1 注意:当同类量的两个数相比,前项和后项单位不同时,要先化成相同的单位,然后再求比值或者化简比。
小升初数学总复习精讲精练5:比和比例及比例的应用(含答案解析)
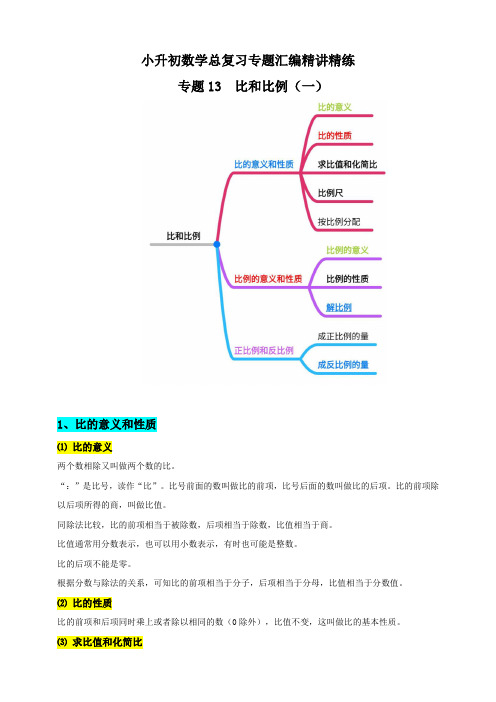
小升初数学总复习专题汇编精讲精练专题13 比和比例(一)1、比的意义和性质⑴比的意义两个数相除又叫做两个数的比。
“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
同除法比较,比的前项相当于被除数,后项相当于除数,比值相当于商。
比值通常用分数表示,也可以用小数表示,有时也可能是整数。
比的后项不能是零。
根据分数与除法的关系,可知比的前项相当于分子,后项相当于分母,比值相当于分数值。
⑵比的性质比的前项和后项同时乘上或者除以相同的数(0除外),比值不变,这叫做比的基本性质。
⑶求比值和化简比求比值的方法:用比的前项除以后项,它的结果是一个数值可以是整数,也可以是小数或分数。
根据比的基本性质可以把比化成最简单的整数比。
它的结果必须是一个最简比,即前、后项是互质的数。
⑷比例尺图上距离:实际距离=比例尺要求会求比例尺;已知图上距离和比例尺求实际距离;已知实际距离和比例尺求图上距离。
线段比例尺:在图上附有一条注有数目的线段,用来表示和地面上相对应的实际距离。
⑸按比例分配在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。
这种分配的方法通常叫做按比例分配。
方法:首先求出各部分占总量的几分之几,然后求出总数的几分之几是多少。
2、比例的意义和性质⑴比例的意义表示两个比相等的式子叫做比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
⑵比例的性质在比例里,两个外项的积等于两个两个内向的积。
这叫做比例的基本性质。
⑶解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个数比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
3、正比例和反比例⑴成正比例的量两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。
用字母表示y/x=k(一定)⑵成反比例的量两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。
六年级数学毕业复习_比和比例知识点资料讲解

六年级数学毕业复习_比和比例知识点比和比例知识点---------判断两个量是否成正比例、反比例或不成比例一、写(写出数量关系式)1、根据数量间的关系或公式,写出数量关系式。
如,①宽一定,长方形的面积和长是否成正比例。
根据“长方形的面积=长×宽”得到“宽(一定)长长方形的面积”,因为长方形的面积和长是相关联的量,宽一定,也就是它们的比值一定,所以“宽一定,长方形的面积和长是成正比例”。
②圆锥的体积一定,底面积和高是否成反比例。
根据“底面积×高×31=圆锥的体积”得到“底面积×高=圆锥的体积×3”,因为底面积和高是相关联的量,圆锥的体积一定,“圆锥的体积×3"的结果也一定,就是底面积和高的积一定(底面积×高=圆锥的体积×3(一定)),所以圆锥的体积一定,底面积和高是成反比例。
2、注意:写出的数量关系式,其中的一边(左边)只能有这两个相关联的量,不能有多余的量和数字。
如,“(长+宽)×2=长方形的周长”的左边就多了×2,长方形的周长”应变为“(长+宽)=2又如,梯形的上底和下底不变,面积和高。
可以这样写关系式:(a+b)×h÷2=s→(a+b)×h÷2÷h=s÷h→(a+b)÷2 =s÷h→s÷h=(a+b)÷2,因为上底和下底不变,(a+b)÷2的结果也是一定的,所以梯形的上底和下底不变,面积和高成正比例。
3、还有些数量之间是无法写关系式的。
如,“小明的身高和跳高的高度成正比例”是无法写出关系式的。
二、看(1、看是否相关联2、看是否能变化3、看是否商(积)一定)1、看是否相关联:也就是一个量变化了,另一个量是否也会随着变化。
如,长方形的面积一定,长和宽就是相关联的量,因为长变化了,宽也会随着变化。
小升初真题特训:比和比例-小学数学六年级下册人教版(有答案 有解析)

小升初真题特训:比和比例-小学数学六年级下册人教版(有答案有解析)小升初真题特训:比和比例-小学数学六年级下册人教版学校:___________姓名:___________班级:___________考号:___________一、选择题1.(2023·江苏·小升初真题)学校田径队中有四名队员的身高在140厘米至150厘米.小明身高170厘米,如果他加入田径队后,这五名田径队员的平均身高( ).A.不会有变化B.增加12.5厘米C.最多增加4厘米D.增加4厘米至6厘米2.(2023·全国·小升初真题)两地间的实际距离是80千米,画在地图上是4厘米.这幅地图的比例尺是().A.1:20 B.1:20000 C.1:20000003.(2022·福建南平·统考小升初真题)如图,阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么甲和乙两个圆的面积比是()。
A.6∶1 B.6∶5 C.5∶64.(2023·全国·小升初真题)甲数的等于乙数的,甲数和乙数的比是()A.7:4 B.4:7 C.:5.(2023·全国·小升初真题)图上距离1厘米,表示实际距离20米,那么比例尺是()A.1:20 B.1:200 C.1:20006.(2022·广东惠州·统考小升初真题)甲数的等于乙数的(甲数、乙数不为),那么甲数与乙数的比是()。
A.B.C.D.7.(2023春·全国·六年级小升初模拟)从圆中剪出一个最大的正方形,则正方形的面积与圆的面积之比为()。
A.π∶4 B.2∶π C.3∶π8.(2022·浙江宁波·统考小升初真题)下面各题中,成反比例关系的是()。
A.路程一定,速度和时间B.时间一定,路程和速度C.单价一定,总价和数量D.数量一定、总价和单价二、判断题9.(2023·全国·小升初真题)若2X=5Y,则X和Y一定成正比例关系.( ).10.(2022·湖南衡阳·统考小升初真题)某班男、女生人数的比是7∶8,男生占全班人数的。
六年级下册数学知识点解析:比和比例

次火车自北京西站开往安庆西站,行驶至全程的511再向前56千米处所用时间比提速前减少了60分钟,而到达安庆西站比提速前早了2小时.问北京西站、安庆西站两地相距多少千米两地相距多少千米? ?【分析与解】设北京西站、安庆西站相距多少千米?设北京西站、安庆西站相距多少千米?(511x+56)x+56)::x=60x=60::120120,即,即,即((511x+56)x+56)::x=1x=1::2,即x=1011x+112x+112,解得,解得x=1232x=1232.. 即北京西站、安庆西站两地相距即北京西站、安庆西站两地相距1232千米,千米,3.两座房屋A 和B 各被分成两个单元.若干只猫和狗住在其中.已知:各被分成两个单元.若干只猫和狗住在其中.已知:A A 房第一单元内猫的比率房第一单元内猫的比率((即住在该单元内猫的数目与住在该单元内猫狗总数之比在该单元内猫的数目与住在该单元内猫狗总数之比))大于B 房第一单元内猫的比率;并且A 房第二单元内猫的比率也大于B 房第二单元内猫的比率.试问是否整座房屋A 内猫的比率必定大于整座房屋B 内猫的比率的比率? ?【分析与解】 如下表给出的反例指出:如下表给出的反例指出:如下表给出的反例指出:对所提出问题的回答应该是否定的.对所提出问题的回答应该是否定的.对所提出问题的回答应该是否定的.表中具体写出了各个表中具体写出了各个单元及整座房屋中的宠物情况和猫占宠物总数的比率.单元及整座房屋中的宠物情况和猫占宠物总数的比率. 小升初数学知识点解析:比和比例两个数相除又叫做两个数的比.两个数相除又叫做两个数的比.一、比和比例的性质性质1:若a: b=c a: b=c::d ,则,则(a + c)(a + c)(a + c)::(b + d)= a (b + d)= a::b=c b=c::d ;性质2:若a: b=c a: b=c::d ,则,则(a - c)(a - c)(a - c)::(b - d)= a (b - d)= a::b=c b=c::d ;性质3:若a: b=c a: b=c::d ,则,则(a +x c)(a +x c)(a +x c)::(b +x d)=a (b +x d)=a::b=c b=c::d ;(x 为常数)性质4:若a: b=c a: b=c::d ,则a ×d ×d = = = b×b×b×c c ;(即外项积等于内项积即外项积等于内项积) )正比例:如果a ÷b=k(k 为常数为常数)),则称a 、b 成正比;成正比;反比例:如果a ×b=k(k 为常数为常数)),则称a 、b 成反比.成反比.二、比和比例在行程问题中的体现在行程问题中,因为有在行程问题中,因为有速度速度=路程时间,所以:,所以: 当一组物体行走速度相等,那么行走的路程比等于对应时间的反比;当一组物体行走速度相等,那么行走的路程比等于对应时间的反比;当一组物体行走路程相等,那么行走的速度比等于对应时间的反比;当一组物体行走路程相等,那么行走的速度比等于对应时间的反比;当一组物体行走时间相等,那么行走的速度比等于对应路程的正比.当一组物体行走时间相等,那么行走的速度比等于对应路程的正比.1.A 和B 两个数的比是8:5,每一数都减少34后,后,A A 是B 的2倍,试求这两个数.倍,试求这两个数.【分析与解】方法一:设A 为8x 8x,则,则B 为5x 5x,于是有,于是有,于是有(8x-34):(5x-34)=2(8x-34):(5x-34)=2(8x-34):(5x-34)=2::1,x=17x=17,所以,所以A 为136136,,B 为8585.. 方法二:因为减少的数相同,所以前后A A 、、B 的差不变,开始时差占3份,后来差占1份且与B 一样多,也就是说减少的3434,占开始的,占开始的3-1=2份,所以开始的1份为34÷2=17,所以A 为17×8=136,B 为17×5=85.17×5=85.2.近年来.近年来火车火车大提速,大提速,142714274.家禽场里鸡、鸭、鹅三种家禽中公篱与母篱数量之比是2:3,已知鸡、鸭、鹅数量之比是8:7:5,公鸡、母鸡数量之比是1:3,公鸭、母鸭数量之比是3:4.试求公鹅、母鹅的数量比..试求公鹅、母鹅的数量比.【分析与解】 公鸡占家禽场家禽总数的公鸡占家禽场家禽总数的公鸡占家禽场家禽总数的 =21124615:(3544)45:46:(3544)46:47.333345´´+´´=´´+´´=8118751310´=+++,母鸡占总数的310; 公鸭占总数的8338753420´=+++,母鸭占总数的420; 公鹅占总数的213332102020-+=+(),母鹅占总数的234232102020-+=+(),公鹅、母鹅数量之比【分析与解】70cm 的杆子产生影子的长度为175cm;所以影子的长度与杆子的长度比为:所以影子的长度与杆子的长度比为:175175175::70=2.5倍.为322020::3:2.5.在古巴比伦的在古巴比伦的金字塔金字塔旁,旁,其朝西下降的阶梯旁其朝西下降的阶梯旁6m 的地方树立有1根走子,其影子的其影子的前端前端正好到达阶梯的第3阶(箭头箭头)).另外,此时树立l 根长70cm 自杆子,其影子的长度为175cm 175cm,设阶梯各阶的高度,设阶梯各阶的高度与深度都是50cm 50cm,求柱子的高度为多少?,求柱子的高度为多少? 于是,影子的长度为6+1.5+1.6+1.5+1.5×25×25×2.5=11.25.5=11.25.5=11.25,所以杆子的长度为,所以杆子的长度为11.11.25÷225÷225÷2.5=4.5m .5=4.5m .5=4.5m..6.已知三种.已知三种混合物混合物由三种成分A 、B 、C 组成,第一种仅含成分A 和B ,重量比为3:5;第二种只含成分B 和C ,重量比为I :2;第三种只含成分A 和C ,重量之比为2:3.以什么.以什么比例比例取这些混合物,才能使所得的混合物中A ,B 和C ,这三种成分的重量比为3:5:2 ?【分析与解】注意到第一种混合物种A 、B 重量比与最终混合物的A 、B 重量比相同,均为3:5.5.所以,所以,k=65. 标准的时钟每隔56511分钟重合一次.分钟重合一次. 假设经历了假设经历了x 分钟.分钟. 于是,甲钟每隔于是,甲钟每隔52460651124605´´´-分钟重合一次,甲钟重合了246052460´-´×x 次;次; 同理,乙钟重合了同理,乙钟重合了246052460´+´×x 次;次; 于是,需要乙钟比甲钟多重合于是,需要乙钟比甲钟多重合于是,需要乙钟比甲钟多重合 246052460´+´×x-246052460´-´×x=102460´×x=10; 所以,所以,x=24x=24x=24×60;×60;×60; 所以要经历24×60×65511分钟,则为5246065 51165246011´´=´天.于是为65天510(24)10()1111´=天.后来,由一队工人23与二队工人13组成新一队,其余的工人组成新二队.其余的工人组成新二队.两支新队又同时分别接受两项工作量与条件完全相同的工程,两支新队又同时分别接受两项工作量与条件完全相同的工程,两支新队又同时分别接受两项工作量与条件完全相同的工程,结果新二队结果新二队先将第二种、第三种先将第二种、第三种混合物混合物的A 、B 重量比调整到重量比调整到 3 3 3::5,再将第二种、第三种混合物中A 、B 与第一种混合物中A 、B 视为单一物质视为单一物质. .第二种混合物不含第二种混合物不含A ,第三种混合物不含B ,所以1.5倍第三种混合物含A 为3,5倍第二种混合物含B 为5,即第二种、第三种混合物的重量比为5:1.51.5..于是此时含有于是此时含有C 为5×2+15×2+1..5×3=145×3=14.5.5.5,在最终混合物中,在最终混合物中C 的含量为3A 3A//5B 含量的2倍.有14.14.5÷25÷25÷2-1=6.25-1=6.25-1=6.25,所以含有第一种混合物,所以含有第一种混合物6.256.25..即第一、二、三这三种混合物的即第一、二、三这三种混合物的比例比例为6.256.25::5:1.5=251.5=25::2020::6.7.现有男、女职工共1100人,其中全体男工和全体女工可用同样人,其中全体男工和全体女工可用同样天数天数完成同样的工作;若将男工人数和女工人数对调一下,则全体男25天完成的工作,全体女工需36天才能完成,问:男、女工各多少人女工各多少人? ?【分析与解】 直接设出男、女工人数,然后在通过直接设出男、女工人数,然后在通过直接设出男、女工人数,然后在通过方程方程求解,过程会比较繁琐.求解,过程会比较繁琐.设开始男工为“1”,此时女工为“设开始男工为“1”,此时女工为“k k ”,有1名男工相当k 名女工.男工、女工人数对调以后,则男工为“男工为“k k ”,相当于女工“,相当于女工“k k 2”,女工为“I”.,女工为“I”.有k 2:1=361=36::2525,所以,所以于是,开始有男工数为11k+×1100=500人,女工600人.人.8.有甲乙两个钟,甲每天比.有甲乙两个钟,甲每天比标准时间标准时间慢5分钟,而乙每天比标准时间快5分钟,在3月15日的日的零点零点零分的时候两钟正好对准.若已知在某一时刻,乙钟和甲钟时针与分针都分别重合,且在从3月15日开始到这个时候,乙钟时针与分针重合的次数比甲钟多10次,那么这个时候的标准时间是多少次,那么这个时候的标准时间是多少? ?【分析与解】 小时106(60)541111´=分钟.分钟.9.一队和二队两个.一队和二队两个施工施工队的人数之比为3:4,每人工作效率之比为5:4,两队同时分别接受两项工作量与条件完全相同的工程,结果二队比一队早完工96÷147=282´´´´282×4645天.天.144:(282×:(282×4645)=(144×45):(282×46))=(144×45):(282×46)=540。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2022-2023学年小升初数学精讲精练专题汇编讲义第5讲比和比例知识点一:比1.比的意义:两个数相除又叫作两个数的比。
2.比的各部分名称及比的读法:4 : 5=4÷5=0.8↓↓↓↓前项比号后项比值3.比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变4.求比值与化简比(1)求比值:前项除以后项所得的商是比的结果,叫比值。
同类量的比,其比值没有单位名称; 不同类量的比,其比值有单位名称。
例如: 100千米:5时=20千米/时(2)化简比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
把两个数的比化成最简整数比的,称为化简比或比的化简。
5.比与分数、除法的关系关系:比与分数相比,比的前项相当于分子,比的后项相当于分母,比值相当于分数值,比号相当于分数线;比与除法比较,比的前项相当于除法中的被除数,比的后项相当于除法中的除数,比值相当于商,比号相当于除号。
(1)比、分数和除法之间的联系与区别如下表所示:名称比分数除法联系前项分子被除法:(比号)一(分数线)÷(除号)后项分母除数比值分数值商知识精讲除法各部分间的关系可知,比的基本性质、分数的基本性质以及商不变的规律三者只是说法不同,其实质是一样的。
6.按比分配:(1)在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫作按比分配。
(2)按比分配应用题的特征:已知总数量和部分数量的比,求各部分数量。
(3)常用的解题方法有两种:一种是先求总份数,再求各部分量占总量的几分之几,最后求各部分数量;另一种是先求每份是多少,再求几份是多少。
知识点二:比例1.比例的意义:表示两个比相等的式子叫做比例。
2.比例的各部分名称:组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
3.比例的基本性质:在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
4.比和比例的区别(1)比表示两个量相除的关系,它有两项(即前、后项);比例表示两个比相等的式子,它有四项(即两个内项和两个外项)。
(2)比有基本性质,它是化简比的依据;比例出有基本性质,它是解比例的依据。
5.解比例: 解比例就是求比例中的未知项,也就是已知比例中的任意三项,就可以求出未知项。
解比例的依据是比例的基本性质。
知识点三:正比例和反比例1.判断正比例和反比例的方法:(1)分析数量关系,确定哪两种量是相关联的量。
(2)分析两种相关联的量,看它们之间是比值一定还是积一定。
(3)如果是比值一定,就成正比例;如果是积一定,就成反比例;如果比值和积都不是一定的,就不成比例。
2.正比例图像:正比例图像是一条直线。
3.用比例的知识解决实际问题(1)用比例知识解决的实际问题可分为正比例问题和反比例问题两类。
(2)应用比例知识解决实际问题的一般方法和步骤: ①判断题中两种相关联的量是成正比例还是成反比例;②设未知量为x;③列出比例,解比例;④检验并作答。
知识点四:比例尺1.比例尺的意义(1)图上距离和实际距离的比,叫做这幅图的比例尺。
即,(2)图上距离:实际距离=比例尺或图上距离实际距离=比例尺2.比例尺的分类(1)数值比例尺:1:200000或1200000,比例尺一般写成前项是1或后项是1的形式(2)线段比例尺:这种用线段表示的比例尺,叫作线段比例尺3求图上距离或实际距离:图上距离=实际距离×比例尺实际距离=图上距离÷比例尺一、精挑细选(共5题;每题1分,共5分)1.(1分)(2022·开平)下面各组中的两个比,可以组成比例的是()。
A.15:34和13:45B.0.03:0.6和0.4:8C.5:4和12:15 D.2.5:12和16:0.24【答案】B【规范解答】解:A项中,15÷34=415,13÷45=512,415≠512,故不能组成比例;提高达标百分练B项中,0.03÷0.6=0.05,0.4÷8=0.05,故能组成比例;C项中,5÷4=54,12÷15=45,54≠45,故不能组成比例;D项中,2.5÷12=5,16÷0.24=2536,5≠2536,故不能组成比例。
故答案为:B。
【思路点拨】能够组成比例的两个比的比值相等,据此作答即可。
2.(1分)(2022·三水)下面选项中两种量成正比例关系的是()。
A.一袋糖果,已经吃了的数量和剩下的数量B.正方形的边长和面积C.百米比赛中运动员的速度和时间D.圆的直径和周长【答案】D【规范解答】解:A项:一袋糖果,已经吃了的数量和剩下的数量,不成比例;B项:正方形的面积=边长×边长,正方形的边长和面积,不成比例;C项:速度×时间=路程(一定),百米比赛中运动员的速度和时间成反比例;D项:圆的周长÷直径=π(一定),圆的直径和周长成正比例。
故答案为:D。
【思路点拨】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
3.(1分)(2022·西城)有6个完全相同的小长方形纸片,每个小长方形的长是7cm,宽是2cm。
将它们不重叠的放在长方形ABCD中(如图),图中的阴影部分是没有被小长方形覆盖的部分。
长方形ABCD的长和宽的比是()。
A.15:11 B.14:11 C.7:5 D.7:2 【答案】A【规范解答】解:长方形的长=7+2×4=7+8=15(cm);长方形的宽=7+2×2=7+4=11(cm),所以长方形的长和宽的比=15:11。
故答案为:A。
【思路点拨】观察图形可得长方形ABCD的长=小长方形的长+小长方形的宽×4,长方形ABCD的宽=小长方形的长+小长方形的宽×2,再进行相比即可得出答案。
4.(1分)(2022·黄山)甲数的23等于乙的35,甲数和乙数的比是()。
A.2:3 B.2:5 C.3:5 D.9:10 【答案】D【规范解答】解:甲数×23=乙数×35,甲数:乙数=35:23;3 5:23=(35×15):(23×15)=9:10。
故答案为:D。
【思路点拨】在甲数×23=乙数×35中,根据比例的外项之积等于比例的内项之积。
把甲数×23看做比例的外项,乙数×35看做比例的內项,据此改写成比例的形式。
再根据比例的基本性质,比的前项和后项同时乘以或除以同一个数,化为最简整数比。
5.(1分)(2022·新荣)下面各组中的两种量,成正比例的是()。
A.平行四边形的面积一定,它的底与高B.比例尺一定,图上距离与实际距离C.小敏做口算题的总数一定,做对的题数与做错的题数【答案】B【规范解答】选项A,因为底×高=平行四边形的面积,所以平行四边形的面积一定,它的底与高成反比例;选项B,因为图上距离:实际距离=比例尺,所以比例尺一定,图上距离与实际距离成正比例;选项C,因为做对的题数+做错的题数=口算题的总数,这里是和一定,所以不成比例。
故答案为:B。
【思路点拨】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
二、判断正误(共5题;每题1分,共5分)6.(1分)(2022·安新)60米赛跑,甲用15秒,乙用12秒。
甲和乙跑步速度的比是5:4。
()【答案】(1)错误【规范解答】解:(60÷15):(60÷12)=4:5。
原题说法错误。
故答案为:错误。
【思路点拨】用路程除以时间分别求出两人的速度,然后写出速度的比并化成最简整数比即可。
7.(1分)(2022·灵武)每袋大米的质量一定,大米的总质量和袋数成正比例。
()【答案】(1)正确【规范解答】解:每袋大米的质量一定,大米的总质量和袋数成正比例。
故答案为:正确。
【思路点拨】若y=kx(k为常数,x,y≠0),那么x和y成正比例。
8.(1分)(2022·蕲春)含糖率10%的糖水中,糖和水的比是1:10。
()【答案】(1)错误【规范解答】解:含糖率10%的糖水中,糖和水的比是10%:(1-10%)=10%:90%=1:9。
原题说法错误。
故答案为:错误。
【思路点拨】把糖水的重量看作“1”,那么糖的重量是10%,水的重量是(1-10%)。
由此写出糖与糖水的比并化成最简整数比即可。
9.(1分)(2022·平山)如果a×b=12×7,那么a:b=12:7。
()【答案】(1)错误【规范解答】解:a:b=(12×7):b2,原题干说法错误。
故答案为:错误。
【思路点拨】比例的基本性质:在比例里,两个内项积等于两个外项积。
10.(1分)(2022·宁强)在浓度为10%的1000克盐水中加入100克盐,溶解之后,盐与盐水的质量比是2:11。
()【答案】(1)正确【规范解答】解:1000×10%=100(克),(100+100):(1000+100)=2:11,所以盐与盐水的质量比是2:11。
故答案为:正确。
【思路点拨】原来盐水中盐的质量=原来盐水的质量×浓度,所以溶解之后盐与盐水的质量比=(原来盐水中盐的质量+加入的盐的质量):(盐水的质量+加入的盐的质量)。
三、仔细想,认真填(共8题;每空1分,共14分)11.(1分)(2022·合阳)在一个比例中,两个外项互为倒数,其中一个内项是10以内最大的质数,另一个内项是。
【答案】1 7【规范解答】解:在一个比例中,两个外项互为倒数,其中一个内项是10以内最大的质数,另一个内项是17。
故答案为:17。
【思路点拨】乘积是1的两个数互为倒数。
10以内最大的质数是7。
根据比例的基本性质可知,另一个内项就是7的倒数。
12.(2分)(2022·安新)观察如图数轴上的点,点A到0的距离与点D到0的距离相等,但方向相反。
点A是,点B与点C表示的数的最简整数比是。
【答案】﹣1;8:21【规范解答】解:点A是-1;点B与点C表示的数的最简整数比是:23:74=8:21。
故答案为:-1;8:21。
【思路点拨】点A在0的左边,0的左边都是负数;点B是23,点C是74,写出两个数的比并化成最简整数比即可。
