(完整版)小学六年级_比和比例知识点梳理
小学六年级_比和比例知识点梳理(最新整理)
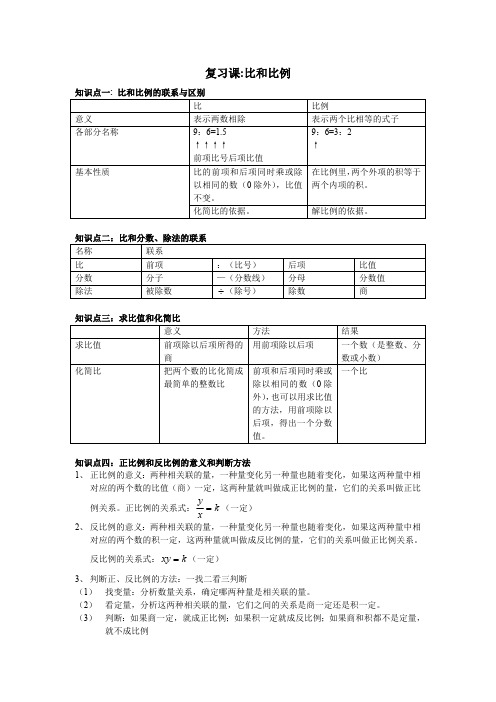
复习课:比和比例知识点一: 比和比例的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9:6=1.5↑↑↑↑前项比号后项比值9:6=3:2↑比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
基本性质化简比的依据。
解比例的依据。
知识点二:比和分数、除法的联系名称联系比前项:(比号)后项比值分数分子—(分数线)分母分数值除法被除数(除号)÷除数商知识点三:求比值和化简比意义方法结果求比值前项除以后项所得的商用前项除以后项一个数(是整数、分数或小数)化简比把两个数的比化简成最简单的整数比前项和后项同时乘或除以相同的数(0除外),也可以用求比值的方法,用前项除以后项,得出一个分数值。
一个比知识点四:正比例和反比例的意义和判断方法1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:(一定)k xy=2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:(一定)k xy =3、判断正、反比例的方法:一找二看三判断(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例4、正比例、反比例的区别与联系不同点名称意义不相同变化方向不相同关系式不同相同点正比例两种量中相对应的两个数的比值,也就是商一定一种量扩大(或缩小),另一种量也随之扩大(或缩小)。
(一定)k xy =反比例两种量中相对应的两个数的积一定一种量扩大(或缩小),另一种量也随之缩小(或扩大)。
小学六年级--比和比例知识点梳理

复习课:比和比例知识点三:求比值和化简比 知识点四:正比例和反比例的意义和判断方法1、 正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:k xy=(一定) 2、 反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:k xy =(一定)3、 判断正、反比例的方法:一找二看三判断(1) 找变量:分析数量关系,确定哪两种量是相关联的量。
(2) 看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3) 判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例知识点五:用比例知识解决问题1、按比例分配问题(1)按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2)解题方法一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量÷总份数=平均每份的量(归一)”,再用“一份的量⨯各部分量所对应的份数”,求出各部分的量。
用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式,再解比例求出x。
2、用正、反比例知识解答应用题的步骤(1)分析数量关系。
判断成什么比例。
(2)找等量关系。
如果成正比例,则按等比找等量关系式;如果成反比例,则按等积找等量关系式。
(3)解比例式。
设未知数为x,并代入等量关系式,得正比例式或反比例式。
(4)解比例。
(5)检验并写出答语。
小学六年级比与比例知识点梳理
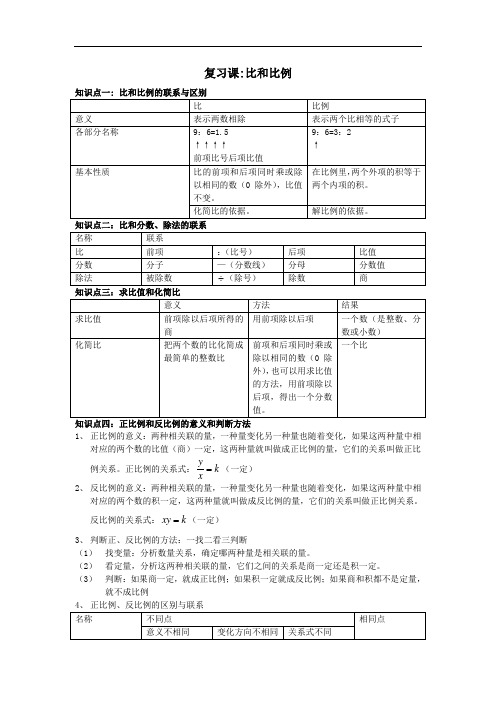
复习课:比和比例知识点三:求比值和化简比1、 正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:k xy=(一定) 2、 反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:k xy =(一定)3、 判断正、反比例的方法:一找二看三判断(1) 找变量:分析数量关系,确定哪两种量是相关联的量。
(2) 看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3) 判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例知识点五:用比例知识解决问题 1、 按比例分配问题 (1) 按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2) 解题方法一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量÷总份数=平均每份的量(归一)”,再用“一份的量⨯各部分量所对应的份数”,求出各部分的量。
用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x 的比例式,再解比例求出x 。
2、 用正、反比例知识解答应用题的步骤(1)分析数量关系。
判断成什么比例。
(2)找等量关系。
如果成正比例,则按等比找等量关系式;如果成反比例,则按等积找等量关系式。
(3)解比例式。
设未知数为x ,并代入等量关系式,得正比例式或反比例式。
(4)解比例。
(5)检验并写出答语。
精讲典型题 例题1(1) 一项工程,甲单独做要4天,乙单独做要5天完成,甲和乙的工作效率比是():()(2) 把2米:4厘米化成最简单的整数比是(),比值是()。
六年级数学必考知识点

六年级数学必考知识点六年级数学必考知识点1.比和比例的意义比的意义是两个数的除又叫做两个数的比,而比例的意义是表示两个比相等的式子是叫做比例。
比是表示两个数相除,有两项;比例是一个等式,表示两个比相等,有四项。
因此,比和比例的意义也有所不同。
而且,比号没有括号的含义而另一种形式,分数有括号的含义!2.比的基本性质:比的前项和后项都乘以或除以一个不为零的数。
比值不变。
用于化简比。
3.比例的性质:在比例里,两个外项的乘积等于两个内项的乘积。
比例的性质用于解比例。
4.比和比例的联系:比和比例有着密切联系。
比是研究两个量之间的关系,所以它有两项;比例是研究相关联的两种量中两组相对应数的关系,所以比例是由四项组成。
比例是由比组成的,成比例的两个比的比值一定相等。
5.比和比例的区别(1)意义、项数、各部分名称不同。
比表示两个数相除;只有两个项:比的前项和后项。
如:a:b这是比比例是一个等式,表示两个比相等;有四个项:两个外项和两个内项。
a:b=3:4这是比例。
(2)比的基本性质和比例的基本性质意义不同、应用不同。
联系:比例是由两个相等的比组成。
6.正比例:若A扩大或缩小几倍,B也扩大或缩小几倍(AB的商不变时),则A与B成正比。
反比例:若A扩大或缩小几倍,B也缩小或扩大几倍(AB的积不变时),则A与B成反比。
比例尺:图上距离与实际距离的比叫做比例尺。
六年级数学常考知识点1.百分数与分数的区别(1)意义不同。
百分数是“表示一个数是另一个数的百分之几的数。
”它只能表示两数之间的倍数关系,不能表示某一具体数量。
分数是“把单位‘1’平均分成若干份,表示这样一份或几份的数”。
分数还可以表示两数之间的倍数关系。
(2)应用范围不同。
百分数在生产、工作和生活中,常用于调查、统计、分析与比较。
而分数常常是在测量、计算中,得不到整数结果时使用。
(3)书写形式不同。
百分数通常不写成分数形式,而采用百分号“%”来表示。
而分数的分子只能是自然数,它的表示形式有:真分数、假分数、带分数,计算结果不是最简分数的一般要通过约分化成最简分数,是假分数的要化成带分数。
(完整版)小学六年级__比和比例知识点梳理
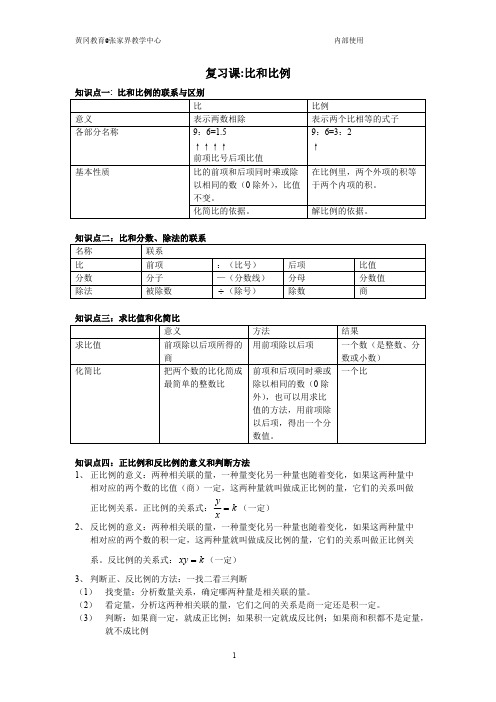
复习课:比和比例知识点一: 比和比例的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9:6=1.5↑↑↑↑前项比号后项比值9:6=3:2↑比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
基本性质化简比的依据。
解比例的依据。
知识点二:比和分数、除法的联系名称联系比前项:(比号)后项比值分数分子—(分数线)分母分数值除法被除数(除号)÷除数商知识点三:求比值和化简比意义方法结果求比值前项除以后项所得的商用前项除以后项一个数(是整数、分数或小数)化简比把两个数的比化简成最简单的整数比前项和后项同时乘或除以相同的数(0除外),也可以用求比值的方法,用前项除以后项,得出一个分数值。
一个比知识点四:正比例和反比例的意义和判断方法1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:(一定)k xy=2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:(一定)k xy =3、判断正、反比例的方法:一找二看三判断(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例4、正比例、反比例的区别与联系不同点名称意义不相同变化方向不相同关系式不同相同点正比例两种量中相对应的两个数的比值,也就是商一定一种量扩大(或缩小),另一种量也随之扩大(或缩小)。
(一定)kxy=反比例两种量中相对应的两个数的积一定一种量扩大(或缩小),另一种量也随之缩小(或扩大)。
小学六年级__比和比例知识点梳理.docx

复习课 :比和比例知识点一 :比和比例的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9: 6=9:6=3: 2↑↑↑↑↑前项比号后项比值基本性质比的前项和后项同时乘或除在比例里,两个外项的积等于以相同的数(0 除外),比值两个内项的积。
不变。
化简比的依据。
解比例的依据。
知识点二:比和分数、除法的联系名称联系比前项:(比号)后项比值分数分子—(分数线)分母分数值除法被除数(除号)除数商知识点三:求比值和化简比意义方法结果求比值前项除以后项所得的用前项除以后项一个数(是整数、分商数或小数)化简比把两个数的比化简成前项和后项同时乘或一个比最简单的整数比除以相同的数( 0除外),也可以用求比值的方法,用前项除以后项,得出一个分数值。
知识点四:正比例和反比例的意义和判断方法1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:y k(一定)x2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:xy k (一定)3、判断正、反比例的方法:一找二看三判断(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例4、正比例、反比例的区别与联系名称不同点意义不相同正比例两种量中相对应的两个数的比值,也就是商一定反比例两种量中相对应的两个数的积一定变化方向不相同关系式不同一种量扩大(或yk (一定)缩小),另一种量x也随之扩大(或缩小)。
一种量扩大(或xy k (一定)缩小),另一种量也随之缩小(或扩大)。
小学六年级:比与比例知识点梳理

小学六年级:比与比例知识点梳理YUKI was compiled on the morning of December 16, 2020复习课:比和比例知识点一: 比和比例的联系与区别知识点二:比和分数、除法的联系知识点三:求比值和化简比知识点四:正比例和反比例的意义和判断方法1、 正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:k xy =(一定) 2、 反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:k xy =(一定)3、 判断正、反比例的方法:一找二看三判断(1) 找变量:分析数量关系,确定哪两种量是相关联的量。
(2) 看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3) 判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量,就不成比例4、 正比例、反比例的区别与联系知识点五:用比例知识解决问题1、按比例分配问题(1)按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2)解题方法一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量÷总份数=平均每份的量(归一)”,再用“一份的量⨯各部分量所对应的份数”,求出各部分的量。
用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式,再解比例求出x。
2、用正、反比例知识解答应用题的步骤(1)分析数量关系。
小学六年级比和比例知识点

小学六年级比和比例知识点1、比和比例的联系与区别:比与比例的区别1、意义不同比的意义两个数相除又叫做两个数的比。
比例的意义表示两个比相等的式子叫做比例。
2、名称不同比的名称两点读作比,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比例的名称组成比例的四个数叫做比例的项,两端的两项叫做比例的的外项,中间的两项叫做比例的内项。
3、性质不同比的性质比的前项和后项同时乘或者除以相同的数(0除外),比值不变。
比例的性质在比例里,两个外项的积等于两个内项的积。
4、应用不同应用比的意义求比值。
应用比的性质化简比。
应用比例的意义判断两个不能否组成比例。
应用比例的性质不但可以判断两个比能否组成比例,还可以解比例。
2、比同分数、除法的联系与区别:比分数除法联系前项分子被除数比号分数线除号后项分母除数比值分数值商比的基本性质分数的基本性质除法的商不变性质区别比表示两个数之间的关系。
分数表示一个数。
除法表示一种运算。
3、求比值与化简比的区别:一般方法结果求比值根据比值的意义,用前项除以后项。
是一个数。
可以是整数、小数或分数。
化简比根据比的基本性质,把比的前项和后项都乘或除以相同的数(零除外)。
是一个比。
它的前项和后项都是整数,并且是互质数。
4、化简比:(1)整数比的化简方法是:用比的前项和后项同时除以它们的最大公约数。
(2)小数比的化简方法是:先把小数比化成整数比,再按整数比化简方法化简。
(3)分数比的化简方法是:用比的前项和后项同时乘以分母的最小公倍数。
5、比例尺:图上距离和实际距离的比叫做这幅图的比例尺。
6、比例尺=图上距离︰实际距离7、正比例和反比例(1)正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
(2)反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习课:比和比例
知识点四:正比例和反比例的意义和判断方法
1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相
对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:〜 k (一定)
x
2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积
一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:xy k (一定)
3、判断正、反比例的方法:一找二看三判断
(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量, 就不成比例
4、正比例、反比例的区别与联系
知识点五:用比例知识解决问题
1、按比例分配问题
(1)按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2)解题方法
一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量
占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的
量是多少
归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量总份数=平均每份的量(归一)",再用"一份的量各部分量所对应的份数”,求出各部分的量。
用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式,再解比例求出X。
2、用正、反比例知识解答应用题的步骤
(1)分析数量关系。
判断成什么比例。
(2)找等量关系。
如果成正比例,则按等比找等量关系式;如果成反比例,则按等积找等量关系式。
(3)解比例式。
设未知数为X,
并代入等量关系式,得正比例式或反比例式。
(4)解比例。
(5)检验并写出答语。
精讲典型题
例题1填空
(1)一项工程,甲单独做要4天,乙单独做要5天完成,甲和乙的工作效率比是(): ()
(2)把2米:4厘米化成最简单的整数比是(),比值是()。
分析:(1)要求甲乙的工作效率比,关键是要根据工作总量和工作时间求出甲、乙的工作效
11 -. ..................................................................................
率,即用一:-5:4 ;(2)为了简便,化简比和求比值时可以都用前项除以后项,但要注
4 5
意结果的区别。
由于单位不统一,化简要先统一单位,即2米:4厘米=200厘米:4厘米
=50:1=50。
解答(1) 5:4
(2)50:1 50
例题2汉江码头第一货场有750吨货物,分给两个运输队运到另一货场。
甲队有载重6吨
的汽车6辆,乙队有载重8吨的汽车3量,按两个队的运输能力分配,甲、乙两队各应运货多少吨?
解法一分数方法
甲乙两个队的运输能力比(6 6): (8 3) =36:24=3:2 3+2=5
甲队:750 3=450 (吨)
5
乙队:750 2=300 (吨)
5
解法二归一法
解答甲乙两个队的运输能力比(6 6): (8 3) =36:24=3:2
甲队:750 (3+2) 3=450 (吨)
乙队:750 (3+2) 2=300 (吨)
解法三用比例知识解答
解答解:设甲队应运货物X吨。
X : (750— X) = (6 6): (8 3)
X : (750— X) =3:2
5X =2250
X=450
750- 450=300 (吨)
答:甲队应运货物450吨,乙队应运货物300吨。
例题三李阿姨是个剪纸艺人,平时李阿姨每天工作6小时,能剪出72张剪纸;节假日期间,李阿姨每天工作8小时,能剪出96张剪纸。
(1) 写出李阿姨平时和节假日剪纸张数及相应工作时间的比
(2) 上面的两个比能组成比例吗?为什么?
(3) 如果李阿姨要剪120张剪纸,需要多少个小时?
解答(1)平时剪纸张数和工作时间的比:72:6=12:1
节假日剪纸张数和工作时间的比:96:8=12:1
(2) 两个比的比值相等,能组成比例。
72:6=96:8
(3) 解:设需要X小时。
72 120
6 X
72 X =6 120
X =10
答:需要10小时。
巧练考点题
1. 请你填一填
(1) 2.1:0.9化简成最简单的整数比是(),比值是()。
(2) 甲乙两数的比是4:5,甲数是乙数的(),乙数是甲乙和的()
(3) 一个最简单的整数比的比值是 1.5,这个比是()
(4) 4.5与它的倒数的比是() (5) ()
24= - =24: () = () %
8
(6) 如果 a 7= b 2(a 、b 都不为 0),那么 a : b =():()
(7)
除数、被除数的比是 1:3,被除数、除数、商的和是
35,被除数是()
(8) 一汽车工人加工一批零件,如下表
① 请按每天生产量与需要时间的关系填表。
② 这批零件有()个
③ 表中两种量是否成比例:(),如果成比例成()比例
(10)判断一些生活中的实例。
① 用煤的大数一定,每天用煤量与总用煤量()比例。
② 一本书的页数一定,已看的页数与没看的页数()比例 ③ 三角形的面积一定,三角形的底与高()比例。
2判断题 (1)
化简比的结果是一个商,可以使小数、
分数或整数。
()
………
1,, F 1,,F …、一 I
(2) 走同一段路,甲用 —小
时,乙用一小时,甲、乙的速度之比是 5:4。
()
(4) 一条道路,已修的米数和未修的米数成反比例。
()
3选择题
k 5
(1) ------- y ,且x 和y 都不为0,当k 一正时,x 和y 成()比例。
4. 解决问题。
(1) 药液与水的比是1:1500,如果倒入药液20.5g,需要加多少克水呢?
(2)
从儿童节那天开始,亮亮前七天看书 210页,照这样计算,
这个月亮亮一共看书多少
5
4
(3)在一个比例里,如果两个外项互为倒数,那么两个内项也互为倒数。
A. 成正比例
B. 成反比例
C. 不成比例
(2)杭州西湖南北长 3.3km ,东西宽2.8km 。
南北长和东西宽的比是() A.33km : 28km B.3.3. : 2.8
(3) 一个三角形,三个内角的度数比是
A.锐角三角形
B.直角三角形
C.33: 8
1:4:5,这个三角形是()
C.钝角三角形
(4)在比例尺
一!一的地图上,量得
100000
A 、
B 两地的距离是 2cm,那么A 、B 两地的实际
距离是()。
A.0.2km
B.2km
C.20km
(3)如果用边长30cm的方砖给一个房间铺地,需要100块。
如果改用边长50cm的方砖铺地,需要多少块?。
