第一章 半导体物理基础2要点
第一章 半导体物理基础2
Ec
Ei
EV
(c) (d) (e)
EF
(a)
(b )
强p型
p型
本征
n型
强n型
费米能级EF反映的是电子在不同能态上的填充水平
半导体材料与器件
当温度一定时,n0 、p0之积与EF无关;这表明:导带电 子浓度与价带空穴浓度是相互制约的,这是动态热平 衡的一个反映。
Ec EF EF Ev n0 p0 N c N v exp exp kT kT Ec Ev Eg / kT N c N v exp Nc Nve kT
由于kT是个很小的能量值(常温下),对于常见的 半导体(Si、Ge、GaAs)来说,其禁带能量要远 大于kT,从而使得费米能级相对于禁带中央的偏移 总是很小(几十meV) Eg(Si): 1.12eV
50meV
半导体材料与器件
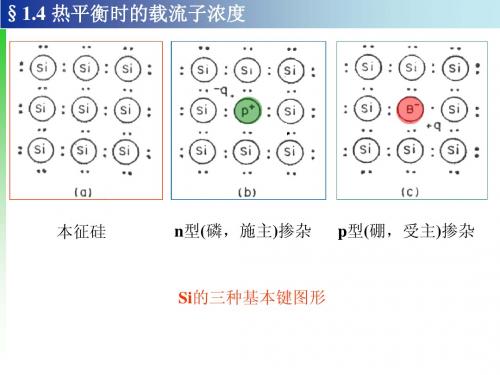
掺杂原子与能级 为什么要掺杂?
半导体的导电性强烈地随掺杂而变化
硅中的施主杂质与受主杂质
*
3/ 2
其中Nv为价带的有效状态密度
2 m p kT Nv 2 2 h
*
3/ 2
半导体材料与器件
有效状态密度和有效质量有关 在一定温度下,特定半导体的有效状态密度为常量 平衡半导体的载流子浓度和费米能级EF的位臵密切相 关 Ec EF 指数项里的分子总 n0 N c exp 为负数,这保证了 kT EF Ev 指数项小于1,对应 于载流子浓度小于 p0 N v exp kT 状态密度的事实
3/ 2
T↑,NC、NV↑
f(EC) 、 f(EV) ~T
半导体物理_01基础知识概论

3、晶体中电子的状态——布洛赫定理与波函数的形式
波函数的形式——布洛赫定理证明:
定义平移算符Tˆ
r am
:
Tˆ
r am
f
xr
f
xr
mar
特点:Tˆ arm Tˆ arn Tˆ arn Tˆ arm 互易性
可以证明:Tˆ
r am
Hˆ
xr
HˆTˆ
r am
xr
Hˆ
xr
mar
因此,若 xr 是 Hˆ 的本征函数,则经过平移后的 xr mar
− N个Si原子组成晶体,形成的两个能带不与s、p能级相对
应,它们都包含2N个状态,各可容纳4N个电子:下面一个 能带填满4N个价电子,通常称为满带(价带);上面一个能带 是空的,称为空带(导带);二者之间是不允许电子状态存在 的禁区——禁带。
1.2.2 半导体中电子的状态和能带(数学分析)1
1、数学物理模型和近似
0
a
k
a
布里渊区按照E(k)的不连续点进行划分,对于一维晶体:
第一布里渊区 第二布里渊区
k
a
a
2 k ,
a
a
k 2
a
a
禁带在布里渊区边界,允带 在布里渊区之内
以此类推,有第三、第四布里渊区
1.2.2 半导体中电子的状态和能带(数学分析)11
3、晶体中电子的状态——布里渊区与能带 − E~ k关系的不连续点对应禁带,在布里渊区边界;
uk x na uk x
以上就是布洛赫定理
自由电子波函数
1.2.2 半导体中电子的状态和能带(数学分析)7
3、晶体中电子的状态——晶体中的电子与自由电子的比较 ➢ 波函数形式相似
半导体物理器

特点:对于光学波,相邻两种不同原子的振动方向是相反的。原胞的质心保持不动,由此也可以定性的看出,波长很长的光学波(长光学波)代表原胞中两个原子的相对振动。
晶格振动能量的量子化 ---声子
电离杂质散射
平均自由时间与驰豫时间 载流子在电场中作漂移运动时,只有在连续两次散射之间的时间称为自由时间,取极多次而求平均值,则称之为载流子的平均自由时间,常用τ表示。
第一章 半导体物理基础
单击添加副标题
方法:
1、本课程的主要内容
概述
01
02
1.1半导体中的电子状态
1.2载流子的统计分布
●导带电子浓度
(1-57)
其中
称为导带有效状态密度
●价带空穴密度
(1-60)
其中
称为价带有效状态密度
1.2载流子的统计分布
●导带电子浓度和价带空穴浓度之积
散射机构 平均自由时间与散射几率互为倒数。 晶格振动散射
2.载流子的散射
1.5载流子的输运
——扩散系数
(1-129)
(1-133)
扩散运动和扩散电流 电子扩散电流密度
流密度 空穴扩散电流密度 在漂移和扩散同时存在的情况下,空穴和电子的流密度分别为:
1.5载流子的输运
1.5载流子的输运
4. 电流密度
1.6非平衡载流子
3.修正的欧姆定律
其中:
分别称为电子和空穴的等效电导率。修正欧姆定律虽然在形式上和欧姆定律一致,但它包括了载流子的漂移和扩散的综合效应。
从修正欧姆定律可以看出,费米能级恒定(即 )是电流为零的条件。处于热平衡的半导体,费米能级恒定。或者说,热平衡系统具有统一的费米能级。
1.6非平衡载流子
半导体物理基础第一章课件

1.7.5只有一种杂质的半导体
• 2、P型半导体
• 在杂质饱和电离的温度范围内有:p N a • 导带电子浓度为: n ni2 ni2
p Na
• 费米能级为
EF
EV
KT ln
NV Na
EF
Ei
KT
ln
Na ni
43
1.7.5只有一种杂质的半导体
• 结论:对于P型半导体,在杂质饱和电离 温度范围之内,费米能级位于价带顶之上, 本征费米能级之下。随着掺杂浓度提高, 费米能级接近价带顶;随着温度升高,费 米能级远离价带顶。
成共价键时,将因缺少一个价电子而形 成一个空穴,于是半导体中的空穴数目 大量增加。
22
1.6杂质能级
• Acceptor,掺入半导体的杂质原子向半导 体中提供导电的空穴,并成为带负电的 离子。
• 掺入受主杂质的半导体为P(Positive)型 半导体。施主杂质的浓度记为NA。
23
1.6杂质能级
• 受主接受电子称为受主杂 志,提供了一个局域化的 电子态,相应的能级称为 受主能级—Ea。
NV
2 2mdp KT
h3
3 2
• 称为价带有效状态密度
34
1.7.3能带中电子和空穴的浓度
• 导带电子浓度和价带空穴浓度之积
Eg
np Nc NV e KT • 式 把中它E写g为成禁经带验宽关度系。式与E温g 度有E关g0 , 可T以
• 其 时中的Eg值为。禁带宽度温度系数,Eg0为0K
Chap1 半导体物理基础
1
1.2 能带
一、能带的形成 • 能级:电子所处的能量状态。 • 当原子结合成晶体时,原子最外层的价
半导体物理1-8章重点总结

半导体重点总结(1-7章)绪论1. 制作pn 结的基本步骤。
(重点,要求能够画图和看图标出步骤)第一章. 固体晶体结构1. 半导体基本上可以分为两类:位于元素周期表IV 元素半导体材料和化合物半导体材料。
大部分化合物半导体材料是III 族和V 族化合形成的。
2. 元素半导体,如:Si 、Ge ; 双元素化合物半导体,如:GaAs (III 族和V 族元素化合而成)、InP 、ZnS 。
类似的也有三元素化合物半导体。
3. 固体类型:(a )无定形(b )多晶(c )单晶 图见P6 多晶:由两个以上的同种或异种单晶组成的结晶物质。
多晶没有单晶所特有的各向异性特征 准晶体: 有长程的取向序,沿取向序的对称轴方向有准周期性,但无长程周期性。
似晶非晶。
4. 原胞和晶胞:原胞是可以通过重复形成晶格的最小晶胞。
晶胞就是可以复制出整个晶体 的小部分晶体。
5. (a )简立方 1 个原子(b )体心立方 2 个原子(c )面心立方 4 个原子计算方法:顶点的一个原子同时被8个晶胞共享,因此对于所求晶胞而言只占有了该原子的1/8;边上、面心和体心原子分别同时被4,2,1个晶胞共享,对于所求晶胞而言分别占有了该原子的1/4,1/2,1/2.如此计算。
例如(c )图中8*1/8+6*1/2=1+3=4. 6. 晶格常数:所取的立方体晶胞的边长。
单位为A ,1A=10^-8cm. 7. 原子体密度:原子个数/体积。
比如上图(c )假设晶格常数为5A 。
求原子体密度。
8.密勒指数(取面与x,y,z 平面截距的倒数):密勒指数描述晶面的方向,任何平行平面都有相同的密勒指数。
9. 特定原子面密度:原子数/截面面积。
计算方法:计算原子面密度时求原子个数的方法与求体密度时的方法类似,但是应当根据面的原子共用情况来计算。
其中有一种较为简便的算法:计算该面截下该原子的截面的角度除处以360,即为该面实际占有该原子的比例。
举例1:计算下图(a )中所显示面所拥有的原子个数和原子面密度:该面截取了顶角四个原子和体心一个原子,顶角每个原子与面的截面角度为90度,90/360=1/4,体心原子与面的截面角度为360度,360/360=1,所以原子总数,1+1+1/4*4=2()223384 3.210510cm ρ-==⨯⨯个原子/举例2:第一次作业中有一道小题是计算硅晶体在晶面(1,1,1)的面密度,晶格常数为a ,如下图可以知道如图所示的等边三角形的边长为√2*a,三个角顶点截面角度为60度,所以该面实际占据这个三个点的比率都为1/6,三个面心点截面角度为180度,所以该面实际占据这个三个点的比率都为1/2.所以该面拥有原子数为3*1/6+3*1/2=1/2+3/2=2.等边三角形面积为√3/2*a^2,所以可以算出面密度为4/(√3a^2).10. 晶向:与晶面垂直的矢量(在非简立方体晶格中不一定成立)。
半导体物理复习资料全

第一章 半导体中的电子状态1. 如何表示晶胞中的几何元素?规定以阵胞的基矢群为坐标轴,即以阵胞的三个棱为坐标轴,并且以各自的棱长为单位,也称晶轴。
2. 什么是倒易点阵(倒格矢)?为什么要引入倒易点阵的概念?它有哪些基本性质? 倒格子: 2311232()a a b a a a π⨯=⋅⨯3122312()a a b a a a π⨯=⋅⨯1233122()a a b a a a π⨯=⋅⨯倒格子空间实际上是波矢空间,用它可很方便地将周期性函数展开为傅里叶级数,而傅里叶级数是研究周期性函数的基本数学工具。
3. 波尔的氢原子理论基本假设是什么?(1)原子只能处在一系列不连续的稳定状态。
处在这些稳定状态的原子不辐射。
(2)原子吸收或发射光子的频率必须满足。
(3)电子与核之间的相互作用力主要是库仑力,万有引力相对很小,可忽略不计。
(4)电子轨道角动量满足:h m vr nn π== 1,2,3,24. 波尔氢原子理论基本结论是什么? (1) 电子轨道方程:0224πεe r mv = (2) 电子第n 个无辐射轨道半径为:2022meh n r n πε= (3) 电子在第n 个无辐射轨道大巷的能量为:222042821hn me mv E n n ε== 5. 晶体中的电子状态与孤立原子中的电子状态有哪些不同?(1)与孤立原子不同,由于电子壳层的交迭,晶体中的电子不再属于某个原子,使得电子在整个晶体中运动,这样的运动称为电子共有化运动,这种运动只能在相似壳间进行,也只有在最外层的电子共有化运动才最为显著。
(2)孤立原子钟的电子运动状态由四个量子数决定,用非连续的能级描述电子的能量状态,在晶体中由于电子共有化运动使能级分裂为而成能带,用准连续的能带来描述电子的运动状态。
6. 硅、锗原子的电子结构特点是什么?硅电子排布:2262233221p s p s s锗电子排布:22106262244333221p s d p s p s s价电子有四个:2个s 电子,2个p 电子。
半导体器件物理教案课件

半导体器件物理教案课件PPT第一章:半导体物理基础知识1.1 半导体的基本概念介绍半导体的定义、特点和分类解释n型和p型半导体的概念1.2 能带理论介绍能带的概念和能带结构解释导带和价带的概念讲解半导体的导电机制第二章:半导体材料与制备2.1 半导体材料介绍常见的半导体材料,如硅、锗、砷化镓等解释半导体材料的制备方法,如拉晶、外延等2.2 半导体器件的制备工艺介绍半导体器件的制备工艺,如掺杂、氧化、光刻等解释各种制备工艺的作用和重要性第三章:半导体器件的基本原理3.1 晶体管的基本原理介绍晶体管的结构和工作原理解释n型和p型晶体管的概念讲解晶体管的导电特性3.2 半导体二极管的基本原理介绍半导体二极管的结构和工作原理解释PN结的概念和特性讲解二极管的导电特性第四章:半导体器件的特性与测量4.1 晶体管的特性介绍晶体管的主要参数,如电流放大倍数、截止电流等解释晶体管的转移特性、输出特性和开关特性4.2 半导体二极管的特性介绍半导体二极管的主要参数,如正向压降、反向漏电流等解释二极管的伏安特性、温度特性和频率特性第五章:半导体器件的应用5.1 晶体管的应用介绍晶体管在放大电路、开关电路和模拟电路中的应用解释晶体管在不同应用电路中的作用和性能要求5.2 半导体二极管的应用介绍半导体二极管在整流电路、滤波电路和稳压电路中的应用解释二极管在不同应用电路中的作用和性能要求第六章:场效应晶体管(FET)6.1 FET的基本结构和工作原理介绍FET的结构类型,包括MOSFET、JFET等解释FET的工作原理和导电机制讲解FET的输入阻抗和输出阻抗6.2 FET的特性介绍FET的主要参数,如饱和电流、跨导、漏极电流等解释FET的转移特性、输出特性和开关特性分析FET的静态和动态特性第七章:双极型晶体管(BJT)7.1 BJT的基本结构和工作原理介绍BJT的结构类型,包括NPN型和PNP型解释BJT的工作原理和导电机制讲解BJT的输入阻抗和输出阻抗7.2 BJT的特性介绍BJT的主要参数,如放大倍数、截止电流、饱和电流等解释BJT的转移特性、输出特性和开关特性分析BJT的静态和动态特性第八章:半导体存储器8.1 动态随机存储器(DRAM)介绍DRAM的基本结构和工作原理解释DRAM的存储原理和读写过程分析DRAM的性能特点和应用领域8.2 静态随机存储器(SRAM)介绍SRAM的基本结构和工作原理解释SRAM的存储原理和读写过程分析SRAM的性能特点和应用领域第九章:半导体集成电路9.1 集成电路的基本概念介绍集成电路的定义、分类和特点解释集成电路的制造工艺和封装方式9.2 集成电路的设计与应用介绍集成电路的设计方法和流程分析集成电路在电子设备中的应用和性能要求第十章:半导体器件的测试与故障诊断10.1 半导体器件的测试方法介绍半导体器件测试的基本原理和方法解释半导体器件测试仪器和测试电路10.2 半导体器件的故障诊断介绍半导体器件故障的类型和原因讲解半导体器件故障诊断的方法和步骤第十一章:功率半导体器件11.1 功率二极管和晶闸管介绍功率二极管和晶闸管的结构、原理和特性分析功率二极管和晶闸管在电力电子设备中的应用11.2 功率MOSFET和IGBT介绍功率MOSFET和IGBT的结构、原理和特性分析功率MOSFET和IGBT在电力电子设备中的应用第十二章:光电器件12.1 光电二极管和太阳能电池介绍光电二极管和太阳能电池的结构、原理和特性分析光电二极管和太阳能电池在光电子设备中的应用12.2 光电晶体管和光开关介绍光电晶体管和光开关的结构、原理和特性分析光电晶体管和光开关在光电子设备中的应用第十三章:半导体传感器13.1 温度传感器和压力传感器介绍温度传感器和压力传感器的结构、原理和特性分析温度传感器和压力传感器在电子测量中的应用13.2 光传感器和磁传感器介绍光传感器和磁传感器的结构、原理和特性分析光传感器和磁传感器在电子测量中的应用第十四章:半导体器件的可靠性14.1 半导体器件的可靠性基本概念介绍半导体器件可靠性的定义、指标和分类解释半导体器件可靠性的重要性14.2 半导体器件可靠性的影响因素分析半导体器件可靠性受材料、工艺、封装等因素的影响14.3 提高半导体器件可靠性的方法介绍提高半导体器件可靠性的设计和工艺措施第十五章:半导体器件的发展趋势15.1 纳米晶体管和新型存储器介绍纳米晶体管和新型存储器的研究进展和应用前景15.2 新型半导体材料和器件介绍石墨烯、碳纳米管等新型半导体材料和器件的研究进展和应用前景15.3 半导体器件技术的未来发展趋势分析半导体器件技术的未来发展趋势和挑战重点和难点解析重点:1. 半导体的基本概念、分类和特点。
半导体物理课件:第一章 半导体中的电子状态

14
1.1 半导体的晶格结构和结合性质
4. 闪锌矿结构和混合键
与金刚石结构的区别
▪ 共价键具有一定的极性 (两类原子的电负性不 同),因此晶体不同晶面 的性质不同。
▪ 不同双原子复式晶格。
常见闪锌矿结构半导体材料 ▪ Ⅲ-Ⅴ族化合物 ▪ 部分Ⅱ-Ⅵ族化合物,如硒化汞,碲化汞等半金属材料。
2024/1/4
量子力学认为微观粒子(如电子)的运动须用波 函数来描述,经典意义上的轨道实质上是电子出 现几率最大的地方。电子的状态可用四个量子数 表示。 (主量子数、角量子数、磁量子数、自旋量子数)
▪ 能级存在简并
2024/1/4
19
1.2 半导体中的电子状态和能带
▪ 电子共有化运动
原子中的电子在原子核的势场和其它电子的作用 下,分列在不同的能级上,形成所谓电子壳层 不同支壳层的电子分别用 1s;2s,2p;3s,3p,3d;4s…等符号表示,每一壳层对 应于确定的能量。
29
1.2 半导体中的电子状态和能带
▪ 金刚石结构的第一布里渊区是一个十四面体。
2024/1/4
30
1.2 半导体中的电子状态和能带
3. 导体、半导体、绝缘体的能带
能带产生的原因:
▪ 定性理论(物理概念):晶体中原子之间的相 互作用,使能级分裂形成能带。
▪ 定量理论(量子力学计算):电子在周期场中 运动,其能量不连续形成能带。
•结果每个二度简并的能级都分裂为二个彼此相距 很近的能级;两个原子靠得越近,分裂得越厉害。
2024/1/4
22
1.2 半导体中的电子状态和能带
▪ 内壳层的电子,轨道交叠少,共有化运动弱,可忽略 ▪ 外层的价电子,轨道交叠多,共有化运动强,能级分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常温下(300K):
半导体材料与器件
计算过程中近似假设的合理性 波尔兹曼近似的合理性:EF一般位于禁带中,和导 带底和价带顶的距离都比较远 在状态密度的推导过程中我们使用的E-k关系(抛 物线近似)实际上只在能带极值附近成立 将积分范围从导带顶Ec’(价带底Ev’)推广到了正 无穷大∞(负无穷大-∞),这样做的合理性在于: 导带(价带)中的电子(空穴)基本集中在导带底 (价带顶)附近
3/ 2
T↑,NC、NV↑
f(EC) 、 f(EV) ~T
Ec EF exp kT EF Ev exp kT
T↑,几率↑
半导体材料与器件
EF 位臵的影响
EF→Ec,Ec-EF↓,n0↑ — EF越高,电子(导带)的填充 水平(几率)越高,对应ND(施主杂质浓度)较高; EF→Ev,EF-Ev↓,po↑ — EF越低,电子(价带)的填充 水平越低(空位几率越高),对应NA(受主杂质浓度)较 高。
半导体材料与器件
载流子:在半导体内可以运动形成电流的电子或 (空穴)
载流子的定向运动形成电流; 半导体中电流的大小取决于:载流子的浓度,载流子 的运动速度(定向的平均速度) 对热平衡状态下载流子浓度的推导和计算需要用到状 态密度和分布函数
半导体材料与器件
导带电子和价带空穴的浓度n0和p0方程
fF(E)=0
半导体材料与器件
因而可化简为:
n0
4 2mn h
3
* 3/ 2
Ec
E EF E Ec exp dE kT
为了方便计算,变量代换:
E Ec kT
积分项被称为伽 马函数 / 2
n0
4 2mn kT
III-V族半导体中的替位式杂质 III-V族化合物半导体材料中的掺杂原子对于III-V族化合 物半导体材料来说,其掺杂的情况比较复杂。以砷化镓材 料为例,通常II价元素的杂质(例如Be、Mg、Zn等)在 砷化镓材料中往往取代镓原子的位臵,因而表现为受主特 性,而VI价元素的杂质(例如S、Se、Te等)在砷化镓材 料中则往往取代砷原子的位臵,因而表现为施主特性。至 于IV价元素硅、锗等,在砷化镓晶体材料中则既可以取代 镓原子的位臵,表现出施主特性,也可以取代砷原子的位 臵,表现出受主特性,通常我们把这类杂质称为两性杂质。 实验结果表明,在砷化镓材料中,锗原子往往倾向于表现 为受主杂质,而硅原子则倾向于表现为施主杂质。
*
3/ 2
h
3
Ec EF 1/ 2 exp 0 exp d kT
半导体材料与器件
因而:
Ec EF exp kT Ec EF N c exp kT 2 mn kT n0 2 2 h
半导体材料与器件
Ec
Ec
Ed
Ev
施主杂质电离, n型半导体
电离能:ΔED= EC – ED ;ΔEA= EA – EV Ea 下表中给出了近似计 Ev 算出的电离能。表明 受主杂质电离, 施主杂质在硅和锗中 p型半导体 的电离能大约为几十 个meV。 常温下,这些杂质处 于完全电离状态
半导体材料与器件
半导体材料与器件
对于本征半导体,费米能级位于 禁带中心(附近)
费米能级的位臵需保证 电子和空穴浓度的相等 如果电子和空穴的有效 质量相同,状态密度函数 关于禁带对称。 对于普通的半导体(Si) 来说,禁带宽度的一半, 远大于kT(~21kT),从 而导带电子和价带空穴的 分布可用波尔兹曼近似来 代替
*
3/ 2
其中Nv为价带的有效状态密度
2 m p kT Nv 2 2 h
*
3/ 2
半导体材料与器件
有效状态密度和有效质量有关 在一定温度下,特定半导体的有效状态密度为常量 平衡半导体的载流子浓度和费米能级EF的位臵密切相 关 Ec EF 指数项里的分子总 n0 N c exp 为负数,这保证了 kT EF Ev 指数项小于1,对应 于载流子浓度小于 p0 N v exp kT 状态密度的事实
半导体材料与器件
掺入施主杂质,费米能级 向上(导带)移动,导带 电子浓度增加,空穴浓度 减少 过程:施主电子热激发跃 迁到导带增加导带电子浓 度;施主电子跃迁到价带 与空穴复合,减少空穴浓 度;施主原子改变费米能 级位臵
半导体材料与器件
掺入受主杂质,费米 能级向下(价带)移 动,导带电子浓度减 少,空穴浓度增加
no和po与掺杂有关,决定于掺 杂的类型和数量。
半导体材料与器件
Boltzmann近似的有效性与简并半导体
当费米能级移动到导带内或价带内时,费米能级以下 的所有电子态都几乎被占据。这时称为载流子的简并 化,相应的称该半导体为简并半导体,处理简并半导 体必须应用费米-狄拉克分布函数。
EF
EF
EF EA EF
半导体材料与器件
本征费米能级位臵
由本征半导体的电中性条件: no
po
EC E F N C exp kT
E F Ev Nv kT
EC EF E F EV ln N C ln NV kT kT
EC EV kT NV EF ln 2 2 NC
* 3/ 2
其中Nc为导带的有效状态密度(数量级一般 在1019):
2 mn kT Nc 2 2 h
*
3/ 2
半导体材料与器件
相应的计算表明空穴浓度:
2 m p kT EF Ev p0 2 exp 2 h kT EF Ev N v exp kT
4 2mn h
3
* 3/ 2
Ec
状态密度函数
费米分布函数
1 E Ec E EF 1 exp kT
波尔兹曼近 似
dE
p0
Ev
4 2m p h3
* 3/ 2
Ev '
1 dE Ev E EF E 1 exp kT
过程:价带电子热激发到 受主能级产生空穴,增加 空穴浓度;导带电子跃迁 到受主能级减少导带电子 浓度;受主原子改变费米 能级位臵,导致重新分布
n0 p0 ni ni ni Nc Nve
2
Eg / kT
可见本征载流子浓度只和温度、禁带宽度Eg有关。
半导体材料与器件
Eg 1 3 ln ni A ln T 2 2k T
本征载流子浓度和温度、禁带宽度的关系
T↑,lnT↑,1/T↓,ni↑ 计算出的硅材料本 征载流子浓度与实 测的本征载流子浓 度有偏离,这是因 为我们使用的有效 质量等参数是在低 温下测出的,而随 着温度变化E-k关 系可能变化,因而 理论值与实际值有 偏差。
半导体材料与器件
非本征半导体 非本征半导体:掺入定量的特定的杂质原子(施 主或受主),从而热平衡电子和空穴浓度不同于 本征载流子浓度的半导体材料。
掺入的杂质原子会改变电子和空穴的分布。费米能级 偏离禁带中心位臵。 掺入施主杂质,杂质电离形成导带电子和正电中心 (施主离子),而不产生空穴(实际上空穴减少), 因而电子浓度会超过空穴,我们把这种半导体叫做n型 半导体;在n型半导体中,电子称为多数载流子,相应 空穴成为少数载流子。 相反,掺入受主杂质,形成价带空穴和负电中心(受 主离子),空穴浓度超过电子,p型,多子为空穴。
半导体材料与器件
半导体材料与器件
影响n0 和p0 的因素 mn* 和 mp* 的影响 — 材料的影响 温度的影响
NC、NV ~T
2 kTmn* Nc 2 2 h
2 kTm p* Nv 2 2 h
3/ 2
3/ 2
NC T 3/ 2 NV T
半导体材料与器件
本征半导体在应用上的限制
本征半导体的纯度 对于硅,常温下本征载流子浓度~1010cm-3。为达 到本征条件,要求施主杂质(受主杂质)的浓度小 于本征载流子浓度(考虑完全电离)。则知道杂质 浓度ND(NA)<1010cm-3,则要求硅材料的纯度大 于99.99999999999% 本征载流子浓度随温度变化很大 在室温附近:Si: T ↑, 8K ni↑ 一倍;Ge: T ↑, 12K ni↑ 一倍 本征半导体的电导率不能控制
p E gv E 1 f F E
对应于该能量的空位几率
对应于该能量的状态密度
则整个价带范围内的空穴浓度为:
p0 ' gv E 1 f F E dE
Ev Ev
半导体材料与器件
将上节得到的状态密度和分布函数代入公式得到
n0
Ec '
kT NV 3 Emidgap ln Emidgap kT ln * 2 NC 4 mn
m p*
半导体材料与器件
当空穴有效质量大时,相对应价带有效状态密度大, 因而费米能级向导带偏移以保证导带电子与价带空穴 相等。相反亦然 * *
m p mn , EF Emidgap m p* mn* , EF Emidgap
Ec
Ei
EV
(c) (d) (e)
EF
(a)
(b )
强p型
p型
本征
n型
强n型
费米能级EF反映的是电子在不同能态上的填充水平
半导体材料与器件
当温度一定时,n0 、p0之积与EF无关;这表明:导带电 子浓度与价带空穴浓度是相互制约的,这是动态热平 衡的一个反映。
