初中数学专题等边三角形(1)含答案

合集下载

初中数学三角形专题训练50题-含答案

初中数学三角形专题训练50题含答案(单选、填空、解答题)一、单选题1．根据下列图中所给定的条件，找出全等的三角形（）A ．①和①B ．①和①C ．①和①D ．①和① 2．在ABC 中，作BC 边上的高，以下作图正确的是（）A ．B ．C ．D ． 3．在ABCD 中，①ABC ＝30°，AB ＝8，AC ＝5，则ABCD 的周长是( )A ．11+B ．10+C ．11++5D ．2210++4．如图，在ABC ∆中，=30A ∠，=50ABC ∠，若EDC ABC ∆≅∆，且,,A C D 在同一条直线上，则=BCE ∠（）A ．20B ．30C ．40D ．50 5．如图，在ABC 中，90,70C B ∠=∠=︒︒，点D 、E 分别在AB AC 、上，将ADE 沿DE 折叠，使点A 落在点F 处．则BDF CEF ∠-∠=（）A．20︒B．30︒C．40︒D．50︒6．，则下列结论正确的是（）A．B．C．D．7．如图，在四边形ABCD中，90⊥，A∠=︒，4AD，连接BD，BD CD=∠=∠．若P是BC边上一动点，则DP长的最小值为（）ADB CA．3B．4C．5D．68．如图，在四边形ABCD中①A＝①C＝90°，AB＝CD＜AD，则下列说法中不正确的是()A．AD①BC B．BC＝CD C．AD＝BC D．AB①CD 9．已知：如图，①ABC中，BD为①ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA，过E作EF①AB，F为垂足．下列结论：①①ABD①①EBC；①BE平分①FEC；①AE＝AD＝EC；①S四边形ABCE＝BF×EF．其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个 10．如图，已知①ABC①①DEF ，若AC ＝22，CF ＝4，则CD 的长是（）A ．22B ．18C ．16D ．411．已知Rt △ABC 的周长是4+，斜边上的中线长是2，则S △ABC 为（） A ．16 B ．8 C ．4 D ．12 12．下列结论中，正确的有（）①①ABC 的三边长分别为a ，b ，c ，若b 2+c 2＝a 2，则①ABC 是直角三角形； ①在Rt①ABC 中，已知两边长分别为6和8，则第三边的长为10；①在①ABC 中，若①A ：①B ：①C ＝1：5：6，则①ABC 是直角三角形；①若三角形的三边长之比为1：2A ．3个B ．2个C ．1个D ．0个 13．如图，AC 与BD 相交于点O ，且OA OC =，OB OD =，则下列结论错误的是()A ．AB CD = B ．AC ∠=∠ C ．//AB CD D ．OA OD = 14．下列说法正确的是（）A ．所有的等边三角形是全等形B ．面积相等的三角形是全等三角形C ．到三角形三边距离相等的点是三边中线的交点D ．到三角形三个顶点距离相等的是三边中垂线的交点15．如图：在①ABC 中，G 是它的重心，AG ①CG ，如果32BG AC ⋅=，则①AGC 的面积的最大值是（）A ．B ．8C ．D ．616．如图，在ABC 中，AB AC =，AF 是①BAC 的角平分线，DE 是边AB 上的中垂线．连接BE 、EF ，若BE AC ⊥，EF FC =，则①BEF 的度数是（）A ．30°B ．20°C ．22.5°D ．15° 17．如图，正方形ABCD 中，E 为BC 的中点，CG DE ⊥于G ，延长BG 交CD 于点F ，延长CG 交BD 于点H ，交AB 于N 下列结论：①DE CN =；①13BH BD =；①3DEC BNH S S ∆∆=；①45BGN ∠=︒；①GN EG +=；其中正确结论的个数有（）A ．2个B ．3个C ．4个D ．5个二、填空题18．如图，在①ABC 中，①ABC ＝①ACB ，AB 的垂直平分线交AC 于点M ，交AB 于点N ．连接MB ，若AB ＝8，①MBC 的周长是14，则BC 的长为____．19．如图，①ABC中，①ACB=90°，D、E是边AB上两点，且CD垂直平分BE，CE平分①ACD，若BC=2，则AC的长为_______.20．用同样粗细、同种材料的金属线，制作两个全等的①ABC和①DEF．已知①B=①E，若AC边的质量为20千克，则DF边的质量为________千克．21．等边ΔABC的高为3cm，则以AB为边的正方形面积为__________.22．如图所示，AD①BC，BD平分①ABC．若①ABD=30°，①BDC=90°，CD=2，则BC=_______．23．小敏设计了一种挂衣架，在挂衣服的时候可以任意角度收扰两个挂衣杆OA和OB，然后套进衣服后松开即可.如图1，衣架杆OA=OB.如图2，若衣架收拢时衣服领口宽AB=22cm，且①AOB=60°，那么这个衣架杆的长OA=OB=______cm.24．如图，直线EF∥GH，点A在EF上，AC交GH于点B，若∠F AC＝72°，∠ACD ＝58°，点D在H上，则∠BDC的度数为____．25．两根长度分别为3，5的木棒，若想钉一个三角形木架，第三根木棒的长度可以是________．（写一个值即可）26．如图，点C 是线段AB 的中点，DA EC ∥．请你只添加一个条件，使得DAC △①ECB ．（1）你添加的条件是______；（要求：不再添加辅助线，只需填一个答案即可）（2）依据所添条件，判定DAC △与ECB 全等的理由是______．27．如图，在ABC 中，已知AB AC BD ==，215∠=︒，那么1∠的度数为________．28．在①ABC 中，点E 、F 分别为边AB 、AC 上的点，把①ABC 沿EF 翻折，翻折后的图形如图所示．若1+2110∠∠=︒，则A ∠的度数为___________．29．如图，G 为ABC 的重心，AG =12，则AD =__________．30．如图，将月牙①绕点A 按逆时针方向旋转得到月牙①，线段AB 与线段AC 重合，连接BC，过B点作BD①AC于点D，若CD长为3，BC长为AD的长为_____．31．如图，在①ABC中，中线AD、BE交于O，若S△BOD=5，则S△BOA=_____．32．已知一个菱形的周长为24cm，有一个内角为60︒，则较长的一条对角线长为_________cm．33．如图，四边形ABCD中，点P是对角线BD的中点，点E，F分别是AB，CD的中点，AD=BC，①PEF=35°，则①PFE的度数是_____．34．如图，在△ABC中，AD平分△BAC，AD△BD于点D，DE△AC交AB于点E，若AB=8，则DE=_______35．如图，在平行四边形ABCD中，45∠=︒，AAD AB与CD之间的距离为______．36．在直角坐标系中有过点(3,4)A 的反比例函数(0)k y x x=>，在x 轴上有一点(1,0)P ，在反比例函数图象上有一个动点Q ，以PQ 为一边作一个正方形PQRS ，当正方形PQRS 有两个顶点在坐标轴上时，点S 坐标为__________． 37．如图，在①ABC 中，AB=AC ，BC=6，AF①BC 于点F ，BE①AC 于点E ，且点D 是AB 的中点，①DEF 的周长是11，则AB=______．三、解答题38．如图，在①ABC 中，①ACB=90°，①A=30°，AB 的垂直平分线分别交AB 和AC 于点D ，E.(1)求证:AE=2CE ;(2)连接CD ，请判断①BCD 的形状，并说明理由.39．已知：如图，在①ABC 中，AD 平分①BAC ，CE①AD 于点E ，EF①AB 交AC 于点F ．求证：①FEC 是等腰三角形．40．如图，已知ABC 中，,90AC BC ACB =∠=︒，点D 与点E 都在射线AP 上，且CD CE =，90DCE ∠=︒．(1)说明AD BE =的理由；(2)说明BE AE ⊥的理由．41．如图，在△ABC 中，AB BC =，点D 在边AB 上，AE CD ∥，CA 平分①BCE ，连接DE ，交AC 于点F ．(1)求证：四边形ADCE 是平行四边形；(2)当DE BC ∥，10AC =，13BC =时，sin AFD ∠的值为．42．如图，以等腰直角三角形ABC 的斜边AB 为边作等边ABD ∆，连接DC ，以DC 当边作等边DCE ∆，B 、E 在C 、D 的同侧，若AB BE 的长．43．已知：如图，ABC 和CDE 都是等边三角形，且点A 、C 、E 在一条直线上，AD 与BE 相交于点P ，AD 与BC 相交于点M ，BE 与CD 相交于点N ．求证：()1APB 60∠=︒；()2CM CN =．44．已知，如图，在边长为2的等边三角形ABC 中，点D 为直线BC 上的一点（不与点B ，C 重合），连接AD ，将AD 绕点A 逆时针旋转60︒到AE ，连接DE ，过点E 作//EF BC 交直线AB 于点F ．（1）如图1，点D 在线段BC 上，①猜想线段AC ，DC ，CE 之间的数量关系，并说明理由．①求出EF 的长度．（2）如图2，当点D 在BC 的延长线上时，直接写出（1）中的两个结论．45．如图1，在边长为4cm 的等边①ABC 中，点P 从点A 出发沿着AB 以2cm/s 的速度向点B 运动，点Q 从B 点出发沿着BC 以相同的速度向点C 运动，P 、Q 两点同时出发，设运动时间为t 秒．(1)当t =1时，试判断①PBQ 的形状，并说明理由；(2)当PQ ①BC 时，求t 的值；(3)如图2，过点P 作PH ①BC ，垂足为H ，连接PQ ，以PQ 为边向左作等边①PQE ，连接BE ．①用含t 的代数式表示QH 的长；①当0≤t ≤23时，BE 的长度能否为2cm ？若能，求出此时QH 的长；若不能，请说明理由．46．如图，在正方形ABCD 中，1AB =，延长BC 至M ，使5BM =．以,BD BM 为邻边作DBMN ．动点P 从点D 出发，以每秒1个单位的速度沿DN 向终点N 运动，过点 P 作PQ ⊥BM 交BM 或BM 的延长线于点Q ，以PQ 为边向右作正方形PQRS ．设正方形PQRS ．设正方形PQRS 与DBMN 的重叠部分的面积为y ，点P 运动的时间为x （0x >．单位：秒）．（1）用含x 的代数式表示线段PN 为；（2）当点S 与点N 重合时，求x 的值；（3）当正方形PQRS 与DBMN 的重叠部分不是正方形时，求y 与x 之间的函数关系式；（4）当DQS △或PRN △是直角三角形时，直接写出x 的值．47．在ABC 中，90BAC ∠=︒，点O 是斜边BC 上的一点，连接AO ，点D 是AO 上一点，过点D 分别作//DE AB ，//DF AC ，交BC 于点E 、F ．（1）如图1，若点O 为斜边BC 的中点，求证：点O 是线段EF 的中点．（2）如图2，在（1）的条件下，将DEF 绕点O 顺时针旋转任意一个角度，连接AD ，CF ，请写出线段AD 和线段CF 的数量关系，并说明理由．（3）如图3，若点O 是斜边BC 的三等分点，且靠近点B ，当30ABC ∠=︒时，将DEF 绕点O 顺时针旋转任意一个角度，连接AD 、BE 、CF ，请求出BE AD的值．参考答案：1．D【分析】根据三角形全等的判定定理，结合已知条件，判断条件与定理相一致的即可．【详解】①①和①符合了SAS ，①①和①两个三角形全等；故选D ．【点睛】本题考查了三角形全等的判定方法，熟练掌握判定方法是解题的关键． 2．A【分析】根据三角形高的定义，即可求解．【详解】解：解：在ABC 中，画出边BC 上的高，即是过点A 作BC 边的垂线段，正确的是A ．故选A ．【点睛】本题主要考查了三角形高线的作法，正确把握相关定义是解题关键，经过三角形的顶点（与底相对的点）向对边（底）作垂线，顶点和垂足之间的线段就是三角形的一条高．3．D【分析】根据题意分别画出图形，BC 边上的高在平行四边形的内部和外部，进而利用勾股定理求出即可．【详解】解：作BC 边上的高AE①BC 于E ，分两种情况：AE 在平行四边形的内部和外部.．① 如图所示：AE 在平行四边形的内部，①在ABCD 中，①ABC ＝30°，AB ＝8，AC ＝5，AE①BC①AE=12AB=4，3 ，=①▱ABCD 的周长等于：()()2222AB BC AB BE EC +=++=+；①如图所示：AE 在平行四边形的外部，①在ABCD 中，①ABC ＝30°，AB ＝8，AC ＝5，AE①BC①AE=12AB=4，3 ，=①▱ABCD 的周长等于：()()2210AB BC AB BE EC +=+-=+．故选D ．【点睛】本题考查平行四边形的性质、勾股定理、直角三角形30度角性质，利用分类讨论得出是解题的关键．4．A【分析】根据三角形内角和定理求出①ACB 的度数，根据全等三角形的性质得到①DCE =①ACB =100°，由A 、C 、D 在同一条直线上，得到①ACD =180°，根据角的和差即可得到结论.【详解】①①A =30°，①ABC =50°，①①ACB =180°－30°－50°=100°.①①EDC ①①ABC ，①①DCE =①ACB =100°.①A 、C 、D 在同一条直线上，①①ACD =180°，①①BCE =①ACB +①DCE ﹣①ACD =20°.故选：A.【点睛】本题考查了三角形内角和定理、全等三角形的性质，平角的定义，熟记全等三角形的性质是解题的关键.5．C【分析】先利用平角用①1表示出①BDF ，再利用三角形的内角和定理及推论用①1表示出①CEF ，两式相减可得结论．【详解】如图，①①DEF是由①DEA折叠成的，①①1=①2，①3=①DEF．①①BDF+①1+①2=180°，①①BDF=180°-2①1．①①CEF+①CED=①DEF，①CED=①1+①A，①3+①1+①A=180°，①①CEF=①3-①CED=180°-①1-①A-①1-①A=180°-2①1-40°=140°-2①1．①①BDF-①CEF=180°-2①1-（140°-2①1）=180°-2①1-140°+2①1=40°．故选：C．【点睛】本题主要考查了三角形的内角和定理，掌握“三角形的内角和等于180°”、折叠的性质是解决本题的关键．6．A【详解】试题分析：由AB=AC，根据等边对等角，即可得①B=①C，又由BF=CD，BD=CE，可证得①BDF①①CED（SAS），根据全等三角形的性质，即可求得①B=①C=α，根据三角形的内角和定理，即可求得答案．①AB=AC，①①B=①C，①BF=CD，BD=CE，①①BDF①①CED（SAS），①①BFD=①EDC ，①α+①BDF+①EDC=180°，①α+①BDF+①BFD=180°，①①B+①BDF+①BFD=180°，①①B=α，①①C=①B=α，①①A+①B+①C=180°，①2α+①A=180°．故选A ．考点：等腰三角形的性质，全等三角形的判定与性质点评：全等三角形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.7．B【分析】当DP BC ⊥时，DP 最短，通过等角的余角相等，得出ABD CBD ∠=∠，即可得出BD 平分ABC ∠，再根据角平分线的性质即可进行解答．【详解】解：过点D 作DP BC ⊥于点P ，此时DP 最短．①90A ∠=︒，BD CD ⊥，①90,90ABD ADB CBD C ∠+∠=︒∠+∠=︒，①ADB C ∠=∠，①ABD CBD ∠=∠，即BD 平分ABC ∠，①90A ∠=︒，DP BC ⊥，4=AD ，①4DP AD ==，故选：B ．【点睛】本题主要考查了角平分线的性质，解题的关键是熟练掌握“垂线段最短”，“等角的余角相等”，“角平分线上的点到两边距离相等”．8．B【分析】先根据HL 证明Rt①ABD ①Rt①CDB ，再根据全等三角形的性质即可进一步判断各项.【详解】解：在Rt①ABD 和Rt①CDB 中，BD DB AB CD =⎧⎨=⎩， ①Rt①ABD ①Rt①CDB (HL)，①AD ＝BC ，①ABD =①CDB ，①ADB =①CBD ，①AB ①CD ，AD ①BC ；所以A 、C 、D 三项是正确的，错误的是B 项.故选B.【点睛】本题考查的是直角三角形的判定和性质、平行线的判定，属于基础题型，熟练掌握直角三角形的判定和性质是关键.9．C【分析】过点E 作EG ①BC ，通过证明①ABD ①①EBC 和①AFE ①①CGE ，结合割补法求面积即可求解；【详解】解：在①ABD 和①EBC 中，AB BE ABD EBC BD BC =⎧⎪∠=∠⎨⎪=⎩(角平分线定义) ①①ABD ①①EBC ；故①正确；①BE ＝BA ，BD ＝BC ，①①AEB =1(180)2ABE ︒-∠， 1(180)2ADE BDC CBE ∠=∠=︒-∠, 又①=ABE CBE ∠∠，①=AEB ADE ∠∠，①AE ＝AD ，又①ABD ①①EBC ，①AD ＝EC①AE ＝AD ＝EC ；故①正确；过点E 作EG ①BC ，交BC 于点G ，①BD 平分ABC ∠，在Rt ①AFE 和Rt ①CGE 中，AE EC EF EG =⎧⎨=⎩, ①Rt ①AFE ①Rt ①CGE (HL )，同理可证：Rt ①BFE ①Rt ①BGES 四边形ABCE ＝2AEF CGE BEF EFBC EFBC SS S S S EF BF +=+==⨯四边形四边形，故①正确，由Rt ①BFE ①Rt ①BGE ，①=FEB BEG ∠∠,①FEB BEC ∠≠∠，①BE 不平分①FEC ，故①不正确；综上，正确的个数为3个，故选择：C【点睛】本题主要考查了全等三角形的判定和性质，角平分线的性质，等腰三角形的判定，证明线段AE =AD =CE 是解题的关键．10．B【分析】根据全等三角形的性质得AC ＝DF ，则依据CF ＝4可得CD 的长．【详解】△ABC①①DEF ，①A 与①D 是对应角，AB 与DE 是对应边，①AC ＝DF ＝22，又①CF ＝4，①CD ＝DF ﹣CF ＝22﹣4＝18，【点睛】本题考查了全等三角形的性质：全等三角形的对应边相等；全等三角形的性质是证明线段和角相等的理论依据，应用时要会找对应角和对应边．11．C【分析】由斜边上的中线长是2，可以得到斜边长为4，设两个直角边的长为x ，y 则x y +=x 2+y 2=16，解这个方程组求出xy 的值即可求出三角形的面积．【详解】解：①Rt ①ABC 的周长是4+，斜边上的中线长是2，①斜边长为4，设两个直角边的长为x ，y ，则x +y =x 2+y 2=16，解得：xy =8，①S △ABC =12xy =4．故选：C ．【点睛】本题考查了直角三角形的性质：直角三角形斜边上的中线等于斜边的一半；还考查了勾股定理．解题时要注意方程思想与整体思想的应用．12．A【分析】根据勾股定理的逆定理、勾股定理和三角形内角和逐个判断即可．【详解】解：①①ABC 的三边长分别为a ，b ，c ，若b 2+c 2＝a 2，则①ABC 是直角三角形，选项说法正确；①在Rt①ABC 中，已知两边长分别为6和8，则第三边的长为10或，选项说法错误； ①在①ABC 中，若①A ：①B ：①C ＝1：5：6，根据三角形内角和是180︒可得11801512A ∠=︒⨯=︒，51807512B ∠=︒⨯=︒，61809012C ∠=︒⨯=︒，则①ABC 是直角三角形，选项说法正确；①若三角形的三边长之比为1：2x ，2x ，根据勾股定理的逆定理即可得到该三角形是直角三角形，选项说法正确；故选：A ．【点睛】本题考查了勾股定理的逆定理、勾股定理和三角形内角和，能熟记勾股定理的逆定理的内容是解此题的关键．13．D【分析】由SAS 证明①AOB①①COD ，得出AB=CD ，①A=①C ，OA=OC ，再由内错角相等，即可得出AB①CD ，即可判断.【详解】在①AOB 和①COD 中，OA OC AOB COD OB OD ⎧⎪∠∠⎨⎪⎩＝＝＝，①①AOB①①COD （SAS ）①AB=CD ，①A=①C ，OA=OC ，①AB①CD ．故答案为：D.【点睛】本题考查了全等三角形的判定与性质、平行线的判定方法；熟练掌握全等三角形的判定方法，并能进行推理论证是解决问题的关键．14．D【分析】根据全等三角形的判定知两个等边三角形不一定全等即可判定A 错误；面积相等的三角形不一定是全等三角形可判定B 错误；根据到三角形三边距离相等的点是内角平分线的交点，可判定C 错误；根据到三角形三个顶点距离相等的点是三边中垂线的交点即可判定D 正确．【详解】解：A 、两个等边三角形不一定全等，故此选项不符合题意；B 、面相等的三角形不一定是全等三角形，故此选项不符合题意；C 、到三角形三边距离相等的点是内角平分线的交点，故此选项不符合题意；D 、到三个顶点距离相等的是三边中垂线的交点，故此选项符合题意；故选：D ．【点睛】本题考查全等三角形的判定，熟练掌握全等三角形的判定的判定定理，等边三角形的性质，三角形三边垂直平分线的交点的性质，三角形内角平分线的交点性质是解题的关键．15．B【分析】延长BG 交AC 于D ．由重心的性质得到 BG =2GD ，D 为AC 的中点，再由直角三角形斜边上的中线等于斜边的一半，得到AC =2GD ，即有BG =AC ，从而得到AC 、GD 的长．当GD ①AC 时，①AGC 的面积的最大，最大值为：12AC •GD ，即可得出结论．【详解】解：延长BG 交AC 于D ．①G 是①ABC 的重心，①BG =2GD ，D 为AC 的中点．①AG ①CG ，①①AGC 是直角三角形，①AC =2GD ，①BG =AC ．①BG •AC =32，①AC GD =当GD ①AC 时，①AGC 的面积的最大，最大值为：12AC •GD =12⨯．故选：B ．【点睛】本题考查了重心的性质和直角三角形的性质．解题的关键是熟知三角形的重心到顶点的距离等于它到对边中点距离的2倍．16．C【分析】由垂直平分线的性质得出AE ＝BE ，由等腰三角形的性质得出①BAE ＝①ABE ＝45°，求出①F AC ＝12①BAC ＝22.5°，AF ①BC ，由直角三角形的性质可求出答案．【详解】解：①BE ①AC ，①①BEC ＝①AEB ＝90°，①DE 是边AB 上的中垂线，①AE ＝BE ，①①BAE ＝①ABE ＝45°，①AB ＝AC ，AF 平分①BAC ，①①F AC ＝12①BAC ＝22.5°，AF ①BC ，①①C ＝90°−①F AC ＝67.5°，①EF ＝FC ，①①FEC ＝①C ＝67.5°，①①BEF ＝①BEC −①FEC ＝90°−67.5°＝22.5°，故选：C ．【点睛】本题考查了等腰三角形的性质，垂直平分线的性质，直角三角形的性质，熟练掌握等腰三角形的性质是解题的关键．17．D【分析】由四边形ABCD 是正方形得90CD BC DCE CBN =∠=∠=︒，，因为CG DE ⊥于G ，90CDE BCN DCG ∠=∠=︒-∠，即可证明DEC CNB ≌，得DE CN =，可判断①正确；由E 为BC 的中点得111222BN CE BC CD AB ====，则12BN CD =，由AB CD ∥证明BHN DHC ∽，据此计算，可判断①正确；求得13NH CN =，则13BNH CNBS S ∆∆=，所以3DEC CNB BNH S S S ∆∆∆==，可判断①正确；先证明BNT BER ≌，得BT BR =，再证明Rt Rt BTG BRG ≌，得45BGN BGR ∠=∠=︒，可判断①正确；由TN ER GT GR ==，可推导出2GN EG GT TN EG GT GR GT +=++=+=，而45TBG BGN ∠=∠=︒，则BT GT =，由勾股定理得22222GT GT BT BG =+=，所以2GT =，则GN EG +，可判断①正确．【详解】解：①四边形ABCD 是正方形，①90CD BC DCE CBN =∠=∠=︒，，①CG DE ⊥于G ，①90CGD ∠=︒，①90CDE BCN DCG ∠=∠=︒-∠，在△DCE 和△CBN 中，CDE BCN CD BCDCE BCN ∠=∠⎧⎪=⎨⎪∠=∠⎩， ①()SAS DEC CNB ≌，①DE CN =，故①正确；①E 为BC 的中点，BC CD AB ==，①111222BN CE BC CD AB ====， ①1122AB BN CD AB ==， ①AB CD ∥，①BHN DHC ∽， ①12BH BN DN CD ==，即13BH BD =，故①正确； ①12NH BN CH CD ==， ①13NH CN =， ①13BNH CNB S S ∆∆=， ①3DEC CNB BNH S S S ∆∆∆==，故①正确；如图，作BT DN ⊥于点T ，BR DE ⊥交DE 的延长线于点R ，则90BTN R BTG ∠=∠=∠=︒，①CE BN CE BE ==，，①BN BE =，①BNT CED BER CED ∠=∠∠=∠，，①BNT BER ∠=∠，在BNT 和BER △中，BTN R BNT BER BN BE ∠=∠⎧⎪∠=∠⎨⎪=⎩，①()AAS BNT BER ≌，①BT BR =，在Rt BTG 和Rt BRG 中，BG BG BT BR=⎧⎨=⎩， ①()Rt Rt HL BTG BRG ≌，①BGN BGR ∠=∠，①90RGN ∠=︒， ①1452BGN RGN ∠=∠=︒，故①正确； ①TN ER GT GR ==，，①2GN EG GT TN EG GT ER EG GT GR GT +=++=++=+=，①45TBG BGN ∠=∠=︒，①BT GT =，①22222GT GT BT BG =+=，BG =，①2GT =，①GN EG +=，故①正确，综上，①①①①①均正确，故选：D ．【点睛】此题考查正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识，正确地作出辅助线构造全等三角形是解题的关键．18．6【分析】根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AM=BM ，然后求出△MBC 的周长=AC+BC ，再代入数据进行计算即可得解．【详解】①M 、N 是AB 的垂直平分线①AM=BM ，①△MBC 的周长=BM+CM+BC=AM+CM+BC=AC+BC ，①AB ＝8，①MBC 的周长是14，①BC=14-8=6．故答案为6．【点睛】线段垂直平分线的性质, 等腰三角形的性质．19．【分析】先根据线段垂直平分线的性质得到CE=CB，①BDC=90°，再根据等腰三角形的性质和角平分线的定义得到①BCD=13①ACB=30°，则①A=30°，然后可得答案．【详解】解：①CD垂直平分BE，①CE=CB，①BDC=90°，①CD平分①BCE，即①BCD=①ECD，①CE平分①ACD，①①ECD=①ACE，而①ACB=90°，①①BCD=13①ACB=30°，①①B=60°，①①A=30°，①2BC=，①AB=4，①AC=．故答案为：【点睛】本题考查了线段垂直平分线的性质：垂直平分线上任意一点，到线段两端点的距离相等，考查了等腰三角形的三线合一的性质，三角形的内角和定理，勾股定理，掌握以上知识是解题的关键．20．20【详解】①①ABC①①DEF，①AC=DF，①AC边的质量为20千克，①DF边的质量为20千克.21．12【分析】首先作出图形，利用等边三角形的性质以及解直角三角形的知识求出BC的长，以AB为边的正方形面积．【详解】如图，过A作AD①BC，①AB=AC=BC，①BD=CD=12BC=12AB，①BAD=30°，①AD=3，222AB AD BD=+，①AB=①以AB为边的正方形面积为212=cm2．22．4．【详解】试题分析：如图，①BD平分①ABC．①ABD=30°，①①DBC=30°．①①BDC=90°，CD=2，①BC=2CD=4．故答案是：4．考点：含30度角的直角三角形．23．22【分析】图一、图二①AOB的度数发生变化，但是OA、OB的长度没有改变，在通过①AOB=60°，OA=OB，得到三角形AOB为等边三角形求解．【详解】图一、图二①AOB的度数发生变化，但是OA、OB的长度没有改变,仍然有OA=OB．①OA=OB，①AOB=60°，①①AOB为等边三角形，①OA=OB=AB=22cm.【点睛】本题比较简单，主要是对三角形中等腰、等边三角形的考查，熟练掌握这块的基础知识是解答本题的关键．24．50°【分析】利用平行线的性质求出①DBC，再根据三角形内角和定理求出①BDC即可．【详解】解：①EF①GH，①①FAC=①DBC=72°，①①C+①DBC+①BDC=180°，①①BDC=180°−72°−58°=50°，故答案为50°.【点睛】本题主要考查了平行线的性质，掌握平行线的性质是解题的关键.25．4（答案不唯一）【分析】根据三角形中“两边之和大于第三边，两边之差小于第三边”，进行分析得到第三边的取值范围；再进一步找到符合条件的数值．【详解】解：根据三角形的三边关系，得第三边应大于两边之差，即532-=；而小于两边之和，即538+=，即2<第三边8<，故第三根木棒的长度可以是4．故答案为：4（答案不唯一）．【点睛】本题主要考查了三角形三边关系，熟练掌握两边之和大于第三边，两边之差小于第三边是解题的关键．26． AD =CE （或①D =①E 或①ACD =①B ）（答案不唯一） SAS【分析】（1）由已知条件可得两个三角形有一组对应边相等，一组对应角相等，根据三角形全等的判定方法添加条件即可；（2）根据添加的条件，写出判断的理由即可．【详解】解：（1）添加的条件是：AD =CE （或①D =①E 或①ACD =①B ）故答案为：AD =CE （或①D =①E 或①ACD =①B ）（2）若添加：AD =CE①点C 是线段AB 的中点，①AC =BC①DA EC ∥①A BCE ∠=∠①DAC △①ECB (SAS )故答案为：SAS【点睛】本题主要考查了添加条件判断三角形全等，熟练掌握全等三角形的判断方法是解答本题的关键．27．65︒【分析】根据AB AC BD ==，可得C B ∠=∠,13∠=∠，根据三角形的内角和定理，以及三角形的外角性质列出方程组解方程组即可求解．【详解】解：如图，①AB AC BD ==①C B ∠=∠,13∠=∠，23180B C ∠+∠+∠+∠=︒1318022C ∴∠=∠=︒-∠-∠又12C ∠=∠+∠218022C C ∴∠+∠=︒-∠-∠318022C ∴∠=︒-∠18030503C ︒-︒∴∠==︒ 12155065C ∴∠=∠+∠=︒+︒=︒故答案为：65︒【点睛】本题考查了三角形内角和定理以及三角形的外角性质，等边对等角求角度，二元一次方程组的应用，掌握以上知识是解题的关键．28．55︒【分析】如图，延长B ′E 交C ′F 的延长线于点A ′，连接AA ′．证明①1+①2=2①EAF ，可得结论．【详解】解：如图，延长B ′E 交C ′F 的延长线于点A ′，连接AA ′．①①1=①EAA ′+①EA ′A ，①2=①F AA ′+①F A ′A ,①①1+①2=①EAF +①EA ′F ，①①EAF =①EA ′F ，①①1+①2=2①EAF =110°，①①A =55°．故答案为：55°．【点睛】本题考查三角形内角和定理，翻折变换等知识，解题的关键是证明①1+①2=2①EAF．29．18【分析】连接CG并延长交AB于点E，连接DE，根据题意，可以得到DE时①ABC的中位线，从而可以得到DE①AC且DE=12AC，然后即可得到①DEG①①ACG，由相似三角形的性质得到DG和AG的比值，求出然后DG，即可得到结果．【详解】解：如图，连接CG并延长交AB于点E，连接DE，①点G是①ABC的重心，①点E和点D分别是AB和BC的中点，①DE是①ABC的中位线，①DE①AC且DE=12AC，①①DEG①①ACG，①12 DE DGAC AG==，①AG=12，①DG=6，①AD=AG+GD=18．故答案为：18．【点睛】本题考查三角形的重心、三角形的中位线、三角形相似，解答本题的关键是明确题意，利用数形结合的思想解答．30．12．【分析】由旋转的性质可求AB AC =，由勾股定理可求BD 的长，AD 的长.【详解】①线段AB 与线段AC 重合AB AC ∴=3,CD BC BD AD ==⊥9BD ∴==222,3AB AC CD AD A D D A BD AB ===+=++2281(3)AD AD ∴+=+12AD ∴=故答案为：12.【点睛】本题考查了旋转的性质、勾股定理，根据旋转的性质得出AB AC =是解题关键. 31．10【详解】试题分析：根据三角形的重心到顶点的长度等于到对边中点的长度的2倍可得OD=12AO ，再根据等高的三角形的面积等于底边的比求出①AOB 的面积为22510AOB BOD S S ==⨯=．考点：三角形的重心，三角形的面积（等高，等底同高）32．【分析】根据菱形的四条边都相等，菱形的两条对角线互相垂直平分，并且每一条对角线平分一组对角；利用30°直角三角形的边长关系和勾股定理计算求值即可．【详解】解：由题意得作图如下：菱形ABCD 中，①DAB =60°，①ABCD 是菱形，①AC 、BD 互相垂直平分，AC 平分①DAB ，①①CAB=30°，①AOB=90°，①菱形周长为24cm，①AB=24÷4=6cm，①OB=12AB=3cm，AO=，①BD=2OB=6cm，AC=2AO=，①较长的一条对角线长，故答案为：【点睛】本题考查了菱形的性质，30°直角三角形，勾股定理；掌握菱形的性质是解题关键．33．35°【详解】①四边形ABCD中，点P是对角线BD的中点，点E，F分别是AB，CD的中点，①PE是①ABD的中位线，PF是①BDC的中位线，①PE=12AD，PF=12BC，又①AD=BC，①PE=PF，①①PFE=①PEF=35°.故答案为35°.34．4【详解】试题分析：根据角平分线的定义可得①CAD=①BAD，再根据两直线平行，内错角相等可得①CAD=①ADE，然后求出①ADE=①BAD，根据等角对等边可得AE=DE，然后根据等角的余角相等求出①ABD=①BDE，根据等角对等边可得DE=BE，从而得到DE= AB．解：①AD是①BAC的平分线，①①CAD=①BAD，①DE①AC，①①CAD=①ADE，①①ADE=①BAD，①AE=DE ，①BD①AD ，①①ADE+①BDE=①BAD+①ABD=90°，①①ABD=①BDE ，①DE=BE ，①DE=AB ，①AB=8，①DE=×8=4．故答案为4．考点：等腰三角形的判定与性质．35【分析】作DE AB ⊥，在Rt ADE 中根据勾股定理求出DE 的长即可．【详解】解：作DE AB ⊥，则90AED ∠=︒，又①45A ∠=︒，45ADE ∴∠=︒，AE DE ∴=，222AE DE AD +=，222DE ∴=，23DE =，DE ∴=，①AB 与CD【点睛】本题主要考查了平行线之间的距离和勾股定理，如果两条直线互相平行，则其中一条直线上任意一点到另一条直线的距离都相等，这个距离称为平行线之间的距离，掌握平行线之间距离的定义并能用勾股定理计算时解题的关键．36．(13,0)或(11,0)-或(4,3)-或(0,11)或(11)-【分析】利用待定系数法求出反比例函数表达式，再分情形画出图形分别求解即可解决问题．【详解】解：反比例函数(0)ky x x=>，过点(3,4)A ， 12k ∴=，12y x ∴=，①如图1中，四边形PQRS 是正方形，PS PQ ∴=，(1,0)P ，(1,12)Q ∴，12PQ ∴=，12PS ∴=，13OS ∴=，(13,0)S ∴．则当S 在负半轴时，(11,0)S -．①如图2中，四边形PQRS 是正方形，Q ∴、S 关于x 轴对称，设(1,)Q m m +代入12y x=中，(1)12m m +=， 3m ∴=或4-（舍弃），(4,3)Q ∴，(4,3)S ∴-．①如图3中，作QE x ⊥轴于E ．四边形PQRS 是正方形，PS PQ ∴=，①SPQ=90°，①①SPO+①QPE=90°，又①SPO+①PSO=90°，①①QPE=①PSO ，又①POS=①PEQ ，①PQE SPO ∆≅∆（AAS ），1EQ OP ∴==，(12,1)Q ∴，11PE SO ∴==，(0,11)S ∴，①如图4中，作QE x ⊥轴于E ，QF y ⊥轴于F ．四边形PQRS 是正方形，①PQ=RQ ，①PQR=90°，①①FQR+①FQP=90°，①EQP+①FQP=90°，①①FQR=①EQP ，又①QFR=①QEP=90°，①PQE RQF ∆≅∆（AAS ），QE QF ∴=，RF PE =，设(,)Q n n ，则Q ，(0R ∴，1)，设(,)S a b ，102+=，1a ∴=-1b =，(1S ∴-1)．综上：点S 的坐标为：(13,0)或(11,0)-或(4,3)-或(0,11)或(11)-，故答案为：(13,0)或(11,0)-或(4,3)-或(0,11)或(11)-．【点睛】本题考查反比例函数综合题、正方形的判定和性质、全等三角形的判定和性质、待定系数法、中点坐标公式等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．37．8【详解】①AB=AC，AF①BC，①①AFB=90°，BF=CF，又①BE①AC，①①BEC=①BEA=90°，①EF=12BC=3，又①D为AB中点，①DE=DF=12AB，①DE+DF+EF=11，①DE+DF=8，①AB=8.38．见解析【分析】（1）连接BE，根据线段垂直平分线的性质可得AE=BE，利用等边对等角的性质可得①ABE=①A；结合三角形外角的性质可得①BEC的度数，再在Rt①BCE中结合含30°角的直角三角形的性质，即可证明第（1）问的结论；（2）根据直角三角形斜边中线的性质可得BD=CD，再利用直角三角形锐角互余的性质可得到①ABC=60°，至此不难判断①BCD的形状【详解】（1）证明：连结BE，如图．①DE是AB的垂直平分线，①AE＝BE，①①ABE＝①A＝30°，①①CBE＝①ABC－①ABE＝30°，在Rt①BCE中，BE＝2CE，①AE＝2CE.（2）解：①BCD是等边三角形．理由如下：①DE垂直平分AB，①D为AB的中点．①①ACB＝90°，①CD＝BD.又①①ABC＝60°，①①BCD是等边三角形．【点睛】此题考查了线段垂直平分线的性质、30°角的直角三角形的性质，等腰三角形的性质，直角三角形斜边的中线等于斜边的一半，等边三角形的判定，熟练掌握30°角的直角三角形的性质是解（1）的关键，熟练掌握直角三角形斜边的中线等于斜边的一半是解（2）的关键，39．见解析.【分析】利用平行线以及角平分线的定义证明①2=①3，再根据等角的余角相等证明①4=①5即可解决问题.【详解】证明：如图，①AD平分①BAC，①①1=①2，①EF①AB，①①1=①3，①①2=①3，①CE①AD 于点E，①①AEC=90°，①①3+①4=90°，①①2+①5=90°，①①4=①5，①FE=FC，①①FEC是等腰三角形．【点睛】本题考查平行线的性质，等腰三角形的判定和性质等知识，解题的关键是熟练掌握基本知识．40．(1)见解析(2)见解析。

初中数学：等边三角形练习(含解析)

初中数学：等边三角形练习（含解析）一、选择题1、下面的图形是轴对称图形，而且对称轴最多的是（）A．等腰三角形B．等腰直角三角形C．等边三角形D．直角三角形【答案】C【解析】试题分析：根据等腰三角形的性质和等边三角形的性质进行判断.解：等腰三角形有1条对称轴，等腰直角三角形有1条对称轴，等边三角形有3条对称轴，一般的直角三角形不是轴对称图形，所以对称轴最多的是等边三角形.故应选C.考点：等边三角形2、如图所示，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE，AD 与CE交于点F，则∠DFC的度数为（）A. 60°B. 45°C. 40°D. 30°【答案】A【解析】试题分析：根据等边三角形的性质可得：AC=AB，∠CAE=∠B，根据SAS可证△AEC≌△BDA，根据全等三角形的性质可证∠BAD=∠ACE，所以∠DAC+∠ACE=60°，所以∠DFC=60°.解：∵△ABC是等边三角形，∴∠CAE=∠B=60°，在△AEC和△BDA中，AE BD EAC DBA AC AB =⎧⎪∠=∠⎨⎪=⎩，∴△AEC ≌△BDA ，∴∠BAD=∠ACE ，∵∠DAC+∠BAD=60°，∴∠DAC+∠ACE=60°，∴∠DFC=∠DAC+∠ACE=60°.故应选A.考点：1.等边三角形的性质；2.全等三角形的判定与性质3、下面给出的几种三角形：①三个内角都相等；②有两个外角为120°；③一边上的高也是这边所对的角的角平分线；④三条边上的高相等的三角形．其中是等边三角形的有（）A ．4个B ．3个C ．2个D ．1个【答案】B【解析】试题分析：根据等边三角形的定义和判定定理进行判断.解：①三角形个内角都相等的三角形是等边三角形；②有两个外角是120°的三角形的两个内角一定是60°，根据三角形内角和定理可得：第三个内角也是60°，所以这个三角形是等边三角形；③一边上的高也是这边所对的角的角平分线一定是等腰三角形，不一定是等边三角形；④根据三角形的面积公式可得：当三角形三条边上的高相等时，三角形的三条边也相等，所以这个三角形是等边三角形.所以正确的有3个.故应选B.考点：等边三角形的判定二、填空题4、在△ABC 中，如果AB=AC=BC ，则∠A ＝_________，∠B ＝___________，∠C ＝_________。

经典精选--初中数学三角形专题训练及例题解析

知识点梳理考点一、三角形1、三角形的定义 : 由不在同一条直线上的三条线段首尾按序相接所构成的图形叫做三角形 .2、三角形的分类 .锐角三角形直角三角形钝角三角形不等边三角形三角形(按边分 )等腰三角形 (等边三角形 )3、三角形的三边关系：三角形随意两边之和大于第三边 , 随意两边之差小于第三边 . 4、三角形的重要线段①三角形的中线：极点与对边中点的连线 , 三条中线交点叫重心②三角形的角均分线：内角均分线与对边订交 , 极点和交点间的线段, 三个角的角均分线的交点叫心里③三角形的高：极点向对边作垂线 , 极点和垂足间的线段 . 三条高的交点叫垂心( 分锐角三角形 , 钝角三角形和直角三角形的交点的地点不一样 )5、三角形拥有稳固性6、三角形的内角和定理及性质定理：三角形的内角和等于 180°. 推论 1：直角三角形的两个锐角互补。

推论 2：三角形的一个外角等于不相邻的两个内角的和。

推论 3：三角形的一个外角大于与它不相邻的任何一个内角。

7、多边形的外角和恒为 360° 8、多边形及多边形的对角线①正多边形：各个角都相等，各条边都相等的多边形叫做正多边形．②凸凹多边形：画出多边形的任何一条边所在的直线，若整个图形都在这条直线的同一侧，这样的多边形称为凸多边形；，若整个多边形不都在这条直线的同一侧，称这样的多边形为凹多边形。

③多边形的对角线的条数 :A.从 n 边形的一个极点能够引（ n-3）条对角线，将多边形分红（ n-2）个三角形。

B.n 边形共有n(n3)条对角线。

29、边形的内角和公式及外角和①多边形的内角和等于（ n-2）×180°(n ≥3) 。

②多边形的外角和等于 360°。

10、平面镶嵌及平面镶嵌的条件。

①平面镶嵌：用形状同样或不一样的图形关闭平面，把平面的一部分既无空隙，又不重叠地所有覆盖。

②平面镶嵌的条件：有公共极点、公共边；在一个极点处各多边形的内角和为 360°。

等边三角形的判定-初中数学习题集含答案

等边三角形的判定（北京习题集）（教师版）一．选择题（共5小题）1．（2016秋•西城区校级期中）下列条件中，不能得到等边三角形的是 A ．有两个内角是的三角形B ．有两边相等且是轴对称图形的三角形C ．三边都相等的三角形D ．有一个角是且是轴对称图形的三角形2．（2016秋•西城区校级期中）下列条件中，不能得到等边三角形的是 A ．有两个外角相等的等腰三角形是等边三角形B ．三边都相等的三角形是等边三角形C ．有一个角是的等腰三角形是等边三角形D ．有两个内角是的三角形是等边三角形3．（2011秋•东城区期末）若一个三角形成轴对称图形，且有一个内角为，则这个三角形一定是 A ．直角三角形B ．等腰直角三角形C ．等边三角形D ．上述三种情形都有可能 4．（2010秋•海淀区期末）的三边、、满足：，则为A ．直角三角形B ．等腰直角三角形C ．等腰三角形D ．等边三角形5．（2006秋•西城区期末）下面给出几种三角形，其中是等边三角形的个数有个①有两个内角为的三角形②外角都相等的三角形③一边上的高也是这边上中线的三角形④有一个角是的三角形．A ．4B ．3C ．2D ．1二．解答题（共3小题）6．（2015秋•东城区期末）在中，，，所对的边，满足．（1）证明：是边长为2的等边三角形．（2）若，两边上的中线，交于点，求的值．()60︒60︒()60︒60︒60︒()ABC ∆a b c 2222223a b c a b c ++--=-ABC ∆()()60︒60︒ABC ∆60A ∠=︒ABC ∠ACB ∠b c 224()80b c b c +-++=ABC ∆b c BD CE O :OD OB7．（2016•门头沟区二模）如图，在中，，，为边上的中线．求证：是等边三角形．8．（2009秋•海淀区校级期末）如图，，，，试判断三角形的形状，并说明理由．ABC ∆90BAC ∠=︒30C ∠=︒AE BC ABE ∆15BAD BDA ∠=∠=︒45CAD ∠=︒30CDA ∠=︒ABC等边三角形的判定（北京习题集）（教师版）参考答案与试题解析一．选择题（共5小题）1．（2016秋•西城区校级期中）下列条件中，不能得到等边三角形的是 A ．有两个内角是的三角形B ．有两边相等且是轴对称图形的三角形C ．三边都相等的三角形D ．有一个角是且是轴对称图形的三角形【分析】根据等边三角形的定义可知：满足三边相等、有一内角为且两边相等或有两个内角为中任意一个条件的三角形都是等边三角形．【解答】解：、两个内角为，根据三角形的内角和为，可知另一个内角也为，所以该三角形为等边三角形．故不符合题意；、两边相等说明是等腰三角形或等边三角形，而这两种三角形都满足“轴对称”的条件，所以不能确定该三角形是等边三角形．故符合题意；、三边都相等的三角形当然是等边三角形．故不符合题意；、“轴对称”说明该三角形有两边相等，且有一个角是，有两边相等且一角为的三角形是等边三角形．故不符合题意；故选：．【点评】此题主要考查了等边三角形的判定，轴对称图形的定义，掌握等边三角形的判定是解本题的关键．2．（2016秋•西城区校级期中）下列条件中，不能得到等边三角形的是 A ．有两个外角相等的等腰三角形是等边三角形B ．三边都相等的三角形是等边三角形C ．有一个角是的等腰三角形是等边三角形D ．有两个内角是的三角形是等边三角形【分析】根据等边三角形的定义可知：满足三边相等、有一内角为且两边相等或有两个内角为中任意一个条件的三角形都是等边三角形．【解答】、两个外角相等说明该三角形中两个内角相等，而等腰三角形的两个底角是相等的，故不能确定该三角形是等边三角形．故本选项符合题意；、三边都相等的三角形是等边三角形；故本选项不符合题意；、有一个角是的等腰三角形是等边三角形；故本选项不符合题意；()60︒60︒60︒60︒A 60︒180︒60︒B C D 60︒60︒B ()60︒60︒60︒60︒A B C 60︒、两个内角为，因为三角形的内角和为，可知另一个内角也为，故该三角形为等边三角形；故本选项不符合题意；故选：．【点评】本题考查了等边三角形的判定：（1）由定义判定：三条边都相等的三角形是等边三角形．（2）判定定理1：三个角都相等的三角形是等边三角形．（3）判定定理2：有一个角是的等腰三角形是等边三角形．3．（2011秋•东城区期末）若一个三角形成轴对称图形，且有一个内角为，则这个三角形一定是 A ．直角三角形B ．等腰直角三角形C ．等边三角形D ．上述三种情形都有可能【分析】三角形是轴对称图形，则该三角形是等腰三角形，根据有一个内角是的等腰三角形是等边三角形，即可作出判断．【解答】解：因为三角形是轴对称图形，则该三角形是等腰三角形，根据有一个内角是的等腰三角形是等边三角形．故选：．【点评】本题主要考查了等边三角形的判定方法，解题的关键是熟练掌握判定方法，此题比较简单，易于掌握．4．（2010秋•海淀区期末）的三边、、满足：，则为 A ．直角三角形B ．等腰直角三角形C ．等腰三角形D ．等边三角形【分析】原式可化为，即，根据完全平方公式得，由非负数的性质可得三边相等．【解答】解：原式可化为，即，，，，，，，，故，为等边三角形．故选：．【点评】本题主要考查等边三角形的判断，此题要转化为偶次方的和，根据非负数的性质解答．D 60︒180︒60︒A 60︒60︒()60︒60︒C ABC ∆a b c 2222223a b c a b c ++--=-ABC ∆()22222230a b c a b c ++---+=2222121210a a b b c c -++-++-+=222(1)(1)(1)0a b c -+-+-=22222230a b c a b c ++---+=2222121210a a b b c c -++-++-+=222(1)(1)(1)0a b c ∴-+-+-=10a ∴-=1a =10b -=1b =10c -=1c =a b c ==ABC ∴∆D非负数的性质：有限个非负数的和为零，那么每一个加数也必为零，即若，，，为非负数，且，则必有．5．（2006秋•西城区期末）下面给出几种三角形，其中是等边三角形的个数有个①有两个内角为的三角形②外角都相等的三角形③一边上的高也是这边上中线的三角形④有一个角是的三角形．A ．4B ．3C ．2D ．1【分析】①一个三角形有两个角为，利用内角和定理得到第三个也为，可得出此三角形三内角相等，利用等角对等边得到三条边相等，故此三角形为等边三角形；②外角都相等，利用外角与相邻的内角互补，得到三内角相等，进而确定出三角形为等边三角形；③等腰三角形底边上的高为这边的中线，但不一定为等边三角形；④有一个角为的三角形不一定为等边三角形，比如中，，，．【解答】解：①有两个内角为的三角形，由三角形的内角和定理得到第三个角为，可得此三角形三内角相等，即三角形为等边三角形，本选项符合题意；②若一个三角形三外角都相等，可得出三内角相等，故此三角形为等边三角形，本选项符合题意；③一边上的高也是这边上中线的三角形为等腰三角形，不一定为等边三角形，本选项不合题意；④有一个角是的三角形不一定为等边三角形，例如：中，，，，则是等边三角形的个数有2个．故选：．【点评】此题考查了等边三角形的判定，其中等边三角形的判定方法有：三边相等的三角形为等边三角形；三内角相等的三角形为等边三角形；有一个角为的等腰三角形为等边三角形．二．解答题（共3小题）6．（2015秋•东城区期末）在中，，，所对的边，满足．（1）证明：是边长为2的等边三角形．（2）若，两边上的中线，交于点，求的值．1a 2a ⋯n a 120n a a a ++⋯+=120n a a a ==⋯==()60︒60︒60︒60︒60︒Rt ABC ∆90A ∠=︒60B ∠=︒30C ∠=︒60︒60︒60︒Rt ABC ∆90A ∠=︒60B ∠=︒30C ∠=︒C 60︒ABC ∆60A ∠=︒ABC ∠ACB ∠b c 224()80b c b c +-++=ABC ∆b c BD CE O :OD OB【分析】（1）由，可以判定，可以确定是边长为1的等边三角形；（2）连接，点、分别是边、边上的中点，所以，，，即可得到答案．【解答】解：（1），，，又，所以是边长为2的等边三角形；（2）连接，点、分别是边、边上的中点，所以，，，，【点评】本题考查因式分解的应用以及相似三角形的综合应用，解答本题的关在在于熟记公式的转化和相似三角形的判定方法和性质的综合应用．7．（2016•门头沟区二模）如图，在中，，，为边上的中线．求证：是等边三角形．222()20b c b c +-++=b c =60A ∠=︒ABC ∆DE D E AC AB //DE BC 12DE BC =DEO BOC ∴∆∆∽224()80b c b c +-++=Q 22(2)(2)0b c ∴-+-=2b c ∴==60A ∠=︒Q ABC ∆DE Q D E AC AB //DE BC 12DE BC =//DE BC Q DEO BOC ∴∆∆∽∴12DE OD BC OB ==ABC ∆90BAC ∠=︒30C ∠=︒AE BC ABE ∆【分析】根据直角三角形的性质得出，即可得出答案．【解答】证明：，，，为边上的中线，，，是等边三角形．【点评】本题考查了等边三角形的性质，掌握等边三角形的判定：三边都相等的三角形是等边三角形．8．（2009秋•海淀区校级期末）如图，，，，试判断三角形的形状，并说明理由．【分析】，，因此首先将绕点旋转，使点与点重合，得，连接，则得到，再由角的关系及等腰三角形的性质证明△，，得出，从而得证．【解答】解：三角形为等边三角形；理由：，，因此将绕点旋转，使点与点重合，连接，则，，，，，，，，，，又，AE BE CE AB ===90BAC ∠=︒Q 30C ∠=︒12AB BC ∴=AE Q BC AE BE CE ∴==AB AE BE ∴==ABE ∴∆15BAD BDA ∠=∠=︒45CAD ∠=︒30CDA ∠=︒ABC 15BAD BDA ∠=∠=︒Q AB DB ∴=ABC ∆B A D ABC ∆'CC 'ABC ABC ∆≅∆'ACD ∆≅C DC 'ABD CBC ∆≅∆'60ACB BAC ABC ∠=∠=∠=︒ABC 15BAD BDA ∠=∠=︒Q AB DB ∴=ABC ∆B A D CC 'ABC ABC ∆≅∆'BC BC ∴='AC DC ='BDC BAC ∠=∠ABC DBC ∠=∠'15BAD BDA ∠=∠=︒Q 45CAD ∠=︒30CDA ∠=︒30154515105CDC CDA BDA BDC CDA BDA ABC CDA BDA CAD BAD ∴∠'=∠+∠+∠'=∠+∠+∠=∠+∠+∠+∠=︒+︒+︒+︒=︒1801804530105ACD CAD CDA ∴∠=︒-∠-∠=︒-︒-︒=︒CD CD =△，，，，，，，，，，，为等边三角形．【点评】此题考查的知识点是等边三角形的判定，关键是通过旋转三角形及证明△和得出结论．ACD ∴∆≅C DC 'AD CC ∴='CBC DBC CBD ∠'=∠'+∠ABD ABC CBD ∠=∠+∠ABC DBC ∠=∠'Q 1801515150CBC ABD ∴∠'=∠=︒-︒-︒=︒15BCC BC C ∴∠'=∠'=︒ABD CBC ∴∆≅∆'AB BC ∴=154560ACB BAC BAD CAD ∴∠=∠=∠+∠=︒+︒=︒60ABC ∴∠=︒ABC ∴∆ACD ∴∆≅C DC 'ABD CBC ∆≅∆'。

初中数学专题：共顶点的等边三角形与全等

共顶点的等边三角形与全等
【例】如图，以△ ABC 的边 AB，AC 为边，向外作等边△ ABD 和等边△ ACE，连接 BE，CD 相交于点 F.
(1)求证：DC＝BE；证明：∵△ABD和△ACE都为等边三角形， ∴AD＝AB，AE＝AC，∠DAB＝∠EAC＝∠AEC＝∠ACE ＝60°. ∴∠DAB＋∠BAC＝∠EAC＋∠BAC，即∠DAC＝∠BAE. 在△DAC和△BAE中，A∠DD＝AACB＝，∠BAE，
1．如图，C 为线段 AE 上一动点(不与点 A，E 重合)，在 AE 同侧分别作等边三角形 ABC 和等边三角形 CDE，AD 与 BE 相交于点 O， AD 与 BC 相交于点 P，BE 与 CD 相交于点 Q，连接 PQ.以下结论： ①AD＝BE；②PQ∥AE；③AP＝BQ；④DE＝DP；⑤∠AOB＝60°； ⑥△CPQ 是等边三角形；⑦OC 平分∠AOE；⑧OC⊥PQ.恒成立的结论有 ①②③⑤⑥⑦ ．(把你认为正确的序号都填上)
(4)求证：DF＝AF＋BF. 证明：在DF上截取DM＝BF，连接AM. 在△ADM和△ABF中，A∠DA＝DAMB＝，∠ABF，
DM＝BF， ∴△ADM≌△ABF(SAS)． ∴AM＝AF，∠DAM＝∠BAF. ∵∠DAB＝60°， ∴∠DAM＋∠MAG＝60°.
∴∠BAF＋∠MAG＝60°，即∠MAF＝60°. ∴△AMF是等边三角形． ∴MF＝AF. ∴DCE＝α， ∴∠ACD＝∠BCE. 在△ACD和△BCE中， C∠AA＝CCD＝B，∠BCE， CD＝CE， ∴△ACD≌△BCE(SAS)． ∴BE＝AD.
(2)∠AMB＝α.
(3)△ CPQ为等腰直角三角形．证明：∵AD，BE的中点分别为点P，Q，BE＝AD， ∴AP＝BQ. ∵△ACD≌△BCE， ∴∠CAP＝∠CBQ. 在△ACP和△BCQ中， C∠AC＝ACP＝B，∠CBQ， AP＝BQ，

中考复习三角形专题一(含答案)

2018年02月28日刘笑天的初中数学组卷一．选择题（共12小题）1．如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m﹣n等于（）A．2 B．3 C．4 D．无法确定2．如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（）A．有且只有1个B．有且只有2个C．组成∠E的角平分线D．组成∠E的角平分线所在的直线（E点除外）3．如图，AD是△ABC的角平分线，则AB：AC等于（）A．BD：CD B．AD：CD C．BC：AD D．BC：AC4．如图，在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线．若在边AB 上截取BE=BC，连接DE，则图中等腰三角形共有（）A．2个 B．3个 C．4个 D．5个5．平面直角坐标系中，已知A（2，2）、B（4，0）．若在坐标轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是（）A．5 B．6 C．7 D．86．如图，已知△ABC的面积为12，AD平分∠BAC，且AD⊥BD于点D，则△ADC 的面积是（）A．10 B．8 C．6 D．47．如图，在下列三角形中，若AB=AC，则不能被一条直线分成两个小等腰三角形的是（）A．B．C． D．8．如图，P为边长为2的正三角形内任意一点，过P点分别作三边的垂线，垂足分别为D，E，F，则PD+PE+PF的值为（）A．B．C．2 D．29．如图，△ABC 的面积为20，点D 是BC 边上一点，且BD=BC ，点G 是AB 上一点，点H 在△ABC 内部，且四边形BDHG 是平行四边形，则图中阴影部分的面积是（）A ．5B ．10C ．15D ．2010．如图，在四边形ABCD 中，∠ABC=90°，AB=BC=2，E 、F 分别是AD 、CD 的中点，连接BE 、BF 、EF ．若四边形ABCD 的面积为6，则△BEF 的面积为（）A ．2B ．C ．D ．3二．填空题（共14小题）11．如图，在△ABC 中，已知∠1=∠2，BE=CD ，AB=5，AE=2，则CE= ．12．如图，△ABC 的三边AB 、BC 、CA 长分别为40、50、60．其三条角平分线交于点O ，则S △ABO ：S △BCO ：S △CAO = ．13．如图，在△ABC中，∠B=40°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=．14．如图，矩形EFGH内接于△ABC，且边FG落在BC上，若AD⊥BC，BC=3，AD=2，EF=EH，那么EH的长为．15．在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为（用含a的式子表示）．16．如图，Rt△ABC中，∠B=90°，AB=4，BC=3，AC的垂直平分线DE分别交AB，AC于D，E两点，则CD的长为．17．如图，△ABC中，∠C=90°，CA=CB，点M在线段AB上，∠GMB=∠A，BG ⊥MG，垂足为G，MG与BC相交于点H．若MH=8cm，则BG=cm．18．如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10=．19．如图，在△ABC中，CD是高，CE是中线，CE=CB，点A、D关于点F对称，过点F作FG∥CD，交AC边于点G，连接GE．若AC=18，BC=12，则△CEG的周长为．20．如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x 轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2017次变换后，等边△ABC的顶点C的坐标为．21．如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为．22．如图，在一张长为7cm，宽为5cm的矩形纸片上，现要剪下一个腰长为4cm 的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为．23．在△ABC中，AB=13，AC=20，BC边上的高为12，则△ABC的面积为．24．如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=10，DA=5，则四边形ABCD的面积为=，BD的长为．三．解答题（共4小题）25．如图，在四边形ABCD中，∠A=∠C=45°，∠ADB=∠ABC=105°．（1）若AD=2，求AB；（2）若AB+CD=2+2，求AB．26．如图：在矩形ABCD中，AD=60cm，CD=120cm，E、F为AB边的三等分点，以EF为边在矩形内作等边三角形MEF，N为AB边上一点，EN=10cm；请在矩形内找一点P，使△PMN为等边三角形（画出图形，并直接写出△PMF 的面积）．27．如图，已知Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，过点A作AE ⊥CD，AE分别与CD、CB相交于点H、E，AH=2CH．（1）求sinB的值；（2）如果CD=，求BE的值．28．如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．（1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．（2）如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE 中AE边上的高，试证明：AE=2CM+BN．2018年02月28日刘笑天的初中数学组卷参考答案与试题解析一．选择题（共12小题）1．如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m﹣n等于（）A．2 B．3 C．4 D．无法确定【分析】设空白出的面积为x，根据题意列出关系式，相减即可求出m﹣n的值．【解答】解：设空白出图形的面积为x，根据题意得：m+x=9，n+x=6，则m﹣n=9﹣6=3．故选B．【点评】本题考查了三角形的面积；设出未知数，根据三角形的面积得出关系式是解决问题的关键．2．如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（）A．有且只有1个B．有且只有2个C．组成∠E的角平分线D．组成∠E的角平分线所在的直线（E点除外）【分析】根据角平分线的性质分析，作∠E 的平分线，点P 到AB 和CD 的距离相等，即可得到S △PAB =S △PCD ．【解答】解：作∠E 的平分线，可得点P 到AB 和CD 的距离相等，因为AB=CD ，所以此时点P 满足S △PAB =S △PCD ．故选D ．【点评】此题考查角平分线的性质，关键是根据AB=CD 和三角形等底作出等高即可．3．如图，AD 是△ABC 的角平分线，则AB ：AC 等于（）A ．BD ：CDB ．AD ：CDC ．BC ：AD D ．BC ：AC【分析】先过点B 作BE ∥AC 交AD 延长线于点E ，由于BE ∥AC ，利用平行线分线段成比例定理的推论、平行线的性质，可得∴△BDE ∽△CDA ，∠E=∠DAC ，再利用相似三角形的性质可有=，而利用AD 时角平分线又知∠E=∠DAC=∠BAD ，于是BE=AB ，等量代换即可证．【解答】解：如图过点B作BE∥AC交AD延长线于点E，∵BE∥AC，∴∠DBE=∠C，∠E=∠CAD，∴△BDE∽△CDA，∴=，又∵AD是角平分线，∴∠E=∠DAC=∠BAD，∴BE=AB，∴=，∴AB：AC=BD：CD．故选：A．【点评】此题考查了角平分线的定义、相似三角形的判定和性质、平行线分线段成比例定理的推论．关键是作平行线．4．如图，在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线．若在边AB 上截取BE=BC，连接DE，则图中等腰三角形共有（）A．2个 B．3个 C．4个 D．5个【分析】根据已知条件分别求出图中三角形的内角度数，再根据等腰三角形的判定即可找出图中的等腰三角形．【解答】解：∵AB=AC，∴△ABC是等腰三角形；∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，∵BD是△ABC的角平分线，∴∠ABD=∠DBC=∠ABC=36°，∴∠A=∠ABD=36°，∴BD=AD，∴△ABD是等腰三角形；在△BCD中，∵∠BDC=180°﹣∠DBC﹣∠C=180°﹣36°﹣72°=72°，∴∠C=∠BDC=72°，∴BD=BC，∴△BCD是等腰三角形；∵BE=BC，∴BD=BE，∴△BDE是等腰三角形；∴∠BED=（180°﹣36°）÷2=72°，∴∠ADE=∠BED﹣∠A=72°﹣36°=36°，∴∠A=∠ADE，∴DE=AE，∴△ADE是等腰三角形；∴图中的等腰三角形有5个．故选D．【点评】此题考查了等腰三角形的判定，用到的知识点是等腰三角形的判定、三角形内角和定理、三角形外角的性质、三角形的角平分线定义等，解题时要找出所有的等腰三角形，不要遗漏．5．平面直角坐标系中，已知A（2，2）、B（4，0）．若在坐标轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是（）A．5 B．6 C．7 D．8【分析】由点A、B的坐标可得到AB=2，然后分类讨论：若AC=AB；若BC=AB；若CA=CB，确定C点的个数．【解答】解：∵点A、B的坐标分别为（2，2）、B（4，0）．∴AB=2，①若AC=AB，以A为圆心，AB为半径画弧与坐标轴有3个交点（含B点），即（0，0）、（4，0）、（0，4），∵点（0，4）与直线AB共线，∴满足△ABC是等腰三角形的C点有1个；②若BC=AB，以B为圆心，BA为半径画弧与坐标轴有2个交点（A点除外），即满足△ABC是等腰三角形的C点有2个；③若CA=CB，作AB的垂直平分线与坐标轴有两个交点，即满足△ABC是等腰三角形的C点有2个；综上所述：点C在坐标轴上，△ABC是等腰三角形，符合条件的点C共有5个．故选A【点评】本题考查了等腰三角形的判定，也考查了通过坐标确定图形的性质以及分类讨论思想的运用．6．如图，已知△ABC的面积为12，AD平分∠BAC，且AD⊥BD于点D，则△ADC 的面积是（）A．10 B．8 C．6 D．4【分析】延长BD交AC于点E，则可知△ABE为等腰三角形，则S△ABD =S△ADE，S△BDC=S△CDE，可得出S△ADC=S△ABC．【解答】解：如图，延长BD交AC于点E，∵AD平分∠BAE，AD⊥BD，∴∠BAD=∠EAD ，∠ADB=∠ADE ，在△ABD 和△AED 中，，∴△ABD ≌△AED （ASA ），∴BD=DE ，∴S △ABD =S △ADE ，S △BDC =S △CDE ，∴S △ABD +S △BDC =S △ADE +S △CDE =S △ADC ，∴S △ADC ═S △ABC =×12=6，故选C ．【点评】本题考查了等腰三角形的性质和判定的应用，由BD=DE 得到S △ABD =S △ADE ，S △BDC =S △CDE 是解题的关键．7．如图，在下列三角形中，若AB=AC ，则不能被一条直线分成两个小等腰三角形的是（）A ．B ．C ．D ．【分析】A 、D 是黄金三角形，C 、过A 点作BC 的垂线即可；只有B 选项不能被一条直线分成两个小等腰三角形．【解答】解：A 、中作∠B 的角平分线即可；C 、过A 点作BC 的垂线即可；D 、中以A 为顶点AB 为一边在三角形内部作一个72度的角即可；只有B选项不能被一条直线分成两个小等腰三角形．故选B．【点评】此题主要考查学生对等腰三角形的判定与性质的理解和掌握，此题的4个选项中只有D选项有点难度，所以此题属于中档题．8．如图，P为边长为2的正三角形内任意一点，过P点分别作三边的垂线，垂足分别为D，E，F，则PD+PE+PF的值为（）A．B．C．2 D．2【分析】首先连接PA、PB、PC，再根据正三角形的面积的求法，求出边长为2的正三角形的面积是多少；然后判断出S ABC=S APB+S APC+S BPC=PD+PE+PF，据此求出PD+PE+PF的值为多少即可．【解答】解：如图，连接PA、PB、PC，，∵△ABC是边长为2的正三角形，∴△ABC的面积为：；∵S ABC=S APB+S APC+S BPC=×2×PD+×2×PF+×2×PE=PD+PE+PF∴PD+PE+PF=，即PD+PE+PF的值为．故选：B．【点评】（1）此题主要考查了等边三角形的性质和应用，要熟练掌握，解答此题的关键是要明确：①等边三角形的三个内角都相等，且都等于60°．②等边三角形是轴对称图形，它有三条对称轴；③它的任意一角的平分线都垂直平分对边，三边的垂直平分线是对称轴．（2）此题还考查了等边三角形的面积的求法，要熟练掌握，解答此题的关键是要明确：边长是a的等边三角形的面积是a2．9．如图，△ABC的面积为20，点D是BC边上一点，且BD=BC，点G是AB上一点，点H在△ABC内部，且四边形BDHG是平行四边形，则图中阴影部分的面积是（）A．5 B．10 C．15 D．20【分析】设△ABC底边BC上的高为h，△AGH底边GH上的高为h1，△CGH底边GH上的高为h2，根据图形可知h=h1+h2．利用三角形的面积公式结合平行四边形的性质即可得出S阴影=S△ABC，由此即可得出结论．【解答】解：设△ABC底边BC上的高为h，△AGH底边GH上的高为h1，△CGH 底边GH上的高为h2，则有h=h1+h2，S△ABC=BC•h=2，∴S阴影=S△AGH+S△CGH=GH•h1+GH•h2=GH•（h1+h2）=GH•h．∵四边形BDHG是平行四边形，且BD=BC，∴GH=BD=BC，∴S阴影=×（BC•h）=S△ABC=5．故选A．【点评】本题考查了三角形的面积公式以及平行四边形的性质，解题的关键是找出S阴影=S△ABC．本题属于基础题，难度不大，解决该题型题目时，根据三角形的面积公式找出阴影部分的面积与△ABC的面积之间的关系是关键．10．如图，在四边形ABCD中，∠ABC=90°，AB=BC=2，E、F分别是AD、CD 的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（）A．2 B．C．D．3【分析】连接AC，过B作EF的垂线，利用勾股定理可得AC，易得△ABC的面积，可得BG和△ADC的面积，三角形ABC与三角形ACD同底，利用面积比可得它们高的比，而GH又是△ACD以AC为底的高的一半，可得GH，易得BH，由中位线的性质可得EF的长，利用三角形的面积公式可得结果．【解答】解：连接AC，过B作EF的垂线交AC于点G，交EF于点H，∵∠ABC=90°，AB=BC=2，∴AC===4，∵△ABC为等腰三角形，BH⊥AC，∴△ABG，△BCG为等腰直角三角形，∴AG=BG=2∵S△ABC=•AB•BC=×2×2=4，∴S△ADC=2，∵=2，∵△DEF∽△DAC，∴GH=BG=，∴BH=，又∵EF=AC=2，∴S△BEF=•EF•BH=×2×=，故选C．方法二：S△BEF =S四边形ABCD﹣S△ABE﹣S△BCF﹣S△FED，易知S△ABE +S△BCF=S四边形ABCD=3，S△EDF=，∴S△BEF =S四边形ABCD﹣S△ABE﹣S△BCF﹣S△FED=6﹣3﹣=．故选C．【点评】此题主要考查了三角形面积的运算，作出恰当的辅助线得到三角形的底和高是解答此题的关键．二．填空题（共14小题）11．如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE=3．【分析】由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．【解答】解：△ABE和△ACD中，，∴△ABE≌△ACD（AAS），∴AD=AE=2，AC=AB=5，∴CE=BD=AB﹣AD=3，故答案为3．【点评】本题主要考查了全等三角形的性质和判定，熟记定理是解题的关键．12．如图，△ABC 的三边AB 、BC 、CA 长分别为40、50、60．其三条角平分线交于点O ，则S △ABO ：S △BCO ：S △CAO = 4：5：6 ．【分析】首先过点O 作OD ⊥AB 于点D ，作OE ⊥AC 于点E ，作OF ⊥BC 于点F ，由OA ，OB ，OC 是△ABC 的三条角平分线，根据角平分线的性质，可得OD=OE=OF ，又由△ABC 的三边AB 、BC 、CA 长分别为40、50、60，即可求得S △ABO ：S △BCO ：S △CAO 的值．【解答】解：过点O 作OD ⊥AB 于点D ，作OE ⊥AC 于点E ，作OF ⊥BC 于点F ， ∵OA ，OB ，OC 是△ABC 的三条角平分线，∴OD=OE=OF ，∵△ABC 的三边AB 、BC 、CA 长分别为40、50、60，∴S △ABO ：S △BCO ：S △CAO =（AB•OD ）：（BC•OF ）：（AC•OE ）=AB ：BC ：AC=40：50：60=4：5：6．故答案为：4：5：6．【点评】此题考查了角平分线的性质．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．13．如图，在△ABC 中，∠B=40°，三角形的外角∠DAC 和∠ACF 的平分线交于点E ，则∠AEC= 70° ．【分析】根据三角形内角和定理、角平分线的定义以及三角形外角定理求得∠DAC+∠ACF=（∠B+∠B+∠1+∠2）；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数．【解答】解：∵三角形的外角∠DAC和∠ACF的平分线交于点E，∴∠EAC=∠DAC，∠ECA=∠ACF；又∵∠B=40°（已知），∠B+∠1+∠2=180°（三角形内角和定理），∴∠DAC+∠ACF=（∠B+∠2）+（∠B+∠1）=（∠B+∠B+∠1+∠2）=110°（外角定理），∴∠AEC=180°﹣（∠DAC+∠ACF）=70°．故答案为：70°．【点评】此题主要考查了三角形内角和定理以及角平分线的性质，熟练应用角平分线的性质是解题关键．14．如图，矩形EFGH内接于△ABC，且边FG落在BC上，若AD⊥BC，BC=3，AD=2，EF=EH，那么EH的长为．【分析】设EH=3x，表示出EF，由AD﹣EF表示出三角形AEH的边EH上的高，根据三角形AEH与三角形ABC相似，利用相似三角形对应边上的高之比等于相似比求出x的值，即为EH的长．【解答】解：如图所示：∵四边形EFGH是矩形，∴EH∥BC，∴△AEH∽△ABC，∵AM⊥EH，AD⊥BC，∴，设EH=3x，则有EF=2x，AM=AD﹣EF=2﹣2x，∴，解得：x=，则EH=．故答案为：．【点评】此题考查了相似三角形的判定与性质，以及矩形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．15．在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为3a（用含a的式子表示）．【分析】由折叠的性质得出BE=EF=a，DE=BE，则BF=2a，由含30°角的直角三角形的性质得出DF=BF=a，即可得出△DEF的周长．【解答】解：由折叠的性质得：B点和D点是对称关系，DE=BE，则BE=EF=a，∴BF=2a，∵∠B=30°，∴DF=BF=a，∴△DEF的周长=DE+EF+DF=BF+DF=2a+a=3a；故答案为：3a．【点评】本题考查了翻折变换的性质、含30°角的直角三角形的性质、三角形周长的计算；熟练掌握翻折变换的性质，由含30°角的直角三角形的性质得出DF=a 是解决问题的关键．16．如图，Rt△ABC中，∠B=90°，AB=4，BC=3，AC的垂直平分线DE分别交AB，AC于D，E两点，则CD的长为．【分析】先根据线段垂直平分线的性质得出CD=AD，故AB=BD+AD=BD+CD，设CD=x，则BD=4﹣x，在Rt△BCD中根据勾股定理求出x的值即可．【解答】解：∵DE是AC的垂直平分线，∴CD=AD，∴AB=BD+AD=BD+CD，设CD=x，则BD=4﹣x，在Rt△BCD中，CD2=BC2+BD2，即x2=32+（4﹣x）2，解得x=．故答案为：．【点评】本题考查的是线段垂直平分线的性质，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．17．如图，△ABC中，∠C=90°，CA=CB，点M在线段AB上，∠GMB=∠A，BG ⊥MG，垂足为G，MG与BC相交于点H．若MH=8cm，则BG=4cm．【分析】如图，作MD⊥BC于D，延长DE交BG的延长线于E，构建等腰△BDM、全等三角形△BED和△MHD，利用等腰三角形的性质和全等三角形的对应边相等得到：BE=MH，所以BG=MH=4．【解答】解：如图，作MD⊥BC于D，延长MD交BG的延长线于E，∵△ABC中，∠C=90°，CA=CB，∴∠ABC=∠A=45°，∵∠GMB=∠A，∴∠GMB=∠A=22.5°，∵BG⊥MG，∴∠BGM=90°，∴∠GBM=90°﹣22.5°=67.5°，∴∠GBH=∠EBM﹣∠ABC=22.5°．∵MD∥AC，∴∠BMD=∠A=45°，∴△BDM为等腰直角三角形∴BD=DM，而∠GBH=22.5°，∴GM平分∠BMD，而BG⊥MG，∴BG=EG，即BG=BE，∵∠MHD+∠HMD=∠E+∠HMD=90°，∴∠MHD=∠E，∵∠GBD=90°﹣∠E，∠HMD=90°﹣∠E，∴∠GBD=∠HMD，∴在△BED和△MHD中，，∴△BED≌△MHD（AAS），∴BE=MH，∴BG=MH=4．故答案是：4．【点评】本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了等腰直角三角形的性质．18．如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10=π．【分析】（1）图1，作辅助线构建正方形OECF，设圆O的半径为r，根据切线长定理表示出AD和BD的长，利用AD+BD=5列方程求出半径r=（a、b是直角边，c为斜边），运用圆面积公式=πr2求出面积=π；（2）图2，先求斜边上的高CD的长，再由勾股定理求出AD和BD，利用半径r=（a、b是直角边，c为斜边）求两个圆的半径，从而求出两圆的面积和=π；（3）图3，继续求高DM和CM、BM，利用半径r=（a、b是直角边，c 为斜边）求三个圆的半径，从而求出三个圆的面积和=π；综上所述：发现S1+S2+S3+…+S10=π．【解答】解：（1）图1，过点O做OE⊥AC，OF⊥BC，垂足为E、F，则∠OEC=∠OFC=90°∵∠C=90°∴四边形OECF为矩形∵OE=OF∴矩形OECF为正方形设圆O的半径为r，则OE=OF=r，AD=AE=3﹣r，BD=4﹣r∴3﹣r+4﹣r=5，r==1∴S1=π×12=π（2）图2，由S=×3×4=×5×CD△ABC∴CD=由勾股定理得：AD==，BD=5﹣=由（1）得：⊙O的半径==，⊙E的半径==∴S1+S2=π×+π×=π=××=×4×MD（3）图3，由S△CDB∴MD=由勾股定理得：CM==，MB=4﹣=由（1）得：⊙O的半径=，：⊙E的半径==，：⊙F的半径==∴S1+S2+S3=π×+π×+π×=π∴图4中的S1+S2+S3+S4=π则S1+S2+S3+…+S10=π故答案为：π．【点评】本题考查了直角三角形的内切圆，这是一个图形变化类的规律题，首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解；解决此题的思路为：①先找出计算直角三角形内切圆半径的规律：半径r=（a、b是直角边，c为斜边）；②利用面积相等计算斜边上的高；③运用勾股定理计算直角三角形的边长．19．如图，在△ABC中，CD是高，CE是中线，CE=CB，点A、D关于点F对称，过点F作FG∥CD，交AC边于点G，连接GE．若AC=18，BC=12，则△CEG的周长为27．【分析】先根据点A、D关于点F对称可知点F是AD的中点，再由CD⊥AB，FG ∥CD可知FG是△ACD的中位线，故可得出CG的长，再根据点E是AB的中点可知GE是△ABC的中位线，故可得出GE的长，由此可得出结论．【解答】解：∵点A、D关于点F对称，∴点F是AD的中点．∵CD⊥AB，FG∥CD，∴FG是△ACD的中位线，AC=18，BC=12，∴CG=AC=9．∵点E是AB的中点，∴GE是△ABC的中位线，∵CE=CB=12，∴GE=BC=6，∴△CEG的周长=CG+GE+CE=9+6+12=27．故答案为：27．【点评】本题考查的是三角形中位线定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．20．如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x 轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2017次变换后，等边△ABC的顶点C的坐标为（﹣2015，﹣﹣1）．【分析】据轴对称判断出点A变换后在x轴下方，然后求出点A纵坐标，再根据平移的距离求出点A变换后的横坐标，最后写出即可．【解答】解：∵△ABC是等边三角形AB=3﹣1=2，∴点C到x轴的距离为1+2×=+1，横坐标为2，∴C（2，+1），第2017次变换后的三角形在x轴下方，点C的纵坐标为﹣﹣1，横坐标为2﹣2017×1=﹣2015，所以，点C的对应点C′的坐标是（﹣2015，﹣﹣1），故答案为：（﹣2015，﹣﹣1）．【点评】本题考查了坐标与图形变化﹣平移，等边三角形的性质，读懂题目信息，确定出连续2016次这样的变换得到三角形在x轴上方是解题的关键．21．如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为2或2或2．【分析】利用分类讨论，当∠ABP=90°时，如图2，由对顶角的性质可得∠AOC=∠BOP=60°，易得∠BPO=30°，易得BP的长，利用勾股定理可得AP的长；当∠APB=90°时，分两种情况讨论，情况一：如图1，利用直角三角形斜边的中线等于斜边的一半得出PO=BO，易得△BOP为等边三角形，利用锐角三角函数可得AP的长；易得BP，利用勾股定理可得AP的长；情况二：如图3，利用直角三角形斜边的中线等于斜边的一半可得结论．【解答】解：当∠APB=90°时（如图1），∵AO=BO，∴PO=BO，∵∠AOC=60°，∴∠BOP=60°，∴△BOP为等边三角形，∵AB=BC=4，∴AP=AB•sin60°=4×=2；当∠ABP=90°时（如图2），∵∠AOC=∠BOP=60°，∴∠BPO=30°，∴BP===2，在直角三角形ABP中，AP==2，情况二：如图3，∵AO=BO，∠APB=90°，∴PO=AO，∵∠AOC=60°，∴△AOP为等边三角形，∴AP=AO=2，故答案为：2或2或2．【点评】本题主要考查了勾股定理，含30°直角三角形的性质和直角三角形斜边的中线，分类讨论，数形结合是解答此题的关键．22．如图，在一张长为7cm，宽为5cm的矩形纸片上，现要剪下一个腰长为4cm 的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为8cm2或2cm2或2cm2．【分析】因为等腰三角形腰的位置不明确，所以分三种情况进行讨论：（1）△AEF为等腰直角三角形，直接利用面积公式求解即可；（2）先利用勾股定理求出AE边上的高BF，再代入面积公式求解；（3）先求出AE边上的高DF，再代入面积公式求解．【解答】解：分三种情况计算：（1）当AE=AF=4时，如图：∴S=AE•AF=×4×4=8（cm2）；△AEF（2）当AE=EF=4时，如图：则BE=5﹣4=1，BF===，∴S=•AE•BF=×4×=2（cm2）；△AEF（3）当AE=EF=4时，如图：则DE=7﹣4=3，DF===，=AE•DF=×4×=2（cm2）；∴S△AEF故答案为：8或2或2．【点评】本题主要考查矩形的角是直角的性质和勾股定理的运用，要根据三角形的腰长的不确定分情况讨论，有一定的难度．23．在△ABC中，AB=13，AC=20，BC边上的高为12，则△ABC的面积为126或66．【分析】分两种情况：①∠B为锐角；②∠B为钝角；利用勾股定理求出BD、CD，即可求出BC的长．【解答】解：分两种情况：①当∠B为锐角时，如图1所示，在Rt△ABD中，BD===5，在Rt△ADC中，CD===16，∴BC=BD+CD=21，∴△ABC的面积为×21×12=126；②当∠B为钝角时，如图2所示，在Rt△ABD中，BC=CD﹣BD=16﹣5=11，所以△ABC的面积为×11×12=66；故答案为：126或66．【点评】本题主要考查了勾股定理；熟练掌握勾股定理，画出图形，分类讨论是解答此题的关键．24．如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=10，DA=5，则四边形ABCD的面积为=31，BD的长为2．【分析】连接AC ，在Rt △ABC 中，根据勾股定理求出AC 的长，利用勾股定理的逆定理，说明△ACD 是直角三角形．利用Rt △ABC 和Rt △ACD 的面积和求出四边形ABCD 的面积．过点D 作DE ⊥BC ，交BC 的延长线与点E ．易证明△ABC ∽△CED ，求出DE 、CE 的长，再利用勾股定理求出BD 的长，【解答】解：连接AC ，过点D 作DE ⊥BC ，交BC 的延长线与点E ．因为∠ABC=90°，AB=3，BC=4，∴AC==5，由于AC 2+CD 2=25+100=125，AD 2=（5）2=125， ∴AC 2+CD 2=AD 2．所以∠ACD=90°．所以S 四边形ABCD =S △ABD +S △ACD = =×3×4+×5×10=6+25=31．∵∠DEC=90°，∴∠DCE +∠CDE=90°，所以∠DCE +∠ACB=90°，∴∠CDE=∠ACB ，又∵∠ABC=90°，∴△ABC ∽△CED∴CE=6，DE=8．∴BE=BC +CE=10，在Rt △DEB 中， DB===2故答案为：31，2【点评】本题考查了直角三角形的勾股定理和逆定理及相似三角形的判定．解决本题的关键是连接AC利用直角三角形的面积求出四边形的面积．三．解答题（共4小题）25．如图，在四边形ABCD中，∠A=∠C=45°，∠ADB=∠ABC=105°．（1）若AD=2，求AB；（2）若AB+CD=2+2，求AB．【分析】（1）在四边形ABCD中，由∠A=∠C=45°，∠ADB=∠ABC=105°，得∠BDF=∠ADC﹣∠ADB=165°﹣105°=60°，△ADE与△BCF为等腰直角三角形，求得AE，利用锐角三角函数得BE，得AB；（2）设DE=x，利用（1）的某些结论，特殊角的三角函数和勾股定理，表示AB，CD，得结果．【解答】解：（1）过D点作DE⊥AB，过点B作BF⊥CD，∵∠A=∠C=45°，∠ADB=∠ABC=105°，∴∠ADC=360°﹣∠A﹣∠C﹣∠ABC=360°﹣45°﹣45°﹣105°=165°，∴∠BDF=∠ADC﹣∠ADB=165°﹣105°=60°，△ADE与△BCF为等腰直角三角形，∵AD=2，∴AE=DE==，∵∠ABC=105°，∴∠ABD=105°﹣45°﹣30°=30°，∴BE===，∴AB=；（2）设DE=x，则AE=x，BE===，∴BD==2x，∵∠BDF=60°，∴∠DBF=30°，∴DF==x，∴BF===，∴CF=，∵AB=AE+BE=，CD=DF+CF=x，AB+CD=2+2，∴AB=+1【点评】本题考查了勾股定理、等腰直角三角形的判定和性质、含有30°角的直角三角形的性质，解题的关键是作辅助线DE、BF，构造直角三角形，求出相应角的度数．26．如图：在矩形ABCD中，AD=60cm，CD=120cm，E、F为AB边的三等分点，以EF为边在矩形内作等边三角形MEF，N为AB边上一点，EN=10cm；请在矩形内找一点P，使△PMN为等边三角形（画出图形，并直接写出△PMF 的面积）．【分析】如图，以MN为边容易作出等边三角形，结合等边三角形的性质，连接PE，可证明△MPE≌△MNF，可证明PE∥MF，容易求得S△PMF=S△MEF，可求得答案．【解答】解：如图，以MN为边，可作等边三角形PMN；△PMF的面积为400．（求解过程如下）．连接PE，∵△MEF和△PMN为等边三角形，∴∠PMN=∠EMF=∠MFE=60°，MN=MP，ME=MF，∴∠PME=∠NMF，在△MPE和△MNF中，，∴△MPE≌△MNF（SAS），∴∠MEP=∠MFE=60°，∴∠PEN=60°，∴PE∥MF，∴S△PMF =S△MEF=EF2=400．【点评】本题主要考查等边三角形的性质及全等三角形的性质和判定，利用全等证得PE∥MF，得到S△PMF =S△MEF是解题的关键．27．如图，已知Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，过点A作AE ⊥CD，AE分别与CD、CB相交于点H、E，AH=2CH．（1）求sinB的值；（2）如果CD=，求BE的值．【分析】（1）根据∠ACB=90°，CD是斜边AB上的中线，可得出CD=BD，则∠B=∠BCD，再由AE⊥CD，可证明∠B=∠CAH，由AH=2CH，可得出CH：AC=1：，即可得出sinB的值；（2）根据sinB的值，可得出AC：AB=1：，再由AB=2，得AC=2，则CE=1，从而得出BE．【解答】解：（1）∵∠ACB=90°，CD是斜边AB上的中线，∴CD=BD，∴∠B=∠BCD，∵AE⊥CD，∴∠CAH+∠ACH=90°，又∠ACB=90°∴∠BCD+∠ACH=90°∴∠B=∠BCD=∠CAH，即∠B=∠CAH，∵AH=2CH，∴由勾股定理得AC=CH，∴CH：AC=1：，∴sinB=；（2）∵sinB=，∴AC：AB=1：，∴AC=2．∵∠CAH=∠B，∴sin∠CAH=sinB==，设CE=x（x＞0），则AE=x，则x2+22=（x）2，∴CE=x=1，AC=2，在Rt△ABC中，AC2+BC2=AB2，∵AB=2CD=2，∴BC=4，∴BE=BC﹣CE=3．【点评】本题考查了解直角三角形，以及直角三角形斜边上的中线，注意性质的应用，难度不大．28．如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．（1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．（2）如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE 中AE边上的高，试证明：AE=2CM+BN．【分析】（1）①通过角的计算找出∠ACD=∠BCE，再结合△ACB和△DCE均为等腰三角形可得出“AC=BC，DC=EC”，利用全等三角形的判定（SAS）即可证出△ACD ≌△BCE，由此即可得出结论AD=BE；②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC，再通过角的计算即可算出∠AEB的度数；（2）根据等腰三角形的性质结合顶角的度数，即可得出底角的度数，利用（1）的结论，通过解直角三角形即可求出线段AD、DE的长度，二者相加即可证出结论．【解答】（1）①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°，∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB，∠DCE=∠DCB+∠BCE，∴∠ACD=∠BCE．∵△ACB和△DCE均为等腰三角形，∴AC=BC，DC=EC．在△ACD和△BCE中，有，∴△ACD≌△BCE（SAS），∴AD=BE．②解：∵△ACD≌△BCE，∴∠ADC=∠BEC．∵点A，D，E在同一直线上，且∠CDE=50°，∴∠ADC=180°﹣∠CDE=130°，∴∠BEC=130°．∵∠BEC=∠CED+∠AEB，且∠CED=50°，∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．（2）证明：∵△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=120°，∴∠CDM=∠CEM=×（180°﹣120°）=30°．∵CM⊥DE，∴∠CMD=90°，DM=EM．在Rt△CMD中，∠CMD=90°，∠CDM=30°，∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°，∠BEC=∠CEM+∠AEB，∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°，∴∠BEN=180°﹣120°=60°．在Rt△BNE中，∠BNE=90°，∠BEN=60°，∴BE==BN．∵AD=BE，AE=AD+DE，∴AE=BE+DE=BN+2CM．【点评】本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算，解题的关键是：（1）通过角的计算结合等腰三角形的性质证出△ACD≌△BCE；（2）找出线段AD、DE的长．本题属于中档题，难度不大，但稍显繁琐，解决该题型题目时，利用角的计算找出相等的角，再利用等腰三角形的性质找出相等的边或角，最后根据全等三角形的判定定理证出三角形全是关键．。

中考数学复习专项之三角形全等 (含答案)

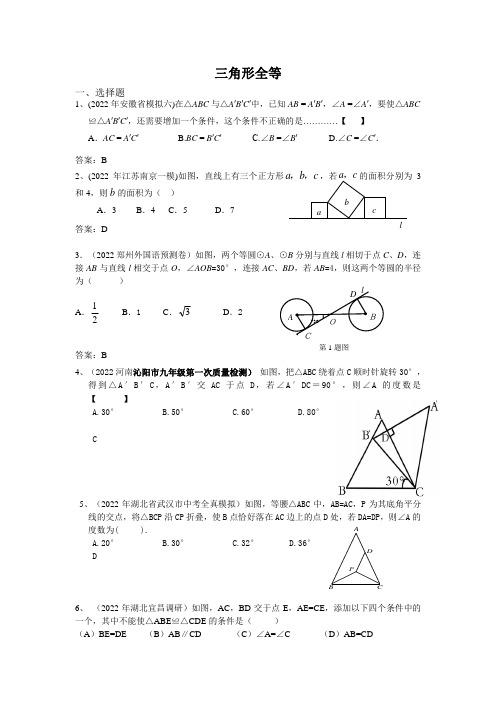
30°AＢＯＣl D 第1题图C A P B D三角形全等一、选择题1、(2022年安徽省模拟六)在△ABC 与△A ′B ′C ′中，已知AB = A ′B ′，∠A =∠A ′，要使△ABC ≌△A ′B ′C ′，还需要增加一个条件，这个条件不正确的是…………【】 A ．AC = A ′C ′ B.BC = B ′C ′ C.∠B =∠B ′ D.∠C =∠C ′．答案：B2、(2022年江苏南京一模)如图，直线上有三个正方形a b c ，，，若a c ，的面积分别为3和4，则b 的面积为（） A ．3 B ．4 C ．5 D ．7 答案：D3．（2022郑州外国语预测卷）如图，两个等圆⊙A 、⊙B 分别与直线l 相切于点C 、D ，连接AB 与直线l 相交于点O ，∠AOB =30°，连接AC 、BD ，若AB =4，则这两个等圆的半径为（） A ．21B ．1C ．3D ．2 答案：B4、（2022河南沁阳市九年级第一次质量检测）如图，把△ABC 绕着点C 顺时针旋转30°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC ＝90°，则∠A 的度数是【】A.30°B.50°C.60°D.80°C5、（2022年湖北省武汉市中考全真模拟）如图，等腰△ABC 中，AB=AC ，P 为其底角平分线的交点，将△BCP 沿CP 折叠，使B 点恰好落在AC 边上的点D 处，若DA=DP ，则∠A 的度数为( ).A.20°B.30°C.32°D.36°D6、（2022年湖北宜昌调研）如图，AC ，BD 交于点E ，AE=CE ，添加以下四个条件中的一个，其中不能使△ABE ≌△CDE 的条件是（）（A ）BE=DE （B ）AB ∥CD （C ）∠A=∠C （D ）AB=CDabclEABCD答案：D7、（2022年唐山市二模）在锐角△ABC 中，∠BAC =60°，BN 、CM 为高，P 为BC 的中点，连接MN 、MP 、NP ，则结论：①NP =MP ②当∠ABC =60°时，MN ∥BC ③ BN =2AN ④AN︰AB =AM ︰AC ，一定正确的有（）A 、1个B 、2个C 、3个D 、4个答案：C8.（2022年上海闵行区二摸）在△ABC 与△A ′B ′C ′中，已知AB = A ′B ′，∠A =∠A ′，要使△ABC ≌△A ′B ′C ′，还需要增加一个条件，这个条件不正确的是（A ）AC = A ′C ′；（B ）BC = B ′C ′；（C ）∠B =∠B ′；（D ）∠C =∠C ′．答案：B二、填空题1、（2022云南勐捧中学二模）如图，AB CD ，相交于点O ，AO=CO ，试添加一个条件使得AOD COB △≌△，你添加的条件是（只需写一个）．【答案】∠A= ∠C 、∠D= ∠B 、OD=OB （答案不唯一）2．（2022年安徽初中毕业考试模拟卷一）如图，ABC ∆为等边三角形，AQ =PQ ，PR =PS ，PR ⊥AB 于R ，PS ⊥AC 于S ，则四个结论正确的是．（把所有正确答案的序号都填写在横线上）①AP 平分∠BAC ；②AS =AR ；③QP ∥AR ；④BRP ∆≌△QSP ．答案：①②③④三、解答题1、(2022年湖北荆州模拟5)（本题满分8分）将两块斜边长度相等的等腰直角三角纸板如图(1)摆放，若把图(1)中的△BCN 逆时针旋转90°，得到图(2)，图(2)中除△ABC ≌△CED 、△BCN ≌△ACF 外，你还能找到一对全等的三角形吗?写出你的结论并说明理由．AC BDO第1题答案：解：△FCM ≌△NCM ，理由如下： ∵把图中的△BCN 逆时针旋转90°， ∴∠FCN=90°，CN=CF ， ∵∠MCN=45°， ∴∠FCM=90°-45°=45°，在△FCM 和△NCM 中∵CM=CM ，∠FCM=∠NCM ， FC=CN∴△FCM ≌△NCM （SAS ）．2、(2022年湖北荆州模拟6)（本题满分8分）如图，正方形ABCD 和BEFG 在直线AB 的同侧，连接AG 、EC ,易证AG=EC ，现在将正方形BEFG 顺时针旋转30°，那么AG=EC 还成立吗？请作出旋转后的图形，并证明你的结论. 答案：解：成立. 理由如下：在ΔABG 与ΔCBE 中，0120AB CB ABG CBE BG BE =⎧⎪∠=∠=⎨⎪=⎩∴ ΔABG ≌ΔCBE ∴ AG=CE3、(2022年江苏南京一模)（7分）如图， AB =AC ，CD ⊥AB 于D ，BE ⊥AC 于E ，BE 与CD 相交于点O ． (1) 求证：AD =AE ；(2) 连接BC ，DE ，试判断BC 与DE 的位置关系并说明理由．答案：（1）证明：在△ACD 与△ABE 中， ∵∠A =∠A ，∠ADC =∠AEB =90°，AB =AC ， ∴ △ACD ≌△ABE ．…………………… 2分 ∴ AD=AE ． ……………………3分 (2) 互相平行 ……………………4分在△ADE 与△ABC 中， ∵AD=AE ，AB=AC ，∴ ∠ADE=∠AED ,∠ABC=∠ACB ……………6分且 ∠ADE =180－∠A =∠ABC.∴ DE ∥BC ． ……………7分第1题图第2题图第2题解答CACBB第2题图14．（2022年北京房山区一模）如图，点C、B、E在同一条直线上，AB∥DE，∠ACB=∠CDE，AC=CD．求证：AB=CD ．答案：证明：∵AB∥DE∴∠ABC=∠E ------------------------------1分∵∠ACB=∠CDE，AC=CD --------------------- --------3分∴△ABC≌△CED -------------------------4分∴AB=CD--------------------------5分5．（2022年北京房山区一模）（1）如图1，△ABC和△CDE都是等边三角形，且B、C、D三点共线，联结AD、BE相交于点P，求证：BE = AD.（2）如图2，在△BCD中，∠BCD＜120°，分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF，联结AD、BE和CF交于点P，下列结论中正确的是（只填序号即可）①AD=BE=CF；②∠BEC=∠ADC；③∠DPE=∠EPC=∠CPA=60°；（3）如图2，在（2）的条件下，求证：PB+PC+PD=BE.答案：(1)证明：∵△ABC和△CDE都是等边三角形∴BC=AC，CE=CD，∠ACB=∠DCE=60°∴∠BCE=∠ACD∴△BCE≌△ACD（SAS）∴BE=AD--------------1分（2）①②③都正确--------------4分（3）证明：在PE上截取PM=PC，联结CM由（1）可知，△BCE≌△ACD（SAS）EDC BA第1题图ADAB∴∠1=∠2设CD 与BE 交于点G ,,在△CGE 和△PGD 中 ∵∠1=∠2，∠CGE =∠PGD∴∠DPG =∠ECG =60°同理∠CPE =60° ∴△CPM 是等边三角形--------------5分 ∴CP =CM ，∠PMC =60° ∴∠CPD =∠CME =120°∵∠1=∠2,∴△CPD ≌△CME （AAS ）---6分 ∴PD =ME∴BE =PB +PM +ME =PB +PC +PD . -------7分即PB+PC+PD=BE .6．（2022年北京龙文教育一模）已知：如图，AB ∥CD ，AB =CD ，点E 、F 在线段AD 上，且AF=DE ．求证：BE =CF ．答案：证明: AF=DE ， ∴ AF-EF=DE –EF ．即 AE=DF ．………………1分AB ∥CD ，∴∠A =∠D ．……2分在△ABE 和△DCF 中， AB =CD ， ∠A =∠D ， AE=DF ．∴△ABE ≌△DCF ．……….4分 ∴ BE =CF ．…………….5分7. （2022年北京龙文教育一模）阅读下面材料：问题：如图①，在△ABC 中， D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =45°，DC =2．求BD 的长．小明同学的解题思路是：利用轴对称，把△ADC 进行翻折，再经过推理、计算使问题得到解决．（1）请你回答：图中BD 的长为；（2）参考小明的思路，探究并解答问题：如图②，在△ABC 中，D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =30°，DC =2，求BD 和AB 的长．FE ACDB第3题图答案：解：（1）22=BD . ……………………………… ………………………1分（2）把△ADC 沿AC 翻折，得△AEC ，连接DE ， ∴△ADC ≌△AEC .∴∠DAC =∠EAC ，∠DCA =∠ECA ， DC ＝EC . ∵∠BAD =∠BCA =2∠DAC =30°， ∴∠BAD =∠DAE =30°，∠DCE =60°.∴△CDE 为等边三角形. ……………………2分 ∴DC ＝DE .在AE 上截取AF ＝AB ，连接DF ， ∴△ABD ≌△AFD . ∴BD ＝DF .在△ABD 中，∠ADB =∠DAC ＋∠DCA =45°， ∴∠ADE =∠AED =75°，∠ABD =105°. ∴∠AFD =105°. ∴∠DFE =75°. ∴∠DFE =∠DEF . ∴DF ＝DE .∴BD ＝DC ＝2. …………………………………………………………………3分作BG ⊥AD 于点G ， ∴在Rt △BDG 中， 2=BG . ……………………………………………4分∴在Rt △ABG 中，22=AB . ……………………………………………5分 8．（2022年北京平谷区一模）已知：如图，AB ∥CD ，AB =EC ，BC =CD . 求证：AC =ED .答案：证明：∵ AB //CD ，∴B DCE ∠=∠．………………… ………………………1分在△ABC 和△ECD 中，= =B DCE AB EC BC CD ∠∠⎧⎪=⎨⎪⎩，，， ∴ △ABC ≌△ECD ． …………………… ………………4分∴ AC =ED ．………………………… ……………………5分9．（2022年北京顺义区一模）已知：如图，CA 平分BCD ∠, 点E 在AC 上，BC EC =，AC DC =．求证：A D ∠=∠．答案：证明：∵CA 平分BCD∠∴ ACB DCE ∠=∠ ……………1分在ABC ∆和DEC ∆中∵BC EC ACB DCE AC DC =⎧⎪∠=∠⎨⎪=⎩……………3分 ∴ABC ∆≌DEC ∆ …………………………………………… 4分 ∴A D ∠=∠ ……………………………………………5分10．（2022年北京平谷区一模）（1）如图(1)，△ABC 是等边三角形，D 、E 分别是 AB 、BC 上的点，且BD CE =，连接AE 、CD 相交于点P . 请你补全图形，并直接写出∠APD 的度数；= （2）如图（2）,Rt △ABC 中，∠B =90°，M 、N 分别是 AB 、BC 上的点，且,AM BC =BM CN =，连接AN 、CM 相交于点P . 请你猜想∠APM = °，并写出你的推理过程.答案：解：（1）60° （2）45° ………………………………..2分证明：作AE ⊥AB 且AE CN BM ==. 可证EAM MBC ∆≅∆. ……………………………..3分 ∴ ,.ME MC AME BCM =∠=∠∵ 90,CMB MCB ∠+∠=︒∴ 90.CMB AME ∠+∠=︒∴ 90.EMC ∠=︒∴ EMC ∆是等腰直角三角形,45.MCE ∠=︒ ……………….5分又△AEC ≌△CAN （s ， a ， s ）∴ .ECA NAC ∠=∠ ∴ EC ∥AN.∴ 45.APM ECM ∠=∠=︒…………………………………………………………………..7分EDCBA第6题图第7题图11.（2022浙江东阳吴宇模拟题）(本题12分) 如图，平面直角坐标系中，点A （0，4），B （3，0），D 、E 在x 轴上，F 为平面上一点，且EF ⊥x 轴，直线DF 与直线AB 互相垂直，垂足为H ，△AOB ≌△DEF ，设BD ＝h 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考必练试题
年级教学媒体教学目标知识技能过程方法情感态度教学重点教学难点
八年级
课题
12.3.2 等边三角形（1）多媒体
课型
新授
1. 掌握并会运用等边三角形的性质. 2. 掌握并会运用等边三角形的判定. 经过应用等边三角形的性质与判定的过程培养学生分析问题、解决问题的能力.
经过应用等边三角形的性质与判定的过程增强学生挑战困难的勇气，体会成功的喜悦，增强学习的信心. 等边三角形的性质和判定. 等边三角形的性质的应用.
教学过程设计
教师展示问题，板在一次探究活动中，老师给同学们出了一道题目：书课题。 “如果等腰三角形有一个角是 60°，那么这个三角形的。学生观察图形，回三边有什么关系？” 。答问题。小明假设底角为 60°，得出了三个角都是 60°，小教师给出性质、判亮假设顶角为 60°，也得出了三个角都是 60°，根据 “等定的准确描述，并角对等边” ，最后得出结论：三边都相等. 板书性质、判定。老师告诉他们“这种三条边都相等的叫做等边三角（ 1 ）、（ 2 ）教师引形” 。小明、小亮也发表了自己的看法，小明认为“三条导学生根据图形选边都相等的三角形是等边三角形，而不是等腰三角形” ；择恰当的方法证明（3）小亮认为“等边三角形也还是等腰三角形，只是比一般两条线段相等。的等腰三角形特殊而已” .，小明、小亮谁说的有道理呢？教师引导学生选择恰当的判定方法证学完这节课就能见分晓。明等边三角形。二、探究新知学生相互交流、相 A 探究：互讨论解决问题。观察右图，回答下面的问题学生独立思考，自 1. 等边三角形边、角具有什么性质？己解决问题。学生独立思考，自 2. 在△ABC 中，∠A=∠B=∠C， C 己解决问题。你能得到 AB=BC=CA 吗？为 B 第 3、 4 题学生画图、什么？比较，体会前后图 3. 在△ABC 中，AB=BC，∠A=60°（ ∠B=60°或形底边的变化，然 ∠C =60°）你能得到 AB=BC=CA 吗？为什么？后选择答案。 4. 等边三角形是轴对称图形吗？有几条对称轴？学生先独立思考， 5. 等边三角形与等腰三角形有什么关系呢？在相互交流。归纳等边三角形的性质：教师引导学生把外等边三角形的三个内角都相等，并且每一个内角都角∠APE 转化。学生观察图形，选等于 60°。教学程序及教学内容一、情境引入师生行为设计意图通过情境引入本节课课题，增加学生的学习兴趣。学生通过观察、思考、证明、归纳，培养学生的语言表达能力、观察能力、归纳能力、养成良好的自觉探索几何命题的习惯。巩固等边三角形性质与判定。培养学生合作意识及分析问题、解决问题的能力。考察学生对等边三角形性质的掌握。考察学生对等边三角形判定的掌握。考察学生对等边三角形判定的掌握，培养学生的动手能力。考察学生对等边三角形性质的掌握，体会数学中转化的思想。考察学生对等边三角形性质的掌握。
择恰当的方法证明两条线段相等。学生先独立思考，在相互交流。教师引导学生证出 △ABE≌△ACD。学生先独立思考，在相互交流，通过观察、画图猜出结论。教师引导学生延长 EC。（1）教师引导学生证出运用等式的性质证出 AF=CE。（2）教师引导学生运用恰当的方法判定等边三角形。教师引导学生回顾本节课知识，并总结、归纳本节课的重点。
考察学生对等边三角形性质、判定的掌握。培养学生分析问题、解决问题的能力。考察学生对等边三角形性质的掌握，知道等腰三角形的 “三线合一”对等边三角形也适用。培养学生大胆尝试，勇于探索，提高学生的思维能力和证明能力。
4．若等腰三角形的腰长为 2，顶角大于底角，则这个等腰三角形的周长为（ A．6 B．大于 6
5．如图，已知等边 ABC 中，BD=CE，AD 与 BE 交于点 P，求∠APE 的度数. 6．已知 ABC 、 DBE 都是等边三角形. 求证：AE=CD. 7．如图所示， E 是等边 ABC 中 AC 边上的点， BE=CD，
中考必练试题ຫໍສະໝຸດ ∠1=∠2. 求证： ADE 为等边三角形. 8．在 ABC 中，∠ACB=90°， ACD 、 BCE 都是等边三角形，请你探究 EC 与 AD 的位置关系，并证明你的结论. 拓展思维：如图，延长 ABC 的各边，使得 BF=AC，AE=CD=AB，顺次连接 D、E、F，得到
中考必练试题
等边三角形的判定：三个角都相等的三角形是等边三角形。有一个角是 60°的等腰三角形是等边三角形。【例题】如图，已知 ABC 、 DCE 均为等边三角形，且 B、C、E 在一条直线上，连结 BD、AE 分别交 AC、 DC 于 F、G. (1) 求证：AE=BD； (2) 求证：CF=CG； (3)连结 FG，求证： CFG 为等边三角形. 【分析】（1）由于等边三角形各边都相等，各角都是 60° ，不难证明 ACE BCD ，所以 AE＝BD；（2）利用（1）中的全等，不难证明 ACG BCF ，所以 CF=CG；（3）因 CFG 为等腰三角形，只须证其有 60° 角。【点拨】本题条件中，即使 B、C、E 不在一条直线上，所证线段依然相等，只是 CFG 为一般等腰三角形，请同学们自己验证。三、当堂训练 1. 对于等边三角形，下列说法不成立的是（ A．三条边都相等 B．每个角都是 60° C．有三条对称轴 D．两条高互相垂直 2．下列说法中正确的个数是（） ①有三条对称轴的三角形是等边三角形； ②三个外角都相等的三角形是等边三角形； ③有一个外角为 120°的等腰三角形是等边三角形； ④腰上的高与底边上的高相等的等腰三角形是等边三角形。 A．1 B．2 C．3 ） D．无法确定） C．小于 6 D 无法确定 D．4 3．等腰三角形的腰长为 2，顶角与底角相等，则这个等腰三角形的周长为（ A．4 B．5 C．6 ）