200671380521_常用弹塑性材料模型
[工学]第五章 弹塑性模型理论
![[工学]第五章 弹塑性模型理论](https://img.taocdn.com/s3/m/2794070ecfc789eb172dc8bc.png)
第五章 弹塑性模型理论5.1 概述弹塑性理论可以分为两种,塑性增量理论和塑性全量理论。
塑性增量理论又称塑性流动理论,塑性全量理论又称塑性形变理论。
在塑性增量理论中,将物体在弹塑性变形阶段的应变ij ε分为两部分:弹性应变e ij ε和塑性应变p ij ε。
塑性应变增量ij d ε的表达式为e p ij ij ij d d d εεε=+ (5.1.1)式中,弹性应变增量d e ij ε可以用广义虎克定律计算,塑性应变增量d p ij ε可以根据塑性增量理论计算。
塑性增量理论主要包括三部分:(1) 屈服面理论;(2) 流动规则理论;(3) 加工硬化(或软化)理论。
在塑性形变理论中是按全量来分析问题的。
它在盈利状态和相应的应变状态之间建立一一对应的关系。
塑性形变理论实质上是把弹塑性变形过程看成是非线性弹性变形过程。
严格说,在弹塑性变形理论的应用是有条件的。
严格讲,只有在等比例加载条件下,应用塑性变形理论可以得到精确解。
所谓等比例加载是指在加载过程中,各应力分量是按同一比例增加的。
严格的等比例加载是很难满足的,在土工问题中可以说是不可能的。
在简单加载条件下应用塑性形变理论分析有时也可以取得较好效果。
近些年来建立的土体弹塑性模型大部分是根据塑性增量理论建立的。
本章主要介绍塑性增量理论,在最后一节简要介绍塑性形变理论。
5.2 屈服面得概念首先讨论理想弹塑性材料。
理想弹塑性材料受力到什么程度才开始发生塑性变形呢?在简单拉伸时,问题是很明显的。
当应力等于屈服应力σs 时,塑性变形开始产生。
σs 值是可以在拉伸试验应力-应变曲线上找到的。
然而在复杂应力状态时,问题就不是这样简单了。
一点的应力状态由六个应力分量确定。
在复杂应力状态下,显然不能任意选取某一个应力分量的数值作为判断材料是否进入塑性状态的标准。
因此需要在应力空间或应变空间来考虑这一问题。
在土塑性力学中,常用的应力空间有三维主应力空间、p 、q (或σm ,σ1-σ3)应力平面、以及132σσ+,132σσ-应力平面等。
钢丝帘线弹塑性材料模型探讨

旦 一 A — A 一 / o o
一
( )
n ( 1+ 十 n e n ) ( 5 )
真实 塑性 应变 ( £ 。 ) 可 以 由真 实 总 应 变 ( e ) 和
及杨 氏模 量 ( E) 得 到
e 一 et一
关 系[ 引。
而 钢丝 帘线 又是子 午线 轮胎结 构 中的 主要受 力材 料; 因此 , 对其 进行 受力 分析 已经成 为现 代轮 胎结 构 设计 和分 析 的重要工 作之 一 。 由于轮 胎结 构及
其材 料 的复 杂性 , 至今 还 没有 有 效 的试 验 手段 来 直观、 定 量地 分析 轮胎 内部材 料 的受力 变形 情况 。 随 着计 算机 和数 学 、 力 学等 自然科 学 的发展 , 有 限
采用试 验 与 Ab a q u s软 件 模 拟 相 结 合 的 方 式, 在 充分 考虑 材料 非线 性 、 多股 加捻钢 丝之 间复 杂 接触 和拉 伸后 截面变 化 的情况 下 , 较直观 、 简 便
地 获得 了钢 丝帘线 弹 塑性材 料模 型参 数 。结果 表
关键词 : 钢丝帘线; 有 限 元分 析 ; 材 料 模 型
中 图分 类 号 : T Q3 3 o . 3 8 9
文献 标 志 码 : B
文章编号: 1 0 0 6 — 8 1 7 1 ( 2 0 1 4 ) 1 0 — 0 6 0 2 — 0 3
众所 周 知 , 轮胎 是汽 车安 全 的关键 部件 之一 ,
考虑 塑性 变 形 的不 可 压 缩 性 , 并 假 设 弹 性 变
形 也是 不可压 缩 的 , 建 立真 实应 力 ( ) 与 名 义应 力
两种材料的弹性、塑性仿真参数及应用

一、05Cr17Ni4Cu4Nb弹性、塑性仿真参数及应用
1.材料简介
05Cr17Ni4Cu4Nb即17-4PH,属马氏体不锈钢。
2.弹性、塑性仿真参数
MAT PLASTIC KINEMATIC模型参数:σ0=1076Mpa,E=186.8Gpa,Ep=1705Mpa,C=21999S-1,P=1.632。
3.材料应用
沉淀硬化型不锈钢,常用在高强度冲击结构,耐腐蚀性与304相当。
适用于400℃以下的高强度耐蚀件,例如,飞机、导弹的紧固件,涡轮发动机安装边和阀门等。
二、022Cr17Ni12Mo2弹性、塑性仿真参数及应用
1.材料简介
022Cr17Ni12Mo2即316L,属奥氏体不锈钢。
2.弹性、塑性仿真参数
弹性模量E=2.1E11pa,泊松比v=0.33;Johnson-Cook模型参数A=280MPa,B=1250Mpa,n=0.76,C=0.070,m=0.82,Tm=1800K,Tr=198K。
3.材料应用
主要做耐点蚀材料,常用于海水或其他其他介质,广泛应用于医疗器械行业。
也可用做耐热材料。
弹塑性材料

这两个选项中的所有数据点必须升序排列
Copyright © 2012 Altair Engineering, Inc. Proprietary and Confidential. All rights reserved.
NLSTAT MATS1 – 硬化准则
• HR-参数
• • • • 1 = isotropic hardening 2 = kinematic hardening 3 = mixed hardening (30% kinematic 和 70% isotropic hardening) 0<HR<1 = mixed hardening (HR*100% kinematic 和 (1-HR)*100% isotropic hardening)
V RBE3单元用于施加载荷
操作:
• 单元属性
材料:
理想的塑钢
• 材料定义
• 边界条件和载荷 • 输出请求 • 工况
Young‘s modulus: 210,000 N/mm² Poisson‘s ratio: 0.3 Yield stress: 230 N/mm²
σ
σy
E
查看:
• Out文件/收敛过程 • 应力 • 塑性应变
Copyright © 2012 Altair Engineering, Inc. Proprietary and Confidential. All rights reserved.
NLSTAT Ex.3.1: 建模 – 梁
模型:
V 3D网格
文件:beam_bending_blank.fem 600N
Copyright © 2012 Altair Engineering, Inc. Proprietary and Confidential. All rights reserved.
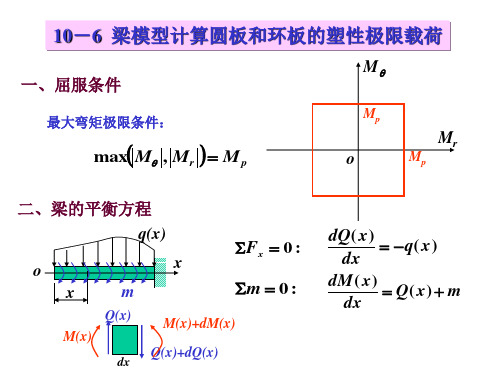
弹塑性力学10-6梁模型计算圆板和环板的塑形极限载荷(精)
例题1:边长为 a 的正方形薄板,一边固支、两边简支,自由边中点A受集 中载荷 P 作用,板的塑性极限弯矩为: Mp ,求塑性极限载荷。 D
b
b
C
a
h
E A B
解:设A点的挠度为d
ABC与ACD的相对转角为q :
a
q
d
AC
cota cot b 5
j d
a
d
2 AC
j
d
ACD与CD的相对转角为j:
dr
梁计算模型
板 x o r
q(r) r
o x
m
Mx Qx
m
q(x) 极限条件:
2rMr 2rQr 2Mq
2rq(r) Mmax Mp
若梁和圆板的边界条 件在形式上相同,可 通过求解变量转换后 梁的问题得到圆板的 解答。
四、 梁模型计算圆板和环板的塑性极限载荷的步骤
1. 结构转换 o
r
o
解:
o
z
r
r a
a
z
2rM r 2rM p r r 2rq 2 3
m= 2Mp
qr 2 Mr M p 6
Mr
r a
qa2 M p M p M p 6
ql 12
Mp a2
简支圆板:
Mr
r a
0
ql 6
Mp a2
例题2:半径为 a 的简支环板,内半径为 b ,受均布载荷 q 作用,圆板单 位塑性极限弯矩为: Mp ,求塑性极限载荷。 2rq q
i 1
ai bi
( n 2) 2n 2 n
Pl M P cota i cot b i
弹塑性力学基础与有限元分析-接触分析实例

06
结论与展望
结论
1
本文通过理论分析和有限元模拟,深入研究了弹 塑性力学基础与有限元分析在接触分析中的应用。
2
研究结果表明,弹塑性力学基础与有限元分析在 接触分析中具有较高的精度和可靠性,能够有效 地模拟复杂接触问题。
3
本文所采用的有限元分析方法在处理接触问题时 具有较好的通用性和扩展性,为进一步研究复杂 接触问题提供了有力支持。
弹塑性本构模型
弹塑性本构模型的定义
弹塑性本构模型是描述弹塑性材料力学行为的数学模型,它通过应力应变关系来描述材料的弹塑性行 为。
常见的弹塑性本构模型
常见的弹塑性本构模型包括Mohr-Coulomb模型、Drucker-Prager模型、Cam-Clay模型等。这些模 型在描述材料的弹塑性行为方面各有特点,适用于不同的材料和工程问题。
接触面完全贴合,无相对运动。
滑动状态
接触面部分贴合,存在相对运动。
混合状态
接触面同时存在分离、粘结和滑动。
接触检测与跟踪
初始接触检测
确定初始状态下接触面的位置和状态。
接触状态跟踪
实时监测接触面的运动状态和相互作用。
接触面更新
根据接触状态调整接触面的几何形状和参数。
接触刚度与阻尼
1 2
接触刚度
描述接触面间的相互作用力与相对位移的关系。
求解阶段主要进行有限元 方程的求解,得到各节点 的位移和应力等结果。
ABCD
前处理阶段主要完成有限元 模型的建立和网格划分,为 求解阶段提供输入数据。
后处理阶段主要对求解结果进 行可视化、分析和评估,为工 程设计和优化提供依据。
04
接触分析原理
接触状态描述
分离状态
常用材料弹性模量和剪切模量

常用材料弹性模量和剪切模量常用材料的弹性模量和剪切模量指的是材料在受力时的弹性性质,即材料在受力后发生形变后能够恢复到原来形状的程度。
弹性模量和剪切模量是用来描述材料的弹性行为的参数,对于材料的力学性质和设计有着重要的意义。
弹性模量(Young's Modulus)通常以E表示,是描述材料拉伸或压缩时的弹性变形性能的参数。
它的定义是材料应力和应变之间的比值,即E = σ/ε,其中σ是材料的应力,ε是材料的应变。
弹性模量的单位是帕斯卡(Pascal),常用的单位还包括千帕斯卡(Kilopascal)和兆帕斯卡(Megapascal)等。
弹性模量越大,表示材料的抵抗变形的能力越强。
常见材料的弹性模量差别很大,以下是一些常用材料的弹性模量的范围:-铁:100-220GPa-钢:200-210GPa-铝:70-80GPa-铜:100-150GPa-橡胶:0.01-0.1GPa-塑料:1-5GPa-木材:10-20GPa剪切模量(Shear Modulus)通常以G表示,是描述材料在剪切应力作用下发生剪切变形时的弹性变形性能的参数。
剪切应力指的是一种在材料中形成剪切力的应力,剪切变形是指材料在受到剪切力时产生的形变。
剪切模量定义为剪切应力和剪切应变之间的比值,即G = τ/γ,其中τ是剪切应力,γ是剪切应变。
剪切模量的单位也是帕斯卡(Pascal)。
常见材料的剪切模量范围如下所示:-钢:70-85GPa-铝:25-30GPa-铜:40-50GPa-橡胶:0.001-0.1GPa-塑料:1-5GPa-木材:1-5GPa弹性模量和剪切模量之间存在一定的关系,通过杨氏模量和剪切模量可以计算出材料的泊松比(Poisson's Ratio)。
泊松比(Poisson's Ratio)通常以ν表示,是描述材料杨氏模量和剪切模量之间关系的参数。
泊松比定义为材料横向应变和纵向应变之间的比值,即ν = - ε_t/ε_l,其中ε_t是材料的横向(剪切)应变,ε_l是材料的纵向(拉伸或压缩)应变。
常用材料弹性模量

弹性模量:一般地讲,对弹性体施加一个外界作用力,弹性体会发生形状的改变(称为“形变”),“弹性模量”的一般定义是:单向应力状态下应力除以该方向的应变。
材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。
弹性模量的单位是达因每平方厘米。
“弹性模量”是描述物质弹性的一个物理量,是一个统称,表示方法可以是“杨氏模量”、“体积模量”等。
常用材料弹性模量:1 镍铬钢、合金钢206 79.38 0.25~0.32 碳钢196~206 79 0.24~0.283 铸钢172~202 - 0.34 球墨铸铁140~154 73~76 -5 灰铸铁、白口铸铁113~157 44 0.23~0.276 冷拔纯铜127 48 -7 轧制磷青铜113 41 0.32~0.358 轧制纯铜108 39 0.31~0.349 轧制锰青铜108 39 0.3510 铸铝青铜103 41 -11 冷拔黄铜89~97 34~36 0.32~0.4212 轧制锌82 31 0.2713 硬铝合金70 26 -14 轧制铝68 25~26 0.32~0.3615 铅17 7 0.4216 玻璃55 22 0.2517 混凝土14~23 4.9~15.7 0.1~0.1818 纵纹木材9.8~12 0.5 -19 横纹木材0.5~0.98 0.44~0.64 -20 橡胶0.00784 - 0.4721 电木1.96~2.94 0.69~2.06 0.35~0.3822 尼龙28.3 10.1 0.423 可锻铸铁152 - -24 拔制铝线69 - -25 大理石55 - -26 花岗石48 - -27 石灰石41 - -28 尼龙1010 1.07 - -29 夹布酚醛塑料4~8.8 - -30 石棉酚醛塑料1.3 - -31 高压聚乙烯0.15~0.25 - -32 低压聚乙烯0.49~0.78 - -33 聚丙烯1.32~1.42 - -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用弹塑性材料模型
MP,ex,1,210e9! Pa
MP,nuxy,1,.29! No units
MP,dens,1,7850! kg/m3
7.2.3.1 双线性各向同性模型
使用两种斜率(弹性和塑性)来表示材料应力应变行为的经典双线性各向同性硬化模型(与应变率无关)。
仅可在一个温度条件下定义应力应变特性。
(也有温度相关的本构模型;参看Temperature
Dependent Bilinear Isotropic Model)。
用MP命令输入弹性模量(Exx),泊松比(NUXY)和密度(DENS),程序用EX和NUXY值计算体积模量(K)。
用TB和TBDATA命令的1和2项输入屈服强度和切线模量:
TB,BISO
TBDATA,1,(屈服应力)
TBDATA,2,(切线模量)
例题参看B.2.7,Bilinear Isotropic Plasticity Example:Nickel Alloy。
B.2.7. Bilinear Isotropic Plasticity Example: Nickel Alloy MP,ex,1,180e9! Pa
MP,nuxy,1,.31! No units
MP,dens,1,8490! kg/m3
TB,BISO,1
TBDATA,1,900e6! Yield stress (Pa)
TBDATA,2,445e6! Tangent modulus (Pa)
7.2.3.5双线性随动模型
(与应变率无关)经典的双线性随动硬化模型,用两个斜率(弹性和塑性)来表示材料的应力应变特性。
用MP命令输入弹性模量(Exx),密度(DENS)和泊松比(NUXY)。
可以用TB,BKIN和TBDATA命令中的1-2项输入屈服强度和切线模量:
TB,BKIN
TBDATA,1,(屈服应力)
TBDATA,2,(切线模量)
例题参看B.2.10,Bilinear Kinematic Plasticity Example :Titanium Alloy。
B.2.10. Bilinear Kinematic Plasticity Example: Titanium Alloy MP,ex,1,100e9! Pa
MP,nuxy,1,.36! No units
MP,dens,1,4650! kg/m3
TB,BKIN,1
TBDATA,1,70e6! Yield stress (Pa)
TBDATA,2,112e6! Tangent modulus (Pa)
7.2.3.6塑性随动模型
各向同性、随动硬化或各向同性和随动硬化的混合模型,与应变率相关,可考虑失效。
通过在0(仅随动硬化)和1(仅各向同性硬化)间调整硬化参数β来选择各向同性或随动硬化。
应变率用Cowper-Symonds模型来考虑,用与应变率有关的因数表示屈服应力,如下所示:
这里—初始屈服应力,—应变率,C和P-Cowper Symonds为应变率参数。
—有效塑性应变,—塑性硬化模量,由下式给出:应力应变特性只能在一个温度条件下给定。
用MP命令输入弹性模量(Exx),密度(DENS)和泊松比(NUXY)。
用TB,PLAW,,,,1和TBDATA命令中的1-6项输入屈服应力,切线斜率,硬化参数,应变率参数C和P以及失效应变:
如下所示,可以用TB,PLAW,,,,10和TBDATA命令中的1-5项定义其它参数。
TB,PLAW,,,,1
TBDATA,1,(屈服应力)
TBDATA,2,(切线模量)
TBDATA,3,β(硬化参数)
TBDATA,4, C(应变率参数)
TBDATA,5,P(应变率参数)
TBDATA,6,(失效应变)
例题参看B.2.11,Plastic Kinematic Example:1018 Steel。
B.2.11. Plastic Kinematic Example: 1018 Steel
MP,ex,1,200e9! Pa
MP,nuxy,1,.27! No units
MP,dens,1,7865! kg/m3
TB,PLAW,,,,1
TBDATA,1,310e6! Yield stress (Pa)
TBDATA,2,763e6! Tangent modulus (Pa)
TBDATA,4,40.0! C (s-1)
TBDATA,5,5.0! P
TBDATA,6,.75! Failure strain
7.2.3.13分段线性塑性模型
多线性弹塑性材料模型,可输入与应变率相关的应力应变曲线。
它是一个很常用的塑性准则,特别用于钢。
采用这个材料模型,也可根据塑性应变定义失效。
采用Cowper-Symbols模型考虑应变率的影
响,它与屈服应力的关系为:
这里——有效应变率,C和P——应变率参数,——常应变率处的屈服应力,而是基于有效塑性应变的硬化函数。
用MP命令输入弹性模量(Exx),密度(DENS)和泊松比(NUXY)。
用TB,PLAW,,,,8和TBDATA命令的1-7项输入屈服应力、切线模量、失效的有效真实塑性
应变、应变率参数C、应变率参数P、定义有效全应力相对于有效塑性真应变的载荷曲线ID 以及定义应变率缩放的载荷曲线ID。
TB,PLAW,,,, 8
TBDATA,1,(屈服应力)
TBDATA,2,(切线模量)
TBDATA,3,(失效时的有效塑性真应变)
TBDATA,4,C(应变率参数)
TBDATA,5,P(应变率参数)
TBDATA,6,LCID1(定义全真应力相对于塑性真实应变的载荷曲
线)
TBDATA,7,LCID2(关于应变率缩放的载荷曲线)
注--如果采用载荷曲线LCID1,则用TBDATA命令输入的屈服应力
和切线模量将被忽略。
另外,如果C和P设为0,则略去应变率影响。
如果使用LCID2,用TBDATA命令输入的应变率参数C和P将被覆盖。
只
考虑真实应力和真实应变数据。
在数据曲线一节中讲述了此种类型的例题。
注--例题参看B.2.16,Piecewise Linear Plasticity Example:High Carbon Steel。
B.2.16. Piecewise Linear Plasticity Example: High Carbon Steel MP,ex,1,207e9! Pa
MP,nuxy,1,.30! No units
MP,dens,1,7830! kg/m3
TB,PLAW,,,,8
TBDATA,1,207e6! Yield stress (Pa)
TBDATA,3,.75! Failure strain
TBDATA,4,40.0! C (strain rate parameter)
TBDATA,5,5.0! P (strain rate parameter)
TBDATA,6,1! LCID for true stress vs. true strain (see EDCURVE below)
*DIM,TruStran,,5
*DIM,TruStres,,5
TruStran(1)=0,.08,.16,.4,.75
TruStres(1)=207e6,250e6,275e6,290e6,3000e6
5 约束Y和Z方向的旋转
6 约束Z和X方向的旋转
7 约束X,Y和Z方向的旋转
例如,命令EDMP,IGID,2,7,7将约束材料的刚体单元的所有自由度。
在定义刚体之后,可以用EDIPART命令指定惯性特性、质量和初始速度矢量。
如果没有定义刚性体的惯性特性,程序将会依据有限元模型计算它们。
例题参看B.2.25,Rigid Material Example:Steel。
B.2.25. Rigid Material Example: Steel
MP,ex,1,207e9! Pa
MP,nuxy,1,.3! No units
MP,dens,1,7580! kg/m3
EDMP,rigid,1,7,7
性能参数
1、密度:2.10~2.30*103 kg/m3
2、熔点:327℃
3、热变形温度:55℃
4、维卡软化点;110℃
5、热分解度:>415℃
6、导热系数:0.256 W/M.K
7、表面张力:18.5*10-5
8、介电常数(106Hz):≤1.8-2.2
9、拉伸强度:27.6mpa
10、断率伸长率:238%
11、压缩强度(变形5%):12.9mpa
12、冲击强度(缺口):2.KJ/m2
13、弯曲强度:20.7mpa
14、摩擦系数:(负荷2mpa 时间30min)249mg
以下聚四氟乙烯软管性能(我厂送至无锡质检的检测结果)
1、密度 2.14 ~2.15* 103 kg/m3
2、使用温度:-54~204℃
3、拉伸强度:26mpa
4、断率伸长率:166 ~171%
二、可熔性聚四氟乙烯(PFA)材质颜色透明和FEP相同,性能和PTFE相同,只是机械强度高于PTFE.。
三、聚全氟乙丙烯(FEP)颜色透明,性能和PTFE及PFA基本相同,只是温度上有所区别。
使用温度在-150 ~180℃之间。
