柏拉图多面体
2024高中数学高考高频考点经典题型练习卷 (82)

一、单选题1. 正多面体统称为柏拉图体,被喻为最有规律的立体结构,其所有面都只由一种正多边形构成(各面都是全等的正多边形,且每个顶点所接的面数都一样,各相邻面所成的二面角都相等),正多面体共有5种,它们分别是正四面体、正六面体(即正方体)、正八面体、正十二面体、正二十面体.连接正方体中相邻面的中心(如图1),得到另一个柏拉图体,即正八面体(如图2),设分别为的中点,则下列说法正确的是()A.与为异面直线B.经过的平面截此正八面体所得的截面为正五边形C.平面平面D.平面平面2. 已知,若,则x的取值范围为()A.B.C.D.3. “”是“函数在区间上单调递增”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4. 已知集合,,则()A.B.C.M D.5. 已知,,,则的最小值是A.2B.C.4D.36. 如图所示,△ABC是边长为8的等边三角形,P为AC边上的一个动点,EF是以B为圆心,3为半径的圆的直径,则的取值范围是()A.B.C.D.7. 若函数的图象上存在不同的两点,使得函数的图象在这两点处的切线的斜率之和等于常数t,则称函数为“t函数”.下列函数中为“2函数”的是()①,②,③,④A.①②B.③④C.①③D.②④8. 在棱长为的正方体中,点、分别是棱、的中点,是上底面内一点,若平面,则二、多选题线段长度的取值范围是( )A.B.C.D.9. 下列函数中,为奇函数的是( )A.B.C.D.10. 把函数的图象上所有点向左平行移动个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数是( )A.B.C.D.11.已知命题数列的通项公式为为实数,,且恒为等差数列;命题数列的通项公式为时,数列为递增数列.若为真,则实数的取值范围为A.B.C.D.12. 已知集合,.若“”是“”的充分不必要条件,则的取值范围是( )A.B.C.D.13. 如图所示,在中,,.若平面外的点P 和线段上的点D 满足,,则四面体的体积的最大值为()A.B.C.D .114..、为两个确定的相交平面,a 、b 为一对异面直线,下列条件中能使a 、b 所成的角为定值的有( ▲ )(1)a∥,b (2)a⊥,b∥ (3)a ⊥,b⊥(4)a∥,b∥,且a 与的距离等于b 与的距离A .0个B .1个C .2个D .4个15.已知函数是偶函数或是奇函数,当时,,则a =( )A .1或B .1或2C .或D .或216. 已知是双曲线:的右焦点,是坐标原点,过作的一条渐近线的垂线,垂足为,并交轴于点.若,则的离心率为( )A.B.C .2D.17. 将平面向量称为二维向量,由此可推广至维向量.对于维向量,,其运算与平面向量类似,如数量积(为向量,的夹角),其向量的模,则下列说法正确的有( )A.不等式可能成立B.不等式一定成立C.不等式可能成立D.若,则不等式一定成立18. 某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例:用该样本估计总体,以下四个选项正确的是()A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群20%19. 已知定义在上的函数,其导函数分别为,若,,则()A.是奇函数B.是周期函数C.D.20. 已知是函数的零点,则下列说法正确的是()A.B.C.D.21. 设,是复数,则()A.B.若,则C.若,则D.若,则22. 设函数,则下列结论正确的是()A.的一个周期为B .的图象关于直线对称C .函数向左平移后所得函数为奇函数D.在区间上单调递增23. 某校举行劳动技能大赛,统计了名学生的比赛成绩,得到如图所示的频率分布直方图,已知成绩均在区间内,不低于分的视为优秀,低于分的视为不及格.若同一组中数据用该组区间中间值做代表值,则下列说法中正确的是()三、填空题四、解答题A.B.优秀学生人数比不及格学生人数少人C.该次比赛成绩的平均分约为D.这次比赛成绩的分位数为24.已知函数的图象关于直线对称,则( )A.B .若,则的最小值为C.将图象向左平移个单位得到的图象D .若函数在单调递增,则的最大值为25. 的展开式中的常数项为___________(用数字作答).26. 定义:若有穷数列,,…,,满足,,…,,即(,且),则称该数列为“对称数列”.若数列是项数为的对称数列,且,,…,构成首项为,公差为的等差数列,记数列的前项的和为,则取得最大值时的值为__________.27. 已知是椭圆的左、右焦点,P在椭圆上运动,则的最小值为___.28.已知(1)求的值;(2)若是第三象限的角,化简三角式,并求值.29. 已知函数.(1)二次函数,在“①曲线,有1个交点;②”中选择一个作为条件,另一个作为结论,进行证明;(2)若关于x 的不等式在上能成立,求实数m 的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.30.已知函数.从下面的两个条件中任选其中一个:①;②若,且的最小值为,,求解下列问题:(1)化简的表达式并求的单调递增区间;(2)已知,求的值.31.设,.(1)求的展开式中系数最大的项;(2)时,化简;五、解答题(3)求证:.32. 已知向量,(,),令().(1)化简,并求当时方程的解集;(2)已知集合,是函数与定义域的交集且不是空集,判断元素与集合的关系,说明理由.33. 已知函数,,.(1)将函数化简成,(,,),的形式;(2)求函数的值域.34. 在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:表一:男生男生等级优秀合格尚待改进频数155表二:女生女生等级优秀合格尚待改进频数153(1)求,的值;(2)从表二的非优秀学生中随机抽取2人交谈,求所选2人中恰有1人测评等级为合格的概率;(3)由表中统计数据填写列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.男生女生总计优秀非优秀总计45参考公式:,其中.参考数据:0.010.050.012.7063.8416.63535. 1766年;人类已经发现的太阳系中的行星有金星、地球、火星、木星和土星.德国的一位中学教师戴维一提丢斯在研究了各行星离太阳的距离(单位:AU ,AU 是天文学中计量天体之间距离的一种单位)的排列规律后,预测在火星和木星之间应该还有一颗未被发现的行星存在,并按离太阳的距离从小到大列出了如下表所示的数据:行星编号(x)1(金星)2(地球)3(火星)4()5(木星)6(土星)离太阳的距离(y)0.7 1.0 1.6 5.210.0受他的启发,意大利天文学家皮亚齐于1801年终于发现了位于火星和木星之间的谷神星.(1)为了描述行星离太阳的距离y与行星编号之间的关系,根据表中已有的数据画出散点图,并根据散点图的分布状况,从以下三种模型中选出你认为最符合实际的一种函数模型(直接给出结论即可);①;②;③.(2)根据你的选择,依表中前几组数据求出函数解析式,并用剩下的数据检验模型的吻合情况;(3)请用你求得的模型,计算谷神星离太阳的距离.36. 车胎凹槽深度是影响汽车刹车的因素,汽车行驶会导致轮胎胎面磨损.某实验室通过试验测得行驶里程与某品牌轮胎凹槽深度的数据如下:行驶里程/万km0.000.64 1.29 1.93 2.57 3.22 3.86 4.51 5.15轮胎凹槽深度/mm10.028.377.39 6.48 5.82 5.20 4.55 4.16 3.82以行驶里程为横坐标、轮胎凹槽深度为纵坐标作散点图,如图所示.(1)根据散点图,可认为散点集中在直线附近,由此判断行驶里程与轮胎凹槽深度线性相关,并计算得如下数据,请求出行驶里程与轮胎凹槽深度的相关系数(保留两位有效数字),并推断它们线性相关程度的强弱;2.57 6.20115.1029.46附:相关系数(2)通过散点图,也可认为散点集中在曲线附近,考虑使用对数回归模型,并求得经验回归方程及该模型的决定系数.已知(1)中的线性回归模型为,在同一坐标系作出这两个模型,据图直观回答:哪个模型的拟合效果更好?并用决定系数验证你的观察所得.六、解答题附:线性回归模型中,决定系数等于相关系数的平方,即.37. 某公司响应国家“节能减排,低碳经济”号召,鼓励员工节约用电,制定奖励政策,若公司一个月的总用电量低于30万,将对员工们发放节能奖励,该公司为了了解9月份日最高气温对当天用电量的影响,随机抽取了去年9月份7天的日最高气温x (℃)和用电量y(万)数据,并计算得,,,气温方差,用电量方差.(1)求y 关于x 的线性回归方程;(2)根据天气预测,今年9月份的日最高气温频率分布直方图如图,以(1)中的回归方程为依据,试估计该公司员工为了获得奖励,是否需要作出节能努力?(注:9月份共30天,同一组中的数据用该组区间的中点值为代表)参考公式:回归方程中斜率和截距的最小二乘估计公式分别为:,.38. 保障性租赁住房,是政府为缓解新市民、青年人住房困难,作出的重要决策部署.2021年7月,国务院办公厅发布《关于加快发展保障性租赁住房的意见》后,国内多个城市陆续发布了保障性租赁住房相关政策或征求意见稿.为了响应国家号召,某地区计划2021年新建住房40万平方米,其中有25万平方米是保障性租赁住房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长,另外,每年新建住房中,保障性租赁住房的面积均比上一年增加5万平方米.(1)到哪一年底,该市历年所建保障性租赁住房的累计面积(以2021年为累计的第一年)将首次不少于475万平方米?(2)到哪一年底,当年建造的保障性租赁住房的面积占该年建造住房面积的比例首次大于?39. 我国核电建设占全球在建核电机组的40%以上,是全球核电在建规模最大的国家.核电抗飞防爆结构是保障核电工程安全的重要基础设施,为此国家制定了一系列核电钢筋混凝土施工强制规范,连接技术全面采用HRB500高强钢筋替代HRB400及以下钢筋.某项目课题组针对HRB500高强钢筋的现场加工难题,对螺纹滚道几何成形机理进行了深入研究,研究中发现某S 型螺纹丝杠旋铣的滚道径向残留高度y (单位:mm )关于滚道径向方位角x (单位:rad )的函数近似地满足,其图象的一部分如图所示.(1)求函数的解析式;(2)为制造一批特殊钢筋混凝土,现需一批滚道径向残留高度不低于0.015mm 且不高于0.02mm 的钢筋,若这批钢筋由题中这种S 型螺纹丝杠旋铣制作,求这种S 型螺纹丝杠旋铣能制作出符合要求的钢筋的比例.40.已知函数.(1)当时,若,求实数的值;(2)若,求证:.41. 如图,等腰直角△ACD 的斜边AC 为直角△ABC 的直角边,E 是AC 的中点,F 在BC 上.将三角形ACD 沿AC 翻折,分别连接DE ,DF ,EF ,使得平面平面ABC .已知,,(1)证明:平面ABD;(2)若,求二面角的余弦值.42. 如图,在三棱柱中,侧面底面,侧面是菱形,,,.(1)若为的中点,求证:;(2)求二面角的正弦值.43. 在四棱锥中,底面是边长为的正方形,平面为中点.(1)如果与平面所成的线面角为,求证:平面.(2)当与平面所成角的正弦值最大时,求三棱锥的体积.44.如图,四棱锥中,,,,,,,点为中点.(1)求证:;(2)求直线与平面所成角的正弦值.45. 如图,矩形与梯形所在的平面垂直,,为的中点.(1)求证:平面平面;七、解答题(2)求二面角的余弦值.46. “黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”江南梅雨的点点滴滴都流润着浓洌的诗情每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q 镇年梅雨季节的降雨量单位:的频率分布直方图,试用样本频率估计总体概率,解答下列问题:Ⅰ“梅实初黄暮雨深”假设每年的梅雨天气相互独立,求Q 镇未来三年里至少有两年梅雨季节的降雨量超过350mm 的概率;Ⅱ“江南梅雨无限愁”在Q 镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元而乙品种杨梅的亩产量亩与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为元,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润万元的期望更大?需说明理由降雨量亩产量50070060040047. 甲、乙两人进行投篮比赛,分轮次进行,每轮比赛甲、乙各投篮一次.比赛规定:若甲投中,乙未投中,甲得1分,乙得-1分;若甲未投中,乙投中,甲得-1分,乙得1分;若甲、乙都投中或都未投中,甲、乙均得0分.当甲、乙两人累计得分的差值大于或等于4分时,就停止比赛,分数多的获胜:4轮比赛后,若甲、乙两人累计得分的差值小于4分也停止比赛,分数多的获胜,分数相同则平局、甲、乙两人投篮的命中率分别为0.5和0.6,且互不影响.一轮比赛中甲的得分记为X .(1)求X 的分布列;(2)求甲、乙两人最终平局的概率;(3)记甲、乙一共进行了Y 轮比赛,求Y 的分布列及期望.48. 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费对年销售量(单位:)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费(万元)和年销售量(单位:)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.(万元)24536(单位:)2.544.536(1)根据表中数据建立年销售量关于年宣传费的回归方程;(2)已知这种产品的年利润与,的关系为,根据(1)中的结果回答下列问题:①当年宣传费为10万元时,年销售量及年利润的预报值是多少?②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.附:问归方程中的斜率和截距的最小二乘估计公式分别为,.参考数据:,.49. 2023年5月31日,习近平主席在学校考察时指出:“体育锻炼是增强少年儿童体质的最有效手段”.为提升学生身体素质,某班组织投篮比赛,比赛分为,两个项目.(i )选手在每个项目中投篮5次,每个项目中投中3次及以上为合格;(ii )第一个项目投完5次并且合格后可以进入下一个项目,否则该选手结束比赛;(iii )选手进入第二个项目后,投篮5次,无论投中与否均结束比赛.若选手甲在项目比赛中每次投中的概率都是.(1)求选手甲参加项目合格的概率;(2)已知选手甲参加项目合格的概率为.比赛规定每个项目合格得5分,不合格得0分.设累计得分为,为使累计得分的期望最大,选手甲应选择先进行哪个项目的比赛(每个项目合格的概率与次序无关)?并说明理由.50. 为落实十三五规划节能减排的国家政策,某职能部门对市场上两种设备的使用寿命进行调查统计,随机抽取A型和B型设备各100台,得到如下频率分布直方图:(1)将使用寿命超过2500小时和不超过2500小时的台数填入下面的列联表:超过2500小时不超过2500小时总计A型B型总计根据上面的列联表,能否有99%的把握认为使用寿命是否超过2500小时与型号有关?(2)用分层抽样的方法从不超过2500小时A型和B型设备中抽取8台,再从这8台设备中随机抽取3台,其中A型设备为台,求的分布列和数学期望;(3)已知用频率估计概率,现有一项工作需要10台同型号设备同时工作2500小时才能完成,工作期间设备损坏立即更换同型号设备(更换设备时间忽略不计),A型和B型设备每台的价格分别为1万元和0.6万元,A型和B型设备每台每小时耗电分别为2度和6度,电价为0.75元/度.只考虑设备的成本和电费,你认为应选择哪种型号的设备,请说明理由.参考公式:,.参考数据:0.0500.0100.0013.841 6.63510.82851. 随着科技的发展,移动互联已进入全新的时代,远程实时遥控已成为现实.某无人机生产厂家计划在年将新技术应用到生产中去,经过市场调研分析,生产某种型号的无人机全年需投入固定成本万元,每生产千台无人机,需投入成本万元,且由市场调研知,每台无人机售价为万元,且全年内生产的无人机当年能全部售完.(1)求出年的利润(万元)关于年产量(千台)的函数关系式(利润销售额成本);(2)年产量为多少时,该厂家所获利润最大?最大利润为多少?。
立体构成-几何多面体(柏拉图多面体).
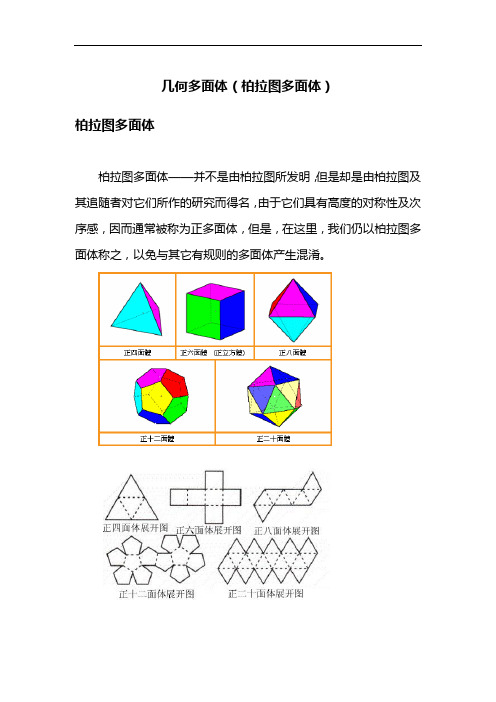
几何多面体(柏拉图多面体)
柏拉图多面体
柏拉图多面体——并不是由柏拉图所发明,但是却是由柏拉图及其追随者对它们所作的研究而得名,由于它们具有高度的对称性及次序感,因而通常被称为正多面体,但是,在这里,我们仍以柏拉图多面体称之,以免与其它有规则的多面体产生混淆。
正四面体特征
(1)重心、四条高的交点、外接球、内切球球心共点,此点称为中心。
(2)一个在其内部的内切球和七个与四个面都相切的旁切球,其中有三个旁切球球心在无穷远处。
(3)四条三重旋转对称轴,六个对称面。
(4)可与正八面体填满空间,在一顶点周围有八个正四面体和六个正八面体。
(5)对边相互垂直。
正六面体特征
〔1〕有六个面,每个面面积相等,形状完全相同;
〔2〕有八个顶点;
〔3〕有十二条棱,每条棱长度相等。
正八面体特征
由6个顶点与8个正三角形构成,4个三角形相交于一个顶点。
柏拉图认为八面体是介于四面体(火)和二十面体(水)之间,因此认为它代表的元素是空气。
八面体有6条二次旋转轴,通过对边中点;4条三次旋转轴,通过对面中心;以及3条四次旋转轴,通过对面的
顶点。
任何符合这些旋转轴的多面体,我们说它具有八面体对称。
正十二面体
是五个柏拉图立体之一,属准晶体,结晶学全称为正五角十二面体,共有二十个顶点、三十条边和十二个面,而每一个面皆是正五边形。
正二十面体
是由20个等边三角形所组成的正多面体,共有12个顶点,30条棱,20个面。
5个柏拉图正多面体和13个阿基米德多面体的中英文名称和图形

5个柏拉图正多面体和13个阿基米德多面体的中英文名称
和图形
看到很多人画多面体,我一直没搞清楚这些多面体的中英文名称,在网上查了一下,请大家指正名称是否正确。
The 5 Platonic Solids
1、正四面体_Tetrahedron
2、正六面体(立方体)Hexahedron
3、正八面体_Octahedron
4、正十二面体
_Dodecahedron5、正二十面体_Icosahedron13 Archimedean Solids
1、截角四面体_Truncatedtetrahedron
2、截角立方体
_Truncatedhexahedron3、截半立方体_Cuboctahedron4、小斜方截半立方体_Rhombicuboctahedron5、大斜方截半立方体_Truncatedcuboctahedron6、扭棱立方体
_Snubhexahedronccw7、截角八面体
_Truncatedoctahedron8、截角十二面体
_Truncateddodecahedron9、扭棱十二面体
_Snubdodecahedronccw10、截角二十面体
_Truncatedicosahedron11、截半二十面体
_Icosidodecahedron12、小斜方截半二十面体
_Rhombicosidodecahedron13、大斜方截半二十面体_Truncatedicosidodecahedron。
柏拉图多面体

从柏拉图多面体到尤拉公式壹、柏拉图多面体“多面体”是日常生活中经常看到的立体,它是被一些平面所包围的立体,例如粉笔盒、三棱镜、新光摩天大楼等等,那些包围多面体的多边形叫做多面体的面,两个面相交的线段叫做多面体的棱,棱与棱的交点叫做多面体的顶点。
顶点是由三个或三个以上的面交会出来的。
例如:右图中的立体中有5个面,9条棱,6个顶点。
所谓“柏拉图多面体”(Platonic Polyhedra)就是指正多面体,正多面体就是每个顶点处交会着相同数目全等的正凸多面体且每个立体角相等。
正多面体会称为柏拉图多面体并不是因为柏拉图发现了正多面体,而是因为柏拉图及其追随者对它们所作的研究而得名。
貳、柏拉图多面体有多少个?(1)要谈柏拉图多面体有几个之前,先观察平面上的凸正n边形,n至少等于3,且每一个内角为(n-2)⨯180︒n,而(n-2)⨯180︒n<180︒,因此平面上的正凸n边形有无限多个。
在空间中,柏拉图多面体是否会有无限多个呢?答案令人很惊讶!不仅不是无限多个,而且只有5个。
古人对于这个事实虽不愿相信,却不得不接受,最后只好搬出“神的旨意”来承认这个事实。
为何会说是“神的旨意”呢?原来在伽利略(Galiep1564~1642意大利人)发明望远镜之前,当时天空中人类只观察到五颗行星,因此这五个正多面体就分别代表那五颗行星,这么的巧合,那一定是“神的旨意”,这样的想法,甚至影响了天文学家克卜勒(Kepler 1571~1630德国人),他曾试图去观察、计算各行星的轨道半径,周期与五个正多面体对应,可惜并未成功。
(2)接下来我们来讨论柏拉图多面体的个数:我们从一个顶点出发,因为正多面体的每一个顶点处都是正n边形内角的顶点,我们先从简单的正多边形讨论起:(1︒)当正多边形是正三角形时,每一个正三角形的内角为60︒,若每一个顶点有3个正三角形,则会形成正四面体(Tetrahedon)若每一个顶点有4个正三角形,则会形成正八面体(Octahedron)若每一个顶点有5个正三角形,则会形成正二十面体(Icsoahedon)但是当每一个顶点处有6个正三角形时,那么交会在这个顶点的面的角之总和为360︒,于是这些三角形构成一平面或是凹面,故表面是正三角形的柏拉图多面体只有3种。
山东省青岛第五十八中学2023-2024学年高二上学期9月月考检测数学试题

山东省青岛第五十八中学2023-2024学年高二上学期9月月考检测数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题A .π6B .π34.如图,在三棱锥-P ABC AC方向上的投影向量为(A .34AC -B .-5.柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.下图是棱长均为1的柏拉图多面体A .12B .146.在正方体1111ABCD A B C D -中,点的取值范围是()A .ππ,43⎡⎤⎢⎥⎣⎦B .π0,2⎡⎤⎢⎥⎣⎦7.三面角是立体几何的基本概念之一,而三面角余弦定理是解决三面角问题的重要依据.三面角-P ABC 是由有公共端点线间的平面部分所组成的图形,设面BPC 所成的角为θ,由三面角余弦定理得-P ABC 中,6PA =,60APC ∠=棱锥-P ABC 体积的最大值为(A .2724B .2748.“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图,将一个正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形,六个面为正方形的米德多面体”,则该多面体中具有公共顶点的两个正三角形所在平面的夹角正切值为A .22B .1二、多选题A .166AC =B .1BC AB ⊥C .111,120DA C B ︒=D .直线1BD 与AC 所成角的余弦值为11.已知正方体111ABCD A B C D -A .1AB AD AA ⨯= B .AB AD AD AB⨯=⨯ C .111()AB AD AA AB AA AD AA +⨯=⨯+⨯D .11111()ABCD C D B A V AB AD CC -=⨯⋅ 三、填空题13.已知,,i j k是不共面向量,,a i j k b =-+=- 个向量共面,则实数λ=.14.已知向量()()0,1,1,4,1,0,a b a b λ=-=+=15.如图,在棱长为2的正方体1111ABCD A B C D -则△MAD 的重心到直线BN 的距离为16.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.古希腊历史学家希罗多德记载:胡夫金字塔的每一个侧面三角形的面积等于金字塔高的平方,则其侧面三角形底边上的高与底面正方形的边长的比值为面角的余弦值为.四、解答题17.如图,在三棱柱111ABC A B C -中,线段11A C 上一点.若直线1AB 与平面BCM 18.如图,在棱长为1的正四面体OABC 在MN 上,且2MG GN =,设OA a = (1)试用向量a ,b ,c 表示向量(1)求二面角11A BD B --所成角的正弦值;(2)点P 是矩形11AA B B (包含边界)内任一点,且的正弦值的取值范围.20.空间中,两两互相垂直且有公共原点的三条数轴构成直角坐标系,如果坐标系中有①若1BE EB =,求向量1 ED 的斜60 坐标;埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造,设边长均为形n n n n A B C D ,1,2,3n =的顶点为“框架点”,定义两正方形交线为记为,n n P Q ,将极点11,P Q ,分别与正方形2222A B C D 的顶点连线,1,2,3,4m =,如(图3).埃舍尔多面体可视部分是由12点均为“框架点”,底面四边形由两个“极点”与两个“中点们构造了其中两个四棱锥11122A P E P E -与22131A P E P F -(1)求异面直线12P A 与12QB 成角余弦值;(2)求平面111P A E 与平面122A E P 的夹角正弦值;(3)求埃舍尔体的表面积与体积(直接写出答案).22.学习几何体结构素描是学习素描的重要一步.如图所示,这是一个用来练习几何体。
柏拉图的多面体

并不是由柏拉图所发明,但是却是由柏拉图及其追随者对它们所作的研究而得名,由于它们具有高度的对称性及次序感,因而通常被称为正多面体,但是,在这里,我们仍以柏拉图多面体称之,以免与其它有规则的多面体产生混淆。
柏拉图多面体所有的面都是不自交、以直线段为边长的正凸多边形平面,每一种多面体都只有一种正多边形的表面,而且在每一个顶点处都有相同数目的面交会。
不仅在每一个顶点处都有相同数目的面交会,而且在每一个顶点处所有交会的面的内角之总和会相等。
简介熟悉柏拉图多面体的最佳方法莫过于经由构造模型并透过模型研究它们。
下图表示一种称之为”展开图”的个别柏拉图多面体平面排列图示。
为了构造柏拉图多面体的模型,一组类似的展开图必须被描绘在适当的材料上。
同学可以将本资料所附之多面体的展开图直接剪下或经放大、缩小影印在合适的漂亮纸张上。
如果材料不方便影印,您也可以依样绘制或把影印展开图并贴在所用材料上。
Albrecht Durei早在1525年,于他所著的《Unterweisung der Messung Mit dem Zirkel und Richtsheit》一书中,给出了几个多面体的展开图。
编辑本段为什么只有五个柏拉图多面体很容易看出柏拉图多面体每一个都是凸的,并且在每一个顶点处交会着相同数目、相似、正的凸多边形。
要理解为什么只有五个柏拉图多面体是相当简单的,这是因为在每一个顶点处交会着至少三个面才能构造出一个立体图形,而且围绕每一个顶点的面的角度和不能等于或超过360°,否则所得的面将是平的或是凹的。
具有最少边数的正多边形是正三角形,三个如此的多边形可以使它们交会在一个顶点上,接下来,加入第四个面,如此,每三个面就会交会在图形的四个顶点处之一。
由于这个图形有四个全等的面,故称之为正四面体(TETRAHEDRON)。
四个正三角形可以使它们交会在一个顶点上,而且加入四个面之后,在图形的六个顶点处都会有四个面交会在这里。
多面体的文化历史及有关知识
多面体的文化历史及有关知识早在古典时代就已为人所知的多面体,不仅在数学中,而且在哲学中扮演了重要角色,并且在不同的科学领域之间架起了桥梁。
约公元前6世纪哲学在希腊诞生了。
哲学家们革新了思想史:对于林林总总的解释世界与人类的起源与演变的神谱和神话,他们代之以理论构造,这些理论排除了神力,建基于与观测事实相容的一些基本原则。
从那以后,“人是万物的尺度”(普罗泰戈拉)。
回忆一下词源,“尺度”的法语是“mesure”,和谐与节律的观念里就包含了这个词,这些观念都从属于“对称”概念,对称的法语是“symétrie”,由希腊语词素syn与metron构成,意为具有同样的尺度,或者根据同样的尺度。
(视频Henry Segerman 讲解柏拉图立体与阿基米德立体,请前往“返朴”观看)毕达哥拉斯及其正多面体球形、圆形及其性质一直以来就被与宇宙的某种表现联系起来。
先驱者毕达哥拉斯(公元前6世纪)教导说,关于大自然的知识建基于从某些整数的性质导出的和谐。
他的门徒将5种完美立体的发现归功于他,完美立体的面是全等的多边形:等边三角形,不等腰或等腰直角三角形与正五边形。
注意,除了正五边形之外,这些图形都很容易尺规作图,此后尺规可作图是统治着《几何原本》(公元前3世纪)中阐述的欧氏几何的隐含条件(原注2:第八卷)。
毕达哥拉斯的同代几何学家已经证明,借助于三种正多边形(正三角形、正方形、正五边形)就可以构造出五种凸正多面体(原注3:每个面都是全等的正多边形,每两个相邻的面之间的二面角都相等):正四面体、立方体、正八面体、正十二面体与正二十面体。
柏拉图的前苏格拉底学术环境在物理学史上有两大派针锋相对的学说:1.元素论:恩培多克勒(公元前5世纪)从四大元素(水、气、火、土)出发来描述我们所处的连续结构的月下世界中的各种变化,四大元素受到两种彼此对抗的力的作用而改变其组合的比例:爱力使元素结合,恨力使元素分离。
亚里士多德继承了四元素说,为其增加了两对性质:热与冷,干与湿。
2023-2024学年湖北省武汉市常青联合体高二(上)期中数学试卷【答案版】
2023-2024学年湖北省武汉市常青联合体高二(上)期中数学试卷一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某中学高三年级共有学生900人,为了解他们视力状况,用分层抽样的方法从中抽取一个容量为45的样本,若样本中共有女生11人,该校高三年级共有男生( )人.A .220B .225C .680D .6852.方程x 2+y 2+4x ﹣2y +5m =0表示圆,则m 的范围是( )A .m >1B .m <1C .m ≥1D .m ≤13.已知直线l 1:(2m 2+m −3)x +(m 2−m)y =4m −1,l 2:x ﹣3y ﹣5=0互相垂直,则实数m 的值为( )A .3B .3或1C .1D .﹣3或﹣1 4.如图,空间四边形OABC 中,OA →=a →,OB →=b →,OC →=c →,点M 在OA →上,且OM =2MA ,2BN =3NC ,则MN →=( )A .−13a →−25b →+35c → B .−23a →+35b →+25c → C .−23a →+25b →+35c → D .23a →+35b →−25c → 5.直线sin41°x +sin49°y ﹣4=0的倾斜角是( )A .41°B .49°C .131°D .139°6.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果、可以判断出一定没有出现点数6的是( )A .平均数为2,方差为3.1B .中位数为3,方差为1.6C .中位数为3,众数为2D .平均数为3,中位数为27.柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.如图是棱长均为1的柏拉图多面体EABCDF ,P ,Q ,M ,N 分别为DE ,AB ,AD ,BF 的中点,则PQ →⋅MN →=( )A .12B .14C .−14D .−12 8.已知三棱锥P ﹣ABC 的体积为15,M 是空间中一点,PM →=−115PA →+315PB →+415PC →,则三棱锥A ﹣MBC 的体积是( )A .7B .8C .9D .10二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.下列说法,不正确的是( )A .在空间直角坐标系中,j →=(0,0,1)是坐标平面Oxy 的一个法向量B .若v →是直线l 的方向向量,则λv →(λ∈R )也是直线l 的方向向量C .若{a →,b →,c →}为空间的一个基底,则{a →+b →,b →+c →,c →+a →}构成空间的另一个基底D .对空间任意一点O 和不共线的三点A ,B ,C ,若OP →=2OA →−2OB →−OC →,则P ,A ,B ,C 四点共面10.从装有2个红球和3个白球的口袋内任取两个球,则下列选项中的两个事件为不是互斥事件的是( )A .至多有1个白球;都是红球B .至少有1个白球;至少有1个红球C .恰好有1个白球;都是红球D .至多有1个白球;全是白球11.如图,在直三棱柱ABC ﹣A 1B 1C 1中,AC =BC =CC 1=6,AC ⊥BC ,E 、F 分别为BB 1,A 1C 1的中点,过点A 、E 、F 作三棱柱的截面α,则下列结论中正确的是( )A .三棱柱ABC ﹣A 1B 1C 1外接球的表面积为108πB.BC1∥αC.若α交B1C1于M,则EM=3√2D.α将三棱柱ABC﹣A1B1C1分成体积较大部分和体积较小部分的体积比为13:512.已知在平面直角坐标系xOy中,M(﹣3,0),N(3,0),动点P是平面上动点,其轨迹为C.则下列结论正确的是()A.若动点P满足|PM||PN|=2,则曲线C的方程为x2+y2﹣10x+6=0B.若动点P轨迹为C:x2+y2+8x=0,Q(4,0)则|PQ|+2|PN|的最小值为10C.若动点P满足|PM|•|PN|=12,则曲线C关于y轴对称D.若动点P满足|PM|•|PN|=12,则△PMN面积的最大值为6三、填空题(本题共4小题,每小题5分,共20分.请把答案直接填写在答题卡相应位置上.)13.甲、乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92,则该题被乙独立解出的概率为.14.设点A(2,﹣3)、B(﹣3,﹣2),若直线l过点P(1,1)且与线段AB不相交,则直线l的斜率k的取值范围是.15.若直线l1:x+my﹣2=0,l2:mx﹣y+2=0(m∈R)相交于点P,过P作圆C:(x+3)2+(y+3)2=1的切线,切点为Q,则|PQ|的最大值为.16.数学中有许多形状优美,寓意独特的几何体,图1所示的礼品包装盒就是其中之一,该礼品包装盒可以看成是一个十面体,其中上、下底面为全等的正方形,所有的侧面是全等的三角形.将长方体ABCD ﹣A1B1C1D1的上底面A1B1C1D1绕着其中心旋转60°得到如图2所示的十面体ABCD﹣EFGH.已知AB=AD=2,AE=√6,P是底面正方形ABCD内的点,且P到AB和AD的距离都为√32,过直线EP作平面α,则十面体ABCD﹣EFGH外接球被平面α所截的截面圆面积的最小值是.四、解答题(本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.)17.(10分)在△ABC中,边AB所在的直线斜率为k AB=−12,其中顶点A点坐标为(﹣1,1),顶点C的坐标为(1,2).(1)求AB边上的高所在的直线方程;(2)若CA,CB的中点分别为E,F,求直线EF的方程.18.(12分)2022年4月16日,神舟十三号载人飞船返回舱成功着陆,航天员翟志刚、王亚平、叶光富完成在轨驻留半年的太空飞行任务,标志着中国空间站关键技术验证阶段圆满完成.并将进入建造阶段,洪山区为了激发市民对天文学的兴趣,开展了天文知识比赛,满分100分(95分及以上为认知程度高),结果认知程度高的有m人,这m人按年龄分成5组,其中第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45],得到如图所示的频率分布直方图,已知第一组有10人.(1)根据频率分布直方图,估计这m人的第60百分位数;(精确到0.1)(2)现从第四组和第五组用分层随机抽样的方法抽取6人,担任“党章党史”宣传使者.①有甲(年龄36),乙(年龄42),且甲、乙确定入选,从6人中要选择两个人担任组长,求甲、乙两人至少有一人被选上组长的概率;②若第四组宣传使者的年龄的平均数与方差分别为36和52,第五组宣传使者的年龄的平均数与方差分别为42和1,据此估计这m人中35~45岁所有人的年龄平均数和方差.19.(12分)如图,在平行六面体ABCD﹣A1B1C1D1中,E,F,G分别在A1A,B1B,D1D上,且A1E=2EA,BF=2FB1,DG=2GD1.(1)求证:EG∥FC1;(2)若底面ABCD,侧面A1ADD1都是正方形,且二面角A1﹣AD﹣B的大小为120°,AB=2,若P是C1G的中点,求AP的长度.20.(12分)第19届亚运会2023年9月在杭州市举办,本届亚运会以“绿色、智能、节俭、文明”为办会理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,从而促进经济快速发展.本次亚运会吉祥物是一组名为“江南忆”的机器人.三个吉祥物分别取名“琮琮”、“莲莲”和“宸宸”,分别代表世界遗产“良渚古城遗址”、“西湖”、“京杭大运河”.亚运期间,篮球比赛间隙安排了机器人吉祥物表演,由后台志愿者操控A,B,C三个开关,分别可操控“琮琮”、“莲莲”和“宸宸”,当A闭合时“琮琮”、“莲莲”表演;当B闭合时“莲莲”和“宸宸”表演;当C闭合时“琮琮”和“宸宸”表演,若A,B,C三个开关闭合的概率分别为12,13,14,且相互独立.(1)求机器人“琮琮”表演的概率;(2)求机器人“莲莲”和“宸宸”都表演的概率.21.(12分)在三棱锥S﹣ABC中,底面△ABC为等腰直角三角形,∠SAB=∠SCB=∠ABC=90°.(1)求证:AC⊥SB;(2)若AB=2√2,SC=4,求平面SAC与平面SBC夹角的余弦值.22.(12分)已知圆C1:(x﹣4)2+(y﹣2)2=20与y轴交于O,A两点,圆C2过O,A两点,且直线C2O 与圆C1相切;(1)求圆C2的方程;(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN 始终成立,若存在求出定点坐标,若不存在,说明理由.2023-2024学年湖北省武汉市常青联合体高二(上)期中数学试卷参考答案与试题解析一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某中学高三年级共有学生900人,为了解他们视力状况,用分层抽样的方法从中抽取一个容量为45的样本,若样本中共有女生11人,该校高三年级共有男生( )人.A .220B .225C .680D .685解:依题意,设高三男生人数为n 人,则高三女生人数为(900﹣n )人,由分层抽样可得900−n 900=1145,解得n =680. 故选:C .2.方程x 2+y 2+4x ﹣2y +5m =0表示圆,则m 的范围是( )A .m >1B .m <1C .m ≥1D .m ≤1 解:因为方程x 2+y 2+4x ﹣2y +5m =0表示圆,所以42+(﹣2)2﹣4×5m >0,解得:m <1. 故选:B .3.已知直线l 1:(2m 2+m −3)x +(m 2−m)y =4m −1,l 2:x ﹣3y ﹣5=0互相垂直,则实数m 的值为( )A .3B .3或1C .1D .﹣3或﹣1解:因为直线l 1:(2m 2+m −3)x +(m 2−m)y =4m −1,l 2:x ﹣3y ﹣5=0互相垂直,所以(2m 2+m ﹣3)×1+(m 2﹣m )×(﹣3)=0,所以 m =3或1,当m =1,直线l 1:0×x +0×y =﹣1不存在,故m =3.故选:A .4.如图,空间四边形OABC 中,OA →=a →,OB →=b →,OC →=c →,点M 在OA →上,且OM =2MA ,2BN =3NC ,则MN →=( )A .−13a →−25b →+35c →B .−23a →+35b →+25c →C .−23a →+25b →+35c → D .23a →+35b →−25c → 解:由OA →=a →,OB →=b →,OC →=c →,且OM =2MA ,2BN =3NC ,可得MA →=13OA →,BN →=35BC →, 所以MN →=MA →+AB →+BN →=13OA →+(OB →−OA →)+35(OC →−OB →) =−23OA →+25OB →+35OC → =−23a →+25b →+35c →. 故选:C .5.直线sin41°x +sin49°y ﹣4=0的倾斜角是( )A .41°B .49°C .131°D .139°解:直线sin41°x +sin49°y ﹣4=0的斜率为k =−sin41°sin49°=sin139°cos139°=tan139°, 故直线的倾斜角为139°.故选:D . 6.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果、可以判断出一定没有出现点数6的是( )A .平均数为2,方差为3.1B .中位数为3,方差为1.6C .中位数为3,众数为2D .平均数为3,中位数为2解:对于选项A ,若平均数为2,则方差S 2>15(6−2)2=3.2>3.1,平均数为2,方差为3.1, 所以一定没有出现点数6,故选项A 正确;对于选项B ,当投掷骰子出现的结果为3,3,3,5,6时,满足中位数为3,方差为:S 2=15[(3−4)2+(3−4)2+(3−4)2+(5−4)2+(6−4)2]=1.6, 此时出现点数为6,故选项B 错误;对于选项C ,当投掷骰子出现结果为2,2,3,4,6时,满足中位数为3,众数为2,可以出现点数6,故选项C 错误;对于选项D ,当投掷骰子出现的结果为1,1,2,5,6时,满足平均数为3,中位数为2,可以出现点数6,故选项D 错误.故选:A .7.柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.如图是棱长均为1的柏拉图多面体EABCDF ,P ,Q ,M ,N 分别为DE ,AB ,AD ,BF 的中点,则PQ →⋅MN →=( )A .12B .14C .−14D .−12解:由柏拉图多面体的性质可知,侧面均为等边三角形,四边形ABCD 为边长为1的菱形,又△AEC ≌△BED ,所以AC =BD ,故四边形ABCD 为正方形,同理四边形BEDF 也为正方形, 取AE 的中点K ,连接PK ,KQ ,则PQ →=PK →+KQ →=12DA →+12EB →,同理MN →=12DF →+12AB →, 所以PQ →⋅MN →=(12DA →+12EB →)•(12DF →+12AB →)=14DA →⋅DF →+14DA →⋅AB →+14EB →⋅DF →+14EB →⋅AB →=14×1×1×cos60°+0+14×1×1+14×1×1×cos60°=12. 故选:A .8.已知三棱锥P ﹣ABC 的体积为15,M 是空间中一点,PM →=−115PA →+315PB →+415PC →,则三棱锥A ﹣MBC 的体积是( )A .7B .8C .9D .10 解:已知PM →=−115PA →+315PB →+415PC →,则15PM →=−PA →+3PB →+4PC →, 即15PM →=−PM →−MA →+3PM →+3MB →+4PM →+4MC →,即9PM →=−MA →+3MB →+4MC →,即32PM →=−16MA →+12MB →+23MC →, 因为−16+12+23=1, 由空间向量基本定理可得:在平面ABC 内存在一点D ,使得MD →=−16MA →+12MB →+23MC →成立,即32PM →=MD →,即MD →=35PD →, 又三棱锥P ﹣ABC 的体积为15,则V A−MBC =V M−ABC =35V P−ABC =35×15=9. 故选:C .二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.下列说法,不正确的是( )A .在空间直角坐标系中,j →=(0,0,1)是坐标平面Oxy 的一个法向量B .若v →是直线l 的方向向量,则λv →(λ∈R )也是直线l 的方向向量C .若{a →,b →,c →}为空间的一个基底,则{a →+b →,b →+c →,c →+a →}构成空间的另一个基底D .对空间任意一点O 和不共线的三点A ,B ,C ,若OP →=2OA →−2OB →−OC →,则P ,A ,B ,C 四点共面解:对于A ,由j →=(0,0,1),得到j →=(0,0,1)是坐标平面Oxy 的一个法向量,故A 正确;对于B ,当λ=0时,不合题意,故B 错误;对于C ,由{a →,b →,c →}为空间的一个基底,得a →,b →,c →不共面,假设a →+b →,b →+c →,c →+a →共面,则存在唯一实数对(x ,y ),使得a →+b →=x(b →+c →)+y(c →+a →),即a →+b →=xb →+ya →+(x +y)c →,显然不成立,故a →+b →,b →+c →,c →+a →不共面,故{a →+b →,b →+c →,c →+a →}构成空间的另一个基底,故C 正确;对于D ,若OP →=xOA →+yOB →+zOC →(x ,y ,z ∈R),则当且仅当x +y +z =1时,P ,A ,B ,C 四点共面,而OP →=2OA →−2OB →−OC →,2﹣2﹣1=﹣1≠1,故P ,A ,B ,C 四点不共面,故D 错误.故选:BD .10.从装有2个红球和3个白球的口袋内任取两个球,则下列选项中的两个事件为不是互斥事件的是( )A.至多有1个白球;都是红球B.至少有1个白球;至少有1个红球C.恰好有1个白球;都是红球D.至多有1个白球;全是白球解:对于A:“至多有1个白球”包含都是红球和一红一白,“都是红球”包含都是红球,所以“至多有1个白球”与“都是红球”不是互斥事件.故A正确;对于B:“至少有1个白球”包含都是白球和一红一白,“至少有1个红球”包含都是红球和一红一白,所以“至少有1个白球”与“至少有1个红球”不是互斥事件.故B正确;对于C:“恰好有1个白球”包含一红一白,“都是红球”包含都是红球,所以“恰好有1个白球”与“都是红球”是互斥事件.故C错误;对于D:“至多有1个白球”包含都是红球和一红一白,“全是白球”包含都是白球,所以“至多有1个白球”与“全是白球”是互斥事件.故D错误.故选:AB.11.如图,在直三棱柱ABC﹣A1B1C1中,AC=BC=CC1=6,AC⊥BC,E、F分别为BB1,A1C1的中点,过点A、E、F作三棱柱的截面α,则下列结论中正确的是()A.三棱柱ABC﹣A1B1C1外接球的表面积为108πB.BC1∥αC.若α交B1C1于M,则EM=3√2D.α将三棱柱ABC﹣A1B1C1分成体积较大部分和体积较小部分的体积比为13:5解:如图所示,将该三棱柱视为正方体ACBD﹣A1C1B1D1的一部分,则三棱柱ABC﹣A1B1C1外接球的直径2R=6√3,R=3√3,其表面积为4πR2=108π,故A项正确;延长AF与CC1的延长线交于点P,连接PE交B1C1于M,连接FM,则平面AEMF即为截面α.若BC1∥α,则BC1∥ME.因为FC1∥AC,F是中点,所以C1是PC的中点,由△MPC1与△MEB1相似,得PC1EB1=MC1MB1=2,得B1M=13B1C1,而E是BB1的中点,所以ME 与BC 1不平行,故B 项错误;因为B 1M =2,又B 1E =3,所以在Rt △B 1EM 中,EM =√22+32=√13,故C 项错误;延长PE 交BC 于点Q ,则α将三棱柱ABC ﹣A 1B 1C 1分成体积较大部分的体积为:V P−ACQ −V P−FMC 1−V A−QBE =13×12×6×8×12−13×12×3×4×6−13×12×2×6×3=78, 所以剩余部分的体积为12×6×6×6−78=30,所以体积之比为7830=135,故D 项正确.故选:AD .12.已知在平面直角坐标系xOy 中,M (﹣3,0),N (3,0),动点P 是平面上动点,其轨迹为C .则下列结论正确的是( ) A .若动点P 满足|PM||PN|=2,则曲线C 的方程为x 2+y 2﹣10x +6=0B .若动点P 轨迹为C :x 2+y 2+8x =0,Q (4,0)则|PQ |+2|PN |的最小值为10C .若动点P 满足|PM |•|PN |=12,则曲线C 关于y 轴对称D .若动点P 满足|PM |•|PN |=12,则△PMN 面积的最大值为6 解:不妨设P (x ,y ), 对于选项A :当|PM||PN|=2时,2222=2,整理得x 2+y 2﹣10x +9=0,故选项A 错误;对于选项B :因为动点P 轨迹为C :x 2+y 2+8x =0,其表示以(﹣4,0)为圆心,4为半径的圆, 不妨设A (﹣2,0),连接P A ,PC ,因为|CP |=4,|CA |=2,|CQ |=8,所以|CA||CP|=|CP||CQ|=12, 又∠ACP =∠PQC ,所以△ACP ∽△PCQ ,此时|PA||PQ|=|CA||CP|=|CP||CQ|=12,则|PQ|=2|P A|,所以|PQ|+2|PN|=2|P A|+2|PN|=2(|P A|+|PN),当P与O重合时,|P A|+|PN|取得最小值,最小值为|OA|+|ON|=2+3=5,则(|PQ|+2|PN|)min=2×5=10,故选项B正确;对于选项C:若动点P满足|PM|•|PN|=12,此时√(x−3)2+y2⋅√(x+3)2+y2=12,即x4+(2y2﹣18)x2+y4+18y2﹣63=0,当x=﹣x时,(﹣x)4+(2y2﹣18)(﹣x)2+y4+18y2﹣63x4+(2y2﹣18)x2+y4+18y2﹣63=0,所以曲线C关于y轴对称,故选项C正确;对于选项D:由选项C可知方程x4+(2y2﹣18)x2+y4+18y2﹣63=0一定有解,所以Δ=(2y2﹣18)2﹣4(y4+18y2﹣63)=576﹣144y2=144(4﹣y2)≥0,解得﹣2≤y≤2,即|y|≤2,则S△PMN=12⋅|MN|⋅|y|≤12⋅6⋅2=6,当且仅当|y|=2时,等号成立,故选项D正确.故选:BCD.三、填空题(本题共4小题,每小题5分,共20分.请把答案直接填写在答题卡相应位置上.)13.甲、乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92,则该题被乙独立解出的概率为0.8.解:设该题被乙独立解出的概率为p,并且甲独立解出的概率为0.6,则甲、乙两人都解不出来的概率为p1=(1﹣0.6)•(1﹣p),又因被甲或乙解出的概率为0.92,故1﹣p1=0.92,即1﹣(1﹣0.6)•(1﹣p)=0.92,故0.4(1﹣p)=0.08,解得p=0.8.故答案为:0.8.14.设点A(2,﹣3)、B(﹣3,﹣2),若直线l过点P(1,1)且与线段AB不相交,则直线l的斜率k的取值范围是(−4,34).解:k PA=1+31−2=−4,k PB=1+21+3=34,直线l过点P(1,1)且与线段AB不相交,故−4<k<34,即k∈(−4,34).故答案为:(−4,34 ).15.若直线l1:x+my﹣2=0,l2:mx﹣y+2=0(m∈R)相交于点P,过P作圆C:(x+3)2+(y+3)2=1的切线,切点为Q,则|PQ|的最大值为7.解:由直线l1:x+my﹣2=0,可得直线l1恒过定点A(2,0),由直线l2:mx﹣y+2=0,可得直线l1恒过定点B(0,2),又易得直线l1与直线l2互相垂直,故点P轨迹是以AB为直径的圆,从而可得P的轨迹方程为(x﹣1)2+(y﹣1)2=2,圆心为D(1,1),半径为√2,由圆C:(x+3)2+(y+3)2=1,可得圆心C(﹣3,﹣3),半径为1,由题意|PQ|=√|PC|2−|QC|2=√|PC|2−1,又|PC|max=|CD|+√2=5√2,∴|PQ|max=√50−1=7.故答案为:7.16.数学中有许多形状优美,寓意独特的几何体,图1所示的礼品包装盒就是其中之一,该礼品包装盒可以看成是一个十面体,其中上、下底面为全等的正方形,所有的侧面是全等的三角形.将长方体ABCD ﹣A1B1C1D1的上底面A1B1C1D1绕着其中心旋转60°得到如图2所示的十面体ABCD﹣EFGH.已知AB=AD=2,AE=√6,P是底面正方形ABCD内的点,且P到AB和AD的距离都为√32,过直线EP作平面α,则十面体ABCD﹣EFGH外接球被平面α所截的截面圆面积的最小值是√3解:由下图可知,上底面的平面图如下所示:记A1B1C1D1的中心为O1,连接A1O1,O1E,因为旋转了60°,所以△O 1A 1E 为等边三角形,A 1E =O 1A 1=√2,又因为长方体ABCD ﹣A 1B 1C 1D 1中,AA 1⊥平面EFGH ,A 1E ⊂平面EFGH ,所以AA 1⊥A 1E ,所以AE 2=AA 12+A 1E 2=6,解得AA 1=2,因为十面体ABCD ﹣EFGH 是将长方体ABCD ﹣A 1B 1C 1D 1的上底面绕着其中心旋转60°得到的, 所以长方体ABCD ﹣A 1B 1C 1D 1的外接球就是十面体ABCD ﹣EFGH 的外接球, 设十面体ABCD ﹣EFGH 的外接球半径为R ,则4R 2=AB 2+AD 2+AA 12,即R=√22+22+224=√3,以D 为原点建立如下图所示的空间直角坐标系,结合第一幅图可知∠BA 1E =60°﹣45°=15°, 可得A 1Esin∠BA 1E =√2sin15°=√3−12,A 1Ecos∠BA 1E =√2cos15°=√3+12,所以E(√3+32,√3+12,2),又因为P 到AB ,AD 的距离为√32,所以P(2−√32,√32,0),球心O (1,1,1),所以PE →=(√3−12,12,2),OE →=(√3+12,√3−12,1),所以最小截面圆的半径为|PE →⋅OE →||PE →|,此时截面圆面积为π(|PE →⋅OE →||PE →|)2=39+12330−4√3.故答案为:√330−4√3π.四、解答题(本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.)17.(10分)在△ABC 中,边AB 所在的直线斜率为k AB =−12,其中顶点A 点坐标为(﹣1,1),顶点C 的坐标为(1,2).(1)求AB 边上的高所在的直线方程;(2)若CA ,CB 的中点分别为E ,F ,求直线EF 的方程.解:(1)由题意知AB边上的高过C(1,2),k AB=−1 2,因为AB边上的高所在的直线与AB所在的直线互相垂直,故高线的斜率为2,所以AB边上的高所在的直线方程为:y﹣2=2(x﹣1),即2x﹣y=0;(2)由已知A(﹣1,1),C(1,2),故CA的中点为E(0,32 ),因为E,F分别是CA,CB的中点,所以EF是△ABC的一条中位线,所以EF∥AB,而k AB=−12,所以直线EF的斜率为−12,所以直线EF的方程为:y−32=−12(x−0),化简可得:x+2y﹣3=0.18.(12分)2022年4月16日,神舟十三号载人飞船返回舱成功着陆,航天员翟志刚、王亚平、叶光富完成在轨驻留半年的太空飞行任务,标志着中国空间站关键技术验证阶段圆满完成.并将进入建造阶段,洪山区为了激发市民对天文学的兴趣,开展了天文知识比赛,满分100分(95分及以上为认知程度高),结果认知程度高的有m人,这m人按年龄分成5组,其中第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45],得到如图所示的频率分布直方图,已知第一组有10人.(1)根据频率分布直方图,估计这m人的第60百分位数;(精确到0.1)(2)现从第四组和第五组用分层随机抽样的方法抽取6人,担任“党章党史”宣传使者.①有甲(年龄36),乙(年龄42),且甲、乙确定入选,从6人中要选择两个人担任组长,求甲、乙两人至少有一人被选上组长的概率;②若第四组宣传使者的年龄的平均数与方差分别为36和52,第五组宣传使者的年龄的平均数与方差分别为42和1,据此估计这m人中35~45岁所有人的年龄平均数和方差.解:(1)设第60百分位数为a,∵0.01×5+0.07×5=0.4<0.6,0.01×5+0.07×5+0.06×5=0.7>0.6,∴a 位于第三组:[30,35)内, ∴a =30+0.6−0.45×0.06×(35−30)≈33.3;(2)①由题意得,第四组和第五组抽取人数之比为2:1,即第四组4人,记为A ,B ,C ,甲, 第五组2人,记为D ,乙,对应的样本空间为:AB ,AC ,A 甲,AD ,A 乙,BC ,B 甲,BD ,B 乙,C 甲,CD ,C 乙,甲D ,甲乙,D 乙,共15个样本点,设事件M 为“甲、乙两人至少一人被选上”,则有A 甲,A 乙,B 甲,B 乙,C 甲,C 乙,甲D ,甲乙,D 乙,共有9个样本点, ∴P (M )=915=35; ②设第四组的宣传使者的年龄平均数分为x =36,方差为s 12=52,设第五组的宣传使者的年龄平均数为y =42,方差为s 22=1,第四组和第五组所有宣传使者的年龄平均数为z ,方差为s 2, 则z =4x 6+2y 6=4×36+2×426=38, 即第四组和第五组所有宣传使者的年龄平均数为38,s 2=16{4×[s 12+(x −z)2]+2×[s 22+(y −z)2]}=10.即第四组和第五组所有宣传使者的年龄方差为10.19.(12分)如图,在平行六面体ABCD ﹣A 1B 1C 1D 1中,E ,F ,G 分别在A 1A ,B 1B ,D 1D 上,且A 1E =2EA ,BF =2FB 1,DG =2GD 1. (1)求证:EG ∥FC 1;(2)若底面ABCD ,侧面A 1ADD 1都是正方形,且二面角A 1﹣AD ﹣B 的大小为120°,AB =2,若P 是C 1G 的中点,求AP 的长度.解:(1)证明:在平行六面体ABCD ﹣A 1B 1C 1D 1中,∵E ,F ,G 分别在A 1A ,B 1B ,D 1D 上,且A 1E =2EA ,BF =2FB 1,DG =2GD 1,∴EA 1→=23AA 1→,D 1G →=−13DD 1→,FB 1→=13BB 1→,A 1D 1→=B 1C 1→,AA 1→=BB 1→=DD 1→,∴EG →=EA 1→+A 1D 1→+D 1G →=23AA 1→+B 1C 1→−13AA 1→=13BB 1→+B 1C 1→=FB 1→+B 1C 1→=FC 1→,∴EG ∥FC 1.(2)由题意可知:A 1A ⊥AD ,AB ⊥AD ,面ABCD ∩面AA 1D 1D =AD , ∴∠A 1AB 为二面角A 1﹣AD ﹣B 的平面角,又二面角A 1﹣AD ﹣B 的大小为120°,∴∠A 1AB =120°, 在平行六面体ABCD ﹣A 1B 1C 1D 1中有: ∵底面ABCD ,侧面A 1ADD 1都是正方形,∴AB →•AD →=0,AB →•AA 1→=|AB →|•|AA 1→|cos120°=2×2×(−12)=﹣2,AD →•AA 1→=0,∵P 是C 1G 的中点,∴AP →=12(AG →+AC 1→)=12(AD →+DG →+AB →+BC →+CC 1→)=AD →+56AA 1→+12AB →,AP →2=(AD →+56AA 1→+12AB →)2=AD →2+2536AA 1→2+14AB →2+53AD →⋅AA 1→+56AB →⋅AA 1→+AD →⋅AB →=4+2536×4+14×4+0+56×(−2)+0=559, 即AP =√553.20.(12分)第19届亚运会2023年9月在杭州市举办,本届亚运会以“绿色、智能、节俭、文明”为办会理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,从而促进经济快速发展.本次亚运会吉祥物是一组名为“江南忆”的机器人.三个吉祥物分别取名“琮琮”、“莲莲”和“宸宸”,分别代表世界遗产“良渚古城遗址”、“西湖”、“京杭大运河”.亚运期间,篮球比赛间隙安排了机器人吉祥物表演,由后台志愿者操控A ,B ,C 三个开关,分别可操控“琮琮”、“莲莲”和“宸宸”,当A 闭合时“琮琮”、“莲莲”表演;当B 闭合时“莲莲”和“宸宸”表演;当C 闭合时“琮琮”和“宸宸”表演,若A ,B ,C 三个开关闭合的概率分别为12,13,14,且相互独立.(1)求机器人“琮琮”表演的概率;(2)求机器人“莲莲”和“宸宸”都表演的概率.解:(1)设P (A ),P (B ),P (C )分别为开关A ,B ,C 闭合的概率,则P(A)=12,P(B)=13,P(C)=14,记“机器人“琮琮”表演”为事件M ,M 发生则需要A 、C 两个开关至少一个闭合, ∴P (M )=P (A ∪C ),由于开关闭合相互独立,则P(A ∪C)=P(AC)+P(AC)+P(AC)=P(A)P(C)+P(A)P(C)+P(A)P(C)=12×(1−14)+(1−12)×14+12×14=58,所以,机器人“琮琮”表演的概率为5 8.(2)记“机器人“莲莲”和“宸宸”都表演”为事件N,分为两种情况:B开关闭合;或B开关不闭合且A、C同时闭合,则P(N)=P(B)+P(B)P(A∩C)=P(B)+[1−P(B)]P(AC)=13+(1−13)×12×14=512.所以,机器人“莲莲”和“宸宸”都表演的概率为5 12.21.(12分)在三棱锥S﹣ABC中,底面△ABC为等腰直角三角形,∠SAB=∠SCB=∠ABC=90°.(1)求证:AC⊥SB;(2)若AB=2√2,SC=4,求平面SAC与平面SBC夹角的余弦值.解:(1)证明:取AC的中点为E,连结SE,BE,∵AB=BC,∴BE⊥AC,在△SCB和△SAB中,∠SAB=∠SCB=90°,AB=BC,SB=SB,∴△SCB≌△SAB,∴SA=SC,∵AC的中点为E,∴SE⊥AC,∵SE∩BE=E,SE⊂平面SBE,BE⊂平面SBE,∴AC⊥面SBE,∵SB⊂面SBE,∴AC⊥SB;(2)过S作SD⊥面ABC,垂足为D,连接AD,CD,∴SD⊥AB,∵AB⊥SA,AB⊥SD,SA∩AD=A,AB⊥平面SAD,∴AB ⊥AD ,同理,BC ⊥CD ,∵底面△ABC 为等腰直角三角形,AB =2√2,SC =4, ∴四边形ABCD 为正方形且边长为2√2.以D 为原点,DA ,DC ,DS 所在直线分别为x ,y ,z 轴建立空间直角坐标系D ﹣xyz , 则A (2√2,0,0),S (0,0,2),C (0,2√2,0),B (2√2,2√2,0), ∴SC →=(0,2√2,﹣2√2),AC →=(﹣2√2,2√2,0),BC →=(﹣2√2,0,0), 设平面SAC 的一个法向量为n →=(x 1,y 1,z 1),则{n →⋅SC →=2√2y 1−2√2z 1=0n →⋅AC →=−2√2x 1+2√2y 1=0,令x 1=1,则y 1=1,z 1=1, ∴平面SAC 的一个法向量为n →=(1,1,1), 设平面SBC 的一个法向量为m →=(x 2,y 2,z 2),则{m →⋅SC →=2√2y 2−2√2z 2=0m →⋅BC →=−2√2x 2=0,令y 2=1,则x 1=0,z 1=1, ∴平面SBC 的一个法向量为m →=(0,1,1),设平面SAC 与平面SBC 夹角为θ,cos θ=|cos <m →,n →>|=|m →⋅n →||m →|⋅|n →|=3×2=√63,故平面SAC 与平面SBC 夹角的余弦值为√63. 22.(12分)已知圆C 1:(x ﹣4)2+(y ﹣2)2=20与y 轴交于O ,A 两点,圆C 2过O ,A 两点,且直线C 2O 与圆C 1相切; (1)求圆C 2的方程;(2)若圆C 2上一动点M ,直线MO 与圆C 1的另一交点为N ,在平面内是否存在定点P 使得PM =PN 始终成立,若存在求出定点坐标,若不存在,说明理由.解:(1)由(x ﹣4)2+(y ﹣2)2=20,令x =0,解得y =0或4. ∵圆C 2过O ,A 两点,∴可设圆C 2的圆心C 1(a ,2).直线C 2的方程为:y =2ax .∵直线C 2O 与圆C 1相切,∴2a ×24=−1,解得a =﹣1,∴圆C 2的方程为:(x +1)2+(y ﹣2)2=(√5)2,化为:x 2+y 2+2x ﹣4y =0. (2)存在,且为P (3,4). 设直线OM 的方程为:y =kx .代入圆C 2的方程可得:(1+k 2)x 2+(2﹣4k )x =0.x M =4k−21+k 2,y M =4k 2−2k 1+k2.代入圆C 1的方程可得:(1+k 2)x 2﹣(8+4k )x =0.x N =8+4k 1+k 2,y N =4k 2+8k1+k2.设P (x ,y ),线段MN 的中点E (4k+31+k 2,4k 2+3k 1+k 2).则4k 2+3k1+k 2−y 4k+31+k 2−x×k =﹣1,化为:k (4﹣y )+(3﹣x )=0,令4﹣y =3﹣x =0,解得x =3,y =4. ∴P (3,4)与k 无关系.∴在平面内是存在定点P (3,4)使得PM =PN 始终成立.。
哲学家柏拉图的简介
哲学家柏拉图的简介柏拉图是古希腊著名的哲学家。
他对古希腊的哲学乃至整个西方的哲学发展起到了不可估量的作用。
下面是店铺搜集整理的哲学家柏拉图的简介,希望对你有帮助。
哲学家柏拉图的简介柏拉图(Πλάτων,约公元前427年-前347年)是著名的古希腊哲学家,他写下了许多哲学的对话录,并且在雅典创办了著名的学院。
柏拉图是苏格拉底的学生,也是亚里士多德的老师,他们三人被广泛认为是西方哲学的奠基者。
如同许多古老的文献,柏拉图留下的文集残缺不全、而且依然存在争议。
他记载的苏格拉底对话录成为后人研究他们思想的主要来源,但许多内容其实记载的是柏拉图自己的看法,而不是苏格拉底的原意。
柏拉图的哲学思想柏拉图是西方客观唯心主义的创始人,其哲学体系博大精深,对其教学思想影响尤甚。
柏拉图认为世界由“理念世界”和“现象世界”所组成。
理念的世界是真实的存在,永恒不变,而人类感官所接触到的这个现实的世界,只不过是理念世界的微弱的影子,它由现象所组成,而每种现象是因时空等因素而表现出暂时变动等特征。
由此出发,柏拉图提出了一种理念论和回忆说的认识论,并将它作为其教学理论的哲学基础。
柏拉图认为任何一种哲学要能具有普遍性,必须包括一个关于自然和宇宙的学说在内。
柏拉图试图掌握有关个人和大自然永恒不变的真理,因此发展一种适合并从属于他的政治见解和神学见解的自然哲学。
柏拉图认为,自然界中有形的东西是流动的,但是构成这些有形物质的“形式”或“理念”却是永恒不变的。
柏拉图指出,当我们说到“马”时,我们没有指任何一匹马,而是称任何一种马。
而“马”的含义本身独立于各种马(“有形的”),它不存在于空间和时间中,因此是永恒的。
但是某一匹特定的、有形的、存在于感官世界的马,却是“流动”的,会死亡,会腐烂。
这可以作为柏拉图的“理念论”的一个初步的解说。
柏拉图认为,我们对那些变换的、流动的事物不可能有真正的认识,我们对它们只有意见或看法,我们唯一能够真正了解的,只有那些我们能够运用我们的理智来了解的“形式”或者“理念”。
多面体
对偶立体
对偶立体
将一个立体的所有边沿着中点转90°延长后围成的 立体称为此立体的对偶立体。
正六面体和正八面体互为对偶立体 正十二面体和正二十面体互为对偶立体 正四面体为本身对偶立体 阿基米得多面体的对偶立体为卡塔兰立体
图中V指的是Vertex(顶点)的个数 E指的是Edge(边)的个数 F指的是Face(面)的个数
柏拉图多面体
4) 正十二面体 (Dodecahedron) 十二面体是一由十二个正五角形组成的多面体, 其每个顶点旁边 都有三个五边形.
V=20 E=30 F=12 象征宇宙
图中V指的是Vertex(顶点)的个数 E指的是Edge(边)的个数 F指的是Face(面)的个数
当每个面的边数为3,每个顶点可连接3、4、5个 面:
只连接1或2个面,无法围成立体 连接3个面,可围成正四面体 连接4个面,可围成正八面体 连接5个面,可围成正二十面体 连接6个面以上,顶点上的角度的总度数
﹥60°×6=360°,不能围成立体。
证明柏拉图多面体只有五个
当每个面的边数为4,每个顶点可连接3个面:
多面体
目录
研
研研研研
究 欧约对正阿证柏多究 究 究 究
心 得
拉 公
翰 逊
偶 立
多 角
基 米
明 柏 拉
拉 图
面 体
内 容
方 法
目 的
动 机
式 多 体 柱 得 图多 简
面 与多多面介
体
反 多
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从柏拉图多面体到尤拉公式壹、柏拉图多面体“多面体”是日常生活中经常看到的立体,它是被一些平面所包围的立体,例如粉笔盒、三棱镜、新光摩天大楼等等,那些包围多面体的多边形叫做多面体的面,两个面相交的线段叫做多面体的棱,棱与棱的交点叫做多面体的顶点。
顶点是由三个或三个以上的面交会出来的。
例如:右图中的立体中有5个面,9条棱,6个顶点。
所谓“柏拉图多面体”(Platonic Polyhedra)就是指正多面体,正多面体就是每个顶点处交会着相同数目全等的正凸多面体且每个立体角相等。
正多面体会称为柏拉图多面体并不是因为柏拉图发现了正多面体,而是因为柏拉图及其追随者对它们所作的研究而得名。
貳、柏拉图多面体有多少个?(1)要谈柏拉图多面体有几个之前,先观察平面上的凸正n边形,n至少等于3,且每一个内角为(n-2)⨯180︒n,而(n-2)⨯180︒n<180︒,因此平面上的正凸n边形有无限多个。
在空间中,柏拉图多面体是否会有无限多个呢?答案令人很惊讶!不仅不是无限多个,而且只有5个。
古人对于这个事实虽不愿相信,却不得不接受,最后只好搬出“神的旨意”来承认这个事实。
为何会说是“神的旨意”呢?原来在伽利略(Galiep1564~1642意大利人)发明望远镜之前,当时天空中人类只观察到五颗行星,因此这五个正多面体就分别代表那五颗行星,这么的巧合,那一定是“神的旨意”,这样的想法,甚至影响了天文学家克卜勒(Kepler 1571~1630德国人),他曾试图去观察、计算各行星的轨道半径,周期与五个正多面体对应,可惜并未成功。
(2)接下来我们来讨论柏拉图多面体的个数:我们从一个顶点出发,因为正多面体的每一个顶点处都是正n边形内角的顶点,我们先从简单的正多边形讨论起:(1︒)当正多边形是正三角形时,每一个正三角形的内角为60︒,若每一个顶点有3个正三角形,则会形成正四面体(Tetrahedon)若每一个顶点有4个正三角形,则会形成正八面体(Octahedron)若每一个顶点有5个正三角形,则会形成正二十面体(Icsoahedon)但是当每一个顶点处有6个正三角形时,那么交会在这个顶点的面的角之总和为360︒,于是这些三角形构成一平面或是凹面,故表面是正三角形的柏拉图多面体只有3种。
タ砰タ砰(2︒)当正多边形是正方形时,每一个正方形的内角为90︒若每一个顶点处有3个正方形,则会形成正立方体(Hexahedron)。
但是当每一个顶点处有4个正方形,那么交会在这个顶点的面的角之总和为360︒,于是这些三角形构成一平面或是凹面,故表面是正方形的柏拉图多面体只有1种。
(3︒)当正多边形是正五边形时,每一个正五边形的内角为108︒若每一个顶点处有3个正五边形,则会形成正十二面体(Dodecahedron)。
但是当每一个顶点处有4个正五边形,那么交会在这个顶点的面的角之总和为360︒,于是这些三角形构成一平面或是凹面,故表面是正五边形的柏拉图多面体只有1种。
(4︒)当正多边形是正六边形时,假如3个正六边形交会在一顶点处,那么这些面的角之总和=360︒,于是构成一个平面。
从此处亦可看出多边形的面数愈多,它们的内角愈大,多于六边的正多边形其三个内角之总和将超过360︒,于是,无法将它们连接在一起而构成一正的凸多面体。
我们将上面的讨论整理如下:设正多面体的所有面都是正n 边形,每一个顶点的棱数都是m ,换句话说,每个顶点的角都是m 个角的顶点。
タ砰正二十面体正六面体因为正n 边形的每个内角=(n-2)⨯180︒n ,就每个顶点而言,因为它是m 个角的顶点,所以在每个顶点的所有角度和=(n-2)⨯180︒n⨯m 因为正多面体是凸多面体,所以在每一个顶点的所有角度和<360︒, 所以(n-2)⨯180︒n⨯m<360︒ ⇒m(n -2)<2n ⇒m<2nn-2 (m,n 都是不小于3的正整数) 解这个不等式当n=3时,m<6,得m=3,4,5; 当n=4时,m<4,得m=3; 当n=5时,m<103,得m=3;当n ≥6时,m<2n n-2≤12n-2≤3,得此时m,n 无解。
因此,我们只能得到五个关于m,n 的解:參、 尤拉公式-多面体的面数、棱数、顶点间的关系(1)几个立体的面数、棱数、顶点数一数柏拉图多面体的面数、棱数、顶点,结果如下表所示:顶点数(V)、面数(F)、棱数(E)之间有何关系呢?光看上面的表或许无法归纳出来,我们再多看几个立体:(2)几个找规律的想法:(a)V是否随F增大呢?(b)F和V是否为一致地随着E的增大而增大呢?(c)F+V是否随着E的增大而增大呢?(d)F+V=E+2成立吗?经过前面几个方向的推测,上述的立体都有面数+顶点数=棱数+2的规则虽然上述的10个立体都符合F+V=E+2这个规则,但我们需要更多的事实来支持我们的猜想。
(3)更多的证据:证据一:让我们考虑两类立体有n个侧面的柱体、有n个侧面的锥体:假如一个柱体有n个侧面,则F=n+2,V=2n,E=3n假如一个锥体有n个侧面,则F=n+1,V=n+1,E=2n因此这两类的立体亦满足F+V=E+2这个例子。
证据二、在观察上述10个立体中曾提及的类似屋顶的“塔顶体”,我们取任何多面体代替立方体,在这个多面体的任一各面在上放一个“屋顶”。
假如原来的多面体有F个面、V个顶点、E条边,且假定所选的面有n个边。
我们在上面放上一个有n个侧面的锥体,从而得到一个新的立体(“塔顶体”),我们来看看新的立体的面数、顶点数、棱数。
新的立体面数=F-1+V,顶点数=V+1,棱数=E+n于是我们可得(新的立体面数)+(新的立体点数)-[(新的立体棱数)+2]=F+V-E-2若原来的立体满足F+V=E+2则(新的立体面数)+(新的立体点数)=(新的立体棱数)+2这个结果告诉我们,如果我们原先的猜测是真的,那么在这个立体的一个面加上一个“屋顶”,这个式子还是会成立。
亦是我们的猜想经得起加“屋顶”这个考验。
问题:如果将任一个多面体截去任意一个顶点,形成一个新的多面体,假如原来的多面体有F 张面、V 个顶点、E 条边,新的立体有F /张面、V /个顶点、E /条边,你能检验F /+V /=E /+2是否成立吗?(3)尤拉公式从前面的讨论,可知有很多种类型的立体都满足V -E+F=2,其实早在200多年前(公元1750年)瑞士数学家尤拉就发现了这个关系,因此我们把它称为尤拉公式。
以四面体ABCD 为例来体验这个公式:设四面体的顶点数V 、棱数E 、面数F ,将四面体ABCD 投影到一个平面上, 如下图所示:A 的投影点为A /,所以−A /B 、−A /C 、−A /D 分别是−AB 、−AC 、−AD 的投影线段,底面△BCD 之外的三面△ABC 、△ACD 、△ABD 分别投影到△A /BC 、△A /CD 、△A /BD ,经过投影可以把立体变成平面图形,那么计算点、线、面的数目时,会比较容易处理。
假设平面图形上顶点、棱及面的数目分别以V /、E /、F /表示,显然的顶点及棱的数目并不会头影而改变, 所以V=V / E=E /但是计算面的时候,我们只计算小三角形△A /BC 、△A /CD 、△A /BD ,而外围的大三角形△BCD 却不计在内,可知F /=F -1 因此,对于四面体证明公式V -E+F=2B CB CD就相当于对它在平面上的投影图形证明公式V /-E /+F /=1…………..(★) 底下来证明(★)式:首先将棱−BC 去掉,同时△A /BC 也去掉了,如下图所示计算右上图的顶点、棱、面数时,会发现:棱固然减少一个,但是面数也相对减少一个,所以V /-E /+F /这个数不会改变。
这也就是说,当我们去掉外围的一条棱之后,图形有所改变,可是V /-E /+F /这个数却不会改变。
因此我们继续把外围的棱−CD 、−BD 去掉,如下图所示显然上面得三个图形V /-E /+F /这个数不会改变,我们可以继续简化图形,将B 点去掉,同时也将−A /B 去掉,此时顶点数目少一个,但是棱数也同时少了一个,所以对V /-E /+F /这个数没有影响。
换句话说,当去掉外围一个顶点及其相连的棱时,图形没有改变,可是V /-E /+F /这个数不会改变。
所以我们继续将顶点C,D 去掉如下图所示:最后,图形只剩下一个点A /,显然不用计算,一看便知V /-E /+F / =1。
以上我们用四面体为例说明尤拉公式的验证方法,其余立体都可依循同样的方法得到尤拉公式。
B CDBDBBBA /问题:可否将在四面体中验证尤拉公式的方法,同样在六面体中验证?问题:如果从尤拉公式出发,如何证明正多面体只有5种?(4)正多面体的内切球半径、外接球半径与其他的性质我们知道正多面体共有五种:正四面体、正六面体、正八面体、正十二面体、正二十面体。
透过尤拉公式V -E+F=2,可以得知各多面体的顶点(V)、棱(E)、面(F)的个数,接下来讨论正多面体各个面之夹角、内切球、外接球半径。
[例題1] 给定一个正四面体的边长为a ,求其外接球半径R 、内切球半径r ,表面积S ,体积V 及相邻两个面的夹角φ。
Ans :R=64a ,r = 612a ,S= 3 a 2,V=212a 3,φ=2tan -112(=cos -113)(練習1) 给定一个正六面体的边长为a ,求其外接球半径、内切球半径r ,表面积S ,体积V 及相邻两个面的夹角φ。
BC[例題2] 给定一个正八面体的边长为a ,求其外接球半径R 、内切球半径r ,表面积S ,体积V 及相邻两个面的夹角φ。
Ans :R=22a ,r =66a ,S=2 3 a 2,V=23a 3, φ=2tan -12 (=cos -1-13)(練習2) (a)观察正四面体与正八面体相邻两个面的夹角,它们之间有什么关系?(b)取一个正四面体及正八面体,两立体的面全等,将两个立体的一面密合贴 在一起,得一个新的立体,请判断这个新立体是几面体?(練習3) 给定一个正四面体,若以它的六条棱的中点为顶点,会形成一个什么样的多面体?A BD[例題3] 给定一个正十二面体的边长为a ,求其外接球半径R 、内切球半径r ,表面积S ,体积V 及相邻两个面的夹角φ。
Ans :R=3(5+1)4a ,r =a 20)51125(10+,S=325+10 5 a 2,V=15+754a 3 φ=cos -1(-55)O[例題4] 给定一个正二十面体的边长为a ,求其外接球半径R 、内切球半径r ,表面积S ,体积V 及相邻两个面的夹角φ。
Ans :R=10+254,r =3(3+5)12,S=5 3 a 2,V=512(3+ 5 )a 3,φ=2tan -13+52(練習4) 试求内接于单位球内的正多面体的边长、内切球半径r 、外接球半径R 、表面积S 、体积V 。
