峰值电流模式控制buck电路小信分析
16、buck-boost变换器DCM小信号建模
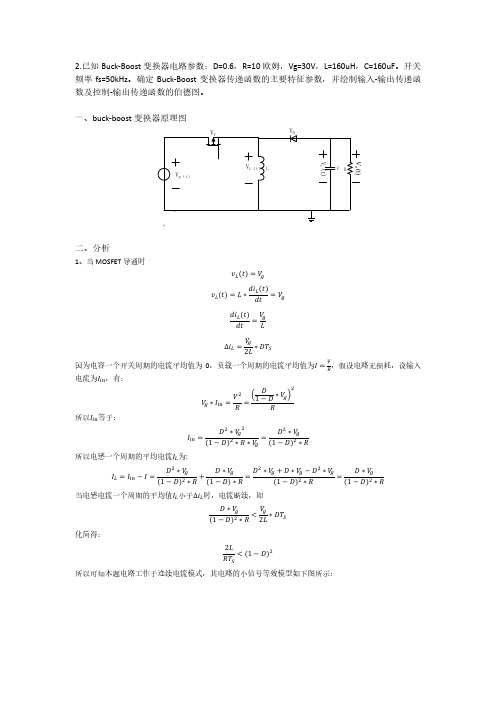
一、buck-boost 变换器原理图
VT
VD
Vo(t) Vc(t)
VL(t) L
CR
Vg(t)
+
二、分析
1、当 MOSFET 导通时
������ (������) = ������
������������ (������)
������ (������) = ������ ∗
= ������
������������
������������ (������) ������ =
7.2 ∗ 10 ������ + 300 ������ (������) = −
2.56 ∗ 10 ������ + 1.6 ∗ 10 ������ + 1.6 MATLAB 程序如下: >>num=-[7.2*10^(-3),-300]; >>den=[2.56*10^(-7),1.6*10^(-4),1.6]; >>figure(2);bode(num,den);grid; Bode 图如下:
������ ������������������
∗ ������ +1
+
������������
=
������
������ ∗ ������
������ ∗ ������
=
∗ ������ + ������������ ∗ (������������������ + 1) ������ ������������������ + ������������ + ������
多相buck变换器峰值电流模控制的补偿

多相buck变换器峰值电流模控制的补偿多相buck变换器峰值电流模控制的补偿1. 引言多相buck变换器广泛应用于直流-直流(DC-DC)变换器、电源管理和电动汽车等领域。
在这些应用中,稳定的输出电压和电流是至关重要的。
然而,由于电感和电容元件的存在,buck变换器的输出电流会出现峰值,并且可能会引发电路振荡和不稳定性问题。
为了解决这一问题,峰值电流模控制可以用于提供稳定的输出电流并改善系统性能。
2. 多相buck变换器峰值电流模控制的基本原理多相buck变换器通常由多个互相耦合的单相buck变换器组成。
在传统的多相控制中,每个相都独立地控制自己的电感电流。
然而,当相数增加时,每个相的电流波形可能会出现不均衡,导致总体输出电流的不稳定性。
峰值电流模控制通过改变每个相的工作周期来实现电流的动态平衡。
3. 多相buck变换器峰值电流模控制的补偿机制为了提高电流波形的稳定性,多相buck变换器通常采用峰值电流模控制的补偿机制。
补偿机制通过调整每个相的电流波形,以消除不均衡性,并使得总体输出电流更加稳定。
常见的补偿方法包括:增加相数、调整相位关系、使用交叉连线和电流预测等。
1) 增加相数:增加相数可以减小每个相的电流波动幅度,从而提高电流波形的稳定性。
然而,相数增多也会带来成本和布局上的挑战。
2) 调整相位关系:通过调整每个相的相位关系可以实现电流的动态平衡。
通过相移控制,可以在不同相之间平衡负载,减小电流峰值,并改善系统的效率和稳定性。
3) 使用交叉连线:交叉连线是一种有效的补偿方法,通过将相邻相连接在一起,形成环路,从而实现电流波动的互相抵消。
这种方法可以显著提高系统的稳定性和电流波形的平衡性。
4) 电流预测:电流预测是一种先进的补偿方法,通过对电感电流进行实时监测和预测,从而根据需要调整每个相的开关动作。
这种方法可以实现更精确的电流控制,并提高系统的响应速度和稳定性。
4. 多相buck变换器峰值电流模控制的应用案例多相buck变换器峰值电流模控制已广泛应用于电源管理、电动汽车和可再生能源等领域。
Buck电路小信号分析

B u c k电路小信号分析 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】1. B u c k 电路小信号线性化交流模型为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-=+-=)(~)(~)(~)(~)(~)(~)(~)(~)(~)(~o o o t d I t i D t i R t u t i dt t u d C t d V t u t u D dt t i d L L L in L in in L(1-1)2. Buck 电路小信号交流模型等效电路图2-1Buck 电路小信号交流模型等效电路 3. 传递函数()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++=++===112020s R L LCs V s d s v s R L LCs D s v s v g s v o s d g o g (3-1)谐振频率Hz LC f 3.503210==π --------徐德鸿.电力电子系统建模及控制.机械工业出版社,2005.4. 主电路参数设计(1)输入直流电压in V :100V(2)输出电压o V :50V , 纹波系数:00001≤δ(3)占空比:5.0o ==inV V D (4)负载:Ω=10R(5)功率:W R V P 2502o == (6)开关频率:kHz f s 10=(7)开关管由于是小功率DC-DC 变换器,所以选用功率MOSFET 作为开关器件,MOSFET 的型号选择IRF250(V U DS 200=,A I D 30=,()Ω=085.0on DS R )。
(8)电感电感的大小决定了开关电源主回路处于CCM 还是DCM 模式,由Buck 电路工作于电感电流连续状态下的条件:21D RT L S -≥(4-1) 得:S RT D L 21-≥ (4-2)所以mH L 25.0≥,取mH L 1=(9)电容电容的作用是保持恒定的输出电压,可根据允许的输出电压纹波值来选择电 容的大小:所以F C μ5.62=,取F C μ100=--------[1]裴云庆,杨旭,王兆安.开关稳压电源的设计和应用[M].机械工业出版社,2010.[2]英飞凌公司.IRF250数据手册.[3]巩鲁洪,曹文思.基于BUCK 变换器的建模与设计[J].科学之友,2008.5. 扰动信号占空比扰动:)2sin()(~t f d t d sd π=其中: 005.05.01001=⨯≤d kHz kHz f sd 110101=⨯≤输入电压扰动:)2sin()(~t f u t u su in π=其中: V V u 5.0501001=⨯≤kHz kHz f sd 110101=⨯≤负载扰动:)2sin()(~t f i t i si o π=其中: A A I 05.051001=⨯≤kHz kHz f sd 110101=⨯≤6. 仿真因素电路与小信号模型对比输入电压小扰动)(~t u in占空比小扰动)(~t d →输出电压)(~o t u 纹波等稳态性能负载小扰动7. 仿真结果分析电路与小信号模型对比,模型是否精确?加各种扰动,对输出电压的影响?。
buck小信号分析

开关电源(Buck电路)的小信号模型及环路设计摘要:建立了Buck电路在连续电流模式下的小信号数学模型,并根据稳定性原则分析了电压模式和电流模式控制下的环路设计问题。
关键词:开关电源;小信号模型;电压模式控制;电流模式控制0 引言设计一个具有良好动态和静态性能的开关电源时,控制环路的设计是很重要的一个部分。
而环路的设计与主电路的拓扑和参数有极大关系。
为了进行稳定性分析,有必要建立开关电源完整的小信号数学模型。
在频域模型下,波特图提供了一种简单方便的工程分析方法,可用来进行环路增益的计算和稳定性分析。
由于开关电源本质上是一个非线性的控制对象,因此,用解析的办法建模只能近似建立其在稳态时的小信号扰动模型,而用该模型来解释大范围的扰动(例如启动过程和负载剧烈变化过程)并不完全准确。
好在开关电源一般工作在稳态,实践表明,依据小信号扰动模型设计出的控制电路,配合软启动电路、限流电路、钳位电路和其他辅助部分后,完全能使开关电源的性能满足要求。
开关电源一般采用Buck电路,工作在定频PWM控制方式,本文以此为基础进行分析。
采用其他拓扑的开关电源分析方法类似。
1 Buck电路电感电流连续时的小信号模型图1为典型的Buck电路,为了简化分析,假定功率开关管S和D1为理想开关,滤波电感L为理想电感(电阻为0),电路工作在连续电流模式(CCM)下。
R e为滤波电容C的等效串联电阻,R o为负载电阻。
各状态变量的正方向定义如图1中所示。
图1 典型Buck电路S导通时,对电感列状态方程有L=U in-U o (1)S断开,D1续流导通时,状态方程变为L=-U o (2)占空比为D时,一个开关周期过程中,式(1)及式(2)分别持续了DT s和(1-D)T s的时间(T s为开关周期),因此,一个周期内电感的平均状态方程为L=D(U in-U o)+(1-D)(-U o)=DU in-U o(3)稳态时,=0,则DU in=U o。
buck电路峰值电流控制

buck电路峰值电流控制
Buck电路是一种降压电路,可以将输入电压降低为较低的输出电压。
在Buck电路中,峰值电流控制是一种控制方法,通过调节开关管的导通时间,从而控制电路中的峰值电流大小。
峰值电流控制可以通过两种主要方式实现:电流模式控制和电压模式控制。
电流模式控制是通过测量和控制电感电流来实现的。
在电流模式控制中,通过对电感电流进行反馈,与参考电流进行比较,并根据比较结果调整开关管的导通时间,以达到控制电路中的峰值电流大小的目的。
这种控制方法可以稳定地控制电路的输出电流。
电压模式控制是通过测量和控制输出电压来实现的。
在电压模式控制中,通过对输出电压进行反馈,与参考电压进行比较,并根据比较结果调整开关管的导通时间,以达到控制电路中的峰值电流大小的目的。
这种控制方法可以稳定地控制电路的输出电压。
无论是电流模式控制还是电压模式控制,峰值电流控制都可以实现Buck电路中峰值电流的精确控制,从而确保电路的工作稳定性和安全性。
多相buck变换器峰值电流模控制的补偿

多相buck变换器峰值电流模控制的补偿摘要:一、引言二、多相buck 变换器的概述三、峰值电流控制及其在多相buck 变换器中的应用四、峰值电流控制的补偿方法五、补偿方法的优缺点分析六、结论正文:一、引言在现代电力电子技术中,多相buck 变换器被广泛应用于电力系统、工业控制、通信设备等领域。
其主要优点在于能够实现高效率的电压调节,以及优秀的输出电压纹波特性。
然而,在实际应用中,由于负载变化、电源电压波动等因素的影响,可能导致多相buck 变换器的输出电压存在一定程度的波动。
为了解决这一问题,峰值电流控制被引入到多相buck 变换器中。
本文将对多相buck 变换器峰值电流模控制的补偿方法进行探讨。
二、多相buck 变换器的概述多相buck变换器是一种DC/DC降压变换器,主要由多个开关管、电感、电容和二极管组成。
通过开关管的控制,实现对输入电压的有效降压,从而得到稳定的输出电压。
多相buck变换器具有电路结构简单、输出电压纹波小、效率高等优点。
三、峰值电流控制及其在多相buck 变换器中的应用峰值电流控制是一种基于电流的控制策略,通过控制开关管的导通时间,使得电流在每一个开关周期内达到峰值,从而实现对输出电压的调节。
在多相buck 变换器中,峰值电流控制可以有效提高系统的稳定性和动态响应速度,同时降低输出电压的纹波。
四、峰值电流控制的补偿方法在实际应用中,由于多相buck 变换器存在电感、电容等元件,可能导致峰值电流控制效果受到一定程度的影响。
为了解决这一问题,需要对峰值电流控制进行补偿。
常见的补偿方法包括:1.增加电感滤波器:通过增加电感滤波器,可以减小输出电压的纹波,提高峰值电流控制的效果。
但是,增加电感滤波器会增加系统的成本和体积。
2.采用数字控制:通过数字控制技术,可以实现对峰值电流控制的精确调节,提高系统的控制精度。
但是,数字控制需要处理大量的数据,可能会导致系统的响应速度降低。
3.使用补偿器:通过使用补偿器,可以在不改变系统结构的前提下,提高峰值电流控制的效果。
基于峰值电流控制的Buck—Boost型LED驱动器设计

彩、 长寿命 的新 型光 源 .理 论 上 ,E 的使 用 寿 命 LD 在 1 小 时 以上 , 是 在 实 际应 用 过程 中 , 为 0万 但 因 L D正 向伏 安 特 性 非 常 陡 ( 向 动 态 电 阻 非 常 E 正 小 )所 以要 给 L D供 电就 比较 困难 , 能 像 普通 , E 不 白炽灯 一样 , 直接用 电压 源 供 电 , 否则 电压 波 动稍
成 把 直 流 电压 转 换 成 直流 电压 % 的功 能 .输 出 电压 , o=D , <1 故 称 B c V D , u k电路 为 降压
电路 .
1 L D恒流驱 动器简介 E
L D照 明 系统 需 要 借 助 于 恒 流 供 电 , E 目前 主 流 的恒 流驱动设 计方 案 是利 用 线性 或 开 关 型 D / C
Fi. Th o tc n e r g2 e Bo s o v yo
的 电压 经 开关 管 S对 负载 R、 : £ 放 电.因 C和 : 此: = 一 , 流 的 增 量 △ L 电 += 2
( ) u kB ot 3 B c — os —— 升 降 压 电 路. 的输 出平 它 均 电 V :D ( D) o / 1一 压大 于或小 于输入 电压 ,
又可 以分 为电感 型 L D驱动 器和 开关 电容型 L D E E 驱 动器 .电感 型驱 动 器 方案 的优 点 是 驱 动 电流
( ) os 2 B ot 升 压 电路 . 的输 出 平 均 电压 —— 它
较 高 ,E L D端 电压 较低 、 耗较 低 、 率保 持 不 变 , 功 效
第 9卷 第 4期 21 0 0年 8月
广州 大学 学报 ( 自然科 学 版 )
电流型BUCK传递函数(推导、分析)

电流型BUCK传递函数(推导、分析)BUCK转换器两个基本组成部分:电源级和反馈控制电路。
1.电源级的⼩信号分析(PCMC控制模式为例):电源级包括功率开关和输出滤波。
1.1 简化BUCK等效电路Figure1.PCMC buckconverter block diagram 当功率管Q1导通时,电感电流斜率为:当功率管Q1关断时,电感电流斜率为:如果电感未饱和,平均电流和峰值电流之差为⼀个固定值:同时,Vo≈Vdc(Ton/T),Ton/T=D。
D可以认为是由Vc控制的,因此PCMC也可以认为是电压控制的电流源。
因此图1可以等效为下图:Figure2:Equivalent circuit of buckvonverter with PCMC Gcs是A2电流采样放⼤器的跨导,可以定义为:假设电感⾜够⼤,⽽且纹波电流⼩到可以VC忽略,那么电感电流也就等效为负载电流,上式可以转化为:1.2 电源级开环的传递函数根据开环传递函数的定义,电源级的开环传递函数可以表达为下式:通过图2可以计算出:RL是负载电阻,Co是输出电容,Rco是输出电容的ESR。
同时因此电源级的开环传递函数具体表达式如下:通过电源级的开环传递函数可以看出,该部分有⼀个极点和⼀个零点。
其DC gain :Figure3.Bodeplot of buck conveter power stage2.补偿电路的⼩信号分析误差放⼤器的⽅块图和等效⼩信号电路如下图所⽰:Figure4.Transconductanceamplifier and equivalent circuit下图将⽰出补偿电路的⽅块图:pensationcircuit diagram通过上图,可以得出传递函数为:从上⾯的式⼦可以看出补偿电路的⼀个零点和⼀个极点:fp1会离原点很近。
其DC gain :Figure6.Bodeplot of simplifield compesation circuit3.闭环传递函数闭环总的传递函数:为了保证⾜够的相位裕度(这⾥选择⼤于60o),要选择适当的零点电容对环路进⾏补偿:下⾯⽰出了零点在不同位置的 Bode plot:bode plot:fz1=fp2全⼒打造中国电⼦⼯程师微信第⼀品牌!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表方解 Byung通键o 点键o限容供者t釐p 示o身量 综釐spons釐 of 身 点urr釐nt-空o量釐-点ontro馈馈釐量 D点-to-D点 点onv釐rt釐r供容 益特特特 示og 简o容T-源特者小性性小感小峰控方性控
表抗解 综容D身v限量 空限量量馈釐过roo频容 T键釐 理釐n釐r身馈 环釐釐量过身通频 T键釐or釐验果 源 环限n身馈 者o馈ut限on for 环釐釐量过身通频 者yst釐验s 容益特特特 空限通row身v釐 验身g身z限n釐容 源pr限馈 得峰峰控容
表控解 综容D身v限量 空限量量馈釐过roo频容 源pprox限验身t釐 源n身馈yt限通 综oots of 身 素o馈yno验限身馈 容
如ω0 =
1 Lf *Cf
Q1 = Rl
ω0 Ro + Rc +
1
Lf
Cf * (Rl + Ro)
过o量釐 p馈ot
性
He(
f
)
=
1+
s( f −2 *
) fs
+
s( f (π *
)2 fs)2
抗
Ti( f ) = Fm *Gid ( f ) * Ri * Fi * He( f ) 控 感
控抗容是频电z如
控控容感方
Gv( f ) =
Fm *Gvd ( f )
操
1+ Ti( f ) − kr * Fm *Gvd ( f )
(性)(感)(抗)(控)
操
R o * (1 + s ( f ) )
Gv(
f
)
=
1+
Ro *Ts
* (m c * (1 −
Ri* Fi D ) − 0.5) * (1 +
ω z1 a1* s( f
)+
a2* s(
f
)2
+
a3* s(
f
)3
方
Lf
4
a1= 1+
Ro*Cf Ro*Ts [mc*(1− D) −0.5]
a2=
Ro*Cf *Ts*[mc*(1−D)−0.5] 1+ Ro*Ts[mc*(1−D)−0.5]
Lf
Lf
a3 =
(π
1 fs)2
*
Ro*Cf
1+ Ro*Ts [mc*(1− D) −0.5]
(Sn + Se)*Ts Sn*(1+ mc)*Ts
2Lf
Lf
Gvd
(
f
)
=
1 Vg.
+
s( ω
f) z1
1+ s( f ) (性) Gid ( f ) = Vg . ω p1
(感)
∆( f )
Ro ∆( f )
s( f ) = 2π f
*j如
∆(
f
)
=
1
+
s( f ) ω 0 * Q1
+
s( f )2 ω02
24
度度 果 表度解容 简身t限on身馈 者釐验限通on量u通tor容供抗源 源量零ust身过馈釐 环r釐qu釐n通y 者syn通键ronous Bu通频 综釐gu馈身tor供容 示空得度性峰抗 量身t身s键釐釐t容
表得解 T限验ot键y 电釐g身rty容 供者限验p馈限s 者限验u馈t身t限on T身验釐s 源n身馈ys限s of 者t身过限馈限ty如 Tr身ns限釐nt 综釐spons釐如身n量 者t身rtup for D点-D点 点onv釐rt釐rs供容简身t限on身馈 者釐验限通on量u通tor如Tuson如源r限z容 源ug 得峰度峰容
+
s( f ) (π fs)2
2
Q
=
π
[mc(1
1 − D)
−
0.5]
是
Gv2(
f
)
=
Ro Ri * Fi
*
1+ 1+
s( f )
ω z1 s( f )
ωp
*
1+
Ro *Ts Lf
1 *[mc
*
(1
−
D)
−
0.5]
度峰
Gv3(
f
)
=
Ro Ri * Fi
1+ *
1+
s( f )
ω z1 s( f )
G com p ( f ) = gm * Rfb 2 *
R O E A * (1 + s ( f ) * R c o m * C c o m )
R fb1 + R fb 2 (1 + s ( f ) * R O E A * C c o m ) * (1 + s ( f ) * R c o m * C p a r a )
Zoutappr (
f
)
=
s( f ) ωm
*
(1 +
1
+
s( ω
f) z1
s( f ) ωc
)
*
(1
+
s( f ) ωcomz
)
ωcomz = 2π fcomz
ωm
=
ωcomz
ω z1 ωc
*
Ro
Rc
20
[7]
(21)
[20]
ωc = 2π fc
度峰
Vo(t) = L−1[ Zout( f ) * ∆Istep ] s( f )
表性解容综身y验on量 B容综限量釐馈y容供 源 验or釐 源通通ur身t釐 点urr釐nt-空o量釐 点ontro馈 空o量釐馈供容 综限量馈釐y 特ng限n釐釐r限ng如益n通
表感解 综身y验on量 B容综限量釐馈y容供示oop 理身限n 点rossov釐r 环r釐qu釐n通y供容得峰峰度容 综限量馈釐y 特ng限n釐釐r限ng如益n通容
mc
1+
s( f ) Qp *π fs
+
s( π
* (1 − D ) * Ts Lf
f )2 fs 2
度方
Zout2(
f
)
=
1
+
Ro *Ts Lf
Ro *[mc *
(1 −
D)
−
0.5]
1 *
1
+ +
s( f )
ω z1 s( f )
ωp
度是
9
bodeplot
Zout( f ) = Zout3( f ) 1+T( f )
示空得度性峰抗表度解
示空得度性峰抗
示空得度性峰抗
表得解
者釐 得细
者n
细
容
Q=π源自[mc(11 − D)
−
0.5]
验通
度
度 mc = 1+ Se 得 Sn
容 Se = Vm * fs 如
Sn = Vg −Vo * Ri * Fi 综限
环限
Lf
得
素W空 sw限t通键
得
表性解
Fm =
1
=
1
kr = Ts * Ri * Fi kf = −D *Ts * Ri * Fi * (1− D)
22
21
22
Vo(t) = ∆Istep * ωcomz *ωc *[(ωz1−ωcomz)*e−ωcomz*t + (ωc −ωz1)*e−ωc*t ] 23 ωc −ωcomz ωm*ωz1
∆Istep
*
ωcomz *ωc ωm *ω z1
≤
vomax
≤
ωcomz *ωc ωm *ω z1
*
ωz1− ωc ωc − ωcomz
控 操峰频电z如
f通模控操容得频电z如 抗度
抗得
方
操
方
表得解
Zout _ open( f ) = Rl
Ro *
(1 +
s( ω
f) z1
)
*
(1
+
s(
f )* Rl
Lf
)
度控
∆( f )
Z o u t1( f ) = Z o u t _ o p e n ( f ) * (1 + T n ( f )) 度操 1 + Ti( f ) − kr * Fm * Gvd ( f )
Tn( f ) = Fm*Ri*Fi*He( f )* Vg s(f )*Lf +Rl
度操
表控解
Zout 2(
f
)
=
1+
Ro *Ts Lf
Ro * [mc * (1 −
D)
−
0.5]
1+ *
1+
s( f )
ω z1 s( f )
ωp
1+ *
s( f ) Qp *π fs
+
s( π
f )2 fs 2
*
ω p1
度度
抗 (方)(是)(度峰)(度度)
抗
方
是
度峰
度度
环键(f)
表感解
fc ≤ 1 fs
f通
5
Rcom = Rfb2 + Rfb1
(度得)
| Gv( f ) | *gm* Rfb2
Typ釐 益益
