利率期限结构的主成分分析
利率期限结构理论讲解
利率期限结构理论讲解利率期限结构理论，也称为利率结构理论或期限结构理论，是描述不同期限债券的利率之间关系的一种理论框架。
它试图解释为什么不同期限债券的利率不同，以及它们之间的关系如何变化。
利率期限结构理论是金融市场和债券投资者常用的分析工具，有助于理解债券市场的运作和预测未来的利率走势。
在利率期限结构理论中，利率分为短期利率和长期利率。
短期利率指的是短期债券的利率或即期利率，而长期利率指的是长期债券的利率。
利率期限结构曲线是以利率期限为横轴、利率为纵轴，绘制不同期限债券利率的曲线图。
利率期限结构曲线有很多形状，常见的形状包括上升型、下降型和平坦型等。
1.期望理论：该理论认为利率期限结构取决于投资者对未来利率走势的预期。
如果投资者预期未来的利率将上升，他们就要求更高的利率来补偿风险，从而使长期利率高于短期利率。
反之，如果预期未来的利率将下降，投资者就会接受较低的利率，使长期利率低于短期利率。
期望理论解释了利率期限结构曲线上升型和下降型的形状。
2.流动性偏好理论：该理论认为投资者会对长期债券的投资具有风险厌恶，因为长期债券更容易受到利率变动的影响。
因此，投资者要求较高的利率来补偿他们对风险的担忧，使长期利率高于短期利率。
流动性偏好理论解释了利率期限结构曲线上升型的形状。
3.市场分割理论：该理论认为市场上的不同债券投资者有不同的投资偏好，从而导致不同期限债券之间的利率差异。
例如，机构投资者可能更喜欢长期债券，而个人投资者则更偏好短期债券。
因此，市场分割理论认为不同期限债券的利率取决于它们所面对的不同投资者的需求和供给关系。
市场分割理论解释了利率期限结构曲线平坦型的形状。
需要注意的是，利率期限结构理论并不是完美的，它只是提供了一种解释和描述不同期限债券利率之间关系的框架。
实际上，利率期限结构受到很多因素的影响，包括货币政策、通胀预期、经济周期和市场供需等。
因此，利率期限结构的变化和预测并不总是准确，需要综合考虑多种因素进行分析。
基于主成分分析我国利率期限结构及其影响因素
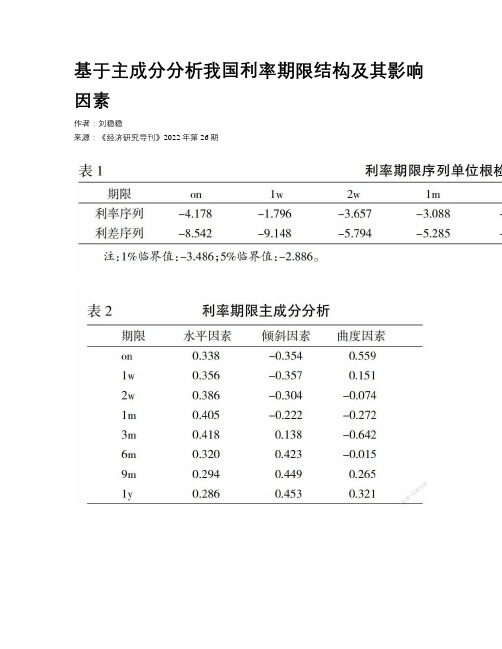
基于主成分分析我国利率期限结构及其影响因素作者：***来源：《经济研究导刊》2022年第26期摘要：上海银行间同业拆放利率（SHIBOR）作为我国基准利率，自运行以来不断发展完善。
以其为研究对象，通过主成分分析提取出3个可反映利率期限结构变动96%以上变动的特征要素，即“水平”、“倾斜”及“曲度”因素;另加入宏观经济变量，利用结构向量自回归（SVAR）模型，发现实体经济因素的冲击主要导致利率期限结构水平变动及倾斜变动，货币政策冲击对利率期限结构曲度变动有一定影响。
关键词：主成分分析;利率期限结构;结构向量自回归;影响因素中图分类号：F832.0 文献标志码：A 文章编号：1673-291X（2022）26-0074-04引言上海银行间同业拆放利率（SHIBOR）自2007年1月4日起正式运行，并不断发展和完善，努力培育成我国货币市场的基准利率，进一步推进了我国利率市场化的改革。
戴国强和李良松（2010）指出，利率作为一个重要的经济变量，不仅是金融产品定价和金融宏观调控的基础，而且其利率期限结构的变动及包含的宏观信息可为央行依据宏观经济走势制定相应利率政策提供直接支持[1]。
在宏观经济发展阶段中，价格水平、货币政策等多种宏观经济因素与利率有着重要的联系。
Litterman和Scheinkman（1991）以美国国债市场为研究对象，首次利用主成分分析法，考察了债券收益率与系统风险因素及非系统风险因素之间的关系，分析其在利率期限结构变化中的作用，且将其归结为水平因素、倾斜因素和曲度因素3种[2]。
刘金全等（2007）利用VAR模型研究宏观因素对不同期限的银行间短期拆借利率水平的影响，得出宏观经济冲击对短期利率水平存在显著的影响[3]。
张笑峰、郭菊娥（2012）对SHIBOR利率期限结构的变动影响因素及其作用机理进行了探讨，发现宏观经济中，物价水平是导致利率期限结构中水平移动的主要因素[4]。
本文利用主成分分析方法对SHIBOR利率期限结构变动因素分析，将SHIBOR利率期限结构的复杂变动用三种特征要素的变化来反映，并基于SVAR模型，分析各种宏观经济变量变化对SHIBOR利率期限结构变动特征要素的冲击效应。
利率期限结构
利率期限结构(term structure),是某个时点不同期限的利率所组成的一条曲线.因为在某个时点,零息票债券的到期收益率等于该时期的利率,所以利率期限结构也可以表示为某个时点零息票债券的收益率曲线(yield curve).它是资产定价、金融产品设计、保值和风险管理、套利以及投机等的基准.因此,对利率期限结构问题的研究一直是金融领域的一个基本课题.利率期限结构是一个非常广阔的研究领域,不同的学者都从不同的角度对该问题进行了探讨,从某一方面得出了一些结论和建议.根据不同的角度和方向,这些研究基本上可以分为5类:1)利率期限结构形成假设;2)利率期限结构静态估计;3)利率期限结构自身形态的微观分析;4)利率期限结构动态模型;5)利率期限结构动态模型的实证检验.1利率期限结构形成假设利率期限结构是由不同期限的利率所构成的一条曲线.由于不同期限的利率之间存在差异,所以利率期限结构可能有好几种形状:向上倾斜、向下倾斜、下凹、上凸等.为了解释这些不同形状的利率期限结构,人们就提出了几种不同的理论假设.这些假设包括:市场预期假设(expectation hy-pothesis),市场分割假设(market segmentation hy-pothesis)和流动性偏好假设(liquidity preference hy-pothesis).为了对这些假设进行验证,不同的学者从不同的角度进行了分析.不同的学者利用不同的方法,使用不同国家的数据对利率期限结构形成假设进行了检验.在3个假设中,市场预期假设是最重要的假设,所以大多数的研究都是立足于市场预期假设,并在此基础上考虑流动性溢酬.4)中国市场.庄东辰[19]和宋淮松[20]分别利用非线性回归和线性回归的方法对我国的零息票债券进行分析.唐齐鸣和高翔[21]用同业拆借市场的利率数据对预期理论进行了实证.实证结果表明:同业拆借利率基本上符合市场预期理论,即长短期利率的差可以作为未来利率变动的良好预测,但是短期利率也存在着一些过度反应的现象.此外,还有杨大楷、杨勇[22],姚长辉、梁跃军[23]对国债收益率的研究.但这些研究大部分都是停留在息票债券的到期收益率上,没有研究真正意义上的利率期限结构.2利率期限结构静态估计当市场上存在的债券种类有限时(特别对债券市场不发达国家而言),如何根据有效的债券价格资料对整个利率期限结构进行估计,是进行债券研究的一个重要内容.不同的学者提出了不同的估计方法,其核心就是对贴现函数δ(m)的估计.郑振龙和林海[31]利用McCulloch[25]样条函数和息票剥离法对我国市场利率期限结构进行了静态估计,构造出中国真正的市场利率期限结构.朱世武和陈健恒[32]则使用Nelson-Siege-Svensson[33]方法对我国交易所市场的利率期限结构进行了估计.郑振龙和林海[34]估计出中国债券市场的违约风险溢酬并进行了分析.林海和郑振龙[35]对中国市场利率的流动性溢酬进行了估计和分析.林海和郑振龙[36]对这些问题进行了统一和归纳,并分析了其在中国金融市场的具体运用.3利率期限结构自身形态微观分析利率期限结构的变动也有平行移动和非平行移动.由于利率直接和债券的收益率相关,这些不同方式的移动对债券组合的收益会产生很大的影响,并进而影响债券组合管理的技术.为了衡量利率期限结构的形状变动对债券投资组合的影响并在此基础上进行有效的管理,达到“免疫”的目的,众多的学者对利率期限结构本身的形态作了大量的分析,并对利率期限结构的平行移动和非平行移动条件下的债券组合套期保值的问题进行了深入研究. Zimmermann[40],D'Ecclesia&Zenios[41], Sherris[42],Martellini&Priaulet[43],Maitland[44], Schere&Avellaneda[45]分别对德国、瑞士、意大利、澳大利亚、法国、南非、拉美等国家和地区的利率期限结构进行了主成分和因子分析.朱峰[46]和林海[47]对中国的市场利率期限结构进行了主成分分析,并在此基础上对中国债券组合的套期保值提出了若干建议.4利率期限结构动态模型4.1基本利率期限结构动态模型根据利率期限结构模型的推导过程,可以分为两种类型:第一种类型就是一般均衡模型(Equilibriummodel),根据市场的均衡条件求出利率所必须遵循的一个过程,在这些模型中,相关的经济变量是输入变量,利率水平是输出变量;另一种类型是无套利模型(No arbitrage model),通过相关债券等资产之间必须满足的无套利条件进行分析,此时利率水平是一个输入变量,相关金融工具的价格是输出变量.必须特别指出的是,这些模型都是建立在风险中性世界中,所描述的均是风险中性世界中的利率变动行为.而实证检验都是利用现实世界的利率数据进行的.因此,在将现实世界中的估计结果运用于衍生产品定价时,必须先利用模型相对应的风险价格②通过Girsanov定理将现实世界转换为风险中性世界,然后再利用风险中性世界中的相应结果进行定价.1)一般均衡模型.主要包括Vasicek[66]模型和Cox,Ingersoll&Ross(CIR)[67,68]模型,此外还有Rendleman&Barter[69],Brennan&Schwartz[55]等.2)无套利模型.主要包括HJM[70]模型,Ho&Lee[71]以及Hull&White[72]模型.此外,还有Black,Derman&Toy[73]等.4.2一般化扩展模型1)仿射模型(Affine Model)2)二次高斯模型(Quadratic Gaussian model)3)非线性随机波动模型(Nonlinear StochasticV olatility Model)4)存在跳跃的利率期限结构模型(Diffusion-jump Model)5)机制转换模型(Regime ShiftModel)5利率期限结构动态模型的实证检验在对利率期限结构模型的理论研究基础之上,众多的学者都对不同的期限结构模型进行了实证检验,以对不同的模型进行判别和比较.实证分析可以分成几个类别:(1)对利率单位根问题的检验;(2)对不同期限结构模型的比较研究;(3)对某个特定期限结构模型的分析;(4)对模型可靠性的分析.5.1对利率单位根的检验Wang&Zhang[89]对利率的单位根问题进行了实证分析,以对利率市场的有效性进行验证5.2对不同期限结构模型的比较研究Durham[92]利用Durham&Gallant[93]的计量分析方法对不同的期限结构模型进行了实证检验. 陈典发[108]对Vasicek模型中参数和实际市场数据的一致性问题进行了研究,并探讨了它在公司融资决策中的应用.谢赤和吴雄伟[109]通过一个广义矩方法,使用中国货币市场的数据,对Vasicek模型和CIR模型进行了实证检验.6利率期限结构研究现状总结性分析根据上面对利率期限结构的文献回顾,可以从中发现利率期限结构研究目前的发展方向.(1)在利率期限结构形成假设方面,市场分割假设逐渐地被人们所遗忘,因为随着市场的发展,技术的进步,市场交易规模的扩大,市场已经逐渐形成一个统一的整体;而且市场预期假设如果没有同流动性溢酬相结合,都会被市场资料所拒绝.流动性溢酬呈现出不断变化的特征.因此,今后的研究方向应该是在市场预期假设的模型框架中引入流动性溢酬假设.(2)在利率期限结构静态估计方面,基本上采用样条函数和息票剥离法.为了保证估计的精确性,样条函数的选择越来越复杂.(3)在利率期限结构自身微观形态分析方面,如何通过对久期的进一步修正,从而使之能够地在利率期限结构非平行移动条件下更为有效地达到套期保值的效果,是该领域未来重要的研究方向.但是由于主成分分析受数据的影响很大,结果很不稳定,所以对主成分分析可靠性的检验,也是一个重要的研究内容.(4)根据对利率期限结构动态模型的实证分析,可以发现:1)不同的模型,不同的计量分析方法,不同的数据,所得出的实证结果都会产生差异.因此,对不同的市场,重要的是模型的适用性.2)实证分析也得出一些基本一致的结论:a.漂移率的假设不会对利率期限结构模型产生太大的影响;b.波动率是利率期限结构模型的重要因素;c.多因子模型要比单因子模型表现得好,但是多因子要牺牲自由度,因此,根据实证结果,两因子模型可能是一个比较好的模型.d.利率一般服从一个均值回归过程.3)基于概率密度预测(density forecast)的样本外检验是利率期限结构实证分析未来的发展方向.4)目前大部分对动态模型的检验都是直接利用实际数据在现实世界中进行的,对现实世界和风险中性世界的差异并未引起足够的重视.1.4 利率期限结构模型的最新进展近年来在HJM 模型类的推动下，利率期限结构理论研究的各种新模型层出不穷，如市场模型、随机弦模型、随机域模型、跳跃过程模型和随机折现因子模型等。
第8章_利率及利率期限结构《金融市场学》
复利就是假定每个计息期所得的利息可以自动地转成投资本金以在 下一个计息期赚取利息，每年复利的情况下，初始投资为P，n年后
这一投资增长为： S p (1 r)n
复利可以以任何频率进行，假设年利率为r，每年复利m次（复利期
长短相同），则每期复利的利率为r/m，有效利率r*与名义利率r之
平上升。
二、凯恩斯流动性偏好理论
凯恩斯认为，利率是使公众愿意以货币形式持有的财富量（货币 需求量）等于现有货币存量（货币供给）的价格，因此均衡利率r0是 由货币供给MS和货币需求Md共同决定的。货币供给是由银行体系决定 的外生变量（由基础货币和存款准备金率决定），与利率没有关系。 货币需求由消费性需求、预防性需求和投机需求组成，其中消费性 需求和预防性需求是外生的，投机性需求与利率相关。凯恩斯认为 利率是由货币供求决定的，在本质上是一种货币现象，与实质性因 素无关。
第三节 利率期限结构理论 一、即期利率与远期利率
（一）、即期利率 即期利率是指债券票面所标明的利率或购买债券时所获得的折价收
益与债券面值的比率。t年期即期利率的计算公式：
Pt
Ft (1 rt )t
其中，Pt为t年零息债券的市场价格， Ft为面值， rt为年期即期利率。 （二）、远期利率
远期利率则是指隐含在给定的即期利率之中从未来的某一时点到另 一时点的利率。如以ft-1，t代表第t-1年至第t年间的远期利率， rt代表t
二、利率的种类
按利率的地位来分 ：基准利率和一般利率 按借贷期内利率是否浮动来分 ：固定利率与浮动利率
按利率的真实水平来分：名义利率与实际利率 按利率的决定方式来分 ：官方利率、公定利率与市场利
率 按计算利率的期限单位来分 ：年利率、月利率与日利率
利率期限结构的模型分析报告
利率期限结构的模型分析摘要：利率期限结构是资产定价、金融产品设计、保值和风险管理、套利以及投机等的基准，所以利率期限结构模型以及利率行为的特点一直以来就是金融学研究的重点。
随着我国债券市场的发展、金融创新的不断深入以及利率市场化进程的逐步推进，利率期限结构问题研究的重要性日益凸显。
本文即分析利率期限结构的四个模型，并运用Matlab软件分别作出图形，在图形的基础上解释说明。
关键词：利率期限结构多项式指数 NS NSS一、前言利率期限结构是指某个时点不同期限的即期利率与到期期限的关系及变化规律，一般由债券市场的实际交易价格确定。
在成熟金融市场中，国债利率期限结构不但能够反映国债市场各期限国债的供求关系、市场利率的总体水平和变化方向，是市场重要的定价基准，而且是精细化设计国债及其衍生产品，科学制定财政和货币政策，完善国债发行和管理的重要依据。
2000年以后，随着国债发行机制的日趋规和完善，期限结构的不断丰富，国债市场的日臻成熟，利率市场化水平的显著提高，鉴于此，我们开展了国债利率期限结构模型的研究，本文在此讨论的有四种模型，分别是多项式样条模型、指数样条模型、NS模型和NNS模型，解释说明不同模型的拟合精度。
利率期限结构是利率水平与期限相联系的函数，收益率曲线的变化本质上体现了债券的到期收益率与期限之间的关系。
即债券的短期利率和长期利率表现的差异性。
而利率期限结构所研究的就是决定长期利率和短期利率关系的原因到底是什么。
随着对利率期限结构研究的发展，理论界也形成了不同的理论流派。
（一）预期理论：预期理论提出了以下命题：长期债券的利率等于在其有效期人们所预期的短期利率的平均值。
这一理论关键的假定是，债券投资者对于不同到期期限的债券没有特别的偏好，因此如果某债券的预期回报率低于到期期限不同的其他债券，投资者就不会持有这种债券。
具有这种特点的债券被称为完全替代品。
在实践中，这意味着如果不同期限的债券是完全替代品，这些债券的预期回报率必须相等。
利率期限结构主成分分析
利率期限结构主成分分析摘要：文章通过Nelson-Siegel模型描述我国国债收益率曲线的变动模式，依据β0、β1、β2、τ取得的最佳值建立方程式，进行不同期限的N-S估计利率分析，以及利率期限结构的主成分分析，得出我国国债收益率进行主要受到三个因素的影响，且收益率曲线的波动方式主要有三种形式：平行移动、斜率变动、曲率变动。
这三个主成分在一定程度上解释了利率非平行移动的原理，因此在此基础上构建的主成分久期相对于麦考利久期和修正久期而言，就可以更加准确的衡量债券的利率风险，达到更好的套期保值效果。
关键词：国债收益率；主成分分析；固定收益证券；利率期限结构；套期保值一个国家的国债收益率一向是重要的指标，从宏观经济上看，国债收益率高说明市场经济走势好，稳定增长，投资回报稳定，投向国债的资金少；利率低说明宏观经济开始波动，市场对经济前景不看好，大量资金涌向国债。
从货币政策上看，如果国家执行稳健的货币政策，国债利率稍高，如果因为刺激经济执行宽松的货币政策，降低利率，这样国债利率也会降低。
因此我们对我国国债收益率曲线的变动模式进行探究，找出其主要受到哪些因素的影响，以及其收益率曲线的主要波动方式。
同时，我们试图找出可以更加准确的衡量债券的利率风险的方法，以达到更好的套期保值效果。
1 理论基础Nelson-Siegel模型是一种通过参数模型来描述曲线动态变化的方法，大量应用于利率期限结构的估计中，由Nelson和Siegel在1987年提出。
瞬时远期利率可以用包含参数的如下模型来描述：由于R（t，x）是f（t，x）的一种积分，因此两者的图形属性一定是一致的，为了研究？茁0、？茁1、？茁2的性质，我们可以对τ取一个假定值，得到R （t，x）相对？茁0、？茁1、？茁2的偏导数。
式中，？茁0是R（t，x）在期限t趋于无穷大时的渐进值，其变动整体改变利率期限结构的水平高度，可以理解为“水平因子”；？茁1参数可以理解为“斜率因子”；？茁2参数可以理解为“曲率因子”；τ参数，在其他参数固定不变的情况下，决定了收益率曲线第一次驼峰出现的时间。
6.利率期限结构分析
利率期限结构
Shape of the yield curve
humped yield curve is the yield curve that yields increasing with maturity for a range of maturities and then the yield curve becoming inverted.
The more common practice is to use the spread between the 30-year and 2-year yield.
10
利率期限结构
Yield Curve Shifts
A shift in the yield curve refers to the relative change in the yield for each Treasury maturity.
Think about: ▪ What does a flattening of the yield curve mean? Under what circumstance a flattening of the yield curve will happen?
9
利率期限结构
the steepness or slope of the yield curve
The spread between these yields for long-term Treasury yields and short-term Treasury yields is referred to as the steepness or slope of the yield curve.
A parallel shift nonparallel shift
中期借贷便利工具对国债利率期限结构的影响——基于主成分分析和VEC模型的实证检验
n
7
金融论坛 2021年第7期(总第307期)
关未来短期利率和量化宽松(QE)操作的前瞻性指导，通过预期渠道调节债券预期风险溢价和收益率。潘敏 和刘姗(2018)认为.预期效应在中央银行借贷便利工具对市场利率的影响中起到了重要作用。从中国的情 况看,近年来预期引导和中央银行沟通已成为宏观调控的重要手段。伴随央行投放流动性方式由外汇占款 逐渐转变为公开市场操作和结构性货币政策工具，金融机构对结构性货币政策工具的关注日益密切。人民 银行在2017年一季度提出MLF操作将以一年期为主，在调节流动性的同时，向市场释放长期资金稳定的 信号，稳定市场预期。
四、研究设计
(变一量)选择和数据来源 1.国债利率指标 中国的债券市场体系可分为银行间债券市场和交易所债券市场。银行间债券市场的参与者是各类机构 投资者，属于大宗交易批发市场,交易所债券市场属于场内集中撮合交易零售市场。但自2005年以来，交易 所国债市场成交量不断萎缩.而银行间国债市场市场化程度高，托管规模、交易金额、交易量等各项指标都 远远超过交易所市场，银行间市场己成为中国国债发行和流通的主导市场，也是中央银行公开市场操作进 行间接货币政策调控的主要场所①。鉴于债券回购交易主要在银行同业拆借中心进行,本文选取银行间债券 市场数据分析国债的期限结构。 在国债即期收益率和到期收益率的选择上，银行间国债即期收益率数据包括市场双边报价、柜台交易 等各方面国债交易信息，数据覆盖面较广,并且在数据制作过程中对异常点进行了科学处理,能够很好地反 映市场价格。国内学者的研究也提供了较多参考:李宏瑾等(2010)认为要分析国债收益率曲线对通胀的预 测作用，应该采用即期收益率曲线以反映当期市场交易者对未来经济的预期，而非假定在未来投资收益不 变的名义到期收益率。王晓芳、郑斌(2015)也选用中央登记结算公司银行间国债即期收益率数据。 关于国债期限的选取，袁靖和薛伟(2012)选取了银行间国债市场6个月、1年、3年、5年、7年、10年、 20年和30年为关键年限的收益率月度数据。本文参考现有文献，选择中央登记结算公司银行间国债即期收
上交所利率期限结构的变动因素分析
上交所利率期限结构的变动因素分析内容摘要：本文通过对我国上交所国债市场利率期限结构变化的分析，得到了影响我国国债市场利率曲线变化的三个最主要的因子，即水平度、倾斜度和曲度，并讨论了几个因子变化的意义，给债券利率风险管理提供了重要的参考价值。
关键词：利率期限结构主成分分析因子变化市场利率是决定债券价格变化的最主要的因素。
正是由于利率的变化，导致固定收益市场金融产品价格的波动，因而必须对债券组合进行利率风险管理以避免利率的大幅波动对组合价值的影响。
而对利率期限结构形状的变化的分析就成为利率风险管理的关键所在。
传统的利率风险管理侧重于久期和久期管理，也就是说，仅仅考虑利率期限结构平行移动的风险。
但事实上利率期限结构在发生平行移动的同时，倾斜度和曲度也在发生改变，表现出另外一个很重要的风险源。
国外的研究文献已经说明有三个潜在的不确定因素影响期限结构的跨期变化，本文的目的就是以上交所市场债券价格隐含的利率期限结构数据作为分析对象，运用主成分分析从主导我国债券市场利率期限结构的实际运动的历史收益率曲线中找出影响我国债券市场利率期限结构变化的几个因子来，找出我国利率期限结构变化的主要形式，以期对我国债券市场利率风险管理提供有益的参考价值。
上交所国债市场利率期限结构变化分析在对利率期限结构的变化的研究中，可以选取一些有代表性的参考期限做为主成分分析的对象，也就是分析这些参考期限的利率的变化情况，可以构造出每个参考期限利率的日变化(或周变化等)的序列，然后计算这些变化序列的协方差矩阵，下一步就是计算该协方差矩阵的特征值以及对应的特征向量。
这些特征向量可以看作是独立的利率期限结构的基本变化形式。
也就是说,任何时点的利率期限结构变化都可以看作是这些不同的、独立的、基本的利率期限结构变化形式的组合，我们可以从特征向量所对应的特征值大小判断哪一种变动形式起主导作用。
由于交易所交易的国债的品种较少，因而无法从市场上观测到某个时间点的利率期限结构，利率期限结构必须采用适当的方法通过市场上债券的交易数据估计出来。
利率期限结构的主成分分析
p值 0.0000 0.0001 0.0011 0.0108 0.0628 0.2176 0.4974 0.8450 0.8237 0.5586 0.2409 0.1048 0.0486 0.0244 0.0133 0.0016 0.0005 0.0002 0.0001
残差平方 和 3.8567 3.1736 2.9430 2.8868 2.8867 2.8980 2.9072 2.9114 2.9112 2.9080 2.8965 2.8828 2.8695 2.8576 2.8473 2.8143 2.7987 2.7904 2.7855
β2 估计值 -6.1596 -3.1371 -2.2315 -1.6419 -1.1754 -0.7834 -0.4409 -0.1315 0.1564 0.4312 0.9633 1.4950 2.0432 2.6177 3.2244 6.8364 11.5086 17.2852 24.1794
由于rtx是ftx的一种积分因此两者的图形属性一定是一致的为了研究的性质所以暂时假定5得到rtx相对是rtx在期限t趋于无穷大时的渐进值且必为正数当期限t无穷大时长期利率无限接近渐近线也即收益率无限接近于的敏感度恒为1短期利率的变动对所有的收益率引起的变化是一样且恒定的对于任意的t的变动整体改变利率期限结构的水平高度可以理解为水平因子
4、运行参数估计程序“NS固定参数取值”， 得到τ去不同值时的OLS估计结果： file/open/program…/run 5、比较τ不同取值时的模型估计效果，然后 选取合适的取值（此例τ=8）得到N-S模型的 估计结果
由Nelson-Siegel模型参数的意义可以看出,β0代表 长期水平，应该是一个正值; β1代表短期利率和 长期的利差，在上升形的利率期限结构中，该利 差应该为负值，因此β1应该为负值; β2代表了中 期利率，在t为正且有限的时候， 应该为正值。 综合考虑上述因素，而且同时满足残差平方和尽 可能小，模型拟合的R2尽可能大，各参数在5%的 显著水平下尽可能显著，从之前的讨论已经知道 τ的取值会影响 β1和β2 的衰减速度，τ的值越大， 衰减越慢，越适合拟合期限较长的数据，由于本 次样本中到期期限在15年之内的数据占绝大部分， 因此选取τ=8作为适合的取值。
十二章利率期限结构汇总
(1 s j ) (1 si ) (1 f i, j )
j i
• （2）每年m期复利：
• •
j i
(1 s j ) f 即 i , j (1 s ) i i
j
j 1 /( j i )
1
j i
(1 s j / m) (1 si / m) (1 f i, j / m)
–
P(0, T )
P(0, T ) e
TY (T )
（12-1）
债券收益率曲线
• 收益率曲线一般具备以下特点：（1）短期收益率一般比 长期收益率更富有变化性；（2）收益率曲线一般向上倾 斜；（3）当利息率整体水平较高时，收益率曲线会呈现 向下倾斜（甚至是倒转的）形状。
到期收益率曲线
5.00% 4.80% 4.60% 4.40% 4.20% 4.00% 3.80% 3.60% 3.40% 3.20% 3.00% 2.80% 2006-09-30.YTC
收益率曲线
– 描述债券到期收益率和到期期限之间关系的曲线叫做收益率曲线。 – 我们可以将收益率 表示为年到期的债券现在应支付的年利率， 也就是说在时间区间 Y (T ) 上的平均年利率。对到期前不支付利息
[0, T ] 的债券而言，收益率是由债券目前的价格和面值（到期价格）的
比求出。如果 表示该比值，则：
P0 e
rT
t时刻
P(t ) e
r (T t )
– 假定短期利率是可变但可确定的。 r (t ) 表示t时刻当期 的利率，称为短期利率（short rate）,则：
–
P(t ) exp[ r (s)ds]
t
T
远期利率与零息券
我国利率期限结构的静态分析和动态特征
我国利率期限结构的静态分析和动态特征摘要:利率期限结构反映的是利率和到期期限之间的关系。
文章利用指数样条法估计出我国上交所国债的利率期限结构，对其进行静态的分析，得到上交所国债利率期限结构统计特征。
同时，应用主成分分析方法研究国债利率期限结构的动态特征，发现水平因素、斜度因素和凸度因素对我国国债即期利率曲线变动的解释能力分别达到51．28％、26．63％和10．86％，累计贡献率达到88．77％，不同因素对各个到期期限即期利率的影响程度也有所不同。
关键词:利率期限结构指数样条法主成分分析一、引言利率期限结构是某个时点不同期限的利率所组成的一条曲线，它是资产定价、金融产品设计、保值和风险管理、套利以及投机等金融活动的基础。
对利率期限结构的估计是资产定价领域一个基础性的研究问题。
随着我国债券市场的发展、金融创新的不断深入以及利率市场化进程的逐步推进，利率期限结构问题研究的重要性日益凸现出来。
在一个存在零息票债券的市场上，我们通过直接求出这些零息票债券的到期收益率就可以估计出某个时点的利率期限结构并进行分析。
但是如果不存在零息票债券或者数量十分有限，那么这种方法就受到很大的限制，中国债券市场就是如此。
在中国债券市场上，大部分债券都是息票债券，零息票债券的数量很少。
上海证券交易所和银行同业间债券交易市场上交易的国债都是息票债券。
因此，我们就不能通过求到期收益率的方法来估计利率期限结构，而只能采取其他的估计方法。
在本文我们使用Vasicek(1982)提出的指数样条估计方法，利用我国上交所2002～2005年国债现货市场的交易数据，估计出我国国债利率期限结构的一个时间序列数据。
有了即期利率这一基准利率曲线，我们就可以用其给国债、公司债以及其他利率金融产品进行定价，为投资者提供投资参考和依据。
但是，我们知道，由于各种宏观经济因素及国债市场本身众多的因素处于不断的变动之中，即期利率曲线也在不断的发生着变化。
利率的变化会导致利率金融产品尤其是固定收益证券价格的变化。
利率期限结构理论分析
利率期限结构理论三、利率期限结构理论（4+4+6=14分）1、简述利率期限结构的含义和流动性偏好理论的主要内容。
答：（1）利率期限结构的含义利率期限结构（Term Structure of Interest Rates）是指在某一时点上，不同期限资金的收益率（Yield）与到期期限（Maturity）之间的关系。
利率的期限结构反映了不同期限的资金供求关系，揭示了市场利率的总体水平和变化方向，为投资者从事债券投资和政府有关部门加强债券管理提供可参考的依据。
（2）流动性偏好理论的内容流动性偏好理论是解释债券(金融资产) 利率期限结构的一种理论。
该理论认为，债券的到期期限越长，价格变化越大，流动性越差，其风险也越大；为补偿这种流动性风险，投资者对长期债券所要求的收益率比短期债券要求收益率要高。
流动性偏好理论和预期理论结合起来，能更好地解释利率期限结构的实际情况。
2、简述债券收益率曲线的含义和债券收益率曲线的四种形态。
答：（1）债券收益率曲线的含义债券收益率曲线又叫“孳息曲线”，是描述在某一时点上一组可交易债券的收益率与其剩余到期期限之间数量关系的一条曲线，即在直角坐标系中，以债券剩余到期期限为横坐标、债券收益率为纵坐标而绘制的曲线。
一条合理的债券收益率曲线将反映出某一时点上(或某一天)不同期限债券的到期收益率水平。
（2）债券收益率曲线通常表现为四种形态图3-1 债券收益率曲线四周形态a.正向收益率曲线。
它表明在某一时点，债券的投资期限越长，收益率越高，也就是说，此时社会经济正处于增长期阶段，这是收益率曲线最为常见的形态。
b.水平收益率曲线。
它表明收益率的高低与投资期限的长短无关，也就意味着社会经济出现极不正常情况。
c.反向收益率曲线。
它表明在某一时点上，债券的投资期限越长，收益率越低，也就意味着社会经济进入衰退期。
d.波动收益率曲线。
这表明债券收益率随投资期限不同，呈现出波浪变动，也就意味着社会经济未来有可能出现波动。
利率期限结构实证分析
利率期限结构实证分析作者：梁慧来源：《商场现代化》2010年第22期[摘要]本文首先介绍了利率期限结构的相关理论;再利用上获得的六月四日美国国债数据计算出国债利率期限结构,并将该期限结构与国内的利率期限结构作对比。
[关键词]利率期限结构分析一、选题背景和意义1. 名词解释利率期限结构:是指某个时点不同期限的即期利率与到期期限的关系及变化规律。
由于零息债券的到期收益率等于相同期限的市场即期利率,从对应关系上来说,任何时刻的利率期限结构是利率水平和期限相联系的函数。
因此,利率的期限结构,即零息债券的到期收益率与期限的关系可以用一条曲线来表示,如水平线、向上倾斜和向下倾斜的曲线。
甚至还可能出现更复杂的收益率曲线,即债券收益率曲线是上述部分或全部收益率曲线的组合。
收益率曲线的变化本质上体现了债券的到期收益率与期限之间的关系,即债券的短期利率和长期利率表现的差异性。
2. 文献综述利率期限结构的主流理论主要有三:一是流动性偏好(liquidity preference)理论,第二是市场分割理论(market segmentation),第三是期望理论(Expectation Hypothesis)。
他们是在不同的假设上,对不同形状的收益率曲线给予了合理的解释,即回答了为什么各种不同的国债即期利率会有差别,而且这种差别会随期限的长短而变化。
二、利率期限结构的估计要研究利率期限结构以及相关的模型理论,对利率期限结构的估计是第一部的工作。
对那些零息票债券而言,它的到期收益率就是这个时期的利率水平,因此可以直接从零息债券的价格以及期限中求出利率的期限结构。
但是对于息票债券而言,它就没有办法直接求出,只能通过其它方法进行估计。
如果息票债券的付息日相同或者相近,我们就可以使用息票剥离法(bootstrap method)求出利率的期限结构。
1. 数据收集从上获取债券数据。
时间:2010年6月7日。
2. 模型建立息票剥离法将息票从债券中进行剥离并在此基础上估计无息票债券利率水平,具体计算方法如下:设Tn为某债券的到期期限,In 表示现金流;F表示债券的面值;P表示债券全价;Sn即期利率,根据债券定价公式从而得到:3. 模型求解由的数据求解得:3个月,6个月,12个月的年收益率分别为:0.12%;0.21%;0.32%。
固定收益证券—第三章—利率期限结构
利率期限结构变动的主成份分析
• 主成份分析的一般步骤
采集不同期限即期利率变动ΔR(t,ti)的历史数据并 __________ 将其标准化 R t , ti R t , ti * R t , ti
Rt ,t
i
计算不同期限ΔR*(t,ti)之间的方差－协方差阵Ω
2
• 类似的，可以认为1.25年期利率等于10.61%， 1.75年利率为10.745% • 第二，由于2.25年利率可以用2.75年利率表示为 2 1 R 0, 2.25 R 0, 2 R 0, 2.75
3 3
• 将其代入债券6的定价方程， R(0, 2)已知，可 解出方程中惟一的未知数R(0, 2.75)为10.87%， 并得R(0, 2.25) 35
• 纯预期理论的三个版本
• 由于长期的即期利率是短期的即期利率和远期利 率的加权平均，当市场预期利率上升（下降或不 变）时，远期利率就会上升（下降或不变），利 率期限结构就会呈现相应的形状
19
纯预期理论
• 纯预期理论的三个版本
版本2：短期零息票债券滚动投资n年的预期 收益率应该等于n年期零息票债券一次性投资 的收益率 1 R t ,t 1 R t ,t n n
26
无风险即期利率期限结构的拟合
• 方法分类
直接法与间接法
评价利率期限结构拟合方法的标准
• 准确性
• 平滑性
• 稳定性 • 灵活性
27
直接法
• 求解债券定价方程：引例
假设有4只付息日相同的债券（一年支付一次 利息）：
息票 债券1 债券2 债券3 3 3.5 3 剩余期限（年） 1 2 3 市场价格 99 99.5 96
金融市场工具-利率期限结构分析报告
⾦融市场⼯具-利率期限结构分析报告利率期限结构分析报告⼀、原理分析（⼀）收益率曲线与率期限结构理论在⾏情表上可以获得各期国债的收益率，若将国债的到期期限绘于横轴，并将其收益率绘于纵轴。
即可观察国债到期期限与收益率的关系，这就是所谓的收益率曲线(Yield-Curve)。
图1 收益率曲线的基本型态收益率曲线可以看出⽬前长短期国债的利差关系。
例如(a)图的收益率曲线是⽔平的，代表短期国债与长期国债的收益率相等；(b)图的收益率曲线是正斜率，代表长期国债的收益率⾼于短期国债，这也是最常见的收益率曲线；(c)图与(b)图恰好相反，短期国债收益率⾼于长期国债；(d)图则是中期国债收益率最⾼，短期与长期国债较低。
然⽽，收益率曲线并不能提供债券投资⼈正确的利率信息，理由在于部分国债含有票息，因存在再投资风险，到期收益率（YTM）未必能充分实现，加以各国债票⾯利率各不相同，导致“相同到期期限”的债券利率敏感性不尽相同，因此其收益率⽆法充分代表市场对此到期期限的真实利率。
⾄此，便有所谓的“利率期限结构”（Term Structure of Interest Rate）——以⽆风险的零息国债收益率所建构的“收益率—到期期限”关系。
原理在于：任何⼀种债券的价值都等于⼀系列现⾦流量的现值之和，这说明任何⼀种债券都可以⽤⼀揽⼦的⽆息票债券组合去替换。
例如，1 张每年付息⼀次的 5 年期附息票债券就等于 6 张与此附息债券息票及⾯值⽀付具有相同期限的⽆息票债券的现值。
换句话说，证券的价值等于具有相同期限结构的⼀揽⼦⽆息票债券的价值。
要进⼀步确定每种⽆息票债券的价值，就必须找到与其期限相同的⽆息票国债的即期利率（Spot Rate），作为确定贴现率的基础。
利率期限结构是由⽆风险的“零息国债”所推导出的收益率曲线。
因零息国债⽆再投资风险，其收益率⼜称为即期利率（Spot Rate），即未来的实际报酬率，所以其收益率曲线可作为其他债券的评价基础。
我国国债利率期限结构研究
我国国债利率期限结构研究作者：马海龙来源：《时代金融》2012年第27期【摘要】文章主要研究了银行间国债的期限结构。
首先，通过主成分分析发现，前三个主成分解释的利率期限结构变异高达97.3%，可分别表示为水平、斜率、曲率因子。
其次，通过构建的结构模型，我们得到这三个参数的走势，为进行后续的研究提供了数据及理论支持。
【关键词】利率期限结构主成分分析国债一、研究背景国债收益率曲线反映了国债收益率与到期期限间的关系。
国债收益率曲线对金融市场及整个市场经济的作用非常大，它是无风险证券的买卖，体现了真实市场利率。
随着市场化的进行，我国将大力发展和完善国债市场，丰富产品结构，充分发挥其基准利率的指示作用，因此对利率期限结构的研究迫在眉睫。
二、文献综述大量的研究表明国债利率期限结构可以由三因素来解释，且这三个参数中蕴藏着丰富的政策信息，可以对未来宏观经济形势进行预测。
Litterman and Scheinkman（1991）运用主成分分析法将美国收益率曲线的主要变动因素进行提取，发现前三个主成分可以解释利率曲线的绝大部分的变动，他将这三个因素分别称为水平因素、斜度因素和曲率因素；于鑫（2009）运用脉冲响应函数发现，与成熟市场相似，我国90%以上的利率曲线变化可以由水平、斜率和曲率三个因素进行解释，价格水平对水平因素的影响最大，而货币政策是斜率与曲率因素变化的最重要原因。
三、数据选取本文选取了中债网2006年5月-2012年2月的3月期、9月期、1年期、2年期、3年期、5年期、7年期、10年期、15年期的银行间国债即期利率。
利率的月度加权平均数据虽然比日度数据缺失了很多信息，但是可以消除异常市场环境的影响。
数据来源为wind数据库。
各期限国债即期收益率的描述性统计量如下表所示，可以看出，3月期、9月期等短期限的债券利率标准差比较大，波动幅度较大，10年期与15年等长期限的变动较小。
这与预期理论相符：长期利率是短期利率的平均，数据相对比较平滑。
中美两国利率期限结构的主成分分析
成分矩阵ａ
中国
２
３
１
．６５４ ．２１３ ．８１７
．６０１ ．１１９ ．８８４
．５０６ ．０１０ ．９３０
．４０９ －．０５８ ．９５９
．３０５ －．０９８ ．９８３
．２３９ －．１００ ．９９２
．１５０ －．１０３ ．９９８
．０７４ －．０９７ ．９９９
．０００ －．０８４ ．９９９
－．０７２ －．０７５ ．９９７
３ ．１７３ ．８６６ ９９．６８７ ．０２３ ．１５５ ９９．９４２
中国国债数据前三个主成分累积解释了总方差变动 的 ９９１０６％，美国国债数据前三个主成分累积解释了总 方差变动的 ９９９４２％。另外，对中国数据的主成分分析 从每个原始变量中至少提取了 ９７８％的信息，对美国数 据的主成分分析从每个原始变量中至少提取了 ９９８％的 信息 ３。综合来看，用本文选取的样本数据进行主成分 分析的效果很好。
［关键词］ 利率期限结构；主成分分析；斜度因素 ［中图分类号］ Ｆ８３２５ ［文献标识码］ Ａ ［文章编号］２０９５－３２８３（２０１４）０１－００４７－０３
一、引言 利率是金融领域的核心变量，它实质上是资产价格，
反映了资金的供求。利率期限结构是指在相同的风险水 平下，利率与到期期限之间的关系，同时也是零息债券的 利率曲线。利率期限结构的变化反映了市场对未来利率 变化的预期。通过对利率期限结构的研究，可以在一定 程度上预测经济周期，从而为投融资活动提供指导。目 前，很多金融机构持有包括大量债券头寸的投资组合，一 旦利率向着价值减少的方向发展，将会使这些机构蒙受 重大损失。因此，预测利率期限结构的变化是风险控制 中不可或缺的内容。
对于利率期限结构的研究，一直是国内外学者关注 的热点。目前国际上研究利率期限结构问题的常用方法 是主成分分析法。主成分分析法由 Ｋ·Ｐｅａｒｓｏｎ于 １９０１ 年创立，而 将 该 法 首 先 用 于 研 究 利 率 期 限 结 构 的 则 是 ＬｉｔｔｅｒｍａｎａｎｄＳｃｈｅｉｎｋｍａｎ（１９９１）。他 们 运 用 主 成 分 分 析 法将美国收益率曲线的主要变动因素进行提取，发现前 三个主成分可以解释利率曲线的绝大部分变动，分别为 水平因素、斜度因素和曲率因素。此后，一些学者运用类 似的方法 对 各 自 国 家 的 利 率 期 限 结 构 进 行 了 研 究，如 Ｅｃｃｌｅｃｉａａｎｄ Ｚｅｎｉｏｓ（１９９４）和 Ｂｕｈｌｅｒａｎｄ Ｚｉｍｍｅｒｍａｎｎ （１９９６）分别研究了意大利和德国的收益率曲线，得出了 三因素能够分别解释利率变动总方差 ９９４％和 ９４％的 结论。我国学者朱世武（２００３）对我国上交所国债的交易 数据进行主成分分析，认为三因素解释了利率变动总方 差的 ９４％以上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 主成分分析结果
初始特征值 成份 1 2 3 合计 26.657 2.722 1.098 方差的 % 85.991 8.782 3.541 累积 % 85.991 94.772 98.314
Байду номын сангаас
-4
-2
0
2
4
-4
-2
0
2
4
• 对于多维变量的情况和二维类似，也有高 维的椭球，只不过无法直观地看见罢了。 • 首先把高维椭球的主轴找出来，再用代表 大多数数据信息的最长的几个轴作为新变 量；这样，主成分分析就基本完成了。 • 注意，和二维情况类似，高维椭球的主轴 也是互相垂直的。这些互相正交的新变量 是原先变量的线性组合，叫做主成分 (principal component)。
图2 τ=1.5时，利率对参数的敏感度
因此对期限结构进行估计时，需要选取合 适的τ的取值，这里采用试值法。 数据选取2008年6月至2013年6月每个月的 最后一天的的上交所国债数据作为样本，数 据全部来源于wind，具体数据见附表1。 分别取τ=0.5,1,1.5,…,5,6,7,8,9,10,15,20,25,30 对公式(2)进行最小二乘估计，分析软件为 Eviews,得到估计结果的统计表如下表所示：
β1 参数，当t不断增加时，从上图可以看出的 β1 系数衰减为0，说明 β1 的影响力在t递增的 过程中逐渐减弱，因此可以将 β1 看作是短期 因素，它在短期中发挥重要作用，长期而言 作用微乎其微。同时，由于 β1 >0时，收益率 曲线斜率为负， β1 <0时，收益率曲线为正， 且 的绝对值越大，收益率曲线越陡峭，因此 也可以将 β1 理解为“斜率因子”。
• 主成分分析通常的做法是，寻求原指标的 线性组合 。即：
主成分 满足如下条件： 1.每个主成分的系数平方和为1。即
2.主成分之间相互独立，即无重叠的信息。即 3.主成分的方差依次递减，重要性依次递减， 即 为了分析原始变量和主成分之间的关系，我 们可以利用原始变量与主成分之间的相关系 数:
写成矩阵形式：
β2 估计值 -6.1596 -3.1371 -2.2315 -1.6419 -1.1754 -0.7834 -0.4409 -0.1315 0.1564 0.4312 0.9633 1.4950 2.0432 2.6177 3.2244 6.8364 11.5086 17.2852 24.1794
• 几种不同类型的利率期限结构
在使用久期和凸度来衡量债券的利率风险 时，能有效发挥作用的一个重要前提是利率 期限结构的平行移动。 但是研究发现，国债收益率曲线的移动方 式并不是只有平行移动一种，同时也存在着 收益率曲线的斜率和曲率变化。收益率曲线 的非平行移动的存在，削弱了债券组合投资 中久期和凸性利率风险管理策略的有效性。 因此，久期和凸性在利率市场化逐步推进， 市场上利率风险逐渐扩大的今天，已经显得 较为落后。
在τ=8时，Nelson-Siegel模型的估计方程为:
对2008年6月-2013年6月的月度样本数据根据 上述方法拟合，得到每个月的N-S拟合模型， 然后每个模型取t=0.5，1，2，3，…, 30得到 对应期限利率估计值，为之后的主成分分析 提供数据，具体结果见附表2
利率期限结构的主成分分析 1、将N-S模型估计的利率期限结构数据导入 SPSS软件中： file/open/data,然后选择文件类型(execl)，以及 数据所在的sheet，完成数据导入 2、进行主成分分析： Analyze/dimension reduction/factor,然后选取 需要进行主成分分析的变量 3、对主成分分析的结果进行分析，得到影响 利率期限结构变动的三个主成分
利率期限结构的主成分分析
胡志强 马文博
利率期限结构的相关概念
主成分分析法
利率期限结构的主成分分析
利率期限结构的相关概念
• 利率期限结构的定义
利率期限结构是指某个时点不同期限的即期利率 与到期期限的关系及变化规律。 由于零息债券的到期收益率等于相同期限的市场 即期利率，因此利率期限结构一般用反映零息债券 的到期收益率与期限之间的一条曲线来表示，如水 平线、向上倾斜和向下倾斜的曲线。
R2 0.6843 0.7402 0.7591 0.7637 0.7637 0.7627 0.7620 0.7617 0.7617 0.7619 0.7629 0.7640 0.7651 0.7661 0.7669 0.7696 0.7709 0.7716 0.7720
具体操作： 1、新建一个workfile,选择文件类型为 unstructured/undated,输入样本数据个数（本 例为42） 2、导入收益率y和时间t的数据: data y data t 3、构建序列l1和n1: series l1=(1-exp(-t/0.5))/(t/0.5) series n1=(1-exp(-t/0.5))/(t/0.5)-exp(-t/0.5)
则 其中 为 对应的特征根，所以原始变量和主 成分之间的相关系数可以写为： 因此可以通过比较Y的特征根来决定主成分的 顺序，从而达到降维的目的
利率期限结构的主成分分析
利率期限结构的估计
Nelson-Siegel模型是一种通过参数模型来描述曲线动态变化 的方法，大量应用于利率期限结构的估计中，由Nelson和 Siegel在1987年提出。瞬时远期利率可以用包含参数的如下 模型来描述： （1） 其中，x是参数向量，τ是固定时间常数，之后讨论τ的取值方 法。Nelson和Siegel运用拉盖尔函数构造出了到期收益率的表 达式如下：
设A是n阶矩阵，若有n维非零列向量x使得以下关 系成立：
则称λ是A的一个特征值，而x是A的属于特征值λ 的一个特征向量
若A有n个线性无关的特征向量 我们还可以将其对角化：令 则 ，其中 由特征值组成的对角矩阵
， ， 是
主成分分析法简介
主成分分析是将多指标化为少数几个综合指标的 一种统计分析方法。 在实际问题中，由于变量太多，彼此之间往往还 存在着一定的相关性，因而使得所观测到的数据在 一定程度上反映的信息有所重叠。而且当变量较多 时，在高维空间中研究样本数据的分布规律比较复 杂，势必会增加问题分析的难度。人们自然希望能 够用较少的综合变量来代替原来复杂的多变量，而 这几个综合变量又能够尽可能多的反映原始变量的 信息，并且彼此之间互不相关，利用这种降维的思 想，产生了主成分分析的统计方法。
先假定只有二维，即只有两个变量，它们 由横坐标和纵坐标所代表；因此每个观测值 都有相应于这两个坐标轴的两个坐标值；如 果这些数据形成一个椭圆形状的点阵（这在 变量的二维正态的假定下是可能的）,那么这 个椭圆有一个长轴和一个短轴。在短轴方向 上，数据变化很少；在极端的情况，短轴如 果退化成一点，那只有在长轴的方向才能够 解释这些点的变化了；这样，由二维到一维 的降维就自然完成了。
4、运行参数估计程序“NS固定参数取值”， 得到τ去不同值时的OLS估计结果： file/open/program…/run 5、比较τ不同取值时的模型估计效果，然后 选取合适的取值（此例τ=8）得到N-S模型的 估计结果
由Nelson-Siegel模型参数的意义可以看出,β0代表 长期水平，应该是一个正值; β1代表短期利率和 长期的利差，在上升形的利率期限结构中，该利 差应该为负值，因此β1应该为负值; β2代表了中 期利率，在t为正且有限的时候， 应该为正值。 综合考虑上述因素，而且同时满足残差平方和尽 可能小，模型拟合的R2尽可能大，各参数在5%的 显著水平下尽可能显著，从之前的讨论已经知道 τ的取值会影响 β1和β2 的衰减速度，τ的值越大， 衰减越慢，越适合拟合期限较长的数据，由于本 次样本中到期期限在15年之内的数据占绝大部分， 因此选取τ=8作为适合的取值。
β2 参数，从上图中可以看出， β2 的系数随着t 的递增先增加后减小，因为 β2 的系数可以从0 开始，所以不是长期因素，同时它又不是单 调递减迅速衰减到0的，因此也不是短期因素， 可以将 β2 理解为中期因素。同时 β2 对不同期 限的收益率影响程度是不一样的，因此可以 理解为“曲率因子”。
τ参数，在其他参数固定不变的情况下，τ决定了收益率曲线第一次 驼峰出现的时间，而且也影响了 和 的衰减速度，对比图1和2就可 以直观的看出τ的不同取值对图形的影响
τ 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 15 20 25 30
β0 估计值 3.9800 4.1521 4.2804 4.3647 4.4167 4.4464 4.4597 4.4598 4.4481 4.4254 4.3481 4.2281 4.0652 3.8589 3.6087 1.6915 -1.3464 -5.5102 -10.8018
β1 p值 估计值 0.0000 0.2977 0.0000 -1.2274 0.0000 -1.6191 0.0000 -1.8331 0.0000 -1.9610 0.0000 -2.0357 0.0000 -2.0753 0.0000 -2.0902 0.0000 -2.0862 0.0000 -2.0669 0.0000 -1.9890 0.0000 -1.8640 0.0000 -1.6944 0.0000 -1.4812 0.0000 -1.2243 0.1651 0.7194 0.5060 3.7742 0.0776 7.9493 0.0162 13.2489 p值 0.6749 0.0012 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0023 0.0293 0.5249 0.0578 0.0107 0.0032
20世纪90年代之后，主成分分析技术被运 用到从时间序列角度捕捉影响收益率曲线变 化的风险因素，成为了债券投资组合的重要 的风险管理工具。 本次实验课的主要目的就是运用主成分分 析的方法来研究我国国债收益率曲线的变动 模式及其在国债投资组合中利率风险管理中 的应用。