具有时滞和脉冲的中立型Cohen-Grossberg神经网络的正p-不变集与全局p-吸引集
【国家自然科学基金】_bam神经网络_基金支持热词逐年推荐_【万方软件创新助手】_20140801
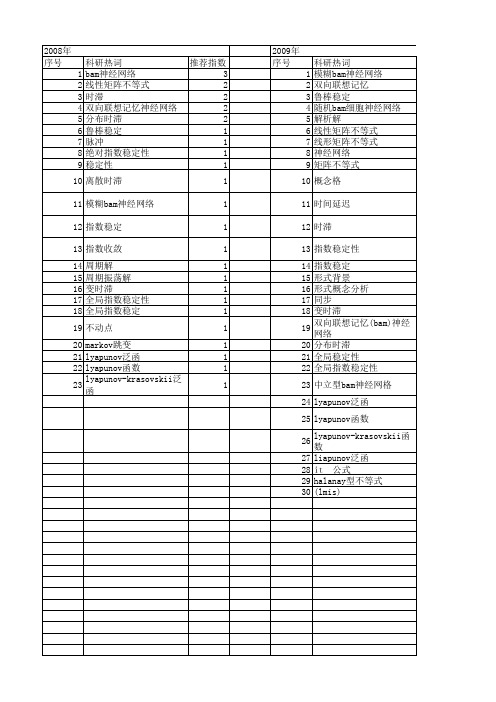
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 bam神经网络 神经网络 时滞 故障诊断 故障树分析 指数稳定性 拓扑度 微分不等式 平衡点 全局指数稳定性 lyapunov泛函
2009年 序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 halanay型不等式 30 (lmis)
科研热词 模糊bam神经网络 双向联想记忆 鲁棒稳定 随机bam细胞神经网络 解析解 线性矩阵不等式 线形矩阵不等式 神经网络 矩阵不等式 概念 时间延迟 时滞 指数稳定性 指数稳定 形式背景 形式概念分析 同步 变时滞 双向联想记忆(bam)神经网络 分布时滞 全局稳定性 全局指数稳定性 中立型bam神经网格 lyapunov泛函 lyapunov函数 lyapunov-krasovskii函数 liapunov泛函
推荐指数 2 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2011年 科研热词 推荐指数 时滞 3 双向联想记忆神经网络 3 脉冲 1 稳定性 1 概周期解 1 振动性 1 平衡点 1 存在性 1 周期解 1 双向联想记忆神经网络:m-矩阵 1 分布时滞 1 全局渐近稳定性 1 全局指数稳定性 1 不稳定性 1 n个神经元bam神经网络 1 mawhin连续定理 1
2014年 序号 1 2 3 4
2014年 科研热词 随机 指数同步 s-分布时滞 bam神经网络 推荐指数 1 1 1 1
光皮木瓜真空脉动干燥特性及神经网络模型

水 分 迁 移 孔 道 坍 塌 堵 塞 当 干 燥 温 度 为 &" a 时 物 料 表 -82;9,F-8P1K689E;,.89:?3;7+3>9238F-F:9>3R-8BE:.,<9;Q->*
面呈 蜂 窝 状 多 孔 结 构 有 助 于 水 分 扩 散 迁 移 结 论 真 空 >98.,<9;,8>3E:BE:.,<9;1HQ9-8BE:.,<9;-82.E>9>R3E;89E;38F
摘要目的提 高 光 皮 木 瓜 干 燥 效 率 和 品 质 方 法以 光 #!1#Q复水比$1!/`"1"&维 生 素 N总 黄 酮 含 量 分 别 为
皮木瓜为试验原料选取干燥温度&"$"V" a真 空 时 V#1!$`"1V(b#"U!#'1!V`"1%%+PPK6 神 经 网
间&#"#&!" +-8和 常 压 时 间 !(/ +-8为 影 响 因 络模型可以很好地描述光皮木瓜的真空脉动干燥过程
素以干燥时间复 水 比维 生 素 N 含 量总 黄 酮 含 量微 关键词光皮木瓜真空 脉 动 干 燥K6 神 经 网 络复 水 比
观结构为指标进行单因素试验建立 K6 神 经 网 络 模 型 并 维生素 N总黄酮
%
V"
#"
为蔷薇科木瓜属植物木瓜的 干 燥 成 熟 果 实$具 有 抗 肿 瘤+
(
$"
&
抗癌+免疫调 节 等 功 效$是 中 国 重 要 的 药 食 两 用 资 源(#)%
混合时滞随机Hopfield神经网络的均方渐近 稳定性

+
D
t
∫−∞
K
(t
−
s
)
h
(
x
(
s
))
ds
dt
( ) +
1 2
trace
σ
T
x
(
t
)
,
x
(t
−
τ
)
,
t
∫−∞
K
(
t
−
s
)
其中 i = 1, 2,, n , n (n > 1) 是网络中神经元的数量, xi 是在时间 t 第 i 个神经元的状态变量,
= x (t ) x1 (t= ), x2 (t ),, xn (t )T ∈ Rn , f ( x (t )) f1 ( x1 (t )), f2 ( x2 (t )),, fn ( xn (t ))T ∈ Rn ,
( ) ∑ ∫ +
( ) d n
j =1 ij
t
−∞ kij
t−s
hj
x j (s) ds dt
(1)
( ( ) ( ) ) ∑ +
σ n
j =1 ij
xj (t), xj
t −τ j
∫,
( ) t
−∞ kij
t−s
ϕj
xj (s) ds
dω j (t ),
= xi (u) ξi (u), − ∞ < u < 0,
【国家自然科学基金】_神经网络系统_基金支持热词逐年推荐_【万方软件创新助手】_20140730
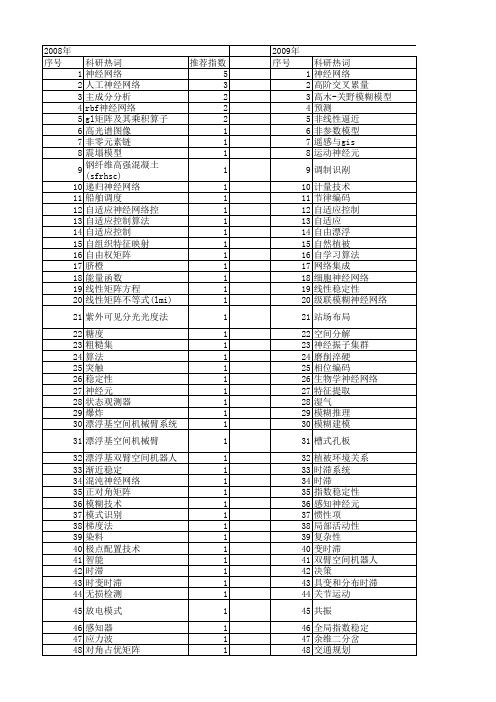
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57
n元神经网络 lyapunov泛函 l-m算法 gl矩阵及其乘积算子 bp神经网络
推荐指数 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 神经网络 高阶交叉累量 高木-关野模糊模型 预测 非线性逼近 非参数模型 遥感与gis 运动神经元 调制识剐 计量技术 节律编码 自适应控制 自适应 自由漂浮 自然植被 自学习算法 网络集成 细胞神经网络 线性稳定性 级联模糊神经网络 站场布局 空间分解 神经振子集群 磨削淬硬 相位编码 生物学神经网络 特征提取 湿气 模糊推理 模糊建模 槽式孔板 植被环境关系 时滞系统 时滞 指数稳定性 感知神经元 惯性项 局部活动性 复杂性 变时滞 双臂空间机器人 决策 具变和分布时滞 关节运动 共振 全局指数稳定 余维二分岔 交通规划 主成分分析 中间神经元 rbf神经元网络 pi-sigma神经网络
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
反同步 危岩 协调运动 加速度 关节运动 入侵检测 信用风险 五级分类 主控结构面 rbf神经元网络 matlab仿真 kronecker乘积 hopfield神经网络系统 gl矩阵及乘积算子 elman神经网络 bp神经网络
211151047_基于改进残差网络的轴承故障诊断方法

图 %!融合示意图
#)(!全局平均池化
全 局 平 均 池 化 ! <B8P;B;J?E;<? L88B45<" =+]# ,#%- " 其主要思想就是通过对上一层的输出
按照通道维度" 依此对每一个通道特征图的所有
像素进行均值计算% 它相对于全连接层大大降低
了参数量并提高了诊断效率" 有效降低了发生过
!X#为了有效地利用空间和时序特征" 使用
## 卷积在通道维度上融合 G::和 30&C 提取
的特征%
!*# 为保证模型轻量化" 减少网络参数量"
提高训练效率" 采用 =+]代替全连接层和 # #
卷积来增加网络的非线性%
!.# 第一层卷积使用大的卷积核来增加其感
受视野" 为下一层提供更多的信息" 并减弱高频
!##为了避免对信号处理知识的依赖" 实现 端到端的轴承故障诊断" 直接采用一维时间序列 振动信号作为网络模型的输入%
!%#为了获得 信 号 的 空 间 和 时 序 信 息" 将 G::和 30&C结合使用以获得信号的空间和时序 信息%
!(# 为了避免 G::操作破坏信号的时序信 息" 为此" 将 30&C 以残差的形式与 G::并行 联合使用" 使两者同时提取原始信号的特征" 获 得真实有效的空间和时序信息%
$!前言
轴承作为旋转机械的核心部件" 其正常运行 至关重要% 一旦轴承出现故障" 不但会造成财产 损失" 还有可能造成人员伤亡,#- " 因此轴承故
收稿日期 %$%% ,#% ,%W& 修订日期 %$%( ,$# ,(# 基金项目 辽宁省教育厅基金项目! ^k3%$%$$#(# & 国家自然科
基于神经网络的非线性时间序列故障预报

2007 年 7 月
自 动 化 学 报
ACTA AUTOMATICA SINICA
Vol. 33, No. 7 July, 2007
基于神经网络的非线性时间序列故障预报
胡寿松 1 张正道 2
摘 要 对模型未知非线性系统, 将系统输出组成时间序列并通过空间嵌入的方法转化为一个离散动态系统. 利用线性 AR 模型拟合时间序列的线性部分, 用神经网络拟合时间序列的非线性部分并补偿外界未知的扰动, 提出了通过对状态的观测实 现时间序列一步预测的方法. 利用滚动优化的思想将一步预测推广, 提出了时间序列的 N 步预测方法, 证明了时间序列预测 误差有界. 通过对预测误差进行概率密度估计和检验, 提出了故障的预报方法. 对 F-16 歼击机的结构故障预报结果表明了方 法的有效性. 关键词 非线性时间序列, 神经网络, 滚动预测, 概率密度估计, 故障预报 中图分类号 TP18
(2)
x(T − p + 1) x(T − p + 2) . . = . x ( T ) x(T + 1) x(T − p) 0 1 0 ... 0 x(T − p + 1) 0 0 1 ... 0 0 x(T − p + 2) ... ... ... 0 . . 0 0 ... 1 0 . ηp ηp−1 ηp−2 ... η0 x(T ) 0 0 . . . 0 f (x(T ), x(T − 1), · · · , x(T − p))
引理 1[10] . 对于任意定义在紧集 Ω 上的非线性 函数 f (x) 及 ε > 0, 一定存在一个 RBF 神经网络 fN N (x) = W ∗ϕ (x), 满足:sup |f (x) − fN N (x)| ≤
【国家自然科学基金】_时变时滞系统_基金支持热词逐年推荐_【万方软件创新助手】_20140801
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
连续分布时滞 还原法 输入时滞 输入受限 自适应重复控制 自适应边界技术 自由权 脆弱性 网络化控制系统 线性系统 线性矩阵不等式方法 稳定性分析 积分变结构 积分不等式 离散和分布时变时滞 电力系统 灰色预测 渐进稳定性 混沌神经网络 混沌同步 混合时滞 正实控制 模糊逻辑系统 模糊辨识 模糊时滞互联系统 模糊双线性系统 模糊分散控制 模糊lyapunov-krasovskii泛函 时滞自由权值矩阵 时滞相关稳定性 时滞依赖条件 时滞依赖指标 时变结构不确定性 时变延滞 无源控制 故障检测滤波器 描述系统 指数稳定 拥塞控制 广义投影同步 带记忆状态反馈 完整性 奇异摄动系统 复合能量函数 增广lyapunov-krasovskii泛函 基于descriptor form的lyapunov-krasovskii 均方指数稳定性 均方指数稳定 固定时滞及时变时滞 变时滞 单刀具垂直切削 区间递归神经网络 动态而控制 切换系统
积分反推 离散奇异系统 状态反馈 特征根分析 ห้องสมุดไป่ตู้波器设计 渐近稳定 流量控制 机床 有限和不等式 有向图 最大允许时滞 最优保成本控制 时滞相关稳定 时滞滤波器 时滞依赖准则 时延 时变时滞系统 时变时延 时变主轴转速 时变 无源控制 方差解法 数据包处理器 数据包丢失 捕食一食饵系统 振荡模式 拉什密辛型定理 执行器故障 性能评价 广义最小方差基准 小波脊法 学习控制 大系统 多变量控制系统 多主体系统 复合能量函数 同伦 变时滞系统 变时滞 参数不确定性 动态领导者 功能反应 列车-桥梁耦合振动 再生型切削 关联矩阵 共享控制 互高阶累积量 二次镇定控制 二次稳定 主动队列管理 中立系统 中立型系统 中立 不确定奇异系统
代数中常用英语词汇
(0,2) 插值||(0,2) interpolation0#||zero-sharp; 读作零井或零开。
0+||zero-dagger; 读作零正。
1-因子||1-factor3-流形||3-manifold; 又称“三维流形”。
AIC准则||AIC criterion, Akaike information criterionAp 权||Ap-weightA稳定性||A-stability, absolute stabilityA最优设计||A-optimal designBCH 码||BCH code, Bose-Chaudhuri-Hocquenghem codeBIC准则||BIC criterion, Bayesian modification of the AICBMOA函数||analytic function of bounded mean oscillation; 全称“有界平均振动解析函数”。
BMO鞅||BMO martingaleBSD猜想||Birch and Swinnerton-Dyer conjecture; 全称“伯奇与斯温纳顿-戴尔猜想”。
B样条||B-splineC*代数||C*-algebra; 读作“C星代数”。
C0 类函数||function of class C0; 又称“连续函数类”。
CA T准则||CAT criterion, criterion for autoregressiveCM域||CM fieldCN 群||CN-groupCW 复形的同调||homology of CW complexCW复形||CW complexCW复形的同伦群||homotopy group of CW complexesCW剖分||CW decompositionCn 类函数||function of class Cn; 又称“n次连续可微函数类”。
Cp统计量||Cp-statisticC。
混合时滞Cohen—grossberg神经网络周期解的存在性
I () t I t 一 。 ) ≤Ml 一 f一 V > ,= , , n ( I , 0 l2 …, , e t
那 么该 系统 的周 期解 是 ’ t ()=( 1()X t , , () 全 局指数稳 定 的 , 中 () () X t ,2() … z t) " 其 t , t分别 满足 初 值 条件 : ’=( () () … , () ∈C [一 ,]R ) t , t , t) ( r0 ,
1 引言 及 引理
本 文讨论 如下 神经 网络模 型 :
。
,)= n x( )b t 。 ) 一∑c( (— O) 一 ( 一 。 )[。 ,( ) f £ ( f q£ ( t T)) ) .
J l
n
.
∞
∑ ( g f () ( Ⅱd) l £]i ,, n t i ux 卜 )u + i ), :12…,, )( i (
Z A G We —w iX N G Y u— i, i —b n H N i e, I A o j WU Xa e o a
( i a o 1M dl Sho, i a 7 60 C ia Wes nN . idec olWe hn27 0 , hn ) h s
Ab t a t:I h sl te x se c fp ro i olto sfrCo e - r sb r el lrn u a ewo k t sr c n t i etre it n e o e id c s ui n o h n— g o s e g c lu a e r ln t r swi h mie e a sa e c n i e e x d d ly r o sd rd. S fiintc n iin r t e e it n e o h  ̄ 6o i o u in r sa — u ce o d t s f h x se c ft e o o d e s lt sae etb o
【国家自然科学基金】_随机时滞_基金支持热词逐年推荐_【万方软件创新助手】_20140730
107 108 109 110 111 112 113 114
lmi leap条件 l2-l∞滤波 ito类型随机时滞系统 h∞滤波 dτ l算法 dk-leap算法 cohen-grossberg随机神经网络
1 1 1 1 1 1 1 1
推荐指数 8 6 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 线性矩阵不等式 随机系统 网络控制系统 机床 时滞系统 时滞相关 均方指数稳定性 变时滞 再生切削 互高阶累积量 h∞控制 鲁棒控制 马尔可夫链 马尔可夫过程 马尔可夫跳变系统 马尔可夫跳变 马尔可夫处理 风险管理 非脆弱滤波 非线性系统 随机时滞系统 随机延迟微分方程 随机大系统 随机分布系统 随机mathieu-duffing系统 镇定 递归神经网络 透皮吸收 输出反馈 输入时滞 跳跃线性离散系统 谐参数估计 自由权矩阵 网络时滞 网络化控制系统 缓释贴片 线性矩阵不等式. 线性矩阵不等式(lmi) 稳定性 矩阵不等式 矩稳定件 盐酸哌唑嗪 灵敏性 模态耦合效应 概率密度函数 最小二乘法 时滞补偿 时滞相关稳定性 时滞实时在线估计 时滞依赖 时滞 时变时滞
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0引言及准备知识近年来,对神经网络吸引集的研究引起学者们的广泛关注,并取得了许多好的结果[1-6].然而,这些结果都是针对细胞神经网络,而对中立型Cohen-Grossberg神经网络的全局吸引集却很少有人研究,因此,本文讨论下面一类具有时滞和脉冲的Cohen-Grossberg中立型神经网络
!"#$%&#!#$#!#$&'(%)#($*#(!($&'(%+#($,#(!($&
#($[
&'(%-#($.#(!"($&/#($&0#$]$$$$1!#$%2#1!$&!$&!'$&34#1!$&#$&!$&#$&!'$&#'$&$$$%$1
(1)
的全局吸引集问题,这里,αi(·)表示放大函数,βi(·)表示行为函数,τij
(t),rij(t)表示传输时滞,且满足0≤τij(t)≤τ,0≤rij(t)≤τ,aij(t),bij(t),cij(t)表示神经网络连接权,fij
(t),
gij(t),hij(t)表示神经元激励函数,Ii(t)表示额外输出.系统(1)的初始条件为
初始函数φ(s)=(φ1(s),φ2(s),…,φn(s))T∈PC1,脉冲函数Pk=(p1k,…,pnk)T∈C[Rn,Rn],Qk=(q1k,…,qnk
)T
∈C
[Rn,Rn],并且固定的脉冲时刻tk
满足t
1
<…,
=∞,k=1,2,….
易知在方程(1)中x′(t)=(x′(t)1,…,x′(t)n)T在固定的脉冲时刻tk
有第一类间断点;而且在某些时刻
有第一类间断点.为了方便起见,我们假设
.
设E为n维单位矩阵,对于A,B∈Rm×n或意味着A与B的对应
的每一对元素满足不等式“≥(≤,>,<)”.特别地,如果A≥0,则称A为非负矩阵,并且如果z>0,则z称为正向量.记为从拓扑空间X到拓扑空间Y的连续映射全体.特殊地,记,其中
第30卷第4期2015年8月柳州师专学报
JournalofLiuzhouTeachersCollege
Vol.30No.4
Aug.2015
具有时滞和脉冲的中立型Cohen-Grossberg神经网络的正p-不变集与全局p-吸引集
秦发金(广西科技师范学院数学与计算机科学系,广西来宾546199)
摘要:研究了一类具有时滞和脉冲的中立型Cohen-Grossberg神经网络的全局吸引集.通过利用一个奇异时滞微分不等式和M-锥理论,获得了其正p-不变集与全局p-吸引集的充分条件.关键词:脉冲中立型;Cohen-Grossberg神经网络;正p-不变集;全局p-吸引集;M-锥理论中图分类号:O175.13文献标识码:A文章编号:1003-7020(2015)04-0127-09
[收稿日期]2015-07-10[基金项目]广西高校科学技术研究项目(2013YB282;YB2014468)。[作者简介]秦发金(1967—),男,广西临桂人,教授,研究方向:微分方程、神经网络。127除了在有限个点s∈J以外连续,并且在这些点s∈J,
以及
存
在,,其中是有界区间,记和分别为的右极限和左极限.特别地,令
PC1[J,Rn]={ψ:J→Rnψ(s)除了在可数个点s∈J以外连续可微,并且在这些点s∈J,ψ(s+),ψ(s-),ψ′(s+)以
及ψ′(s-)存在,ψ(s)=ψ(s+),ψ′(s)=ψ′(s+)},其中记ψ′(s)为ψ(s)的导数.特别地,令PC1=PC1[[-τ,0],Rn].
正的可积函数,且满足.
对于,定义!"#$!#!%#&'"$()*%+%,
对于或,定义,
,并且记D+
φ(t)为φ(t)在时间t的右上导数.对于φ∈C
或φ∈PC,定义范数
{}
.
对于φ∈PC1,定义范数
{}
.
令y(t)=x′(t),则系统(1)转换成以下2n-维奇异脉冲时滞微分系统!"#$%&#!#$[#!#$&'(%)#($*#(!($&'(%+#($,#(!($&#($
&'(%-#($.#(/($&0#($&1#$]$$$$2%&/#$&#!#$[#!#$&'(%)#($*#(!($&'(%+#($,#(!($&#($&'(%-#($.#(/($&0#($&1#$]$$$$2!#$%3#2!$&!$&!'$&45#2!$&#$&!$&#$&!'$&#'$&/#$%/#$4#$$
(2)
系统(2)的初值为!"#$%&"%'"#$%&("%)%"*
注1:显然,研究系统(1)在中的渐近行为等价于研究系统(2)在中的渐近行为.
对,我们总假设系统(1)过至少存在一个解,记为或者
.
定义1集合S⊂PC1被称为系统(1)的正不变集,是指如果对任意初始值φ∈S,都有.x(t0,φ)∈S,t≥t0
.
定义2集合S⊂PC1被称为系统(1)的全局吸引集,是指如果对任意初始值φ∈PC1,都有x(t0
,φ)→S,t→∞,
也即其中,这里表示x到y的距离.定义3令矩阵D=(dij)n×n,dii
>0以及
,则D称为M-矩阵,如果下列条件中的其中之一成立:
(i)D的所有前主子式都为正的;(ii)存在一个正向量z使得Dz>0;(iii)D是逆正矩阵,即D-1存在并且D-1≥0.
对一个M-矩阵D,我们定义
由定义3的(ii),可得下面的引理:引理1如果D是一个M-矩阵,则ΩM(D)非空,并且对任意的z1,z2∈ΩM
(D)有
所以
是一个没有底面的锥,我们称之为“M-锥”.
128
