(中考快递)2019届中考数学复习检测:专题一-开放探索问题(word版,有答案)-推荐
2019届人教版中考复习数学练习专题三:开放型探索专题(含答案)

专题三开放型探索专题的青睐,中考题型以填空题、解答题为【课堂精讲】例1如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.分析:(1)根据全等三角形的判定方法,可得出当EH=FH,BE∥CF,∠EBH=∠FCH时,都可以证明△BEH≌△CFH,(2)由(1)可得出四边形BFCE是平行四边形,再根据对角线相等的平行四边形为矩形可得出BH=EH时,四边形BFCE是矩形.解答:(1)添加:EH=FH,证明:∵点H是BC的中点,∴BH=CH,在△△BEH和△CFH中,,∴△BEH≌△CFH(SAS);(2)解:∵BH=CH,EH=FH,∴四边形BFCE是平行四边形(对角线互相平分的四边形为平行四边形),∵当BH=EH时,则BC=EF,∴平行四边形BFCE为矩形(对角线相等的平行四边形为矩形).本题考查了全等三角形的判定和性质以及平行四边形的判定基础题,难度不大例2.如图2-1-3,边长为1的正方形ABCD 的对角线AC ,BD 相交于点O .有直角∠MPN ,使直角顶点P 与点O 重合,直角边PM ,PN 分别与OA ,OB 重合,然后逆时针旋转∠MPN ,旋转角为θ(0°<θ<90°),PM ,PN 分别交AB ,BC 于E ,F 两点,连结EF 交OB 于点G ,则下列结论中正确的是____. ①EF =2OE ;②S四边形OEBF∶S正方形ABCD=1∶4;③BE +BF =2OA ;④在旋转过程中,当△BEF 与△COF 的面积之和最大时,AE =34;⑤OG ·BD =AE 2+CF 2.图2-1-3 第4题答图【解析】 ∵四边形ABCD 是正方形,∴OB =OC ,∠OBE =∠OCF =45°,∠BOC =90°,∴∠BOF +∠COF =90°,∵∠EOF =90°,∴∠BOF +∠BOE =90°,∴∠BOE =∠COF ,∴△BOE ≌△COF (ASA ),∴OE =OF ,BE =CF ,∴EF =2OE .故①正确;∵S 四边形OE BF =S △BOE +S △BOF =S △BOF +S △COF =S △BOC =14S 正方形ABCD ,∴S 四边形OEBF ∶S 正方形ABCD =1∶4.故②正确;∵BE +BF =BF +CF =BC =2OA .故③正确;如答图,过点O 作OH ⊥BC 交BC 于点H ,∵BC =1,∴OH =12BC =12,设AE =x ,则BE =CF=1-x ,BF =x ,∴S △BEF +S △COF =12BE ·BF +12CF ·OH =12x (1-x )+12(1-x )×12=-12⎝ ⎛⎭⎪⎫x -142+932,∵a =-12<0,∴当x =14时,S △BEF +S △COF 最大,即在旋转过程中,当△BEF 与△COF 的面积之和最大时,AE =14.故④错误;∵∠EOG =∠BOE ,∠OEG =∠OBE =45°,∴△OEG ∽△OBE ,∴OE ∶OB =OG ∶OE ,∴OG ·OB =OE 2,∵OB =12BD ,OE =22EF ,∴OG ·BD =EF 2,∵在△BEF 中,EF 2=BE 2+BF 2,∴EF2=AE 2+CF 2,∴OG ·BD =AE 2+CF 2.故⑤正确.故答案为①②③⑤.【课堂提升】1.如图,直线a、b被直线c所截,若满足,则a、b平行.2.写出一个运算结果是a6的算式.3.如图2-1-5,CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图①,若∠BCA=90°,∠α=90°,则BE____CF;EF____|BE-AF|(选填“>”“<”或“=”);②如图②,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件____,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图③,若直线CD经过∠BCA的外部,∠α=∠BCA,请写出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).图2-1-54.如图2-1-6①,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形;(2)如图②,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.①判断四边形BFDG的形状,并说明理由;②若AB=6,AD=8,求FG的长.5.如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G,(1)观察图形,写出图中所有与∠AED相等的角。
2019年中考数学二轮复习 开放探究型问题 讲解与练习(共44张PPT)

2.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D, 交AB于点E,点F在DE的延长线上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形; (2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.
解:(1)证明:∵DE 垂直平分 BC,∴∠FDC=90°,BD=12BC, ∠BED=∠CED.∵∠FDC=∠ACB=90°.∴FD∥AC. ∴△BED∽△BAC.∴BBAE=BBDC=12.∴CE 为 Rt△ABC 的中线. ∴CE=AE=12AB.∵AF=CE,∴AE=AF.∴∠F=∠AEF.
2019年中考数学二轮复习
开放探究型问题讲解与训练
开放探究型问题常用的方法
【例题】 已知:如图,在▱ABCD中,O是CD的中点,连结AO并延长, 交BC的延长线于点E.
(1)求证:△AOD≌△EOC; (2)连结AC,DE,当∠B=∠AEB=____°时,四边形ACED是正方形?请 说明理由.
审题视角 (1)根据平行线的性质可得∠D=∠OCE,∠DAO=∠E,再根据 中点定义可得DO=CO,然后可利用AAS证明△AOD≌△EOC;
解:成立.证明:由(1)易知 AD=AE,
∴由旋转性质可知∠DAB=∠EAC.在△DAB 和△EAC 中,
AD=AE, ∠DAB=∠EAC, AB=AC,
∴△DAB≌△EAC.∴DB=CE.
(3)拓展运用:如图③,P是等腰直角三角形ABC内一点,∠ACB=90°, 且PB=1,PC=2,PA=3,求∠BPC的度数.
解:如图,将△CPB 绕点 C 旋转 90°得△CEA,连结 PE, ∴△CPB≌△CEA,∴CE=CP=2,AE=BP=1,∠PCE=90°. ∴∠CEP=∠CPE=45°.在 Rt△PCE 中,由勾股定理可得,PE=2 2, 在△PEA 中,PE2=(2 2)2=8,AE2=12=1,PA2=32=9, ∴PE2+AE2=AP2.∴△PEA 是直角三角形,∴∠PEA=90°, ∴∠CEA=135°.又∵△CPB≌△CEA,∴∠BPC=∠CEA=135°.
2019版中考专题(2)开放探究问题(含答案)

专题二开放探究问题一、填空题1.(原创题)写出第三象限内的一个点,并使得它在直线y=x上,这个点可以是________.解析写出的点只要横纵坐标相等,且都是负数即可.答案答案不唯一,如(-1,-1)二、解答题2.(改编题)提出问题(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.类比探究(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.拓展延伸(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN 的数量关系,并说明理由.(1)证明∵等边△ABC,等边△AMN,∴AB=AC,AM=AN,∠BAC=∠MAN=60°.∴∠BAM=∠CAN.∴△BAM≌△CAN(SAS).∴∠ABC=∠ACN.(2)解结论∠ABC=∠ACN仍成立.理由如下:∵等边△ABC,等边△AMN,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,∴△BAM≌△CAN.∴∠ABC=∠ACN.(3)解∠ABC=∠ACN.理由如下:∵BA =BC ,MA =MN ,顶角∠ABC =∠AMN , ∴底角∠BAC =∠MAN ,∴△ABC ∽△AMN . ∴AB AM =ACAN .又∠BAM =∠BAC -∠MAC , ∠CAN =∠MAN -∠MAC , ∴∠BAM =∠CAN .∴△BAM ∽△CAN . ∴∠ABC =∠ACN .3.(原创题)如图,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该直角坐标系内的一个动点.(1)使∠APB =30°的点P 有________个;(2)若点P 在y 轴上,且∠APB =30°,求满足条件的点P 的坐标;(3)当点P 在y 轴上移动时,∠APB 是否有最大值?若有,求点P 的坐标,并说明此时∠APB 最大的理由;若没有,也请说明理由.解 (1)以AB 为边,在第一象限内作等边三角形ABC , 以点C 为圆心,AC 为半径作⊙C ,交y 轴于点P 1,P 2. 在优弧AP 1B 上任取一点P ,如图1,图1则∠APB =12∠ACB =12×60°=30°. ∴使∠APB =30°的点P 有无数个.填无数.(2)①当点P在y轴的正半轴上时,过点C作CG⊥AB,垂足为G,如图1. ∵点A(1,0),点B(5,0),∴OA=1,OB=5.∴AB=4.∵点C为圆心,CG⊥AB,∴AG=BG=12AB=2.∴OG=OA+AG=3.∵△ABC是等边三角形,∴AC=BC=AB=4.∴CG=AC2-AG2=42-22=2 3.∴点C的坐标为(3,23).过点C作CD⊥y轴,垂足为D,连结CP2,如图1,∵点C的坐标为(3,23),∴CD=3,OD=2 3.∵P1,P2是⊙C与y轴的交点,∴∠AP1B=∠AP2B=30°.∵CP2=CA=4,CD=3,∴DP2=42-32=7.∵点C为圆心,CD⊥P1P2,∴P1D=P2D=7.∴P2(0,23-7).P1(0,23+7).②当点P在y轴的负半轴上时,同理可得:P3(0,-23-7).P4(0,-23+7).综上所述:满足条件的点P的坐标有:(0,23-7),(0,23+7),(0,-23-7),(0,-23+7).(3)当过点A,B的⊙E与y轴相切于点P时,∠APB最大.①当点P在y轴的正半轴上时,连结EA,作EH⊥x轴,垂足为H,如图2. ∵⊙E与y轴相切于点P,∴PE⊥OP.∵EH⊥AB,OP⊥OH,∴∠EPO=∠POH=∠EHO=90°.∴四边形OPEH是矩形.∴OP=EH,PE=OH=3.∴EA=3.∵∠EHA=90°,AH=2,EA=3,∴EH=EA2-AH2=32-22=5,∴OP=5,∴P(0,5).图2②当点P 在y 轴的负半轴上时, 同理可得:P (0,-5).理由:①若点P 在y 轴的正半轴上,在y 轴的正半轴上任取一点M (不与点P 重合), 连结MA ,MB ,交⊙E 于点N ,连结NA ,如图2所示. ∵∠ANB 是△AMN 的外角, ∴∠ANB >∠AMB .∵∠APB =∠ANB ,∴∠APB >∠AMB .②若点P 在y 轴的负半轴上,同理可证得:∠APB >∠AMB .综上所述:当点P 在y 轴上移动时,∠APB 有最大值,此时点P 的坐标为(0,5)和(0,-5).4.(改编题)如图,平面直角坐标系xOy 中,一次函数y =-34x +b (b 为常数,b >0)的图象与x轴、y 轴分别相交于点A ,B ,半径为4的⊙O 与x 轴正半轴相交于点C ,与y 轴相交于点D ,E ,点D 在点E 上方.(1)若直线AB 与CD ︵有两个交点F 、G . ①求∠CFE 的度数;②用含b 的代数式表示FG 2,并直接写出b 的取值范围;(2)设b ≥5,在线段AB 上是否存在点P ,使∠CPE =45°?若存在,请求出P 点坐标;若不存在,请说明理由.解 (1)①如图1∵∠CFE =12∠COE ,∠COE =90°, ∴∠CFE =45°,②如图2,作OM ⊥AB 点M ,连结OF , ∵直线AB 的解析式为:y = -34x +b , 图1图2当x =0时,y =-34x +b =b ;当y =0时,0=-34x +b ,解得x =43b ,∴B (0,b ),A (43b ,0). ∴AB =b 2+⎝ ⎛⎭⎪⎫43b 2=53b .∵S △AOB =12OA ×OB =12AB ×OM ,∴OM =45b ;∴FM 2=OF 2-OM 2=42-⎝ ⎛⎭⎪⎫45b 2,∴FG 2=4FM 2=4×⎣⎢⎡⎦⎥⎤42-⎝ ⎛⎭⎪⎫45b 2,=64-6425b 2=64×⎝ ⎛⎭⎪⎫1-125b 2,∵直线AB 与CD ︵有两个交点F 、G . ∴4≤b <5,(2)如图3,当b =5时,直线AB 与⊙O 相切, 存在点P ,这时点P 就是线段AB 与⊙O 的切点,作PH ⊥x 轴于点H ,连结OP , ∵P 是切点,∴OP ⊥AB , ∴∠OAB +∠AOP =90°, ∠OPH +∠POH =90°; ∴∠OAB =∠OPH , ∴△AOB ∽△PHO , ∴OB OH =OA PH =AB PO ;∴OH =125,PH =165;∴P ⎝ ⎛⎭⎪⎫125,165;当b >5时,如图4,这时AB 与⊙O 相离,不存在点P ,理由如下.连结EP 交⊙O于N ,再连结CN ,CP ,图3图4∵∠ENC=45°>∠CPE,∴∠CPE<45°.2019-2020学年数学中考模拟试卷一、选择题1.如图,AD 是∆ABC 中∠BAC 的平分线,DE ⊥AB 于点E ,ABCS7 ,DE=2,AB=4,则AC 的长是( )A.3B.4C.5D.62.比较的大小,正确的是 ( )A .B .CD <23.如图是洛阳市某周内日最高气温的折线统计图,关于这7天的日最高气温说法正确的是( )A.众数是28B.中位数是24C.平均数是26D.方差是84.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度为( )米A.B.4C. D.4π5.如图,小亮从A 点出发前进10m ,向右转15º,再前进10m ,再右转15º,这样一直走下去,他第一次回到出发点A 时,一共走了多少米( )A .120米B .240米C .360米D .480米6.如图,△ABC 中,AB=AC ,点D 、E 分别是边AB 、AC 的中点,点G 、F 在BC 边上,四边形DEFG 是正方形.若DE=2cm ,则AC 的长为 ( )A.cmB.4cmC.cmD.cm7.如图,等腰直角ABC ∆中,AC BC =,90ACB ∠=︒,点O 在斜边AB 上,且满足:BO OA =,将BOC ∆绕C 点顺时针方向旋转到AQC ∆的位置,则AQC ∠的大小为( )A .100︒B .105︒C .120︒D .135︒8.甲,乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛,他们成绩的平均数、中位数、方差如下表所示,规定成绩大于等于95分为优异,则下列说法正确的是( )A .甲、乙两班的平均水平相同B .甲、乙两班竞赛成绩的众数相同C .甲班的成绩比乙班的成绩稳定D .甲班成绩优异的人数比乙班多9.如图,A 、B 两地之间有一池塘,要测量A 、B 两地之间的距离.选择一点O ,连接AO 并延长到点C ,使OC =12AO ,连接BO 并延长到点D ,使OD =12BO .测得C 、D 间距离为30米,则A 、B 两地之间的距离为( )A .30米B .45米C .60米D .90米10.如图,经过直线l 外一点A 作l 的垂线,能画出( )A.4条B.3条C.2条D.1条11.二次函数y =ax 2+bx+c 的部分图象如图,则下列说法错误的是( )A.对称轴是直线x=﹣1B.abc<0C.b2﹣4ac>0D.方程ax2+bx+c=0的根是x1=﹣3和x2=112.关于x、y的方程组239x y mx y m+=⎧⎨-=⎩的解是方程3x+2y=34的一组解,那么m的值是( )A.﹣2 B.﹣1 C.1 D.2二、填空题13.菱形ABCD中,∠B=60°,AB=5,以AC为边长作正方形ACFE,则点D到EF的距离为_____.14.如图,四边形ABCD是矩形,AD=5,AB=163,点E在CD边上,DE=2,连接BE,F是BE边上的一点,过点F作FG⊥AB于G,连接DG,将△ADG沿DG翻折的△PDG,设EF=x,当P落在△EBC内部时(包括边界),x的取值范围是__.15.已知反比例函数k1yx-=的图象在第二、四象限内,那么k的取值范围是________.16.(2016四川省甘孜州)如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,﹣1),(﹣2,0),则点P4的坐标为______________.17.如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.18.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=12,BC=9,则EF的长是_____.三、解答题19.现有24个劳力和1000亩鱼塘可供对虾、大黄鱼、蛏子养殖,所需劳力与每十亩产值如下表所示.另外设对虾10x亩,大黄鱼10y亩,蛏子10z亩.(1)用x的式子分别表示y、z;(2)问如何安排劳力与养殖亩数收益最大?20.中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:请根据所给信息,解答下列问题:(1)m=,n=;(2)请补全频数分布直方图;(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?21.随着“互联网+购物”的快速发展,快递业务也越来越红火,某小区物业为了解本小区1200户家庭在过去的一年中收到快递的情况,随机调查了80户家庭去年一年共收到的快递件数,并绘制了如下的频数分布表和频数分布直方图(不完整).根据以上提供的信息,解答下列问题(1)表格中a=,b=,m=;补全频数分布直方图;(2)这80户家庭一年中收到的快递件数的中位数落在哪一个小组?(3)请估计该小区去年一年共收到快递件数大约是多少?22.某水果批发商经销一种高档水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.1元,销售量将减少1千克(1)现该商场保证每天盈利1500元,同时又要照顾顾客,那么每千克应涨价多少元?(2)若该商场单纯从经济利益角度考虑,这种水果每千克涨价多少元,使该商场获利最大?23.如图,二次函数图象的顶点为(﹣1,1),且与反比例函数的图象交于点A(﹣3,﹣3)(1)求二次函数与反比例函数的解析式;(2)判断原点(0,0)是否在二次函数的图象上,并说明理由;(3)根据图象直接写出二次函数的值小于反比例函数的值时自变量x的取值范围.24.如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E.(1)求证:PA是⊙O的切线;(2)若sinE=35,PA=6,求AC的长.25.某足球队为了解运动员的年龄情况,作了一次年龄调查,根据足球运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:(Ⅰ)本次接受调查的足球运动员人数为______,图①中m的值为______;(Ⅱ)求统计的这组足球运动员年龄数据的平均数、众数和中位数.【参考答案】***一、选择题二、填空题13.或51415.k <1 16.(8,0). 17.1 18.5 三、解答题19.(1)y =140﹣2x ,z =x ﹣40.(2)对虾400亩,大黄鱼600亩,蛏子0亩;养植对虾的劳动力是12人,养殖大黄鱼的劳动力是12人,养殖蛏子的劳动力是0人. 【解析】 【分析】(1)本题考查对方程组的应用能力,要注意由题中提炼出的两个等量关系,即所需劳动力的总和是24、所养殖的总亩数是1000,据此可列方程组解应用题;(2)设对虾10x 亩,大黄鱼10y 亩,蛏子10z 亩的收益为T ,则T=2x+8y+1.6z ,再根据实际问题,求出定义域,然后,由函数的单调性来求值即可. 【详解】解:(1)根据题意,得1010101000(1)0.30.20.124(2)x y z x y z ++=⎧⎨++=⎩解得,140240y xz x =-⎧⎨=-⎩∴y =140﹣2x ,z =x ﹣40.(2)设对虾10x 亩,大黄鱼10y 亩,蛏子10z 亩的收益为T ,则 T =2x+8y+1.6z ① 由(1)解得,140240y xz x =-⎧⎨=-⎩将其代入①并整理,得 T =﹣12.4x+1056,∵0<10x≤1000,即0<x≤100,又∵01000100y z <⎧⎨<⎩……即01402100040100x x <-⎧⎨<-⎩……解得40≤x≤70,∵函数T =﹣12.4x+1056在[40,70]上是减函数, ∴当x =40时,T 最大,∴y=140﹣2×40=60,z=40﹣40=0,10x=400,10y=600,10z=0,20.(1)70,0.2(2)70(3)750【解析】【分析】(1)根据题意和统计表中的数据可以求得m、n的值;(2)根据(1)中求得的m的值,从而可以将条形统计图补充完整;(3)根据统计表中的数据可以估计该校参加这次比赛的3000名学生中成绩“优”等约有多少人.【详解】解:(1)由题意可得,m=200×0.35=70,n=40÷200=0.2,故答案为:70,0.2;(2)由(1)知,m=70,补全的频数分布直方图,如下图所示;(3)由题意可得,该校参加这次比赛的3000名学生中成绩“优”等约有:3000×0.25=750(人),答:该校参加这次比赛的3000名学生中成绩“优”等约有750人.【点睛】本题考查频数分布直方图、频数分布表、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.21.(1)见解析(2)3(4)16050【解析】【分析】(1)总数乘以第3组频率可得a,总数减去其它分组人数可得b,依据频率=频数÷总数可得m;(2)根据中位数的定义求解可得;(3)总户数乘以样本的平均值即可得.【详解】解:(1)a=80×0.45=36,b=80﹣(4+12+36+18+4)=6,m=6÷80=0.075,补全直方图如下:故答案为:36、6、0.075;(2)这组数据的中位数是第40、41个数据的平均数,而这两个数据均落在第3组, 所以这80户家庭一年中收到的快递件数的中位数落在第3组; (3)2471212361718226274107012001200160508080⨯+⨯+⨯+⨯+⨯+⨯⨯=⨯=(件),估计该小区去年一年共收到快递件数大约是16050件. 【点睛】本题考查搜集信息的能力(读图、表),分析问题和解决问题的能力.正确解答本题的关键在于准确读图表.22.(1)涨价5元;(2)涨价7.5元 【解析】 【分析】(1)根据题意列出一元二次方程,然后求出其解,最后根据题意确定其值; (2)根据题意列出二次函数解析式,然后转化为顶点式,最后求其最值即可. 【详解】解:(1)设每千克应涨价x 元,由题意列方程得: (5+x )(200﹣0.1x)=1500 解得:x =5或x =10,答:为了使顾客得到实惠,那么每千克应涨价5元; (2)设涨价x 元时总利润为y , 则y =(5+x )(200﹣0.1x) =﹣10x 2+150x+1000 =﹣10(x 2﹣15x )+1000 =﹣10(x ﹣7.5)2+1562.5,答:若该商场单纯从经济角度看,每千克这种水果涨价7.5元,能使商场获利最多. 【点睛】本题考查了二次函数的应用,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a 的绝对值是较小的整数时,用配方法较好,如y =﹣x 2﹣2x+5,y =3x 2﹣6x+1等用配方法求解比较简单.23.(1)y=﹣(x+1)2+1,9yx=;(2)原点(0,0)是在二次函数的图象上;(3)当x<﹣3或x>0时二次函数的值小于反比例函数的值.【解析】【分析】(1)设二次函数为y=a(x+1)2+1,设反比例函数的解析式为y=kx,把A点的坐标代入,关键待定系数法即可求得;(2)把x=0代入求得的二次函数的解析式即可判断;(3)由两函数的图象直接写出x的取值范围即可.【详解】解:(1)设二次函数为y=a(x+1)2+1,∵经过点A(﹣3,﹣3)∴﹣3=4a+1,∴a=﹣1,∴二次函数的解析式为y=﹣(x+1)2+1,设反比例函数的解析式为y=kx,∵二次函数的图象与反比例函数的图象交于点A(﹣3,﹣3)∴k=﹣3×(﹣3)=9,∴反比例函数的解析式为y=9x;(2)把x=0代入y=﹣(x+1)2+1,得y=﹣1+1=0,∴原点(0,0)是在二次函数的图象上;(3)由图象可知,二次函数与反比例函数图象的交点为A(﹣3,﹣3),当x<﹣3或x>0时二次函数的值小于反比例函数的值.【点睛】本题是一道函数的综合试题,考查了待定系数法求反比例函数的解析式和求二次函数的解析式,由图象特征确定自变量的取值范围.24.(1)见解析;(2)5AC=.【解析】【分析】(1)先利用平行线的性质得到∠ACO=∠POB,∠CAO=∠POA,加上∠ACO=∠CAO,则∠POA=∠POB,于是可根据“SAS”判断△PAO≌△PBO,则∠PAO=∠PBO=90°,然后根据切线的判定定理即可得到PA是⊙O的切线;(2)先由△PAO≌△PBO得PB=PA=6,在Rt△PBE中,利用正弦的定义可计算PE=10,则AE=PE-PA=4,再在Rt△AOE中,由sinE=35OAOE=,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出EAC∽△EPO,再利用相似比可计算出AC . 【详解】(1)证明:连接OA ,如图,∵AC ∥OP ,∴∠ACO =∠POB ,∠CAO =∠POA , 又∵OA =OC , ∴∠ACO =∠CAO , ∴∠POA =∠POB , 在△PAO 和△PBO 中,PO PO POA POB 0A 0B =⎧⎪∠=∠⎨⎪=⎩, ∴△PAO ≌△PBO (SAS ), ∴∠PAO =∠PBO , 又∵PB ⊥BC , ∴∠PBO =90°, ∴∠PAO =90°, ∴OA ⊥PE , ∴PA 是⊙O 的切线; (2)解:∵△PAO ≌△PBO , ∴PB =PA =6, 在Rt △PBE 中,∵sinE =35PB PE = ∴635PE =,解得PE =10, ∴AE =PE ﹣PA =4, 在Rt △AOE 中,sinE =35OA OE =, 设OA =3t ,则OE =5t , ∴AE4t , ∴4t =4,解得t =1, ∴OA =3,在Rt △PBO 中,∵OB =3,PB =6,∴OP=∵AC∥OP,∴△EAC∽△EPO,∴AC EAPO EP=410=,∴AC.【点睛】本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了全等三角形的判定与性质.25.(Ⅰ)50,24;(Ⅱ)平均数是14.8;众数为15;中位数为15.【解析】【分析】(1)频数÷所占百分比=样本容量,m=100-28-20-10-18=24,据此解答即可;(2)根据平均数、众数和中位数的定义求解即可.【详解】(Ⅰ)9÷18%=50(名)m=100-28-20-10-18=24,故答案为:50,24.(Ⅱ)观察条形统计图,139141215141610175x14.850⨯+⨯+⨯+⨯+⨯==,∴这组数据的平均数是14.8.∵在这组样本数据中,15出现了14次,出现的次数最多, ∴这组样本数据的众数为15.∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是15,有1515152+=,∴这组样本数据的中位数为15.【点睛】本题考查了条形统计图,扇形统计图,掌握平均数、众数和中位数的定义是解题的关键.2019-2020学年数学中考模拟试卷一、选择题1.若二次函数2()1y x m =--,当1x ≤时,y 随x 的增大而减小,则m 的取值范围是( ) A .1m =B .1m >C .1m ≥D .1m ≤2.新中国成立70年以来,中国铁路营业里程由52000公里增长到131000公里,将数据131000用科学记数法表示为( ) A .13.1×105B .13.1×104C .1.31×106D .1.31×1053.如图,小明站在自家阳台上A 处观测到对面大楼底部C 的俯角为α,A 处到地面B 处的距离AB =35m ,则两栋楼之间的距离BC (单位:m )为( )A .35tan αB .35sin αC .35sin αD .35tan α4.如图是二次函数y =ax 2+bx+c (a 、b 、c 为常数,且a≠0)图象的一部分,与x 轴的右交点在点(2,0)和(3,0)之间,对称轴是x =1,对于下列说法:①abc <0; ②2a+b =0; ③3a+c >0; ④当﹣1<x <2时,y >0; ⑤b 2﹣4ac >0.其中正确的个数是( )A.2B.3C.4D.55.如图,AB 是⊙O 的直径,BC 是⊙O 的弦AD CD =.若BD =2,CD =6,则BC 的长为( )D.56.下列函数中,自变量x 的取值范围是x >3的是( ) A.y =B.y =C.y =D.y =7.如图所示的几何体的俯视图是( )A .B .C .D .8.某市去年完成了城市绿化面积共8210000m 2,将8210000用科学记数法表示应为( ) A .821×102B .82.1×105C .8.21×106D .0.821×1079.在平面直角坐标系中,若直线y =x+n 与直线y =mx+6(m 、n 为常数,m <0)相交于点P (3,5),则关于x 的不等式x+n+1<mx+7的解集是( ) A .x <3B .x <4C .x >4D .x >610.如图,在矩形ABCD 中,AD =3,AB =4,将△ABC 沿CF 折叠,点B 落在AC 上的点E 处,则AFFB等于( )A .12B .35C .53D .211.不等式2x+3>3x+2的解集在数轴上表示正确的是( )A .B .C .D .12.下列分解因式正确的是( ) A .﹣x 2+4x =﹣x (x+4) B .x 2+xy+x =x (x+y )C .x 2﹣4x+4=(x+2)(x+2)D .x (x ﹣y )+y (y ﹣x )=(x ﹣y )2二、填空题13.如图,正方形ABCD 的对角线相交于点O ,正三角形OEF 绕点O 旋转,在旋转过程中,当CF =DE 时,∠DOF 的大小是_____.14.若关于x 的一元二次方程x 2﹣4x+m =0有实数根,则实数m 满足_____.15.计算: __________.16.如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为﹣1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为_____.17.如图,在Rt△ABC中,∠A=90°,AB=AC,,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_____.18.如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是_____.三、解答题19.如图,在△ABC中,AD是△ABC的中线,点E是AD的中点,连接BE并延长,交AC于点F.(1)根据题意补全图形.(2)如果AF=1,求CF的长.20.如图,在平面直角坐标系内,直线y1=kx+b(k≠0)与双曲线y2=(a≠0)交于A、B两点,已知点A(m,2),点B(-1,-4).(1)求直线和双曲线的解析式;(2)把直线y1沿x轴向负方向平移1个单位,得到直线y3,直接写出y3解析式及当y3>y2时,自变量x 的取值范围.21.观察下面的变形规律:11=1122-⨯;111=2323-⨯;111=3434-⨯;…. 解答下面的问题: (1)若n 为正整数,请你猜想1(1)n n += ; (2)证明你猜想的结论;(3)求和:112⨯+123⨯+134⨯+…+120092010⨯. 22.线段AB 在由边长为1的小正方形组成的网格中,端点A 、B 为格点(即网格线的交点).(1)线段AB 的长度为________;(2)在网格中找出一个格点C ,使得△ABC 是以AB 为直角边的等腰直角三角形,请画出△ABC ;(3)在网格中找出一个格点D ,使得△ABD 是以AB 为斜边的等腰直角三角形,请画出△ABD .23.如图,已知()()()3,3,2,1,1,2A B C ------是直角坐标平面上三点.(1)将ABC ∆先向右平移3个单位,再向上平移3个单位,画出平移后的图形111A B C ∆;(2)以点()0,2为位似中心,位似比为2,将111A B C ∆放大,在y 轴右侧画出放大后的图形222A B C ∆;(3)填空:222A B C ∆面积为 .24.已知抛物线y =ax 2+bx+2经过点A (﹣1,﹣1)和点B (3,﹣1).(1)求这条抛物线所对应的二次函数的表达式.(2)写出抛物线的开口方向、对称轴、顶点坐标和二次函数的最值.25.如图是云梯升降车示意图,其点A位置固定,AC可伸缩且可绕点A转动,已知点A距离地面BD的高度AH为3.4米.当AC长度为9米,张角∠HAC为119°时,求云梯升降车最高点C距离地面的高度.(结果保留一位小数)参考数据:sin29°≈0.49,cos29°≈0.88,tan29°≈0.55【参考答案】***一、选择题二、填空题13.165°或15°.14.4m≤15.116.(32,258)1712+或118.(-10,3)三、解答题19.(1)如图所示,见解析;(2)CF=2.【解析】【分析】(1)根据线段垂直平分线的作法画出图形即可;(2)过点D作DG∥BF,交AC于点G,根据三角形中位线定理即可得出结论.【详解】(1)如图,(2)作DH ∥AC 交BF 于H ,如图,∵DH ∥AF ,∴∠EDH =∠EAF ,∠EHD =∠EFA ,∴△EDH ≌△EAF ,∴DH =AF =1,∵点D 为BC 的中点,DH ∥CF ,∴DH 为△BCF 的中位线,∴CF =2DH =2.【点睛】本题考查的是作图-复杂作图,熟知线段垂直平分线的作法是解答此题的关键.20.(1)双曲线的解析式为y 2=4x ,直线的解析式为y=2x-2;(2)y 3=2x ,当y 3>y 2时,自变量x 的取值范围是:0x <或x >【解析】【分析】(1)因为A 、B 是直线y 1=kx+b (k≠0)与双曲线y 2=a x(a≠0)的图象的两个交点,所以把A 点、B 点坐标代入反比例函数解析式,即可求出a 和m 的值,从而求出反比例函数的解析式和A 点坐标,进而把A 、B 点的坐标代入一次函数y 1=kx+b 的解析式,就可求出k 、b 的值;(2)根据图象和交点坐标,从而求得x 的取值范围.【详解】解:(1)∵点B (-1,-4)在双曲线y 2=a x (a≠0)上, ∴a=-1×(-4)=4.∴双曲线的解析式为y 2=4x∵点A (m ,2)在反比例函数y 2=4x 的图象上, ∴2=4m, ∴m=2.∵点A (2,2)和点B (-1,-4)在直线y 1=kx+b (k≠0)上,224k b k b +=⎧∴⎨-+=-⎩解得22k b =⎧⎨=-⎩∴直线的解析式为y=2x-2.(2)直线y1沿x轴向负方向平移1个单位,得到直线y3=2(x+1)-2=2x,解24y xyx=⎧⎪⎨=⎪⎩,得xy⎧=⎪⎨=⎪⎩或xy⎧=⎪⎨=-⎪⎩∴直线y3和双曲线的交点为和(-.∴当y3>y2时,自变量x的取值范围是:0x-<<或x>【点睛】题考查了反比例函数和一次函数的交点问题,能够熟练运用待定系数法求得函数的解析式;能够运用数形结合的思想观察两个函数值的大小关系21.(1)111=(1)1n n n n-++;(2)见解析;(3)20092010.【解析】【分析】(1)观察规律可得:111 (1)1n n n n=-++;(2)根据分式加减法的运算法则求解即可证得结论的正确性;(3)利用上面的结论,首先原式可化为:111111112233420092010-+-+-++-继而可求得答案.【详解】(1)由111111111;;121223233434=-=-=-⨯⨯⨯,…则:111(1)1n n n n=-++;(2)111111(1)(1)(1)(1)n n n nn n n n n n n n n n++--=-==+++++;(3)1111 12233420092010 ++++⨯⨯⨯⨯=1111111 12233420092010 -+-+-+-=1﹣1 2010=2009 2010.【点睛】此题考查了分式的加减运算法则,解题的关键是仔细观察,得到规律:111 (1)1 n nn n=-++,然后利用规律求解.22.(1)(2)见解析(答案不唯一);(3)见解析(答案不唯一).【解析】(1)直接利用勾股定理进而得出答案;(2)直接利用网格结合勾股定理得出符合题意的图形;(3)直接利用网格结合勾股定理和圆周角定理得出符合题意的图形.【详解】解:(1)如图所示:=(2)如图,△ABC 就是所要求的等腰直角三角形(答案不唯一);(3)如图,△ABD 就是所要求的等腰直角三角形(答案不唯一).【点睛】此题主要考查了应用设计与作图,正确应用勾股定理和圆周角定理是解题关键.23.(1)详见解析;(2)详见解析;(3)6.【解析】【分析】(1)分别画出A 、B 、C 三点的对应点即可解决问题;(2)由(1)得111A B C ∆各顶点的坐标,然后利用位似图形的性质,即可求得222A B C ∆各点的坐标,然后在图中作出位似三角形即可.(3)求得222A B C ∆所在矩形的面积减去三个三角形的面积即可.【详解】(1)如图,111A B C ∆即为所求作;(2)如图,222A B C ∆即为所求作;(3)222A B C ∆面积=4×4-12×2×4-12×2×2-12×2×4=6.本题主要考查了利用平移变换作图、位似作图以及求三角形的面积,作图时要先找到图形的关键点,把这几个关键点按平移的方向和距离确定对应点后,再顺序连接对应点即可得到平移后的图形.24.(1)y=﹣x2+2x+2;(2)抛物线开口向下,对称轴是:x=1,顶点坐标为(1,3),二次函数的最大值为3.【解析】【分析】(1)由条件可知点A和点B的坐标,代入解析式可得到关于a和b的二元一次方程组,解得a和b,可写出二次函数解析式;(2)根据a的值可确定开口方向,并将抛物线的解析式配方后可得对称轴、顶点坐标和二次函数的最值.【详解】解:(1)将点A(﹣1,﹣1)和点B(3,﹣1)代入y=ax2+bx+2中,得21 9321 a ba b-+=-⎧⎨++=-⎩,∴a=﹣1,b=2,∴y=﹣x2+2x+2;(2)∵y=﹣x2+2x+2=﹣(x2﹣2x+1﹣1)+2=﹣(x﹣1)2+3,∵a=﹣1,∴抛物线开口向下,对称轴是:x=1,顶点坐标为(1,3),二次函数的最大值为3.【点睛】本题考查二次函数的性质、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,学会利用配方法确定二次函数的顶点坐标和对称轴,属于基础题.25.云梯升降车最高点C距离地面的高度为7.8m.【解析】【分析】作CE⊥BD于E,AF⊥CE于F,如图,易得四边形AHEF为矩形,则EF=AH=3.4m,∠HAF=90°,再计算出∠CAF=29°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF即可.【详解】作CE⊥BD于E,AF⊥CE于F,如图,易得四边形AHEF为矩形,∴EF=AH=3.4m,∠HAF=90°,∴∠CAF=∠CAH-∠HAF=119°-90°=29°,在Rt△ACF中,∵sin∠CAF=CF AC,∴CF=9sin29°=9×0.49=4.41,∴CE=CF+EF=4.41+3.4≈7.8(m),答:云梯升降车最高点C距离地面的高度为7.8m.【点睛】本题考查了解直角三角形的应用:先将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),然后利用勾股定理和三角函数的定义进行计算.。
2019年中考数学练习题:开放性问题

2019年中考数学练习题:开放性问题若选择a 、b 、c .在Rt △ EBC 中,由勾股定理:若选择b 、c ,则有关系式2r 3+br 2-bc 2=0.例4.如图所示,△ ABC 中,点D 在AB 上,点E 在BC 上, BD=BE _ (1)请你再添加一个条件,使得△BEA^A BDC ?并给出证明?, ?你添加的条件是:概述: 这类题在命题条件不变的情况下,命题结论不唯一, ?或在命题结论不变的条件下,条 件不唯一,解答这类题要求较高,要求对所学基础知识全面掌握. 典型例题精析 例1 .如图,D ABC 边AB 上一点,满足 _________ 条件时,△ AD3A ACB _ 分析:要求对相似三角形的判定定理全面掌握. (1) Z ACD=/ B, (2) Z ADC=/ ACB (3) AC 2=AD- AB. 例2.如图,四边形 ABCD 是矩形,O 是它的中心,E 、 F 是对角线AC?上的点.(1)如果 ________ ,则△ DEC^^ BFA(请你填上能使结论成立的一个条件) (2)证明你的结论. (1) AE=CF (OE=OF DEI AC BF 丄 AC; DE// BF 等等) (2) 证明:•••四边形 ABCD 是矩形, ••• AB=C□且 AB / CD •••/ CDE=/ BAF •/ AE=CF •- AC-AE=AC-CF _ 即 AF=CE DEC^A BFA 例3.如图,AB 是O O 的直径,CB CD 分别切O O 于点B DCA BD, CD 与 BA 的延长线交于点 E ,连结 OC OD _ (1) 求证:△ OBC^A ODC _ (2) 已知 DE=a AE=b BC=c 请你思考后,选用以上 适当的数,设计出算O O?半径的一种方案: ① ____________________________ 你选用的已知数是 ; _ ② 写出求解的过程.(结果用字母表示) (1) 证明:T CD CB 是O O 的切线,_•••/ ODC N OBC=90 , OD=OB OC=OC_ •••△ OBC^A ODC( HL ).(2) ①选择a 、b 、c ,或其中2个均可. ②若选择 a 、b .由切割线定理:a 2=b ( b+2r ),得r= 2b ,得r=• a 2 2ac -b2b+2r ) 2+c 2= ( a+c )___________ ,根据你添加的条件,再写出图中的一对全等三角形 一对全等三角形,不再添加其他线段,不再标注或使用其他字母,解:添加条件列举: BA=BC / AEBK CDB / BAC H BCA / BCD " BAE 等,证明列举(以添加条件/AEB=Z CDB 为例)•••/ AEB 玄 CDB BE=BD / B=Z B, •••△ BEA^A BDC另一对全等三角形是:△ ADF ^A CEF 或△ AEC^A CDA 中考样题训练1如图1 ,已知AC=BD?要使△ ABCI ^A DCB?只需增加的一个条件是 ____________________________________________________________________________________(1) ⑵ ⑶2. _______________________________________________________ 如图2, AB=AC 要使△ ABE ^A ACD 应添加的条件是 ____________________________________ (?添加一个条件即可). 3•聪明的亮亮用含有 30?°角的两个完全相等的三角板拼成如图 3所示的图案,并发现图中有等腰三角形,请你帮他找出两个等腰三角形: _______ .4. 已知,如图 4,AC 丄BC, BD 丄BC, AC>BC>B , ?请你添加一个条件使△ ABC^A CDB 你添 加的条件是 __________________ .(4) (5)5. 若二次函数y=x 2-4x+c 的图象与x 轴没有交点,其中 c 为整数,?则c= __________ (只要求 写出一个).6. 已知:如图 5,点C 、D 在线段 AB 上,PC=PD请你添加一个条件,使图中存在全等三角形,并给予证明. 所添条件为 ______________ ,得到的一对全等三角形是△ _______ 7 __________ .考前热身训练1. 已知x 2-ax+6在整数范围内可分解因式,则整数 a 的值是2. 有一个二次函数的图象,三位学生分别说出了它的一些特点.甲:对称轴是x=4;乙:与x 轴两个交点的横坐标都是整数; 丙:与y 轴交点的纵坐标也为整数._______ •( ?只要求写出 ?不必写出证明过程)(只填一个)且以这三个交点为顶点的三角形面积为3. 请你写出一个满足上述全部特点的二次函数.3. 如图,已知AD// BC,要使四边形 ABCD 为平行四边形, 需要增加的条件 ____________________ . ( ?只填一个 你认为正确的条件即可)4. 以x=1为根,并且包含加减乘除运算的一元一次方 程是 ____________________________ . ( ?只需写满足条 件的一个方程即可)5. 如图,O O 是等边△ ABC 的外接圆,AB=2, M N 分别是边AB AC 的中点,直线 MN 交O 0于E 、F 两点,BD// AC 交直线MN 于点D,求出图中线 段DN 上已有的线段的长.6. 已知点0是正六边形的中心,现要用一条直线把它的面积分成相等的两部分, 两种不同的方法画出这条直线•(画图工具不限)7.如图,/ 1 = / 2,若再增加一个条件就能使结论“AB. DE=AD BC'成立,?则这个条件可以是 __________ .?请分别用答案:中考样题看台1. AB=DC 2 ./ B=Z C 3 .△ ABE △ BEQ △ CED 只要写出个即可4. ? / CAB=?/ BCD或/ CBA玄BDC或BC2=AC- BD5. 只要大于4的整数均可6. / A=Z B (或PA=PB ? ?PAC PBD 心APD^A BPC考前热身训练1. 5 或-5 , 7 或-71 8 i 82. y= x2- x+3 或y=- x2+ x-35 5 5 51 2 8 1 2 8或y= x - x+1 或y=- x + x-17 7 7 73. AD=BC或AB// DC 4 . 3x-3=015. 由已知不难得出MN/ BC, MN~BC=1,2△ BMD^ AMN••• DM=MN=1 连结OA交MN于点G,贝U OAL BC•••OAL EF ,•EG=FG MG=NG•EM=FN ME- MF=MA MB• EM(EM+1 =1 ,解之得DE=DM-E M=^6. 过正六边形的中心画直线.7./ B=/ D或/ C=/ AED或AD AB=AE AC等.。
2019-中考数学第二轮复习专题讲解开放性探索题
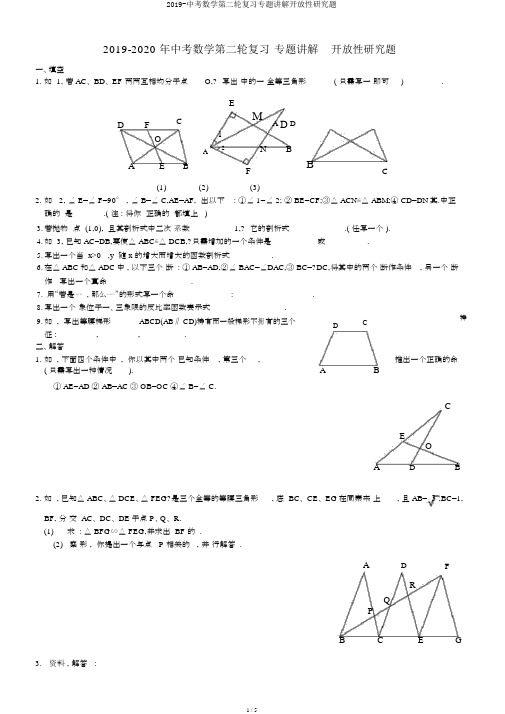
2019-2020 年中考数学第二轮复习专题讲解开放性研究题一、填空1. 如 1, 若 AC、 BD、 EF 两两互相均分于点O,? 写出中的一全等三角形( 只需写一即可)_________.ED F CO1A2A E BMA D DN BFBC(1)(2)(3)2.如 2, ∠ E=∠ F=90° , ∠ B=∠ C,AE=AF, 出以下 : ①∠ 1=∠ 2; ② BE=CF;③△ ACN≌△ ABM;④ CD=DN其.中正确的是 ______.( 注 : 将你正确的都填上 )3.若抛物点 (1,0), 且其剖析式中二次系数1,? 它的剖析式 ___________.( 任写一个 ).4.如 3, 已知 AC=DB,要使△ ABC≌△ DCB,?只需增加的一个条件是 _________或 _________.5.写出一个当 x>0 ,y 随 x 的增大而增大的函数剖析式 ________.6.在△ ABC和△ ADC中 , 以下三个断 : ① AB=AD,②∠ BAC=∠DAC,③ BC=?DC,将其中的两个断作条件, 另一个断作写出一个真命__________.7.用“若是⋯⋯ , 那么⋯⋯”的形式写一个命:__________________.8.写出一个象位于一、三象限的反比率函数表示式_________.9.如 , 写出等腰梯形ABCD(AB∥ CD)特有而一般梯形不拥有的三个D 征 :_________,_________,__________.二、解答1.如 , 下面四个条件中 , 你以其中两个已知条件 , 第三个 ,( 只需写出一种情况).A① AE=AD ② AB=AC ③ OB=OC ④∠ B=∠ C.C特推出一个正确的命BCEOA D B2. 如 , 已知△ ABC、△ DCE、△ FEG?是三个全等的等腰三角形, 底 BC、 CE、 EG在同素来上, 且 AB= 3 ,BC=1,BF, 分交 AC、 DC、 DE于点 P、Q、 R.(1)求 : △ BFG∽△ FEG,并求出 BF 的 .(2)察形 , 你提出一个与点 P 相关的 , 并行解答 .A D FRQPB C E G3.资料 , 解答 :资料 :“小的一个子游是 : 一子跳蚤从 P1(-3,9) 开始 , 按点的横坐依次增加 1 的律 , 在抛物 y=x2上向右跳 , 获取点 P2、 P3、P4、 P5⋯ ( 如① ?所示 ), P1、 P2、 P3分作 P1H2、 P2H2、P3H3垂直于 x ,垂足 H、H、H, S=S-S-S111× 1=1.,即△PPP=(9+1) × 2-(9+4) × 1- (4+1)123△ P1P2P3梯形 P1H1H3P3梯形 P1H1H2P2梯形 P2H2H3P3 1 2 3222的面1”:(1)? 求四形 P1P2P3P4?和四形 P2P3P4P5的面 ( 要求 : 写出其中一个四形面的求解程, 另一个直接写出答案 );(2)猜想四形 P n-1 P n P n+1P n+2的面 , 并明原由 ( 利用② ).(3)若将抛物 y=x2改抛物 y=x 2+bx+c, 其他条件不 , 猜想四形 P n-1 P n P n+1P n+2的面 ( 直接写出答案 ).①②4. 如 , 梯形 ABCD,AB∥ DC,AD=DC=CB,AD、 BC?的延订交于G,CE⊥ AG于 E,CF⊥ AB于 F.(1)写出中 4 相等的段 ( 已知的相等段除外 );(2)(1) 中你所写出的一相等段 , 明它相等的原由 .GED CA F B参照答案一、1. △ DOF ≌△ BOE2. ①②③3.y=x 2-1 或 y=x 2-2x+1 等4.AB=DC, ∠ACB=?∠ DBC5.y=x 或 y=-1x或 y=x 2 等6. 已知 :AB=AD,∠ BAC=∠ DAC,求证 :BC=DC.或已知 :AB=AD,BC=DC, 求证 : ∠ BAC=∠ DAC.7. 略8.y= k, 其中 k>0.x9. ∠ A=∠ B, ∠ D=∠ C,AD=BC 二、AE AD, AB AC, AEAD,1.已知:①或②B或③BCABACC求证 : ①∠ B=∠ C,或② AE=AD,或③ AB=AC.AEAD,证明:①AB, △ ABE ≌△ ACD ∠ B=∠C;ABAC.或②或③AB AC,B C,A A.B C, AD AE,AA.△ ABE ≌△ ACD AE=AD;△ ABE ≌△ ACD AB=AC.2.(1) 证明 : ∵△ ABC ≌△ DCE ≌△ FEG,1∴ BC=CE=EG= BG=1,即 BG=3.3∴ FG=AB= 3 , ∴FGBG 3 = 3 EGFG 3又∠ BGF=∠ FGE,∴△ BFG ∽△ FEG.∵△ FEG 是等腰三角形 , ∴△ BFG 是等腰三角形 . ∴ BF=BG=3. (2)A层问题 ( 较简易的 , 仅用到了 1 个知识点 ).比方 : ①求证 : ∠PCB=∠ REC(或问∠ PCB 与∠ REC 可否相等 ?)等 ; ②求证 :PC ∥ RE.( 或问线段 PC 与 RE 可否平行 ?) 等 . B层问题 ( 有必然思虑的 , 用到了 2~ 3 个知识点 ). 比方 : ①求证 : ∠ BPC=∠ BFG 等 ,? 求证 :BP=PR 等 . ②求证 : △ ABP ∽△ CQP 等, 求证 : △ BPC ∽△ BRE 等 ; ③求证 : △ APB ∽△ DQR 等; ④求 BP:PF 的值等 .C 层问题 ( 有深刻思虑的 , 用到了 4 个或 4 个以上知识点或用到了 (1) 中结论 ).比方 : ①求证 : △APB ≌△ ERF;②求证 :PQ=RQ 等 ;③求证 : △BPC 是等腰三角形 ;? ④求证 : △PCQ ≌△ RDQ 等 ; ⑤求 AP:PC 的值等 ; ⑥求 BP 的长 ;⑦求证 :PC=3( 或求 PC 的长 ) 等.3A 层解答举例 . 求证 :PC ∥ RE.证明 : ∵△ ABC ≌△ DCE, ∴∠ PCB=∠ REB. ∴ PC ∥RE.B 层解答举例 . 求证 :BP=PR.证明 : ∵∠ ACB=∠ REC,∴ AC ∥ DE.又∵ BC=CE,∴ BP=PR.C 层解答举例 .求 AP:PC 的值 .解 : ∵ AC ∥ FG,∴PCBC1 , ∴PC= 3 . FG BG3 3∵AC= 3 , ∴AP= 3 -3 = 2 3, ∴ AP:PC=2. 3 33. 解 :(1) 如图 , 由题意知 :P1(-3,9),P 2(-2,4),P3(-1,1),P4(0,0).S 四边形 P1P2P3P4=S △ P1H1P4-S 梯形 P1H1H2P2-S 梯形 P2H2H3P3-S △P3H3P4 =1× 9×3- 1 × (9+4) × 1-1×(4+1) × -1× 1× 1=4.2222S 四边形 P2P3P4P5=4.(2)四边形 P n-1 P n P n+1P n+2 的面积为 4.原由 :过点 P n-1 、P n 、 P n+1、 P n+2 分别作 P n-1 H n-1 、 P n H n 、 P n+1H n+1、 P n+2H n+2 垂直于 x 轴, 垂足分别为H n-1 、 H n 、 H n+1、H n+2.设 P n-1 、 P n 、 P n+1 、 P n+2 四 点 的 横 坐 标 依 次 为 x-1,x,x+1,x+2,?则 这 两 个 点 的 纵 坐 标 分 别 为(x-1) 2,x 2,(x+1) 2 ,(x+2) 2.所以四边形 P PP P 的面积n-1n n+1 n+2=梯形 P n-1 H n-1 H n+1P n+2 的面积 - 梯形 P n-1 H n-1 H n P n 的面积 -? 梯形 P n H n H n+1P n+1- 梯形 P n+1H n+1H n+2P n+2 的面积 =3[(x-1)2+(x+2) 2]-1[(x-1)2+x 2]- 1· [x 2+(x+1) 2]-1[(x+1) 2+(x+2) 2]2222=(x-1) 2222+(x+2) -x -(x+1) =4.(3) 四边形 P n-1 P n P n+1P n+2 的面积为 4. 4.(1)DG=CG;DE=BF;CF=CE;AF=AE;AG=BG.(2)举例说明 AG=BG.∵在梯形 ABCD 中 ,AB ∥ DC,AD=BC, ∴梯形 ABCD 为等腰梯形 .∴∠ GAB=∠ GBA.∴ AG=BG.。
2019年中考数学一轮复习 第八章 专题拓展 8.3 开放探究型(试卷部分)课件

(江苏专用)
§8.3
开放探究型
பைடு நூலகம்
好题精练
一、选择题
1.(2015枣庄,10,3分)如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部 分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这 两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方 形的作法共有 ( )
.
①EF= 2 OE;②S四边形OEBF∶S正方形ABCD=1∶4;③BE+BF= OA 2;④在旋转过程中,当△BEF与△COF
3 ;⑤OG· 的面积之和最大时,AE= BD=AE2+CF2. 4
答案 ①②③⑤
解析 ∵四边形ABCD是正方形,∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,∴∠BOF+ OF=90°,∵∠EOF=90°,∴∠BOF+∠BOE=90°,∴∠BOE=∠COF,∴△BOE≌△COF(ASA),
点E、F都存在,连接EF,如图②所示,问:点D是否存在某一位置,使ED平分∠BEF且FD平分∠
BD CFE?若存在,求出 的值;若不存在,请说明理由; BC
【探索】如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点 放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的 顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为 (用含α的表达式表示).
3.(2016随州)如图,边长为1的正方形ABCD的对角线AC,BD相交于点O.有直角∠MPN,使直角 顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<
2019年中考数学试卷分类汇编:开放性问题(含答案)
数学精品复习资料开放性问题1. (2014•四川巴中,第28题10分)如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.考点:矩形的判定.分析:(1)根据全等三角形的判定方法,可得出当EH=FH,BE∥CF,∠EBH=∠FCH 时,都可以证明△BEH≌△CFH,(2)由(1)可得出四边形BFCE是平行四边形,再根据对角线相等的平行四边形为矩形可得出BH=EH时,四边形BFCE是矩形.解答:(1)答:添加:EH=FH,证明:∵点H是BC的中点,∴BH=CH,在△△BEH和△CFH中,,∴△BEH≌△CFH(SAS);(2)解:∵BH=CH,EH=FH,∴四边形BFCE是平行四边形(对角线互相平分的四边形为平行四边形),∵当BH=EH时,则BC=EF,∴平行四边形BFCE为矩形(对角线相等的平行四边形为矩形).点评:本题考查了全等三角形的判定和性质以及平行四边形的判定,是基础题,难度不大.2. (2014•山东威海,第24题11分)猜想与证明:如图1摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD 上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.拓展与延伸:(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为DM=DE.(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF 的中点,试证明(1)中的结论仍然成立.3. (2014•山东枣庄,第22题8分)如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.(1)求证:△BOE≌△DOF;(2)若OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.,出发,以相同的速度在直线DC,CB上移动.(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明)(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最小值.考点:全等三角形,正方形的性质,勾股定理,运动与变化的思想.分析:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;(4)由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD的中点为O,连接OC交弧于点P,此时CP的长度最小,再由勾股定理可得OC的长,再求CP即可.解答:(1)AE=DF,AE⊥DF.理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.∵DE=CF,∴△ADE≌△DCF.∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;(3)成立.理由:由(1)同理可证AE=DF,∠DAE=∠CDF延长FD交AE于点G,则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图:由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为O,连接OC交弧于点P,此时CP的长度最小,在Rt△ODC中,OC=,∴CP=OC﹣OP=.点评:本题主要考查了四边形的综合知识.综合性较强,特别是第(4)题要认真分析.5. (2014•浙江杭州,第23题,12分)复习课中,教师给出关于x的函数y=2kx2﹣(4kx+1)x﹣k+1(k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选出以下四条:①存在函数,其图象经过(1,0)点;②函数图象与坐标轴总有三个不同的交点;③当x>1时,不是y随x的增大而增大就是y随x的增大而减小;④若函数有最大值,则最大值比为正数,若函数有最小值,则最小值比为负数.教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法.,﹣﹣。
2019届人教版中考复习数学练习专题三:开放型探索专题(含答案)
专题三开放型探索专题的青睐,中考题型以填空题、解答题为【课堂精讲】例如图,在四边形中,点是的中点,作射线,在线段及其延长线上分别取点,,连结,.()请你添加一个条件,使得△≌△,你添加的条件是,并证明.()在问题()中,当与满足什么关系时,四边形是矩形,请说明理由.分析:()根据全等三角形的判定方法,可得出当,∥,∠∠时,都可以证明△≌△,()由()可得出四边形是平行四边形,再根据对角线相等的平行四边形为矩形可得出时,四边形是矩形.解答:()添加:,证明:∵点是的中点,∴,在△△和△中,,∴△≌△();()解:∵,,∴四边形是平行四边形(对角线互相平分的四边形为平行四边形),∵当时,则,∴平行四边形为矩形(对角线相等的平行四边形为矩形).本题考查了全等三角形的判定和性质以及平行四边形的判定基础题,难度不大例.如图--,边长为的正方形的对角线,相交于点.有直角∠,使直角顶点与点重合,直角边,分别与,重合,然后逆时针旋转∠,旋转角为θ(°<θ<°),,分别交,于,两点,连结交于点,则下列结论中正确的是.①=;②四边形∶正方形=∶;③+=;④在旋转过程中,当△与△的面积之和最大时,=;⑤·=+.图--第题答图【解析】∵四边形是正方形,∴=,∠=∠=°,∠=°,∴∠+∠=°,∵∠=°,∴∠+∠=°,∴∠=∠,∴△≌△(),∴=,=,∴=.故①正确;∵四边形=△+△=△+△=△=正方形,∴四边形∶正方形=∶.故②正确;∵+=+==.故③正确;如答图,过点作⊥交于点,∵=,∴==,设=,则==-,=,∴△+△=·+·=(-)+(-)×=-+,∵=-<,∴当=时,△+△最大,即在旋转过程中,当△与△的面积之和最大时,=.故④错误;∵∠=∠,∠=∠=°,∴△∽△,∴∶=∶,∴·=,∵=,=,∴·=,∵在△中,=+,∴=+,∴·=+.故⑤正确.故答案为①②③⑤.【课堂提升】.如图,直线、被直线所截,若满足,则、平行..写出一个运算结果是的算式..如图--,是经过∠顶点的一条直线,=,分别是直线上两点,且∠=∠=∠α.()若直线经过∠的内部,且,在射线上,请解决下面两个问题:①如图①,若∠=°,∠α=°,则;-(选填“>”“<”或“=”);②如图②,若°<∠<°,请添加一个关于∠α与∠关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.()如图③,若直线经过∠的外部,∠α=∠,请写出,,三条线段数量关系的合理猜想(不要求证明).图--.如图--①,将一张矩形纸片沿着对角线向上折叠,顶点落到点处,交于点.()求证:△是等腰三角形;()如图②,过点作∥,交于点,连结交于点.①判断四边形的形状,并说明理由;②若=,=,求的长..如图,正方形中,点,分别在边,上,,和相交于点,()观察图形,写出图中所有与∠相等的角。
【复习必备】2019【提分必备】中考数学专题复习 开放性问题复习当堂达标题 (新版)新人教版
开放性问题一、填空题1.如图,已知AC ⊥BD 于点P ,AP =CP ,请增加一个条件,使得△ABP ≌△CDP (不能添加辅助线),你增加的条件是________.2.反比例函数y =m x(m ≠0)与一次函数y =kx +b (k ≠0)的图象如图所示,请写出一条正确的结论:________.3.两个不相等的无理数,它们的乘积为有理数,这两个数可以是______.4.已知x 2-ax -24在整数范围内可以分解因式,则整数a 的值是______(只需填一个). 5.有一个二次函数的图象三位学生分别说出了它的一些特点: 甲:对称轴是直线x =4;乙:与x 轴两个交点的横坐标都是整数;丙:与y 轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式:______. 二、选择题6.如图,△ABC 是不等边三角形,DE =BC ,以D 、E 为两个顶点作不同位置的三角形,使所作三角形与△ABC 全等,这种三角形最多可以画出( ) .A .2个B .4个C .6个D .8个 7.已知道三角形的三边长分别为4, 5, x ,则x 不可能是( ) . A.3 B.5 C.7 D.98.点A ,B ,C ,D 在同一平面内,从①AB 平行CD ;②AB =CD ;③BC 平行AD ;④BC =AD 这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有( ) . A.2种 B.3种 C.4种 D.5种三、解答题9.在一服装厂里有大量形状为等腰直角三角形的边角余布料.现找出其中的一种,测得∠C =90°,AC =BC =4,今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC 的边上,且扇形的弧与△ABC 的其他边相切.请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径).10.阅读函数图象,并根据你所获得的信息回答问题:(1)折线OAB 表示某个实际问题的函数图象,请你编写一道符合该图象意义的应用题; (2)根据你给出的应用题分别指出x 轴、y 轴所表示的意义,并写出A 、B 两点的坐标; (3)求出图象AB 的函数解析式,并注明自变量x 的取值范围.开放性问题复习当堂达标题答案1.答案不唯一,如BP =DP 或AB =CD 或∠A =∠C 或∠B =∠D 或AB //CD .2.答案不唯一,如反比例函数解析式为y =2x或一次函数解析式为y =x +1等.故存在点P 1(-3,-9)和点P 2(9,-9)满足题意.3. 2+1和2-1等4.略5. :y =±(51x 2-58x -3) y =±(71x 2-78x +1) 6. B 7. D 8. C9.10. 答:张老师从家里出发,乘汽车去学校,汽车的速度为每小时25 km ,经过2h 到达学校.到校后由于家中有事,立即骑自行车返回,再经过5h 到家.(2)x 轴表示运动时间,单位是小时,y 轴表示运动的路程,单位是千米.A (2,50),B (7,0) (3)设AB 的解析式为y =kx +b ,则⎩⎨⎧=+=+07502b k b k 解之,得⎩⎨⎧=-=7010b k∴ y =-10x +70(2≤x ≤7).。
中考数学专题复习突破篇四开放探索问题课件
【解析】答案不唯一. (1)水塔上面的蓄水池深8米,往里蓄满水用5分钟,接着 打开底部的排水管放完全部的水用去了10分钟.
(2)x轴表示时间(分),y轴表示蓄水池的深度(米). A(5,8),B(15,0).
(3)设图象AB的函数解析式为y=kx+b.把A(5,8),B(15,0)
代入上式,得
(1)上述三个条件中,由哪两个条件可以判定△ABC是等 腰三角形?(用序号写出所有成立的情形) (2)请选择(1)中的一种情形,写出证明过程.
【解析】(1)①②;①③. (2)选①②证明如下: 如图,
在△BOE和△COD中, ∵∠EBO =∠DCO,∠EOB=∠DOC,BE=CD, ∴△BOE ≌△COD(AAS). ∴BO=CO.∴∠OBC=∠OCB. ∴∠EBO+∠OBC=∠DCO+∠OCB.
(2)设☉O的半径为r.
在Rt△OBE中,∵OE2=EB2+OB2,
∴(4-r)2=22+r2,∴r=1.5, ∵tan E= OB=CD,
EB DE
∴ 1.5=,C∴DCD=BC=3,
24
在Rt△ABC中,AC= AB2 BC2= 32 32=3 2. ∴圆的半径为1.5,AC的长为 3 .2
(2)①当四边形ADOE是正方形时,利用正方形的性质解 答即可; ②当四边形ADCE是菱形时,利用菱形的性质解答即可.
【自主解答】 略
【规律方法】 解决条件开放类问题的方法
从所给的结论出发,设想出合乎要求的一些条件,逐一 列出,运用所学的定理,进行逻辑推理,从而找出满足结 论的条件.
【题组过关】 1.如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交 于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;] ③OB=OC.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题综合检测(一)
(30分钟 50分)
一、选择题(每小题5分,共15分)
1.(2018·莆田中考)等腰三角形的两条边长分别为3,6,那么它的周长为( )
(A)15 (B)12
(C)12或15 (D)不能确定
2.如图,直线y=x+2与双曲线m3yx在第二象限有两个交点,那么m的取值范围在数轴上表示为( )
3.(2017·宁波中考)如图,用邻边长分别为a,b(a﹤b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与
矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的
侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),
则a与b满足的关系式是( )
(A)b3a (B)51ba2
(C)5ba2 (D)b2a
二、填空题(每小题5分,共10分)
4.已知x2+x-1=0,则代数式2x3+4x2+3的值为________________________.
5.(2018·潜江中考)已知ABCD的周长为28,自顶点A作AE⊥CD于点E,AF⊥CB于点F.若AE=3,AF=4,
则CE-CF=_______________.
三、解答题(共25分)
6.(12分)(2017·黄冈中考)新星小学门口有一直线马路,为方便学生过马路,交警在门口设有一定宽度的斑
马线,斑马线的宽度为4 米,为安全起见,规定车头距斑马线后端的水平距离不得低于2 米,现有一旅游
车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15° 和∠FAD=30° .司机距
车头的水平距离为0.8 米,试问该旅游车停车是否符合上述安全标准(E,D,C,B 四点在平行于斑马线的同一直
线上)?
6262(tan1523sin15cos1531.73221.414)44
参考数据:,,,,
【探究创新】
7.(13分)(2017·河北中考)如图1和图2,在△ABC中,AB=13,BC=14,cos∠ABC=513.
探究如图1,AH⊥BC于点H,则AH=________,AC=________,
△ABC的面积S△ABC=__________.
拓展 如图2,点D在AC上(可与点A,C重合),分别过点A,C作直线BD的垂线,垂
足为E,F,设BD=x,AE=m,CF=n.(当点D与点A重合时,我们认为S△ABD=0)
(1)用含x,m或n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现请你确定一条直线,使得A,B,C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
答案解析
1.【解析】选A.由题意可知:当6是腰时,三角形的周长是15;当3是腰时,3+3=6,不能组成三角形.
2.【解析】选B.由题意可得m-3<0,故m<3;由直线y=x+2与双曲线m3yx在第二象限有两个交点,可
得m3x2x,即x2+2x-(m-3)=0,即Δ=4+4(m-3)>0,所以m>2.综上,可得2
得1ra.4
在Rt△O1O2H中,O1O2=13raa24, O1H=12b,211OHara.24
又O1O22=O1H2+O2H2,
所以222311(a)(b)(a)424,解得b2a.故选D.
4.【解析】把x2+x看成一个整体,得x2+x=1,所以2x3+4x2+3=2x3+2x2+2x2+3=
2x(x2+x)+2x2+3=2x+2x2+3=2(x2+x)+3=2+3=5.
答案:5
5.【解析】(1)当E,F分别在线段CD和CB上时,如图所示:
设BC=x,DC=y,则根据题意可得:xy144x3y,,
解得x6y8,,即BC=6,DC=8,根据勾股定理可知2222DE6333BF8443,,
所以CE-CF= 83364323.
(2)当E,F分别在CD,CB的延长线上时,如图所示:
同理可得CE-CF=2-3.
答案:2323或
6.【解析】由题意得:∠FAE=15°,∠FAD=30°,
∴∠EAD=15°.
∵FA∥BE, ∴∠AED=15°,即AD=DE=4米.
在Rt△ADB中,∠ADB=∠FAD=30°,
∴BD=AD·cos30°34232≈3.464米,
DC=BD-BC=3.464-0.8=2.664米>2米,
∴该车停车符合上述安全标准.
7.【解析】探究 12 15 84
拓展 (1)由三角形面积公式,得ABDCBD11Smx,Snx.22VV
(2)由(1)得CBDABD2S2Sm,n,xxVV
∴m+n= CBDABD2S2S168.xxxVV
由于AC边上的高为ABC2S28456,15155V
∴x的取值范围是565≤x≤14.
∵(m+n)随x的增大而减小,
∴当x=565时,(m+n)的最大值为15;
当x=14时,(m+n)的最小值为12.
(3)x的取值范围是x=565或13
【高手支招】解压轴题时遇到困难的原因及应对策略
原因:在解压轴题时遇到的困难可能来自多方面,如基础知识和基本技能欠缺、解题经验缺失或训练程度
不够、自信心不足等,具体表现可能是“不知从何处下手,不知向何方前进”.
应对策略:在求解中考数学压轴题时,要重视一些数学思想方法的灵活应用.数学思想方法是解好压轴题的
重要工具,也是保证压轴题能求解的“对而全、全而美”的重要前提.
针对近年全国各地中考数学压轴题的特点,在学习中要狠抓基础知识的落实,因为基础知识是“不变量”,
而所谓的考试“热点”只是与题目的形式有关.有效地解答中考压轴题的关键是要以不变应万变.加大综合题
的训练力度,加强解题方法的训练,加强数学思想方法的渗透,注重“基本模式”的积累与变化
