电磁学第1章
合集下载
电磁学习题案1-3章
第一章 习题一1、电量Q 相同的四个点电荷置于正方形的四个顶点上，0点为正方形中心，欲使每个顶点的电荷所受电场力为零，则应在0点放置一个电量q ＝－(1+2√2)Q/4 的点电荷。
2、在点电荷系的电场中，任一点的电场强度等于各点电荷单独在该点产生场强的矢量和，这称为电场强度叠加原理。
3、一点电荷电场中某点受到的电场力很大，则该点的电场强度E ：( C )(A)一定很大 (B)一定很小 (C)可能大也可能小4、两个电量均为+q 的点电荷相距为2a ，O 为其连线的中点，求在其中垂线上场强具有极大值的点与O 点的距离R 。
解法一：22020214141aR qπεr q πεE E +=== 21E E E ϖϖϖ+=，θE θE θE E cos 2cos cos 121=+=2222042a R R a R q πε++=()2/32202a R R πεq +=E 有极值的条件是：()0222/522220=+-=a R R a πεq dR dE 即 0222=-R a ，解得极值点的位置为：a R 22=∵ ()2/722220223223a R a R πεqR dR E d +-=，而 0398402/222<-==aπεqdR E d a R ∴ 中垂线上场强具有极大值的点与O 点的距离为a R 22= 且 ()202/3220max 332/2/2aπεq a a a πεq E =+=解法二：θaq πεr q πεE E 2202021sin 4141===，21E E E ϖϖϖ+=ϖ+qθE θE θE E cos 2cos cos 121=+=θθaq πεcos sin 21220=)cos (cos 21320θθaq πε-=E 有极值的条件是：0)sin 3sin 2(2320=-=θθaπεq θd dE E 有极值时的θ满足：31cos 32sin 1cos 0sin 2211====θ，θ；θ，θ )cos 7cos 9(2)cos sin 9cos 2(232022022θθaπεq θθθa πεq θd E d -=-= 0)cos 7cos 9(22011320221>=-==aπεq θθa πεq θd E d θθ 032)cos 7cos 9(22022320222<-=-==aπεq θθa πεq θd E d θθ 可见 θ = θ2时，E 有极大值。
04-1-第1章-静止电荷的电场-电磁学-大学物理-海南大学
相当于电荷集中在盘心的一个点电荷所 产生的电场。
四、点电荷电场强度
例 P.17定： （ 1 ）曲线上每一点的切线方向表示该点场强 的方向；
五、电场线和电通量 规定： （2）曲线的疏密表示该点场强的大小，即该点 附近垂直于电场方向的单位面积所通过的电力 线条数满足
xdq 1 x 2d dE P 2 2 3/ 2 4 0 ( x ) 4 0 ( x 2 2 ) 3 / 2 1
四、点电荷电场强度
E P dE P 1 4 0
R
0
x 2d ( x 2 2 )3 / 2
2 0
x 1 ( R 2 x 2 )1 / 2
1 e 3 或 2 e 3
至今尚未从实验中直接发现单独存在的夸克 或反夸克，仅在一些间接的实验中得到验证。
一、电荷
5.电荷的连续分布
电磁现象的宏观规律 大量电荷 电荷在带电体上连续分布
一、电荷
6.电荷守恒定律
由摩擦生电的实验可见，当一种电荷出现 时，必然有相等量值的异号电荷同时出现；一 种电荷消失时，必然有相等量值的异号电荷同 时消失。 因此，在孤立系统中，不管其中的电荷如何迁 移，系统的电荷的代数和保持不变，这就是电 荷守恒定律。
q E dS
S
0
对包含电荷 q 的任意闭合 曲面都成立。
四、点电荷电场强度
讨论： 当 x <<R
EP 2 0
x 时， ( R 2 x 2 )1 / 2 0
为无限大均匀带电 平板附近的电场分 布，是匀强电场。
四、点电荷电场强度 如果将两块无限大平板平行放置，板间距离 远小于板面线度，当两板带等量异号电荷， 面密度为σ 时， 两板内侧场强为
第1章磁路
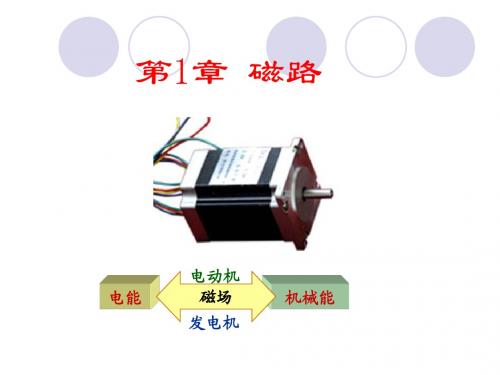
T 1T
从铸钢磁化曲线查得：与BFe对应的HFe=9×102A/m 铁心段的磁位降： H Fe l Fe 9 10 0 . 3 A 270 A
2
空气隙中： B
H
A B
0 . 0009 3 . 05 10
2 4
T 0 . 967 T
4
0 . 967 4 10
电磁力方向：左手定则判断
f
在旋转电机里，作用在转子载流导体上的电磁力将 使转子受到一个力矩，即为电磁力矩。在电机进行 机电能量转换过程中起着重要作用。
上一张下一张
4. 磁路欧姆定律
Φ 铁心中： Bc = u Ac Bc － Φ = Hc = c c Ac 气隙中： B0 = Φ A0 B0 Φ = H0 = 0 0 A0 安培环路定律: ∮H dl = I =F
N I 一定时， 因 Rm0 的存在，使Φ 大大减小； 若要保持 Φ 一定，则需增大磁动势 F。
上一张下一张
5、磁路的基尔霍夫第一定律
任何磁路中，流进节点的磁通代数和为零 A
1
2
3
节点A： 1+ 2+ 3=0
6、磁路的基尔霍夫第二定律 在闭合磁回路中，磁路各段磁压降代数和等于 作用于该磁路上的磁动势之和。 Hl Ni 该定律的本质是全电流定律。
上一张下一张
(3)铁芯损耗
铁芯中的磁滞损耗和涡流损耗之合称为铁芯损耗， 即有：
p Fe p h p w
1 .3
对于一般的电工硅钢片，可以近似写成：
PFe C Fe f
B G
2 m
铁心损耗与频率的1.3次方、磁通密度的平方和 铁心重量成正比。
第1章电磁学的基本知识与基本定律
则上式变为:
e(t) 2fN m sin(t 900 )
2 E sin(t 900 )
若取 m m0 为参考相量，则：
E j4.44 fN m
(1-5)
速度电势：
图1.3 磁通与感应电势的相量图
图1.4 感应电势与磁场、导体运动速度之间的右手定则
e Blv
(1-6)
1.3.3 电磁力定律
精品课件！
精品课件！
图1.1 磁力线与电流之间的右螺旋关系
磁通量
SB dS
(1-1)
若对于均匀磁场，若B与S垂直，则
BS
磁场强度H
B H
(1-2)
磁势：
F Ni
磁链：
N
1.3 基本电磁定律
电生磁的基本定律——安培环路定律 磁生电的基本定律——法拉第电磁感应定律 电磁力定律 磁路的欧姆定律
1.3.5 线圈电感
根据 N 和式（1-8）得：
L i
L
N 2m
N2
S
l
上式给出了电感与结构参数以及磁性材料之间的关系式。
1.4 常用磁性材料及其特性
1.4.1 铁磁材料的磁化及磁滞回线
图1.10 铁磁材料的磁化
图1.11 磁性材料的磁滞回线
1.4.2 磁化曲线与饱和现象
图1.12 铁磁材料与非铁磁材料的磁化曲线
1.3.1 电生磁的基本定律——安培环路定律
LH dl ik Ni
(1-3)
若闭合磁力线上 H 处处相等,则上式变为: HL Ni
1.3.2 磁生电的基本定律——法拉第电磁感应定律
图1.2 磁通与其感应电势的正方向假定
d d
变压器电势：
e N
第1章 交变电磁场
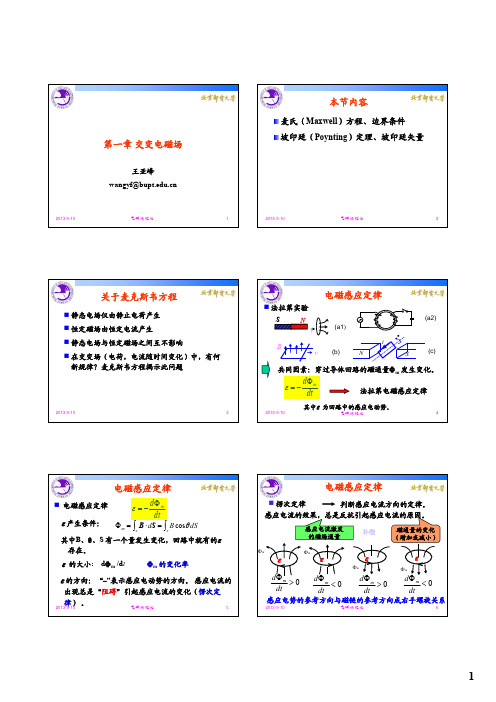
dq S J c dS dt
H dl 0
l
I
矛盾，环路定理需要修正
2013-9-10
电磁场理论
~
（对于S1面） （对于S2面）
11
S
S
D dS q
D dS 0 t
12
得到
J
2013-9-10
c
电磁场理论
(6.25)
2013-9-10
电磁场理论
31
2013-9-10
32
复数形式的麦克斯韦方程
对下面的瞬时表示式
E ( x, y , z , t ) B ( x, y , z , t ) t
复数形式的麦克斯韦方程
由于以上两式相等，则得
E ( x , y , z ) j B (x , y , z )
29
5
复数形式的麦克斯韦方程
假定电场强度E的瞬时值表示式为
复数形式的麦克斯韦方程
取其实部(用Re表示)则得到瞬时值的表示式
j t E (x, y , z, t ) Re E ( x, y , z ) e
E (x, y , z, t ) E0 ( x, y , z ) cos(t )
24
4
微分形式麦克斯韦方程组
D H J t E B t D B 0
本构关系
在各向同性的媒质中
D E B H J E
2013-9-10
电磁场理论
25
2013-9-10
电磁场理论
26
麦克斯韦方程组的意义
27 2013-9-10 28
第一章静电场的基本规律 大学电磁学
六、计算
1、两个相同的导体球带有异号电荷，相距0.5m时彼此以0.108N的力相吸，两球用一导线连接，然后将导线拿去，此后彼此以0.036N的力相斥。问两球上原来的电量各是多少？
解：设两导体球带电量分别为 、 ，由库仑定律得
．．．．．．．．．．．．．．．．．．．．．．．．①
两球用导线连接后，两球带相等电量 ，再由库仑定律得
（C）高斯面内必无净电荷
（D）高斯面外必无电荷
8、两个点电荷 固定在一条直线上。相距为d，把第三个点电荷 放在 的延长在线，与 相距为d，故使 保持静止，则（C）
（A） （B）
（C） （D）
9、电偶极矩 的电偶极子位于电量为Q的点电荷的电场中，点电荷Q到偶极子中心O的距离为r（r>>l）当P与r平行时，偶极子所受的力和力矩为（A）
不变化变化不变化变化
4、一均匀带电球面，电量为Ｑ，半径为Ｒ，在球内离球心Ｒ／２处放一电量为q的点电荷，假定点电荷的引入并不破坏球面上电荷的均匀分布，整个带电系统在球外Ｐ点产生的电场强度（）。
5、电偶极子在外电场中的能量（）。
6、（1）先把偶极子的负电荷从无限远处搬到电场中r处，再把正电荷从无限远处搬到 处，反抗电场力作的功（）;（2）把偶极子作为一整体（保持 恒定），从无限远处搬到电场中给定的位置，反抗电场力作的功（）。
二、选择题（答案中，只有一个是正确的）
1、将一带电量为Q的金属小球靠近一个不带电的静电感应带电，总电量为-Q
（B）金属导体因感应带电，靠近小球的一端带-Q，远端带+Q
（C）金属导体两端带等量异号电荷，且电量q<Q
（D）当金属小球与金属导体相接触后再分离，金属导体所带电量大于金属小球所带电量
9、两个小球都带正电，总共带有电荷 ，如果当这两个小球相距2.0m时，任一球受另一球之斥力为1.0N，则两球所带电量分别是（）（）。
1、两个相同的导体球带有异号电荷，相距0.5m时彼此以0.108N的力相吸，两球用一导线连接，然后将导线拿去，此后彼此以0.036N的力相斥。问两球上原来的电量各是多少？
解：设两导体球带电量分别为 、 ，由库仑定律得
．．．．．．．．．．．．．．．．．．．．．．．．①
两球用导线连接后，两球带相等电量 ，再由库仑定律得
（C）高斯面内必无净电荷
（D）高斯面外必无电荷
8、两个点电荷 固定在一条直线上。相距为d，把第三个点电荷 放在 的延长在线，与 相距为d，故使 保持静止，则（C）
（A） （B）
（C） （D）
9、电偶极矩 的电偶极子位于电量为Q的点电荷的电场中，点电荷Q到偶极子中心O的距离为r（r>>l）当P与r平行时，偶极子所受的力和力矩为（A）
不变化变化不变化变化
4、一均匀带电球面，电量为Ｑ，半径为Ｒ，在球内离球心Ｒ／２处放一电量为q的点电荷，假定点电荷的引入并不破坏球面上电荷的均匀分布，整个带电系统在球外Ｐ点产生的电场强度（）。
5、电偶极子在外电场中的能量（）。
6、（1）先把偶极子的负电荷从无限远处搬到电场中r处，再把正电荷从无限远处搬到 处，反抗电场力作的功（）;（2）把偶极子作为一整体（保持 恒定），从无限远处搬到电场中给定的位置，反抗电场力作的功（）。
二、选择题（答案中，只有一个是正确的）
1、将一带电量为Q的金属小球靠近一个不带电的静电感应带电，总电量为-Q
（B）金属导体因感应带电，靠近小球的一端带-Q，远端带+Q
（C）金属导体两端带等量异号电荷，且电量q<Q
（D）当金属小球与金属导体相接触后再分离，金属导体所带电量大于金属小球所带电量
9、两个小球都带正电，总共带有电荷 ，如果当这两个小球相距2.0m时，任一球受另一球之斥力为1.0N，则两球所带电量分别是（）（）。
电磁场课件第一章电磁场的四个基本量
电荷作用力研究带给我们的启示
• 从万有引力得到的启示
但是卡文迪什的同心球实验结果和他自己的许多看法， 却没有公开发表。直到19世纪中叶，开尔文（即W.汤 姆生）发现卡文迪什的手稿中有圆盘和同半径的圆球所 带电荷的正确比值，才注意到这些手稿的价值，经他催 促，才于1879年由麦克斯韦整理发表。卡文迪什的许 多重要发现竟埋藏了一百年之久。
F12
q1q2
4 0 r 2
ar
q1q2
4 0 r 3
r , F21
...
r q1
F12 q2
Q
q
q q
库仑力的特点
• 库仑力大小与相对距离有关系（平方反 比）；
• 库仑力大小与电荷电量有关系（成正比）； • 库仑力作用方向在电荷连线上且和两电荷
属性有关。 • 库仑力具有非接触的分布特性。
1.2 理论解释和电场强度的定义
每米平方），求平面前距离为R的P 点处的电场强度。
dx
x
p dE
0
R
dE
图1- 3 无限大均匀带电平面电场
二、用场的方法分析电场
已知电场分布，分析其通量、散度、环 量和旋度。 2.1 高斯定律 2.2 静电场的散度 2.3 静电场的环量和旋度 2.4 电势函数
2.1 高斯定律
点电荷通过以电荷为中
电荷作用力研究带给我们的启示
麦克斯韦对卡文迪什的评价
“这些关于数学和电学实验的手稿近20捆，” 其中 “物体 上电荷 （分布）的实验，卡文迪什早就写好了详细的叙述， 并且费了很大气力书写得十分工整（就象要拿出去发表的 样子），而且所有这些工作在1774年以前就已完成，但卡 文迪什（并不急于发表）仍是兢兢业业地继续做电学实验， 直到1810年去世时，手稿仍在他自己身边。”
赵凯华-电磁学-第三版-第一章-静电场-129-pages
rˆ
变形
F q0
(1)
4 0 r
q
2
rˆ
与试探电荷无关：
仅与q、空间位置有关 ，反映场的性质 单位正电荷所受的力
定义 E F q0
是描述场中各点电场强弱的 物理量即:电场强度 为矢量：大小、方向与单位 正电荷所受电场力的相同
量纲、单位
国际单位制量纲
E
F
则令： K=1(如牛顿第二定律中的K)a=F/m
库仑定律的k值确定 (两种方法) SI
第一种 国际单位制中
K 9 109m2 N / c2
第二种 高斯制中 电量的单位尚未确定
f
q1q2 r2
令 K = 1 库仑定律的常用形式
目前使用率低
有 理 化
令
K 1
4 0
0
8.85 1012
条形永久强磁体， 由外部磁场驱动）； ②能摄像: 通过微型摄像机， ③能图像传输：无线发射图像信号（直播）。
（5）优点：无创检查和小 损伤手术。 （比较：内窥镜透视、放射造影或手术检查）
3）电磁现象的普遍性
(a) 各种宏观接触力（如摩擦力、弹力等）
的微观本质是电、磁作用力；
(b) 电磁作用力是四种基本相互作用的一种：
E F q0
r
下页）
从源电荷指向场点
由上述 两式得
E
4
q
0r2
rˆ
场强方向： 正电荷受力方向
z
F q0
q
4 0r 2
rˆ
o
A
y 球对称！
j x
静电场基本 特性的原因
！！！
电磁学 (王楚 李椿 周乐柱 著) 北京大学出版社 课后答案 第一章 课后答案【khdaw_lxywyl】
R x/2
课
后 答
w.
1.19
案 网
co
1.16 (1) a
带正电， b 带负电
m
I (3.1 1.1) 1018 1.6 1019 0.67 A
第一章习题答案 1.20 忽略电子的质量 达到平衡后有 F q(v B E ) 0 v B E 0 v是电子速度
4
(1)
M
(2) Lmax MB 2.12 4 103 8.48 103 Nm
kh
0 I1 1 1 ( ) 2 x x a
2a
F ( x) I 2 a[( B ( x) b(a x)]
IN
课
0 I1 I 2 a 2 a 1 1 ( )dx a 2 x xa
w.
案 网
x cos 2
co
-L/2
m
o
θ
1 Q 1 1 ( ) ( x l ) 4 0 L x L x L 0 2 2 Q 1 L (x ) 2 4 0 2 L 2 x 4 4 L
L 2
Q
L 2
d
根据对称性知
E ( x) Q 4 0 1 x2 L 4
w.
Q dl L E ( x) L 2 4 ( x l ) 2 0
L 2
kh
Q L 2 L2 x2 4 Q
L 2
课
L 2
da
2 0 x L2 4 x 2ቤተ መጻሕፍቲ ባይዱ
x 0
4 L
0
Q
L 2
dl ( x l )2
后 答
电磁学复习提纲 赵凯华
0 Il 2
2
dΦ dt
r l1
0 I
2 x
b
l2 dx
l1
c
l2
r
ln
r l1 r
dΦ dr dr dt dΦ dr
I
v
x a r o
dx d x
0 I 0l1l2 v
2r ( r l2 )
方向：顺时针方向
28
一直导线CD在一无限长直电流磁场中作 切割磁力线运动。求：动生电动势。 解： 方法一
18
三、掌握复杂电路的基尔霍夫定律 掌握电压、电流的规定，会列节点电流方程和 回路电压方程 流入节点的电流前面取“-”号， ±I 0 在流出节点的电流前面取“+” U ( ) 号 ( IR ) 0
(2) 电阻元件的端电压为 ±RI，当电流 I 的参考 方向与回路绕行方向一致时，选取“+”号；反之， 选取“”号； (3) 电源电动势为 E，当电源电动势的方向与回 路绕行方向一致时，选取“-”号，反之应选取“+” 号。
V x
电场强度和电势是描述静电场的两个物理量能， 两者的关系是微积分的关系。
2
二、 计算电场强度和电势
电场
(3) E V q ˆ 点电荷：E r 2 4 r
◆常见带电体的场强及电势
(1) 场强公式； (2) 高斯定理；
电势
(1) 定义法
(2) 叠加法
q 4 r
电介质的分类及其极化机理
有极分子介质——取向极化 无极分子介质——位移极化
会计算极化电荷的面分布及退极化场 P ( r 1) 0 E ' P n
2
dΦ dt
r l1
0 I
2 x
b
l2 dx
l1
c
l2
r
ln
r l1 r
dΦ dr dr dt dΦ dr
I
v
x a r o
dx d x
0 I 0l1l2 v
2r ( r l2 )
方向：顺时针方向
28
一直导线CD在一无限长直电流磁场中作 切割磁力线运动。求：动生电动势。 解： 方法一
18
三、掌握复杂电路的基尔霍夫定律 掌握电压、电流的规定，会列节点电流方程和 回路电压方程 流入节点的电流前面取“-”号， ±I 0 在流出节点的电流前面取“+” U ( ) 号 ( IR ) 0
(2) 电阻元件的端电压为 ±RI，当电流 I 的参考 方向与回路绕行方向一致时，选取“+”号；反之， 选取“”号； (3) 电源电动势为 E，当电源电动势的方向与回 路绕行方向一致时，选取“-”号，反之应选取“+” 号。
V x
电场强度和电势是描述静电场的两个物理量能， 两者的关系是微积分的关系。
2
二、 计算电场强度和电势
电场
(3) E V q ˆ 点电荷：E r 2 4 r
◆常见带电体的场强及电势
(1) 场强公式； (2) 高斯定理；
电势
(1) 定义法
(2) 叠加法
q 4 r
电介质的分类及其极化机理
有极分子介质——取向极化 无极分子介质——位移极化
会计算极化电荷的面分布及退极化场 P ( r 1) 0 E ' P n